A distributionally robust optimization approach for two-stage facility location problems

Abstract

In this paper, we consider a facility location problem where customer demand constitutes considerable uncertainty, and where complete information on the distribution of the uncertainty is unavailable. We formulate the optimal decision problem as a two-stage stochastic mixed integer programming problem: an optimal selection of facility locations in the first stage and an optimal decision on the operation of each facility in the second stage. A distributionally robust optimization framework is proposed to hedge risks arising from incomplete information on the distribution of the uncertainty. Specifically, by exploiting the moment information, we construct a set of distributions which contains the true distribution and where the optimal decision is based on the worst distribution from the set. We then develop two numerical schemes for solving the distributionally robust facility location problem: a semi-infinite programming approach which exploits moments of certain reference random variables and a semi-definite programming approach which utilizes the mean and correlation of the underlying random variables describing the demand uncertainty. In the semi-infinite programming approach, we apply the well-known linear decision rule approach to the robust dual problem and then approximate the semi-infinite constraints through the conditional value at risk measure. We provide numerical tests to demonstrate the computation and properties of the robust solutions.

1 Introduction

The classic discrete facility location problem (FLP) involves selecting a subset of facility locations within a finite set of available locations and assigning customers to the selected facilities with the aim to minimize the combined facility setup cost and transportation cost. In the most basic form, the discrete FLPs consist of allocating p facilities to a given list of candidate locations. In these so-called p-median problems, the fixed setup cost of all candidate sites is assumed to be equal. The objective function is only to minimize the total service cost to the customers, i.e., the transportation cost. Under the non-homogeneity of the facilities’ setup cost, the p-median problem can be extended to uncapacitated facility location problems (UFLP) in which the setup cost is also added to the objective function. The UFLP assumes that facilities can serve an unlimited amount of demand. However, in many practical problems, facilities have capacity constraints and this leads to an important family of FLPs called capacitated facility location problems (CFLP) in which the cheapest-assignment criterion is not sufficient for the optimality of the solution. Note that in the p-median problem, the number of facilities to be installed is fixed to p whereas, in UFLP and CFLP, no such constraints are posed. The p-median, UFLP, and CFLP have been subjects of extensive research, and interested readers might refer to Daskin (2011), Daskin (2008) and ReVelle and Eiselt (2005) for some comprehensive reviews.

The aforementioned models share certain characteristics such as single-period planning horizon, single product and facility type, and deterministic parameters (i.e., demands, supplies, and costs). However, the deterministic assumption is one of the major drawbacks in coping with many real-world problems. The strategic decisions on facility setup are often capital-intensive, non-repetitive, and span a long time horizon. The decision has to be made at present and hence is subject to risks arising from uncertainties in demands and operations of the established facilities. Hedging the risk, therefore, becomes a vital component of the decision-making process. The facility location problem under uncertainty has attracted considerable attention recently; see, for examples, reviews in Owen and Daskin (1998), Snyder (2006) and Lim et al. (2010). Two major frameworks used to model uncertainty in the facility location problems are stochastic optimization and robust optimization.

In the first framework, stochastic optimization has long been a well-known mathematical method for finding optimal decisions under uncertainty. A key assumption in this approach is that the decision maker has complete information on the distribution of the uncertainty, through either empirical data or subjective judgment. However, in some circumstances, this might turn out to be difficult if not impossible when a strategic decision has to be made well in advance of the realization of the uncertainty.

In the second approach, the robust optimization framework, no assumption is made on the probability distribution of the uncertainty. The traditional proposed measure of robustness is the minmax cost approach in which the cost associated with the worst case scenario is minimized. Some of the examples of the minmax approach can be found in Averbakh and Berman (1997), Averbakh and Berman (2000), Conde (2007) and Snyder and Daskin (2006).

A feasible way to address the issue of distributional uncertainty in stochastic optimization is to use the available data to construct a set of distributions which contains the true distribution of the uncertainty and make an optimal decision on the basis of the worst distribution from the set. This approach is known as distributionally robust optimization which was proposed by Scarf et al. (1958) and has now been extensively studied over the past few decades. [For some recent developments see Delage and Ye (2010), Esfahani and Kuhn (2018), Wiesemann et al. (2014), Xu et al. (2018), Lu et al. (2015), Santiváñez and Carlo (2018) and references therein.] How to construct the set of distributions depends on the available information and there is no unified framework for this. For examples, if there are some empirical data which allow one to construct a nominal empirical distribution, then one may use the Kantorovich/Wasserstein metric or $\phi$-divergence to construct a ball of distributions (Esfahani and Kuhn (2018) and Love and Bayraksan (2015)); if the information comes with statistical quantities such as mean and variance, then one may use moment type conditions (Delage and Ye (2010), Wiesemann et al. (2014) and Xu et al. (2018)). In this paper, we use the moment approach. Specifically, we propose a distributionally robust optimization model for the capacitated facility location problem to deal with future demand uncertainty. We then propose two numerical schemes—namely a semi-definite program and a semi-infinite program—to solve the distributionally robust optimization model. Finally, we provide numerical results for medium size instances taken from the literature.

The remainder of this paper is organized as follows.

• 1. In Sect. 2, we formally describe the deterministic model, a two-stage stochastic model and a distributionally robust formulation of the stochastic model.

• 2. We then proceed with discussions on numerical schemes in the following two consecutive sections for solving the robust model depending on the availability of information on the distribution of demands: a semi-definite programming (SDP) scheme in Sect. 3 and a semi-infinite programming (SIP) scheme in Sect. 4.

• 3. In Sect. 5, we report numerical test results of the two schemes and draw some conclusions in Sect. 6.

2 Facility location models

We first introduce the classic deterministic capacitated facility location (D-FLP) problem. By taking into account future uncertainty, we extend it to a two-stage stochastic facility location (S-FLP) modeling framework, which then forms the basis for developing a distributionally robust facility location (R-FLP) model.

2.1 Deterministic facility location model

There is a vast body of literature on the deterministic facility location problem. A good review of the related literature is carried out by Owen and Daskin (1998) and Daskin (2011). Suppose there are up to n facilities to be opened in a set of possible locations $I=\{1,\ldots ,n\}$, indexed by i. Let $J=\{1,\ldots ,m\}$ be the set of customers, indexed by j. The location decision variable $z_i$ is defined as:

$$\begin{aligned} z_i = \left\{ \begin{array}{l l} 1 &{} \quad \text {if the facility }i\text { is opened},\\ 0 &{} \quad \text {otherwise},\\ \end{array} \right. \end{aligned}$$

and continuous assignment variable $x_{ij}$ determines the service quantity or the transportation quantity as we refer to it in this work, assigned from facility i to customer j. Each facility $i \in I$ has a fixed opening cost of $b_i$ and, if opened, has a service capacity $s_i$ that can be used by one or more customers. Likewise, each customer $j \in J$ is characterized by a demand $d_j$ that needs to be satisfied by one or more facilities. In the deterministic framework, it is assumed that the customer demand and the capacity of the facilities are known. The unit service cost of facility i for serving customer j is denoted by $c_{ij}$ and assumed to be known; for example, transportation costs are proportional to the distances between the facilities and the customers. Note that real-life transportation problems are likely to be unbalanced; that is, the total demand might exceed the total supply (Goyal 1984). To avoid the unbalance in the transportation problem, we assume that an external supplier will serve the excess demand $w_j$ of customer j. The unit service cost of this external supply facility, denoted by $C_j$, is assumed to be sufficiently large, $C_j \ge \max _{i \in I} c_{ij}$, so that the external supply is invoked only when the total supply from all facilities fails to satisfy the demand.

The objective of the facility location problem is to minimize the total fixed cost of opening the facilities and the future transportation costs while satisfying the customer demand and supply capacity constraints. The deterministic FLP is formulated as follows:

$$\begin{aligned} \text {(D-FLP)} \quad \quad \min \limits _{\mathbf {z, x, w}}&\sum _i b_i z_i + \sum _{i,j} c_{ij} x_{ij} + \sum _{j} {C_j} w_{j} \nonumber \\ \text {s.t.}&\sum _i x_{ij} + w_j \ge d_j,~\forall ~j \in J, \end{aligned}$$

(2.1a)

$$\begin{aligned}&\sum _j x_{ij} \le z_i s_i,~\forall ~i \in I, \end{aligned}$$

(2.1b)

$$\begin{aligned}&x_{ij} \ge 0 , ~\forall ~j \in J,~i \in I, \end{aligned}$$

(2.1c)

$$\begin{aligned}&w_{j} \ge 0 , ~\forall ~j \in J, \end{aligned}$$

(2.1d)

$$\begin{aligned}&z_i \in \{0,1\} , ~\forall ~i \in I. \end{aligned}$$

(2.1e)

Balance constraint (2.1a) ensures that the demands of all customers are met. Constraint (2.1b) prevents the service level assigned to each facility from exceeding its capacity and also ensures that the customers cannot be served by un-built facilities (i.e., when $z_i = 0$, $x_{ij}$ must be equal to zero). Finally, constraints (2.1c)–(2.1e) enforce the nonnegativity of the service quantities and the binary nature of the facility allocating decisions, respectively. Variations of deterministic facility location formulations similar to the D-FLP have been well studied in the literature. We refer the readers to Daskin (2011) for more details about these.

2.2 Two-stage stochastic model

The facility location problems involve uncertainties that stem from unpredictability of demand, supply and service costs. Since the facility location decisions are irreversible and capital intensive, it is vital to take into account the future uncertainties when the facility location decisions are made. Louveaux (1986) first introduced a two-stage stochastic program with recourse for solving simple plant location problems and p-median problems where uncertainties in demand, production and transportation costs are considered. Wu et al. (2015) develop a distributionally robust model for the uncapaciated facility location problem under demand uncertainty and derive some nice reformulation of the stochastic model. We follow this approach but extend it to the capacitated cases. There are several differences between our model and that in Wu et al. (2015) which are described below. First of all, Wu et al.’s model is for the uncapacitated case, which means each facility can serve as many customers as it wishes as long as the total transportation distances are minimized as part of the objective function. Their decision variables are which facilities to fully serve which customers while our decision variables are to what extend each facility, if opened, serves each customer. When the facilities have unlimited capacity, the demand uncertainty does not play as much of an important role as when there is capacity limitation. This is because, despite uncertain demand, each customer is still being fully served by the nearest facility. In our case, it is possible that the demand exceeds the nearby facilities’ capacities and hence we have to buy and transport from one or more expensive sources.

To extend the deterministic model described in Sect. 2.1 to a stochastic setting, customer demand is assumed to be stochastic with a known probability distribution. Instead of having a deterministic demand vector $\mathbf {d}$, we use the notation $\mathbf {d}({\varvec{\xi }})$ for the stochastic demands that depend on a random vector ${\varvec{\xi }}$. For convenience in notation, we use $\mathbf {d}({\varvec{\xi }})$ and ${\varvec{\xi }}$ interchangeably; that is, both ${d_j}({\varvec{\xi }})$ and $\xi _j$ refer to the stochastic demand of customer j. The objective of the two-stage problem is to minimize the sum of fixed investment cost of allocating the facilities and the expected future transportation costs. The resulting mathematical model is given as follows,

$$\begin{aligned} \begin{array}{lll} \text {(S-FLP)} \quad \quad &{}\min \limits _{\mathbf {z}} &{} \sum _i b_i z_i + \mathbb {E} \left[ g(\mathbf {z},{\varvec{\xi }})\right] \\ &{}\text {s.t.} &{} z_i \in \{0,1\},~ \forall ~i \in I, \end{array} \end{aligned}$$

(2.2)

where $g(\mathbf {z},{\varvec{\xi }})$ is the optimal value of the second-stage transportation problem

$$\begin{aligned} g(\mathbf {z},{\varvec{\xi }}) :=&\min \limits _{x,w}&\sum _{i,j} c_{ij} x_{ij} + \sum _{j} {C_j} w_{j}, \nonumber \\&\text {s.t.}&\sum _i x_{ij} + w_j \ge d_j({\varvec{\xi }}),~ \forall ~j \in J, \end{aligned}$$

(2.3a)

$$\begin{aligned}&\sum _j x_{ij} \le z_i s_i,~\forall ~i \in I, \end{aligned}$$

(2.3b)

$$\begin{aligned}&x_{ij} \ge 0,~ \forall ~i \in I,~j \in J, \end{aligned}$$

(2.3c)

$$\begin{aligned}&w_{j} \ge 0,~\forall ~j \in J, \end{aligned}$$

(2.3d)

and the expectation is taken w.r.t. the distribution of random vector ${\varvec{\xi }}$. In this formulation, the decision on $\mathbf {z}$ in the first stage determines the location of new facilities to be built, before the realization of the uncertain demand $\mathbf {d}({\varvec{\xi }})$, while in the second stage a decision is made to specify allocation of transportation resources after the demand is realized. The optimal value $g({\mathbf {z}},{\varvec{\xi }})$ of the second-stage problem therefore depends on $\mathbf {z}$ and ${\varvec{\xi }}$.

2.3 Distributionally robust facility location model

One of the major difficulties which often arises in facility location problems is the lack of complete information on the probability distribution of future customer demands at different locations. We consider a setting where there might be limited information on the probability distribution P of the random parameters ${\varvec{\xi }}$. Suppose that we are able to construct a set of probability distributions, denoted by $\mathcal {P}$, which contains the true probability distribution P. In order to hedge the risk against ambiguity of the true distribution, we may consider a robust model where the optimal decision on the location of the new facilities to be built and the operation of all facilities is based on the worst distribution from $\mathcal {P}$. In the literature of robust optimization, $\mathcal {P}$ is called the ambiguity set which reflects the fact that there is an ambiguity in the true probability distribution in this setup. The corresponding distributionally robust optimization problem can be formulated as

$$\begin{aligned} \begin{array}{lll} \text {(R-FLP)} \quad \quad &{}\min \limits _{\mathbf {z}} &{} {{\mathbf {b}^{T} \mathbf {z}}} + \sup \limits _{P \in \mathcal {P}} \mathbb {E}_{P} \left[ g(\mathbf {z},{\varvec{\xi }}))\right] \\ &{}\text {s.t.} &{} \mathbf {z} \in \{0,1\}^n. \end{array} \end{aligned}$$

(2.4)

One of the key elements in distributionally robust optimization is construction of the ambiguity set. Over the past few decades, various statistical methods have been proposed among which the method using moment information of the underlying probability distribution seems to be popular; see Delage and Ye (2010) and references therein. Another widely adopted approach is a mixture distribution which uses a convex combination of some observed and/or predicted distributions. In this paper, we will consider the moment approach which seems to be relevant in the problem setting. We will proceed our discussions through two distinct mathematical formulations: In the first formulation, we assume the mean value and covariance of ${\varvec{\xi }}$ are known and consequently we reformulate problem (2.4) as a semi-definite program (SDP). In the second formulation, we weaken the assumption by merely assuming the mean value of ${\varvec{\xi }}$ is known and subsequently reformulate problem (2.4) as a semi-infinite program (SIP). We then develop appropriate numerical procedures for solving the resulting optimization problems.

3 A semi-definite programming approach

In this section, we first formulate the (R-FLP) problem as an integer semi-definite program in Sect. 3.1. The resulting model, however, has a large number of SDP constraints in addition to the inherent binary variables for the facility location decisions. We propose to resolve the integrality issue by using a generic genetic algorithm in Sect. 3.2 and the large number of SDP constraints by using a row generation algorithm in Sect. 3.3.

3.1 SDP formulation

We first investigate (R-FLP) with some moment information of ${\varvec{\xi }}$.

Let $\Xi$ denote the range of ${\varvec{\xi }}$ and $\mathscr {P}(\Xi )$ the set of all probability measures over $\Xi$. We consider the following ambiguity set,

$$\begin{aligned} \mathcal {P} = \left\{ P\in { \mathscr {P}(\Xi )}: \mathbb {E}_{P}[{\varvec{\xi }}]={\varvec{\mu }}, \quad \mathbb {E}_{P}[{\varvec{\xi }}{\varvec{\xi }}^{T}]=\mathbf {Q} \right\} , \end{aligned}$$

(3.1)

where ${\varvec{\mu }}$ and $\mathbf {Q}$ denote the first and second moments of ${\varvec{\xi }}$. In practice, the true moments may be unknown. In the literature of distributionally robust optimization, one often specifies a range for these statistical quantities; see for instance Delage and Ye (2010). Assume here that both ${\varvec{\mu }}$ and $\mathbf {Q}$ can be approximated using empirical data. Quantification of the difference between the ambiguity using true moments and the one using sample average approximation is well documented in Sun and Xu (2015) and Zhang et al. (2016). Its impact on the optimal value and optimal solutions can also be found in these papers.

Let

$$\begin{aligned} H({{\mathbf {z}}})= \sup \limits _{P \in \mathcal {P}} \mathbb {E}_{P} \left[ g(\mathbf {z},{\varvec{\xi }})\right] . \end{aligned}$$

(3.2)

Problem (3.2) is related to the classical problem of moments. Here, instead of finding a feasible distribution $P \in \mathcal {P}$, we want to find one which maximizes the expected value of $g(\mathbf {z},{\varvec{\xi }})$. For a discussion on the background of the problem of moments, interested readers are referred to Landau (1987). Let $\mathscr {M}^+$ denote the set of all nonnegative finite measures on measurable space $(\Xi , \mathscr {B})$. Then

$$\begin{aligned} \begin{array}{lll} H({{\mathbf {z}}}) := &{}\sup \limits _{P\in \mathscr {M}^+} &{}\displaystyle \int _{\Xi } g({\mathbf {z}},{\varvec{\xi }}) P(\hbox {d}{\varvec{\xi }}) \\ &{}\text {s.t.} &{}\displaystyle \int _{\Xi } {\xi }_{i}{\xi }_{j} P(\hbox {d}{\varvec{\xi }}) = Q_{ij}, ~ \forall i,j = 1,\ldots ,m, \\ &{} &{}\displaystyle \int _{\Xi } {\xi }_{i} P(\hbox {d}{\varvec{\xi }}) = \mu _{i}, ~ \forall i= 1,\ldots ,m, \\ &{} &{}\displaystyle \int _{\Xi } P(\hbox {d}{\varvec{\xi }}) = 1, \end{array} \end{aligned}$$

(3.3)

where $Q_{ij}$ denotes the (ij)th component of $\mathbf {Q}$, and $\mu _j$ the jth component of ${\varvec{\mu }}$.

Let $\mathbb {S}^{m\times m}$ denote the space of m by m real matrices. Let $\mathbf {Y} \in \mathbb {S}^{m\times m}$, $\mathbf {y} \in \mathbb {R}^m$ and $y_0 \in \mathbb {R}$ denote the dual variables associated with the moment constraints in (3.3). We can then write the Lagrangian dual problem of (3.3) as follows,

$$\begin{aligned} \begin{array}{lll} H_D({ {\mathbf {z}}}) := &{}\min \limits _{\mathbf {Y},\mathbf {y}, {y_0}} &{} {\mathbf {Q}}\bullet {\mathbf {Y}} + {\mathbf {{{\varvec{\mu }}}^{T} y}} + y_0 \\ &{} \text {s.t.} &{} {{\varvec{\xi }}}^{T} {\mathbf {Y}} {{\varvec{\xi }}} + {{\varvec{\xi }}}^{T} {\mathbf {y}}+ y_0 \ge g(\mathbf {z},{\varvec{\xi }}), ~ \forall {\varvec{\xi }}\in {\mathbb {R}^m}. \end{array} \end{aligned}$$

(3.4)

Here and later on $A\bullet B$ denotes the Frobenius inner product of matrices A and B. This kind of dual formulation is well-known; see for instance Zymler et al. (2013) and (Shapiro et al. 2009, Chapter 6) for general moment problems. It is easy to prove that $H(\mathbf {z}) \le H_D(\mathbf {z})$; see for instance Bertsimas and Sethuraman (2000).

For strong duality results to hold, we make the following assumption

Assumption 3.1

The linear matrix inequality $\mathbf {Q}-{{\varvec{\mu }}}{{\varvec{\mu }}}^T \succ 0$ holds, where $A \succ 0$ means A is positive definite.

Here and later on we write $A \succeq 0$ for matrix A being positive semi-definite. Note that, for $({\varvec{\mu }},\mathbf {Q})$ to be valid first and second moments of some random variable, it is necessary to have condition $\{\mathbf {Q}-{{\varvec{\mu }}}{{\varvec{\mu }}}^T \succeq 0\}$ satisfied. Indeed, for any vector v, we have

$$\begin{aligned} v^{\mathrm{{T}}}(\mathbf {Q}-{{\varvec{\mu }}}{{\varvec{\mu }}}^T)v= & {} v^{\mathrm{{T}}}{\text {E}} \left[ (\mathbf {{\varvec{\xi }}} -{\text {E}} [\mathbf {{\varvec{\xi }}} ])(\mathbf {{\varvec{\xi }}} -{\text {E}} [\mathbf {{\varvec{\xi }}} ])^{\mathrm{{T}}}\right] v\\= & {} {\text {E}} \left[ v^{\mathrm{{T}}}(\mathbf {{\varvec{\xi }}} -{\text {E}} [\mathbf {{\varvec{\xi }}} ])(\mathbf {{\varvec{\xi }}} -{\text {E}} [\mathbf {{\varvec{\xi }}} ])^{\mathrm{{T}}}v\right] \\= & {} {\text {E}} {\big [}{\big (}v^{\mathrm{{T}}}(\mathbf {{\varvec{\xi }}} -{\text {E}} [\mathbf {{\varvec{\xi }}} ]){\big )}^{2}{\big ]}\ge 0, \end{aligned}$$

since $v^{\mathrm{{T}}}(\mathbf {{\varvec{\xi }}} -{\text {E}} [\mathbf {{\varvec{\xi }}} ])$ is a scalar. Thus, the covariance matrix is positive definite unless the uncertain sources $\mathbf {{\varvec{\xi }}}$ are linearly dependent. Assumption 3.1 is slightly stronger as we replace positive semi-definiteness with positive definiteness, i.e., we explicitly assume that there is no linear dependency among the sources of uncertainty. This is needed for reasons of technicality in proving the strong duality result, which is formally stated in the following proposition.

Proposition 3.1

Under Assumption 3.1, $H(\mathbf {z}) = H_D(\mathbf {z})$.

Proof

Let us define $\mathcal{H} = \left\{ (M,v) ~|~ M = M^T,~M \succ v v^T \right\}$. For any fixed $(M,v) \in \mathcal{H}$, there exists a symmetric matrix W such that $W^2 =(M - v v^T)$. We can then construct a random variable ${\varvec{\xi }}= W X + v$ such that ${\varvec{\xi }}$ has a mean value of v and a covariance matrix of $(M - v v^T)$, where $X \in {\mathbb {R}}^n$ is a random vector which follows the standard multivariate normal distribution. It is easy to verify that $\xi$ satisfies the following:

$$\begin{aligned} \begin{array}{lll} &{}&{}\displaystyle \int _{\Xi } {\xi }_{i}{\xi }_{j} P(\hbox {d}{\varvec{\xi }}) = M_{ij}, ~ \forall i,j = 1,\ldots ,m, \\ &{} &{}\displaystyle \int _{\Xi } {\xi }_{i} P(\hbox {d}{\varvec{\xi }}) = v_{i}, ~ \forall i= 1,\ldots ,m, \\ &{} &{}\displaystyle \int _{\Xi } P(\hbox {d}{\varvec{\xi }}) = 1. \end{array} \end{aligned}$$

(3.5)

In other words, using any choice of $(M,v) \in \mathcal{H}$ to replace $(\mathbf {Q},{\varvec{\mu }})$ in the right-hand side of (3.5) would lead to a feasible ${\varvec{\xi }}$. In addition, we can show that $\mathcal{H}$ is an open set. Therefore, under Assumption 3.1, i.e., $(\mathbf {Q},{\varvec{\mu }}) \in \mathcal{H}$, we also have $(\mathbf {Q},{\varvec{\mu }})$ to belong to the interior of $\mathcal{H}$. As a result, there exists a neighborhood $\mathcal{B}$ small enough around $(\mathbf {Q},{\varvec{\mu }})$ such that if we replace the right-hand side of (3.5) by any $(M,v) \in \mathcal{B}$, the system of equations (3.5) is still feasible (for some different ${\varvec{\xi }}$). This is the sufficient condition for having strong duality result to hold, i.e., $H(\mathbf {z}) = H_D(\mathbf {z})$, as stated in (Shapiro 2001, Proposition 3.4). $\square$

From the strong duality result, problem (2.4) can be equivalently written as

$$\begin{aligned} \begin{array}{ll} \min \limits _{\mathbf {z},\mathbf {Y},\mathbf {y}, {y_0}} &{} \mathbf {b}^{T} \mathbf {z} + {\mathbf {Q}}\bullet {\mathbf {Y}} + {\mathbf {{{\varvec{\mu }}}^{T} y}} + y_0 \\ ~\text {s.t.} &{} {{\varvec{\xi }}}^{T} {\mathbf {Y}} {{\varvec{\xi }}} + {{\varvec{\xi }}}^{T} {\mathbf {y}}+ y_0 \ge g(\mathbf {z},{\varvec{\xi }}), ~ \forall {\varvec{\xi }}\in {\Xi },\\ &{}{\mathbf {z} \in \{0,1\}^n}. \end{array} \end{aligned}$$

(3.6)

Let us now write down the dual of the transportation problem described in problem (2.3),

$$\begin{aligned} \begin{array}{lll} g_D(\mathbf {z},{\varvec{\xi }})= &{}\max \limits _{\varvec{\alpha , \beta }} &{} \sum _{j} \alpha _j {\xi _j} - \sum _{i} \beta _i (s_i z_i) \\ &{}~\text {s.t.} &{} \alpha _j - \beta _i \le c_{ij},~ \forall ~i \in I, ~j \in J, \\ &{}&{} \alpha _j \le {C_j}, ~ \forall ~j \in J,\\ &{}&{} \alpha _j, \beta _i \ge 0, ~ \forall ~i \in I, ~j \in J, \end{array} \end{aligned}$$

(3.7)

where $\alpha _j$, $j \in J$, are dual variables associated with demand constraints (2.3a) and $\beta _i$, $i\in I$, are dual variables associated with supply constraints  (2.3b). Observe that problem (2.3) satisfies the Mangasarian-Fromovitz constraint qualification (MFCQ). Thus the Lagrange multipliers of the problem are bounded and there exists a positive number $C'$ such that the problem above is equivalent to the following,

$$\begin{aligned} \begin{array}{lll} \text {(DTP)} \quad \quad g_D(\mathbf {z},{\varvec{\xi }})= &{}\max \limits {\varvec{\alpha , \beta }} &{} \sum _{j} \alpha _j {\xi _j} - \sum _{i} \beta _i (s_i z_i) \\ &{}~\text {s.t.} &{} {\hbox {constraints of problem }(3.7)},\\ &{}&{}{\beta _i\le C', \forall i\in I}. \end{array} \end{aligned}$$

To ease the notation, let ${{\varvec{\gamma }}}_{\alpha } := {\varvec{\alpha }}$, ${{\varvec{\gamma }}}_{\beta } := {\varvec{\beta }}$, and ${{\varvec{\gamma }}}:=({{\varvec{\gamma }}}_{\alpha },{{\varvec{\gamma }}}_{\beta })$. Let $\Gamma$ denote the feasible set of (DTP). It is easy to observe that $\Gamma$ is a polyhedral in ${\mathbb {R}}^{|I|+|J|}$ where |I| and |J| denote the cardinality of the index sets I and J, respectively.

It is easy to observe that $\Gamma$ is a bounded polyhedral. In addition, the finiteness number of vertices of $\Gamma$ follows from Balinski and Russakoff (1984).

Let $\{{{\varvec{\gamma }}^1}, \ldots , {{\varvec{\gamma }}^{N}}\}$ denote the set of vertices. Using the notation introduced above, we can rewrite (DTP) in a neater form,

$$\begin{aligned} \begin{array}{lll} g_{D}(\mathbf {z},{{\varvec{\xi }}})= &{}\max \limits {\varvec{\gamma } (\mathbf {z})} &{} {{\varvec{\xi }}}^{T}{{\varvec{\gamma }}_\alpha }- {{\varvec{\gamma }}_\beta }^{T}(\mathbf {s\circ z})\\ &{}~\text {s.t.} &{} {\varvec{\gamma }}\in \Gamma , \end{array} \end{aligned}$$

(3.8)

where $(\mathbf {s\circ z})$ denotes an m-dimensional vector with components $s_iz_i$ for $i \in I$. Combining (3.6) and (DTP), we can recast the robust facility location problem (2.4) as a semi-definite program through the following proposition.

Proposition 3.2

Let $\mathcal{P}$ be defined as in (3.1) and $\Xi {=} {\mathbb {R}}^m$. Under Assumption 3.1, the two-stage distributionally robust facility location problem (2.4) can be reformulated as the following semi-definite optimization problem:

$$\begin{aligned} \begin{array}{lll} \text {(R-SDP)} \quad \quad &{}\min \limits _{\mathbf {z},\mathbf {Y},\mathbf {y}, {y_0}} &{} \mathbf {b}^{T} \mathbf {z} + {\mathbf {Q}}\bullet {\mathbf {Y}} + {\mathbf {{{\varvec{\mu }}}^{T} y}} + y_0 \\ &{}~\text {s.t.}&{} \begin{bmatrix} y_0 + {{\varvec{\gamma }}_\beta }^{T}(\mathbf {s\circ z}) &{} \frac{1}{2}({\mathbf {y}-{{\varvec{\gamma }}_\alpha }})^{T} \\ \frac{1}{2}({\mathbf {y}}-{{\varvec{\gamma }}_\alpha }) &{} \mathbf {Y} \end{bmatrix} \succeq 0, ~\forall {{\varvec{\gamma }}}\in \{{{\varvec{\gamma }}^1}, \ldots , {{\varvec{\gamma }}^{N}}\}\\ &{}&{} {\mathbf {z} \in \{0,1\}^n}. \end{array} \nonumber \\ \end{aligned}$$

(3.9)

Proof

It follows from Proposition 3.1 that, under Assumption 3.1, $H(\mathbf {z}) = H_D(\mathbf {z})$ and problem (2.4) can be reformulated as problem (3.6). Note that the reformulation still involves $g(\mathbf {z},{{\varvec{\xi }}})$. Since $g(\mathbf {z},{{\varvec{\xi }}})$ and $g_{D}(\mathbf {z},{{\varvec{\xi }}})$ are primal and dual LPs of each other and since both of them are feasible (i.e., by setting $\mathbf {x} = 0$, $\omega _j = d_j, \forall j \in J$ in the primal and $\mathbf {\alpha } = \mathbf {\beta } = 0$ in the dual), strong duality result holds and we have $g(\mathbf {z},{{\varvec{\xi }}})=g_{D}(\mathbf {z},{{\varvec{\xi }}})$.

Thus, we can replace the second-stage transportation problem through its dual and rewrite the constraint of problem (3.6) as

$$\begin{aligned} {{\varvec{\xi }}}^{T} {\mathbf {Y}} {{\varvec{\xi }}} + {{\varvec{\xi }}}^{T} {\mathbf {y}}+ y_0 \ge \max \limits {\varvec{\gamma } \in \Gamma }\Big \{{{\varvec{\xi }}}^{T}{{\varvec{\gamma }}_\alpha }- {{\varvec{\gamma }}_\beta }^{T}(\mathbf {s\circ z})\Big \}, \quad \forall {\varvec{\xi }}\in {\mathbb {R}^m}. \end{aligned}$$

(3.10)

Since $\Gamma$ is bounded with a finite set of extreme points $\{{{\varvec{\gamma }}^1}, \ldots , {{\varvec{\gamma }}^{N}}\}$, the maximizer of the LP on the R.H.S of (3.10) occurs at one of the extreme points. Thus, (3.10) can be equivalently rewritten as

$$\begin{aligned} {{\varvec{\xi }}}^{T} {\mathbf {Y}} {{\varvec{\xi }}} + {{\varvec{\xi }}}^{T} {\mathbf {y}}+ y_0 \ge {{\varvec{\xi }}}^{T}{{\varvec{\gamma }}_\alpha }- {{\varvec{\gamma }}_\beta }^{T}(\mathbf {s\circ z}), \quad \forall {\varvec{\xi }}\in {\mathbb {R}^m},~\forall \varvec{\gamma } \in \{{{\varvec{\gamma }}^1}, \ldots , {{\varvec{\gamma }}^{N}}\}. \end{aligned}$$

A simple rearrangement yields

$$\begin{aligned} \min \limits _{\varvec{\xi }}\Big \{{{\varvec{\xi }}}^{T} {\mathbf {Y}} {{\varvec{\xi }}} + {{\varvec{\xi }}}^{T} ({\mathbf {y}}-{{\varvec{\gamma }}_\alpha })+ y_0 + {{\varvec{\gamma }}_\beta }^{T}(\mathbf {s\circ z})\Big \} \ge 0, \quad \forall \varvec{\gamma } \in \{{{\varvec{\gamma }}^1}, \ldots , {{\varvec{\gamma }}^{N}}\}.\nonumber \\ \end{aligned}$$

(3.11)

We can show that inequality (3.11) holds if and only if

$$\begin{aligned} \begin{bmatrix} y_0 + {{\varvec{\gamma }}_\beta }^{T}(\mathbf {s\circ z}) &{} \frac{1}{2}({\mathbf {y}-{{\varvec{\gamma }}_\alpha }})^{T} \\ \frac{1}{2}({\mathbf {y}}-{{\varvec{\gamma }}_\alpha }) &{} \mathbf {Y} \end{bmatrix} \succeq 0, \quad \forall {\varvec{\gamma }}\in \{{{\varvec{\gamma }}^1}, \ldots , {{\varvec{\gamma }}^{N}}\}. \end{aligned}$$

(3.12)

Here, it is very clear that (3.12) implies (3.11). For the reverse, suppose that (3.12) does not hold, i.e., there exists $\gamma$ and $(q_0, {\varvec{q}})$ such that

$$\begin{aligned} \begin{bmatrix} q_0&{\varvec{q}}^T \end{bmatrix} \begin{bmatrix} y_0 + {{\varvec{\gamma }}_\beta }^{T}(\mathbf {s\circ z}) &{} \frac{1}{2}({\mathbf {y}-{{\varvec{\gamma }}_\alpha }})^{T} \\ \frac{1}{2}({\mathbf {y}}-{{\varvec{\gamma }}_\alpha }) &{} \mathbf {Y} \end{bmatrix} \begin{bmatrix} q_0 \\ {\varvec{q}}\end{bmatrix} < 0. \end{aligned}$$

We then need to show that (3.11) does not hold either. If $q_0 \ne 0$, then we can construct ${\varvec{\xi }}= {\varvec{q}}/q_0$ and obtain ${{\varvec{\xi }}}^{T} {\mathbf {Y}} {{\varvec{\xi }}} + {{\varvec{\xi }}}^{T} ({\mathbf {y}}-{{\varvec{\gamma }}_\alpha })+ y_0 + {{\varvec{\gamma }}_\beta }^{T}(\mathbf {s\circ z}) < 0$ which means that (3.11) does not hold. If $q_0 = 0$, we have ${\varvec{q}}^T \mathbf {Y} {\varvec{q}}< 0$. We can then construct ${\varvec{\xi }}= \delta {\varvec{q}}$ with sufficiently large $\delta$ such that $\delta ^2 {{\varvec{q}}}^{T} {\mathbf {Y}} {{\varvec{q}}} + \delta {\varvec{q}}^{T} ({\mathbf {y}}-{{\varvec{\gamma }}_\alpha })+ y_0 + {{\varvec{\gamma }}_\beta }^{T}(\mathbf {s\circ z}) < 0$ which also means that (3.11) does not hold.

Finally, we can replace the constraint in (3.4) with the SDP constraint (3.12) and obtain the SDP  (3.9). $\square$

Notice that the derivation from inequality (3.11) to inequality (3.12) requires $\Xi \equiv {\mathbb {R}}^m$. In practice, there is often some information on the bounds of the uncertain parameters. For example the customer demand cannot take negative values. In order to handle the indefinite set of constraints that appears in problem (3.6) for this case, we will approximate the indefinite constraint with a finite set of semi-definite constraints as shown next.

Suppose the support set is specified as $\Xi = \prod \nolimits _{j \in J} \Xi _j$, where $\Xi _j = [{\underline{\xi }}_j,{\bar{\xi }}_j]$ for all $j \in J$ and ${\underline{{{\varvec{\xi }}}}}$ and ${\overline{{{\varvec{\xi }}}}}$ are some given lower and upper bounds. For reasons of technicality in proving strong duality, we make an assumption that there exists a random vector X with support set $\Xi$ such that $E[X] = 0$ and $E[X X^T] = I$, where $I \in {\mathbb {R}}^{m \times m}$ is the identity matrix. In practice, the support set of $\xi$ may not be necessarily box structured. In such a case, we might consider a box within the support set of $\xi$ such that the probability of $\xi$ taking values outside the box is negligible. It is possible to investigate the difference between the ambiguity sets before and after cut and its impact on the optimal value and optimal decisions although we have not attempted to do so in this paper.

Under this new assumption and Assumption 3.1, we can show that the strong duality result still holds and the proof is very similar to that of Proposition 3.1. The only difference is in the way that we construct the random variable X (i.e., instead of choosing a multivariate normal random variable, we choose a random vector X such that $E[X] = 0$ and $E[X X^T] = I$). It is noted that the new assumption can be relaxed further by a proper scaling of the random variables ${\varvec{\xi }}$.

Once we have derived the strong duality result, problem (3.4) becomes

$$\begin{aligned} \begin{array}{lll} H_D({ {\mathbf {z}}})= &{}\min \limits _{\mathbf {Y},\mathbf {y}, {y_0}} &{} {\mathbf {Q}}\bullet {\mathbf {Y}} + {\mathbf {{{\varvec{\mu }}}^{T} y}} + y_0 \\ &{} \text {s.t.} &{} {{\varvec{\xi }}}^{T} {\mathbf {Y}} {{\varvec{\xi }}} + {{\varvec{\xi }}}^{T} {\mathbf {y}}+ y_0 \ge g(\mathbf {z},{\varvec{\xi }}), ~ \forall {\varvec{\xi }}\in \Xi , \end{array} \end{aligned}$$

(3.13)

where the only difference compared to problem (3.4) is that we have replaced the semi-infinite constraint $\{\forall {\varvec{\xi }}\in {\mathbb {R}}^n\}$ with $\{\forall {\varvec{\xi }}\in \Xi \}$. Inequality (3.11) now become

$$\begin{aligned} \min \limits _{\varvec{\underline{\xi }}~\le ~\varvec{\xi }~ \le ~ \varvec{\bar{\xi }}}\left[ {{\varvec{\xi }}}^{T} {\mathbf {Y}} {{\varvec{\xi }}} + {{\varvec{\xi }}}^{T} ({\mathbf {y}}-{{\varvec{\gamma }}_\alpha })+ y_0 + {{\varvec{\gamma }}_\beta }^{T}(\mathbf {s\circ z})\right] \ge 0, \quad \forall {\varvec{\gamma }}\in \{{\varvec{\gamma }}^1, \ldots , {\varvec{\gamma }}^{N}\},\nonumber \\ \end{aligned}$$

(3.14)

which is equivalent to

$$\begin{aligned} \begin{array}{l} \phi ({\varvec{\gamma }}) \ge 0,~ \forall {\varvec{\gamma }}\in \{{\varvec{\gamma }}^1, \ldots , {\varvec{\gamma }}^{N}\},\\ \end{array} \end{aligned}$$

(3.15)

where $\phi ({\varvec{\gamma }})$ is the optimal value of the following program

$$\begin{aligned} \begin{array}{l} \begin{aligned} \min \limits _{\varvec{\xi }}&\left\{ \begin{bmatrix} 1 &{} {\varvec{\xi }}\end{bmatrix} \begin{bmatrix} y_0 + {{\varvec{\gamma }}_\beta }^{T}(\mathbf {s\circ z}) &{} \frac{1}{2}({\mathbf {y}-{{\varvec{\gamma }}_\alpha }})^{T} \\ \frac{1}{2}({\mathbf {y}}-{{\varvec{\gamma }}_\alpha }) &{} \mathbf {Y} \end{bmatrix}\begin{bmatrix} 1 \\ {\varvec{\xi }}\end{bmatrix}\right\} \\ \text {s.t.} &{}\quad \begin{bmatrix} 1 &{} {\varvec{\xi }}\end{bmatrix} V_j \begin{bmatrix} 1 \\ {\varvec{\xi }}\end{bmatrix}\le 0, \qquad \qquad \forall j \in J, \end{aligned} \end{array} \end{aligned}$$

and where $\displaystyle V_j = \begin{bmatrix} {\overline{\xi }_j} {\underline{\xi }_j} &{}~ v_j^{T} \\ &{} \\ v_j &{} I_j \end{bmatrix},$ with $I_j$ denoting an $m \times m$ matrix with all elements being 0 except 1 at (j, j), and $v_j$ is an m-dimensional vector with all components are equal to zero except for the jth element which is equal to $-(\underline{\xi }_j +\overline{\xi }_j)/2$. The S-lemma (Derinkuyu and Pınar 2006) provides a sufficient condition for the nonnegativity of the quadratic objective function over the quadratic inequalities corresponding to the bounds. In other words, for the conditions (3.15) to be satisfied for each ${\varvec{\gamma }}\in \Gamma$, it suffices that there exists $\mathbf {h} \ge 0$ such that

$$\begin{aligned} \begin{bmatrix} y_0 + {{\varvec{\gamma }}_\beta }^{T}(\mathbf {s\circ z}) &{} \frac{1}{2}({\mathbf {y}-{{\varvec{\gamma }}_\alpha }})^{T} \\ \frac{1}{2}({\mathbf {y}}-{{\varvec{\gamma }}_\alpha }) &{} \mathbf {Y} \end{bmatrix}+ \sum _{j \in J} h_j V_j\succeq 0, \end{aligned}$$

where $h_j$ denotes the jth component of vector $\mathbf {h}$. Consequently, the SDP problem (3.9) can be reformulated as

$$\begin{aligned} \begin{array}{ll} \min \limits _{\mathbf {z},\mathbf {Y},\mathbf {y}, {y_0},\mathbf {h}} &{} \mathbf {b}^{T} \mathbf {z} + {\mathbf {Q}}\bullet {\mathbf {Y}} + {\mathbf {{{\varvec{\mu }}}^{T} y}} + y_0 \\ ~\text {s.t.}&{} \begin{bmatrix} y_0 + {{\varvec{\gamma }}_\beta }^{T}(\mathbf {s\circ z}) &{} \frac{1}{2}({\mathbf {y}-{{\varvec{\gamma }}_\alpha }})^{T} \\ \frac{1}{2}({\mathbf {y}}-{{\varvec{\gamma }}_\alpha }) &{} \mathbf {Y} \end{bmatrix}\\ &{}\quad + \sum _{j \in J} h_j V_j \succeq 0, ~\forall {\varvec{\gamma }}\in \{{\varvec{\gamma }}^1, \ldots , {\varvec{\gamma }}^{N}\},\\ &{} \mathbf {h} \ge 0, \\ &{} {\mathbf {z} \in \{0,1\}^n}. \end{array} \end{aligned}$$

(3.16)

Remark: Problem (3.16) is very similar to problem (3.9) except for the newly introduced decision variable $\mathbf {h}$. If we restrict $\mathbf {h} = 0$, then problem (3.16) is exactly the same as problem (3.9). Each $\mathbf {h} > 0$ essentially enlarges the feasible domain of $(\mathbf {Y},\mathbf {y}, {y_0})$ in problem (3.9) to a larger feasible domain of $(\mathbf {Y},\mathbf {y}, {y_0})$ in problem (3.16).

3.2 Genetic algorithm for finding $\mathbf {z}$

From a computational perspective, problems (3.9) and (3.16) are complex to solve due to both the presence of the binary variable $\mathbf {z}$ and the potentially large number of SDP constraints.

The issue of having binary variables $\mathbf {z}$ is unavoidable as this is an intrinsic part of the facility location problems, even in the deterministic case. For practical purposes, we utilize a genetic algorithm (GA) to search for the optimal facility location variables. To this end, we rewrite Problem (3.16) in a compact form on decision variable $\mathbf {z}$ as follows,

$$\begin{aligned} \min \limits _{\mathbf {z} \in \{0,1\}^n} \qquad {\mathbf {\mathbf {b}^{T} \mathbf {z}}} +H_D({\mathbf {z}}), \end{aligned}$$

(3.17)

where $H_D({\mathbf {z}})$ is defined in Formulation (3.4) and has a SDP reformulation similar to Formulation (3.16) except that $\mathbf {z}$ is not a decision variable and the fixed term ${\mathbf {\mathbf {b}^{T} \mathbf {z}}}$ is taken out of the objective function.

As long as we are able to evaluate the fitness function ${\mathbf {\mathbf {b}^{T} \mathbf {z}}} +H_D({\mathbf {z}})$ for each $\mathbf {z}$, the optimization problem (3.17) can be embedded in a generic genetic algorithm.¹ In this case, we view the decision variable $\mathbf {z}$ as genomes and the genetic algorithm keeps updating them through operations such as mutation and crossover to find better solutions. The genetic algorithm is a probabilistic search method that mimics the biological model of natural selection. It applies the principle of “survival of the fittest” to a population of potential solutions to produce progressively better solutions over the generations. We refer the interested readers to Davis (1991) for more details about the genetic algorithm.

3.3 Row generation algorithm for evaluating the fitness function

The fitness function is the optimal value of a SDP problem of a similar form as in (3.16) with N semi-definite constraints, where N is the number of vertices of the DTP polyhedra $\Gamma$, that is the feasible space of the DTP. The challenge here is that N grows exponentially as the problem size (n, m) increases (Balinski and Russakoff 1984). We resolve this issue by utilizing a row generation (RG) algorithm. The RG algorithm starts by including only a subset of constraints and solves the restricted problem. The optimal solution obtained might violate some constraints of the original problem. The next step is to identify such violated constraints which are then added to the restricted problem in an iterative manner. This procedure is applied until there is no further violating constraint. In that case, the optimal solution of the restricted problem is also the optimal solution of the original problem.

A key component of a row generation algorithm is to identify violating constraints. Suppose, at iteration k, we solve problem (3.16) with the subset of SDP constraints and obtain $\left( \mathbf {Y}^{(k)},\mathbf {y}^{(k)},y_0^{(k)},\mathbf {h}^{(k)}\right)$. To find a violating constraint, we need to find $\varvec{\gamma } \in \Gamma$ such that

$$\begin{aligned} \min \limits _{\varvec{\underline{\xi }}~\le ~\varvec{\xi }~ \le ~ \varvec{\bar{\xi }}}\left[ {{\varvec{\xi }}}^{T} {\mathbf {Y}} {{\varvec{\xi }}} + {{\varvec{\xi }}}^{T} ({\mathbf {y}}-{{\varvec{\gamma }}_\alpha })+ y_0 + {{\varvec{\gamma }}_\beta }^{T}(\mathbf {s\circ z})\right] < 0, \end{aligned}$$

since this is the complementary condition of the feasibility constraint (3.14).

This can be done by solving

$$\begin{aligned} \min \limits _{\varvec{\gamma } \in \Gamma , \varvec{\underline{\xi }}~\le ~\varvec{\xi }~ \le ~ \varvec{\bar{\xi }}}\left[ {{\varvec{\xi }}}^{T} {\mathbf {Y}}^{(k)} {{\varvec{\xi }}} + {{\varvec{\xi }}}^{T} ({\mathbf {y}^{(k)}-{{\varvec{\gamma }}_\alpha }})+ y_0^{(k)} + {{\varvec{\gamma }}_\beta }^{T}(\mathbf {s\circ z}) \right] \end{aligned}$$

(3.18)

and checking whether the optimal value is less than zero, in which case we have identified a violating constraint. Otherwise, we conclude that the relaxed solution $\left( \mathbf {Y}^{(k)},\mathbf {y}^{(k)},y_0^{(k)},\mathbf {h}^{(k)}\right)$ is an optimal solution of the original SDP problem. Problem (3.18) is a non-convex quadratic optimization problem, i.e., still involving a bilinear term in the objective function between decision variable $\xi$ and $\gamma$. Despite the NP-hardness nature of the problem, there are several numerical schemes for solving practical problems globally such as in Chen and Burer (2012), Bonami et al. (2018), Gondzio and Yildirim (2018) and Xia et al. (2019). In our numerical scheme, we develop a simple iterative approach to alternatively fix $\gamma$ to solve the (convex) quadratic program on $\xi$ and then fix the newly found $\xi$ to solve the linear program on $\gamma$. While this approach does not provide us a definite conclusion on the feasibility of $\left( \mathbf {Y}^{(k)},\mathbf {y}^{(k)},y_0^{(k)},\mathbf {h}^{(k)}\right)$ if the local optimal $(\xi ,\gamma )$ results in a nonnegative objective value, it is still effective in identifying violating constraints when this results in a negative objective value. Here, we note that a global optimization procedure is only needed in the very last iteration of the row generation algorithm to verify the feasibility of the relaxed optimal solution.

4 A semi-infinite approach

In this section, we consider the case when the uncertainty set is defined through the first moment²

$$\begin{aligned} \mathcal {P} = \left\{ P\in \mathscr {P}: \mathbb {E}_{P}[{\varvec{\xi }}]={\varvec{\mu }}\right\} , \end{aligned}$$

(4.1)

where ${\varvec{\mu }}$ is the true mean value of the random demand ${\varvec{\xi }}$.

We first formulate the (R-FLP) problem as an integer semi-infinite program (SIP) in Sect. 4.1. Similar to the SDP formulation, the resulting model still has the inherent binary variables for the facility location decisions and hence we use the same genetic algorithm as described in Sect. 3. The major additional challenge is that the resulting model has an infinite number of constraints. We first utilize a linear decision rule approximation approach in Sect. 4.2 to simplify the SIP model by restricting the second-stage decision variables as linear functions of the uncertainties. We then utilize the conditional value at risk approximations over the sets of infinite constraints. Finally, we use sample approximation to approximate the semi-infinite programs, i.e., both the original SIP and the linear decision rule approximation, and the CVaR formulation in Sect. 4.4.

4.1 Semi-infinite formulation

Let us reconsider the inner maximization problem associated with the robust problem (2.4)

$$\begin{aligned} H({{\mathbf {z}}}) := \sup \limits _{P \in \mathcal {P}} \mathbb {E}_{P} \left[ g({\mathbf {z}},{\varvec{\xi }})\right] . \end{aligned}$$

We can derive the dual formulation with respect to the moment condition as

$$\begin{aligned} \begin{array}{lll} H_D({ {\mathbf {z}}})= &{}\min \limits _{\lambda _0, \varvec{\lambda }} &{} \lambda _0 + {\varvec{\lambda }}^T {\varvec{\mu }}\\ &{}\text {s.t.} &{} g({\mathbf {z}},{\varvec{\xi }}) \le \lambda _0 + {\varvec{\xi }}^T {\varvec{\lambda }}, ~ \forall {\varvec{\xi }}\in \Xi , \end{array} \end{aligned}$$

(4.2)

where $\Xi \subset {\mathbb {R}^m}$ is the support set of ${\varvec{\xi }}$, ${\varvec{\lambda }}\in \mathbb {R}^m$ and $\lambda _0 \in \mathbb {R}$ are the dual variables associated with the moment constraints and the normalization constraint, respectively. Since the support set $\Xi$ is infinite, the dual problem (4.2) is a linear semi-infinite programming problem (SIP). It is important to note that (4.2) is a deterministic semi-infinite programming problem. If $\Xi$ is structured, e.g., polyhedral or semi-algebraic and g is linear or quadratic w.r.t. ${\varvec{\xi }}$, then through the well known S-lemma, the semi-infinite system can be represented as an SDP; see for instance Zymler et al. (2013). Here, we don’t assume any special structure as such. To avoid duality gap, we assume that the regularity conditions specified in Shapiro et al. (2009) hold. Specifically, we assume that the dual problem has a non-empty and bounded set of optimal solutions and also the support set $\Xi$ is convex and compact. The second-stage maximization problem in (2.4) can

be replaced by its dual as follows,

$$\begin{aligned} \begin{array}{lll} \text {(R-SIP)}\quad \quad &{}\min \limits _{\mathbf {z}, \lambda _0, \varvec{\lambda }} &{} {{\mathbf {b}^{T} \mathbf {z}}} + \lambda _0 + {\varvec{\lambda }}^T {\varvec{\mu }}\\ &{}\text {s.t.} &{} g({\mathbf {z}},{\varvec{\xi }}) \le \lambda _0 + {\varvec{\xi }}^T {\varvec{\lambda }}, ~ \forall {\varvec{\xi }}\in \Xi , \\ &{}&{}{\mathbf {z} \in \{0,1\}^n,} \end{array} \end{aligned}$$

(4.3)

or equivalently

$$\begin{aligned} \begin{array}{lll} &{}\min \limits _{\mathbf {z,x(\cdot ),w(\cdot )}, \lambda _0,\varvec{\lambda }} &{} {{\mathbf {b}^{T} \mathbf {z}}} + \lambda _0 + {\varvec{\lambda }}^T {\varvec{\mu }}\\ &{}\qquad \text {s.t.} &{} \mathbf {c}\bullet \mathbf {x}({\varvec{\xi }})+ {\mathbf {C}\bullet } \mathbf {w}({\varvec{\xi }})\le \lambda _0 + {\varvec{\xi }}^T {\varvec{\lambda }}, ~ \forall {\varvec{\xi }}\in \Xi ,\\ &{}&{} \bigg (\mathbf {x}({\varvec{\xi }}),\mathbf {w}({\varvec{\xi }})\bigg )\in \mathcal{{G}}(\mathbf {z},{\varvec{\xi }}), ~ \forall {\varvec{\xi }}\in \Xi ,\\ &{}&{} {\mathbf {z} \in \{0,1\}^n,} \end{array} \end{aligned}$$

(4.4)

where $\mathbf {x}({\varvec{\xi }}) \in \mathbb {R}^{n \times m}$ and $\mathbf {w}({\varvec{\xi }}) \in \mathbb {R}^{m}$ are optimal transportation decisions for each fixed $\mathbf {z}$ and for each realization of ${\varvec{\xi }}$, and where $\mathbf {c}$ is the matrix of transportation cost coefficients and $\mathbf {C}$ is the cost vector of serving customers from the external source. Moreover, $\mathcal {G}(\mathbf {z},{\varvec{\xi }})$ is the feasible regions associated with the second-stage problem (2.3).

4.2 Linear decision rule approximation

One of the main challenges in solving the semi-infinite problem above is the dependence of the second-stage transportation variables $\mathbf {x}({\varvec{\xi }})$ and $\mathbf {w}({\varvec{\xi }})$ on random variable ${\varvec{\xi }}$. These “adjustable” variables are often referred to as decision rules, and their presence could often complicate the solution procedure. Formally, a decision rule $\mathbf {x}({\varvec{\xi }})$ can be defined as a vector-valued function, mapping the random variables ${\varvec{\xi }}\in \mathbb {R}^{m}$ with support set $\Xi$ into the decisions. The decision rule problem can be interpreted as identifying the best decision $\mathbf {x}({\varvec{\xi }}) \in \Delta \subset \mathcal {X}$ once ${\varvec{\xi }}$ is observed, where $\mathcal {X}$ denotes the set of all the mapping from $\Xi$ to $\mathbb {R}^{n\times m}$ and $\Delta$ a subset of $\mathcal {X}$.

A tractable approximation scheme to deal with the decision rules is to restrict their feasible set to the ones that have a functionality affine relation with the uncertain random variables (that are affine functions of the uncertain data). This approach was proposed by Ben-Tal et al. (2004) and was extended in Shapiro and Nemirovski (2005) and Kuhn et al. (2011) to develop tractable numerical procedure for stochastic programming problems. Here, we take the initiative to apply the linear decision rule (LDR) approximation to problem (4.4); that is, we impose the dependence of transportation decisions on the random demand to follow linear functions

$$\begin{aligned} \mathbf {x}({\varvec{\xi }})=&\mathbf {X} {\varvec{\xi }}+ \mathbf {x^0},\\ \mathbf {w}({\varvec{\xi }})=&\mathbf {W} {\varvec{\xi }}+ \mathbf {w^0}, \end{aligned}$$

where $\mathbf {X} \in \mathbb {R}^{(nm \times m)},\mathbf {W} \in \mathbb {R}^{m \times m} \in \mathbb {R}^{n\times m}, \mathbf {x^0} \in \mathbb {R}^{n \times m}, \text {and } \mathbf {w^0} \in \mathbb {R}^m$. Consequently, problem (4.4) can be approximated as

$$\begin{aligned} \begin{array}{lll} \text {(R-LDR)}\quad \quad &{}\min \limits _{\mathbf {z,X,x^0,W,w^0}, \lambda _0,\varvec{\lambda }} &{} {{\mathbf {b}^{T} \mathbf {z}}} + \lambda _0 + {\varvec{\lambda }}^T {\varvec{\mu }}\\ &{}\qquad \text {s.t.} &{} \mathbf {c}\bullet (\mathbf {X} {\varvec{\xi }}) + \mathbf {x^0}+ {\mathbf {C}\bullet } (\mathbf {W} {\varvec{\xi }}) + \mathbf {w^0}\le \lambda _0 \\ &{}&{}\quad + {\varvec{\xi }}^T {\varvec{\lambda }}, ~ \forall {\varvec{\xi }}\in \Xi ,\\ &{}&{} \bigg (\mathbf {X} {\varvec{\xi }}+ \mathbf {x^0},\mathbf {W} {\varvec{\xi }}+ \mathbf {w^0}\bigg )\in \mathcal{{G}}({\mathbf {z}},{\varvec{\xi }}), ~ \forall {\varvec{\xi }}\in \Xi , \\ &{}&{}{\mathbf {z} \in \{0,1\}^n}. \end{array} \end{aligned}$$

(4.5)

Note that here we are slightly abusing the notation in this formulation: ${\varvec{\xi }}$ should be understood as a parameter rather than a random variable. Indeed, it represents a realization of the random vector ${\varvec{\xi }}$. The optimal value of the LDR approximation problem will generate an upper bound on the optimal value of original robust problem (4.4).

4.3 Conditional value at risk approximation

Having defined the LDR formulation of the original robust semi-infinite problem, we approximate the first semi-infinite constraint with Conditional Value at Risk (CVaR) and then approximate the latter through Monte Carlo sampling to reduce the number of constraints. One of the main advantages of using CVaR is that it converts the semi-infinite number of constraints into a single constraint. A recent study by Anderson et al. (2014) has shown promising performance of CVaR approximation in dealing with semi-infinite problems. The CVaR approximation method has been extensively used in stochastic programming for approximating the chance constraints, and we refer the readers to Sun et al. (2014) and Hong et al. (2011) for more details.

In the case of our LDR problem, we start by considering CVaR approximation of the first semi-infinite constraints in problem (4.5). To ease the notation, let

$$\begin{aligned} h(\mathbf {X,x^0,W,w^0}, \lambda _0, \varvec{\lambda , \xi }) := \mathbf {c}\bullet (\mathbf {X} {\varvec{\xi }}) + \mathbf {x^0}+ {\mathbf {C}\bullet } (\mathbf {W} {\varvec{\xi }}) + \mathbf {w^0}-\lambda _0 - {\varvec{\xi }}^T {\varvec{\lambda }}, \end{aligned}$$

and $\mathcal {Q}:=(\mathbf {X,x^0,W,w^0}, \lambda _0, {\varvec{\lambda }})$. The semi-infinite constraint of (4.5) can be written as

$$\begin{aligned} \sup \limits _{\varvec{\xi } \in \Xi } h(\mathcal {Q},{\varvec{\xi }}) \le 0. \end{aligned}$$

Let $\tilde{{\varvec{\xi }}}$ be a continuous random vector with support $\Xi$. Then $\sup _{\varvec{\xi } \in \Xi } h(\mathcal {Q},{\varvec{\xi }})$ can be approximated by CVaR of $h(\mathcal {Q},\tilde{{\varvec{\xi }}})$, which is defined as

$$\begin{aligned} {\text {CVaR}}_\beta (h(\mathcal {Q},\tilde{{\varvec{\xi }}})) := \min \limits _{\eta \in \mathbb {R}} \Phi _{\beta }(\mathcal {Q},\eta ), \end{aligned}$$

where

$$\begin{aligned} \Phi _{\beta }(\mathcal {Q},\eta ) := \eta + \frac{1}{1-\beta } \int _{\tilde{\varvec{\xi }} \in \Xi } \big (h(\mathcal {Q},\tilde{{\varvec{\xi }}})-\eta \big )_{+} ~ \tilde{P}(d\tilde{{\varvec{\xi }}}), \end{aligned}$$

$(\tau )_{+} = \max (0,\tau )$, and $\tilde{P}$ denotes the distribution of $\tilde{{\varvec{\xi }}}$. Consequently, the CVaR approximation of the semi-infinite constraint in problem (4.5) can be expressed as follows:

$$\begin{aligned} \min \limits _{\eta \in \mathbb {R}} \Bigg ( \eta + \frac{1}{1-\beta } \mathbb {E}\bigg [(h\big (\mathcal {Q},\tilde{{\varvec{\xi }}})-\eta \big )_{+}\bigg ]\Bigg ) \le 0. \end{aligned}$$

(4.6)

It is important to distinguish the expectation $\mathbb {E}[\cdot ]$ here from the expectation $\mathbb {E}[\cdot ]$ in (S-FLP). The former should be understood as a mathematical expectation taken w.r.t. any distribution of any random variable $\tilde{{\varvec{\xi }}}$ with support set $\Xi$. In other words, here, the $\tilde{{\varvec{\xi }}}$ does not have to be identical to the ${\varvec{\xi }}$ in (S-FLP). For example, we may set $\tilde{{\varvec{\xi }}}$ as a random variable with uniform distribution over $\Xi$. Of course, the selection of $\tilde{{\varvec{\xi }}}$ and its distribution will affect the quantity of CVaR of h and the rate of approximation to its essential supremum.

Under some mild conditions, we can show that the error arising from the approximation scheme does not have significant impact on the optimal value; see Anderson et al. (2014). By replacing the constraint in the original LDR problem, we can write the CVaR approximation problem as

$$\begin{aligned} \begin{array}{lll} \text {(R-CVaR)}\quad \quad &{}\min \limits _{\eta ,\mathbf {z,X,x^0,W,w^0}, \lambda _0, \varvec{\lambda }} &{} {{\mathbf {b}^{T} \mathbf {z}}} + \lambda _0 + {\varvec{\lambda }}^T {\varvec{\mu }}\\ &{}\qquad \text {s.t.} &{} \eta + \frac{1}{1-\beta } \mathbb {E}\bigg [\Big (h(\mathbf {X,x^0,W,w^0}, \lambda _0, {\varvec{\lambda }},\tilde{{\varvec{\xi }}})-\eta \Big )_{+}\bigg ] \le 0, \\ &{}&{} \bigg (\mathbf {X} {\varvec{\xi }}+ \mathbf {x^0},\mathbf {W} {\varvec{\xi }}+ \mathbf {w^0}\bigg )\in \mathcal{{G}}({\mathbf {z}},{\varvec{\xi }}), ~ \forall {\varvec{\xi }}\in \Xi , \\ &{}&{}{\mathbf {z} \in \{0,1\}^n}. \end{array} \nonumber \\ \end{aligned}$$

(4.7)

Under the Slater constraint qualification of the LDR problem (4.5), we can demonstrate, similar to (Anderson et al. 2014, Theorem 4) that the optimal solution of the CVaR approximation problem (4.7) converges to optimal solution of the LDR problem as $\beta \rightarrow 1$.

4.4 Discretization through sampling

One of the well-known solution approaches for semi-infinite programs is random discretization. The basic idea is to construct a tractable sub-problem by considering a randomly drawn finite subset of constraints and hence enlarging the solution set. Calafiore and Campi (2005), Calafiore and Campi (2006) investigated this approach and used Monte Carlo sampling (often referred to as sample average approximation) to approximate the convex problems consisting of linear objectives and semi-infinite constraints. They showed that the resulting randomized solution fails to satisfy only a small proportion of the original constraints for a sufficiently large sample size. An explicit bound on the measures of the original constraints that may be violated by the randomized solution is derived. The approach has been shown numerically efficient, and it has been widely applied to various stochastic and robust programs. We refer interested readers to Campi and Garatti (2011), Shapiro (2003) and references therein.

In this paper, we apply the Monte Carlo sampling approach respectively to the original semi-infinite problem (4.4), its LDR approximation (4.5) and the CVaR formulation (4.7).

Let $\mathcal {K}=\{1,\ldots ,K\}$ denote the finite set of sample indices and ${\varvec{\xi }}^1,\ldots , {\varvec{\xi }}^{K}$ an independent and identically distributed (i.i.d) sampling of ${\varvec{\xi }}$. We may construct a discretized approximation of problem (4.4) through Monte Carlo sampling as follows,

$$\begin{aligned} \begin{array}{lll} &{}\min \limits _{\mathbf {z},x(\xi ^k),w(\xi ^k):k\in \mathcal {K}, \lambda _0,\varvec{\lambda }} &{} {{\mathbf {b}^{T} \mathbf {z}}} + \lambda _0 + {\varvec{\lambda }}^T {\varvec{\mu }}\\ &{}\qquad \text {s.t.} &{} \mathbf {c}\bullet \mathbf {x}({\varvec{\xi }}^k)+ {\mathbf {C}\bullet } \mathbf {w}({\varvec{\xi }}^k)\le \lambda _0 + {\varvec{\lambda }}^T {\varvec{\xi }}^k, ~ \forall k \in \mathcal {K},\\ &{}&{}\bigg ( \mathbf {x}({\varvec{\xi }}^k),\mathbf {w}({\varvec{\xi }}^k)\bigg )\in \mathcal{{G}}(\mathbf {z},{\varvec{\xi }}^k), ~ \forall k \in \mathcal {K}, \\ &{}&{}{\mathbf {z} \in \{0,1\}^n}. \end{array} \end{aligned}$$

(4.8)

This kind of discretization scheme was recently applied to a distributionally robust formulation of a two-stage stochastic unit commitment problem. From a mathematical perspective, it is justified in that under some mild conditions, one can show the convergence of the optimal value of the discretized problem to its true counterpart almost surely as the sample size increases, see details in (Xu et al. 2018, Sect. 3.1).

Similarly the discretized LDR problem (4.5) can be formulated as

$$\begin{aligned} \begin{array}{lll} &{}\min \limits _{\mathbf {z,X,x^0,W,w^0}, \lambda _0, \varvec{\lambda }} &{} {{\mathbf {b}^{T} \mathbf {z}}} + \lambda _0 + {\varvec{\lambda }}^T {\varvec{\mu }}\\ &{}\qquad \text {s.t.} &{} \mathbf {c}\bullet (\mathbf {X} {\varvec{\xi }}^k)+ \mathbf {x^0}+ {\mathbf {C}\bullet } (\mathbf {W} {\varvec{\xi }}^k) + \mathbf {w^0}\le \lambda _0 +{\varvec{\lambda }}^T {\varvec{\xi }}^k, ~ \forall k \in \mathcal {K},\\ &{}&{} \bigg (\mathbf {X} {\varvec{\xi }}^k + \mathbf {x^0},\mathbf {W} {\varvec{\xi }}^k + \mathbf {w^0}\bigg )\in \mathcal{{G}}({\mathbf {z}},{\varvec{\xi }}^k), ~ \forall k \in \mathcal {K}, \\ &{}&{}{\mathbf {z} \in \{0,1\}^n,} \end{array} \end{aligned}$$

(4.9)

and, finally, we apply the sample average approximation (SAA) scheme to CVaR approximation problem (4.7) as follows,

$$\begin{aligned} \begin{array}{lll} &{}\min \limits _{\eta ,\mathbf {z,X,x^0,W,w^0}, \lambda _0, \varvec{\lambda }} &{} {{\mathbf {b}^{T} \mathbf {z}}} + \lambda _0 + {\varvec{\lambda }}^T {\varvec{\mu }}\\ &{}\qquad \text {s.t.} &{} \eta + \frac{1}{(1-\beta ){K}} \sum _{k=1}^{K} \bigg [\Big (h(\mathbf {X,x^0,W,w^0}, \lambda _0, {\varvec{\lambda }},{\varvec{\xi }}^k)-\eta \Big )_{+}\bigg ] \le 0, \\ &{}&{} \bigg (\mathbf {X} {\varvec{\xi }}^k + \mathbf {x^0},\mathbf {W} {\varvec{\xi }}^k + \mathbf {w^0}\bigg )\in \mathcal{{G}}({\mathbf {z}},{\varvec{\xi }}^k), ~ \forall k \in \mathcal {K}, \\ &{}&{}{\mathbf {z} \in \{0,1\}^n}. \end{array} \end{aligned}$$

(4.10)

Compared to (4.8), the CVaR approximation scheme allows one to take a few samples at the tail rather than essential superemum of h and in that way smooth up or stabilize the numerical computation; see Anderson et al. (2014). In the case of CVaR formulation, we replace the CVaR constraint with the equivalent system of linear inequalities by introducing additional positive dummy variables $\theta ^1, \ldots \theta ^k$ as follows

$$\begin{aligned} \left\{ \begin{array}{ll} \eta + \frac{1}{(1-\beta ){K}} \sum _{k=1}^{K} \theta ^k \le 0, &{}\\ h(\mathbf {X,x^0,W,w^0}, \lambda _0, {\varvec{\lambda }},{\varvec{\xi }}^k)-\eta \le \theta ^k, ~ \forall k \in \mathcal {K},&{}\\ \theta ^k \ge 0,~ \forall k \in \mathcal {K}.&{} \end{array}\right. \end{aligned}$$

(4.11)

The substitution results in

$$\begin{aligned} \begin{array}{lll} &{}\min \limits _{\theta ,\eta ,\mathbf {z,X,x^0,W,w^0}, \lambda _0,\varvec{\lambda }} &{} {{\mathbf {b}^{T} \mathbf {z}}} + \lambda _0 + {\varvec{\lambda }}^T {\varvec{\mu }}\\ &{}\qquad \text {s.t.} &{} \eta + \frac{1}{(1-\beta ){K}} \sum _{k=1}^{K} \theta ^k \le 0, \\ &{}&{} h(\mathbf {X,x^0,W,w^0}, \lambda _0, {\varvec{\lambda }},{\varvec{\xi }}^k)-\eta \le \theta ^k, ~ \forall k \in \mathcal {K},\\ &{}&{} \bigg (\mathbf {X} {\varvec{\xi }}^k + \mathbf {x^0},\mathbf {W} {\varvec{\xi }}^k + \mathbf {w^0}\bigg )\in \mathcal{{G}}({\mathbf {z}},{\varvec{\xi }}^k), ~ \forall k \in \mathcal {K},\\ &{}&{} \theta ^k \ge 0, ~ \forall k \in \mathcal {K} \\ &{}&{}{\mathbf {z} \in \{0,1\}^n}. \end{array} \end{aligned}$$

(4.12)

The reformulation will effectively address the non-smoothness caused by the $(.)_+$ operation but at the cost of introducing additional variables and constraints. It is worthwhile to do that here as the latter formulation will result in an overall MILP.

5 Computational results

In this section, we report the numerical experiments performed to evaluate the proposed methodologies. We have used MATLAB R2015b with CPLEX 12.6 for solving transportation problems and quadratic optimization problems while SEDUMI 1.3 was used for solving SDPs.

We first provide numerical results on a small-case study in Sect. 5.1 with three facilities and four customers. The purpose of this part is to illustrate the performance of various components of the SDP and SIP models such as the constraint generation algorithm and the CVaR approximation. We also use this example to demonstrate how the sample size affects the performance of the SIP model. We then report the numerical results for medium test instances in Sect. 5.2. Here we report the computational times for some test instances in the literature. We also study the robustness of the proposed SDP and SIP solutions by varying the realized demand distributions. For convenience in recapping these methods, Table 1 provides a quick reference on their abbreviations and the key differences among them.

Table 1 Abbreviations and references of methodologies used

5.1 A small case study

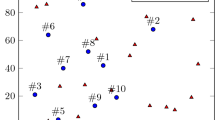
We study a small-scale facility location problem to illustrate the quality of solutions obtained from the proposed solution methods. We randomly generate a facility location problem with 4 demand nodes and 3 potential locations to build facilities. The transportation costs are assumed to be proportional to the distances between the customers and the facilities. Figure 1 shows the network layout of this problem.

Fig. 1

The network of facility location problem

The transportation cost, fixed investment cost and the capacity of each potential facility are given in Table 2.

Table 2 Transportation and investment costs and capacity of the facilities

We assume that customer demands are unknown prior to the construction of facilities and we are only given the first moment information of the demand with ${\varvec{\mu }}=(150,150,100,100)$. Moreover, in the SDP formulation of the problem, we are also provided with the second moment information of the uncertain demand

$$\begin{aligned} \mathbf {Q}= \left( \begin{array}{cccc} 22669.34&{} 22511.07&{} 15038.4 &{} 15026.78\\ 22511.07&{} 22551.57&{} 15000.53&{} 14988.58\\ 15038.4&{} 15000.53&{} 10045.48&{} 10013.84\\ 15026.78&{} 14988.58&{} 10013.84&{} 10031.04 \end{array} \right) \end{aligned}$$

Under the assumption of available first and second moments, we formulate the problem as a robust SDP (R-SDP). Since the problem size is small, we first consider all combinations of the possible facility location decisions ($2^3$ possible combinations of z). For each potential solution, the full R-SDP problem (3.16) is constructed by including all of the extreme points of the dual transportation polytopes [obtained by using the signature method in Balinski and Rispoli (1993)]. The full R-SDP problem is then solved for each potential solution and comparisons between the total cost of each decision are provided in Table 3.

Table 3 Worst expected cost associated with each possible facility location decision

Note that the very high costs of certain facility location solutions, such as with $\mathbf {z} = [0,0,0]$ or $\mathbf {z} = [0,0,1]$, are due to the high costs of using the external facility when the total (random) demand exceeds the capacity of the built facilities. It can be observed that solution number 4, i.e., $\mathbf {z}=(0,1,1)$ has the least cost and therefore is optimal (and is highlighted in bold in Table 3).

In order to illustrate the performance of the proposed constraint generation algorithm for the R-SDP formulation, we first fixed the facility decisions to $\mathbf {z}=(1,1,1)$. In each run, the problem was initiated by randomly selecting one of the SDP constraints corresponding to one of the extreme points of the dual transportation problem. We recorded the objective value after each iteration of the constraint generation process. Figure 2 summarizes the objective value after each iteration of the algorithm (by taking the average over 100 runs, each with a different starting point). It can be observed that the convergence of the constraint generation algorithm to the optimal value takes place after around 15 iterations.

Fig. 2

Convergence of the constraint generation algorithm solutions

After finding the optimal solution for a fixed facility location decision $\mathbf {z}$, the next step of the proposed solution method is to find the optimal $\mathbf {z}$ using GA. However, this is not necessary for this small instance as it has only 8 possible solutions.

5.1.1 Robust SIP formulation

Let us assume that we are only given the first moment information ${\varvec{\mu }}$ and the second moment Q is unknown. We implement the second proposed method and formulate the FLP as a semi-infinite program. For assessing the quality of LDR approximation (R-LDR) of the “true” robust SIP (R-SIP) solution, we limit the support set of the random demand for each customer to 2000 values generated from the uniform distribution $\mathcal {U}(0,250)$. We then solve the full R-SIP and its R-LDR approximation over this support set. As shown in Table 4, the R-LDR solution provides an upper bound approximation with 0.9% deviation from the original R-SIP solution. For comparison purposes, we also solve the deterministic version of the instance by assuming that the demand values are known and given by ${\varvec{\mu }}$. The solution from the deterministic problem (D-FLP) is then benchmarked against the robust solution in Table 4.

Table 4 Deterministic versus robust solutions

The deterministic solution is to install just enough capacity to meet the predicted (assumed to be known) demand values by locating facilities 1 and 2. In other words, the D-FLP solution provides no flexibility for possible variation in future demand. The robust solutions, on the other hand, offers to install the facilities with a higher total capacity at a higher total cost (i.e., constructing facilities 2 and 3 in the R-SDP case and all facilities in the R-SIP case), to hedge against the risk of not meeting the customer demand.

In the next step, we implement the proposed CVaR approximation (R-CVaR) of the R-LDR solution. Using the same support set of 2000 values, we solved the R-CVaR approximation with various $\beta$ values. The results are presented in Fig. 3. It can be observed that the CVaR solution approximates the R-LDR optimal solution consistently and without any error for $\beta \ge 0.7$.

Fig. 3

CVaR approximation of R-LDR problem for various $\beta$ values

5.1.2 Discretization through sampling

The complexity of the R-LDR and R-CVaR schemes increases as the number of scenarios increases. As described in Sect. 4.4, one way to resolve this issue is to use sample approximation (SA) for R-LDR and sample average approximation for R-CVaR. These involve drawing i.i.d samples from the underlying distribution of the uncertainty. In the case of the first instance, we have chosen the samples from the same support set used to run the full R-SIP tests. To assess the quality of sample approximation, we solve R-SIP, R-DLR and R-CVaR using various sample sizes. For each sample size, we carried out 1000 independent runs. The $\beta$ value for all of the CVaR instances was set to 0.99. The normalized deviation of the sample approximations of all problems from the true robust (full R-SIP) solution is shown in Fig. 4 for various choices of the sample sizes.

Fig. 4

Normalized deviation of approximation problems from the true robust solution

It can be observed that, for each sample size, the mean deviation of R-CVaR and R-LDR solutions from the true robust solution is very similar. They range from -0.4% to 0.9% of the true solution. (Here 0.9% deviation means that the approximate solution is 0.9% higher than the true value of the robust solution.) We can also see that the sample approximation of R-CVaR and R-LDR converges to the full R-LDR solution as the sample size increases. Furthermore, the sampling method applied to R-SIP provides a very good approximation of the true solution even for small sample sizes.

The average computation times for 1000 runs of each sample size are shown in the graph below (Fig. 5).

Fig. 5

Average computation time

5.2 Medium size test instances

In this section, we consider a set of larger facility location problems. Test instances are selected from those existing in the literature. We have modified and used test problems presented by Díaz and Fernández (2002) for the single-source capacitated facility location problem.³ The first 6 instances consist of networks of 10 potential facility locations and 20 customer demand points. The network size is increased twice in the last instance to observe how the computational time increases. We have used the given demand values in test instances as the first moment of the customer demand distribution. The second moment matrix for the SDP formulation was randomly generated.⁴

5.2.1 SDP formulation

The test results for the medium size instances are presented in Table 5. The first two columns show the test instances from Díaz and Fernández (2002) and their corresponding network sizes. The third and fourth columns show the optimal solution $\mathbf {z}$ and the corresponding SDP objective values. Columns 5–7 show the CPU computational time while column 8 shows the optimal value of the corresponding deterministic facility location problem as defined in Model 2.

Table 5 Robust facility location solutions

We can see from column 7 that it took between 2–4 hours to run the instances with 20 customers and 10 facilities. This increases sharply to over 11 hours for instance $p_7$ and 22 hours for instance $p_{18}$ when the number of customers and facilities are increased to (30, 15) and (40, 20), respectively. The total CPU times are broken down to the time to (iteratively) run the SDPs and to perform row generations (i.e., to identify violating constraints). We can see that most of the computational time is on solving the SDPs. In theory, the SDP models (3.9) and (3.16) can be solved in polynomial times for fixed numbers of facilities and customers since the problem has a linear objective function with a polynomial number of SDP constraints. While we have made a contribution in transforming the two-stage stochastic, minimax, integer optimization problem into a single-level SDP optimization problem, we acknowledge that there are still drawbacks in the framework. Specifically, despite recent developments in SDP programming, problems (3.9) and (3.16) do not scale well with the number of facilities and the number of customers due to the fast growth in the number of SDP constraints. For practical purposes with larger instances, if being able to find a reasonably robust solution is more crucial than optimality, our framework is still applicable and what we need to do is to set the time limits on the constraint generation algorithm and the genetic algorithms.

The numerical scheme for solving the SDP contains several fine tuning parameters. First of all, the stopping condition for the row generation algorithm is triggered either when a maximum of 100 SDP constraints are added or when the additional constraints do not lead to more than 0.1% changes on the objective value in the 5 consecutive iterations. Second, the number of iterations in the alternating procedure for finding violating constraints is set at most 100 iterations. We implement the constraint generation and utilize the built-in Matlab GA algorithms with mostly default settings except that the GA population size is set to 30 with stopping criteria of a maximum of 10 generations. The population size is the number of solutions under consideration at any point by the GA algorithm to perform various operations in order to produce further solutions. The parameters are set to balance between the run time and the quality of the solutions. All the numerical tests are run in MATLAB R2015b utilizing SeDuMi and Cplex LP solvers version 12.6.

For comparison purposes, we also include the deterministic solutions of the instances in the table above on column 8. As expected, most of the robust solutions have higher costs than deterministic facility decisions as a result of installing higher total capacities, although the lower cost of D-FLP solutions comes at the expense of non-flexibility of the facility decisions against the fluctuation in future customer demand. The only exception is on instance $p_2$. Here, we note that the row generation algorithm have some stopping criteria and the reported SDP solutions might not be the “true optimal” solutions should we have enough computational power to solve the big SDPs with all the constraints included.

In order to verify the performance of GA, we compare its solutions with the exhaustive search technique where the objective values for every combination of $\mathbf {z}$ are evaluated in order to find the optimal solutions. This exhaustive search is only doable when n is small enough, i.e., $n=10$ in the first 6 instances. We found that the solution obtained from GA matched the optimal solution in the first 5 instances while the optimality gap for instance $p_6$ is quite small at 1.5%.⁵

5.2.2 SIP formulation

We now reconsider the problem instance $p_5$ and assume that the only available information on demand uncertainty is the first moment of the distribution ${\varvec{\mu }}$. The R-SIP framework is then used to construct and solve this problem. As before, we limit the support set of the random variable ${\varvec{\xi }}$ to 200 uniformly generated random values. For comparison purposes, we summarize the full R-SIP solution to this problem along with those from D-FLP, S-FLP and full R-SDP versions of the problem in Table 6 below.

Table 6 FLP solutions for various methodologies

It can be observed that R-SIP offers a more flexible solution by installing a higher level of supply capacity. This, of course, comes at the expense of a higher total expected cost. Also, as we include progressively less information on the uncertainty in our models, the solution becomes more and more robust (higher levels of supply capacity installed), which is intuitively sensible.

Having solved the full R-SIP $p_5$, we consider sample approximation of the R-SIP, R-LDR and R-CVaR. Various sample sizes are used for each problem, and we repeat each test for 100 times. The normalized deviation from the full R-SIP solution is computed and presented in Fig. 6.

Fig. 6

Deviation of approximation solutions from the true robust solution

It can be observed that, in all models, the sampling scheme results in approximation of the true robust solution (R-SIP) with a very low error (with < 3% mean deviation). Moreover, in the case of smaller sample sizes, the CVaR model performs much better than the other two models and has a mean deviation of $<0.5$%.

6 Conclusion

In this paper, we consider a capacitated facility location problem with customer demand uncertainty and propose a two-stage distributionally robust model for the problem to tackle the issue of incomplete information on the true distribution of the uncertainty. We construct the uncertainty set using the moments information associated with the distribution of the random demands. Two numerical methods are proposed based on the available moment information. Specifically, we first formulate the robust problem as a semi-definite program on the basis of the first and the second moments which is then solved by using a constraint generation algorithm. Moreover, we formulate the robust problem as a semi-infinite program for the case that only the first moment information is given. The semi-infinite program is then solved by approximation using a linear decision rule, CVaR and Monte Carlo sampling. Finally, we carry out numerical tests for a small instance and also for some medium-sized instances taken from the literature. In each case, the distributionally robust solutions offer the flexibility in hedging against uncertainty compared to the deterministic and the stochastic solutions.

In the future, it would be interesting to study the possibility of extending the results and methodologies presented in this paper to include uncertainty in supply, multistage problems, and the competition in the market. Also, we would like to explore the problem structure to enhance the solution algorithms for a better performance in large-scale instances. Another open direction is to apply the proposed methodologies and numerical schemes to the practical problems with similar structure and characteristics such as uncertain supply and demand. Some examples related to the energy industry could include the wind farm site location problem and liquefied natural gas storage facility location problems.