A Hierarchical Bayes Unit-Level Small Area Estimation Model for Normal Mixture Populations

Abstract

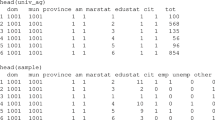
National statistical agencies are regularly required to produce estimates about various subpopulations, formed by demographic and/or geographic classifications, based on a limited number of samples. Traditional direct estimates computed using only sampled data from individual subpopulations are usually unreliable due to small sample sizes. Subpopulations with small samples are termed small areas or small domains. To improve on the less reliable direct estimates, model-based estimates, which borrow information from suitable auxiliary variables, have been extensively proposed in the literature. However, standard model-based estimates rely on the normality assumptions of the error terms. In this research we propose a hierarchical Bayesian (HB) method for the unit-level nested error regression model based on a normal mixture for the unit-level error distribution. Our method proposed here is applicable to model cases with unit-level error outliers as well as cases where each small area population is comprised of two subgroups, neither of which can be treated as an outlier. Our proposed method is more robust than the normality based standard HB method (Datta and Ghosh, Annals Stat. 19, 1748–1770, 1991) to handle outliers or multiple subgroups in the population. Our proposal assumes two subgroups and the two-component mixture model that has been recently proposed by Chakraborty et al. (Int. Stat. Rev. 87, 158–176, 2019) to address outliers. To implement our proposal we use a uniform prior for the regression parameters, random effects variance parameter, and the mixing proportion, and we use a partially proper non-informative prior distribution for the two unit-level error variance components in the mixture. We apply our method to two examples to predict summary characteristics of farm products at the small area level. One of the examples is prediction of twelve county-level crop areas cultivated for corn in some Iowa counties. The other example involves total cash associated in farm operations in twenty-seven farming regions in Australia. We compare predictions of small area characteristics based on the proposed method with those obtained by applying the Datta and Ghosh (Annals Stat. 19, 1748–1770, 1991) and the Chakraborty et al. (Int. Stat. Rev. 87, 158–176, 2019) HB methods. Our simulation study comparing these three Bayesian methods, when the unit-level error distribution is normal, or t, or two-component normal mixture, showed the superiority of our proposed method, measured by prediction mean squared error, coverage probabilities and lengths of credible intervals for the small area means.

Appendix: A

1.1 A Integrability of Joint Posterior Probability Density Function

Chakraborty et al. (2019) showed that the joint posterior density function of $\boldsymbol {\beta }, {\sigma ^{2}_{1}}, {\sigma ^{2}_{2}}, p_{e},$ and ${\sigma _{v}^{2}}$ is proper. In particular, they showed that the function

$$ L(\boldsymbol{\beta}, {\sigma^{2}_{1}}, {\sigma^{2}_{2}}, p_{e},{\sigma_{v}^{2}})\frac{I_{\{{\sigma_{1}^{2}}<{\sigma_{2}^{2}}\}}}{({\sigma_{2}^{2}})^{2}} $$

(A.1)

is integrable with respect to $\boldsymbol {\beta }, {\sigma ^{2}_{1}}, {\sigma ^{2}_{2}}, p_{e},$ and ${\sigma _{v}^{2}}$, where $L(\boldsymbol {\beta }, {\sigma ^{2}_{1}}, {\sigma ^{2}_{2}}, p_{e},{\sigma _{v}^{2}})$ is the likelihood function based on the distribution y_ij,j = 1,…,n_i,i = 1,…,m obtained as the marginal distribution from (I)−(III) in Section 2. Similar arguments show that $L(\boldsymbol {\beta }, {\sigma ^{2}_{1}}, {\sigma ^{2}_{2}}, p_{e},{\sigma _{v}^{2}})\frac {I_{\{{\sigma _{1}^{2}}{\geq \sigma _{2}^{2}}\}}}{({\sigma _{1}^{2}})^{2}}$ is also integrable with respect to the same variables. Now we note that

$$ \begin{array}{@{}rcl@{}} \frac{I_{\{2^{-1}<p_{e}<1\}}}{({\sigma_{1}^{2}}+{\sigma_{2}^{2}})^{2}} & \leq& \frac{1}{({\sigma_{1}^{2}}+{\sigma_{2}^{2}})^{2}} = \frac{I_{\{{\sigma_{1}^{2}}<{\sigma_{2}^{2}}\}}+I_{\{{\sigma_{1}^{2}}{\geq\sigma_{2}^{2}}\}}}{({\sigma_{1}^{2}}+{\sigma_{2}^{2}})^{2}} \\ &=&\frac{1}{({\sigma_{2}^{2}})^{2}}\left( \frac{{\sigma_{2}^{2}}}{{\sigma_{1}^{2}}+{\sigma_{2}^{2}}}\right)^{2}I_{\{{\sigma_{1}^{2}}<{\sigma_{2}^{2}}\}}+\frac{1}{({\sigma_{1}^{2}})^{2}}\left( \frac{{\sigma_{1}^{2}}}{{\sigma_{1}^{2}}+{\sigma_{2}^{2}}}\right)^{2}I_{\{{\sigma_{1}^{2}}{\geq\sigma_{2}^{2}}\}}\\ &<& \frac{I_{\{{\sigma_{1}^{2}}<{\sigma_{2}^{2}}\}}}{({\sigma_{2}^{2}})^{2}}+\frac{I_{\{{\sigma_{1}^{2}}{\geq\sigma_{2}^{2}}\}}}{({\sigma_{1}^{2}})^{2}}. \end{array} $$

This implies,

$$ \begin{array}{@{}rcl@{}} L(\boldsymbol{\beta}, {\sigma^{2}_{1}}, {\sigma^{2}_{2}}, p_{e},{\sigma_{v}^{2}})\frac{I_{\{2^{-1}<p_{e}<1\}}}{({\sigma_{1}^{2}}+{\sigma_{2}^{2}})^{2}} < L(\boldsymbol{\beta}, {\sigma^{2}_{1}}, {\sigma^{2}_{2}}, p_{e},{\sigma_{v}^{2}})\left( \frac{I_{\{{\sigma_{1}^{2}}<{\sigma_{2}^{2}}\}}}{({\sigma_{2}^{2}})^{2}}+\frac{I_{({\sigma_{1}^{2}}{\geq\sigma_{2}^{2}})}}{({\sigma_{1}^{2}})^{2}}\right). \end{array} $$

(A.2)

The LHS of Eq. A.2 is bounded above by two integrable functions, hence it is also integrable.

1.2 A.2 Simulation Results with no Contamination of Unit-Level Errors

Figure 6

Plots of various measures of $\hat {\theta }$s when no unit-level contamination is present