Abstract
Fractional derivatives and integrals for measures and distributions are reviewed. The focus is on domains and co-domains for translation invariant fractional operators. Fractional derivatives and integrals interpreted as  -convolution operators with power law kernels are found to have the largest domains of definition. As a result, extending domains from functions to distributions via convolution operators contributes to far reaching unifications of many previously existing definitions of fractional integrals and derivatives. Weyl fractional operators are thereby extended to distributions using the method of adjoints. In addition, discretized fractional calculus and fractional calculus of periodic distributions can both be formulated and understood in terms of
-convolution operators with power law kernels are found to have the largest domains of definition. As a result, extending domains from functions to distributions via convolution operators contributes to far reaching unifications of many previously existing definitions of fractional integrals and derivatives. Weyl fractional operators are thereby extended to distributions using the method of adjoints. In addition, discretized fractional calculus and fractional calculus of periodic distributions can both be formulated and understood in terms of  -convolution.
-convolution.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
A central motivation behind the development of fractional calculus has been the original idea of Leibniz to treat integrals symbolically as negative powers of differentials [1, p. 105], [2] (and [3] for more). Distribution theory [4, 5], as well as operational calculus [6,7,8], originated from that very same idea [6, p. 574] [5, p. 174] [8, p. 121] of justifying the “symbolic integrations” of physicists and engineers [6, 9,10,11], so that fractional calculus is closely related to both, operational calculus and distribution theory.
Most mathematical implementations, interpretations and investigations of fractional calculus are concerned with ordinary functions as witnessed by recent reviews [3, 12,13,14] and numerous articles in this journal. A fractional calculus for certain generalized functions (distributions) appeared already with the concept of distributions itself in Schwartz’ monograph [5, p. 174]. It was later discussed in [15, Sec. I.5.5] and briefly in [16, Sec. 8.3] and [17, Sec. 2.9], but the “Schwartz fractional calculus” continues to receive little or no attention in most old and new books on fractional calculus and its applications [18,19,20,21,22,23,24]. Our objective in this review is to draw attention to Schwartz’ fractional calculus of distributions as an ideal framework for extending and unifying theory and applications of fractional calculus. Recall that fractional derivatives for functions are usually discussed only for sufficiently “good”, meaning smooth and integrable, functions [19, p. 237]. Extending the domain of definition from “good” functions to less good generalized functions (distributions), however, can make an otherwise unsolvable (fractional) equation solvable. More precisely, extending domains and co-domains can lead to an extended concept of solution by the following general mechanism [25].
Define a mapping \(A:X\rightarrow Y\) between two non-empty sets and consider the problem of solving the equation
for given \(g\in Y\). Equation (1.1) cannot have a solution \(f\in X\), unless \(g\in Y\) lies in the range of A. If, however, the domains X, Y can be extended to larger sets \(\widetilde{X},\widetilde{Y}\) into which f, g are suitably embedded, and if A can be extended to a surjective mapping \(\widetilde{A}:\widetilde{X}\rightarrow \widetilde{Y}\) such that
holds for the embedding \(f\rightarrow \widetilde{f}\), then, if g is the right hand side in eq. (1.1), the extended equation
has at least one (generalized or weak) solution \(u\in \widetilde{X}\), even when \(g\in Y\) is not in the range of A.
Generalized or weak formulations in this sense sometimes lead to unification of operators whereby previously different operators \(A_1,A_2,\ldots \) become restrictions to subdomains of one and the same extended operator \(\widetilde{A}\). Let \(f:[a,b]\rightarrow \mathbb {R}\) be a real-valued function on an interval \([a,b]\subseteq \mathbb {R}\). Operators of interest in this review are fractional derivatives and integrals  ,
,  of order \(\alpha \) and type \(\text {X} \) for which numerous different mathematical interpretations have been proposed in the literature [3, 18,19,20,21, 25,26,27,28,29,30,31,32]. Riemann-Liouville fractional integrals of order \(\alpha >0\) [33, 34] for real valued functions \(f:[a,b]\rightarrow \mathbb {R}\) on a closed interval \([a,b]\subset \mathbb {R}\) are a popular example of fractional integrals, and usually defined as [35, p. 566], [36, p. 181], [16, p. 33], [37, p. 6]
of order \(\alpha \) and type \(\text {X} \) for which numerous different mathematical interpretations have been proposed in the literature [3, 18,19,20,21, 25,26,27,28,29,30,31,32]. Riemann-Liouville fractional integrals of order \(\alpha >0\) [33, 34] for real valued functions \(f:[a,b]\rightarrow \mathbb {R}\) on a closed interval \([a,b]\subset \mathbb {R}\) are a popular example of fractional integrals, and usually defined as [35, p. 566], [36, p. 181], [16, p. 33], [37, p. 6]


It is common to choose

as the domain for these operators [16, 17, 19, 20, 37, 38] with \(L^{1}([a,b])\) the set of integrable functions \(f\!:\![a,b]\!\rightarrow \!\mathbb {R}\). An example for fractional derivatives are the closely related Riemann-Liouville fractional derivatives of order \(\alpha >0\) defined as


where  . Many domains
. Many domains  have been used in the literature [18, 19], a frequent, but by no means maximal, example being [16, p. 37]
have been used in the literature [18, 19], a frequent, but by no means maximal, example being [16, p. 37]

the space of functions such that \(f^{\left\lceil \llceil \alpha \right\rceil \rrceil }\) is absolutely continuous (see [12, 20, 21, 38]).
Riemann-Liouville fractional derivatives depend on the lower, resp. upper, limit of integration a, resp. b. Integer order derivatives, however, do not depend on such a parameter. This difference is fundamental. Integer order derivatives are translation invariant, meaning that they commute with translations, while Riemann-Liouville fractional derivatives are not.
Translation symmetry, i.e. invariance under translations in space and time, is a basic symmetry of nature [39, 40]. In theoretical physics it is closely related by Noethers theorem with the laws of energy and momentum conservation [41]. With respect to applications in physics it is therefore of interest to consider translation invariant fractional derivatives. From a purely mathematical point of view translation invariance is interesting, because it reduces the number of parameters.
Fractional calculus for distributions was introduced in a translation invariant formulation already in [5, p. 174], but has subsequently received little attention. Exceptions are [42, 15, Sec. I.5.5], [43, 29, p. 151] and [16, Sec.8.3]. Possible reasons for this negligence might be that multiplication of distributions is not defined in general [44], and that spaces of distributions tend to be locally convex while the focus was on fractional powers of operators on normed spaces [27, 45,46,47,48]. Later, in [27], fractional powers were extended abstractly to non-negative operators on Frechet spaces, but without providing concrete spaces of distributions for applications. In recent years the extension of fractional calculus from functions to measures [49, 50] and distributions [51,52,53,54,55] has found renewed interest.
A significant number of common interpretations and definitions for translation invariant fractional integrals and derivatives are unified in this review by defining them as convolution operators with power law monomials on spaces of distributions. Thus, the convolution interpretation turns out to be the most general approach to fractional calculus at present.
The present review is concerned mainly with asymmetric convolution kernels. Symmetric kernels, arising e.g. in Riesz-Feller operators or fractional powers of the Laplacian, can often be reduced to linear combinations of asymmetric kernels [16, Sec. 12.1]. Such kernels are mentioned briefly in Section 7.6.
To help readers navigating and finding quickly material of their interest we povide a structured overview of subsequent contents:
-
Section 2 Translation invariant Fractional Calculus for functions (\(\mathbb {R}^1\))
-
Section 3 Translation invariant Fractional Calculus for measures (\(\mathbb {R}^d\))
-
Section 4 Operational Calculus (\(\mathbb {R}^1\))
-
Section 5 Schwartz Fractional Calculus for distributions (\(\mathbb {R}^1\))
-
Section 6 Other approaches for distributions
-
Section 7 Generalized Schwartz Fractional Calculus for distributions
-
Section 8 Laplace multiplier approach for distributions
-
Section 9 Towards unification of Fractional Calculus
-
Section 10 Appendix
As seen above the review begins with operators for functions in Section 2, proceeds to measures in Section 3, then to generalized functions or “hyperfunctions” [56] in Section 4, and discusses fractional calculus for distributions in Sections 5, 6, 7, and 8. Section 7 is the centerpiece of this work. It reviews the generalization of Schwartz’s fractional calculus in [53,54,55] and provides new results for discrete distributional Grünwald-Letnikov fractional derivatives, for their continuum limit and for periodic distributions. Also, the fractional derivative and integral operators for Radon measures in Section 3, the Weyl fractional calculus extended to distributions in Section 6.1 and the Laplace multiplier approach in Section 8, apparently, have not been defined or discussed previously in the literature.
It seems appropriate to conclude this introduction with some remarks concerning applications, even if applications are decidedly outside the scope of this review. Distributional fractional calculus, as presented here, has recently been applied in studies of sequential generalized Riemann-Liouville fractional derivatives [57]. Generalized Riemann-Liouville fractional derivatives [58] are becoming increasingly popular for applications, not only in mathematics [59,60,61,62,63,64], but also in physics [65, 66], engineering [67] and beyond [68, 69], because their “type” parameter is crucial for formulating well-posed initial and boundary value problems. In another recent application of distributional fractional calculus to the linear response theory of dielectric relaxation in glasses [54] this “type” parameter was conjectured to cause the universal observation of nearly constant loss and high frequency excess wings in glasses [70,71,72]. The conjecture is relevant for the question what is the physical origin of the fractional order \(\alpha \). For applications in physics the interpretation and independent measurability of \(\alpha \) is of crucial importance [38, 73]. Spatial fractional derivatives, such as powers of the Laplacian, are plagued with unphysical predictions emerging already within fractional potential theory [74]. Until recently there were, to the best of our knowledge, only two interpretations of \(\alpha \), that are compatible with the fundamental laws (in particular the law of locality) in physics. Firstly, \(\alpha \) has been linked rigorously to critical exponents and the Ehrenfest order of phase transitions in [75, 76], where locality in space and time plays no role. Secondly, fractional time derivatives of order \(\alpha \) were related with anomalous diffusion and long time tails in continuous time random walks in [77,78,79] (semi-Markov processes) and with fractional time evolutions in [58, 80, 81]. The generalizations, unifications and simplifications in this review are hoped to directly generalize, unify and simplify such applications of fractional calculus.
2 Translation invariant fractional calculus for functions (\(\mathbb {R}^1\))
2.1 Liouville-Weyl
The earliest translation invariant formulation of fractional derivatives can be traced back to Liouville’s fractional derivative formula [33, p. 3,(1)]
for functions representable as
a series of exponentials. Liouville’s formula was used by Weyl [82, Satz 2] to define what could be called Liouville-Weyl fractional derivatives and integrals of trigonometric series [82, 83] as


where \(\alpha >0\) and
with \(k=\pm 1,\pm 2,\ldots \) and \(f_0=0\) is the Fourier series of f. The operators  are defined for functions \(f:\mathbb {R}/2\pi \mathbb {Z}\rightarrow \mathbb {C}\) on the unit circle \(\mathbb {G}=\mathbb {R}/2\pi \mathbb {Z}\) (\(2\pi \)-periodic functions on the real line) for which \(f_0=0\), i.e. for functions whose mean or integral over a period vanishes. Contrary to Riemann-Liouville integrals these definitions do not depend on an extra parameter such as a lower or upper limit of integration. A possible domain of definition is
are defined for functions \(f:\mathbb {R}/2\pi \mathbb {Z}\rightarrow \mathbb {C}\) on the unit circle \(\mathbb {G}=\mathbb {R}/2\pi \mathbb {Z}\) (\(2\pi \)-periodic functions on the real line) for which \(f_0=0\), i.e. for functions whose mean or integral over a period vanishes. Contrary to Riemann-Liouville integrals these definitions do not depend on an extra parameter such as a lower or upper limit of integration. A possible domain of definition is

of periodic Lebesgue integrable functions with norms
where \(1\le p<\infty \). The domain

can be used for Liouville-Weyl derivatives.
2.2 Weyl
Recall the formula for convolution of two \(2\pi \)-periodic functions [83, p. 36]
which gives rise to the Weyl fractional integral for periodic functions

on \(L^{p}_{2\pi }\) with \(p\in [1,\infty [\) where

is Weyl’s kernel function from [82, p. 300]. The series is convergent for all \(x\in (0,2\pi )\), \(\alpha >0\), and uniformly convergent for \(\varepsilon \le x\le 2\pi -\varepsilon ,\varepsilon >0\), so that it represents the Fourier series of  .
.
It can be shown [83] that eq. (2.10) coincides with the Riemann-Liouville definition (1.4) for \(a=-\infty \) resp. \(b=\infty \). For this reasonFootnote 1 the Riemann-Liouville fractional integral  resp.
resp.  with infinite limits \(\pm \infty \) is traditionally called a Weyl fractional integral [82, p. 300], [35, p. 567], [85, 36, 16, p. 353], [37, p. 7]. For \(\alpha >0\) and non-periodic functions \(f:\mathbb {R}\rightarrow \mathbb {C}\) the Weyl fractional integral is defined as
with infinite limits \(\pm \infty \) is traditionally called a Weyl fractional integral [82, p. 300], [35, p. 567], [85, 36, 16, p. 353], [37, p. 7]. For \(\alpha >0\) and non-periodic functions \(f:\mathbb {R}\rightarrow \mathbb {C}\) the Weyl fractional integral is defined as

where \(x\in \mathbb {R}\) and \({\Gamma }\) is the Gamma function. The Weyl integral is translation invariant. Interpreting the Weyl integral (2.12) as an absolutely convergent Lebesgue integral, the maximal domain of locally integrable functions is given by

In the context of Weyl’s considerations the integral (2.12) is considered as an improper integral in the upper limit, resulting in the maximal domain

which contains periodic functions for \( 0< \alpha < 1 \). This domain was explicitly considered in [86, p. 116].
Let \(\text {D} ^k=\text {d} ^k/\text {d} x^k\) denote the derivative of integer order \(k\in \mathbb {N}\). The Weyl fractional derivative of order \(\alpha >0\) is defined by

where  is the smallest integer above \(\beta \in \mathbb {R}\). Choosing the set of absolutely continuous functions
is the smallest integer above \(\beta \in \mathbb {R}\). Choosing the set of absolutely continuous functions  as the domain of definition for the derivative \(\text {d} /\text {d} x\), the domain
as the domain of definition for the derivative \(\text {d} /\text {d} x\), the domain

is obtained by  -fold iteration as the domain for partially defined operators.Footnote 2 Note that for \(\alpha \notin \mathbb {N}_0\) the constant function \(x\mapsto c\) is not contained in the domain of the Weyl fractional derivative
-fold iteration as the domain for partially defined operators.Footnote 2 Note that for \(\alpha \notin \mathbb {N}_0\) the constant function \(x\mapsto c\) is not contained in the domain of the Weyl fractional derivative  .
.
Weyl fractional derivatives and integrals have also been studied on the Hölder spaces  [16, Sec. 19.6]. Essentially, fractional integrals, resp. derivatives, of order \(\alpha >0\) increase, resp. decrease, the Hölder order \(\beta \) by \(\alpha \).
[16, Sec. 19.6]. Essentially, fractional integrals, resp. derivatives, of order \(\alpha >0\) increase, resp. decrease, the Hölder order \(\beta \) by \(\alpha \).
2.3 Marchaud
A larger domain of definition than for Weyl fractional derivatives is obtained for Marchaud fractional derivatives [87]. Let \(0<\alpha <\infty \), \(\alpha \notin \mathbb {N}\), and introduce the notation  for \(x\in \mathbb {R}\). The Marchaud fractional derivative is defined as
for \(x\in \mathbb {R}\). The Marchaud fractional derivative is defined as

for all \(t\in \mathbb {R}\), where

and the right differences of order \(m\in \mathbb {N}\) and step size \(s>0\) are

for all \(t\in \mathbb {R}\).
A possible choice for the domain is

and it depends explicitly on \(\alpha \). This domain contains the constant function.
2.4 Grünwald-Letnikov
For \(\alpha >0\) the Grünwald-Letnikov fractional derivative [88, 89] of a function \(f:\mathbb {R}\rightarrow \mathbb {R}\) is defined as

by generalizing the integer order difference quotients from eq. (2.19) to fractional orders. A suitable domain is [16, p. 382]

for any \(1\le p<\infty \). For \(0<\alpha <1\) it was shown in [16, Thm. 20.4] that on this domain the Grünwald-Letnikov fractional derivative  coincides with the Marchaud derivative
coincides with the Marchaud derivative  . An analogous result is obtained in [90] for the Hölder spaces
. An analogous result is obtained in [90] for the Hölder spaces  .
.
Here, in Section 7.4 below, these results for functions are extended and generalized to distributions. It is found that the maximal domains of Marchaud derivatives and Grünwald-Letnikov derivatives for distributions nearly coincide. As shown in Section 9.3, where a weak formulation for fractional derivatives of distributions is introduced, differences may only arise from the fact that  is defined as a pointwise limit, while
is defined as a pointwise limit, while  is defined by a Lebesgue integral.
is defined by a Lebesgue integral.
Similar to the Marchaud case  contains the constant function, but does not contain the Heaviside step function or the Dirac distribution.
contains the constant function, but does not contain the Heaviside step function or the Dirac distribution.
2.5 Liouville-Grünwald
The Weyl calculus for periodic functions has been related rigorously in [37, 91] to the Grünwald-Letnikov approach [88, 89] on the Lebesgue spaces \(L^{p}_{2\pi }\) of periodic functions defined above. These Banach spaces, as well as the space

of continuous \(2\pi \)-periodic functions with norm

were used in [37, 91] to characterize the strong Liouville-Grünwald fractional derivatives. Let \(1\le p<\infty \) and \(\alpha >0\). The strong Liouville-Grünwald fractional derivative of order \(\alpha \) with domain

resp.

is defined as that function

for which the limit

exists. Because  it can be used to define the Liouville-Grünwald fractional integral
it can be used to define the Liouville-Grünwald fractional integral

on  with \(p\in [1,\infty [\) such that
with \(p\in [1,\infty [\) such that

for all \(f\in L^{p}_{2\pi }\). Note that  has a convolution kernel
has a convolution kernel  .
.
Theorem 1
(Thm 3.4, [37]) The following three assertions are equivalent for \(f\in L^{p}_{2\pi }\), \(1\le p<\infty \) and \(\alpha >0\):
-
a)
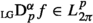 .
. -
b)
There exists \(g\in L^{p}_{2\pi }\) such that \((\text {i} k)^\alpha f_k=g_k\), \(k\in \mathbb {Z}\).
-
c)
There exists \(g\in L^{p}_{2\pi }\) such that
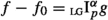 almost everywhere.
almost everywhere.
Here \(f_k,g_k\) are the Fourier coefficients of f, g as defined in (2.5). The following three properties hold for \(f\in L^{p}_{2\pi }\), \(\alpha ,\beta >0\):
-
A)
(Monotonicity)
If
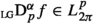 , then
, then 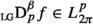 for any \(0<\beta <\alpha \).
for any \(0<\beta <\alpha \). -
B)
(Additivity)
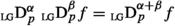 whenever one of the two sides is meaningful.
whenever one of the two sides is meaningful. -
C)
(Fundamental theorem of fractional calculus)
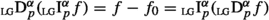 where the second equality holds if
where the second equality holds if 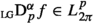 .
.
The Liouville-Grünwald fractional calculus and its applications are further developed in [37, 92,93,94] (see [37] and references therein).
3 Translation invariant fractional calculus for measures (\(\mathbb {R}^d\))
Common domains of definition for translation invariant fractional integrals and derivatives of functions are often small and their intersection may be too small for applications. For this reason an extension of translation invariant fractional calculus from functions to measures was initiated in [49, 50] for the case of Weyl fractional integrals. It was later superseded and unified with the distributional fractional calculus of Section 7 below. The present section reviews some results and ideas from this initial approach in [49, 50] by placing them into the distributional context.
3.1 Radon measures
Let \(1\le p\le \infty \) and let \(\mathfrak {K}\) denote the family of compact subsets of \(\mathbb {R}^d\). The indicator function \(1_\Omega :\Omega \rightarrow \mathbb {R}\) of a set \(\Omega \subseteq \mathbb {R}^d\) is defined by
The notation \(\mathbb {R}^{\Omega }\) is used for the set of real (or sometimes complex) valued functions \(f:\Omega \rightarrow \mathbb {R}\). The Lebesgue space of locally p-integrable functions \(L^{p}_{\text {loc} }(\mathbb {R}^d)\) consists of the measurable functions \(f:\mathbb {R}^d\rightarrow \mathbb {R}\) such that \(f\cdot 1_K\in L^{p}(\mathbb {R}^d)\) for all \(K\in \mathfrak {K}\). It is endowed with the topology generated by the seminorms \(f\mapsto \Vert f\cdot 1_K\Vert _p\) with \(K\in \mathfrak {K}\). The space  of continuous functions is endowed with the subspace topology inherited from \(L^{p}_{\text {loc} }(\mathbb {R}^d)\). The spaces of continuous functions with compact support are defined by
of continuous functions is endowed with the subspace topology inherited from \(L^{p}_{\text {loc} }(\mathbb {R}^d)\). The spaces of continuous functions with compact support are defined by


for any compact set \(K\subseteq \mathbb {R}^d\). The topology on every  is the subspace topology induced from
is the subspace topology induced from  . The locally convex topology on the union
. The locally convex topology on the union  is generated by all seminorms on
is generated by all seminorms on  that have a continuous restriction to
that have a continuous restriction to  .
.
The spaces  ,
,  and \(L^{p}_{\text {loc} }(\mathbb {R}^d)\) are vector lattices (or Riesz spaces) with respect to pointwise (almost everywhere) ordering [95, 96]. Lattice orderings \(\le \) are characterized by the existence of supremum and infimum for any two of its elements. For any x in a vector lattice its absolute value is defined as \(|x|:=\sup \{x,-x\}\).
and \(L^{p}_{\text {loc} }(\mathbb {R}^d)\) are vector lattices (or Riesz spaces) with respect to pointwise (almost everywhere) ordering [95, 96]. Lattice orderings \(\le \) are characterized by the existence of supremum and infimum for any two of its elements. For any x in a vector lattice its absolute value is defined as \(|x|:=\sup \{x,-x\}\).
The locally convex space of Radon measures is defined as the topological dual space

endowed with the  -topology (see Section 10.2). Because the dual of a locally convex vector lattice is again a vector lattice (see Proposition 4.17 in [95, p. 108]) the space
-topology (see Section 10.2). Because the dual of a locally convex vector lattice is again a vector lattice (see Proposition 4.17 in [95, p. 108]) the space  of Radon measures is again a locally convex vector lattice under the dual ordering, i.e.
of Radon measures is again a locally convex vector lattice under the dual ordering, i.e.  satisfy \(\mu \le \nu \) iff \(\mu (\varphi )\le \nu (\varphi )\) for all \(\varphi \ge 0\). Thus, \(|\mu |\) exists for all
satisfy \(\mu \le \nu \) iff \(\mu (\varphi )\le \nu (\varphi )\) for all \(\varphi \ge 0\). Thus, \(|\mu |\) exists for all  and the topology on
and the topology on  is generated by the seminorms \(\mu \mapsto |\mu (\varphi )|\) with
is generated by the seminorms \(\mu \mapsto |\mu (\varphi )|\) with  . The set of real valued Radon measures is a real vector lattice. From this one obtains the Riesz decomposition theorem
. The set of real valued Radon measures is a real vector lattice. From this one obtains the Riesz decomposition theorem  where
where  .
.
3.2 Integration with respect to Radon measures
The evaluation of a Radon measure  on a function
on a function  is written as integration of \(\varphi \) with respect to \(\mu \)
is written as integration of \(\varphi \) with respect to \(\mu \)

and this continuous linear functional can be extended uniquely to more general real valued functions using the “upper” and “lower” integrals from [97, 98, 99, Ch.XI], [100, Sec. 3.2]. Recall, that a function \(f:\mathbb {R}^d\rightarrow [0,+\infty ]\) is lower semicontinuous, if the set \(\{f\ge a\}\) is closed for every \(a\in [0,\infty ]\). The set of lower semicontinuous functions is denoted as  . Let
. Let


denote the set of upper envelopes, where “sup” is the pointwise supremum of \([-\infty ,+\infty ]\)-valued functions. The last equality then allows to extend \(\mu \) from  to upper envelopes by
to upper envelopes by

for all  . The upper \(\mu \)-integral \(\mu ^*(f)\) and the lower \(\mu \)-integral \(\mu _*(f)\) of a function \(f:\mathbb {R}^d\rightarrow [-\infty ,+\infty ]\) are defined as
. The upper \(\mu \)-integral \(\mu ^*(f)\) and the lower \(\mu \)-integral \(\mu _*(f)\) of a function \(f:\mathbb {R}^d\rightarrow [-\infty ,+\infty ]\) are defined as


and f is called \(\mu \)-integrable or integrable with respect to \(\mu \) if
that is, the upper and lower integrals agree.
Accordingly, the domain for integration with respect to \(\mu \) is the space of \(\mu \)-integrable real valued functions, defined as

Let

be the space of functions that vanish \(\mu \)-almost everywhere. Equipped with the norm \(f\mapsto \mu (|f|)\) the quotient space

becomes a Banach space. The definition can be extended to signed Radon measures and complex functions.
The space \(L^{1}_{\text {loc} }(\mathbb {R}^d)\) can be identified with a closed subspace of  by associating to every \(f\in L^{1}_{\text {loc} }(\mathbb {R}^d)\) the measure \(\mu _f\) defined by
by associating to every \(f\in L^{1}_{\text {loc} }(\mathbb {R}^d)\) the measure \(\mu _f\) defined by
for all  . It is equipped with the subspace topology inherited from
. It is equipped with the subspace topology inherited from  via the map \(f\mapsto \mu _f\). The introduced spaces are then related by a chain
via the map \(f\mapsto \mu _f\). The introduced spaces are then related by a chain

of continuous inclusions where \(1\le p\le q\le \infty \).
3.3 Convolution of Radon measures
The convolution of two locally integrable functions \(f,g\in L^{1}_{\text {loc} }(\mathbb {R}^d)\) is commonly defined pointwise in the almost everywhere sense as
for \(x\in \mathbb {R}^d\), if it exists. This is guaranteed in the most common case \( f,g\in L^{1}(\mathbb {R}^d) \). Reformulated weakly for the corresponding measures \(\mu _f,\mu _g\) from eq. (3.11) and  this becomes with Fubini’s theorem
this becomes with Fubini’s theorem
where \(\mu _f\otimes \mu _g\) is the product measure,  is the codiagonal function defined as
is the codiagonal function defined as
and the mapping \(\triangle :\mathbb {R}^d\times \mathbb {R}^d\rightarrow \mathbb {R}^d\) with
denotes addition in \(\mathbb {R}^d\).
The  -convolution of two Radon measures
-convolution of two Radon measures  is defined as the image of their product measure under \(\triangle \),
is defined as the image of their product measure under \(\triangle \),
whenever \(\mu ,\nu \) are convolvable or, equivalently, whenever

for  . Two measures
. Two measures  are called convolvable if and only if
are called convolvable if and only if  or, equivalently,
or, equivalently,
for all  with \(\varphi \ge 0\). The image of a measure under a continuous mapping is defined generally in [97, Ch. V, §6, No. 4, Def. 2]. Here, for
with \(\varphi \ge 0\). The image of a measure under a continuous mapping is defined generally in [97, Ch. V, §6, No. 4, Def. 2]. Here, for  and a continuous mapping \(m:\mathbb {R}^{2d}\rightarrow \mathbb {R}^d\) it is \((m\mu )(\varphi ):=\mu (\varphi \circ m)\),
and a continuous mapping \(m:\mathbb {R}^{2d}\rightarrow \mathbb {R}^d\) it is \((m\mu )(\varphi ):=\mu (\varphi \circ m)\),  whenever \(|\mu |(\varphi \circ m)<\infty \) for all \(\varphi \ge 0\).
whenever \(|\mu |(\varphi \circ m)<\infty \) for all \(\varphi \ge 0\).
Proposition 1
Let \(f,g\in L^{1}_{\text {loc} }(\mathbb {R}^d)\). Then \(\mu _f\) and \(\mu _g\) are  -convolvable if and only if
-convolvable if and only if
-
1)
\((f*g)(x)\) is well defined by equation (3.13) for almost all \(x\in \mathbb {R}^d\) in terms of a Lebesgue integral and
-
2)
\(f*g\in L^{1}_{\text {loc} }(\mathbb {R}^d)\).
If \(\mu _f\) and \(\mu _g\) are  -convolvable, then one has \(\mu _f*\mu _g=\mu _{f*g}\).
-convolvable, then one has \(\mu _f*\mu _g=\mu _{f*g}\).
Proof
Follows from eq. (3.14).
\(\square \)
3.4 Convolution duals and extremal domains
In [49, 50] a constructive method was introduced to define weighted measure spaces on which a given set of convolution operators acts as an equicontinuous family of endomorphisms. The constructive method was later extended to distributions. For \(d=1\) this method was applied in [50, Sec. 9] to linear combinations of fractional Weyl integrals and derivatives with orders and coefficients from a bounded set.
The constructive method is based on the convolution dual  of a set
of a set  of measures defined as [49, 101, 102]
of measures defined as [49, 101, 102]

By construction  is a polarity in the sense of [103, V. 7, p. 122]. Thus the convolution perfection operator
is a polarity in the sense of [103, V. 7, p. 122]. Thus the convolution perfection operator

is a closure operator [103, p. 105, p. 116–120]. The corresponding closures are called convolution perfect. It follows from the definitions that

is a well defined bilinear mapping. Within the class of convolution perfect spaces, convolution operators with kernels from F have maximal domain  and are embedded in the minimal space
and are embedded in the minimal space  .
.
The construction (3.21) does not necessarily give domains on which the convolution operators with kernels from F map  into itself. To construct endomorphic domains the concepts of simultaneous convolution of p-tuples and maximal convolution modules were introduced.
into itself. To construct endomorphic domains the concepts of simultaneous convolution of p-tuples and maximal convolution modules were introduced.
Definition 1
For  the maximal convolution module associated with F is defined as
the maximal convolution module associated with F is defined as

Systematic investigation of  and
and  was carried out in [55] for the more general case of distributions. It resulted in a calculus for convolution perfect spaces as extremal domains of definition (or operation) for convolution operators. The main problem solved by the calculus for convolution perfect spaces is to find extremal and convolution perfect domains
was carried out in [55] for the more general case of distributions. It resulted in a calculus for convolution perfect spaces as extremal domains of definition (or operation) for convolution operators. The main problem solved by the calculus for convolution perfect spaces is to find extremal and convolution perfect domains  ,
,  , and
, and  for inclusion relations such as
for inclusion relations such as
A detailed description in this review would lead too far afield. Instead we mention only Theorem 5 from [49, p. 1561] in the next paragraph.
Let \(u,v,w:\mathbb {R}^d\rightarrow \mathbb {R}_{+}\) be three upper semicontinuous and positive weight functions. Given a weight w define two weighted balls


of measures, respectively for functions. Let \({\circledast }\) denote supremal convolution defined for \(0\le f\in L^{\infty }_{\text {loc} }(\mathbb {R}^d)\) and \(0\le g\in L^{\infty }_{\text {loc} }(\mathbb {R}^d)\) pointwise as

with \((\text {T} _xf)(y)=f(y-x)\) defining translation by x. Theorem 5 in [49, p. 1561] characterizes inclusion relations

between weighted balls in terms of an inequality between the weight functions, that is important for the investigations described in Section 6.1. The proof uses the triangle inequality for Radon measures: Two Radon measures \(\mu ,\nu \) are  -convolvable if and only if their absolute values are convolvable. And in that case \(|\mu *\nu |\le |\mu |*|\nu |\) holds true.
-convolvable if and only if their absolute values are convolvable. And in that case \(|\mu *\nu |\le |\mu |*|\nu |\) holds true.
3.5 Fractional derivatives and integrals for Radon measures
For \(\alpha \in \mathbb {H}\) let  denote the monomial measure with Lebesgue density
denote the monomial measure with Lebesgue density
Let  and \(\alpha =(\alpha _1,\ldots ,\alpha _d)\in \mathbb {C}^d\). The fractional integral of a Radon measure \(\mu \) is defined as the convolution
and \(\alpha =(\alpha _1,\ldots ,\alpha _d)\in \mathbb {C}^d\). The fractional integral of a Radon measure \(\mu \) is defined as the convolution

where the  denotes the reflected measure. Thus
denotes the reflected measure. Thus

for \(\alpha \in \mathbb {C}\).
4 Operational Calculus (\(\mathbb {R}^1\))
Operational calculus was initiated by Leibniz [6] and investigated in the 18th and 19th century by Lagrange, Bernoulli, Laplace, Lorgna, Gruson, Arbogast, Francais, Servois, Oltramare, Liouville, Cauchy, Boole and many others (see [104] for a historical account). Symbolic computation with operational symbols was also practiced by physicists and engineers in the early 20th century [6, 9,10,11, 105] and this motivated Mikusinski [7] and Schwartz [4]. For reviews of operational calculus see [8, 56, 106,107,108,109,110].
Operational calculus is usually formulated for continuous real- or complex-valued continuous functions  on the half-axis \(\mathbb {R}_{0+}=[0,\infty [\). Let \(a\in \mathbb {C}\), \(t\in \mathbb {R}_{0+}\) and
on the half-axis \(\mathbb {R}_{0+}=[0,\infty [\). Let \(a\in \mathbb {C}\), \(t\in \mathbb {R}_{0+}\) and  . Then
. Then  becomes a commutative ring with the operations
becomes a commutative ring with the operations
of scalar multiplication, addition, and convolution  of f and g.
of f and g.
The ring  has no divisors of zero due to a theorem by Titchmarsh [111, Thm 152, p.325] : If f, g are locally integrable and \(f*g=0\), then either \(f=0\) or \(g=0\). As a consequence,
has no divisors of zero due to a theorem by Titchmarsh [111, Thm 152, p.325] : If f, g are locally integrable and \(f*g=0\), then either \(f=0\) or \(g=0\). As a consequence,  is an integral domain [112, p. 115] and can be extended to a field
is an integral domain [112, p. 115] and can be extended to a field  of quotients in the same way as integers are extended to rationals [113, p. 110].
of quotients in the same way as integers are extended to rationals [113, p. 110].
The elements of the quotient field \(Q\) are equivalence classes of ordered pairs, denoted as \((f:\!\!\!/\!\!\!:g)\), representing a convolution numerator f over a convolution denominator \(g\ne 0\). Two convolution quotients \((f_1:\!\!\!/\!\!\!:g_1)\) and \((f_2:\!\!\!/\!\!\!:g_2)\) are equivalent if the relation
holds for all \(g_1,g_2\ne 0\). The multiplication of a pair with numbers \(a\in \mathbb {C}\) is defined such that
holds for all pairs  . The addition and multiplication of pairs is defined such that
. The addition and multiplication of pairs is defined such that
holds for all  . The neutral element for the multiplication \(\times \) of pairs is the pair
. The neutral element for the multiplication \(\times \) of pairs is the pair  . It is not a continuous function and resembles the generalized \(\updelta \)-function. Because the elements in
. It is not a continuous function and resembles the generalized \(\updelta \)-function. Because the elements in  are sets, they are usually called “operators” [108] and sometimes “hyperfunctions” [56]. The two mappings
are sets, they are usually called “operators” [108] and sometimes “hyperfunctions” [56]. The two mappings


are embeddings of \(\mathbb {C}\), resp.  , into
, into  . Obviously, scalar multiplication \(a(f:\!\!\!/\!\!\!:g)\ne a \times (f:\!\!\!/\!\!\!:g)=a 1\times (f:\!\!\!/\!\!\!:g)= a(1*f:\!\!\!/\!\!\!:g)\) is not the same as multiplication with a constant function.
. Obviously, scalar multiplication \(a(f:\!\!\!/\!\!\!:g)\ne a \times (f:\!\!\!/\!\!\!:g)=a 1\times (f:\!\!\!/\!\!\!:g)= a(1*f:\!\!\!/\!\!\!:g)\) is not the same as multiplication with a constant function.
The relevance of the ring  and its quotient field
and its quotient field  for fractional calculus emerges from choosing for f and g in (4.1c) the constant function \(f=1\), defined by \(f(t)=1\) for all \(t\in [0,\infty [\). One has \(1*1=t\) and
for fractional calculus emerges from choosing for f and g in (4.1c) the constant function \(f=1\), defined by \(f(t)=1\) for all \(t\in [0,\infty [\). One has \(1*1=t\) and
by iteration. Choosing \(f=1\) in (4.1c) shows
which identifies convolution with \(f=1\) as the operator of integration.
The operator of fractional integration in operational calculus is then defined by extending iterated convolution with 1 to noninteger n as

with domain

for \(\text {Re} \alpha >0\).
The definition of fractional integration can be extended to all \(\alpha \in \mathbb {C}\) as convolution with the convolution quotient
where \(n=(\left\lfloor \text {Re} \alpha \right\rfloor -1)\) is the smallest positive integer such that \(\text {Re} \alpha +n>1\). For \(\alpha =-1\) one finds
and this is interpreted as the operator of differentiation. The fractional derivative operators are

with domain

by virtue of the embedding (4.4a).
The construction of the quotient field  is quite general. It can be carried out for other spaces such as the space of locally integrable functions \(L^{1}_{\text {loc} }(\mathbb {R}_{0+})\) or distributions
is quite general. It can be carried out for other spaces such as the space of locally integrable functions \(L^{1}_{\text {loc} }(\mathbb {R}_{0+})\) or distributions  on the half axis. One has the algebra isomorphism [114]
on the half axis. One has the algebra isomorphism [114]

relating operational calculus with Schwartz distributional calculus. On the other hand, the construction of  has also a few disadvantages:
has also a few disadvantages:
-
(i)
Although every function in the ring
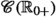 also represents an operator (because it can be represented as \((f*b~:\!\!\!/\!\!\!:~ b)\) with \(b\ne 0\)) not every operator in the quotient field corresponds to a function.
also represents an operator (because it can be represented as \((f*b~:\!\!\!/\!\!\!:~ b)\) with \(b\ne 0\)) not every operator in the quotient field corresponds to a function. -
(ii)
Generalization of the fundamental equation (4.1c) from \(d=1\) to higher dimension is not straightforward, because of the difficulty to specify what happens at the boundary.
5 Schwartz fractional calculus for distributions (\(\mathbb {R}^1\))
The first fractional calculus for distributions was introduced together with the theory of distributions [5, 15, 115] as an application of defining the convolution of distributions [5, p. 174] . Let \(\alpha \in \mathbb {C}\), \(x\in \mathbb {R}\) and
be the Heaviside step function. For \(x\in \mathbb {R}\) define
and its reflection  . This definition is extended as
. This definition is extended as

to \(\alpha \in \mathbb {C}\). Here \(\text {D} ^k\) is the distributional derivative of order k. Note that \(\text {Y} _{1}=\Theta \), that \(\text {Y} _{0}=\text {D} \Theta =\updelta \) is the Dirac distribution, and that \(\text {Y} _{-k}=\text {D} ^{1+k}\Theta =\updelta ^{(k)}\) their k-th derivative for \(k\in \mathbb {N}\). The abbreviation \(\text {Y} =\text {Y} _{1}\) will also be employed. The symbol \(\text {Y} _{\alpha }\) is the notation from [5, p. 43] while it is denoted as \(\Phi _\alpha \) in [15, p. 48]. The notation \(\chi _+^\alpha \) is used in [116, p. 73] and the authors used \(\text {p} _+^\alpha \) for \(\text {Y} _{\alpha }\) and \(\text {q} _+^\alpha \) for \(\text {Y} _{-\alpha }\) in Definition 1 in [54].
The idea is now to define fractional derivatives as convolution with the monomial distribution \(\text {Y} _{\alpha }\) as kernel in analogy with operational calculus. Let \(\alpha \in \mathbb {C}\). The Schwartz fractional derivative is defined as [5, p. 172]

for distributions f in the set

of distributions bounded on the left, also called “causal distributions”. Note that the domain is independent of \(\alpha \). Analogously, a reflected operator  is defined for anticausal distributions.
is defined for anticausal distributions.
The convolution of two locally integrable functions \(f,g\in L^{1}_{\text {loc} }(\mathbb {R})\) is given by eq. (3.13) with \(d=1\). This definition can be extended to distributions along the same lines as the extension to measures discussed above in Section 3.3.
Given two test functions  their tensor product is the bilinear mapping
their tensor product is the bilinear mapping  that assigns to every pair of functions \((\varphi ,\psi )\) the function \((x,y)\mapsto \varphi (x)\psi (y)\). The tensor product of two distributions
that assigns to every pair of functions \((\varphi ,\psi )\) the function \((x,y)\mapsto \varphi (x)\psi (y)\). The tensor product of two distributions  is the unique distribution
is the unique distribution  which satisfies
which satisfies
for all  . The problem with using eq. (3.14) as a definition for convolution of distributions is that \(\varphi ^\triangle \) is smooth, but in general not a test function, i.e.
. The problem with using eq. (3.14) as a definition for convolution of distributions is that \(\varphi ^\triangle \) is smooth, but in general not a test function, i.e.  , because it does not have compact support. Figure 1 illustrates \(\texttt {supp}\varphi ^\triangle \) for a test function with \(\texttt {supp}\varphi = [a,b]\).
, because it does not have compact support. Figure 1 illustrates \(\texttt {supp}\varphi ^\triangle \) for a test function with \(\texttt {supp}\varphi = [a,b]\).
Illustration of \(\texttt {supp}\varphi ^\triangle \) for \(\texttt {supp}\varphi =[a,b]\) and of convolvability by support (condition (2) below) for distributions  . The set \(\texttt {supp}\varphi ^\triangle \) is textured by north east lines, \(\texttt {supp}f\) is textured by horizontal lines, and \(\texttt {supp}g\) is textured by vertical lines
. The set \(\texttt {supp}\varphi ^\triangle \) is textured by north east lines, \(\texttt {supp}f\) is textured by horizontal lines, and \(\texttt {supp}g\) is textured by vertical lines
The problem is circumvented by using a cutoff function  to cut off the integrand. In other words, given \(\varphi \) a cutoff function \(\chi _\varphi \) is chosen such that \(\{\chi _\varphi =1\}\supseteq \texttt {supp}((f\otimes g)\cdot \varphi ^\triangle )\). Note, that such a cutoff cannot be found for all pairs of distributions
to cut off the integrand. In other words, given \(\varphi \) a cutoff function \(\chi _\varphi \) is chosen such that \(\{\chi _\varphi =1\}\supseteq \texttt {supp}((f\otimes g)\cdot \varphi ^\triangle )\). Note, that such a cutoff cannot be found for all pairs of distributions  . If a cutoff function can be found, then f, g are called convolvable by support. If
. If a cutoff function can be found, then f, g are called convolvable by support. If  are convolvable by support, then their convolution is defined by
are convolvable by support, then their convolution is defined by
for  . Two distributions
. Two distributions  are convolvable by support if and only if
are convolvable by support if and only if

for  . This is the most common definition of convolution of distributions, which can be found up to details in [116, 117]. For example, convolvability by support is guaranteed,
. This is the most common definition of convolution of distributions, which can be found up to details in [116, 117]. For example, convolvability by support is guaranteed,
-
(1)
if
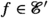 or
or 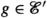 , or
, or -
(2)
if
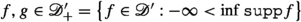 .
.
The set  with the operations of addition and convolution
with the operations of addition and convolution  becomes a convolution algebra without divisors of zero [5, Thm. XIV, p. 173]. Thus, the algebra
becomes a convolution algebra without divisors of zero [5, Thm. XIV, p. 173]. Thus, the algebra  in distribution theory resembles the algebra
in distribution theory resembles the algebra  in operational calculus.
in operational calculus.
While  contains the \(\updelta \)-distribution, \(\text {Y} _{\alpha }\) and the Heaviside function, it does not contain the constant function or the trigonometric functions. Some authors maintain that fractional derivatives of integer powers \(x\mapsto x^n, n\in \mathbb {N}\) cannot exist [118, p. 24, Sec. 3.5.2], [119, Sec. 2.3].
contains the \(\updelta \)-distribution, \(\text {Y} _{\alpha }\) and the Heaviside function, it does not contain the constant function or the trigonometric functions. Some authors maintain that fractional derivatives of integer powers \(x\mapsto x^n, n\in \mathbb {N}\) cannot exist [118, p. 24, Sec. 3.5.2], [119, Sec. 2.3].
Schwartz calculus on the half axis, i.e. on  , was applied to a convolution operator with nonsingular kernel in [120], and has been extended to the cone \(\mathbb {R}_{0+}^d\) in [52]. The well known results from [15] were recently repeated in [121].
, was applied to a convolution operator with nonsingular kernel in [120], and has been extended to the cone \(\mathbb {R}_{0+}^d\) in [52]. The well known results from [15] were recently repeated in [121].
6 Other approaches for distributions
6.1 Method of adjoints
A useful method to define fractional derivatives for distributions is the method of adjoints or transposition [42, 122, 123]. Let \((X,\uptau _X),(Y,\uptau _Y)\) be two locally convex Hausdorff spaces endowed with topologies \(\uptau _X,\uptau _Y\) and let \(X^\prime ,Y^\prime \) be their topological duals. Let \(A:X\rightarrow Y\) be a linear operator. Its adjoint or transpose  is the operator defined by the relation
is the operator defined by the relation

The vector \( ^tAf\) is defined as that linear functional on X, which assigns to each \(\varphi \in X\) the same number, that the functional \(f\in Y^\prime \) assigns to \(A\varphi \). If \(A:(X,\uptau _X)\rightarrow (Y,\uptau _Y)\) is continuous, then also \(A:(X,\sigma (X,X^\prime ))\rightarrow (Y,\sigma (Y,Y^\prime ))\) is continuous, i.e when the spaces are endowed with the weak topologies \(\sigma (X,X^\prime )\) and \(\sigma (Y,Y^\prime )\). Morover, if A is continuous, then the adjoint operator is continuous  ) in the weak and the strong topology, i.e. as a map
) in the weak and the strong topology, i.e. as a map  ) [117, p. 256] [124, eq.(3.23)][25, p. 7]. When A is a fractional operator and X, Y are space of test functions, then
) [117, p. 256] [124, eq.(3.23)][25, p. 7]. When A is a fractional operator and X, Y are space of test functions, then  is a fractional operator for distributions.
is a fractional operator for distributions.
The method of adjoints (6.1) can be used to extend Weyl fractional integrals  with \(\alpha \in \mathbb {H}\) and derivatives
with \(\alpha \in \mathbb {H}\) and derivatives  with \(\alpha \in \mathbb {C}\) to certain weighted space of distributions. This will now be illustrated in this section.
with \(\alpha \in \mathbb {C}\) to certain weighted space of distributions. This will now be illustrated in this section.
In [49, 50, 125] the Weyl operators  and
and  were discussed as continuous endomorphisms of certain weighted spaces of continuous or smooth functions. The results were characterized using the equivalence (3.27). For \(k\in \mathbb {N}_0\cup \{\infty \}\) and a set W of weights with
were discussed as continuous endomorphisms of certain weighted spaces of continuous or smooth functions. The results were characterized using the equivalence (3.27). For \(k\in \mathbb {N}_0\cup \{\infty \}\) and a set W of weights with  define
define

with  and
and  . These spaces are endowed with the locally convex topology generated by the seminorms \(f\mapsto \Vert f^{(m)}w\Vert _\infty \) with \(w\in W,m\in \mathbb {N}_0\). Let the supremal convolution dual for a set
. These spaces are endowed with the locally convex topology generated by the seminorms \(f\mapsto \Vert f^{(m)}w\Vert _\infty \) with \(w\in W,m\in \mathbb {N}_0\). Let the supremal convolution dual for a set  of weights be denoted as (see (3.26) for the definition of \(\circledast \))
of weights be denoted as (see (3.26) for the definition of \(\circledast \))

In the notation of [50, eqs. (2.3), (4.1), (9.1)] the set  corresponds to the intersection of
corresponds to the intersection of  with the expression “
with the expression “ ” in [50, p. 1246]. With notations similar to [50, pp. 1245] one denotes \(P:=\left\langle \left( 1+x^2\right) ^n:n\in \mathbb {N} \right\rangle _{\texttt {tici}}\) and
” in [50, p. 1246]. With notations similar to [50, pp. 1245] one denotes \(P:=\left\langle \left( 1+x^2\right) ^n:n\in \mathbb {N} \right\rangle _{\texttt {tici}}\) and  (compare also (7.25a) below for \(d=1\)). Then
(compare also (7.25a) below for \(d=1\)). Then  and
and  .
.
Retracing the steps in [50, Sec. 11] it can be shown that \(P_-\circledast W\subseteq W\) for all  . From Theorem 8.1 in [50, p. 1240] (see Theorem 6 in [49, p. 1565] for its proof) and Proposition 10.2 in [50, p. 1243] follows that Weyl fractional integrals
. From Theorem 8.1 in [50, p. 1240] (see Theorem 6 in [49, p. 1565] for its proof) and Proposition 10.2 in [50, p. 1243] follows that Weyl fractional integrals  with \(\alpha \in \mathbb {H}\) define continuous endomorphisms of
with \(\alpha \in \mathbb {H}\) define continuous endomorphisms of  . Except for \(W=\left\langle \text {e} ^{-\mu x} \right\rangle _{\texttt {tici}}\) this follows also from Korollar 3.7 in [125, p. 63]. Thus Weyl fractional derivatives
. Except for \(W=\left\langle \text {e} ^{-\mu x} \right\rangle _{\texttt {tici}}\) this follows also from Korollar 3.7 in [125, p. 63]. Thus Weyl fractional derivatives  with \(\alpha \in \mathbb {C}\) are continuous endomorphisms of
with \(\alpha \in \mathbb {C}\) are continuous endomorphisms of  .
.
It was mentioned in Section 8.1 of [54, p. 130] that the locally convex space  can be understood as a translation invariant reflected version of the “space of good functions
can be understood as a translation invariant reflected version of the “space of good functions  ” from [126], which consists of rapidly decreasing smooth functions on \([0,\infty [\). In Chapter VII of [19, p. 236] this space is denoted as \({\textbf {S}}\) and in [16, p. 155] it is written as \(S_+(\mathbb {R}^1_+)\). The set of weights
” from [126], which consists of rapidly decreasing smooth functions on \([0,\infty [\). In Chapter VII of [19, p. 236] this space is denoted as \({\textbf {S}}\) and in [16, p. 155] it is written as \(S_+(\mathbb {R}^1_+)\). The set of weights  fulfills the identity
fulfills the identity  where \(\mathfrak {S}_+\) is the space from [16, p. 146]. In [16, p. 147] it is claimed misleadingly that the “topology in \(\mathfrak {S}_+\) is easily defined by means of a countable set of norms” although this does not hold true for the topology of
where \(\mathfrak {S}_+\) is the space from [16, p. 146]. In [16, p. 147] it is claimed misleadingly that the “topology in \(\mathfrak {S}_+\) is easily defined by means of a countable set of norms” although this does not hold true for the topology of  .
.
Consider now the set  of weights. In this case, as mentioned in [125, p. 67], the dual space of
of weights. In this case, as mentioned in [125, p. 67], the dual space of  is the space
is the space

where  is the space of distributions with finite order [117, p. 339]. This permits to define adjoint Weyl fractional integrals
is the space of distributions with finite order [117, p. 339]. This permits to define adjoint Weyl fractional integrals  for \(\alpha \in \mathbb {H}\) by
for \(\alpha \in \mathbb {H}\) by

and adjoint Weyl fractional derivatives  with \(\alpha \in \mathbb {C}\) by
with \(\alpha \in \mathbb {C}\) by

for all  . Their domains are
. Their domains are

with  and \(\alpha \in \mathbb {C}\) resp. \(\alpha \in \mathbb {H}\). It is known from [5, p. 245] that
and \(\alpha \in \mathbb {C}\) resp. \(\alpha \in \mathbb {H}\). It is known from [5, p. 245] that  and thus that
and thus that  . Comparing this with \(\texttt {dom}\left( \text {I} _{+}^{\alpha }\right) \) in (7.26) below shows that the adjoint extended Weyl operators can be extended further using Schwarz’ approach.
. Comparing this with \(\texttt {dom}\left( \text {I} _{+}^{\alpha }\right) \) in (7.26) below shows that the adjoint extended Weyl operators can be extended further using Schwarz’ approach.
6.2 Lizorkin and Rubin (\(\mathbb {R}^1\))
Interpreting fractional derivatives and integrals as Fourier multiplication operators is a common approach, which will be discussed below in Section 8. It led Lizorkin [42, 43] already in the early 1960’s to introduce the space

named after him. The Lizorkin space  contains those (rapidly decreasing) Schwartz test functions, that are orthogonal to all polynomials. It carries the subspace topology inherited from the Schwartz space
contains those (rapidly decreasing) Schwartz test functions, that are orthogonal to all polynomials. It carries the subspace topology inherited from the Schwartz space  .
.
The Lizorkin fractional derivative \(_{\scriptscriptstyle {\text {Lz} }}\text {D} _{\pm }^{\alpha }\) of order \(\alpha \in \mathbb {R}\) is then defined by the method of adjoints for  as
as

for all  . The domain is
. The domain is

where  is the space of tempered distributions and
is the space of tempered distributions and  the space of polynomials [16, Sec. 8.2]. The operators
the space of polynomials [16, Sec. 8.2]. The operators  obey the general semigroup or index law
obey the general semigroup or index law  for all orders \(\alpha ,\beta \in \mathbb {R}\).
for all orders \(\alpha ,\beta \in \mathbb {R}\).
Lizorkin fractional operators have not found much attention or application, because multiplication of  with a power functions leads out of Lizorkin space. This circumstance renders
with a power functions leads out of Lizorkin space. This circumstance renders  virtually useless as a domain for fractional differential equations.
virtually useless as a domain for fractional differential equations.
Lizorkin’s approach for fractional integration was considered in [127] for the half-axis \(\mathbb {R}_{0+}\), and with Fourier transformation replaced by Mellin transformation. Let  be the space consisting of restrictions of Schwartz functions from the line to the half-line and define
be the space consisting of restrictions of Schwartz functions from the line to the half-line and define



with topology generated by the seminorms
with \(k\in \mathbb {N}_0\). The Rubin fractional integrals of order \(\alpha \in \mathbb {H}\) are defined implicitly by demanding that


holds for all \(\varphi \in \Upphi _+(\mathbb {R}_{0+})\) in the first, resp. \(\varphi \in \Upphi _\alpha (\mathbb {R}_{0+})\) in the second relation. The domains are


the topological duals of the test function spaces \(\Upphi _+(\mathbb {R}_{0+})\) and \(\Upphi _{-\alpha }(\mathbb {R}_{0+})\).
6.3 Erdelyi-McBride (\(\mathbb {R}^1\))
Let \(\alpha \in \mathbb {C}\), \(\text {Re} \alpha >0\), \(m>0\). The Erdelyi-Kober operators are defined for functions \(f:\;]0,\infty [\rightarrow \mathbb {R}\) by [85]
and they are studied in [122, 123] with \(\zeta =\eta +1-m^{-1}\) as \(\text {I} _m^{\eta ,\alpha },K_m^{\eta +1-m^{-1},\alpha }\) with \(m>0\), complex \(\alpha \) and \(\eta \) with \(\text {Re} \alpha >0\), \(\text {Re} \eta > m^{-1}-1\) and \(\text {Re} (\eta +\alpha ) > m^{-1}-1\). Although Erdelyi-Kober operators are related to Riemann-Liouville and Weyl operators as [85]


they are not identical with them. The extension to spaces of distributions via the method of adjoints is based on “fractional integration by parts” [128]

which is written in [122, eq. (1.10)] as

for \(a=0\) and \(b=\infty \). The idea is to define the Erdelyi-McBride fractional integral  of a distribution
of a distribution  by the right hand side of this relation, which remains well defined although in general
by the right hand side of this relation, which remains well defined although in general  .
.
A suitable space of test functions for the Erdelyi-Kober operators is constructed in [123]. Let \(a\in \mathbb {R}\). The set of test functions


is equipped with seminorms
determining the topology on  . The space
. The space  is dense in
is dense in  . Similar but somwhat larger spaces were proposed in [122] and [129]. The Erdelyi-McBride pseudo-fractional integral
. Similar but somwhat larger spaces were proposed in [122] and [129]. The Erdelyi-McBride pseudo-fractional integral  of order \(\alpha \in \mathbb {C}\) is defined by demanding that
of order \(\alpha \in \mathbb {C}\) is defined by demanding that

holds true for all  . Its domain is the dual space
. Its domain is the dual space

with \(a<1\). It contains distributions of order zero having limited growth at \(0+\) but arbitrary growth at \(+\infty \). For fixed \(\alpha \) the operator  is bounded on
is bounded on  .
.
The Erdelyi-McBride calculus of distributions is restricted to the half axis. Hence it is not translation invariant and cannot be applied e.g. to the constant function on \(\mathbb {R}\). Erdelyi-McBride operators for distributions combine convolution with multiplication. Because they differ in this respect from ordinary fractional integrals operators we have called them pseudo-fractional integral operators.
6.4 Braaksma-Schuitman (\(\mathbb {R}^1\))
In [130] multiplicative convolution and Mellin transformation are employed to study the Erdelyi-Kober operators \(\text {I} _m^{\eta ,\alpha }\) and \(K_m^{\eta ,\alpha }\). Let \(\lambda ,\mu \in \mathbb {R}\cup \{\pm \infty \}\), \(\lambda <\mu \). Let \((\lambda _n)^\infty _{n=0}\) and \((\mu _n)^\infty _{n=0}\) be sequences of real numbers with \(\lambda _n\downarrow \lambda \) and \(\mu _n\uparrow \mu \) and \(\lambda _n<\mu _n\) for all \(n\in \mathbb {N}\). The space \(T(\lambda ,\mu )\) is defined as the space of all functions  with the property
with the property

for all \(n\in \mathbb {N}\). \(T(\lambda ,\mu )\) is a locally convex space with topology generated by the norms \(p_n\). The Erdelyi-Kober operators are written multiplicatively as Mellin convolutions
for all \(f\in T(\lambda ,\mu )\), \(m(\text {Re} \eta +1)>\lambda \) and
for all \(f\in T(\lambda ,\mu )\), \(\text {Re} \alpha >0\) and \(m\text {Re} \eta +\mu >0\).
Given a positive number \(a>0\), let \(T([0,a],\lambda )\) denote the subspace of \(T(\lambda ,\infty )\) of functions with support contained in [0, a]. Similarly, let \(T([a,\infty ),\mu )\) denote the subspace of \(T(-\infty ,\mu )\) of functions with support contained in \([a,\infty )\). It is shown in [130] that \(\text {I} _m^{\eta ,\alpha }\) is a continuous operator of \(T([a,\infty ),\mu )\) into itself, if \(\mu \le m(1+\text {Re} \eta )\), and it is an automorphism, if \(\mu \le m(1+\text {Re} \alpha +\text {Re} \eta )\) . Similarly, \(K_m^{\eta ,\alpha }\) is a continuous operator of \(T([0,a],\lambda )\) into itself, if \(\lambda \ge -m\text {Re} \eta \) and it is an automorphism if \(\lambda \ge -m\text {Re} (\alpha +\eta )\).
The operators \(\text {I} _m^{\eta ,\alpha }\) and \(K_m^{\eta ,\alpha }\) are then extended by transposition to distributions as continuous operators with domains
where \(a>0\). Setting \(\eta =0\) and \(m=1\) leads to the definition of the Braaksma-Schuitman pseudo-fractional integral of order \(\alpha \in \mathbb {C}\) via the relation

for all \(g\in T([a,\infty ),1-\lambda )\), \(\lambda \ge 0\), \(a>0\).
As in the Erdelyi-McBride case also the Braaksma-Schuitmann approach is not translation invariant. Braaksma-Schuitmann operators cannot be compared with ordinary fractional calculus operators insofar as they involve not only convolution but also multiplication with fractional powers.
6.5 Lamb (\(\mathbb {R}^1\))
The distributional fractional calculus developed in [131, 132] is based on fractional powers of the integral operators J and K defined as
on test function spaces (\(1\le p <\infty \), \(\mu \in \mathbb {R}\))


where  is the space of smooth functions such that all derivatives are in \(L^{p}\) (defined in [5, p. 199]). For \(p=\infty \) the space
is the space of smooth functions such that all derivatives are in \(L^{p}\) (defined in [5, p. 199]). For \(p=\infty \) the space  is replaced by the subspace of those functions from
is replaced by the subspace of those functions from  , that also converge to zero at infinity, because
, that also converge to zero at infinity, because  is dense in the latter but not the former. Lamb defined the spaces \(D_{p,\mu }\) for \(\mu \in \mathbb {C}\) [131, Def. 3.1], although they do not depend on any non-zero imaginary part of \(\mu \). Hence it suffices to parametrize them with \(\mu \in \mathbb {R}\) as we do it here.
is dense in the latter but not the former. Lamb defined the spaces \(D_{p,\mu }\) for \(\mu \in \mathbb {C}\) [131, Def. 3.1], although they do not depend on any non-zero imaginary part of \(\mu \). Hence it suffices to parametrize them with \(\mu \in \mathbb {R}\) as we do it here.
The spaces \(D_{p,\mu }\) are Frechet spaces equipped with the topology generated by the seminorms
where \(\Vert \cdot \Vert _p\) is the usual \(L^p\)-norm. If \(\mu >0\), then J is a homeomorphism of \(D_{p,\mu }\) onto \(D_{p,\mu }\) with inverse \(J^{-1}=\text {d} /\text {d} x\). If \(\mu <0\), then K is a homeomorphism of \(D_{p,\mu }\) onto \(D_{p,\mu }\) with inverse \(K^{-1}=-\text {d} /\text {d} x\) [131, Thm 3.4] .
Fractional powers of a linear and continuous operator \(A=J,K\) on \(D_{p,\mu }\) are defined by the formula
for the \(\alpha \)-th power of a linear and continuous operator A on X with continuous inverse \(A^{-1}\). Here \(0<\text {Re} \alpha <2\) in eq. (6.39a) and \(n<\text {Re} \alpha <n+2\), \(n=\pm 1,\pm 2,\ldots \) with \((-A)^n=(-A^{-1})^m\) when \(n=-m, m>0\) in eq. (6.39b). The class of admissible operators is restricted by the conditions:
-
(1)
\((0,\infty )\subset \uprho (A)\), where \(\uprho (A)\) is the resolvent set of A.
-
(2)
For each \(q_k\in \{q_k\}_{k=0}^\infty \) there exists a seminorm \(p\in \{q_k\}_{k=0}^\infty \) such that
$$\begin{aligned} q_k\left( \left[ C\lambda (\lambda \textsf {1}-A)^{-1}\right] ^nf\right) \le p(f) \end{aligned}$$(6.40)for all \(f\in X\) where \(\lambda >0\), \(n=1,2,\ldots \) and the constant \(C>0\) is independent of \(f,\lambda \) and n.
These conditions ensure convergence of the integral in (6.39a), intepreted as an improper Riemann integral. It is shown in [131] that on \(D_{p,\mu }\) the fractional powers of J and K are the Weyl fractional integrals  and
and  .
.
The integrals J and K are then extended to operators \(\widetilde{J}\) and \(\widetilde{K}\) on the dual spaces \(D^\prime _{p,\mu }\) by
where \(f\in D^\prime _{p,\mu }\), \(\varphi \in D_{p,\mu }\) and \(\langle \cdot , \cdot \rangle \) is the bilinear pairing of the dual system \((D^\prime _{p,\mu },D_{p,\mu })\). Let \(\alpha \in \mathbb {C}\) with \(\text {Re} \alpha >0\). The distributional Lamb fractional derivatives and integrals are defined as the fractional powers of the extended Weyl fractional derivatives and integrals


with


on \(D^\prime _{p,\mu }\) where \((1/p)+(1/q)=1\).
Although it is defined for functions on the full real axis the Lamb-calculus does not apply to \(\exp (\text {i} \omega x)\) or trigonometric functions.
6.6 Khan-Lamb-McBride (\(\mathbb {R}^1\))
Periodic distributions were considered in [133] with the objective to extend earlier work of Butzer and Westphal [37] on periodic functions to distributions. In [133] \(d=1\) and \(\mathbb {G}=\mathbb {R}/2\pi \mathbb {Z}\). The space  of test functions is defined as
of test functions is defined as

the vector space of smooth and \(2\pi \)-periodic test functions equipped with the topology generated by the seminorms
with \(k\in \mathbb {N}_0\). The direction reversed Liouville-Weyl fractional operators


are defined for all test functions  and \(\alpha >0\).
and \(\alpha >0\).
The dual space  of
of  is equipped with the weak*-topology [133, p. 267]. The periodic fractional derivative and integral of periodic distributions
is equipped with the weak*-topology [133, p. 267]. The periodic fractional derivative and integral of periodic distributions  are then defined for \(\alpha >0\) as
are then defined for \(\alpha >0\) as


Both operators are endomorphisms on the distributional domain

as shown in [133].
7 Generalized Schwartz fractional calculus for distributions
Schwartz’ fractional calculus was significantly extended in [53,54,55]. The extension is based on generalizing the standard definition (5.7) of convolvability by support. The generalized convolution was first introduced already in [134] but has remained relatively unknown (it was rediscovered in [135], see also [136]). It is not usually discussed in books on distributions. Notable exceptions are [137,138,139], but even these books do not give the full picture. Additional information can be found in [135, 136, 140,141,142,143,144]. The generalized concept of convolution allows to extend and unify several translation invariant definitions of fractional derivatives [55].
7.1
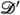 -convolution
-convolution
The generalization of convolution proceeds in two steps. The first step is to define the distributional integral in a way analogous to eq. (3.4) for measures. Because  , when equipped with a suitable topology [138, p. 11], is dual to
, when equipped with a suitable topology [138, p. 11], is dual to  , the distributional integral of a distribution
, the distributional integral of a distribution  is defined as
is defined as
where \(1_{\mathbb {R}^d}\) is the constant function on \(\mathbb {R}^d\). The second step is to generalize convolvability by support (5.8) (or  -convolvability) to
-convolvability) to  -convolvability by replacing
-convolvability by replacing  with
with  in (5.8). For \(x,y\in \mathbb {R}^d\) one has
in (5.8). For \(x,y\in \mathbb {R}^d\) one has  and (5.8) becomes
and (5.8) becomes

when  . Two distributions
. Two distributions  are called
are called  -convolvable if and only if
-convolvable if and only if

for  . This condition is always fulfilled if f, g fulfill (5.8), because
. This condition is always fulfilled if f, g fulfill (5.8), because  . Finally,
. Finally,  -convolution of two
-convolution of two  -convolvable distributions f, g is defined as
-convolvable distributions f, g is defined as
for  . The various definitions of convolution are related as illustrated in Figure 2.
. The various definitions of convolution are related as illustrated in Figure 2.
Schematic set-theoretic illustration of inclusion and subset relations for the various domains of definition for convolution discussed in the text. The equation numbers refer to the definitions of  -convolution (7.4),
-convolution (7.4),  -convolution (5.7),
-convolution (5.7),  -convolution (3.17), \(L^{1}_{\text {loc} }\)-convolution (3.13),
-convolution (3.17), \(L^{1}_{\text {loc} }\)-convolution (3.13),  -convolution (4.1c), and \(d=1\) in (3.13) and (4.1c)
-convolution (4.1c), and \(d=1\) in (3.13) and (4.1c)
 -convolution generalizes also the convolution formula (2.9) for periodic functions as shown in Section 7.5 below. In addition, it generalizes the convolution of Radon measures [98, 138, p. 7] defined as continuous linear functionals on the space
-convolution generalizes also the convolution formula (2.9) for periodic functions as shown in Section 7.5 below. In addition, it generalizes the convolution of Radon measures [98, 138, p. 7] defined as continuous linear functionals on the space  of continuous functions with compact support. Two Radon measures
of continuous functions with compact support. Two Radon measures  are convolvable if and only if \(\varphi ^\triangle (\mu \otimes \nu )\) is an integrable Radon measure on \(\mathbb {R}^{2d}\) for each
are convolvable if and only if \(\varphi ^\triangle (\mu \otimes \nu )\) is an integrable Radon measure on \(\mathbb {R}^{2d}\) for each  . The space
. The space  of integrable measures is defined as the dual of
of integrable measures is defined as the dual of  . Because Radon measures are convolutions [145, p. 300] and
. Because Radon measures are convolutions [145, p. 300] and  -convolution generalizes the convolution of Radon measures, several results of [49, 50] for Weyl fractional integration of measures are contained in the more general results for distributions.
-convolution generalizes the convolution of Radon measures, several results of [49, 50] for Weyl fractional integration of measures are contained in the more general results for distributions.
Let \(L^{1}_{\text {c} }(\mathbb {R}^d)\) and  denote the space of integrable functions with compact support and the space of compactly supported measures. Then all spaces in the diagram
denote the space of integrable functions with compact support and the space of compactly supported measures. Then all spaces in the diagram

are  -convolution algebras [139, p. 69].
-convolution algebras [139, p. 69].
7.2 Associativity of  -convolution
-convolution
Let  , \(d\in \mathbb {N},p\in \mathbb {N},p\ge 2\). The simultaneous
, \(d\in \mathbb {N},p\in \mathbb {N},p\ge 2\). The simultaneous  -convolution is defined as
-convolution is defined as
whenever \((f_1,\ldots ,f_p)\) is  -convolvable, i.e. whenever
-convolvable, i.e. whenever

for all  . Here \({\varphi ^p}^\triangle (x_1,\ldots ,x_p)=\varphi (x_1+\cdots +x_p)\). This definition follows Definition 5 in [136, p. 373] and remarks from [138, Sec. 1.3]. Convolution is linear and convolvability is preserved under addition in each factor. For the construction of convolution modules the following law of associativity is fundamental.
. Here \({\varphi ^p}^\triangle (x_1,\ldots ,x_p)=\varphi (x_1+\cdots +x_p)\). This definition follows Definition 5 in [136, p. 373] and remarks from [138, Sec. 1.3]. Convolution is linear and convolvability is preserved under addition in each factor. For the construction of convolution modules the following law of associativity is fundamental.
Proposition 2
(Thm 2 in [143]) If the p-tuple \((f_1,\ldots ,f_p), p\in \mathbb {N},p\ge 2\) with  is
is  -convolvable, then
-convolvable, then
for \(q\in \{1,\ldots ,p-2\}\), where the right hand side is well defined in the sense of definition (7.6)
The set of lower semicontinuous functions \(f:\mathbb {R}^d\rightarrow [0,\infty ]\) becomes a semigroup for convolution as group operation, if convolution is pointwise defined. This follows from Fubini’s theorem [99, p. 55] and allows to formulate the following convenient convolvability criterion:
Proposition 3
A p-tuple \((f_1,\ldots ,f_p)\), \(p\ge 2\),  is convolvable if and only if for all test functions
is convolvable if and only if for all test functions  the convolution of the regularisations
the convolution of the regularisations
is a finite-valued function.
Proof
The criterion is equivalent to the criterion given in [140, p. 19] after a linear transformation of \(\mathbb {R}^{d p}\). \(\square \)
The construction of convolution duals  , perfection
, perfection  and
and  for measures can be carried over to distributions and
for measures can be carried over to distributions and  -convolution by replacing
-convolution by replacing  with
with  . Let \(\left\langle F \right\rangle _{\mathbb {C},+}\) (resp. \(\left\langle F \right\rangle _{\mathbb {C},+,*}\)) denote the complex linear span (resp. convolution algebra) generated by
. Let \(\left\langle F \right\rangle _{\mathbb {C},+}\) (resp. \(\left\langle F \right\rangle _{\mathbb {C},+,*}\)) denote the complex linear span (resp. convolution algebra) generated by  (resp. by
(resp. by  with
with  ).
).
Theorem 2
(Thm 8, [54]) Let  . If
. If  , then every tuple from F is convolvable and
, then every tuple from F is convolvable and  is a convolution module over \(\left\langle F \right\rangle _{\mathbb {C},+,*}\).
is a convolution module over \(\left\langle F \right\rangle _{\mathbb {C},+,*}\).
Denote as  the space of lower semicontinous functions \(f:\mathbb {R}^d\rightarrow [0,\infty ]\), and let
the space of lower semicontinous functions \(f:\mathbb {R}^d\rightarrow [0,\infty ]\), and let  . The W-weighted \(L^{1}\)-space of distributions is defined as
. The W-weighted \(L^{1}\)-space of distributions is defined as

Its definition depends only on the translation invariant cone ideal generated by W, which is defined as

where \((\text {T} _xf)(y)=f(y-x)\) is translation by x.
Proposition 4
Let  . The convolution dual
. The convolution dual  and the maximal module
and the maximal module  can be represented as weighted \(L^{1}\)-spaces of distributions
can be represented as weighted \(L^{1}\)-spaces of distributions


where \(\left\langle W \right\rangle _{*}\) is the set of simultaneous convolution products formed with elements in W, and  is the reflection of f defined in (10.37).
is the reflection of f defined in (10.37).
Proof
With the notation \(w=|\psi _1*f_1|*\cdots *|\psi _p*f_p|\) one obtains

for all  and
and  . Applying Proposition 3 concludes the proof. \(\square \)
. Applying Proposition 3 concludes the proof. \(\square \)
7.3 Generalized Schwartz fractional derivative
To formulate the extension of Schwartz’ fractional derivatives  and integrals
and integrals  succinctly the following discussion is presented for \(d=1\). The extension to \(d\ne 1\) is considered at the end.
succinctly the following discussion is presented for \(d=1\). The extension to \(d\ne 1\) is considered at the end.
The generalized Schwartz fractional derivative \(\text {D} _{+}^{\alpha }\) is defined exactly as the Schwartz derivative in eq. (5.4) as
for \(\alpha \in \mathbb {C}\) but now using the  -convolution (7.4) resulting in the significantly enlarged domain
-convolution (7.4) resulting in the significantly enlarged domain
for \(\alpha \in \mathbb {C}\). The generalized Schwartz fractional integral is defined as a derivative of negative order \(\text {I} _{+}^{\alpha }:=\text {D} _{+}^{-\alpha }\) for \(\alpha \in \mathbb {C}\).
Using (7.12) and some simple calculations the domain (7.16) can be described more explicitly. Let  . For \(\alpha \in \mathbb {C}\setminus (-\mathbb {N}_0)\) there exists \(C<\infty \) such that
. For \(\alpha \in \mathbb {C}\setminus (-\mathbb {N}_0)\) there exists \(C<\infty \) such that
for all \(x\ge 2y>0\). Using this inequality gives the asymptotic behaviour

for \(x\rightarrow \infty \). The extended domains can now be described as weighted \(L^{1}(\mathbb {R})\)-spaces. Define the power logarithmic weights
for \(\mu ,x\in \mathbb {R},n\in \mathbb {N}_0\). Using the shorthand notation \(f_+:=f\cdot \Theta \) and  , an asymptotic expansion shows that
, an asymptotic expansion shows that

for \(\alpha \in \mathbb {C}\setminus (-\mathbb {N}_0)\). Thus, the enlarged domain \(\texttt {dom}\left( \text {D} _{+}^{\alpha }\right) \) is

for \(\alpha \in \mathbb {C}\setminus \mathbb {N}_0\) by virtue of Proposition 4.
Theorem 3
The index law
holds if \(\{\alpha ,\beta \}\cap (-\mathbb {N}_0)\ne \emptyset \), or if  with \(v_{\alpha ,\beta }:=w_-^{\text {Re} \alpha -1}*w_-^{\text {Re} \beta -1}\).
with \(v_{\alpha ,\beta }:=w_-^{\text {Re} \alpha -1}*w_-^{\text {Re} \beta -1}\).
Proof
Apply Propositions 2 and 3 to the simultaneous convolution \(\text {Y} _{\alpha }*\text {Y} _{\beta }*f\). \(\square \)
Proposition 5
Convolutions of power logarithmic weights satisfy
Proof
Equations (7.24a) and (7.24b) are contained in [146, Lemma 2.2]. Equation (7.24c) follows from [147, VIII.8]. \(\square \)
Let \(\mathbb {H}:=\{z\in \mathbb {C}:\text {Re} z>0\}\), \(\overline{\mathbb {H}}:=\{z\in \mathbb {C}:\text {Re} z\ge 0\}\) and \(\mathbb {H}_0:=\mathbb {H}\cup \{0\}\) and define the following sets
of weights. Then  .
.
Theorem 4
Let \(\alpha \in \mathbb {C}\). The maximal invariant domain of the Schwartz fractional integral is given by

Fractional integrals with orders \(\alpha \in \mathbb {C}\) define a group operating bijectively on  . Fractional integrals with orders \(\alpha \in \text {i} \mathbb {R}\) define a group operating bijectively on
. Fractional integrals with orders \(\alpha \in \text {i} \mathbb {R}\) define a group operating bijectively on  . Fractional integrals with orders \(\alpha \in -\overline{\mathbb {H}}\) define a semigroup operating on
. Fractional integrals with orders \(\alpha \in -\overline{\mathbb {H}}\) define a semigroup operating on  . Fractional integrals with orders \(\alpha \in -\mathbb {H}\) define a semigroup operating on
. Fractional integrals with orders \(\alpha \in -\mathbb {H}\) define a semigroup operating on  .
.
Proof
Apply Proposition 4, Theorem 2 and Proposition 5. \(\square \)
In [119, p. 126] it has been argued at length that fractional derivatives of the power function \(x \mapsto x^n, n\in \mathbb {N}\) do not exist in general, not even in the sense of distributions. The generalized Schwartz derivative \(\text {D} _{+}^{\alpha }(x^n)\) defined above, however, exists if and only if \(\alpha \in \mathbb {N}_0\) or \(\alpha \in \mathbb {C}\) with \(\text {Re} \alpha >n\).
7.4 Discrete Grünwald-Letnikov calculus and the continuum limit
This section discusses discretized fractional integrals and derivatives on domains of sequences and distributional domains in analogy with the continuous case. Discretized functions are sequences, i.e. functions defined on \(\texttt {dom}\left( f\right) =h\mathbb {Z}\) instead of \(\mathbb {R}\) for some step size \(h>0\). Let \(\mathbb {C}^{h\mathbb {Z}}\) be the space of all discrete functions \(h\mathbb {Z}\rightarrow \mathbb {C}\). Analogous to the monomials \(\text {Y} _{\alpha }\) from (5.2) define the discrete power function as
for \(\alpha \in \mathbb {C}\) and \(h>0\). Define the associated discrete Grünwald-Letnikov fractional derivative as

for \(k\in \mathbb {Z}\) and  with the natural domain
with the natural domain

for \(\alpha \in \mathbb {C} \setminus \mathbb {N}_0\) and  for \( \alpha \in \mathbb {N}_0 \). Thus,
for \( \alpha \in \mathbb {N}_0 \). Thus,  is the discrete convolution operator \((\cdot )*\text {y} _{\alpha ,h}\) on the discrete convolution dual of \(\{\text {y} _{\alpha ,h}\}\). The operators (7.28) were considered, for example, in [148]. With Equation (7.29) we provide a precise definition of their natural domain.
is the discrete convolution operator \((\cdot )*\text {y} _{\alpha ,h}\) on the discrete convolution dual of \(\{\text {y} _{\alpha ,h}\}\). The operators (7.28) were considered, for example, in [148]. With Equation (7.29) we provide a precise definition of their natural domain.
Every discrete function \(f\in \mathbb {C}^{h\mathbb {Z}}\) can be identified with a distribution  (even with a Radon measure) via
(even with a Radon measure) via
where \(\updelta _x\) is the Dirac distribution at \(x\in \mathbb {R}\) and \(h>0\) the step size. The distribution corresponding to \(\text {y} _{\alpha ,h}\) is
The generalized Grünwald-Letnikov fractional derivative of order \(\alpha \in \mathbb {C}\) with step \(h>0\) is then defined as

where \((\text {T} _xf)(y):=f(y-x)\) is the translation operator. The domain is

The definition (7.32) can be understood in terms of  -convolution or in terms of the series on the right hand side, that is absolutely convergent in
-convolution or in terms of the series on the right hand side, that is absolutely convergent in  . The second equality in (7.33) is proved analogous to (7.22).
. The second equality in (7.33) is proved analogous to (7.22).
Proposition 6
Let \( \alpha \in \mathbb {C}\setminus -\mathbb {N}_0 \) and  . There exist \( C, x \in \mathbb {R}_{+} \) such that
. There exist \( C, x \in \mathbb {R}_{+} \) such that
Thus, \( \text {Y} _{\alpha ,h} \rightarrow \text {Y} _{\alpha } \) with respect to the normal topology  for all \( \alpha \in \mathbb {C} \).
for all \( \alpha \in \mathbb {C} \).
Proof
The estimate (7.34) is proved similar to Theorem 1.3 in [90]. The second statement is clear from the definition of the normal topology  in Definition 8 from [55] and Theorem 3.11 in [149]. \(\square \)
in Definition 8 from [55] and Theorem 3.11 in [149]. \(\square \)
Proposition 6 and Theorem 8 in [55, p. 143] imply that
for all  .
.
7.5 Periodic distributions
7.5.1 Induced kernels for convolution with periodic distributions
Fractional derivatives and integrals for periodic functions and distributions were already discussed in Sections 2.1, 2.2, 2.5 and 6.6. They are naturally induced by their counterparts on the real line or on the integers.
Periodic functions can be identified with functions on the unit circle understood as the quotient \(\mathbb {R}/2\pi \mathbb {Z}\). More generally, consider two commutative Lie groups G, H. Recall, that every commutative Lie group is isomorphic to \( \mathbb {R}^a \times \mathbb {Z}^b \times (\mathbb {R}/\mathbb {Z})^c \times D \) for some \( a,b,c \in \mathbb {N}_0 \) and a finite Abelian group D. Below, \(G=\mathbb {R}\) or \(G=h\mathbb {Z}\) and \(H=2\pi \mathbb {Z}\) with \(h=2\pi /{\Lambda }\), \({\Lambda }\in \mathbb {N}\) will be considered.
Let \(A:G\rightarrow H\) be an affine mapping, i.e. a homomorphism followed by a shift y with \(y\in H\). Define the image A(f) of a distribution  under A as
under A as
for all  , whenever this is well defined. The image of a distribution under a mapping is analogous to the image of a Radon measure under a mapping, see [97, Ch. V, §6, No. 4, Def. 2] or Subsection 3.3. On the other hand, the pullback of a distribution
, whenever this is well defined. The image of a distribution under a mapping is analogous to the image of a Radon measure under a mapping, see [97, Ch. V, §6, No. 4, Def. 2] or Subsection 3.3. On the other hand, the pullback of a distribution  under A is defined by (the arrow under the limit sign means convergence in \(\mathscr {E}^\prime (H)\))
under A is defined by (the arrow under the limit sign means convergence in \(\mathscr {E}^\prime (H)\))
for all  . This extends the classical definition of \(A^*(f):=f\circ A\) for functions
. This extends the classical definition of \(A^*(f):=f\circ A\) for functions  . See [116, Ch. VI] for a more general discussion of pullbacks.
. See [116, Ch. VI] for a more general discussion of pullbacks.
Let \(H\hookrightarrow G\rightarrow G/H\) be a short exact sequence of commutative Lie groups and denote the projection as  . The pullback
. The pullback  is injective on
is injective on  and induces a bijection on its range
and induces a bijection on its range  , where
, where  denotes the set of distributions from
denotes the set of distributions from  that are invariant under H. The convolution of a distribution
that are invariant under H. The convolution of a distribution  with the projected kernel
with the projected kernel  of a distribution
of a distribution  is related to convolution with the original kernel f via
is related to convolution with the original kernel f via

This can now be applied to the continous case where \(G=\mathbb {R}\) with \(H={2\pi }\mathbb {Z}\) and to the discrete case where \(G=h\mathbb {Z}\) with \(H=2\pi \mathbb {Z}\).
In the special case \( G = \mathbb {R} \) and \( H = \mathbb {Z} \) equation (7.38) follows from
for \( x\in \mathbb {R} \), \( f \in L^1(\mathbb {R}) \) and \( g \in L^1(\mathbb {R}/\mathbb {Z}) \) via Fubini’s Theorem and a unique continuous extension argument using the continuity of  .
.
7.5.2 Continuous case
Here \(G=\mathbb {R}\) with \(H={2\pi }\mathbb {Z}\). The space  of test functions on the unit circle is isomorphic to the space of periodic test functions
of test functions on the unit circle is isomorphic to the space of periodic test functions  from [133]. Thus
from [133]. Thus  is isomorphic to
is isomorphic to  . Define the space of \(2\pi \)-periodic distributions as
. Define the space of \(2\pi \)-periodic distributions as

Distributions from  are lifted uniquely as
are lifted uniquely as

from  to
to  one has
one has  and
and

extending  from eq. (2.11) to negative indices, which is then not convergent as a function, but only as a distribution. The series
from eq. (2.11) to negative indices, which is then not convergent as a function, but only as a distribution. The series

converges absolutely in  [5, Ch. VII §1] for all \(\alpha \in \mathbb {C}\). Eqs. (7.38) and (7.42) imply that for all \(\alpha \in \mathbb {H}\cup \{0\}\) and for
[5, Ch. VII §1] for all \(\alpha \in \mathbb {C}\). Eqs. (7.38) and (7.42) imply that for all \(\alpha \in \mathbb {H}\cup \{0\}\) and for  one has
one has

where the fractional derivative  on
on  is defined as convolution with
is defined as convolution with  . This fractional derivative is naturally induced by the generalized Schwartz fractional derivative \(\text {D} _{+}^{\alpha }\) on the space of periodic distributions.
. This fractional derivative is naturally induced by the generalized Schwartz fractional derivative \(\text {D} _{+}^{\alpha }\) on the space of periodic distributions.
7.5.3 Discrete case
In the discrete case one has \(G=h\mathbb {Z}\) with \(H=2\pi \mathbb {Z}\). Now the projected discrete Grünwald-Letnikov kernel is defined as

with \({\Lambda }\in \mathbb {N}\) and \(h=2\pi /{\Lambda }\) and reads as

for \(m\in \mathbb {N}_0\) and \(0\le m<{\Lambda }\). The generalized Grünwald-Letnikov fractional derivative of order \(\alpha \in \mathbb {C}\) with step \(h=2\pi /{\Lambda }\) and period \({\Lambda }\) is then defined as

with domain

where  is the space of all sequences on the quotient \(h\mathbb {Z}/2\pi \mathbb {Z}\), which can be identified with the space of periodic sequences with period \({\Lambda }=2\pi /h\). For \(\alpha \in \mathbb {C}\) the limit
is the space of all sequences on the quotient \(h\mathbb {Z}/2\pi \mathbb {Z}\), which can be identified with the space of periodic sequences with period \({\Lambda }=2\pi /h\). For \(\alpha \in \mathbb {C}\) the limit

recovers the kernel on \(\mathbb {R}/2\pi \mathbb {Z}\), extending the definition of  to \(\alpha \in \text {i} \mathbb {R}\setminus \{0\}\).
to \(\alpha \in \text {i} \mathbb {R}\setminus \{0\}\).
Due to the generality of  -convolution the continuum limit from discrete to continuous fractional derivatives and the projection from non-periodic to periodic distributions can be freely combined as illustrated in Figure 3.
-convolution the continuum limit from discrete to continuous fractional derivatives and the projection from non-periodic to periodic distributions can be freely combined as illustrated in Figure 3.
Diagram illustrating the continuum limit \(h\rightarrow 0\) and the projections \({\text {P} }_{\Lambda }\), resp. \({\text {P} }_{2\pi }\), of fractional derivative operators on discrete  , resp. continuous \(\text {D} _{+}^{\alpha }\), distributions to their periodic counterparts
, resp. continuous \(\text {D} _{+}^{\alpha }\), distributions to their periodic counterparts  , resp.
, resp.  . The horizontal arrows hold for all \(\alpha \in \mathbb {C}\), the vertical arrows for \(\alpha \in \mathbb {H}\cup \{0\}\)
. The horizontal arrows hold for all \(\alpha \in \mathbb {C}\), the vertical arrows for \(\alpha \in \mathbb {H}\cup \{0\}\)
7.6 Extensions to higher dimension
Let \(\alpha =(\alpha _1,\ldots ,\alpha _d)\in \mathbb {C}^d\), \(x=(x_1,\ldots ,x_d)\in \mathbb {R}^d\), and
the multinomial homogeneous distribution, which generalizes the one-dimensional monomial distribution from (5.2). The generalized Schwartz fractional integral \(\text {I} _{+}^{\alpha }\) is defined as the mapping

for all  -convolvable \((d+1)\)-tuples \((f,\text {Y} _{\alpha _1},\ldots ,\text {Y} _{\alpha _d})\). Its inverse
-convolvable \((d+1)\)-tuples \((f,\text {Y} _{\alpha _1},\ldots ,\text {Y} _{\alpha _d})\). Its inverse
is the generalized Schwartz fractional derivative \(\text {D} _{+}^{\alpha }\). On the severely restricted domain  the generalized law of additivity
the generalized law of additivity
holds true for all \(\alpha ,\beta \in \mathbb {C}^d\) [52]. Note that  , even for \(d=1\).
, even for \(d=1\).
Another often studied generalization of fractional derivatives to higher dimension are fractional powers \((-\Delta )^{\alpha /2}\) of the (negative) Laplacian with general \(\alpha \in \mathbb {C}\) [32, 45, 150,151,152,153,154]. These operators differ from the operators discussed so far, and in particular from the generalized Schwartz fractional derivative \(\text {D} _{+}^{\alpha }\), because their kernel is different. The generalized fractional Riesz derivative  for distributions is defined as the convolution mapping
for distributions is defined as the convolution mapping

where
for all \(\alpha \in \mathbb {H}\setminus (d+2\mathbb {N}_0)\), is the Riesz kernel [32, 136, p. 369], [152]. Because the Riesz kernels are convolvable if and only if \(\text {Re} (\alpha +\beta )<d\) the fractional Laplacian becomes an endomorphism on the domain

for \(\alpha >0\), \(\alpha \notin 2\mathbb {N}\) [55, Sec. 8].
This domain was envisaged in [151, 152] as the dual of the space

equipped with the seminorms \(\varphi \mapsto \Vert (\partial ^\beta \varphi )(1+x^2)^{d+\alpha }\Vert _\infty \) and \(\beta \in \mathbb {N}_0^d\). But with this topology the dual  is not contained in
is not contained in  , contrary to statements in [151, Sec. 2.1] and [152], because
, contrary to statements in [151, Sec. 2.1] and [152], because  is not dense in
is not dense in  . However, using the seminorms \(\varphi \mapsto \Vert (\partial ^\beta \varphi )(1+x^2)^{d+\alpha }\psi \Vert _\infty \) with
. However, using the seminorms \(\varphi \mapsto \Vert (\partial ^\beta \varphi )(1+x^2)^{d+\alpha }\psi \Vert _\infty \) with  and \(\beta \in \mathbb {N}^d\) this shortcoming can be repaired similar to [138, Prop. 1.3.1]. For more details see [55] and [155, II.5.d]
and \(\beta \in \mathbb {N}^d\) this shortcoming can be repaired similar to [138, Prop. 1.3.1]. For more details see [55] and [155, II.5.d]
We remark also that the test function space  introduced for fractional powers of the negative Laplace operator in Definition 3.1 [156, p. 261] is nothing but
introduced for fractional powers of the negative Laplace operator in Definition 3.1 [156, p. 261] is nothing but  . Therefore its dual is
. Therefore its dual is  , which is smaller than our domain
, which is smaller than our domain  above. This follows from the structural properties of amalgam spaces described in [155, Sec. II.3]
above. This follows from the structural properties of amalgam spaces described in [155, Sec. II.3]
For \(d=1\) the generalized fractional Riesz derivatives enjoy special properties [55]. An example is the factorization into causal and anticausal fractional derivatives

for \(\text {Re} \alpha >0\) and all \(f\in \texttt {dom}\left( \text {D} _{+}^{\alpha }\right) \cap \texttt {dom}\left( \text {D} _{-}^{\alpha }\right) \). Thus, the factorization is valid only on a strict subdomain of the fractional Laplacian. Note, that the power of the Laplacian in [55, eq. (8.5)] should be \(\alpha \), not \(2\alpha \).
8 Laplace multiplier approach for distributions
Liouville’s formula as used by Weyl [82, Satz 2] defines fractional derivatives as Laplace multipliers. This mathematical interpretation provides yet another approach to define fractional derivatives of distributions. At the first glance, Fourier transform of tempered distributions [5, Ch. VIII] seems to be the right tool for this. However, defining domains is difficult, because the multiplication of a tempered distribution with a continuous function, such as \( \mathbb {R} \ni x \mapsto x^\alpha \), \( \alpha > 0 \), is not necessarily well defined. This issue will be resolved using pointwise defined  -Fourier-Laplace transforms that are based on integration of distributions. This approach was only briefly mentioned in [5, Ch. VIII] and has, up to some exceptions such as [139], not been discussed further in the literature.
-Fourier-Laplace transforms that are based on integration of distributions. This approach was only briefly mentioned in [5, Ch. VIII] and has, up to some exceptions such as [139], not been discussed further in the literature.
Let \(\exp _z:\mathbb {R}^d\rightarrow \mathbb {C}\) with \(\exp _z(x)=\exp (z\cdot x)\). Because  for all \(z\in \mathbb {C}^d\) a common approach is to define the Fourier-Laplace transform of a distribution via the dual system
for all \(z\in \mathbb {C}^d\) a common approach is to define the Fourier-Laplace transform of a distribution via the dual system  as
as
and then to extend it at least in some subsets of \(\mathbb {C}^d\) to more general distributions [116, 137, 139, 157]. Using the dual pair  Schwartz also studied the Fourier-Laplace transform as the distribution-valued mapping
Schwartz also studied the Fourier-Laplace transform as the distribution-valued mapping

Using the dual pair  instead, the Fourier-Laplace transform can be understood as a function-valued mapping.
instead, the Fourier-Laplace transform can be understood as a function-valued mapping.
For any  define the f-dependent set of E-conjugate (Fourier)Laplace variables as
define the f-dependent set of E-conjugate (Fourier)Laplace variables as
The  -Laplace transform of a distribution
-Laplace transform of a distribution  is defined via the distributional integral at the points
is defined via the distributional integral at the points  as
as
Proofs for the following continuity properties of these Laplace transforms were briefly sketched in [5, Ch. VIII]:
Theorem 5
Let  . The sets
. The sets  ,
,  and
and  are of the form \(A+\text {i} \mathbb {R}^d\) where \(A\subseteq \mathbb {R}^d\) is convex. All three sets have the same interior. The function
are of the form \(A+\text {i} \mathbb {R}^d\) where \(A\subseteq \mathbb {R}^d\) is convex. All three sets have the same interior. The function

is continuous on \(P+\text {i} \mathbb {R}^d\) for every convex polytope  . It is holomorphic on the interior of
. It is holomorphic on the interior of  , where it agrees with the generalized rotated Fourier-Laplace transform \(\widehat{f}(\text {i} z)\) in the sense of [116, Sec. 7.4].
, where it agrees with the generalized rotated Fourier-Laplace transform \(\widehat{f}(\text {i} z)\) in the sense of [116, Sec. 7.4].
Proof
The equation  holds for all \(x\in \mathbb {R}^d\), which proves that
holds for all \(x\in \mathbb {R}^d\), which proves that  .
.
Let P be a convex polytope with vertices  , \(n\in \mathbb {N}\). Set \(h:=\exp _{\xi _1}+\ldots +\exp _{\xi _n}\). Then
, \(n\in \mathbb {N}\). Set \(h:=\exp _{\xi _1}+\ldots +\exp _{\xi _n}\). Then  ,
,  and
and

holds for all \(R>0\), where  is the set of all bounded subsets of
is the set of all bounded subsets of  . From this follows
. From this follows  , because
, because

for all \(z\in P\). This proves that  is convex.
is convex.
If P is a convex polytope contained in  and z a point in its interior, then
and z a point in its interior, then  and
and

implying  . Thus
. Thus  contains the interior of
contains the interior of  .
.
Further, if \(z\in P\) converges to \(z_0\in P\), then \(\exp _z/h\) converges to \(\exp _{z_0}/h\) in  and thus also within
and thus also within  [138, p. 11]. Because multiplication
[138, p. 11]. Because multiplication  is hypocontinuous, it follows that
is hypocontinuous, it follows that
and thus \(\varvec{\textsf {L}}\!\left\{ f\right\} \!\) is continuous on \(P+\text {i} \mathbb {R}^d\).
The convexity of  can be proved in the same way (see [117, p. 191]). For
can be proved in the same way (see [117, p. 191]). For  the function
the function  is continuous with at most polynomial growth by Proposition 1.6.6(2) from [139]. Hence \(\varvec{\textsf {L}}\!\left\{ f\right\} \!(z)=\widetilde{f}(\text {i} z)\) and applying Theorem 7.4.2 from [116] yields analyticity of \(\varvec{\textsf {L}}\!\left\{ f\right\} \!(z)\) on the interior of
is continuous with at most polynomial growth by Proposition 1.6.6(2) from [139]. Hence \(\varvec{\textsf {L}}\!\left\{ f\right\} \!(z)=\widetilde{f}(\text {i} z)\) and applying Theorem 7.4.2 from [116] yields analyticity of \(\varvec{\textsf {L}}\!\left\{ f\right\} \!(z)\) on the interior of  . \(\square \)
. \(\square \)
Remark 1
The injectivity of the Fourier transform on  entails the injectivity of the
entails the injectivity of the  -Fourier-Laplace transform from Equation (8.4).
-Fourier-Laplace transform from Equation (8.4).
Proposition 7
Let  , \(z\in \mathbb {C}^d\) and \(i\in \{1,\ldots ,d\}\).
, \(z\in \mathbb {C}^d\) and \(i\in \{1,\ldots ,d\}\).
-
(1)
If (f, g) is
 -convolvable, then \((f\exp _z,g\exp _z)\) is also
-convolvable, then \((f\exp _z,g\exp _z)\) is also  -convolvable and $$\begin{aligned} (f\exp _z)*(g\exp _z)=(f*g)\exp _z . \end{aligned}$$(8.10)
-convolvable and $$\begin{aligned} (f\exp _z)*(g\exp _z)=(f*g)\exp _z . \end{aligned}$$(8.10) -
(2)
If
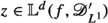 , then $$\begin{aligned} f*\exp _z=\varvec{\textsf {L}}\!\left\{ f\right\} \!(z)\cdot \exp _z. \end{aligned}$$(8.11)
, then $$\begin{aligned} f*\exp _z=\varvec{\textsf {L}}\!\left\{ f\right\} \!(z)\cdot \exp _z. \end{aligned}$$(8.11) -
(3)
If \((\partial _if,g)\) and \((f,\partial _ig)\) are
 -convolvable and
-convolvable and 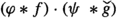 is vanishing at infinity for all
is vanishing at infinity for all 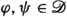 , then $$\begin{aligned} (\partial _if)*g=f*(\partial _ig) \end{aligned}$$(8.12)
, then $$\begin{aligned} (\partial _if)*g=f*(\partial _ig) \end{aligned}$$(8.12)
Proof
Let  .
.
-
(1):
Using \((f\exp _z)\otimes (g\exp _z)=(f\otimes g)\exp _z^\triangle \) and \((\varphi \exp _z)^\triangle =\varphi ^\triangle \exp _z^\triangle \) gives
$$\begin{aligned} \langle (f\exp _z)*(g\exp _z) , \varphi \rangle&= \int \limits (f\otimes g)(\varphi \exp _z)^\triangle \nonumber \\&=\langle f*g , \varphi \exp _z \rangle =\langle (f*g)\exp _z , \varphi \rangle . \end{aligned}$$(8.13) -
(2):
Equation (8.11) is clear for
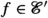 and can be extended to the general case via approximate units using Lemma 3.5 and Theorem 7.1 from [158].
and can be extended to the general case via approximate units using Lemma 3.5 and Theorem 7.1 from [158]. -
(3):
This follows from Proposition 1 in [159, p. 534] and the remarks subsequent to Equation (1) in [160, p. 202–203].
\(\square \)
Theorem 6
(Convolution Theorem) If the pair (f, g) of distributions is  -convolvable, then
-convolvable, then  and
and
for all  .
.
Proof
Let  ,
,  and
and  . Then one has \(|f*\varphi |\cdot \exp _{-z}\in L^{1}(\mathbb {R}^d)\), \(|g*\psi |\cdot \exp _{-z}\in L^{1}(\mathbb {R}^d)\) and thus
. Then one has \(|f*\varphi |\cdot \exp _{-z}\in L^{1}(\mathbb {R}^d)\), \(|g*\psi |\cdot \exp _{-z}\in L^{1}(\mathbb {R}^d)\) and thus
This entails  -convolvability of \((f,g,\exp _z)\) and thus also
-convolvability of \((f,g,\exp _z)\) and thus also  -convolvability of \((f*g,\exp _z)\). Computing
-convolvability of \((f*g,\exp _z)\). Computing
concludes the proof. \(\square \)
Corollary 1
Let  and \(\kappa \in \mathbb {N}_0^d\). Then
and \(\kappa \in \mathbb {N}_0^d\). Then  and
and
for all  .
.
Proof
It is left to the reader to prove that  and \(\varvec{\textsf {L}}\!\left\{ \partial ^\kappa \updelta \right\} \!(z)=z^d\). Then equation (8.17) follows from the convolution theorem. \(\square \)
and \(\varvec{\textsf {L}}\!\left\{ \partial ^\kappa \updelta \right\} \!(z)=z^d\). Then equation (8.17) follows from the convolution theorem. \(\square \)
As stated in Theoreme XXV, 1\(^\circ \) in [5, p. 201] and the corollary of Proposition 3.5.3 in [117, p. 347] the space  can be represented as
can be represented as

where \(\left\langle ~\cdot ~ \right\rangle _{\mathbb {C},+}\) denotes the linear span. Accordingly, represent  as the sums \(f=\sum _\kappa \partial ^\kappa f_\kappa =\sum _\kappa \partial ^\kappa \mu _\kappa \) with a finite number of \(f_\kappa \in L^{1}(\mathbb {R}^d)\) and
as the sums \(f=\sum _\kappa \partial ^\kappa f_\kappa =\sum _\kappa \partial ^\kappa \mu _\kappa \) with a finite number of \(f_\kappa \in L^{1}(\mathbb {R}^d)\) and  . Then Corollary 1 above implies that
. Then Corollary 1 above implies that
holds for the distributional integral. Using this one computes
for all \((\alpha ,z)\in \mathbb {H}^d\times \mathbb {H}^d\). This can be extended to all \((\alpha ,z)\in (\mathbb {H}\cup \{0\})^d\times \overline{\mathbb {H}}^d\) by virtue of Theorem 5, and to all \((\alpha ,z)\in \mathbb {C}^d\times \mathbb {H}^d\) using Corollary 1.
Let \(d=1\) and \(\alpha \in \mathbb {C}\). The Laplace multiplier fractional derivative  is defined implicitly by the relation
is defined implicitly by the relation

for all  , or
, or  in case \(\text {Re} \alpha >0\) or \(\alpha =0\). As usual, the fractional power \(z^\alpha =\exp (\alpha (\log |z|+\text {i} \arg (z)))\) with \(\arg (z)\in (-\pi ,\pi )\) is taken on the principal branch. The distribution
in case \(\text {Re} \alpha >0\) or \(\alpha =0\). As usual, the fractional power \(z^\alpha =\exp (\alpha (\log |z|+\text {i} \arg (z)))\) with \(\arg (z)\in (-\pi ,\pi )\) is taken on the principal branch. The distribution  is well-defined due to Remark 1. The domain of definition
is well-defined due to Remark 1. The domain of definition

with the sets
is smaller than the domain of the corresponding generalized Schwartz fractional operator from equation (7.16). The Laplace multiplier fractional integral  is defined as
is defined as  .
.
A close relation with Lamb’s operators in Section 6.5 emerges from comparison with eq. (6.44). The spaces \(D_{p,\mu }\) with \(\mu <0\) in (6.44) are an inductive system with respect to set-theoretic inclusion. If one takes their inductive limit one obtains the Laplace multiplier domains in (8.22). One finds  for \(\text {Re} \alpha \ge 0\) and \(\alpha \ne 0\), while
for \(\text {Re} \alpha \ge 0\) and \(\alpha \ne 0\), while  for \(\text {Re} \alpha > 0\) or \(\alpha = 0\). The relation between Lamb’s fractional operators and Laplace multipliers may become understandable, because \(z^\alpha \) can be viewed as the fractional power of a multiplication operator, so that both approaches are based on fractional powers.
for \(\text {Re} \alpha > 0\) or \(\alpha = 0\). The relation between Lamb’s fractional operators and Laplace multipliers may become understandable, because \(z^\alpha \) can be viewed as the fractional power of a multiplication operator, so that both approaches are based on fractional powers.
9 Towards unification of fractional calculus
9.1 Illustrative examples
To illustrate the greater generality of \(\text {D} _{+}^{\alpha }\) as compared to other fractional derivatives, this subsection collects various examples of functions and distributions \({f:\mathbb {R}\rightarrow \mathbb {C}}\). They show that \(\text {D} _{+}^{\alpha }\) holds some promise for the unification of translation invariant approaches to fractional calculus. The examples are
-
A
: \(f_{\text A }(x) = 1\)
-
B
: \(f_{\text B }(x) = \text {e} ^{x}\)
-
C
: \(f_{\text C }(x) = \text {e} ^{\text {i} x}\)
-
D
: \(f_{\text D }(x) = \text {e} ^{\text {i} x^2}\)
-
E
: \(f_{\text E } = \text {e} ^{-\sqrt{1+x^2}}\)
-
F
: \(f_{\text F }(x) = \Theta (x)\text {e} ^{x^2-x^{-2}}\)
-
G
: \(f_{\text G }(x) = (\sqrt{1+x^2})^{\alpha -0.1},\quad \alpha >0\)
-
H
: \(f_{\text H }(x) = \Theta (-x)\)
-
I
: \(f_{\text I }(x) = \updelta (x)\)
-
J
: \(f_{\text J }(x) = \updelta ^\prime (x)\)
-
K
: \(f_{\text K }(x) = \text {Y} _{1/2}(x)\) \(\notin _{\text K } : 2\alpha <1\)
-
L
: \(f_{\text L }(x) = \displaystyle \sum _{k=1}^\infty \varphi [k(x+k)]k^{\alpha +1/2},\)
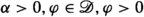 \(\notin _{\text L } : 2\alpha \ge 1\)
\(\notin _{\text L } : 2\alpha \ge 1\) -
M
: \(f_{\text M }(x) = \text {sgn} (\sin (x))\) \(\notin ^1_{\text M } : 2\alpha \ge 1\), \(\notin ^2_{\text M } : \alpha p >1\)
An entry \(\in \) in the table below means that  for all \(\alpha >0\), where XY indicates the type of fractional derivative. An entry \(\notin \) means that
for all \(\alpha >0\), where XY indicates the type of fractional derivative. An entry \(\notin \) means that  for all \(\alpha >0\). The table lists \(\notin _i\) if inclusion or exclusion depends on \(\alpha \), where the condition is given above together with the definition of \(f_i\).
for all \(\alpha >0\). The table lists \(\notin _i\) if inclusion or exclusion depends on \(\alpha \), where the condition is given above together with the definition of \(f_i\).
\(f_{\text A }\) | \(f_{\text B }\) | \(f_{\text C }\) | \(f_{\text D }\) | \(f_{\text E }\) | \(f_{\text F }\) | \(f_{\text G }\) | \(f_{\text H }\) | \(f_{\text I }\) | \(f_{\text J }\) | \(f_{\text K }\) | \(f_{\text L }\) | \(f_{\text M } \) | \(\texttt {dom}\left( ~\cdot ~\right) \) | equation |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
\(\in \) | \(\notin \) | \(\in \) | \(\notin \) | \(\notin \) | \(\notin \) | \(\notin \) | \(\notin \) | \(\notin \) | \(\notin \) | \(\notin \) | \(\in \) | \(\notin ^1_{\text M }\) |
| (2.8) |
\(\in \) | \(\notin \) | \(\in \) | \(\notin \) | \(\notin \) | \(\notin \) | \(\notin \) | \(\notin \) | \(\notin \) | \(\notin \) | \(\notin \) | \(\notin \) | \(\notin ^2_{\text M }\) |
| (2.25) |
\(\in \) | \(\notin \) | \(\in \) | \(\notin \) | \(\notin \) | \(\notin \) | \(\notin \) | \(\notin \) | \(\notin \) | \(\notin \) | \(\notin \) | \(\notin \) | \(\notin \) |
| (2.26) |
\(\in \) | \(\notin \) | \(\in \) | \(\notin \) | \(\notin \) | \(\notin \) | \(\notin \) | \(\notin \) | \(\notin \) | \(\notin \) | \(\notin \) | \(\notin \) | \(\in \) |
| (6.52) |
\(\notin \) | \(\in \) | \(\notin \) | \(\notin \) | \(\in \) | \(\in \) | \(\notin \) | \(\notin \) | \(\notin \) | \(\notin \) | \(\notin _{\text K }\) | \(\notin \) | \(\notin \) |
| (2.16) |
\(\in \) | \(\in \) | \(\in \) | \(\in \) | \(\in \) | \(\in \) | \(\in \) | \(\notin \) | \(\notin \) | \(\notin \) | \(\notin \) | \(\notin \) | \(\notin \) |
| (2.20) |
\(\in \) | \(\in \) | \(\in \) | \(\in \) | \(\in \) | \(\notin \) | \(\in \) | \(\notin \) | \(\notin \) | \(\notin \) | \(\notin \) | \(\in \) | \(\notin \) |
| (2.22) |
\(\notin \) | \(\notin \) | \(\notin \) | \(\notin \) | \(\notin \) | \(\in \) | \(\notin \) | \(\notin \) | \(\in \) | \(\in \) | \(\in \) | \(\notin \) | \(\notin \) |
| (5.5) |
\(\notin \) | \(\notin \) | \(\notin \) | \(\notin \) | \(\in \) | \(\in \) | \(\notin \) | \(\notin \) | \(\in \) | \(\in \) | \(\in \) | \(\notin \) | \(\notin \) |
| (6.7) |
\(\notin \) | \(\in \) | \(\notin \) | \(\in \) | \(\in \) | \(\notin \) | \(\notin \) | \(\notin \) | \(\in \) | \(\in \) | \(\in \) | \(\notin _{\text L }\) | \(\notin \) |
| (8.22) |
\(\in \) | \(\in \) | \(\in \) | \(\in \) | \(\in \) | \(\in \) | \(\in \) | \(\in \) | \(\in \) | \(\in \) | \(\in \) | \(\in \) | \(\in \) | \(\text {D} _{+}^{\alpha }\) | (7.26) |
Riemann-Liouville operators and other non-translation-invariant operators are missing from this table, because they operate on sometimes very different domains. Comparison with translation invariant operators would require extensions, embeddings or projections that influence the comparison. Lizorkin type operators and operational calculus operators are missing, because they operate not on distributions but equivalence classes thereof.
Distributions growing too fast, e.g. exponentially, on the left half axis fall outside the domain of all fractional derivative operators. After they have been excluded, there remains only one domain that contains all examples, namely that of the generalized Schwartz fractional derivative \(\text {D} _{+}^{\alpha }=\text {I} _{+}^{-\alpha }\) in the last row.
9.2 Unification theorem
The following theorem summarizes various examples of translation invariant fractional derivative operators that can be obtained as special cases of the generalized Schwartz fractional derivative \(\text {D} _{+}^{\alpha }\) defined in Section 7.3 with domain (7.26).
Theorem 7
-
(a)
It holds
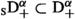 for \(\alpha \in \mathbb {C}\).
for \(\alpha \in \mathbb {C}\). -
(b)
It holds
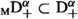 for \(\alpha \in \mathbb {R}_{+}\setminus \mathbb {N}\).
for \(\alpha \in \mathbb {R}_{+}\setminus \mathbb {N}\). -
(c)
It holds
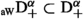 for \(\alpha \in \mathbb {C}\).
for \(\alpha \in \mathbb {C}\). -
(d)
It holds
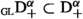 for \(\alpha \in \mathbb {C}\).
for \(\alpha \in \mathbb {C}\). -
(e)
It holds
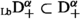 for \(\alpha \in \mathbb {H}\).
for \(\alpha \in \mathbb {H}\). -
(f)
It holds
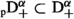 for \(\alpha \in \mathbb {R}_{0+}\).
for \(\alpha \in \mathbb {R}_{0+}\). -
(g)
It holds
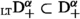 for \(\alpha \in \mathbb {C}\).
for \(\alpha \in \mathbb {C}\).
Proof
The inclusions of the domains are obvious in each case and it remains to verify the extension part. Part (a) is clear from Figure 2. For (c) and (e), one notes first, that

for all  . The equalities (9.1) extend to the respective domains of
. The equalities (9.1) extend to the respective domains of  and
and  by the density of
by the density of  and the continuity of transpose operators. For (b), one uses (9.1) and continuity properties of Lebesgue integrals. Part (d) follows from the considerations in Subsection 7.4. Part (f) was treated in Subsection 7.5.2. Part (g) follows from the convolution theorem (Theorem 6). \(\square \)
and the continuity of transpose operators. For (b), one uses (9.1) and continuity properties of Lebesgue integrals. Part (d) follows from the considerations in Subsection 7.4. Part (f) was treated in Subsection 7.5.2. Part (g) follows from the convolution theorem (Theorem 6). \(\square \)
9.3 Weak Weyl-, Marchaud- and Grünwald-Letnikov derivatives
The generalized Schwartz fractional derivative \(\text {D} _{+}^{\alpha }\) from eq. (7.15) can be interpreted as a weak formulation of fractional derivatives in the following sense:
Theorem 8
-
(a)
Let \(\alpha \in \mathbb {C}\) and
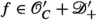 . Then
. Then 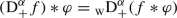 (9.2a)
(9.2a)for all
 with the right hand side defined point wise by eq. (2.15).
with the right hand side defined point wise by eq. (2.15). -
(b)
Let \(\alpha \in \mathbb {R}_{+}\setminus \mathbb {N}\) and
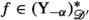 . Then
. Then 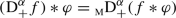 (9.2b)
(9.2b)for all
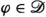 with the right hand side defined point wise by eq. (2.17).
with the right hand side defined point wise by eq. (2.17). -
(c)
Let \(\alpha \in \mathbb {C}\) and
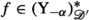 . Then
. Then  (9.2c)
(9.2c)for all
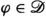 with the right hand side defined point wise by eq. (2.21).
with the right hand side defined point wise by eq. (2.21).
Proof
Associativity yields \((\text {D} _{+}^{\alpha }f)*\varphi =\text {D} _{+}^{\alpha }(f*\varphi )\) for  . Thus, it is clear that the equations hold for
. Thus, it is clear that the equations hold for  . The general case is obtained by considering approximations \(f\theta _n\rightarrow f\) via an approximate unit \((\theta _n)\), that is, a sequence
. The general case is obtained by considering approximations \(f\theta _n\rightarrow f\) via an approximate unit \((\theta _n)\), that is, a sequence  that is bounded in
that is bounded in  and satisfies \(\theta _n\rightarrow 1\) in
and satisfies \(\theta _n\rightarrow 1\) in  . It is readily seen, that the limits
. It is readily seen, that the limits  . \(\square \)
. \(\square \)
The theorem implies that it is possible to employ the Grünwald-Letnikov fractional derivative of functions to define the generalized Schwartz fractional derivative of distributions by the formula

for all \(\alpha \in \mathbb {C}\),  and
and  . The same is possible for the Marchaud fractional derivative if \(\alpha \in \mathbb {R}_{+}\setminus \mathbb {N}\).
. The same is possible for the Marchaud fractional derivative if \(\alpha \in \mathbb {R}_{+}\setminus \mathbb {N}\).
Notes
and because Weyl is credited for being the first to define fractional integrals for functions on the whole real axis [84].
For operators A and B whose domain and range is contained within a common space X the domain of their composition is \(\texttt {dom}\left( A\circ B\right) =\{f\in \texttt {dom}\left( B\right) : Bf\in \texttt {dom}\left( A\right) \}\).
References
Leibniz, G.: IV. Epistola D. Leibnitii ad Wallisium, 28. Maii 1697. In: L. Dutens (ed.) Opera omnia, tomus tertius, continens opera mathematica, pp. 103–107. Fratres de Tournes, Geneva (1767)
Leibniz, G.: Symbolismus memorabilis calculi Algebraici et infinitesimalis, in comparatione potentiarum et differentiarum; et de Lege Homogeneorum Transcendentali. Miscellaneo Berolinensia ad incrementum scientiarum, ex scriptis Societate Regiae Scientiarum exhibitis I, 160 (1710)
Hilfer, R.: Mathematical and physical interpretations of fractional derivatives and integrals. In: A. Kochubei, Y. Luchko (eds.) Handbook of Fractional Calculus with Applications: Basic Theory, vol. 1, pp. 47–86. Walter de Gruyter GmbH, Berlin (2019). https://doi.org/10.1515/9783110571622
Schwartz, L.: Generalisation de la notion de fonction, de derivation, de transformation de Fourier et applications mathematiques et physiques. Annales de l’universite de Grenoble 21, 57–74 (1945)
Schwartz, L.: Theorie des Distributions, vols. 1–2, Nouvelle edn. Hermann, Paris (1966)
Wiener, N.: The operational calculus. Math. Ann. 95, 557–584 (1926)
Mikusinski, J.: Sur les fondements du calcul operatoire. Stud. Math. 11, 41–70 (1950)
Mikusinski, J.: Operational Calculus. PWN, Warszaw (1959)
Dirac, P.: The physical interpretation of the quantum dynamics. Proc. Roy. Soc. Lond. A 113, 621–641 (1927)
Carson, J.: Elektrische Ausgleichvorgänge und Operatorenrechnung. Springer, Berlin (1929)
Vahlen, K.: Über den Heaviside-Kalkül. Z. Angew. Math. Mech. 13, 283–298 (1933)
Kochubei, A., Luchko, Y.: Basic FC operators and their properties. In: Kochubei, A., Luchko, Y. (eds.) Handbook of Fractional Calculus with Applications: Basic Theory, vol. 1, pp. 23–46. Walter de Gruyter GmbH, Berlin (2019)
Luchko, Y.: Fractional derivatives and the fundamental theorem of fractional calculus. Fract. Calc. Appl. Anal. 23, 939–966 (2020). https://doi.org/10.1515/fca-2020-0049
Diethelm, K., Kiryakova, V., Luchko, Y., Tenreiro-Machado, J., Tarasov, V.: Trends, directions for further research, and some open problems of fractional calculus. Nonlinear Dyn. 107, 3245–3270 (2022)
Gelfand, I., Shilov, G.: Generalized Functions, vol. I. Academic Press, New York (1964)
Samko, S., Kilbas, A., Marichev, O.: Fractional Integrals and Derivatives. Gordon and Breach, Berlin (1993)
Rubin, B.: Fractional Integrals and Potentials. Longman, Harlow (1996)
Oldham, K., Spanier, J.: The Fractional Calculus. Academic Press, New York (1974)
Miller, K., Ross, B.: An Introduction to the Fractional Calculus and Fractional Differential Equations. Wiley, New York (1993)
Kilbas, A., Srivastava, H., Trujillo, J.: Theory and Applications of Fractional Differential Equations. Elsevier, Amsterdam (2006)
Diethelm, K.: The Analysis of Fractional Differential Equations. Springer, Berlin (2010)
Uchaikin, V.: Fractional Derivatives for Physicists and Engineers I. Springer, Berlin (2012)
Podlubny, I.: Fractional Differential Equations. Academic Press, London (1999)
Mainardi, F.: Fractional Calculus and Waves in Linear Elasticity. World Scientific, Singapore (2022)
McBride, A.: Fractional Calculus and Integral Transform of Generalized Functions. Pitman Publishing Ltd, San Francisco (1979)
Kochubei, A., Luchko, Yu. (eds.): Handbook of Fractional Calculus with Applications, Vol. 1: Basic Theory. de Gruyter, Berlin (2019)
Martinez Carracedo, C., Sanz Alix, M.: The Theory of Fractional Powers of Operators. Elsevier, Amsterdam (2001)
Kiryakova, V.: Generalized Fractional Calculus and Applications. Longman, Essex (1994)
Ross, B.: Fractional Calculus and Its Applications. Lecture Notes in Mathematics, vol. 457. Springer, Berlin (1975)
Butzer, R., Berens, H.: Semigroups of Operators and Approximation, Die Grundleheren der mathematischen Wissenschaften in Einzeldarstellungen, vol. 145. Springer, Berlin (1967)
Butzer, P., Trebels, W.: Hilberttransformationen, gebrochene Integration und Differentiation. In: L. Brandt (ed.) Forschungsberichte des Landes Nordrhein-Westfalen, Nr. 1889, pp. 1–81. Westdeutscher Verlag, Köln, Opladen (1968)
Riesz, M.: L’integrale de Riemann-Liouville et le probleme de Cauchy. Acta Math. 81, 1 (1949)
Liouville, J.: Mémoire sur quelques Questions de Geometrie et de Mecanique, et sur un nouveau genre de Calcul pour resoudre ces Questions. Journal de l’Ecole Polytechnique XIII, 1 (1832)
Riemann, B.: Versuch einer allgemeinen Auffassung der Integration und Differentiation, (Januar 1847). In: Weber, H. (ed.) Bernhard Riemann’s gesammelte mathematische Werke und wissenschaftlicher Nachlass, pp. 333–344. Teubner, Leipzig (1876)
Hardy, G., Littlewood, J.: Some properties of fractional integrals. I. Math. Zeitschr. XXVII, 565 (1928)
Erdelyi, A., et al.: Tables of Integral Transforms, vol. II. Mc Graw Hill Book Co., New York (1954)
Butzer, P., Westphal, U.: Introduction to fractional calculus. In: Hilfer, R. (ed.) Applications of Fractional Calculus in Physics, pp. 1–86. World Scientific, Singapore (2000)
Hilfer, R.: Threefold introduction to fractional derivatives. In: R. Klages, G. Radons, I. Sokolov (eds.) Anomalous Transport: Foundations and Applications, pp. 17–74. Wiley-VCH, Weinheim (2008). https://www.wiley.com/en-ad/Anomalous+Transport%3A+ Foundations+and+Applications-p-9783527407224
Wigner, E.: Events, laws of nature and invariance principles. Nobel Lecture, December 12, 1963 (1963)
Streater, R., Wightman, A.: PCT, Spin and Statistics, and All That. Benjamin Inc., Reading (1964)
Scheck, F.: Theoretische Physik 1 - Mechanik, 8. Auflage Springer, Berlin (2007)
Lizorkin, P.: Generalized Liouville differentiation and the functional space \(l_p^r(e_n)\). Imbedding theorems. Mat.Sb. (N.S.) 102, 325–353 (1963)
Lizorkin, P.: Generalized Liouville differentiation and the multiplier method in the theory of imbeddings of classes of differentiable functions. Trudy Mat. Inst. Steklov 105, 89–167 (1969)
Schwartz, L.: Sur l’impossibilite de la multiplication des distributions. C. R. Acad. Sci. 239, 847–848 (1954)
Hille, E., Phillips, R.: Functional Analysis and Semi-Groups. American Mathematical Society, Providence (1957)
Balakrishnan, A.: Fractional powers of closed operators and the semigroups generated by them. Pac. J. Math. 10, 419 (1960)
Komatsu, H.: Fractional powers of operators. Pac. J. Math. 19, 285 (1966)
Andersson, M., Sjöstrand, J.: Functional calculus for non-commuting operators with real spectra via an iterated Cauchy formula. J. Funct. Anal. 210, 341–375 (2004)
Kleiner, T., Hilfer, R.: Convolution operators on weighted spaces of continuous functions and supremal convolution. Annali di Matematica 199, 1547–1569 (2020). https://doi.org/10.1007/s10231-019-00931-z
Kleiner, T., Hilfer, R.: Weyl integrals on weighted spaces. Fract. Calc. Appl. Anal. 22, 1225–1248 (2019). https://doi.org/10.1515/fca-2019-0065
Stojanovic, M.: Fractional derivatives in spaces of generalized functions. Fract. Calc. Appl. Anal. 14, 125–137 (2011)
Mincheva-Kaminska, S.: Convolutional approach to fractional calculus for distributions of several variables. Fract. Calc. Appl. Anal. 19, 441–462 (2016). https://doi.org/10.1515/fca-2016-0023
Hilfer, R., Kleiner, T.: Maximal domains for fractional derivatives and integrals. Mathematics 8, 1107 (2020). https://doi.org/10.3390/math8071107
Kleiner, T., Hilfer, R.: Fractional glassy relaxation and convolution modules of distributions. Anal. Math. Phys. 11, 130 (2021). https://doi.org/10.1007/s13324-021-00504-5
Kleiner, T., Hilfer, R.: On extremal domains and codomains for convolution of distributions and fractional calculus. Monatshefte für Mathematik 198, 122–152 (2022). https://doi.org/10.1007/s00605-021-01646-1
Yosida, K.: Operational Calculus. Springer, Berlin (1984)
Kleiner, T., Hilfer, R.: Sequential generalized Riemann-Liouville derivatives based on distributional convolution. Fract. Calc. Appl. Anal. 25, 267–298 (2022). https://doi.org/10.1007/s13540-021-00012-0
Hilfer, R.: Fractional time evolution. In: R. Hilfer (ed.) Applications of Fractional Calculus in Physics, pp. 87–130. World Scientific, Singapore (2000). https://doi.org/10.1142/3779
Garra, R., Gorenflo, R., Polito, F., Tomovski, Z.: Hilfer-Prabhakar derivatives and some applications. Appl. Math. Comput. 242, 576–589 (2014)
Saxena, R., Garra, R., Orsingher, E.: Analytical solution of space-time fractional telegraph-type equations involving Hilfer and Hadamard derivatives. Integral Transform. Spec. Funct. 27, 30–42 (2016)
Kamocki, R.: A new representation formula for the Hilfer fractional derivative and its application. J. Comput. Appl. Math. 308, 39–45 (2016)
Abbas, S., Benchohra, M., Bohner, M.: Weak solutions for implicit differential equations with Hilfer-Hadamard fractional derivative. Adv. Dyn. Syst. Appl. 12, 1–16 (2017)
Sousa, J., Jarad, F., Abdeljawad, T.: Existence of mild solutions to Hilfer fractional evolution equations in Banach space. Ann. Funct. Anal. 12, 12 (2021)
Zhou, Y., He, J.: A Cauchy problem for fractional evolution equations with Hilfer’s fractional derivative on semi-infinite interval. Fract. Calc. Appl. Anal. 25, 924–961 (2022). https://doi.org/10.1007/s13540-022-00057-9
Sandev, T., Metzler, R., Tomovski, Z.: Fractional diffusion equation with a generalized Riemann-Liouville time fractional derivative. J. Phys. A: Math. Theor. 44, 255203 (2011)
Dubbeldam, J., Tomovski, Z., Sandev, T.: Space-time fractional Schrödinger equation with composite time fractional derivative. Fract. Calc. Appl. Anal. 18, 1179–1200 (2015)
Vivek, D., Kanagarajan, K., Sivasundaram, S.: Dynamics and stability results for Hilfer fractional type thermistor problem. Fractal Fract. 1, 5 (2017)
Lv, J., Yang, X.: A class of Hilfer fractional stochastic differential equations and optimal controls. Adv. Differ. Equ. 2019, 17 (2015)
Anastassiou, G.: Unification of Fractional Calculi with Applications. Springer, Berlin (2022)
Lunkenheimer, P., Loidl, A.: Dielectric spectroscopy of glass-forming materials: \(\alpha \)-relaxation and excess wing. Chem. Phys. 284, 205–219 (2002)
Hilfer, R.: Fitting the excess wing in the dielectric alpha-relaxation of propylene carbonate. J. Phys.: Condens. Matter 14, 2297 (2002). https://doi.org/10.1088/0953-8984/14/9/318
Hilfer, R.: Excess wing physics and nearly constant loss in glasses. J. Stat. Mech: Theory Exp. 2019, 104007 (2019). https://doi.org/10.1088/1742-5468/ab38bc
Douglas, J.: Polymer science applications of path-integration, integral equations and fractional calculus. In: Hilfer, R. (ed.) Applications of Fractional Calculus in Physics, pp. 241–330. World Scientific, Singapore (2000)
Hilfer, R.: Experimental implications of Bochner-Levy-Riesz diffusion. Fract. Calc. Appl. Anal. 18, 333–341 (2015). https://doi.org/10.1515/fca-2015-0022
Hilfer, R.: Multiscaling and the classification of continuous phase transitions. Phys. Rev. Lett. 68, 190 (1992). https://doi.org/10.1103/PhysRevLett.68.190
Hilfer, R.: Fractional calculus and regular variation in thermodynamics. In: R. Hilfer (ed.) Applications of Fractional Calculus in Physics, pp. 429–463. World Scientific, Singapore (2000). https://doi.org/10.1142/3779
Hilfer, R., Anton, L.: Fractional master equations and fractal time random walks. Phys. Rev. E Rapid Commun. 51, R848 (1995). https://doi.org/10.1103/PhysRevE.51.R848
Hilfer, R.: Exact solutions for a class of fractal time random walks. Fractals 3(1), 211–216 (1995). https://doi.org/10.1142/S0218348X95000163
Hilfer, R.: Fractional dynamics, irreversibility and ergodicity breaking. Chaos Solitons Fractals 5, 1475 (1995). https://doi.org/10.1016/0960-0779(95)00027-2
Hilfer, R.: Foundations of fractional dynamics. Fractals 3, 549 (1995). https://doi.org/10.1142/S0218348X95000485
Hilfer, R.: Mathematical analysis of time flow. Analysis 36, 49–64 (2016). https://doi.org/10.1515/anly-2015-5005
Weyl, H.: Bemerkungen zum Begriff des Differentialquotienten gebrochener Ordnung. Vierteljahresschrift der Naturforsch. Ges. Zürich 62, 296 (1917)
Zygmund, A.: Trigonometric Series, vol. II. Cambridge University Press, Cambridge (1959)
Love, E.: Fractional integration and almost periodic functions. Proc. Lond. Math. Soc. 2(44), 363–397 (1938)
Kober, H.: On fractional integrals and derivatives. Q. J. Math. 11, 193 (1940)
Martinez, C., Sanz, M., Martinez, D.: About fractional integrals in the space of locally integrable functions. J. Math. Anal. Appl. 167, 111–122 (1992)
Marchaud, A.: Sur les derivees et sur les differences des fonctions de variables reelles. J. Math. Pures Appl. 6, 337–425 (1927)
Grünwald, A.K.: Über “begrenzte” Derivationen und deren Anwendung. Z.f.Math. und Phys. 12, 441 (1867)
Letnikov, A.: Theory of differentiation with an arbitrary index. Mat. Sb. 3, 1–66 (1868)
Abadias, L., DeLeon-Contreras, M., Torrea, J.: Non-local fractional derivatives. Discrete and continuous. J. Math. Anal. Appl. 449, 734–755 (2017)
Butzer, P., Westphal, U.: An access to fractional differentiation via fractional difference quotients. In: B. Ross (ed.) Fractional Calculus and Its Applications. Lecture Notes in Mathematics, vol. 457. Springer, New York (1975)
Diaz, J., Osler, T.: Differences of fractional order. Math. Comput. 28, 185–202 (1974)
Butzer, P., Dyckhoff, H., Görlich, E., Stens, R.: Best trigonometric approximation, fractional order derivatives and Lipschitz classes. Can. J. Math. 29, 781–793 (1977)
Wilmes, G.: On Riesz-type inequalities and \(K\)-functionals related to Riesz potentials in \(\mathbb{R} ^n\). Numer. Funct. Anal. Optim. 1, 57–77 (1977)
Peressini, A.: Ordered Topological Vector Spaces. Harper & Row, New York (1967)
Aliprantis, C., Burkinshaw, O.: Locally Solid Riesz Spaces with Applications to Economics. American Mathematical Society, Providence (2003)
Bourbaki, N.: Elements of Mathematics: Integration I. Springer, Berlin (2004)
Edwards, R.: A theory of Radon measures on locally compact spaces. Acta Math. 89, 133–164 (1953)
Godement, R.: Analysis IV: Integration and Spectral Theory. Springer, Berlin (2015)
Reiter, H., Stegemann, J.: Classical Harmonic Analysis on Locally Compact Groups. Clarendon Press, Oxford (2000)
Hirata, Y.: On convolutions in the theory of distributions. J. Sci. Hiroshima Univ. Ser. A 22, 89–98 (1958)
Yoshinaga, K., Ogata, H.: On convolutions. J. Sci. Hiroshima Univ. Ser. A 22, 15–24 (1958)
Birkhoff, G.: Lattice Theory, 3rd edn. American Mathematical Society, Providence (1973)
Pincherle, S.: Funktionaloperationen und -gleichungen. Encyklopädie der mathematischen Wissenschaften mit Einschluss ihrer Anwendungen II A 11, 761–817 (1906)
Heaviside, O.: On operators in physical mathematics. Part I. Proc. Roy. Soc. A 52, 504–529 (1893)
Erdelyi, A.: Operational Calculus and Generalized Functions. Holt, Rinehart and Winston, New York (1962)
Dimovski, I.: Convolutional Calculus. Kluwer, Dordrecht (1990)
Glaeske, H., Prudnikov, A., Skornik, K.: Operational Calculus and Related Topics. Chapman and Hall, Boca Raton (1996)
Luchko, Y.: Operational methods for fractional ordinary differential equations. In: Kochubei, A., Luchko, Y. (eds.) Handbook of Fractional Calculus with Applications: Basic Theory, vol. 2, pp. 91–118. Walter de Gruyter GmbH, Berlin (2019)
Luchko, Y.: Operational calculus for the general fractional derivative and its applications. Fract. Calc. Appl. Anal. 24, 338–375 (2021). https://doi.org/10.1515/fca-2021-0016
Titchmarsh, E.: Introduction to the Theory of Fourier Integrals. Clarendon Press, Oxford (1948)
Bourbaki, N.: Elements of Mathematics: Agebra I. Springer, Berlin (1989)
Lang, S.: Algebra. Springer, Berlin (1993)
Struble, R.: An algebraic view of distributions and operators. Stud. Math. 37, 103–109 (1971)
Schwartz, L.: Theorie des Distributions. Hermann, Paris (1950)
Hörmander, L.: The Analysis of Linear Partial Differential Operators, vol. 1. Springer, Berlin (1990)
Horvath, J.: Topological Vector Spaces and Distributions. Addison-Wesley, Reading (1966)
Ortigueira, M.: Fractional Calculus for Scientists and Engineers. Springer, Berlin (2011)
Ortigueira, M., Valerio, D., Lopes, A.: Continuous-time fractional linear systems: transient responses. In: Petras, I. (ed.) Handbook of Fractional Calculus with Applications: Applications and Control, vol. 6, pp. 119–148. Walter de Gruyter GmbH, Berlin (2019)
Atanckovic, T., Pilipovic, S., Zorica, D.: Properties of the Caputo-Fabrizio fractional derivative and its distributional setting. Fract. Calc. Appl. Anal. 21, 29–44 (2018). https://doi.org/10.1515/fca-2018-0003
Li, C.: Several results on fractional derivatives in \(\cal{D} ^\prime ({R}_+)\). Fract. Calc. Appl. Anal. 18, 192–207 (2015)
Erdelyi, A., McBride, A.: Fractional integrals of distributions. SIAM J. Math. Anal. 1, 547–557 (1970)
Erdelyi, A.: Fractional integrals of generalized functions. In: B. Ross (ed.) Fractional Calculus and Its Applications. Lecture Notes in Mathematics, vol. 457, pp. 151–170. Springer, New York (1975)
McBride, A.: A theory of fractional integration for generalized functions. SIAM J. Math. Anal. 6, 583–599 (1975)
Kleiner, T.: Lokalkonvexe Funktionenräume und fraktionale Weyl-Ableitungen. Master’s thesis, Universität Stuttgart (2016)
Miller, K.: The Weyl fractional calculus. In: Ross, B. (ed.) Fractional Calculus and Its Applications. Lecture Notes in Mathematics, vol. 457, pp. 80–89. Springer, New York (1975)
Rubin, B.: On fractional integration of generalized functions on a half-line. Proc. Edinb. Math. Soc. 38, 387–396 (1995)
Love, E., Young, L.: On fractional integration by parts. Proc. Lond. Math. Soc. Ser. 2(11), 1–35 (1938)
Erdelyi, A.: Fractional integrals of generalized functions. J. Austral. Math. Soc. 14, 30–37 (1972)
Braaksma, B., Schuitman, A.: Some classes of Watson transforms and related integral equations for generalized functions. SIAM J. Math. Anal. 7, 771–798 (1976)
Lamb, W.: A distributional theory of fractional calculus. Proc. R. Soc. Edinb. 99A, 347–357 (1985)
Schiavone, S., Lamb, W.: A fractional power approach to fractional calculus. J. Math. Anal. Appl. 149, 377–401 (1990)
Khan, K., Lamb, W., McBride, A.: Fractional calculus of periodic distributions. Fract. Calc. Appl. Anal. 14, 260–283 (2011)
Schwartz, L.: Definition integrale de la convolution de deux distributions. Seminaire Schwartz 1, 1–7 (1954)
Horvath, J.: Sur la Convolution des Distributions. Bull. Sci. Math. 98, 183–192 (1974)
Ortner, N.: On some contributions of John Horvath to the theory of distributions. J. Math. Anal. Appl. 297, 353–383 (2004)
Vladimirov, V.: Methods of the Theory of Generalized Functions. Taylor and Francis, London (2002)
Ortner, N., Wagner, P.: Distribution-Valued Analytic Functions-Theory and Applications. tredition GmbH, Hamburg (2013)
Ortner, N., Wagner, P.: Fundamental Solutions of Linear Partial Differential Operators. Springer, Cham (2015)
Shiraishi, R.: On the definition of convolutions for distributions. J. Sci. Hiroshima Univ. Ser. A 23, 19–32 (1959)
Dierolf, P., Voigt, J.: Convolution and S’-convolution of distribuions. Collect. Math. 29, 185–196 (1978)
Youn, H., Richards, I.: On the general definition of convolution for distributions. J. Korean Math. Soc. 17, 13–37 (1980)
Youn, H., Richards, I.: On the general definition of convolution for several distributions. J. Korean Math. Soc. 17, 161–168 (1981)
Ortner, N.: On convolvability conditions for distributions. Monatshefte für Mathematik 160, 313–335 (2010)
Edwards, R.: Functional Analysis. Holt, Rinehart and Winston, New York (1965)
Cui, Z., Omey, E., Wang, W., Wang, Y.: Asymptotics of convolution with the semi-regular-variation tail and its application to risk. Extremes 21, 509–532 (2018)
Feller, W.: An Introduction to Probability Theory and Its Applications, vol. II. Wiley, New York (1971)
Ortigueira, M., Rivero, M., Trujillo, J.: The incremental ratio based causal fractional calculus. Int. J. Bifurc. Chaos 22, 1250078 (2012)
Kleiner, T., Hilfer, R.: Convolution on distribution spaces characterized by regularization. Math. Nachr. 296, 1938–1963 (2023). https://doi.org/10.1002/mana.202100330
Bochner, S.: Stochastic processes. Ann. Math. 48, 1014–1061 (1947)
Silvestre, L.: Regularity of the obstacle problem for a fractional power of the Laplace operator. Commun. Pure Appl. Math. LX, 0067-0112 (2007)
Kwasnicki, M.: Fractional Laplace operator and its properties. In: Kochubei, A., Luchko, Y. (eds.) Handbook of Fractional Calculus with Applications: Basic Theory, vol. 1, pp. 159–193. Walter de Gruyter GmbH, Berlin (2019)
Caffarelli, L., Silvestre, L.: An extension problem related to the fractional Laplacian. Commun. Partial Differ. Equ. 32, 1245–1260 (2007)
Pagnini, G., Runfola, C.: Mellin definition of the fractional Laplacian. Fract. Calc. Appl. Anal. 26, s13540-023-00190-z 2101–2117 (2023)
Kleiner, T.: Faltungskalkül mit translationsinvarianten Amalgamräumen von Distributionen auf Euklidischen Räumen. Ph.D. thesis, Universität Stuttgart (2024)
Martines, C., Sanz, M., Periago, F.: Distributional fractional powers of the Laplacean. Riesz potentials. Stud. Math. 135, 253–271 (1999)
Zemanian, A.: Distribution Theory and Transform Analysis. McGraw-Hill, New York (1965)
Mincheva-Kaminska, S.: Convolution of distributions in sequential approach. Filomat 28, 1543–1557 (2014)
Ortner, N.: Sur la convolution des distributions. C. R. Acad. Sci. Paris 290, 533–536 (1980)
Bargetz, C., Ortner, N.: Kernel identities and vectorial regularisation. Monatsh. Math. 186, 201–214 (2018)
Adams, R.: Sobolev Spaces. Academic Press, New York (1975)
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
Not applicable.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
1.1 General notation
Natural, integer, real and complex numbers are denoted \(\mathbb {N},\mathbb {Z},\mathbb {R},\mathbb {C}\), and \(\mathbb {N}_0\) is the set of natural numbers with zero. Positive real numbers are denoted \(\mathbb {R}_{+}:=]0,\infty [\), non-negative real numbers as \(\mathbb {R}_{0+}:=[0,\infty [\). The set \(\overline{\mathbb {R}}_{+}:=[0,\infty ]\) consists of the non-negative real numbers including infinity with the convention \(0\cdot \infty =0\). The open resp. closed complex half plane is written \(\mathbb {H}\) resp. \(\overline{\mathbb {H}}\). The shorthand notations \(X^d:=X\times \ldots \times X\) for d-fold cartesian products and \(X^\times :=X\setminus \{0\}\) for excluding zero are used.
1.2 Locally convex spaces
A few basic concepts of locally convex spaces are collected here for convenient reference. A seminorm on a vector space X is a function \(q:X\rightarrow \mathbb {R}_{0+}\) such that \(q(\lambda x)=|\lambda |q(x)\) and \(q(x+y)\le q(x)+q(y)\). Let A be an arbitray set of indices. The topology of a locally convex space can be defined by a family \((q_a)_{a\in A}\) of seminorms by choosing the family of sets \((\{x\in X;q_a(x)<\lambda \})_{a\in A, \lambda >0}\) and their finite intersections as neighbourhoods of zero. This topology is Hausdorff if and only if for every \(x\ne 0\) there is an \(a\in A\) such that \(q_a(x)\ne 0\).
A set \(B\subseteq X\) is bounded if every seminorm \(q_a, a\in A\) is bounded on B. The concept of bounded set is not very important in normed spaces \((Y,\Vert ~\cdot ~\Vert )\), because it is then the same as the concept of “subset of a ball”, where a ball of radius R is defined by \(\{y\in Y:\Vert y\Vert \le R\}\). In locally convex spaces there does not in general exist a fundamental system of bounded neighbourhoods of zero. Indeed, a Hausdorff locally convex space is normable if and only if it has at least one bounded neighbourhood of zero [117, p. 108]. A locally convex space is metrizable if and only if it is Hausdorff and its topology can be generated by a countable family of seminorms.
The topological dual space \(X^\prime \) of a locally convex space X is the space of continuous linear functionals \(x^\prime :X\rightarrow \mathbb {C}\), often written as \(x^\prime (x)=\langle x^\prime , x \rangle \) a bracket or product. For any subset \(A\subset X\) its polar \(A^o\) in \(X^\prime \) is the set of all \(x^\prime \in X^\prime \) such that \(|\langle x^\prime , x \rangle |\le 1\) for all \(x\in A\).
Let \(\mathfrak {S}\) denote a family of subsets of X. The so called \(\mathfrak {S}\)-topology on the dual space \(X^\prime \) is the topology which has a fundamental system of neighbourhoods of zero consisting of the finite intersections of the polars of the sets \(A\in \mathfrak {S}\). The most important \(\mathfrak {S}\)-topologies on \(X^\prime \) arise from choosing \(\mathfrak {S}=\{\{x\}\subset X;x\in X\}\) or \(\mathfrak {S}=\{A\subset X; A \text {~bounded} \}\). The former is called topology of pointwise convergence or weak* topology and denoted as \(\sigma (X^\prime ,X)\), while the latter is called topology of bounded convergence or strong topology and denoted as \(\beta (X^\prime ,X)\). When X is a normed space, then \(\beta (X^\prime ,X)\) is the usual dual norm topology.
1.3 Function spaces
Let \(\Omega \subseteq \mathbb {R}^d\) be an open set, \(\mathfrak {M}\) a \(\sigma \)-algebra of subsets of \(\Omega \), and \(\mu \) a measure on \(\mathfrak {M}\). The Lebesgue spaces of equivalence classes of integrable functions over the measure space \((\Omega ,\mathfrak {M},\mu )\) are defined as
with norm
and their locally integrable variants are
For \(p=\infty \)
where
and
is the essential range of f.
Let \(\Omega \subseteq \mathbb {R}^d\) be open with boundary \(\partial \Omega \). For \(\Omega =\mathbb {R}^d\) the phrase “for all \(x\in \partial \Omega \)” means “for all \(|x|\rightarrow \infty \)”. Denote with \(\mathbb {C}^\Omega \) the set of all complex valued functions \(f:\Omega \rightarrow \mathbb {C}\). The notation for spaces of functions is \((\kappa \in \mathbb {N}^d,|\kappa |=\kappa _1+\ldots +\kappa _d\), \(k\in \mathbb {N})\)

















If \(K\subset \Omega \) is compact, the spaces of functions \(f:K\rightarrow \mathbb {C}\) are denoted

where  . In these cases the topology of
. In these cases the topology of  is the subspace topology inherited from
is the subspace topology inherited from  . As an example, for \(d=1\) and \(K=[a,b]\subset \mathbb {R}\)
. As an example, for \(d=1\) and \(K=[a,b]\subset \mathbb {R}\)

are the absolutely continuous functions on [a, b].
The spaces  are known as Hölder spaces. For \(0<\alpha <\beta \le 1\) they obey
are known as Hölder spaces. For \(0<\alpha <\beta \le 1\) they obey  if \(K\subset \Omega \) [161, p. 10]. The space
if \(K\subset \Omega \) [161, p. 10]. The space  , consists of slowly increasing smooth functions, while
, consists of slowly increasing smooth functions, while  is the space of very slowly increasing smooth functions. The spaces
is the space of very slowly increasing smooth functions. The spaces  of Lebesgue integrable test functions are known as Sobolev spaces, and often denoted as \(W^{\infty ,p}(\Omega )\). Table 1 compares our notation for some function spaces with other widespread notations in the literature.
of Lebesgue integrable test functions are known as Sobolev spaces, and often denoted as \(W^{\infty ,p}(\Omega )\). Table 1 compares our notation for some function spaces with other widespread notations in the literature.
 is defined as the space
is defined as the space  equipped with the finest locally convex topology that induces the topology of
equipped with the finest locally convex topology that induces the topology of  on the subsets of
on the subsets of  which are bounded w.r.t its Frechet topology generated by the seminorms \(\varphi \mapsto \Vert \partial ^\kappa \varphi \Vert _\infty \), \(\kappa \in \mathbb {N}_0^d\). This topology is weaker than the Frechet topology on
which are bounded w.r.t its Frechet topology generated by the seminorms \(\varphi \mapsto \Vert \partial ^\kappa \varphi \Vert _\infty \), \(\kappa \in \mathbb {N}_0^d\). This topology is weaker than the Frechet topology on  . However,
. However,  and
and  have the same bounded subsets.
have the same bounded subsets.
1.4 Spaces of Radon measures
Spaces of Radon measures are defined as topological duals of spaces of continuous functions,



where only the case \(p=1\) is needed here.
1.5 Distribution spaces
Spaces of distributions are defined as topological duals \(X^\prime \) of test function spaces  equipped with the strong topology \(\beta (X^\prime ,X)\) of uniform convergence on bounded subsets of X [5, p. 71], [145, p. 300],[117, p. 201].
equipped with the strong topology \(\beta (X^\prime ,X)\) of uniform convergence on bounded subsets of X [5, p. 71], [145, p. 300],[117, p. 201].






The space  of tempered distributions
of tempered distributions  is the dual of the space of rapidly decreasing (Schwartz) functions
is the dual of the space of rapidly decreasing (Schwartz) functions  . The space
. The space  of distributions with compact support is the dual of the space of smooth functions
of distributions with compact support is the dual of the space of smooth functions  .
.  resp.
resp.  are the spaces of rapidly decreasing resp. very rapidly decreasing decreasing distributions. The following continuous inclusions (with \(1/p+1/q=1\) and \(1<p\le q<\infty \))
are the spaces of rapidly decreasing resp. very rapidly decreasing decreasing distributions. The following continuous inclusions (with \(1/p+1/q=1\) and \(1<p\le q<\infty \))

apply to some of the spaces of smooth and continuous functions, Radon measures and distributions. For the first and last row see [5, p. 420]. Other chains of inclusions may exist between some spaces as evident from Figure 4 for differentiable functions and, for \(\Omega =\mathbb {R}^d\) from (3.12) and (7.5). Spaces for the missing entries in the third row can be constructed using Amalgam spaces with local component  , that were considered in [155, Sec. V.2], by choosing suitable global components.
, that were considered in [155, Sec. V.2], by choosing suitable global components.
Given a locally convex space X of distributions, Schwartz defined its pre-image under the maps  as the following set of smooth functions
as the following set of smooth functions

equipped with the coarsest topology such that all the maps  are continuous (projective topology). He then introduced the distribution spaces
are continuous (projective topology). He then introduced the distribution spaces

the space of continuous linear functionals on  equipped with the topology of uniform convergence on bounded subsets of
equipped with the topology of uniform convergence on bounded subsets of  (Table 2).
(Table 2).
The reflection of a locally integrable function f(x) with respect to the origin, denoted  , is defined as [5, p. 167]
, is defined as [5, p. 167]

so that with

the reflection of a distribution is defined by

Rights and permissions
This article is published under an open access license. Please check the 'Copyright Information' section either on this page or in the PDF for details of this license and what re-use is permitted. If your intended use exceeds what is permitted by the license or if you are unable to locate the licence and re-use information, please contact the Rights and Permissions team.
About this article
Cite this article
Hilfer, R., Kleiner, T. Fractional calculus for distributions. Fract Calc Appl Anal (2024). https://doi.org/10.1007/s13540-024-00306-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s13540-024-00306-z



 -convolution
-convolution -convolution
-convolution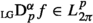 .
.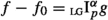 almost everywhere.
almost everywhere.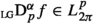 , then
, then 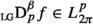 for any
for any 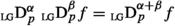 whenever one of the two sides is meaningful.
whenever one of the two sides is meaningful.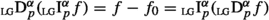 where the second equality holds if
where the second equality holds if  .
.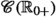 also represents an operator (because it can be represented as
also represents an operator (because it can be represented as 
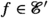 or
or 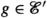 , or
, or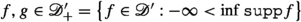 .
.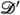 -convolution
-convolution
 -convolution
-convolution
 -convolvable, then
-convolvable, then  -convolvable and
-convolvable and 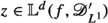 , then
, then  -convolvable and
-convolvable and 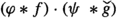 is vanishing at infinity for all
is vanishing at infinity for all 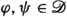 , then
, then 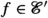 and can be extended to the general case via approximate units using Lemma 3.5 and Theorem 7.1 from [
and can be extended to the general case via approximate units using Lemma 3.5 and Theorem 7.1 from [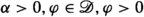










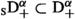 for
for 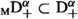 for
for 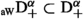 for
for 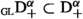 for
for 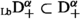 for
for 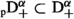 for
for 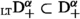 for
for 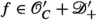 . Then
. Then 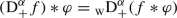
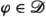 with the right hand side defined point wise by eq. (
with the right hand side defined point wise by eq. (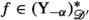 . Then
. Then 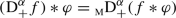
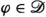 with the right hand side defined point wise by eq. (
with the right hand side defined point wise by eq. (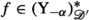 . Then
. Then 
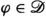 with the right hand side defined point wise by eq. (
with the right hand side defined point wise by eq. (