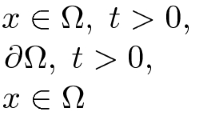Skip to main content
SpringerLink
Log in

Global existence and finite time blowup for a fractional pseudo-parabolic p-Laplacian equation

  • Original Paper
  • Published:
Fractional Calculus and Applied Analysis Aims and scope Submit manuscript

Abstract

In this paper, we study the initial-boundary value problem for a fractional pseudo-parabolic p-Laplacian type equation. First, by means of the imbedding theorems, the theory of potential wells and the Galerkin method, we prove the existence and uniqueness of global solutions with subcritical initial energy, critical initial energy and supercritical initial energy, respectively. Next, we establish the decay estimate of global solutions with subcritical initial energy, critical initial energy and supercritical initial energy, respectively. For supercritical initial energy, we also need to analyze the properties of \(\omega \)-limits of solutions. Finally, we discuss the finite time blowup of solutions with subcritical initial energy and critical initial energy, respectively.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Barenblatt, G.I., Zheltov, Y.P., Kochina, I.N.: Basic concepts in the theory of seepage of homogeneous liquids in fissured rocks. J. Appl. Math. Mech. 24(5), 852–864 (1960). https://doi.org/10.1016/0021-8928(60)90107-6

    Article  MATH  Google Scholar 

  2. Benjamin, T.B., Bona, J.L., Mahony, J.J.: Model equations for long waves in nonlinear dispersive systems. Philos. Trans. R. Soc. Lond Ser. A 272(1220), 47–78 (1972). https://doi.org/10.1098/rsta.1972.0032

    Article  MathSciNet  MATH  Google Scholar 

  3. Bertoin, J.: Levy Processes. Cambridge Tracts in Mathematics, vol. 121. Cambridge University Press, Cambridge (1996)

  4. Budd, C., Dold, B., Stuart, A.: Blowup in a partial differential equation with conserved first integral. SIAM J. Appl. Math. 53(3), 718–742 (1993). https://doi.org/10.1137/0153036

    Article  MathSciNet  MATH  Google Scholar 

  5. Caffarelli, L.: Nonlocal equations, drifts and games. Nonlinear Partial Differential Equations. Abel Symposia 7, 37–52 (2012). https://doi.org/10.1007/978-3-642-25361-4

    Article  MATH  Google Scholar 

  6. Cao, Y., Liu, C.H.: Initial boundary value problem for a mixed pseudo-parabolic \(p\)-Laplacian type equation with logarithmic nonlinearity. Electron. J. Differ. Equ. 2018, 1–19 (2018). http://ejde.math.txstate.edu

  7. Chen, H., Luo, P., Liu, G.W.: Global solution and blow-up of a semilinear heat equation with logarithmic nonlinearity. J. Math. Anal. Appl. 422(1), 84–98 (2015). https://doi.org/10.1016/j.jmaa.2014.08.030

    Article  MathSciNet  MATH  Google Scholar 

  8. Cheng, J.Z., Wang, Q.R.: Global existence and finite time blowup for a mixed pseudo-parabolic \(p\)-Laplacian type equation. Nonlinear Anal. Real World Appl. 73(1), 1–22 (2023). https://doi.org/10.1016/j.nonrwa.2023.103895

    Article  MathSciNet  MATH  Google Scholar 

  9. Childress, S.: Chemotactic Collapse in Two Dimensions. Springer, Berlin (1984)

    Book  Google Scholar 

  10. Chueshov, I.: Global attractors for a class of Kirchhoff wave models with a structural nonlinear damping. J. Abstr. Differ. Equ. Appl. 1(1), 86–106 (2010)

    MathSciNet  MATH  Google Scholar 

  11. Daoud, M., Laamri, E.H.: Fractional Laplacians: A short survey. Discret. Contin. Dyn. Syst. Ser. S 15(1), 95–116 (2022). https://doi.org/10.3934/dcdss.2021027

    Article  MathSciNet  MATH  Google Scholar 

  12. Davis, P.L.: A quasilinear parabolic and a related third order problem. J. Math. Anal. Appl. 40(2), 327–335 (1972). https://doi.org/10.1016/0022-247X(72)90054-6

    Article  MathSciNet  MATH  Google Scholar 

  13. Di, H.F., Qian, X., Peng, X.M.: Blow up and exponential growth for a pseudo-parabolic equation with \(p(x)\)-Laplacian and variable exponents. Appl. Math. Lett. 138, 1–8 (2023). https://doi.org/10.1016/j.aml.2022.108517

    Article  MathSciNet  MATH  Google Scholar 

  14. Di, H.F., Rong, W.J.: The regularized solution approximation of forward/backward problems for a fractional pseudo-parabolic equation with random noise. Acta Math. Sci. Ser. B (Engl. Ed.) 43(1), 324–348 (2023). https://doi.org/10.1007/s10473-023-0118-3

    Article  MathSciNet  MATH  Google Scholar 

  15. Ding, H., Zhou, J.: Global existence and blow-up for a mixed pseudo-parabolic \(p\)-Laplacian type equation with logarithmic nonlinearity. J. Math. Anal. Appl. 478(2), 393–420 (2019). https://doi.org/10.1016/j.jmaa.2019.05.018

    Article  MathSciNet  MATH  Google Scholar 

  16. Evans, L.C.: Partial Differential Equations. American Mathematical Society, Providence (2010)

    MATH  Google Scholar 

  17. Gal, C.G., Warma, M.: On some degenerate non-local parabolic equation associated with the fractional \(p\)-Laplacian. Dyn. Partial Differ. Equ. 14(1), 47–77 (2017). https://doi.org/10.4310/DPDE.2017.v14.n1.a4

    Article  MathSciNet  MATH  Google Scholar 

  18. Giacomoni, J., Tiwari, S.: Existence and global behavior of solutions to fractional \(p\)-laplacian parabolic problems. Electron. J. Differ. Equ. 2018, 1–20 (2018). http://ejde.math.txstate.edu

  19. Gilboa, G., Osher, S.: Nonlocal operators with applications to image processing. Multiscale Model. Simul. 7(3), 1005–1028 (2008). https://doi.org/10.1137/070698592

    Article  MathSciNet  MATH  Google Scholar 

  20. Landkof, N.S.: Foundations of Modern Potential Theory. Grundlehren Math. Wiss., vol. 180. Springer, Berlin (1972)

  21. Laskin, N.: Fractional quantum mechanics and L\(\acute{e}\)vy path integrals. Phys. Lett. A 268(4–6), 298–305 (2000). https://doi.org/10.1016/S0375-9601(00)00201-2

    Article  MathSciNet  MATH  Google Scholar 

  22. Li, Y.H., Cao, Y., Yin, J.X.: A class of viscous \(p\)-Laplace equation with nonlinear sources. Chaos Solitons Fractals 57, 24–34 (2013). https://doi.org/10.1016/j.chaos.2013.07.021

    Article  MathSciNet  MATH  Google Scholar 

  23. Liao, M.L., Liu, Q., Ye, H.L.: Global existence and blow-up of weak solutions for a class of fractional \(p\)-Laplacian evolution equations. Adv. Nonlinear Anal. 9(1), 156–1591 (2020). https://doi.org/10.1515/anona-2020-0066

    Article  MathSciNet  MATH  Google Scholar 

  24. Liu, C.C.: Weak solutions for a viscous \(p\)-Laplacian equation. Electron. J. Differ. Equ. 2003(63), 1–11 (2003). http://ejde.math.swt.edu

  25. Liu, W.J., Yu, J.Y.: A note on blow-up of solution for a class of semilinear pseudo-parabolic equations. J. Funct. Anal. 274(5), 1276–1283 (2018). https://doi.org/10.1016/j.jfa.2018.01.005

    Article  MathSciNet  MATH  Google Scholar 

  26. Liu, Y.C., Wang, F.: A class of multidimensional nonlinear Sobolev–Galpern equations. Acta Math. Appl. Sin. 17(4), 569–577 (1994)

    MathSciNet  Google Scholar 

  27. Liu, Y.C.: On potential wells and vacuum isolating of solutions for semilinear wave equations. J. Differ. Equ. 192(1), 155–169 (2003). https://doi.org/10.1016/S0022-0396(02)00020-7

    Article  MathSciNet  MATH  Google Scholar 

  28. Liu, Y.C., Zhao, J.S.: On potential wells and applications to semilinear hyperbolic equations and parabolic equations. Nonlinear Anal. 64(12), 2665–2687 (2006). https://doi.org/10.1016/j.na.2005.09.011

    Article  MathSciNet  MATH  Google Scholar 

  29. Luo, Y.B., Xu, R.Z., Yang, C.: Global well-posedness for a class of semilinear hyperbolic equations with singular potentials on manifolds with conical singularities. Calc. Var. 61(6), 1–47 (2022). https://doi.org/10.1007/s00526-022-02316-2

    Article  MathSciNet  MATH  Google Scholar 

  30. Mazón, J.M., Rossi, J.D., Toledo, J.: Fractional \(p\)-Laplacian evolution equations. J. Math. Pures Appl. 105(6), 810–844 (2016). https://doi.org/10.1016/j.matpur.2016.02.004

    Article  MathSciNet  MATH  Google Scholar 

  31. Metzler, R., Klafter, J.: The restaurant at the end of the random walk: recent developments in the description of anomalous transport by fractional dynamics. J. Phys. A 37(31), 161–208 (2004). https://doi.org/10.1088/0305-4470/37/31/R01

    Article  MathSciNet  MATH  Google Scholar 

  32. Nezza, E.D., Palatucci, G., Valdinoci, E.: Hitchhiker’s guide to the fractional Sobolev spaces. Bull. Sci. Math. 136(5), 521–573 (2012). https://doi.org/10.1016/j.bulsci.2011.12.004

    Article  MathSciNet  MATH  Google Scholar 

  33. Padron, V.: Effect of aggregation on population recovery modeled by a forward–backward pseudoparabolic equation. Trans. Am. Math. Soc. 356(7), 2739–2756 (2012). https://doi.org/10.1090/S0002-9947-03-03340-3

    Article  MathSciNet  MATH  Google Scholar 

  34. Payne, L.E., Sattinger, D.H.: Saddle points and instability of nonlinear hyperbolic equations. Israel J. Math. 22(3–4), 273–303 (1975). https://doi.org/10.1007/BF02761595

    Article  MathSciNet  MATH  Google Scholar 

  35. Puhst, D.: On the evolutionary fractional \(p\)-Laplacian. AMRX Appl. Math. Res. Express 2015(2), 253–273 (2015). https://doi.org/10.1093/amrx/abv003

    Article  MathSciNet  MATH  Google Scholar 

  36. Rubenstein, J., Sternberg, P.: Nonlocal reaction-diffusion equations and nucleation. IMA J. Appl. Math. 48(3), 249–264 (1992). https://doi.org/10.1093/imamat/48.3.249

    Article  MathSciNet  MATH  Google Scholar 

  37. Sattinger, D.H.: On global solution of nonlinear hyperbolic equations. Arch. Ration. Mech. Anal. 30, 148–172 (1968). https://doi.org/10.1007/BF00250942

    Article  MathSciNet  MATH  Google Scholar 

  38. Schaaf, R.: Stationary solutions of chemotaxis systems. Trans. Am. Math. Soc. 292(2), 531–556 (1985). https://doi.org/10.1090/S0002-9947-1985-0808736-1

    Article  MathSciNet  MATH  Google Scholar 

  39. Servadei, R., Valdinoci, E.: Mountain pass solutions for non-local elliptic operators. J. Math. Anal. Appl. 389(2), 887–898 (2012). https://doi.org/10.1016/j.jmaa.2011.12.032

    Article  MathSciNet  MATH  Google Scholar 

  40. Servadei, R., Valdinoci, E.: Variational methods for non-local operators of elliptic type. Discret. Contin. Dyn. Syst. 33(5), 2105–2137 (2013). https://doi.org/10.3934/dcds.2013.33.2105

    Article  MathSciNet  MATH  Google Scholar 

  41. Shang, Y.D.: Blow-up of solutions for the nonlinear Sobolev–Galpern equations. Math. Appl. (Wuhan) 13(3), 35–39 (2000)

    MathSciNet  MATH  Google Scholar 

  42. Showalter, R.E., Ting, T.W.: Pseudoparabolic partial differential equations. SIAM J. Math. Anal. 1, 1–26 (1970). https://doi.org/10.1137/0501001

    Article  MathSciNet  MATH  Google Scholar 

  43. Stein, E.: Singular Integrals and Differentiability Properties of Functions. Princeton University Press, Princeton (1970)

    MATH  Google Scholar 

  44. Ting, T.W.: Certain non-steady flows of second-order fluids. Arch. Ration. Mech. Anal. 14, 1–26 (1963). https://doi.org/10.1007/BF00250690

    Article  MathSciNet  MATH  Google Scholar 

  45. V\(\acute{a}\)zquez, J.L.: Nonlinear diffusion with fractional Laplacian operators, In: Holden, H., Karlsen, K.H. (eds.) Nonlinear Partial Differential Equations, The Abel Symposium 2010. Springer, Berlin pp. 271–298 (2012)

  46. Vázquez, J.L.: The Dirichlet problem for the fractional \(p\)-Laplacian evolution equation. J. Differ. Equ. 260(7), 6038–6056 (2016). https://doi.org/10.1016/j.jde.2015.12.033

    Article  MathSciNet  MATH  Google Scholar 

  47. Wang, X.C., Xu, R.Z.: Global existence and finite time blowup for a nonlocal semilinear pseudo-parabolic equation. Adv. Nonlinear Anal. 10(1), 261–288 (2021). https://doi.org/10.1515/anona-2020-0141

    Article  MathSciNet  MATH  Google Scholar 

  48. Xu, H.Y.: Existence and blow-up of solutions for finitely degenerate semilinear parabolic equations with singular potentials. Commun. Anal. Mech. 15(2), 132–161 (2023). https://doi.org/10.3934/cam.2023008

    Article  MathSciNet  Google Scholar 

  49. Xu, R.Z.: Initial boundary value problem for semilinear hyperbolic equations and parabolic equations with critical initial data. Q. Appl. Math. 68(3), 459–468 (2010). https://doi.org/10.1090/S0033-569X-2010-01197-0

    Article  MathSciNet  MATH  Google Scholar 

  50. Xu, R.Z., Lian, W., Niu, Y.: Global well-posedness of coupled parabolic systems. Sci. China Math. 63(2), 321–356 (2020). https://doi.org/10.1007/s11425-017-9280-x

    Article  MathSciNet  MATH  Google Scholar 

  51. Xu, R.Z., Niu, Y.: “Addendum to Global existence and finite time blow-up for a class of semilinear pseudo-parabolic equations” [J. Funct. Anal. 264(12) (2013) 2732–2763]. J. Funct. Anal. 270(10), 4039–4041 (2016)

  52. Xu, R.Z., Su, J.: Global existence and finite time blow-up for a class of semilinear pseudo-parabolic equations. J. Funct. Anal. 264(12), 2732–2763 (2013). https://doi.org/10.1016/j.jfa.2013.03.010

    Article  MathSciNet  MATH  Google Scholar 

  53. Xu, R.Z., Wang, X.C., Yang, Y.B.: Blowup and blowup time for a class of semilinear pseudo-parabolic equations with high initial energy. Appl. Math. Lett. 83, 176–181 (2018). https://doi.org/10.1016/j.aml.2018.03.033

    Article  MathSciNet  MATH  Google Scholar 

  54. Yang, C., R\({\check{\rm a}}\)dulescu, V.D., Xu, R.Z., Zhang, M.Y.: Global well-posedness analysis for the nonlinear extensible beam equations in a class of modified Woinowsky–Krieger models. Adv. Nonlinear Stud. 22(1), 436–468 (2022). https://doi.org/10.1515/ans-2022-0024

  55. Yang, M., Wang, Q.R.: Existence of mild solutions for a class of Hilfer fractional evolution equations with nonlocal conditions. Fract. Calc. Appl. Anal. 20(3), 679–705 (2017). https://doi.org/10.1515/fca-2017-0036

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The authors contributed equally to the writing of this paper. All authors read and approved the final manuscript. This research was supported by the National Natural Science Foundation of China (No. 12071491). The authors would like to thank the editors and the referees for their very helpful comments and suggestions.

Author information

Authors and Affiliations

  1. School of Mathematics, Sun Yat-sen University, Guangzhou, 510275, Guangdong, China

    Jiazhuo Cheng & Qiru Wang

Authors
  1. Jiazhuo Cheng
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Qiru Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Qiru Wang.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Cheng, J., Wang, Q. Global existence and finite time blowup for a fractional pseudo-parabolic p-Laplacian equation. Fract Calc Appl Anal 26, 1916–1940 (2023). https://doi.org/10.1007/s13540-023-00179-8

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s13540-023-00179-8

Keywords

Mathematics Subject Classification

Search

Navigation