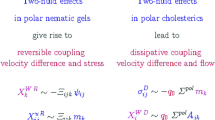Abstract
We present the macroscopic dynamics of nematic liquid crystals in a two-fluid context. We investigate the case of a nematic in a chiral solvent as well as of a cholesteric in a non-chiral solvent. In addition, we analyze how the incorporation of a strain field for nematic gels and elastomers in a chiral solvent modifies the macroscopic dynamics. It turns out that the relative velocity between the nematic subsystem and the chiral solvent gives rise to a number of cross-coupling terms, reversible as well as irreversible, unknown from other two-fluid systems considered so far. Possible experiments to study those novel dynamic cross-coupling terms are suggested. As examples we just mention that gradients of the relative velocity lead, in cholesterics to heat currents. We also find that in cholesterics shear flows give rise to a temporal variation in the velocity difference perpendicular to the shear plane, and in cholesteric gels uniaxial stresses or strains generate temporal variations of the velocity difference. Finally, the exotic chiral Q phase of tetragonal (\(D_4\)) symmetry is analyzed for an isotropic non-chiral solvent in a two-fluid scenario.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The physical properties of cholesteric liquid crystals, which are known for over 100 years [1, 2], have been investigated in detail [3, 4]. Their chirality is manifest on the macroscopic level by a helical superstructure as the ground state, which breaks parity symmetry. Very often immiscible or only partly miscible mixtures involving a cholesteric phase have been prepared to optimize material properties [5, 6]. In other cases two phase regions involving a cholesteric phase and an isotropic liquid phase were studied to bring out effects specific for systems with macroscopic handedness such as Lehmann-type effects [2, 3]. When studying those an external force such as temperature and concentration gradients or electric fields give rise to rotations of the director field in suitably chosen geometries, for example, with the helical axis in the cholesteric drops perpendicular to the bounding plates of the sample [7,8,9,10,11]. We note that the inverse effect [12] has also been observed [13]. For both types of systems, cholesteric mixtures as well as two-phase regions, a natural question arises: are there two-fluid effects in such systems and how could their consequences be detected?
There is a large body of materials for which two-fluid effects turn out to be of considerable physical interest including, as examples, fluid emulsions [14], colloidal suspensions [15], polymer solutions and mixtures [16], fiber networks in a matrix [17], and microtubuli coupled to the cytoskeleton in cells [18].
More recently macroscopic dynamic two-fluid descriptions have been given for a number of soft matter materials and complex fluids starting with immiscible liquids [19, 20] and combinations of ordinary or viscoelastic liquids with nematic liquid crystals [19]. More recently, this approach has been applied to a number of other two-fluid systems including immiscible compound materials in solids and gels [21], bioinspired complex fluids [22, 23], and materials characterized by the formation of clusters, for example of smectic clusters above the nematic to smectic A transition [24] and of clusters above the glass transition [25].
Here, we investigate how two-fluid effects can show up in a system with macroscopic chirality. Specifically, we have in mind two possibilities, which are equivalent for a macroscopic description: a nematic phase in a chiral solvent or a cholesteric phase in a non-chiral solvent. In both cases, one has a ground state that breaks inversion symmetry. Furthermore, we have two additional macroscopic variables: the velocity difference between the two subsystems, \(w_i\), which is a slowly relaxing variable, and the concentration of one component, \(\phi\), which will be considered here to be a conserved quantity. Generally, depending on the material of interest, it could relax on a finite time scale [19].
In macroscopic dynamics, one keeps, in addition to the locally conserved variables (e.g., mass density, density of momentum and energy density) and the variables associated with spontaneously broken continuous symmetries [26,27,28,29], also macroscopic variables that relax on a sufficiently long, but finite time scale to be of interest for the macroscopic behavior of the system [29].
Since the two subsystems move relative to each other, two different velocities are needed for a complete macroscopic description. The barycentric velocity is related to the momentum conservation and the total momentum density is a convenient hydrodynamic variable, just as in the single-fluid case. As the additional variable, it is customary to use the relative velocity, \(w_i\), which generally is not related to any conservation law or broken symmetry and therefore is a (slowly) relaxing quantity. Only for superfluids the superfluid velocity is related to broken gauge invariance and is truly hydrodynamic [30]. This is manifest in the propagation of second sound in the bulk in the long wavelength limit in the superfluid phase of \(^4\)He [30, 31].
In the bulk of this paper, we deal with the two-fluid description of nematic fluids with a chiral solvent or, equivalently, of cholesterics with a non-chiral solvent in detail. In Sect. 3, we analyze how for nematic gels and elastomers the elastic strain field can be incorporated in a two-fluid description. In addition, relative rotations of the preferred direction with respect to the elastic network are considered. In Sect. 4, we discuss some possible dynamic experiments involving the relative velocity. A brief summary and perspective in Sect. 5 concludes the main part of the paper. In a last section, two-fluid effects for the chiral Q \((D_4)\) phase in a non-chiral solvent are briefly discussed.
2 Two-Fluid Model for Nematics in a Chiral Solvent
2.1 Variables
In this paper, we study a chiral two-fluid system with orientational order, namely either a nematic with a chiral liquid as the second, “solvent” fluid or a cholesteric in an isotropic solvent as long as the bulk of the phase is considered. For the nematic order parameter, \(Q_{ij}\) in three dimensions we have \(Q_{ij} = (S/2)(\hat{n}_i \hat{n}_j - (1/3) \delta _{ij})\), where the nematic director \(\hat{n}_i\) describes the broken rotational symmetry [32]. A director is part of the nematic order parameter and is therefore subject to \(\hat{n}_i \rightarrow -\hat{n}_i\) invariance. The additional feature of a cholesteric compared to a nematic is the existence of macroscopic chirality. The latter is described by a pseudoscalar quantity, \(q_0\), that is invariant under proper rotations, but changes sign if a spatial inversion is involved, thus breaking inversion symmetry. Since the 2-fluid system is mixed on the microscopic level, chirality applies to all degrees of freedom, even those of the non-chiral subsystem. That means, we will use the ’local description’ [3, 33], starting from a homogeneous ground state and describe the chiral effects by adding all possible contributions, linear in \(q_0\), to the energy density (statics) and the phenomenological currents (reversible and irreversible dynamics).
The two-fluid character is manifest by the additional macroscopic variables, velocity difference \(w_i\) and concentration \(\phi\) of the solvent component [19, 20]. The other variables are the entropy density, \(\sigma\), the density, \(\rho\), the density of linear momentum, \(g_i\), the director field, \(\hat{n}_i\) and the modulus of the nematic order parameter, S.
The first law of thermodynamics relates changes of the variables to changes of the energy density \(\varepsilon\) by the Gibbs relation [29, 34].
The Gibbs relation contains the entropy density \(\sigma\), representing the thermal degree of freedom, with its thermodynamic conjugate, the temperature T. Other conjugates are the chemical potential \(\mu\), the osmotic pressure \(\Pi\), the mean velocity \(v_i = g_i / \rho\), \(m_i\), the conjugate field to the velocity difference, \(w_i\), the molecular field associated with the director \(\hat{n}_i\), \(h_i^n\), and the molecular field \(h^S\) associated the magnitude of the nematic order parameter, S. The contribution \(E_i d D_i\) guarantees that we can describe Maxwell stresses as well as field-induced pressure changes [29]. The conjugate \(E_i\) is the local electric field containing internal and external contributions. Our notation follows closely that of refs. [24].
2.2 Statics
The static behavior of a macroscopic system can be derived from an energy functional. In harmonic approximation and including the kinetic energy densities, it reads in the present case
where \(\delta\) denotes deviations from the equilibrium value, in particular \(\delta S = S - S_0\), \(\delta \hat{n}_i = \hat{n}_i - \hat{n}_i^0\), \(\delta \phi = \phi - \phi _0\).
The orientation energy due to an external field is governed by the dielectric anisotropy, \(\epsilon _a = \epsilon _{\parallel } - \epsilon _{\bot }\) [3] and the stiffness of order parameter variations is given by \(1/\chi _S)\). Although the energy density expression is given in harmonic approximation only, it can give rise to nonlinear effects, since all material parameters are still functions of the state variables, like temperature and pressure.
Spatially inhomogeneous variations of the nematic order parameter are described by various energy contributions. They comprise the Frank orientational elastic energy (\(\sim K_{ijkl}\) with splay, bend and twist [3]), the energy associated with gradients of the modulus (\(\sim K_{ij}^{(2)}\), of the standard uniaxial form) [29] and a cross-coupling term between gradients of the preferred direction to gradients of the order parameter modulus (\(K_{ijk}^{(3)} =K^{(3)} (\delta _{ik}^\bot \hat{n}_j + \delta _{jk}^\bot \hat{n}_i)\) with \(\delta _{jk}^\bot \equiv \delta _{jk} - \hat{n}_j \hat{n}_k\))) [35]. The flexoelectric contribution \(\sim e_{ijk} (\nabla _i n_j) E_k\) is not considered here.
In addition, there is the energy density of a fluid binary mixture in the third and fourth line. The kinetic energy \((1/2\rho _n) (\varvec{g}^{n})^2 + (1/2\rho _s) (\varvec{g}^{s})^2\) expressed by the momentum densities for the nematic and the solvent subsystem, respectively, leads to \(\alpha = \phi (1-\phi ) \rho\), since \(\varvec{g}^{n} + \varvec{g}^{s} = \varvec{g}\). In line 5 there is the linear twist term (\(\tilde{K}_2\)) well known from chiral nematics, that gives rise to a helical equilibrium structure \(({ \varvec{\hat{n} }\cdot {curl}\,\hat{n}} )_0= q_0 \tilde{K}_2 / K_2\), with \(K_2\) the Frank-like modulus for the quadratic, non-chiral twist energy. Very often \(\tilde{K}_2 = K_2\) is assumed, although there is no a priori reason to do so and in the early discussions the two moduli are indeed discriminated [36, 37]. The last line (\(\sim \alpha _{1,2,3,4}\)) describes couplings between twist and variations of the scalar variables giving rise to the static Lehmann effects [33].
In the following we list the expressions for the conjugated variables in terms of the hydrodynamic and macroscopic variables. They are defined as partial derivatives with respect to the appropriate variable, while all the other variables are kept constant, denoted by ellipses in the following
from which the total molecular fields, used in Eq. (1), \(h^S = h^{'S} - \nabla _j\Phi ^S_{j}\) and \(h_i^n = h^{'n}_i- \nabla _j\Phi _{ij}^{n}\) follow immediately. The \(w_i\)-dependence of the chemical potential and the osmotic pressure are due to the \(\rho\)- and \(\phi\)-dependence of \(\alpha\).
2.3 Dynamics
The dynamic equations have the form
where the electric charge density is related to \(D_i\) by \(\rho _e = \nabla _i D_i\). The electric current density is \(j_i^{eR} +j_i^{eD}\). The pressure p contains the electric field contributions
and \(\sigma ^{th}_{ij}\) contains the Maxwell and the Ericksen-type stresses
where the Maxwell stress has been symmetrized with the help of the requirement that the energy density should be invariant under rigid rotations [29].
The source term of Eq. (13) contains R, the dissipation function, which represents the energy dissipation of the system. Due to the second law of thermodynamics R must satisfy \(R\ge 0\): For reversible processes, this dissipation function is equal to zero, while for irreversible processes it must be positive
The phenomenological currents and quasi-currents with the superscripts \(^* \in \{\)R, D\(\}\) consist of two parts, a reversible and a dissipative one, respectively. The various transport contributions in Eqs. (12)–(19) (as well as p and \(\sigma ^{th}_{ij}\)) are reversible and add up to zero in the entropy production.
These phenomenological currents and quasicurrents are treated in the following subsections within ’linear irreversible thermodynamics’ (guaranteeing general Onsager relations), i.e., as linear relations between currents and thermodynamic forces. The resulting expressions are nevertheless nonlinear, since all material parameters can be functions of the scalar state variables (e.g., p, T, P, \(\phi\)).
The form of Eq. (16) reflects the fact that both densities, \(\rho _n\) and \(\rho _s\), are conserved individually, and Eq. (18) describes the order parameter modulus S as a slowly relaxing quantity [32] (similar to, e.g., the superfluid order [31, 38]).
In a single-fluid description, the transport and convective dynamic contributions are fixed, while in a 2-fluid theory it is a priori not given, which velocity should be used. In Eqs. (12)–(19), the mean velocity, \(v_i\), is employed, since this guarantees zero entropy production. However, there are additional contributions of the transport and convective type in the reversible phenomenological currents involving the relative velocity. By assigning special values to the appropriate reversible transport coefficients, specific models can be realized, where, e.g., variables of the first (second) subsystem are transported and convected with the first (second) velocity. In this manuscript, we will not dwell on this point and refer to appropriate previous discussions [19, 21, 24].
2.4 Reversible Currents
For the reversible dynamic behavior of our two fluid cholesteric macroscopic system, we focus on the chiral terms containing phenomenological parameters, since the terms present in for a two fluid nematic have been discussed in detail in refs. [19, 24]. We obtain
with \(s_{ijk} =\hat{n}_i \hat{n}_m \epsilon _{mjk}\) and where \(\dots\) indicate all the terms already discussed in [19, 24]. There are no chiral additions to \(Y_i^R\) and \(X^{SR}\).
2.5 Dissipative Currents
The dissipative dynamic behavior of our macroscopic system is characterized by the dissipation function R
with \(s_{ijk} = \hat{n}_i \hat{n}_p \epsilon _{pjk}\). The tensors \(\kappa _{ij}\), \(D^{T\phi }_{ij}\), \(D_{ij}\), \(\xi _{ij}\), \(\sigma _{ij}^E\), \(D_{ij}^E\), \(\kappa _{ij}^E\) as well as \(\nu _{ijkl}\), and \(\nu _{ijkl}^{w}\) are of the standard uniaxial form for second and fourth rank tensors [29, 39], while the mixed one, \(\nu _{ijkl}^{c}\), contains six parameters, due to the lack of the \(\nu _{ijkl}^{c} = \nu _{klij}^{c}\) symmetry [19, 39].
The contribution \(\sim b_{||}\) in the entropy production describes the relaxation of the order parameter modulus S, while the contribution associated with \(b_{\bot }\) corresponds to the diffusion of director rotations (often called \(\gamma _1^{-1}\)). The third rank tensor associated with the dynamic flexoelectric effect \(\sim \zeta _{ijk}^E\) is of the form \(\zeta _{ijk}^E = \zeta ^E (\delta _{ij}^{\bot } \hat{n}_k + \delta _{ik}^{\bot } \hat{n}_j\)). Those terms exist already in single-fluid, achiral nematics.
The most interesting dissipative cross-coupling is clearly the contribution \(\sim \Sigma ^{chol}\) describing a direct cross-coupling between relative velocities and symmetrized gradients of the mean velocity. It does not exist for non-chiral nematics and requires for its existence a pseudoscalar as well as a preferred direction.
There are further dissipative coupling terms between the molecular field of the director, \(h_i^n\), and temperature and concentration gradients, electric fields, as well as the force associated with the order modulus, \(h^S\). They are the dissipative parts of the Lehmann effect for cholesterics [12, 33, 40,41,42]—familiar also from chiral smectic liquid crystals [12, 33, 41, 42].
To obtain the dissipative parts of the currents and quasicurrents, we take the partial derivatives of R with respect to the appropriate thermodynamic force
3 Incorporation of a Strain Field for Nematic Gels and Elastomers in a Chiral Solvent
In this section, we discuss how the two-fluid macroscopic dynamics has to be modified for nematic gels and elastomers in a chiral solvent. One needs a strain field \(u_{ij}\) to deal with elasticity and a special vector \(\tilde{\Omega }_i\) to describe relative rotations. We will make extensive use of the macroscopic dynamics for single-fluid cholesteric gels and elastomers [43].
The strain tensor can be written in linearized form as \(u_{ij} = \frac{1}{2} (\nabla _i u_j + \nabla _j u_i)\) with the displacement field \(u_i\). For a nonlinear generalization cf. [44]. Since we will deal with the case of a permanently cross-linked gel or elastomer, \(u_{ij}\) does not relax, but can only diffuse.
As pointed out first by de Gennes [45], rotations of the director \(\delta \hat{n}_i\) relative to the elastic network are an important macroscopic variable. In linear approximation, it can be written as
with \(\Omega _{ij} = \frac{1}{2} (\nabla _i u_j -\nabla _i u_i)\). For a nonlinear definition, cf. [46]. Relative rotations are perpendicular to the director, \(\hat{n}_i \hat{n}_j \tilde{\Omega }_{ij} = 0\). They are not truly hydrodynamic variables, but relax due to the energy dissipation involved.
The Gibbs relation Eq. (1) has to be amended
where the dots denote all the contributions already given in Sect. 2. The additional thermodynamic conjugate quantities are the elastic stress \(\psi _{ij}\) and the relative molecular field \(L_i^{\bot }\) associated with relative rotations.
The strain and the relative rotations bring a host of additional contributions to the energy, Eq. (2). However, none is related to the 2-fluid situation. Therefore, we can refer to the single-fluid expressions [47] without copying them here.
Here, we discuss the chiral part of the energy, which couples to strains and relative rotations
The contributions in Eq. (39) are specific for cholesteric elastic systems. The first one represents a coupling of twist to the strain tensor u, where \(\tau _{ij}^{u}\) takes the form
Thus, this term gives rise to changes in the pitch due to uniaxial mechanical stresses such as compression and dilatation. This effect has been studied for cholesteric sidechain elastomers in detail experimentally [48, 49]. The second one (\(\sim \tau _\Omega\)) relates static director deformations with relative rotations.
Other static effects specific for general cholesteric elastic systems are related to electric fields
and describe electric field-induced relative rotations (rotato-electricity [50, 51]) and deformations with
Next, we give the additional chiral contributions to the thermodynamic conjugate quantities that arise from the chiral energy associated with strains and relative rotations by taking the variational derivative with respect to the appropriate variables
For the dynamic equations, we have in addition
while the other dynamic equations are of the same form as discussed above.
Using the requirement of the rotational invariance of the energy, one can write [29, 44, 47]
where \(\sigma _{ij}^{th}\) is either symmetric or a divergence of an antisymmetric part, which ensures angular momentum conservation. It can be brought into a manifestly symmetric form by some redefinitions [26].
For the reversible chiral currents, we have, in addition to the terms without phenomenological coefficients given above
where
This coupling between the elastic degree of freedom and the relative velocity is specific for a 2-fluid description.
Next, we focus on the dissipative part of the dynamics associated with strains and relative rotations in the presence of the pseudoscalar \(q_0\), which can be discussed most succinctly in terms of the dissipation function R [26, 29].
where
and \(\alpha \in {\sigma , \phi , e}\). All terms in Eq. (53) describe dissipative couplings to elastic deformations and relative rotations.
We stress that these dissipative contributions occur for all gels and elastomers with macroscopic chirality including chiral smectic gels and elastomers.
The chiral parts of the dissipative currents then read
4 Possible Dynamic Experiments
4.1 Reversible Coupling Terms in Cholesterics
Inspecting the reversible coupling terms in Eqs. (24)–(28), some quite intuitive possibilities emerge to detect these contributions. Taking the heat current as an example, we get
with \(s_{ijk} = \hat{n}_i \hat{n}_m \epsilon _{mjk}\)
Taking the director \(\hat{n}_i\) parallel to the \(\hat{z}\)-direction, we have explicitly
meaning the symmetrized gradient of the velocity difference in the \(y-z\)-plane leads to a heat current in \(x-\)direction. A heat current of the same magnitude but of opposite sign in the \(y-\)direction is found for a symmetrized gradient of the velocity difference in the \(x-z\)-plane.
Similarly, concentration currents are found \(\sim \Gamma _5\) from Eq. (27) and electric currents \(\sim \Gamma _{6a,6b}\) from Eq. (28). If one considers gradients of the mean velocity (\(A_{ij}\)), instead of the relative velocity, appropriate effects are found, but they are not specific for a two-fluid description.
The counter terms in Eq. (26), necessary to have zero entropy production, lead to
for a bent temperature field, and similarly \(\sim \Gamma _5\) for a bent concentration field, and \(\sim \Gamma _{6a,6b}\) for a sheared electrical field. The bending or shear plane must contain the preferred direction \(\hat{n}_i\). In all cases the resulting \(X_i^{WR}\) is perpendicular to the bending or shear plane.
A nonzero \(X_i^{WR}\) means that the relative velocity is time-dependent. In the stationary state \(X_i^{WR}\) is compensated by the relaxation \(\alpha \, \xi _{ij} w_j\). Thus, bent temperature and concentration fields, as well as shear electric fields trigger relative velocities in chiral nematic two-fluid systems.
4.2 Dissipative Coupling Terms in Cholesterics
Inspecting the dissipation function for cholesterics there is a chiral term, \(R_{chir}\), which has only one gradient
which gives rise to dissipative contributions to the stress tensor and the quasi-current associated with the velocity difference
This coupling between a relative velocity (or its time derivative) in the plane perpendicular to the preferred direction \(\hat{n}_i\) (taken as the z-direction) with shear flow (or shear stress) of the mean velocity, with the shear plane containing \(\hat{n}_i\), reads explicitly
where we have added the relaxation of the relative velocity.
Taken together, Eqs. (68)–(71) describe a diffusion-like behavior of \(w_x\) and \(w_y\) (along the \(y-\) and \(x-\)direction, respectively) with a diffusion coefficient \(q_0^2 \alpha \rho ^{-1} (\Sigma ^{chol})^2\) that comes in addition to the relaxation with relaxation coefficient \(\alpha \xi _\perp\).
4.3 Reversible Coupling Between Stresses and Relative Velocities
To analyze the consequences of Eqs. (50) and (51), we proceed as follows. For the reversible chiral currents, we take the preferred direction, \(\hat{n}_i\), to be parallel to the \(\hat{z}\)-direction. Then, we obtain from Eq. (50)
Thus, an applied mechanical stress in the \(x-z\)-plane leads to a temporal variation of the velocity difference in \(y-\) direction and a mechanical stress applied in the \(y-z\)-plane results in a temporal variation for the velocity difference in the \(x-\) direction of the same magnitude, but the opposite sign. Conversely, velocity differences can drive temporal variations of strains and stresses. Using the same assumptions as above, we obtain
We emphasize that this coupling between the elastic degree of freedom and the relative velocity is specific for a 2-fluid description.
5 Summary and Perspective
In this work, we have predominantly analyzed the macroscopic dynamics of two-fluid systems from the field of liquid crystals: nematics in a chiral solvent and, equivalently, cholesterics in a non-chiral solvent. It turns out that there are a large number of reversible and dissipative dynamic cross-coupling terms between the velocity difference, on the one hand, and symmetrized velocity gradients and electric fields, temperature gradients, concentration gradients and mechanical stresses, on the other. For several of these coupling terms, we have outlined experimental set-ups to detect these cross-coupling terms not investigated before. These include, for example, the possibility that electric field gradients lead to temporal variations in the relative velocity field and that relative velocities generate oscillatory mechanical stresses in two-fluid cholesteric elastomers. In addition, we have also elucidated a number dynamic aspects of the rather exotic chiral Q phase of \(D_4\) symmetry, thus complementing earlier static studies.
Throughout this manuscript, we have focused on the influence of a macroscopic chirality on the two-fluid macroscopic dynamic behavior. Systems of interest are mainly coming from liquid crystal physics, but also from biological applications. Many of the cross-coupling terms presented are intrinsically connected to their chiral nature giving rise to broken parity symmetry, while time reversal symmetry is maintained.
This observation opens up a natural perspective for the study of another class of two-fluid systems. If the preferred direction is odd under time reversal like in magnetically ordered systems in a solvent, a different class of dynamic cross-coupling terms involving the magnetization will emerge. And this class of systems also already exists experimentally, namely ferromagnetic nematics [52,53,54,55,56] and ferromagnetic cholesterics [57,58,59]. Both classes of systems can we viewed as suspensions of magnetic platelets in a nematic or a cholesteric liquid crystal as a solvent. So far the focus experimentally and theoretically has been on the macroscopic dynamics of one component ferromagnetic nematics and ferromagnetic cholesterics [43, 60,61,62,63] generalizing earlier work on the macroscopic dynamics of ferronematics [64, 65]. As for the two-fluid aspects there appears to be no work on the dynamics of ferromagnetic nematics and ferromagnetic cholesterics, while some static experimental aspects of this type of behavior including converse magneto-electric effects and magneto-optic effects have been already examined for ferromagnetic nematics in the literature [53]. Only rather recently investigations of the macroscopic dynamic aspects of magnetic two-fluid systems have been started for magneto-rheological fluids [66].
Another class of two-fluid systems of interest that should be investigated in a next step are two-fluid systems with a polar preferred direction. Such a system can be ferroelectric. The macroscopic dynamics of polar nematics in a one component system has been presented in ref.[67] and in ref.[68] the issue of phases with spontaneous splay was addressed. Quite recently polar nematic phases have been found experimentally, and their molecular foundations and the associated physical consequences have been elucidated [69,70,71]. Therefore, it appears natural to investigate the two-fluid behavior of these systems, all the more when defect phases are involved.
References
F. Reinitzer, Monatsh. Chemie 9, 421 (1888); English translation: F. Reinitzer, Liq. Cryst., 5 7 (1989)
O. Lehmann, Ann. Phys. 2, 649 (1900)
P.G. de Gennes, The Physics of Liquid Crystals (Clarendon Press, Oxford, 1975)
S. Chandrasekhar, Liquid Crystals (Cambridge University Press, Cambridge, 1977)
A.M.F. Neto, Liq. Cryst. Rev. 2, 47 (2014)
I. Dierking, A.M.F. Neto, Crystals 10, 604 (2020)
N.V. Madhusudana, R. Pratibha, Mol. Cryst. Liq. Cryst. Lett. 5, 43 (1987)
N.V. Madhusudana, R. Pratibha, Liq. Cryst. 5, 1827 (1989)
J. Yoshioka, F. Ito, Y. Suzuki, H. Takahashi, H. Takizawa, Y. Tabe, Soft Matter 10, 5869 (2014)
T. Yamamoto, M. Kuroda, M. Sano, EPL 109, 46001 (2015)
S. Bono, S. Sato, Y. Tabe, Soft Matter 13, 6569 (2017)
D. Svenšek, H. Pleiner, H.R. Brand, Phys. Rev. E 78, 021703 (2008)
S. Sato, S. Bono, Y. Tabe, J. Phys. Soc. Jap. 86, 023601 (2017)
P. Hebraud P, F. Lequeux, and J.F. Palierne, Langmuir 16, 8296 (2000)
D. Lhuillier, J Non-Newtonian Fluid Mech 96, 19 (2001)
R.G. Larson, Constitutive Equations for Polymer Melts and Solutions (Butterworths, Boston, 1988)
A.S. Shahsavari, R.C. Picu, Phys. Rev. E 92, 012401 (2015)
C.P. Brangwynne, F.C. MacKintosh, S. Kumar, N.A. Geisse, J. Talbot, L. Mahadevan, K.K. Parker, D.E. Ingber, D.A. Weitz, J. Cell Biol. 173, 733 (2006)
H. Pleiner, J.L. Harden, Notices of Universities. South of Russia. Natural Sciences, special issue: Nonlinear Problems of Continuum Mechanics, pp. 46–61 (2003). arXiv:cond-mat/0404134
H. Pleiner, J.L. Harden, AIP Proc. 708, 46 (2004)
H. Pleiner, A.M. Menzel, H.R. Brand, Phys. Rev. B 103, 174304 (2021)
H. Pleiner, D. Svenšek, H.R. Brand, Eur. Phys. J. E 36, 135 (2013)
H. Pleiner, D. Svenšek, H.R. Brand, Rheol. Acta 55, 857 (2016)
H.R. Brand, H. Pleiner, Phys. Rev. E 103, 012705 (2021)
H. Pleiner, H.R. Brand, Rheol. Acta 60, 675 (2021)
P.C. Martin, O. Parodi, P.S. Pershan, Phys. Rev. A 6, 2401 (1972)
D. Forster, Ann. Phys. (N.Y.) 84, 505 (1974)
D. Forster, Hydrodynamic Fluctuations, Broken Symmetry, and Correlation Functions (Benjamin, Reading, Mass, 1975)
H. Pleiner, H.R. Brand, in Pattern Formation in Liquid Crystals, edited by A (Buka and L, Kramer (Springer, New York, 1996)
P.C. Hohenberg, P.C. Martin, Ann. Phys. (N.Y.) 34, 291 (1965)
I.M. Khalatnikov, Introduction to the Theory of Superfluidity (W.A. Benjamin, Reading, Mass., 1965)
P.G. de Gennes, Mol. Cryst. Liq. Cryst. 12, 193 (1971)
H.R. Brand, H. Pleiner, Phys. Rev. A 37, 2736 (1988)
H.B. Callen, Thermodynamics and an Introduction to Thermostatics (John Wiley & Sons, New York, 1985)
H.R. Brand, K. Kawasaki, J. Phys. C 19, 937 (1986)
C.W. Oseen, Trans. Faraday Soc. 29, 883 (1933)
H. Zocher, Trans. Faraday Soc. 29, 945 (1933)
L.P. Pitaevskii, Soviet Physics JETP 35, 282 (1959)
W.P. Mason, Physical Acoustics and the Properties of Solids (D. Van Nostrand, New York, 1958)
F. Leslie, Proc. Roy. Soc. A 307, 359 (1968)
H.R. Brand, H. Pleiner, D. Svenšek, Phys. Rev. E 88, 024501 (2013)
H.R. Brand, H. Pleiner, D. Svenšek, Rheol. Acta 57, 773 (2018)
H.R. Brand, A. Fink, H. Pleiner, Eur. Phys. J. E 38, 65 (2015)
H. Pleiner, M. Liu, H.R. Brand, Rheol. Acta 39, 560 (2000)
P.G. de Gennes, in Liquid Crystals of One– and Two–Dimensional Order, edited by W. Helfrich and G. Heppke (Springer, New York, 1980) p. 231
A.M. Menzel, H. Pleiner, H.R. Brand, J. Chem. Phys. 126, 234901 (2007)
H.R. Brand, H. Pleiner, Physica A 208, 359 (1994)
S.T. Kim, H. Finkelmann, Makromol. Chem. Rapid Commun. 22, 429 (2001)
A. Komp, J. Rühe, H. Finkelmann, Makromol. Chem. Rapid Commun. 26, 813 (2005)
H.R. Brand, Makromol. Chem. Rapid Commun. 10, 441 (1989)
A.M. Menzel, H.R. Brand, J. Chem. Phys. 125, 194704 (2006)
A. Mertelj, D. Lisjak, M. Drofenik, M. Čopič, Nature 504, 237 (2013)
A. Mertelj, N. Osterman, D. Lisjak, M. Čopič, Soft Matter 10, 9065 (2014)
Q. Zhang, P.J. Ackerman, Q. Liu, I.I. Smalyukh, Phys. Rev. Lett 115, 097802 (2015)
A.J. Hess, Q. Liu, I.I. Smalyukh, Appl. Phys. Lett. 107, 071906 (2015)
A. Mertelj, D. Lisjak, Liquid Crystals Reviews 5, 1 (2017)
Q. Liu, P.J. Ackerman, T.C. Lubensky, I.I. Smalyukh, Proc. Natl. Acad. Sci. USA 113, 10479 (2016)
P.J. Ackerman, I.I. Smalyukh, Nat. Mater. 16, 426 (2017)
P. Medle Rupnik, D. Lisjak, M. Čopič, S. Čopar, A. Mertelj, Science Advances 3, e1701336 (2017)
R. Sahoo, M.V. Rasna, D. Lisjak, A. Mertelj, S. Dahra, Appl. Phys. Lett. 106, 161905 (2015)
T. Potisk, D. Svenšek, H.R. Brand, H. Pleiner, D. Lisjak, N. Osterman, A. Mertelj, Phys. Rev. Lett. 119, 097802 (2017)
T. Potisk, A. Mertelj, N. Sebastián, N. Osterman, D. Lisjak, H.R. Brand, H. Pleiner, D. Svenšek, Phys. Rev. E 97, 012701 (2018)
T. Potisk, H. Pleiner, D. Svenšek, H.R. Brand, Phys. Rev. E 97, 042705 (2018)
E. Jarkova, H. Pleiner, H.W. Müller, A. Fink, H.R. Brand, Eur. Phys. J. E 5, 583 (2001)
E. Jarkova, H. Pleiner, H.-W. Müller, H.R. Brand, J. Chem. Phys. 118, 2422 (2003)
H. Pleiner, D. Svenšek, T. Potisk, H.R. Brand, Phys. Rev. E 101, 032601 (2020)
H.R. Brand, H. Pleiner, F. Ziebert, Phys. Rev. E 74, 021713 (2006)
H. Pleiner, H.R. Brand, EPL 9, 243 (1989)
N. Sebastian, L. Cmok, R.J. Mandle, M.R. de la Fuente, I.D. Olenik, M. Copic, A. Mertelj, Phys. Rev. Lett. 124, 037801 (2020)
R.J. Mandle, N. Sebastian, J. Martinez-Perdiguero, A. Mertelj, Nature Comm. 12, 4962 (2021)
N. Sebastian, R.J. Mandle, A. Petelin, A. Eremin, A. Mertelj, Liq. Cryst. 48, 2055 (2021)
H. Lu, X. Zeng, G. Ungar, C. Dressel, C. Tschierske, Angew. Chem. Int. Ed. 57, 2835 (2018)
A.M. Levelut, C. Germain, P. Keller, L. Liebert, J. Billard, J. Phys. (France) 44, 623 (1983)
A.M. Levelut, E. Hallouin, D. Bennemann, G. Heppke, D. Loetzsch, J. Phys. II 7, 981 (1997)
B. Pansu, Y. Nastishin, M. Imperor-Clerc, M. Veber, H.T. Nguyen, Eur. Phys. J. E 15, 225 (2004)
M. Tinkham, Group Theory and Quantum Mechanics (McGraw-Hill, New York, 1964)
H.R. Brand, H. Pleiner, Eur. Phys. J. E 42, 142 (2019)
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of Interest
The authors have no relevant financial or non-financial interests to disclose.
Macroscopic Two-Fluid Effects for the Chiral Q (\(D_4\)) - Phase in a Non-Chiral Solvent
Macroscopic Two-Fluid Effects for the Chiral Q (\(D_4\)) - Phase in a Non-Chiral Solvent
The chiral Q phase [72,73,74,75], which has been discussed and characterized recently in detail [72], has a tetragonal structure with chiral symmetry \(D_4\) [39, 76]. It can be viewed as a tetragonal biaxial nematic liquid crystal with a director and 4-fold perpendicular preferred structure \(Q^{tr}_{ijkl}\), whose rotations are additional hydrodynamic variables. Chirality is provided by the existence of a pseudoscalar \(q_0\). For one component systems various aspects of the macroscopic dynamics of this phase have been discussed recently [77].
Here, we focus on two-fluid aspects of a system consisting of two subsystems: a \(D_4\)-phase and an isotropic solvent. We restrict ourselves to the connection between the relative and the mean velocity with the thermal and solutal degree of freedom.
For the variables of interest, we have dynamic equations like in Sect. 2.3
For the reversible parts of the currents, we find, requiring vanishing entropy production, R,
with \(s_{ijk} = \hat{n}_i \hat{n}_p \epsilon _{pjk}\) with \(\hat n_i\) symbolizing the preferred 4-fold axis of the \(D_4\) phase. We have also kept in Eqs. (80)–(83) the non-chiral contributions, since they have not been given before, neither for the non-chiral Q phase of \(D_{4h}\) symmetry nor for the chiral Q phase.
From inspection of Eqs. (80)–(83), we see that there are a number of reversible dynamic cross-coupling terms between the relative velocity and the scalar variables \(\sigma\) and \(\phi\) (and similarly to electric fields \(E_i\)). In addition, we notice that the cross-coupling terms \(\sim \Gamma _2\) and \(\sim \Gamma _3\) also exist already in the one component \(D_4\) phase.
For the dissipative aspects, we focus on the variables \(g_i\) and the velocity difference \(w_i\). For the dissipative contributions associated with the concentration \(\phi\) we refer to ref. [77], where we have discussed already Lehmann effects for the case of a concentration without a relative velocity.
where \(\dots\) stands for the dissipative contributions of all the other variables. The fourth rank tensors \(\sim \nu _{ijkl}\), \(\sim \nu _{ijkl}^{w}\) and \(\sim \nu _{ijkl}^{c}\) all contain six independent coefficients (as it is standard for tetragonal symmetry [39]) due to the existence of a constant \(Q_{ijkl}^{tr}\) in equilibrium.
The most interesting dissipative cross-coupling is clearly the contribution \(\sim \Sigma ^{D4}\) describing a direct cross-coupling between relative velocities and symmetrized velocity gradients. It does not exist for \(D_{4h}\)-symmetry and requires for its existence broken parity symmetry as well as a preferred direction.
From Eq. (84), we obtain the following dissipative currents
demonstrating that the coupling \(\Sigma ^{D_4}\) between relative velocity and symmetrized velocity gradients indeed leads to a dissipative coupling to lowest order in the gradients.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Brand, H.R., Pleiner, H. A Two-Fluid Model for the Macroscopic Behavior of Nematic Fluids and Gels in a Chiral Solvent. Braz J Phys 52, 70 (2022). https://doi.org/10.1007/s13538-022-01052-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s13538-022-01052-4