1 Introduction

Metal oxides and their composites are among the important material groups that always attract the attention of researchers due to their wide application areas. The main reason for this interest is related to their unique mechanical, thermal, optical, magnetic, electrical, and catalytic characteristics [1]. Photocatalysis [2], drug delivery systems [3], flame retardants [4], photodetectors [5], electrochromic devices [6], supercapacitors [7], light–emitting diodes [8], organic solar cells [9], and wastewater treatment [10,11,12] are only a few of their application areas.

Transition metal oxides can be prepared as pure oxides or metal nanocomposites by various methods. These include microwave treatment [13], electrospinning [14, 15], co-precipitation [15, 16], solution combustion synthesis [17], sol–gel spontaneous combustion [18], sonochemical route [19], and hydrothermal method [20]. The hydrothermal method is a processable, simple, low temperature, low cost, and rapid synthesis method. Nowadays, many researchers focus on the biosynthesis of metal oxide nanomaterials using natural substances such as plants or microorganisms. This green synthesis approach can replace harmful chemicals and provide an environmentally friendly synthesis [21, 22]. The green hydrothermal technique has the advantages of both green chemistry and hydrothermal process. Therefore, its application to metal oxide synthesis has attracted attention [21]. Mixed metal oxide systems are unique structures that combine different properties of metal oxides. Among mixed metal oxide systems, nickel oxide and zinc oxide composites are of particular interest because various properties of n-type ZnO and p-type NiO are achieved in a single structure [19, 20].

While NiO has been recognized as a promising electroactive material [23], its wide band gap and low conductivity remain significant challenges. To overcome these limitations, NiO NPs are combined with other metal oxides [24]. The synergistic effect facilitates the oxidation/reduction of ions and the transport of electrons to the electrodes [25]. NiO stands out as one of the most extensively researched pseudocapacitive materials, attributed to its semiconducting nature, p-type wide band gap (3.6–4.0 eV) [26], environmental friendliness [27], high redox activity, impressive theoretical gravimetric capacitance, as well as its applications in photocatalysis and electrochemical sensing [28].

ZnO is another metal oxide having outstanding physical and chemical properties [29]. Its high chemical stability, photostability, and radiation absorption in a wide range provide various application areas, such as electronics, photocatalysts and sensor systems [29, 30]. Recently, ZnO has also been used as a supercapacitor electrode material due to its ease of fabrication, low cost [31], environmental friendliness [32, 33].

Salvia officinalis (S. officinalis), also known as common sage and belonging to the Labiatae/Lamiaceae family, is the genus with the most glandular hairs (Fig. 1) [34, 35]. A wide range of constituents, including alkaloids, carbohydrate, fatty acids, phenolic compounds (e.g., coumarins, tannins, flavonoids), terpenes/terpenoids (e.g., monoterpenoids, sesquiterpenoids, diterpenoids, triterpenoids), glycosidic derivatives (e.g., cardiac glycosides, saponins, flavonoid glycosides), poly acetylenes, steroids, and waxes, are found in S. officinalis [34]. S. officinalis has a rich history of culinary and medicinal application, serving as an antispasmodic, anti-inflammatory, antimicrobial, carminative and mucolytic agent. Its versatility extends to being a natural antioxidant, replacing synthetic alternatives in food and pharmaceuticals. Sage enhances food flavor, prolongs shelf life, and exhibits antibacterial-antifungal properties. Its essential oil finds applications in medicine and cosmetics [34,35,36,37].

Fig. 1
figure 1

Image of S. officinalis

Full size image

To the best of our knowledge, there are no reports in the literature regarding the biosynthesis of NiO NPs and NiO@ZnO nanocomposite using S. officinalis extract-assisted hydrothermal processes. While a green synthesis of NiO NPs using S. officinalis extract was reported previously [35], the hydrothermal process was not utilized in that study for NiO NPs synthesis. Additionally, Abomuti et al. reported the green synthesis of ZnO NPs using S. officinalis extract, investigating their photocatalytic and antifungal activities, but without employing a hydrothermal process [36]. Furthermore, in another study, ZnO NPs were prepared by a S. officinalis extract-assisted hydrothermal process with and without the presence of a polymer [38]. In contrast to this study, the ZnO NPs synthesized here were evaluated for their supercapacitive properties.

Our study introduces a novel synthesis route for NiO NPs and NiO@ZnO nanocomposite using S. officinalis extract as a reducing and capping reagent. ZnO NPs were also synthesized for comparison. The synthesized products underwent comprehensive characterization, including optical, morphological, magnetic, and electrochemical analyses. Specifically, we investigated the specific capacitance of NiO NPs, ZnO NPs, and NiO@ZnO nanocomposite in a 2 M NaOH electrolyte using the cyclic voltammetry (CV) technique. Additionally, we determined the crystallite sizes of the metal oxides through PXRD spectra analysis using Scherrer and Williamson–Hall (W–H) methods. For these calculations, we applied the Uniform Deformation Model (UDM), the Uniform Stress Deformation Model (USDM), and the Uniform Deformation Energy Density Model (UDEDM).

2 Experimental method

2.1 Materials

Ni(NO3)2·6H2O (Alfa Aesar), Zn(NO3)2·6H2O (Merck) and NaOH (Merck) were used. All chemicals were of analytical grade and used for synthesis without further purification. S. officinalis specimens were collected from Çınarlı district, located at 40°37′17" N latitude and 27°32′10" E longitude, with an altitude of 40 m, in Balıkesir, Turkey, in August 2021. Before use, the leaves of S. officinalis were dried for one week at room temperature between 30/20 °C (day/night) without being exposed to sunlight.

2.2 Preparation of the S. officinalis leaf extract

The S. officinalis leaves were cleaned with deionized water (DW) to remove contaminants, and then dried at room temperature for one week, and finely grounded. 5 g of dried leaves were mixed with 100 mL of DW at 60 °C for 1 h. The aqueous extract was cooled, filtered through S&H Labware (125 mm) and centrifuged at 6000 rpm for 5 min. Then, the extract was stored in the refrigerator at 4 °C for later use in experiments [35].

2.3 S. officinalis leaf extract-mediated hydrothermal synthesis of NiO NPs, ZnO NPs and NiO@ZnO nanocomposite

To synthesize NiO NPs, 7 mmol of Ni(NO3)2.6H2O was dissolved in 10 mL of DW, then mixed at once with 25 mL of S. officinalis plant extract at room temperature using a magnetic stirrer. pH of the solution was adjusted to 8.0 using 0.1 M NaOH. After the alkaline mixture was transferred to the 100 mL teflon-lined stainless steel autoclave, it was left in the furnace under operating conditions of 180 °C, 24 h. When the process was completed, the hydrothermal reactor was cooled to room temperature. The precipitates were filtrated and washed several times with DW and dried. The dried NiO NPs were annealed at 500 °C for 2 h. ZnO NPs and NiO@ZnO nanocomposite were synthesized by the same process. A molar ratio of 1:1 (Ni(NO3)2.6H2O: Zn(NO3)2.6H2O) was used for nanocomposite synthesis. The synthetic procedure for synthesis was given in Fig. 2.

Fig. 2
figure 2

Schematic presentation for green-hydrothermal synthesis of NiO and ZnO NPs, and NiO@ZnO nanocomposite

Full size image

2.4 Characterization techniques

The Perkin Elmer Spectrum Two ATR model FT-IR instrument was used in characterization studies (in range of 4000–375 cm−1). The UV–Vis analysis of the samples was performed using a PerkinElmer WinLab-25 series spectrophotometer within the wavelength range of 250–700 nm. The Zeiss Sigma 300 instrument model was used for scanning electron microscopy (SEM) analysis. Transmission electron microscopy (TEM) analysis was conducted using a JEOL JEM-1400 PLUS model instrument. For powder X-ray diffraction (PXRD) analysis, a Rigaku SmartLAB diffractometer (CuKα, 40 kV, 40 mA) was utilized. Diffraction patterns were analyzed between 20° and 80° (2θ) with a step of 0.01°. Vibrating Sample Magnetometer (VSM) measurements were performed using a Lake Shore 7407 instrument (300 K, ± 20 kOe). Cyclic Voltammetric (CV) measurements were conducted with a Metrohm 757 VA Trace Analyzer instrument, utilizing a pencil graphite electrode (PGE) as the working electrode, a platinum wire as the auxiliary electrode, and an Ag/AgCl (3 M KCl) reference electrode. Argon gas (99.5%) was passed through the measured solutions for 1 min. A Rotring Tikky model pen with a Tombow 2B ultrapolymer (0.5 mm diameter) was used as the PGE.

3 Results and discussion

3.1 Green synthesis of NiO and ZnO NPs, and NiO@ZnO nanocomposite

The green synthesis of the NiO and ZnO nanoparticles (NPs) and the NiO@ZnO nanocomposite utilizing S. officinalis extract involves the reduction of Ni(II) and Zn(II) ions. The extract serves as both a reducing and stabilizing agent [39]. This process is eco-friendly and takes place under simple conditions. Flavonoids, polyphenols, and alkaloids in plants have high reduction potentials and act as electron donors, facilitating the reduction of metal ions [40, 41]. The major phenolic contents in S. officinalis extracts have been previously reported [34, 42]. These components, shown in Fig. 3, may be responsible for the reduction process. The reduction process arises from the inherent electron-donating properties of these compounds, which interact with metal ions and their salts. Consequently, there is an increase in electronic density within the conjugated metal salts, promoting the reduction reaction [43].

Fig. 3
figure 3

Demonstration of the formation of NiO NPs, ZnO NPs, and NiO@ZnO nanocomposite via bioreduction using S. officinalis extract

Full size image

3.2 Characterization of NiO NPs, ZnO NPs, and NiO@ZnO nanocomposite

3.2.1 FT-IR and UV–Vis analyses

FT-IR was the first method used here for the characterization. The formations of NiO NPs, ZnO NPs, and NiO@ZnO nanocomposite were confirmed by FT-IR, as shown in Fig. 4 and Table 1. In our previous publication, the FT-IR spectrum of the S. officinalis extract was presented [35].

Fig. 4
figure 4

FT-IR spectra of NiO NPs (a), ZnO NPs (b), and NiO@ZnO nanocomposite (c)

Full size image
Table 1 FT-IR data of NiO NPs, ZnO NPs, NiO@ZnO nanocomposite, and related peak assignments
Full size table

In the FT-IR spectrum of the NiO nanoparticles (NiO NPs) (Fig. 4a), vibrations between 1460–1345 cm–1, 1170–1100 cm–1, and 379 cm–1 were observed. The band at 1460–1345 cm–1 was attributed to C-H deformation vibrations, and the band at 1170–1100 cm-1 was assigned to the C-O bond [44, 45]. The characteristic Ni–O vibrations were observed at 379 cm–1 [44].

ZnO NPs exhibited vibrations at 2341, 1505, 1396, 1070 and 380 cm−1 (Fig. 4b). The sharp peak at 2341 cm–1 belonged to the C = O stretching [46]. The vibrations at 1396 cm−1 were attributed to aliphatic C-H vibrations. The band at 1070 cm−1 corresponded to the C-O stretching vibrations of the plant extracts [35].

For NiO@ZnO nanocomposite, the vibrations at 1498–1371, 1164–1120 and 383 cm−1 were observed (Fig. 4c). The vibrations between 1498–1371 cm−1 belonged to aliphatic C-H vibrations. The band between 1164–1120 cm−1 corresponded to the C-O stretching vibrations of the plant extracts [35, 45]. The presence of a stretching vibration observed at 383 cm−1 confirmed the formation of M–O and O-M–O (M2+ = Ni and Zn) bonds [47].

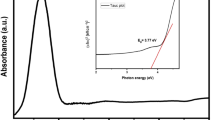
Figure 5a shows the UV–Vis spectra of NiO NPs, ZnO NPs, and NiO@ZnO nanocomposite dispersed in DW. NiO NPs, ZnO NPs, and NiO@ZnO nanocomposite exhibited absorption maxima at 307, 376 and 311 nm, respectively, and in harmony with the literature [24, 48]. NiO@ZnO nanocomposite exhibited a red shifted adsorption edge as compared to NiO NPs [49].

Fig. 5
figure 5

UV–Vis absorption spectra (a), Tauc's plot for direct (b), and indirect (c) band gap energies of NiO NPs, ZnO NPs, and NiO@ZnO nanocomposite

Full size image

The optical band gaps (Eg) of the compounds were calculated by the Tauc equation (Eq. 1):

$$\alpha h\nu ={A\left(h\nu -{E}_{g}\right)}^{n}$$
(1)

where α is the absorption coefficient, hv is the frequency of light, A is a constant, Eg is the band gap energy, and n depends on the bandpass type. n = 1/2 or 2 was the direct and indirect transition band gaps, respectively [50].

In Fig. 5b and 5c, the direct band gap energies of NiO NPs, ZnO NPs, and NiO@ZnO nanocomposite were 3.00, 2.28, 2.71 eV, whereas the indirect band gap energies were 2.63, 1.91, 2.23 eV, respectively. Because of the coupling of NiO and ZnO, electrons can freely move from NiO with a higher Fermi level to ZnO with a lower Fermi level, allowing the separation of holes and electrons. This causes the band gap of NiO@ZnO nanocomposite to be lower than the band gap of NiO NPs [49]. The reduced band gap increases the electron transfer between the valence and conduction bands, thereby enhancing the conductivity of nanomaterials. This enhancement contributes to increased charge storage and consequently higher capacitance, rendering it a promising candidate for supercapacitor applications [51].

3.2.2 Powder X-ray diffraction (PXRD) analyses

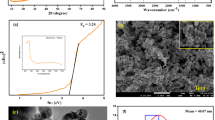
The PXRD patterns of S. officinalis extract-mediated hydrothermal synthesized NiO NPs, ZnO NPs, and NiO@ZnO nanocomposite are shown in Fig. 6. The diffraction peaks at 37.2°, 43.2°, 62.8°, 75.4° and 79.3° in 2θ of NiO NP were assigned to the (111), (200), (220), (311) and (222) planes of cubic NiO (JCPDS card No. 04–0835). The sample was crystalline cubic NiO NPs with lattice constants a = b = c = 4.1769 Å, belonging to the space group: Fm-3 m [52].

Fig. 6
figure 6

PXRD patterns of NiO NPs, ZnO NPs, NiO@ZnO nanocomposite

Full size image

The PXRD patterns of ZnO nanoparticles (ZnO NPs) showed peaks at 31.7°, 34.4°, 36.2°, 47.5°, 56.6°, 62.8°, 66.4°, 67.9°, 69.1°, and 77.0° in 2θ values. These peaks were indexed to the (100), (002), (101), (102), (110), (103), (200), (112), (201), and (202) planes of the hexagonal Wurtzite structured ZnO [53] (JCPDS card No. 36–1451) [54]. The lattice constants are a = b = 3.2501, c = 5.2017 Å, belonging to the space group: P63mc [55]. The presence of diffraction peaks belonging to both NiO and ZnO structures in the patterns proved that two different phases were available in the composite. Moreover, these spectra exhibited no additional peaks due to impurities. Using the Whole Powder Pattern Fitting (WPPF) method, it was possible to calculate the mass fractions of crystalline phases for each phase [56]. WPPF weight fraction analysis indicated that NiO@ZnO nanocomposite consisted of 48% NiO and 52% ZnO. Furthermore, the PXRD patterns exhibited sharp peaks with high intensity, indicating that extract-mediated hydrothermal synthesized NiO NPs, ZnO NPs, and NiO@ZnO nanocomposite had high crystallinity. It was noted that hydrothermal process obviously increased the NiO crystallinity as compared to that of the previously reported ones [35]. The crystal sizes of the metal oxides synthesized here were determined by the Scherrer method and compared with the results obtained by the Williamson–Hall method, and the results were presented in Table 2. The calculations were separately performed for both NiO and ZnO phases in the composite, as given in the literature [57].

Table 2 Calculated parameters of NiO NPs, ZnO NPs, and NiO@ZnO nanocomposite
Full size table

The crystal size of nanomaterials is usually calculated using the Scherrer equation (Eq. 2). In Eq. 2, the full width at half maximum (β) (where β ℎ k l β hkl ​ represents each diffraction peak) of the measured sample (β meas) and the instrument (β inst.) are considered. K is the dimensionless shape factor, usually taken as 0.94, and the wavelength (λ) of radiation for CuKα is 1.54 Å. These parameters are used for determining the crystallite size (D) (Eq. 3) [58].

$${\beta }_{hkl}^{2}={\beta }_{meas.}^{2}-{\beta }_{inst.}^{2}$$
(2)
$$D=\frac{K\lambda }{{\beta }_{hkl} \mathrm{cos}(\theta )}$$
(3)

The uniform deformation model (UDM) presumes uniform stress along all crystallographic directions. In other words, UDM treats the stress isotropically, which affects the physical broadening in the XRD pattern [59]. Therefore, the broadening (βhkl) can be written as in Eq. 4 [60]:

$${\beta }_{hkl}={\beta }_{meas.}-{\beta }_{inst.}$$
(4)

It leads to the estimation of DUDM (crystallite size) and ε (strain) according to the equation in Eq. 5 [61].

$${\beta }_{hkl}\mathrm{cos}\theta = \frac{K\lambda }{D}+4\varepsilon \mathrm{sin}\theta$$
(5)

Figure S1 demonstrates the linear fitting of the βhkl cosθ versus 4sinθ plot. The DUDM was calculated using the y-intercept, and ε was determined from the slope of the fitted line [62].

The uniform stress deformation model (USDM) is another model used here. In this model, the lattice deformation stress is accepted to be uniform for all crystallographic directions, and a small microstrain is presumed to exist in the particles. The relation between stress (σ) and ε is described by the Hooke's law, given in Eq. 6. In here, the proportionality constant is Young's modulus (Yhkl) [63].

$$\upsigma =\upvarepsilon {Y}_{hkl}$$
(6)

In Eqs. (7–14), Yhkl was calculated using Cij (stiffness constant) and Sij (elastic compliances) [63]. For cubic system [63];

$${\mathrm{S}}_{11}= \frac{{\mathrm{C}}_{11}+{\mathrm{C}}_{12}}{\left({\mathrm{C}}_{11}-{\mathrm{C}}_{12}\right)\left({\mathrm{C}}_{11}+{2\mathrm{C}}_{12}\right)}$$
(7)
$${\mathrm{S}}_{12}= \frac{-{\mathrm{C}}_{12}}{\left({\mathrm{C}}_{11}-{\mathrm{C}}_{12}\right)\left({\mathrm{C}}_{11}+{2\mathrm{C}}_{12}\right)}$$
(8)
$${\mathrm{S}}_{44}=\frac{1}{{\mathrm{C}}_{44}}$$
(9)

For hexagonal system [63];

$${\mathrm{S}}_{11}=\frac{1}{2}\left( \frac{{\mathrm{C}}_{33}}{{\mathrm{C}}_{33}\left({\mathrm{C}}_{11}+{\mathrm{C}}_{12}\right)-2{{(\mathrm{C}}_{13})}^{2}}+\frac{1}{{\mathrm{C}}_{11}-{\mathrm{C}}_{12}}\right)$$
(10)
$${\mathrm{S}}_{12}=\frac{1}{2}\left( \frac{{\mathrm{C}}_{33}}{{\mathrm{C}}_{33}\left({\mathrm{C}}_{11}+{\mathrm{C}}_{12}\right)-2{{(\mathrm{C}}_{13})}^{2}}-\frac{1}{{\mathrm{C}}_{11}-{\mathrm{C}}_{12}}\right)$$
(11)
$${\mathrm{S}}_{33}=\frac{{\mathrm{C}}_{11}+{\mathrm{C}}_{12}}{{\mathrm{C}}_{33}\left({\mathrm{C}}_{11}+{\mathrm{C}}_{12}\right)-2{{(\mathrm{C}}_{13})}^{2}}$$
(12)
$${\mathrm{S}}_{13}=\frac{{\mathrm{C}}_{13}}{{\mathrm{C}}_{33}\left({\mathrm{C}}_{11}+{\mathrm{C}}_{12}\right)-2{{(\mathrm{C}}_{13})}^{2}}$$
(13)
$${\mathrm{S}}_{44}=\frac{1}{{\mathrm{C}}_{44}}$$
(14)

Young’s modulus for cubic and hexagonal crystal systems can be given as Eq. (15) and (16). For cubic system [63];

$$\frac{1}{{Y}_{hkl}}= {\mathrm{S}}_{11}-2\left[{(\mathrm{S}}_{11}- {\mathrm{S}}_{12})-\frac{1}{2}{\mathrm{S}}_{44}\right]\left[\frac{{\mathrm{h}}^{2}{\mathrm{k}}^{2}+ {\mathrm{k}}^{2}{\mathrm{l}}^{2}+{\mathrm{l}}^{2}{\mathrm{h}}^{2}}{{\mathrm{h}}^{2}+{\mathrm{k}}^{2}+ {\mathrm{l}}^{2}}\right]$$
(15)

S11, S12 and S44 values for NiO were 6.14 × 10−12, − 2.12 × 10−12 and 14.76 × 10−12 m2 N−1, respectively (C11 = 255.66 GPa, C12 = 134.66 GPa and C44 = 67.73 GPa) [64].

For hexagonal system [63];

$${Y}_{hkl}= \frac{{\left[{\mathrm{h}}^{2}+\frac{{\left(\mathrm{h}+2\mathrm{k}\right)}^{2}}{3}+{\left(\frac{\mathrm{al}}{\mathrm{c}}\right)}^{2}\right]}^{2}}{{\mathrm{S}}_{11}{\left({\mathrm{h}}^{2}+\frac{{\left(\mathrm{h}+2\mathrm{k}\right)}^{2}}{3}\right)}^{2}+{\mathrm{S}}_{33}{\left(\frac{\mathrm{al}}{\mathrm{c}}\right)}^{4}+\left({2\mathrm{S}}_{13}+{\mathrm{S}}_{44}\right)\left({\mathrm{h}}^{2}+\frac{{\left(\mathrm{h}+2\mathrm{k}\right)}^{2}}{3}\right){\left(\frac{\mathrm{al}}{\mathrm{c}}\right)}^{2}}$$
(16)

Here, “a” and “c” are the lattice parameters, and the S11, S13, S33 and S44 values for ZnO were 7.858 × 10−12, − 2.206 × 10−12, 6.940 × 10−12 and 23.57 × 10−12 m2 N−1, respectively [65].

Energy density of a crystal is determined by the uniform deformation energy density model (UDEDM). For an elastic system, the ued is given in Eq. (17) [66];

$${\beta }_{hkl}\mathrm{cos}\theta = \left(\frac{K\lambda }{D}\right)+\left(4 \mathrm{sin}{\theta }_{hkl}{\left(\frac{{2u}_{ed}}{{Y}_{hkl}}\right)}^{1/2}\right)$$
(17)

By plotting βhkl cosθhkl versus 4sinθhkl (2/Yhkl)1/2, ued was calculated from the slope of the linear fit, and the crystallite size D was determined from the y-intercept [65].

Table 2 shows the calculated D, ε, σ, ued structural parameters of the synthesized metal oxides according to the Scherrer and W–H method.

3.2.3 Morphological studies

TEM and SEM analyzes were performed to evaluate the morphology, composition and size characteristics of the synthesized metal oxides. Figure 7(a,b) shows the TEM images of NiO NPs.

Fig. 7
figure 7

TEM images of NiO (a, b), ZnO (d, e) NPs, and NiO@ZnO (g, h) at different magnifications and their related particles size distribution histograms (c, f, i) (histograms were produced from b, e, and h images)

Full size image

As seen in Fig. 7a and b, the particles were almost in spherical shape, and their sizes were in the range of 7.4–25.4 nm. The average particle size was 16.0 nm (SD: 3.5) (Fig. 7c). The TEM images of ZnO NPs given in Fig. 7d and e show the presence of the agglomerated rice shaped particles. The particle sizes ranged from 89.5 to 330.9 nm, and the average particle size was 207.5 nm (SD: 57.8) (Fig. 7f). Figure 7g and h belong to the TEM images of NiO@ZnO. These particles were in a spherical shape as NiO. Unlike NiO, some hexagonal formations were also observed in these images. It was noted that their particle sizes were smaller than those of ZnO NPs, and larger than NiO NPs. The particle sizes ranged from 12.5 to 55.0 nm, and the average size was 31.0 nm (SD: 7.6) (Fig. 7i).

Figure 8a-i indicates the SEM images of NiO, ZnO NPs, and NiO@ZnO nanocomposite. The morphology of NiO and NiO@ZnO was very similar. Hence, their particle sizes were close to each other and varied approximately from 10 up to 200 nm. ZnO NPs exhibited relatively different morphology. The broken-rice like formations were observed from Fig. 8d-f). The elemental composition of NiO@ZnO was evaluated by EDX and EDS mapping analysis (Fig. 8j-o). The elemental ratio of Ni: Zn (as weight) was found to be 43.33:56.67 (Fig. 8o). The distribution of the elementals was almost homogenous, as seen from Fig. 8j-n. The EDX and EDS mapping images of NiO, ZnO NPs were presented in Figure S2. NiO NPs had a composition ratio consisting of 82.64 Ni and 17.36 O as weight %. ZnO NPs contained 87.32 Zn and 12.68 O as weight%.

Fig. 8
figure 8

SEM images of NiO (a-c), ZnO (d-f) NPs, and NiO@ZnO (g-i) at different magnifications, low-resolution SEM image of NiO@ZnO (j), EDS mapping images of NiO@ZnO (k-n), and EDX analysis of NiO@ZnO (o)

Full size image

3.2.4 Magnetic behavior

Figure 9 shows the magnetization-magnetic field hysteresis loops of NiO NPs, ZnO NPs, and NiO@ZnO nanocomposite obtained by the VSM technique at room temperature.

Fig. 9
figure 9

FSM analysis results of NiO NPs, ZnO NPs, and NiO@ZnO nanocomposite

Full size image

The coercivity (Hci), saturation magnetization (Ms) and residual magnetization (Mr) values of NiO NPs were 209.22 Oe, 0.32 emu/g, and 0.007 emu/g, respectively. These values can be compared with our previous study [35]. The presence of the hydrothermal process caused an increase in the Hci values of NiO NPs. In addition, the obtained data here showed that NiO NPs exhibited ferromagnetic behavior in contrast to the antiferromagnetic behavior of bulk NiO. Ferromagnetism in metal oxide NPs is thought to cause point defects originated from oxygen vacancies or other defects instead of the existence of magnetic ions [67]. Additionally, Makhlouf et al. reported ferromagnetic properties in NiO NPs with particles smaller than 30 nm [68]. As a result, the ferromagnetic behavior of high surface area NiO nanoparticles can be attributed to the presence of a high number of unpaired surface spins [69].

ZnO NPs show a diamagnetic behavior at room temperature due to the paired electrons of the d-orbital and the non-permanent magnetic moment [70]. When NiO is doped into pure ZnO NPs, it exhibits weak ferromagnetism. The weak ferromagnetic properties of the NiO@ZnO nanocomposite may be attributed to the defects and oxygen vacancies, and the interactions between the spin moment of NiO and ZnO [71]. The ferromagnetic behavior is weakened when electrons are confined in defect areas, causing the electrons to settle in orbits that overlap the d-shells of neighboring Zn ions. This enhances the interaction between Zn ions, leading to a decrease in the saturation magnetization (Ms). Although the saturation of the M-H loop is low, the presence of a small hysteresis loop in the NiO@ZnO nanocomposite indicates its weak ferromagnetic nature [72,73,74].

Squareness Ratio (SQR) is calculated as the ratio of Mr to Ms of hysteresis loop. The SQR equal to, or greater than, 0.5 points out the studied compound has a single magnetic field, while SQR less than 0.5 points out the presence of multi-field structures [75]. In this study, NiO NPs, ZnO NPs, and NiO@ZnO nanocomposite have SQR of 0.02, 0.035 and 0.03, respectively, indicating that they have a multi-field structure.

The coercivity (Hci), saturation magnetization (Ms), retentivity (Mr) and squareness ratio (SQR = Mr/Ms) values for NiO NPs, ZnO NPs, and NiO@ZnO nanocomposite were given in Table 3.

Table 3 Magnetic parameters of NiO NPs, ZnO NPs, and NiO@/ZnO nanocomposite
Full size table

3.2.5 Electrochemical properties and capacitance performances

The electrochemical properties and capacitance characteristics of NiO NP, ZnO NPs, and NiO@ZnO nanocomposite were determined in 2 M NaOH solution by CV [76]. The CV voltammograms and specific capacitance plots of NiO NPs, ZnO NPs, and NiO@ZnO nanocomposite are given in Fig. 10. The voltammograms for NiO and ZnO nanoparticles were consistent with the literature in terms of both shape and redox potential values, as discussed below and shown in Fig. 10 [76, 77].

Fig. 10
figure 10

Voltammograms recorded by CV in 2 M NaOH aqueous electrolyte using PGE at scan rates of 25–100 mV/s, NiO NPs (a), ZnO NPs (b), NiO@ZnO nanocomposite (c), and specific capacitance values of NiO NPs, ZnO NPs and NiO@ZnO nanocomposite at scan rates of 25, 50, 75, 100 mV/s (d)

Full size image

As seen from Fig. 10a, both anodic (about 0.45 V) and cathodic (about 0.33 V) peaks were observed in voltammograms of NiO NPs. The presence of reversible Ni2+/Ni3+ redox peaks in the cathodic and anodic scans is important evidence of pseudocapacitance character in the electrochemical process [28]. The oxidation peak (Ni2+ ↔ Ni3+) of NiO nanoparticles (NiO NPs) was observed at + 0.45 V for a scan rate of 25 mV/s. This peak was attributed to the oxidation of nickel oxide to nickel oxyhydroxide (NiO/NiOOH). The oxidation mechanism for NiO is described in Eq. (18) [78].

$$\mathrm{NiO}+{\mathrm{OH}}^{-}\leftrightarrow \mathrm{NiOOH}+{\mathrm{e}}^{-}$$
(18)

In the reverse scan, the reduction (Ni3+ ↔ Ni2+) peak of NiO NPs was observed at + 0.33 V for the same scan rate. The related reduction reaction mechanism is given in Eq. (19) [79].

$$\mathrm{NiOOH}+{\mathrm{e}}^{-}\leftrightarrow \mathrm{NiO}$$
(19)

As seen from Fig. 8b, both anodic (about -1.37 V) and cathodic (about -1.56 V) peaks were observed in voltammograms of ZnO NPs [77]. The presence of fast and reversible faradaic Zn2+/Zn3+ redox peaks in the cathodic and anodic scans is evidence of pseudocapacitance character in the electrochemical process [77]. The oxidation peak (Zn2+ ↔ Zn3+) of ZnO NPs was observed at -1.37 V for a scan rate of 25 mV/s. This peak was attributed to the oxidation of zinc oxide to zinc oxyhydroxide (ZnO/ZnOOH). The oxidation mechanism of ZnO is described in Eq. (20) [79].

$$\mathrm{ZnO}+{\mathrm{OH}}^{-}\leftrightarrow \mathrm{ZnOOH}+{\mathrm{e}}^{-}$$
(20)

In the reverse scan, the reduction (Zn3+ ↔ Zn2+) peak of ZnO NPs was observed at -1.56 V for the same scan rate. The related reduction reaction mechanism was given in Eq. (21).

$$\mathrm{ZnOOH}+{\mathrm{e}}^{-}\leftrightarrow \mathrm{ZnO}$$
(21)

CV voltammograms of NiO@ZnO nanocomposite are given in Fig. 10b. During the positive potential scan, a sharp oxidation peak was observed at -1.41 V for 25 mV/s scan rate. This was attributed to the simultaneous electrooxidation of nickel and zinc species (Ni2+ ↔ Ni3+ and Zn2+ ↔ Zn3+), which occurs at approximately the same potential.

The corresponding redox reactions (Eqs. 22 and 23) are defined as follows [79]:

$$\mathrm{ZnO}+{\mathrm{OH}}^{-}\leftrightarrow \mathrm{ZnOOH}+{\mathrm{e}}^{-}$$
(22)
$$\mathrm{NiO}+{\mathrm{OH}}^{-}\leftrightarrow \mathrm{NiOOH}+{\mathrm{e}}^{-}$$
(23)

In the reverse scan, a weaker reduction was observed at -1.57 V. This peak is related to the simultaneous reduction of oxidized nickel and zinc species (Ni3+  ↔ Ni2+ and Zn3+  ↔ Zn2+). These reduction mechanisms are given in Eq. 24 and 25 [79].

$$\mathrm{ZnOOH}+{\mathrm{e}}^{-}\leftrightarrow \mathrm{ZnO}+{\mathrm{OH}}^{-}$$
(24)
$$\mathrm{NiOOH}+{\mathrm{e}}^{-}\leftrightarrow \mathrm{NiO}+{\mathrm{OH}}^{-}$$
(25)

Figure 10d shows the change in the specific capacitance (Cs) of NiO NPs and NiO@ZnO nanocomposite as a function of scan rates. Cs values were calculated from the CV curves using Eq. (26).

$${C}_{s}=\frac{{\int }_{{V}_{i}}^{{V}_{f}}I(\mathrm{v})}{m\times{v}_{s} \times\Delta V}$$
(26)

where Cs is the specific capacitance of the electrode material (Fg−1), I is the current density (A/cm2), m is the mass of the active material (g), υs is the scan rate (V/s), and ΔV is the potential window (Vf -Vi), with Vi​ as the initial potential and Vf ​ as the final potential [80].

The specific capacitance values of NiO NPs calculated at scan rates of 25, 50, 75 and 100 mV/s are 196.8, 105.3, 78.1 and 62.0 Fg−1, respectively. The specific capacitance values of ZnO NPs were 632.4, 436.6, 400.1 and 399.4 Fg−1, respectively. The specific capacitance values of the NiO@ZnO nanocomposite were 785.0, 439.0, 332.0, and 287.3 Fg−1. The higher Cs values of NiO@ZnO as compared to NiO NPs for the same scan rates can be attributed to the formation of the synergistic effect of these two components in the nanocomposite.

4 Conclusion

NiO nanoparticles (NiO NPs) and NiO@ZnO nanocomposite were successfully synthesized using an S. officinalis leaf extract-mediated hydrothermal synthesis method for the first time. The optical band gaps of NiO NPs, ZnO NPs, and NiO@ZnO nanocomposite were determined to be 3.00, 2.28, and 2.71 eV, respectively. The crystallite sizes of all nanomaterials were calculated using the Scherrer and Williamson-Hall methods. According to the Scherrer method, the crystallite sizes of NiO and ZnO were found to be 15.37 nm and 24.06 nm, respectively. The NiO@ZnO nanocomposite had a composition ratio of 48% NiO and 52% ZnO by weight, indicating a successful synthesis in an almost 1:1 stoichiometric ratio, consistent with EDX results. TEM images showed that the shape of NiO NPs and the composite were very similar, both being spherical, while ZnO NPs appeared as rice-shaped formations. VSM results indicated that the NiO@ZnO nanocomposite exhibited a weak ferromagnetic character due to the combination of ferromagnetic NiO NPs with diamagnetic ZnO NPs. The specific capacitance (Cs) values of NiO NPs, ZnO NPs, and NiO@ZnO nanocomposite were 196.8, 632.4, and 785 F/g at a scan rate of 25 mV/s, respectively. The remarkable enhancement in specific capacitance can be attributed to the combined synergistic effect of NiO and ZnO, facilitated by the reduced direct band gap of the NiO@ZnO nanocomposite. The NiO@ZnO nanocomposite prepared here exhibited outstanding supercapacitance performance.