1 Introduction

Methylene blue (MB) is a cationic dye with extensive industrial applications [1]. Despite its seemingly mild toxicity, ingestion of MB-contaminated water, like in the case of every other organic pollutant, could be detrimental to human and animal health—cases of increased heart rate, diarrhea, dizziness, and vomiting as a result of ingesting water with a mild (< 100 mg/L) concentration of MB abound. Similarly, painful micturition, severe headache, and methemoglobinemia could be experienced following accidental ingestion of a large MB concentration (> 150 mg/L) [2]. Due to the concerns for environmental safety and sustainability, the removal of dyes and pigments from waste has been a front-burner issue over the last decade. Consequently, different techniques exist for the efficient treatment of dye-contaminated streams such as degradation [3,4,5], flocculation–coagulation [6, 7], oxidation [8, 9], membrane filtration [10], ion exchange resins [11], and adsorption [12, 13]. Due to its applicational flexibility, cost-effectiveness, and process efficiency, the adsorption technique has been preferred. Meanwhile, different natural, synthetic, and hybrid adsorbents have been applied to methylene blue adsorption.

Notably, starch-based adsorbents are cheap, renewable, and environmentally friendly. Also, the reactive hydroxyl groups present in the starch molecules improve their chemical stability and reactivity. The hydroxyl groups also make starch molecules readily tunable into the array of useful derivatives and biopolymers. Chen et al. [14] prepared starch-humic acid composite hydrogel beads which were applied for MB adsorption. The study reported preferential adsorption of MB molecules at an acidic pH range with a predominant π-π interaction and ion exchange. Similarly, the starch-based high-performance hydrogel was fabricated by Chen et al. [15] by crosslinking polyacrylic acid-g-starch with N, N′-methylene-bisacrylamide. The as-prepared adsorbent was used for the adsorption of aqueous MB. It was noted that the carboxylic and hydroxy groups on the hybrid adsorbent enhanced MB adsorption via hydrogen bonding and electrostatic interaction mechanism. Furthermore, starch/rice husk ash-based superabsorbent composite [16], bioinspired catecholamine/starch superabsorbent [17], biodegradable superabsorbent cassava starch-based hydrogel [18], and succinylated starch nanocrystals [19] were all prepared and effectively utilized for MB adsorption.

Additionally, numerous studies have explored and successfully reported on the use of other agro materials, including microbial biomass, as viable low-cost alternative adsorbents for dye wastewater treatment. Congo red dye was successfully adsorbed onto Trametes versicolor biomass by Munagapati et al. [20], and a maximum adsorption capacity of 415.7 mg/g was obtained at pH 2.0 and 60 °C. Furthermore, reasonable process efficiencies were reported during the respective adsorption of aqueous reactive red 3 and reactive green 6 dye onto Trichoderma harzianum (qmax = 172.63) [21] and immobilized Aspergillus sp. (qmax = 21.2 mg/g) [22] biomasses.

Thus, using methylene blue (MB) dye as the model pollutant, this work investigates the adsorptive potentials of sulfonated starch (HPSS) and Aspergillus oryzae (Asp. oryzae) biomass. The following benefits can be obtained by using microbial biomass as an adsorbent: (i) they can be quickly and easily cultivated on low-cost medium using simple methods, (ii) they exhibit exceptional surface complexation capabilities because of the many functional groups that make up their cell walls, and (iii) they are often non-pathogenic and so safe for use in water treatment. Because of their greater surface area, stronger mechanical strength, cost-effectiveness, and applicational flexibility, dead fungal biomass was specifically chosen in this study [23]. Although Hebeish and Aly [24] previously studied the adsorption of MB using starch hydroxypropyl sulfate, the instrumental characterization of the prepared adsorbent was not extensively conducted and discussed. Similarly, the adsorption studies were limited only to the effect of process variables (pH, initial dye concentration, time, and adsorbent dose). This present study extensively characterized the prepared starch sulfate including the structural, textural, morphological, elemental distribution, and pore distribution analyses. This study also compared the adsorptive performance of the HPSS to that of Asp. oryzae via an in-depth discussion on the isotherm and kinetics modelling, as well as the plausible adsorption mechanisms.

2 Material and methods

2.1 Materials

The Cairo Company for Starch and Glucose supplied the maize starch used in the study, and the culture collection center at the Department of Microbial Chemistry, National Research Center, Cairo, Egypt, graciously provided the Asp. oryzae strain. All other reagents, methylene blue, sodium bisulphite, hydrochloric acid, sodium hydroxide, epichlorohydrin, and ethanol, were laboratory-grade chemicals (Merck, Germany). The molecular formula, molecular weight, maximum wavelength, and structure of the dye are listed in Table 1.

Table 1 General characteristics of methylene blue (MB)
Full size table

2.2 Methods

2.2.1 Preparation of the Asp. oryzae biomass

The culture substrate employed in this study was potato dextrose broth (PDB), and our earlier publications [25] have a detailed technique for the fungus cultivation, as well as the mycelium development, and extraction. After a successful extraction, the fungal mycelium was thoroughly washed, oven-dried at 50 °C until it reached a constant dry weight, and then ground to a fine particle size (~ 50–125 µm).

2.2.2 Preparation of 2-hydroxy-3-chloropropyl sulfate

In the procedure, 1,2-propanediol (1.7 mL, 20 mmol) was introduced into sodium sulfite solution (2.52 g, 20 mmol) contained in a 250-mL conical flask. The resultant emulsion was stirred at 25 °C for 72 h until a clear solution was achieved. Subsequent freeze-drying of the clear solution afforded a gelatinous solid which metamorphosed to a powdery suspension after an overnight stirring with the addition of ethanol (40 mL). The suspension was boiled, filtered while hot (using a sintered glass), and washed with boiling ethanol (25 mL). Upon cooling, the resultant crystals were obtained as filtrate, washed with ethanol, and oven-dried to give a water-soluble whitish monohydrated product. Notably, the NaOH produced during the epoxide ring opening converts some HSO3– to SO32−, thus facilitating the attack of SO32− on –CH2–Cl and producing episulfohydrin.

2.2.3 Synthesis of hydroxypropyl starch sulfate

Sodium hydroxide (NaOH) powder was mixed with neat starch in a dry state using a mechanical stirrer. Then, 2-hydroxy-3-chloropropyl sulfate (in a molar ratio of 1: 1.5 with the NaOH powder) was added to the blended mixture of starch/sodium hydroxide at room temperature. The reactant was transferred to a stoppered bottle, with its temperature maintained at 90 °C for 60 min using a thermostated water bath. The reaction was terminated by pouring 200 mL ethanol with a pH adjustment to pH 8.0. The product was filtered off and then purified with 80% v/v of ethanol in a Soxhlet apparatus for 12 h. This is considered a final step which was followed by a subsequent drying of the product (Scheme 1).

Scheme 1
scheme 1

Preparation of hydroxypropyl hydroxypropyl sulfonated starch (HPSS)

Full size image

2.2.4 Batch adsorption studies

The detailed protocol for the equilibrium and kinetic experiments has been reported previously by the authors. The experiment was conducted at the following reaction conditions: HPSS dosage, 0.2 g/L; initial dye concentration, 10–100 mg/L; temperature, 30 °C; stirring speed, 200 rpm; contact time, 0–180 min. The amount of MB adsorbed at each instant (qt, mg/g) and equilibrium (qe, mg/g) is evaluated from Eqs. (1) and (2), respectively.

$${q}_{{\text{t}}}=\frac{\left({C}_{{\text{o}}}-{C}_{{\text{t}}}\right)\times V}{{\text{W}}}$$
(1)
$${q}_{{\text{e}}}=\frac{\left({C}_{{\text{o}}}-{C}_{{\text{e}}}\right)\times V}{W}$$
(2)

where Co (mg/L), Ce (mg/L), and Ct (mg/L) are the initial, equilibrium, and instantaneous dye concentrations, respectively. V (L) is the volume of adsorbate solution used, and W (g) is the mass of the adsorbent.

2.3 Adsorption isotherm and kinetic modelling

For the isotherm studies, the following 2-parameter [Langmuir, Eq. (3); Freundlich, Eq. (4), and Temkin, Eq. (5)] and 3-parameter [Redlich-Peterson, Eq. (6); Hills, Eq. (7); Sip, Eq. (8); Toth, Eq. (9) and Khan, Eq. (10)] nonlinear models were investigated. The Langmuir and Freundlich models are employed to respectively describe homogeneous and heterogeneous adsorption systems [26]. The Temkin equation applies to studying the adsorption energy in a dominant chemisorption process [27]. The Redlich-Peterson, Hill, Sips, Toth, and Khan models are 3-parameter isotherms that are based on Langmuir and Freundlich model characteristics. Specifically, the Redlich-Peterson model follows a hybrid mix of the monolayer and multi-layer adsorption sorption mechanisms [28]. The Hills model explains solute binding onto homogeneous substrates as a cooperative monolayer binding onto non-uniform sites of the same adsorbent. The cooperative phenomenon implies that solute binding on one site could influence the energy and stability of the other binding sites on the same adsorbent. The Sip model is an upgraded form of the Freundlich model, with features for circumventing the Freundlich model limitations at high adsorbate concentrations [27]. The Toth model postulates a variable energy distribution where the energies of the minimum adsorption site energies fell short of the peak energy values [29].

$${q}_{{\text{e}}}=\frac{{q}_{{\text{max}}}{K}_{{\text{L}}}{C}_{{\text{e}}}}{1+{K}_{{\text{L}}}{C}_{{\text{e}}}}$$
(3)
$${q}_{{\text{e}}}={K}_{{\text{F}}}{C}_{{\text{e}}}^{{~}^{1}\!\left/ \!{~}_{n}\right.}$$
(4)
$${q}_{{\text{e}}}=\frac{{\text{RT}}}{{b}_{{\text{T}}}}{\text{ln}}\left({A}_{{\text{T}}}{C}_{{\text{e}}}\right)$$
(5)
$${q}_{{\text{e}}}= \frac{{K}_{RP}{C}_{e}}{1+ {\alpha }_{RP}{\left({C}_{e}\right)}^{g}}$$
(6)
$${q}_{e}=\frac{{q}_{mH}{{C}_{e}}^{{n}_{H}}}{{K}_{H}+{{C}_{e}}^{{n}_{H}}}$$
(7)
$${{\text{q}}}_{{\text{e}}}= \frac{{K}_{{\text{s}}}\times {C}_{{\text{e}}}^{\upbeta }}{1+{{\text{a}}}_{{\text{s}}}*{{\text{C}}}_{{\text{e}}}^{\upbeta }}$$
(8)
$${{\text{q}}}_{{\text{e}}}= \frac{{k}_{{\text{T}}}\times {C}_{{\text{e}}}}{{\left({a}_{{\text{T}}}+{C}_{{\text{e}}}\right)}^{{t}^{-1}}}$$
(9)
$${q}_{e}=\frac{{q}_{mK}{b}_{K}{C}_{e}}{{\left(1+{b}_{K}{C}_{e}\right)}^{{a}_{K}}}$$
(10)

[aK, Kahn isotherm model exponent; bK, Khan isotherm model constant; qm, maximum adsorption capacity (mg/g); Ks, Sips isotherm model constant (L/g); β, Sips isotherm exponent; aS, Sips isotherm model constant (L/g); aR, Redlich-Peterson isotherm constant (1/mg); aT, Toth isotherm constant (L/mg); g, Redlich-Peterson exponent that lies between 0 and 1; KR, Redlich-Peterson isotherm constant (L/g); KS, Sips isotherm model constant (L/g); nH, Hill cooperativity coefficient of the binding interaction; qSH, Hill isotherm maximum uptake saturation (mg/L); KL, Langmuir adsorption constant (L/mg); KF, Freundlich constant; KD, Hill isotherm constant].

For the kinetic studies, the following nonlinear 2-parameter [pseudo-first-order, Eq. (11), pseudo-second-order, Eq. (12), Elovich, Eq. (13), and the linear form of the Intraparticle diffusion, Eq. (14)] models were investigated. The pseudo-first-order (PFO) model assumes an effective proportionality between the rate of sorption site occupation and the number of unoccupied sites [30, 31], while for the pseudo-second-order (PSO) model, the extent of adsorption is a function of the solute accessibility to the adsorbent sorption site [31]. The second-order kinetic description of an adsorption system containing adsorbents with an energetically heterogeneous surface is achieved using the Elovich model. The intraparticle diffusion postulates a proportional variation between the solute uptake and the square root of adsorption time [32].

$${q}_{{\text{t}}}= {q}_{{\text{e}}}\left[1-{\text{exp}}\left(-{K}_{1 }t\right)\right]$$
(11)
$${q}_{\mathrm{t }}= \frac{{{\text{K}}}_{2} \times {q}_{{\text{e}}}^{2} \times t}{1+ {K}_{2} \times {q}_{{\text{e}}}\times t}$$
(12)
$${q}_{\mathrm{t }}=\left(\frac{1}{\beta }\right){\text{l}}n \left(1+ \alpha \beta t\right)$$
(13)
$${q}_{\mathrm{t }}= {K}_{{\text{id}}}\sqrt{t}+C$$
(14)

[k1, pseudo-first-order rate constant (1/min); k2, pseudo-second-order rate constant (g/mg × min); α, Elovich’s initial adsorption rate (mg/g × min), β, Elovich’s desorption constant (g/mg); kid, intraparticle diffusion rate constant; Kb, Bangham model constants; n, Bangham model exponent].

2.4 Error analysis

The fitting goodness of nonlinear models is generally determined using specialized error models. Table 2 presents the mathematical expression of the different error models adopted in the study. Meanwhile, by applying different error models, varying error values were also generated. Hence, to ensure a holistic model analysis, these error values were normalized following the procedure we previously reported [33] to generate the sum of normalized error (SNE) values.

Table 2 Mathematical expression of the error models
Full size table

3 Results and discussion

3.1 Characterization of HPSS

3.1.1 Surface chemistry

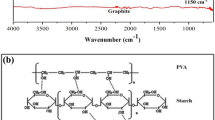
Fourier transform spectroscopy (FTIR) spectra of the HPSS and Asp. oryzae samples were determined using a PerkinElmer spectrophotometer within the 4000 to 400 cm−1 range. The generated FTIR spectra are shown in Fig. 1a, b. For the FTIR spectrum of native starch (black line in Fig. 1a), the glucose unit of the starch gave rise to the –OH and C–O stretching vibration band at 3321 cm−1 and 994 cm−1, respectively. The –OH in-plane bending vibration of the glucose unit and the –CH2 groups are respectively attributed to the bands at 1328 and 2924 cm−1. Comparison of the FTIR spectrum of HPSS (red line in Fig. 1a) with that of the native starch respectively shows the appearance of –SO3 asymmetric and symmetric stretching vibration at 1459 and 1221 cm−1, while the C–O–S stretching vibration is registered at 816 cm−1. Additionally, the sulfate groups can be observed at around 701 and 612 cm−1. The aforementioned sulfate groups are indications of the successful preparation of the HPSS sample. The MB@HPSS spectrum (green line in Fig. 1a) exhibits a slight shift in the wavenumber peaks which are responsible for MB adsorption. For instance, the –NH/–OH overlapped stretching vibration shifted from 3321 cm−1 in the native starch to 3443 cm−1. Similarly, the –SO3 symmetric stretching vibration shifted to 1214 cm−1. Also, the intensity of the –CH2 group at 2924 cm−1 decreased. Additionally, an MB peak (C–S–C–) was observed at 1110 cm−1. From the FTIR spectra, we can conclude that the native starch was modified successfully, with hydroxypropyl sulphonation derivatives obtained and MB adsorbed in HPSS.

Fig. 1
figure 1

FTIR spectra of a native starch, hydroxypropyl starch sulfate, and hydroxypropyl starch sulfate-loaded methylene blue and b raw and loaded Asp. oryzae

Full size image

Only a few broad peaks were observed in the Asp. oryzae FTIR spectra at wavenumbers 3397, 2919, and 1454 cm−1. The broad band stretching at 3397 cm−1 is attributed to the existence of the aliphatic and phenolic –OH stretching chain, the major constituent of cellulose-based material inherent in the raw Asp. oryzae. The stretching vibrations of the phenolic, carbonyl, amide II, and amide III groups of the lignin are responsible for the band at 1454 cm−1. After adsorption, the functional groups that were responsible for the solute binding shrunk considerably while the associated % Transmittance values significantly increased.

3.1.2 Structural properties

X-ray diffraction (XRD) patterns were analyzed on a PAN analytical diffractometer (X’Pert PRO) in continuous scanning mode using a Cu tube (in the reading range of 5 to 80°). The generated X-ray diffraction patterns are presented in Fig. 2a, b. For the HPSS (Fig. 2a, the broad peak which is the signature peak for the amorphous structure of the glucose unit in starch was recorded at 2θ = 13–23°. Also, new sharp peaks appearing at 2θ = 31.3°, 45.1°, and 56.3° are due to increased crystallinity occasioned by the existence of the new starch derivatives (HPSS). The loaded HPSS shows different peaks at 2θ = 14.8°, 17.6°, 23.1°, and 31.3° which corresponds to the chemical structure of starch derivative. The sharp peaks related to starch derivative (HPSS) decreased after adsorption due to the interaction between MB and functional groups of modified starch. This occurred mostly at the upper layer of the HPSS crystalline structure.

Fig. 2
figure 2

XRD spectra of the a HPSS and loaded HPSS and b) raw and dye-loaded Asp. oryzae

Full size image

Concerning Asp. oryzae, two semi-lucid peaks developed around 2θ = 12.39° and 20.23°. It is believed that the semi-lucid peaks are caused by the chitin polysaccharides in the fungal structure. Karthik et al. [21] also noted an analogous semi-lucid peak at 2θ = 22.64° and 41.73° when doing their structural analysis of Trichoderma harzianum. The study concluded that the polysaccharides in the fungal cell wall were responsible for the apparent peaks. After noticing a broad peak on Penicillium sp. at 2θ = 20°, Yu et al. [34] concluded that the fungus adsorbent was amorphous. The dye-loaded samples showed peaks at locations corresponding to the raw sample. This finding shows that the adsorption process did not result in any structural changes.

3.1.3 Surface morphology

Scanning electron microscopy (SEM) micrographs of the samples were analyzed on a scanning electron microscope (model JEOL-JSM-5600) following the standard protocols. The morphological properties of the samples are shown in Fig. 3. From Fig. 3a, a heterogeneous surface due to the presence of polygonal and ellipsoid starch granules was observed. However, the modification completely altered native starch granules’ morphology (Fig. 3b). The starch derivatives show sphere-shaped structures with high adhesion morphology between starch granules, and the size of starch granules after chemical modification became smaller than native starch. After the adsorption process, the size and shape of loaded HPSS were completely different compared with native starch and HPSS (Fig. 3c). The loaded HPSS shows irregular and flat heterogonous shapes, with the observation of adherent small MB molecules. The cited morphological changes were due to the successful chemical modification of starch and the high loading capacity of MB on the starch surface.

Fig. 3
figure 3

SEM micrographs of a raw starch, b HPSS, c loaded HPSS, d raw Asp. oryzae, and e loaded Asp. oryzae

Full size image

Raw Asp. oryzae (Fig. 3d) had noticeably crooked surfaces with a dispersion of pores that resembled conduits and waxy ducts. The open channels on the raw Asp. oryzae were gone on the post-adsorption micrograph (Fig. 3e). These morphological changes serve as evidence that the solute was successfully bound to the adsorbent surface.

3.1.4 BET surface area

The HPSS showed a BET surface area and pore volume of 93.311 m2/g and 0.066 cm3/g, respectively, with an average pore size of 1.924 nm. Therefore, with an average pore size of less than 2 nm, the HPSS is considered a microporous adsorbent. For the Asp. oryzae, it has specific surface areas, pore volume, and pore sizes of 25.593 m2/g, 0.365 cm3/g, and 0.341 nm, respectively. Notably, the surface area and pore radius recorded for the HPSS are higher compared to those of Asp. oryzae. Since higher surface area is synonymous with improved adsorption capacity, therefore, HPSS is expected to exhibit higher adsorption capacity than the Asp. oryzae. Similarly, the pore radius for both adsorbents is smaller than 2 nm; hence, they are classified as micro-mesoporous adsorbents according to the IUPAC [35, 36].

3.2 Process variables studies

3.2.1 Analysis of the adsorbents’ pHpzc and effect of solution pH

The point of zero charge was established in this study using the titrimetric method. The generated plot for both adsorbents is shown in Fig. 4, where it can be seen that the pHpzc for the HPSS and Asp. oryzae occur at pH 6.0 and 6.7, respectively. Thus, the adsorption of MB species is expected to occur more favorably when the solution pH is higher than the pHpzc of the respective adsorbents.

Fig. 4
figure 4

Plot for the determination of pHpzc of both adsorbents

Full size image

Since solution pH sustains a significant effect on the sorption process efficiency, Fig. 5 presents the effect of solution pH on the adsorption capacity. The plot for both adsorbents showed a consistent increase in adsorption capacity as the solution acidity weakened. This is due to an enhanced attraction between the cationic dye molecules and the progressively deprotonated surface of both adsorbents. However, pH 9.0 and pH 8.0 were recorded as the optimum pH for the adsorption of MB species onto Asp. oryzae and HPSS, respectively. Meanwhile, with an increase in solution pH beyond the respective optimums and deep into the alkaline pH ranges, a decrease in adsorption capacity was recorded. This observation is quite uncommon as the optimum adsorption of cationic dye molecules is expected to improve with increased alkalinity. However, this anomaly occurred due to a possible swelling and rupturing of the starch granules and Asp. oryzae cells at alkaline conditions [37]. Therefore, the optimum pH for the study was established at pH 9.0 and pH 8.0 for Asp. oryzae and HPSS, respectively.

Fig. 5
figure 5

Plots of the effect of contact time on MB dye adsorption capacity (reaction conditions: MB conc., 20 mg/L; Temp., 30 °C; time, 2 h; adsorbent conc., 0.15 g/L]

Full size image

3.2.2 Effect of contact time

The effect of adsorption time as presented in Fig. 6 showed a rapid MB uptake at the onset of adsorption in the case of both adsorbents. Notably, at a constant 20 mg/L concentration, about 61.80 mg/g and 41.35 mg/g of the solute were respectively adsorbed onto the HPSS and Asp oryzae within the first 10 min of adsorption. This is due to the presence of a large number of vacant adsorption sites and the shortened diffusion path phenomenon obtainable at the early stages of the adsorption process. Due to active site saturation, the adsorption rate progressively abated after the first 10 min of contact time. This is such that only about 4.30 mg/g of HPSS and 3.65 mg/g of Asp. oryzae was additionally adsorbed afterwards until equilibrium was finally attained at 60 min. Furthermore, at the optimum time of 60 min, HPSS recorded an adsorption capacity of 66.13 mg/g, and this value is quite larger than the 45.0 mg/g recorded by Asp. oryzae. This finding shows that the surface area difference between both adsorbents also had a significant impact on their respective adsorption capacity since HPSS exhibit a larger surface area.

Fig. 6
figure 6

Plots of the effect of contact time on MB dye adsorption capacity [reaction conditions: MB conc., 20 mg/L; Temp., 30 °C; time, 2 h; adsorbent conc., 0.15 g/L; pH 8.0–9.0]

Full size image

3.2.3 Effect of adsorbent dose

The effect of the variation of the adsorbent concentration on the adsorption capacity is presented in Fig. 7. Accordingly, the plot shows a decrease in the adsorption capacity of both adsorbents as the adsorbent concentration increased. Specifically, at least the adsorbent concentration studied (0.15 g/L), HPSS, and Asp. oryzae respectively adsorbed 77.0 and 70.0 mg/g of MB species. Conversely, when the adsorbent concentration was raised to 2.0 g/L, the adsorption capacities were reduced to 4.87 and 6.63 mg/g for HPSS and Asp. oryzae, respectively. This observation is attributed to the disproportionality occasioned by the introduction of a greater number of active sites via the increase in adsorbent dosage even at initial adsorbate concentration. Such development triggers a progressive unsaturation of these active sites, as the amount of MB species adsorbed per gram of adsorbent drops. Also, the probable particle agglomeration and clogging at high dosages could limit the surface area of the respective adsorbents and by extension, their overall adsorption capacity. A similar occurrence of a reduction in adsorption density with an increase in the adsorbent dose was reported by Aljeboree et al. [38] during the adsorption of maxilon blue GRL and direct yellow DY 12 onto coconut husk-activated carbon. The authors claim that the incidences of sustained unsaturation in the face of an increase in the number of available adsorptions was the primary cause of this development.

Fig. 7
figure 7

Plots of the effect of adsorbent concentration on MB dye adsorption capacity [reaction conditions: MB conc., 20 mg/L; Temp., 30 °C; time, 2 h]

Full size image

3.2.4 Effect of temperature

The adsorption process is significantly impacted by temperature variation since it can change the adsorbates’ kinetic energy and physicochemical composition [39]. Figure 8 presents the relationship between temperature and adsorption capacity for both adsorbents. Consequently, a consistent adsorption capacity decrease was observed with temperature rise. For instance, the adsorption capacity decreased from 66.50 to 37.0 mg/g (for HPSS) and from 43.50 to 28.00 mg/g (for Asp. oryzae) as the temperature increased from 30 to 70 °C. This observation suggests the occurrence of an exothermic process where the electrostatic properties of the adsorbents are temperature-dependent. Also, a physisorption interaction which weakens with increasing temperature is postulated.

Fig. 8
figure 8

Plots of the effect of temperature on MB dye adsorption capacity [reaction conditions: MB conc., 20 mg/L; adsorbent conc., 0.15 g/L; time, 2 h; pH 8.0–9.0]

Full size image

3.3 Adsorption modelling

3.3.1 Isotherm studies

The equilibrium data was further described using the dedicated models presented in Eqs. (3)–(10). The generated isotherm model parameters for both adsorbents are presented in Table 3, while the plots for 2-parameter and 3-parameter models are presented in Figs. 9 and 10, respectively. As earlier stated (Section 2.4), the model of best fit is determined based on the magnitude of the SNE value. These SNE values are more appropriate compared to the coefficient of determination (R2) for evaluating the nonlinear models. Generally, the lower the SNE value, the better the model’s description. The number of adsorption model parameters has been shown to have a significant impact on the models’ fitting ability. Therefore, the isotherm models are generally groups based on the number of model parameters and the associated discussion follows a similar pattern.

Table 3 Isotherm model parameters
Full size table
Fig. 9
figure 9

The plots of 2-parameter isotherm models for Asp. oryzae and HPSS [reaction conditions: adsorbent conc., 0.15 g/L; pH, 8; contact time 2 h; Temp., 30 °C]

Full size image
Fig. 10
figure 10

The plots of 3-parameter isotherm models for Asp. oryzae and HPSS [reaction conditions: adsorbent conc., 0.15 g/L; pH, 8; contact time 2 h; temperature, 30 °C]

Full size image

The Freundlich isotherm model with the lowest SNE values of 1.48 and 1.96 for HPSS and Asp. oryzae is regarded as the best fit for 2-parameter models (Fig. 9). The Freundlich isotherm predicts multi-layer adsorption with an equilibrium coverage proportion of roughly 50% on heterogeneous surfaces [27, 40]. According to the existing hypothesis about the range of 1/n-values and how they relate to the adsorption system [40], the 1/n-values obtained in Table 3 are greater than zero but less than unity, thus indicating that the adsorption is favorable. Having identified the best fit, the significance of the magnitude of the constants generated for the other 2-parameter isotherm model to the present adsorption system is further elucidated. The Langmuir KL constant values of 1.3 and 5.43 L/g were obtained respectively for HPSS and Asp. oryzae indicates a reasonable adsorbent-adsorbate interaction [41, 42]. Also, the Langmuir favorability index (RL) value of 0.02 (for HPSS) and 0.07 (for Asp. oryzae) indicates favorable adsorption processes [40, 43]. Also, the Freundlich maximum adsorption capacity parameter (kF) is reasonably larger than unity for both adsorbents.

For the 3-parameter models (Fig. 8), the Khan isotherm model with the lowest SNE value of 1.43 and 2.11 for HPSS and Asp. oryzae is considered the best fit. The magnitude of the models’ exponent (aK) which indicates the nature of the adsorptive interaction is less than unity for both adsorbents and thus suggests a heterogenous adsorption process [27]. Upon further consideration of the parametric implication of other models to the present adsorption system, it is well known that the Sip model respectively reduces to the Freundlich and Langmuir model at βS-value equal to 1 and 0. However, the βS-value obtained for both adsorbents could be approximated to unity, hence, suggesting the predominance of Freundlich. The cooperative adsorption index for the Hill model (nH) was recorded as 0.59 (for HPSS) and 0.74 (for Asp. oryzae), thus indicating negative cooperativities. Consequently, the affinity of the respective adsorbents for MB species is progressively limited as the adsorption duration extends [44, 45]. The “t “ parameter of the Toth model provides insight into the heterogeneity of the adsorption system. Thus, a given adsorption system is considered heterogeneous when (t) does not equal unity [46]. On this basis, the adsorption system for both adsorbents is heterogeneous.

3.3.2 Kinetic studies

The MB dye adsorption onto HPSS and Asp. oryzae at an initial concentration of 20 mg/L and optimum adsorbent dosage was investigated using classical kinetic models whose theoretical background and mathematical expressions are presented in Section 2.3 and Eqs. (11)–(13). The results from the kinetics modelling are presented in Table 4 and Fig. 11. Generally, all the kinetic models gave a satisfactory R2 value (R2 > 0.9). However, taking the magnitude of SNE value as the basis for determining the kinetic model of best fit, just as was the case in isotherm studies, the Elovich and PFO models are considered the best fit for HPSS and Asp. oryzae. The Elovich model signifies the chemisorption of MB onto energetically heterogeneous sorption sites, while the PFO model suggests the predominance of physisorption via interfacial diffusion. An overview of the implication of the different kinetic model parameters shows that Elovich’s initial adsorption rate (α) value was much greater than the desorption constant (β) for both adsorbents, thus indicating a stable uptake process. Also, the k2-value recorded in Table 4 was much lower than the k1-value and implies faster second-order rate sorption.

Table 4 Kinetic model parameters
Full size table
Fig. 11
figure 11

The plots of the PFO, PSO, and Elovich models for Asp. oryzae and HPSS [reaction conditions: MB conc., 20 mg/L; adsorbent conc. 0.15 g/L; pH, 8; temp., 30 °C]

Full size image

The linear form of the intraparticle diffusion models (Eq. 14) and the associated plots (Fig. 12) was applied to elucidate the rate-limiting step during MB removal and the model recorded good R2-values for both adsorbents. This is an indication of the occurrence of film diffusion characteristics during the MB adsorption. Similarly, the fact that the intercept (c-parameter) of the intraparticle diffusion model is far greater than zero corroborates the earlier assertion for the predominance of the film diffusion mechanism [47, 48].

Fig. 12
figure 12

The intraparticle diffusion model plots for Asp. oryzae and HPSS [reaction conditions: MB conc., 20 mg/L; adsorbent conc. 0.15 g/L; pH, 8; temp., 30 °C]

Full size image

3.4 Plausible adsorption mechanism

The efficient adsorption of MB onto HPSS and Asp. oryzae was mainly due to electrostatic interactions and hydrogen bonding mechanisms as shown in Scheme 2. For both adsorbents, the post-adsorption FTIR spectra (Fig. 1) showed a general increase in the % transmittance of the main peaks, particularly the hydroxyl, amino, and sulfate groups. Based on the pH studies, the hydrogen bond donor and acceptor groups (oxygen- and nitrogen-based groups) in the HPSS can also form hydrogen bonds with dye molecules (Scheme 2a). Specifically, the –SO3 groups on the HPSS shared some electrostatic affinity with the MB dye cationic center (N+ backbone), while a hydrogen bond is formed between the hydroxyl groups of the starch and N+ backbone of the MB dye. Also, the post-adsorption XRD spectra showed a decrease in the sharp crystalline peaks of HPSS. This is attributed to the adsorption of MB dye on the upper layer of the crystalline structure of the HPSS via electrostatic interaction and hydrogen bond formation. Additionally, the binding of MB species was significantly influenced by the nitrogen- and oxygen-containing groups on the Asp. oryzae. These functional groups attracted the charged adsorbate species via an electrostatic interaction mechanism, as depicted in Scheme 2b.

Scheme 2
scheme 2

Proposed mechanism for MB sorption onto a HPSS and b Asp. oryzae

Full size image

Table 5 displays a comparison of the MB adsorptive performance of different fungal- and starch-based adsorbents to those of the adsorbents utilized in this study. From the presented data, it is observed that the adsorption performance recorded in this study is well-situated among the previously published works.

Table 5 Comparison of the MB adsorptive performance of different adsorbents
Full size table

3.5 Cost estimation for producing I kg of the adsorbent

When choosing a treatment approach for pollutant removal, cost analysis frequently helps [54]. Because the cost of the adsorbent being utilized is a major determinant of adsorption cost, doing a thorough cost analysis is crucial when choosing an adsorbent [55]. The most common adsorbent used in the water treatment process at the moment is commercial activated carbon, yet it is highly costly. Because of this, activated carbon adsorbent is frequently not a sustainable economic option for treating wastewater containing dyes. Therefore, such costly material is out of reach for small and medium-sized businesses in developing nations. Therefore, there is a great demand for an inexpensive absorbent that is readily available in nature, low cost, and just as effective as activated carbon. The present work is based on the synthesis and dye adsorption application of hydroxypropyl starch sulfate (HPSS) and Aspergillus oryzae (Asp. oryzae). After a detailed evaluation of the cost analyses as shown in Table 6, it is observed that the cost for producing 1 kg of each of the Asp. oryzae and HPSS adsorbents are USD 1.54 and USD 37.95, respectively. Notably, the combined cost of both adsorbents is far lower when compared to the cost per kilogram of commercial activated carbon, which is about USD 172.96 per kg [56]. Thus, the Asp. oryzae and HPSS are both considered effective and low-cost dye adsorbents.

Table 6 Estimated cost of producing 1 kg of the respective adsorbents
Full size table

4 Conclusion

This work successfully generated hydroxypropyl starch sulfate (HPSS) and Aspergillus oryzae (Asp. oryzae) biomass and examined their ability to adsorb methylene blue (MB) dye. By adjusting several process variables, including the initial dye concentration, temperature, time, solution pH, and adsorbent dose, the adsorptive qualities of both adsorbents were efficiently studied in batch mode. To further clarify each adsorbent’s unique functional, textural, and morphological characteristics, a thorough analysis of the materials using the FTIR, XRD, SEM, EDX, and BET surface area studies was also carried out. Based on the result of the pore distribution analyses, both adsorbents are categorized as micro-mesoporous adsorbents since their pore radii are less than 2 nm. The study’s isotherm models and related discussions were categorized according to the number of parameters in each model. The isotherm modelling followed the Freundlich (for 2-parameter models studied) and the Khan (for 3-parameter models studied). Similarly, PFO and Elovich models respectively emerged as the best-fit kinetic model for Asp. oryzae and HPSS. Notably, the nitrogen- and oxygen-containing groups on the Asp. oryzae had a substantial impact on the binding of MB species. Through an electrostatic interaction mechanism, these functional groups attracted the charged adsorbate species. The MB dye ‘s cationic center (N+ backbone) and the –SO3 groups on the HPSS also shared some electrostatic affinity, coupled with a probable formation of hydrogen bond between the hydroxyl groups of the starch and the N+ backbone of the MB dye.