1 Introduction

Non-woody biomass from agricultural residues is abundant, readily available, and cheap. Within these are mainly located agricultural residues such as corn, representing one of the most abundant sources of bioenergy in the world [1] which can be utilized via thermochemical processes such as gasification [2]. In addition to syngas, biochar is considered another valuable product generated in the gasification process due to its potential uses as industrial adsorbent, catalyst [3], soil enricher [4, 5], and carbon sequestrant [6,7,8]. Among the most important properties for its use as a product are the textural characteristics associated with the volume of nanopores, surface area, and pore size distribution. Furthermore, coal, charcoal, and biochar reactivities are related to their physical structure; both porosity and surface area affect the activity and gasification performance [9]. In this sense, the prediction models of textural evolution are a valuable tool for both the design and defining the gasification reactors’ operating conditions whenever the energy utilization of syngas is sought, as well as significant surface area in the biochar [10]. However, these models require detailed knowledge of the chemical reactivity of biochar involving knowing the intrinsic kinetics and the mass transport phenomena as a conversion function [11].

Thermogravimetric analysis (TGA) is the most common technique to evaluate the intrinsic kinetics (kinetics with no or minimal mass transport effects) of charcoal gasification with CO2 and steam. However, this methodology presents two significant disadvantages. First, it involves using a fixed bed, which can cause diffusional and mass transfer in the solid–gas reactions, if operating conditions such as particle size, weight, bed depth, and gasificaction agent volumetric flow are not optimized [12,13,14,15]. Therefore, a fixed bed depth less than 3 mm [16], particle size less than 149 μm [17], and high gas flow [14] are often used to improve the kinetic measurements.

Second, isoconversional methods such as Friedman, Flynn–Wall–Ozawa, Kissinger–Akahira–Sunose, and Coats-Redfern among others are commonly used to determine the kinetic parameters by macro-samples [18,19,20,21], focusing more on estimating the global kinetic model with respect to the conversion than knowing intrinsic kinetic with an established chemical mechanism. Therefore, these methods always include an order parameter with respect to the conversion of char between 0.22 and 1.20 [22], which allows a good experimental data fitting, but hides the effect of both mass transport and mass transfer during the experimental process. As a consequence of this methodology, average activation energy parameters are obtained, consisting of a pre-exponential factor and the order. All these parameters are adjusted during the test and are not considered thermodynamic limits or kinetic orders of an intrinsic mechanism.

Currently, the TGA analysis (experimental test) is processed using a computational model that considers experimental effects and textural properties for char; this allows finding intrinsic kinetics [13, 14, 18, 19, 23]. Authors such as Hodge et al. [24] and Liu et al. [25] have obtained the value of intrinsic kinetics by extrapolating the reaction rate with low-temperature tests. Krishnamoorthy et al. [26] obtained the intrinsic reaction rate for CO2 gasification of coals using a pressurized atmosphere and a thermogravimetric analyzer. It was determined that the activation energy is insensitive to the gasification pressure. Furthermore, the pre-exponential factor is similar when the apparent reaction rate is normalized using the coal surface area.

Prabhakar et al. [27] used an intraparticle diffusion model for gasification, considering an initial structure parameter by the random pore model (RPM), but not the textural evolution in the pore scale. The model development had overall conversion and reaction rate predictions with an average relative error of 3% at 950 °C temperature. However, the conversion prediction error of the model increases to 4.8% when the gasification temperature is 850 °C. Regarding biochar derived from corn cobs, the work of Li et al. [28] studied the effect of biochar reactivity by fitting a global model of random pore model (RPM), volume reaction model (VM), and unreacted core model (URCM). Finally, the best fit model concluded that the RPM better described the conversion behavior with activation energies for gasification with CO2 between 183.1 and 263.4 kJ/mol. Authors [29] evaluated the kinetics of CO2 and steam gasification at temperatures of 900, 950, and 1000 °C of rice husk biochar using the VM, URCM, and RPM models. The RPM is found to agree better with the experimental data than the other two models. They obtained an activation energy of 165.8 kJ/mol and a pre-exponential factor of 2595.4 s−1 for gasification and, respectively, 152.9 kJ/mol and 3473.4 s−1 for steam gasification. However, the last-mentioned methods implement a constant textural property for char, which, in all cases, will estimate an apparent kinetic rate normalized with the initial condition of pore volume or surface area. The pore textural evolution distribution due to conversion is neglected.

Therefore, the global models [30], distributed activation energy models (DAEM) [31], and diffusion of reactants at the multipore level models are used to adjust the kinetic parameters which are dependent on experimental conditions and initial pore texture. There is little evidence of the use of models involving diffusion of reactants at the multipore level with their textural evolution for the determination of kinetic parameters of biomass char gasification.

Intrinsic kinetics contributes to the estimation of the char conversion rate independently of the transport phenometry, scale, and physical structure of the char when it is measured and normalized per unit area (intrinsic heterogeneous kinetics). These kinetics should be universal even for the same char with different textural properties such as pore size distribution and BET surface area. In the present work, the intrinsic kinetics of biochar gasification using CO2 and steam are estimated by TGA kinetic analysis fitting an evolution pore multimodal model. Two samples of corn cob biochar with different initial textural properties were used in TGA analysis under not optimized experimental conditions to validate the independence of the kinetic parameters concerning the textural conditions of the char and mass transport effects. The parameters of the first-order heterogeneous intrinsic kinetics for biochar gasification, such as the activation energy E (kJ/mol) and the pre-exponential factor Ao (kg/m2s), are estimated and compared with values obtained by the use of the adjusted conversion global model.

2 Materials and methods

2.1 Origin of biochar

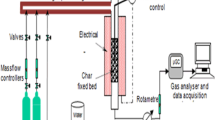
The biochar was obtained by gasification in an autothermal downdraft reactor with a processing capacity of up to 60 kg/h of biomass (WBG-60 from Ankur Scientific). Two types of biochar were obtained with differences in the initial pore structure: biochar A1 and biochar A2. Biochar A1 comes from a gasification process at a maximum throat temperature of 910 °C, and an equivalence ratio (E.R.) of 0.27 ± 0.1; biochar A2 was generated with a gasification process at 910 °C and the addition of steam to a steam/biomass ratio of 0.16 (w/w). The technical details of bioenergy and biochar performances have been described in previous work [32, 33]. Two kilograms of biochar was obtained from the char collector. Samples were dried in an electric oven at 120 °C for 24 h, grinding in a ball mill, and controlled the speed at 50 RPM for 5 min. The samples were mechanically screened using a #100 mesh (< 149 um).

2.2 Biochar characterization

Materials pass-through #100 mesh (< 148 mm) was used for physico-chemical analysis and characterization. ASTM D5373-14 and D4239-14 were implemented for ultimate analysis. The moisture and biogenic oxide content of biochar was measured using ASTM D3173-11 and ASTM D3174-12 methods. Pore volume distribution, pore size distribution (PSD), and BET area distribution were estimated from nitrogen sorption isotherms at − 196 °C using NOVA 3000 gas sorption equipment. For the PSD, the non-local density functional theory model (NLDFT) was implemented for cylindrical carbon nanopores. The Dubinin-Radushkevich model was applied to determine the micropore volume W0 (N2) (0–2 nm). The volume of nitrogen adsorbed at a relative pressure of 0.95 was used to compute mesopore volume—Vmeso (2–50 nm)—following Gurvich’s rule as described in previous studies [33, 34].

Considering that the specific area involved in the reactions is linked to the mass of carbon in the sample, the specific BET area is corrected by removing the oxides as the mass of oxides is estimated. The specific BET area corrected by removing the mass of oxides is estimated as shown in Eq. (1).

$${S}_{c}=\frac{{S}_{BET}}{(1-ASH)}$$
(1)

2.3 Kinetics analysis from TGA

Twenty milligrams of biochars with a particle size of 149μm was subjected to thermogravimetry in pure CO2 and mix of N2—steam atmosphere with a flow of 50 ml/min for temperatures of 850 °C, 900 °C, and 950 °C achieved with a 30 °C/min heating rate. The particle size, volumetric flow, and specific surface area of samples were selected to generate an induced difference of apparent kinetic as a result of textural properties. Two TGA for each experimental treatment were performed to ensure the repeatability of the results.

2.4 Analysis of apparent kinetics

The isothermal gasification degree of conversion \(x\left(t\right)\) is computed using Eq. (2).

$$x\left(t\right)=\left(\frac{{m}_{o}-m\left(t\right)}{{m}_{o}}\right)$$
(2)

\({m}_{\mathrm{o}}\) and \(m\left(\mathrm{t}\right)\) are the ash-free mass of the samples used for thermogravimetry at the initial time (t = 0) and t, respectively. The apparent reaction rate \(R\left(x\right)\) for a given time is measured by the time variation of the conversion \(x(t)\) as shown in Eq. (3).

$$R\left(x\right)=\frac{\partial x(t)}{\partial t}$$
(3)

where the reaction rate is expressed as a function of the apparent activation energy \({E}_{A}(kJ/mol)\) and apparent pre-exponential factor \({A}_{A}\) (1/s) shown in Eq. (4). These parameters are determined by computing the slope and intercepting an Arrhenius plot implementing the Friedman method for TGA with CO2 and steam at 850°, 900 °C, and 950 °C.

$$R\left(x\right)={A}_{A}\left(x\right)exp\left(-\frac{{E}_{A}\left(x\right)}{RT}\right)(1-x)$$
(4)

2.5 Intrinsic kinetic measure

The random capillary model developed by Gavals [35] particle scale, including the diffusive effects, is estimated. The time variation of the conversion x(t) obtained by TGA is a function of the heterogeneous intrinsic reactivity \({\mathfrak{R}}_{int}\) expressed in (kg/m2s), reagent concentration \({C}_{i}\) (mol/m3) and the evolution of the area \({s}_{i}\left(t\right)\) (m2/g) for each i-th pore radius as shown in Eq. (5).

$$x\left(t\right)=\frac{{\mathfrak{R}}_{int}{M}_{C}}{{\rho }_{c}}\int \sum_{i=1}^{n}{s}_{i}\left(t\right){C}_{i}\left(t\right)dt$$
(5)

The mathematical model used in the present work allows for determining the total evolution of the conversion, considering the time variation of the surface area \({s}_{i}\left(t\right)\) and the reactant concentrations \({C}_{i}\left(t\right)\) for each pore radius. This intrinsic reactivity \({\mathfrak{R}}_{int}\) is fitted from experimental conversion function \(x\left(t\right)\) obtained by TGA using Eq. (5). This intrinsic reactivity is expressed as a function of kinetic parameters such as the activation energy \({E}_{int}\) (kJ/mol) and the intrinsic pre-exponential factor \({A}_{int}\) (kg/m2s), using the Arrhenius arrangement shown in Eq. (6).

$${\mathfrak{R}}_{int}={A}_{Int}\mathrm{exp}\left(-\frac{{E}_{int}}{RT}\right)$$
(6)

To estimate the concentrations of reactants \({C}_{i}\left(t\right)\) involved in the availability of area for each pore \({s}_{i}\left(t\right)\), Eq. (7) is used.

$${C}_{i}\left(t\right)={\eta }_{i}{C}_{BC}\left(r\right)$$
(7)

where \({C}_{BC}\left(r\right)\) is the reactant concentration in the boundary condition. For the present work, 100% CO2 concentration is assumed as a boundary concentration, as used in TGA where a pure CO2 flow is introduced for the experiment. Furthermore, pyrolysis reactions are neglected. The effectiveness factor \({\eta }_{i}\) measures the level of participation for each reaction, taking into consideration every i-th pore radius \({r}_{i}\). Because the reactant transport time is very small with respect to the total char conversion time, it is valid to assume pseudo-steady-state conditions, then a solution can be derived to define the reaction effectiveness \({\eta }_{i}\) in terms of the pore-level Thiele modulus \({\Phi }_{i}\) as shown in Eq. (8), which is used assuming a pseudo-homogeneous slab pore model [36].

$${\eta }_{i}=\frac{\mathit{tan}h\left({\Phi }_{i}\right)}{{\Phi }_{i}}$$
(8)

This is defined as the actual conversion rate in an i-pore divided by the theoretical rate if there were no diffusive limitations [36]. To compute the participation in the reaction for each i-pore, the concept of the Thiele module in the pore-scale developed by Gavals is used [35]. The pore Thiele modulus \({\Phi }_{i}\) shown in Eq. (9) evaluates the effects of diffusion and the velocity of the k-th reaction on reactant penetration over the surface area of each pore.

$${\Phi }_{i,k}=\frac{{\mathrm{L}}_{\mathrm{i}}}{2}\sqrt{\frac{2{v}_{c,k}{\mathfrak{R}}_{int,k}{S}_{i}{C}_{BC}}{{r}_{i}{D}_{e,i,j}}}$$
(9)

The characteristic length for diffusion on the porous scale \({L}_{i}\)(m) is estimated from pore length using the capillary Thiele methods developed by Gavalas [35]. Equation (1 ) describes the estimation of \({L}_{i}\) assuming that the distribution of pores presents random intersections and pores have a hierarchical structure.

$${L}_{i}={\left(\sum_{s=i+1}^{n} \frac{\pi {l}_{0,i+1}\left({r}_{i}+{r}_{i+1}\right)}{2}\right)}^{-1}$$
(10)

where \({l}_{0,i}\) is the length of pore per unit volume to cover the porosity of each pore radius \({r}_{i}\). See Eq. (11).

$${l}_{0,i}=\frac{{\varepsilon }_{i}}{\pi {r}_{i}^{2}}$$
(11)

The diffusion length has a physical meaning. As the pore length increases, the probability of radial intersections between pores also increases, so the diffusion length becomes smaller. \({L}_{i}\) represents the distance at which the concentration of reactants present at the boundary condition is consumed when penetrating through the i-th pore. In fact, low porosities with small radii have longer diffusion lengths, thus increasing the Thiele modulus and decreasing the diffusion effectiveness \({\eta }_{i}\) for pore i. \({\varepsilon }_{i}\) is the porosity associated with the void pore volume \(d{V}_{i}\) for each pore radius (see Eq. (12)). Initial \(d{V}_{i}\) is obtaineb by pore size distribution measure.

$${\varepsilon }_{i}={\rho }_{c}d{V}_{i}$$
(12)

The effective diffusion of j-th reactant \({D}_{e,\mathrm{i},\mathrm{j}}\) is described in Eq. (13), each i-th pore radius conjugating the free diffusion coefficient \({\mathrm{D}}_{\mathrm{O},\mathrm{j}}\) and the Knudsen diffusion coefficient \({D}_{Kn,i,j}\) indicated in Eq. (13) and (14), respectively.

$${D}_{e,i,j}={\varepsilon }_{i}^{2}{\left(\frac{1}{{D}_{kn,i,j}}+\frac{1}{{D}_{0,j}}\right)}^{-1}$$
(13)
$${D}_{0,j}=\frac{{10}^{-7}{T}^{1.75}{\left(\frac{1}{{M}_{j}}+\frac{1}{{M}_{CO}}\right)}^{1/2}}{P{\left({{V}_{j}}^{1/3}+{{V}_{CO}}^{1/3}\right)}^{2}}$$
(14)
$${D}_{Kn,i,j}=\frac{2{ r}_{i,j}}{3}\sqrt{\frac{8RT}{\pi {M}_{j}}}$$
(15)

where R is the universal gas constant, \({M}_{\mathrm{j}}\) the molecular mass of reactant j, \({V}_{\mathrm{j}}\) is the atomic volume of reactant j, \(P\) is the thermodynamic pressure of the process taken as 100 kPa for this work, and T is the gasification temperature.

The rate of change of the porosity distribution function is shown in Eq. (16). It is expressed in terms of the effectiveness \({\eta }_{i,j}\) and individual area \({S}_{i}\) computed in Eq. (17).

$$\frac{d{\varepsilon }_{i}}{dt}=\left(\frac{1-{\varepsilon }_{tot}}{{\rho }_{c}}\right){{M}_{c}{\mathfrak{R}}_{int,k}S}_{i}{\eta }_{i,j}{v}_{c,i}$$
(16)
$${S}_{i}=\frac{2{\varepsilon }_{i}}{{r}_{i}}$$
(17)

Boudouard reaction shown in Eq. (18) and steam gasification shown in Eq. (19) are the reactions used for char conversion.

$$C+{CO}_{2}\to 2CO$$
(18)
$$C+{H}_{2}O\to CO+{H}_{2}$$
(19)

To consider the evolution of porosity, a statistical function of the porosity distribution based on RPM is used [35]. Because the probability of pore overlapping for different pore diameters is independent, it is possible to write an expression that determines the individual porosity corresponding to the i-th pore computed, as shown in Eq. (20).

$${\varepsilon }_{i}\left(t\right)=\left[1-\mathit{exp}\left(-\pi {l}_{0,i}{r}_{i}^{2}\right)\right]\mathit{exp}\left(-\pi \sum\limits_{s=i+1}^{n}{l}_{0,i}{r}_{i}^{2}\right)$$
(20)

Finally, a population balance is used for the porosity distribution given by the equation.

$$\frac{\partial {\varepsilon }_{i}}{\partial t}=-\frac{\partial }{\partial {r}_{p}}\left(\frac{d{r}_{p,i}}{dt}{\varepsilon }_{i}\right)$$
(21)

where dr/dt is computed from Eq. (16) as

$$\frac{d{r}_{i}}{dt}=\frac{1}{\pi {l}_{0}{r}_{i}}\frac{d{\varepsilon }_{i}}{dt}$$
(22)

Equations from (7) to (22) are programmed in the Simulink—Matlab software. The solution describes the behavior of structural change, diffusion coefficient, and reactivity. ODE45, which is based on Runge–Kutta (4,5), was used to solve the temporal differential equations due to nonstiff characteristics.

3 Results

3.1 Raw materials and PDS analysis

The elemental and proximate analyses for the raw biomass are shown in Table 1. The biochar ash content and textural properties are shown in Table 2. According to international certification, the H/C ratio of the residues generated during corncob gasification is less than 0.7, classifying this product as biochar [37]. Biochar A1 shows a larger volume in micro- and mesopores than biochar A2. The major difference between the two types of biochar was found in the volume of micropores. Figure 1 shows the pore volume distribution for both biochar samples. For biochar A1, the specific surface area was 54.09 m2/g, where micropores (0–2 nm) contribute 50.71 m2/g, whereas mesopores (2–50 nm) contribute 2.37 m2/g. For biochar A2, the specific surface area was 22.14 m2/g, with 17.96 m2/g contributed by micropores and 4.17 m.2/g by mesopores. In both cases, the mesopores had a minor contribution. Therefore, the main contribution of the specific area was in the range of microporous. Furthermore, biochar A1 shows a higher peak in this zone, which is a characteristic behavior attributed to the reaction of carbon with CO2 creating greater pore length growth [38]

Table 1 Corncob proximate and ultimate analysis
Full size table
Table 2 Biochar ultimate analysis, ASH content and textural parameters
Full size table
Fig. 1
figure 1

Initial pore size distribution

Full size image

3.2 TGA Apparent kinetics analysis

TGA analysis of biochar through gasification with CO2 and steam for biochar A1 and A2 is shown in Fig. 2. Biochar A1 gasification at 850 °C showed a 100% conversion in approximately 0.45 h in the presence of CO2 (Fig. 2a) and 0.34 h for steam (Fig. 2b). As gasification temperature increases to 950 °C, the complete conversion is attained in 0.33 and 0.2 h, in the presence of CO2 and steam, respectively. Biochar A2 gasification at 850 °C showed a 100% conversion in 0.72 h in the presence of CO2 (Fig. 2c) and 0.36 h for steam (Fig. 2d). For a temperature of 950 °C, the total conversion for CO2 and steam is attained at 0.4 and 0.27 h, respectively. Despite both biochars being obtained from the same biomass, they present different conversion times under the same TGA conditions. The difference in initial texture is significantly influencing the apparent reaction rate. Likewise, these differences are more noticeable at lower temperatures, being attributed to the effects of structural evolution due to the greater intraparticle diffusion of reactant.

Fig. 2
figure 2

Conversion during gasification: CO2-A1 (a), H2O-A1 (b), CO2-A2 (c), H2O-A2 (d)

Full size image

The most significant difference is found in the total conversion time for gasification with CO2 at 850 °C. For biochar A1, the conversion time is practically half that of biochar A2. This could be attributed to the larger area of the A1 biochar, which allows CO2 to react inside the particle with a larger active area than the A2 biochar. However, when gasification at 950 °C is compared, there is no difference between the total conversion times. Likewise, biochar A1 at 850 °C gasified with CO2 presents an increasing slope until reaching a conversion fraction of 0.3. On the other hand, biochar A2 presents a less aggressive slope increase. In general, the differences in the apparent kinetics are more noticeable at low temperatures. This suggests that textural evolutions occur inside the porous structure caused by the intraparticle diffusion of reactants, while at high temperatures, the internal evolution may not take place due to the increased reaction rate compared to the diffusive transportation characteristic of a shrinking nuclei model. Regarding gasification with steam, the apparent kinetics do not show a notable difference between biochar A1 and A2. This can be associated because steam reactions are more effective in the mesopore region. Because of a faster steam gasification than CO2, the reactant concentration that reaches the micropores is limited by the faster consumption of reactant in the larger pores. Both types of biochar show a similar pore volume with 0.0114 cm3/g for biochar A1 and 0.0096 cm3/g for biochar A2.

Figure 3 and Fig. 4 show the derivatives of the conversion and an Arrhenius diagram for the gasification of biochar A1 and A2, respectively. For biochar A1 gasification with CO2 at 850 °C (Fig. 3a), an increase in the conversion rate is observed that reaches close the apparent conversion rate at 950 °C in a conversion range between 0.4 and 0.6. This increase in reactivity can be attributed to a porosity opening, increasing the area that participates in the reactions and increasing the diffusion velocity by expanding porosity [39]. On the other hand, the biochar conversion rates for gasification at 900 °C and 950 °C remain similar in ranges between 0.4 and 0.7; this type of behavior is characteristic for diffusive control processes. In this case, the apparent conversion rate is limited by the transport speed of the reactants with temperatures higher than 900 °C. Figure 3b shows the Arrhenius plot for CO2; a change in activation energies with respect to conversion rate is evident. This suggests that there are changes between kinetic control from 850 °C with structural evolution to diffusive control above 900 °C for the particle size studied.

Fig. 3
figure 3

Isoconversional reactivity and Arrhenius plot for char A1. (a), (b) for CO2, (c) and (d) for Steam

Full size image
Fig. 4
figure 4

Isoconversional reactivity and Arrhenius plot for char A2. (a), (b) for CO2, (c) and (d) for Steam

Full size image

Regarding the conversion rate of biochar A2 shown in. Figure 4a, CO2 gasification shows an increasing reaction rate until a 50% conversion is attained. Furthermore, the reaction rate for gasification at temperatures of 900 °C and 950 °C are similar in a conversion ranging between 0.2 and 0.6. The Arrhenius plot shown in Fig. 4b describes steeper slopes compared to biochar A1, thus indicating a higher apparent activation energy.

Figure 3c and Fig. 3d show the conversion rate and the Arrhenius diagram for the steam gasification of biochar A1. It is noticed that the maximum reaction rate is attained for all temperatures before 20% conversion. This suggests a high reactivity at the beginning associated with a better diffusion of reactants and CO2 as well. Unlike the reaction rates with CO2, the reaction rate increases notably with temperature; this indicates that although gasification with steam is faster, the opening of the structure and the greater diffusivity of the steam allow better capturing the kinetic control process in the temperature range studied. However, between 900 and 950 °C, there are similar apparent conversion rates, which suggest diffusive limitations. The Arrhenius diagram also shows changes in activation energy between 850–900 and 900–950 °C.

Regarding biochar A2 gasification with CO2, the conversion ratios are clearly differentiated with respect to temperature (Fig. 4a). Unlike biochar A1, there may be fewer diffusive limitations. This is associated with the fact that biochar A2 initially has a higher initial volume of mesopores and macropores, which increases the transportation rate of reactants. Consequently, the Arrhenius diagram shows activation energies with more homogeneous slopes with respect to x(t) (Fig. 4b). Like biochar A1, steam gasification of biochar A2 shows a maximum apparent reaction rate before reaching a conversion of 0.2 (Fig. 4c). At the same time, the change in these rates is clear between 900 and 950 °C with respect to biochar A1. Again, the effect of the greater volume of meso- and macropores may be affecting the apparent reactivity, revealing more homogeneous activation energies (Fig. 4d).

Figure 5 shows the change in activation energy for gasification with CO2 and steam. There is quite a marked difference between the two types of biochar. The literature shows variations in activation energy between 88 and 250 kJ/mol for CO2 (most between 200 and 250 kJ/mol) and 143 and 237 kJ/mol for steam (most between 200 and 250 kJ/mol) [40]. Based on TGA, these values coincide in some regions with what is shown in the literature. The activation energy for CO2 corresponds to those reported in the literature for conversion ranges greater than 0.75. On the other hand, steam indicates activation energies for all conversions below those shown in the literature, with conversions between 0.1 and 0.35 being the closest to the range shown in the literature.

Fig. 5
figure 5

Activation energy for apparent kinetics vs. char conversion. CO2 (a) and H2O (b)

Full size image

During gasification with CO2 and steam, both biochar A1 and A2, the apparent activation energy decreases until reaching values close to a conversion of 0.7. After this, the value grows again at a faster rate of change. This same behavior was evidenced by the authors Meng et al. [39], which showed that from the conversion of 0.2, the activation energy shows a certain degree of reduction until the conversion reaches 0.6. After this, the activation energy increased, specifically in large particles governed by intraparticle diffusion. The same authors showed that porosity gradually increased with conversion, which can then be reflected as a decrease in activation energy. Subsequently, the reduction of the mass transfer limitation leads to an increase in the apparent activation energy. Therefore, it can be considered that there are important correlations between the evolution of the kinetic parameters and the change in the structure of the pores. Some other authors [41, 42] also identified that the evolution of kinetic parameters is an indication of possible changes in the structure of the char.

3.3 Intrinsic kinetics

Table 3 shows fit values for heterogeneous intrinsic kinetics \({\mathfrak{R}}_{int}\) that best fit the experimental x(t) conversion. Figure 6 shows the model for the best \({\mathfrak{R}}_{int}\) adjusted compared to experimental conversion by TGA. For the model and for the experimental data as well, it is noticed that the total conversion time decreases when temperature increases. Likewise, at high temperatures, both the model and the data show a more linear behavior, possibly attributed to a lower reaction order at higher temperatures, associated with the fact that structural changes at high reactions speeds are not as influential when compared to low-temperature gasification.

Table 3 Fitting parameter for intrinsic heterogeneous kinetics
Full size table
Fig. 6
figure 6

Biochar conversion model fitting. a A1-CO2, b A2-CO2, c A1-H2O, and d A2-H2O

Full size image

Figure 7 shows the Arrhenius plot for the data obtained in Table 3. The activation energy and the pre-exponential factor are obtained with the slope of a trend line and the antilogarithm of the intercept on the ln axis (ℜint). These values are shown in Table 4. It is evident that there is no greater difference between the intrinsic kinetic parameters between biochar A1 and A2 compared to the differences shown in the apparent kinetics obtained by TGA shown in Fig. 5. Indicating that the model has captured both effects due to the diffusion limitations associated with temperature increases (homogeneous slope between 850–900 and 900–950 °C) and because of the initial structure of the biochar type (biochar A1-A2). On the other hand, the activation energy values derived from gasification with CO2 and steam are comparable with those reported in the literature for this type of biochar.

Fig. 7
figure 7

Arrhenius Plot for CO2 (a) and steam (b) heterogeneous intrinsic kinetic parameters

Full size image
Table 4 Intrinsic activation energy and pre-exponential factor estimation
Full size table

For A2 char gasification with CO2 at 850 °C, the total theoretical area develops from 34 to 100 m2/cc at a conversion of x = 0.4. While at 950 °C, the area reached a maximum value of 60 m2/cc at a conversion of x = 0.37. This behavior is similar to that shown by Maya et al. [38], in which gasification in the presence of CO2 under intraparticle gradient showed lower area development in conversions close to x = 0.4, while gasification with CO2 under chemical control showed greater development of the maximum area at conversion over x = 0.5.

4 Conclusions

To validate the methodology for obtaining intrinsic kinetic parameters of char gasification by adjusting the parameters of a multipore capillary particle reaction model, biomass gasification is carried out by varying the gasifying agent (CO2-steam), temperature, and initial porosity distribution. The main conclusions are:

  • The kinetic parameters based on iso-conversion analysis vary considerably both in the evolution of the conversion and the initial structural state of the porosity for the particle size studied.

  • Experimental adjustment of the reaction order is not necessary for detailed models which describe multiporous intraparticle diffusion with structural evolution.

  • The same activation energy is obtained for gasification with CO2 and steam from the same biochar with different initial porous structures, suggesting that the model captures the intrinsic kinetics independent of diffusion effects, initial structural pore parameters, and structural evolution.

  • Besides obtaining the intrinsic heterogeneous kinetics, the model can be used to predict the evolution of the porous structure of biochar by gasification with CO2 and steam. Therefore, it is a reliable tool that allows the valorization of biochar in which the porous structure provides a significant value for the biochar.

  • The main limitations of the model are: (a) it can only be used if the initial pore distribution and initial biochar content are known, (b) biochar must have low volatile content as it does not predict density changes due to devolatilization, and (c) model lacks experimental fit accuracy for conversions above 90%.