Abstract
The generalized Cesàro operators \(C_t\), for \(t\in [0,1]\), were first investigated in the 1980s. They act continuously in many classical Banach sequence spaces contained in \({{\mathbb {C}}}^{{{\mathbb {N}}}_0}\), such as \(\ell ^p\), \(c_0\), c, \(bv_0\), bv and, as recently shown in Curbera et al. (J Math Anal Appl 507:31, 2022) [26], also in the discrete Cesàro spaces ces(p) and their (isomorphic) dual spaces \(d_p\). In most cases \(C_t\) (\(t\not =1\)) is compact and its spectra and point spectrum, together with the corresponding eigenspaces, are known. We study these properties of \(C_t\), as well as their linear dynamics and mean ergodicity, when they act in certain non-normable sequence spaces contained in \({{\mathbb {C}}}^{{{\mathbb {N}}}_0}\). Besides \({{\mathbb {C}}}^{{{\mathbb {N}}}_0}\) itself, the Fréchet spaces considered are \(\ell (p+)\), \(ces(p+)\) and \(d(p+)\), for \(1\le p<\infty \), as well as the (LB)-spaces \(\ell (p-)\), \(ces(p-)\) and \(d(p-)\), for \(1<p\le \infty \).
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The (discrete) generalized Cesàro operators \(C_t\), for \(t\in [0,1]\), were first investigated by Rhaly, [52]. The action of \(C_t\) from \(\omega :={{\mathbb {C}}}^{{{\mathbb {N}}}_0}\) into itself (with \({{\mathbb {N}}}_0:=\{0,1,2,\ldots \}\)) is given by
For \(t=0\) note that \(C_0\) is the diagonal operator
where \(\varphi :=\left( \frac{1}{n+1}\right) _{n\in {{\mathbb {N}}}_0}\), and for \(t=1\) that \(C_1\) is the classical Cesàro averaging operator
The spectra of \(C_1\) have been investigated in various Banach sequence spaces. For instance, we mention \(\ell ^p\) (\(1<p<\infty \)), [22, 23, 30, 40], \(c_0\) [1, 40, 51], c [40], \(\ell ^\infty \) [50, 51], the Bachelis spaces \(N^p\) (\(1<p<\infty \)) [25], bv and \(bv_0\) [47, 48], weighted \(\ell ^p\) spaces [7, 10], the discrete Cesàro spaces ces(p) (for \(p\in \{0\}\cup (1,\infty )\)), [24], and their dual spaces \(d_s\) (\(1<s<\infty \)), [19]. For the class of generalized Cesàro operators \(C_t\), for \(t\in (0,1)\), a study of their spectra and compactness properties (in \(\ell ^2\)) go back to Rhaly, [52, 53]. A similar investigation occurs for \(\ell ^p\) (\(1<p<\infty \)) in [58] and for c and \(c_0\) in [55, 59]. The paper [55] also treats \(C_t\) when it acts on \(bv_0\), bv, c, \(\ell ^1\), \(\ell ^\infty \) and the Hahn sequence space h. In the recent paper [26] the setting for considering the operators \(C_t\) is a large class of Banach lattices in \(\omega \), which includes all rearrangement invariant sequence spaces (over \({{\mathbb {N}}}_0\) for counting measure), and many others.
Our aim is to study the compactness, the spectra and the dynamics of the generalized Cesàro operators \(C_t\), for \(t\in [0,1)\), when they act in certain classical, non-normable sequence spaces \(X\subseteq \omega \). Besides \(\omega \) itself, the Fréchet spaces considered are \(\ell (p+)\), \(ces(p+)\) and \(d(p+)\), for \(1\le p<\infty \), as well as the (LB)-spaces \(\ell (p-)\), \(ces(p-)\) and \(d(p-)\), for \(1<p\le \infty \).
In Sect. 2 we formulate various preliminaries that will be needed in the sequel concerning particular properties of the spaces X that we consider, as well as linear operators between such spaces. We also collect some general results required to determine the spectra of operators T acting in the spaces X and the compactness of their dual operator \(T'\) acting in the strong dual space \(X'_\beta \) of X.
Section 3 is devoted to a detailed study of the operators \(C_t\), for \(t\in [0,1)\), when they act in \(\omega \). These operators are never compact (c.f. Proposition 3.2) and their spectrum is completely described in Theorem 3.7 where, in particular, it is established that the set of all eigenvalues of \(C_t\) is independent of t and equals \(\Lambda :=\{\frac{1}{n+1}:\, n\in {{\mathbb {N}}}_0\}\). The 1-dimensional eigenspace corresponding to \(\frac{1}{n+1}\), for each \(n\in {{\mathbb {N}}}_0\), is identified in Lemma 3.4.
The situation for the other mentioned spaces \(X\subseteq \omega \), which is rather different, is treated in Sects. 4 and 5. The operator \(C_t\), for \(t\in [0,1)\), is always compact in these spaces; see Theorem 4.5(i) for the case of Fréchet spaces and Theorem 5.3(i) for the case of (LB)-spaces. The spectra of \(C_t\) are fully determined in Theorems 4.5(ii) and 5.3(ii), and the 1-dimensional eigenspace corresponding to each eigenvalue of \(C_t\) is identified in Theorems 4.5(iii) and 5.3(iii). We note, for all cases of X and \(t\in [0,1)\), that the set of all eigenvalues of \(C_t\) is again \(\Lambda \). The main tool is a factorization result stating that \(C_t=D_\varphi R_t\), where \(D_\varphi :X\rightarrow X\) is a compact (diagonal) operator in X and \(R_t:X\rightarrow X\) is a continuous linear operator; see Propositions 4.4(iii) and 5.2(iii).
For the definition of a mean ergodic operator and the notion of a supercyclic operator we refer to Sect. 6, where the relevant operators under consideration are \(C_t\) acting in the spaces X, for each \(t\in [0,1)\). It is necessary to determine some abstract results for linear operators in general lcHs’ (c.f., Theorems 6.2 and 6.4), which are then applied to \(C_t\) to show that it is both power bounded and uniformly mean ergodic in all spaces \(X\not =\omega \); see Theorem 6.6. The same is true for \(C_t\) acting in \(\omega \); see Theorem 6.1. In this section we also investigate the properties of the dual operators \(C'_t\) acting in \(X'_\beta \), which are given by (6.6) and (6.8). The operators \(C_t'\) are compact and their spectra are identified in Proposition 6.7, where it is also shown that the set of all eigenvalues of \(C'_t\) is \(\Lambda \). Moreover, for each \(n\in {{\mathbb {N}}}_0\), the eigenvector in \(X'_\beta \) spanning the 1-dimensional eigenspace corresponding to \(\frac{1}{n+1}\in \Lambda \) is also determined. A consequence of \(C'_t\) having a rich supply of eigenvalues is that each operator \(C_t:X\rightarrow X\), for \(t\in [0,1)\), fails to be supercyclic. Moreover, it is established in Proposition 6.8 that \(C'_t:X'_\beta \rightarrow X'_\beta \) is power bounded, uniformly mean ergodic but, not supercyclic. It should be noted that the main results in this section are also new for \(C_t\) acting in the Banach spaces \(\ell ^p\), ces(p) and \(d_p\).
2 Preliminaries
Given locally convex Haudorff spaces X, Y (briefly, lcHs) we denote by \({{\mathcal {L}}}(X,Y)\) the space of all continuous linear operators from X into Y. If \(X=Y\), then we simply write \({{\mathcal {L}}}(X)\) for \({{\mathcal {L}}}(X,X)\). Equipped with the topology of pointwise convergence \(\tau _s\) on X (i.e., the strong operator topology) the lcHs \({{\mathcal {L}}}(X)\) is denoted by \({{\mathcal {L}}}_s(X)\) and for the topology \(\tau _b\) of uniform convergence on bounded sets the lcHs \({{\mathcal {L}}}(X)\) is denoted by \({{\mathcal {L}}}_b(X)\). Denote by \({{\mathcal {B}}}(X)\) the collection of all bounded subsets of X and by \(\Gamma _X\) a system of continuous seminorms determing the topology of X. The identity operator on X is denoted by I. The dual operator of \(T\in {{\mathcal {L}}}(X)\) is denoted by \(T'\); it acts in the topological dual space \(X':={{\mathcal {L}}}(X,{{\mathbb {C}}})\) of X. Denote by \(X'_\sigma \) (resp., by \(X'_\beta \)) the space \(X'\) with the weak* topology \(\sigma (X',X)\) (resp., with the strong topology \(\beta (X',X)\)); see [37, Sect. 21.2] for the definition. It is known that \(T'\in {{\mathcal {L}}}(X'_\sigma )\) and \(T'\in {{\mathcal {L}}}(X_\beta ')\), [38, p. 134]. For the general theory of functional analysis and operator theory relevant to this paper see, for example, [27, 33, 36, 44, 49, 56].
Lemma 2.1
Let X be a lcHs and \(T\in {{\mathcal {L}}}(X)\) be an isomorphism of X onto itself. Then \(T'\) is an isomorphism of \(X'_\beta \) onto itself. If, in addition, X is complete and barrelled, then T is an isomorphism of X onto itself if, and only if, \(T'\) is an isomorphism of \(X'_\beta \) onto itself.
Proof
If T is an isomorphism of X onto itself, then \(T^{-1}\in {{\mathcal {L}}}(X)\) exists with \(TT^{-1}=T^{-1}T=I\). It was already noted that \(T', (T^{-1})'\in {{\mathcal {L}}}(X'_\beta )\) and clearly \((T^{-1})'T'=T'(T^{-1})'=I\). Thus, \((T')^{-1}\) exists in \({{\mathcal {L}}}(X'_\beta )\) and \((T')^{-1}=(T^{-1})'\); that is, \(T'\) is an isomorphism of \(X_\beta '\) onto itself.
Suppose that X is also complete and barrelled and that \(T'\in {{\mathcal {L}}}(X'_\beta )\) is an isomorphism of \(X'_\beta \) onto itself. As proved above, \(T''\) is necessarily an isomorphism of \(X''_\beta \) onto itself. By the proof of Lemma 3 in [6] it follows that T is an isomorphism of X onto itself. This completes the proof. \(\square \)
Given a lcHs X and \(T\in {{\mathcal {L}}}(X)\), the resolvent set \(\rho (T;X)\) of T consists of all \(\lambda \in {{\mathbb {C}}}\) such that \(R(\lambda ,T):=(\lambda I-T)^{-1}\) exists in \({{\mathcal {L}}}(X)\). The set \(\sigma (T;X):={{\mathbb {C}}}{{\setminus }} \rho (T;X)\) is called the spectrum of T. The point spectrum \(\sigma _{pt}(T;X)\) of T consists of all \(\lambda \in {{\mathbb {C}}}\) (also called an eigenvalue of T) such that \((\lambda I-T)\) is not injective. An eigenvalue \(\lambda \) of T is called simple if  . Some authors (e.g. [56]) prefer the subset \(\rho ^*(T;X)\) of \(\rho (T;X)\) consisting of all \(\lambda \in {{\mathbb {C}}}\) for which there exists \(\delta >0\) such that the open disc \(B(\lambda ,\delta ):=\{z\in {{\mathbb {C}}}:\, |z-\lambda |<\delta \}\subseteq \rho (T;X)\) and \(\{R(\mu ,T):\, \mu \in B(\lambda ,\delta )\}\) is an equicontinuous subset of \({{\mathcal {L}}}(X)\). Define \(\sigma ^*(T;X):={{\mathbb {C}}}{\setminus } \rho ^*(T;X)\), which is a closed set with \(\sigma (T;X)\subseteq \sigma ^*(T;X)\). If X is a Banach space, then \(\sigma (T;X)= \sigma ^*(T;X)\). For the spectral theory of compact operators in lcHs’ we refer to [27, 33], for example.
. Some authors (e.g. [56]) prefer the subset \(\rho ^*(T;X)\) of \(\rho (T;X)\) consisting of all \(\lambda \in {{\mathbb {C}}}\) for which there exists \(\delta >0\) such that the open disc \(B(\lambda ,\delta ):=\{z\in {{\mathbb {C}}}:\, |z-\lambda |<\delta \}\subseteq \rho (T;X)\) and \(\{R(\mu ,T):\, \mu \in B(\lambda ,\delta )\}\) is an equicontinuous subset of \({{\mathcal {L}}}(X)\). Define \(\sigma ^*(T;X):={{\mathbb {C}}}{\setminus } \rho ^*(T;X)\), which is a closed set with \(\sigma (T;X)\subseteq \sigma ^*(T;X)\). If X is a Banach space, then \(\sigma (T;X)= \sigma ^*(T;X)\). For the spectral theory of compact operators in lcHs’ we refer to [27, 33], for example.
Corollary 2.2
Let X be a complete, barrelled lcHs and \(T\in {{\mathcal {L}}}(X)\). Then
Moreover,
Proof
The identities in (2.1) are an immediate consequence of Lemma 2.1.
Fix \(\lambda \in \rho ^*(T; X)\). Then there exists \(\delta >0\) such that \(B(\lambda , \delta )\subseteq \rho (T;X)\) and \(\{R(\mu ;T)\,:\, \mu \in B(\lambda ,\delta )\}\subseteq {{\mathcal {L}}}(X)\) is equicontinuous. For each \(\mu \in B(\lambda ,\delta )\) it follows from the proof of Lemma 2.1 that \(R(\mu , T)'=((\mu I-T)^{-1})'=(\mu I-T')^{-1}=R(\mu , T')\). Then [38, Sect. 39.3(6), p.138] implies that \(\{R(\mu , T')\,:\, \mu \in B(\lambda ,\delta )\}\subseteq {{\mathcal {L}}}(X'_\beta )\) is equicontinuous, that is, \(\lambda \in \rho ^*(T';X'_\beta )\). So, we have established that \(\rho ^*(T;X)\subseteq \rho ^*(T';X'_\beta )\); taking complements yields (2.2). \(\square \)
A linear map \(T:X\rightarrow Y\), with X, Y lcHs’, is called compact if there exists a neighbourhood \({{\mathcal {U}}}\) of 0 in X such that \(T({{\mathcal {U}}})\) is a relatively compact set in Y. It is routine to show that necessarily \(T\in {{\mathcal {L}}}(X,Y)\). For the following result see [38, Sect. 42.1(1)] or [36, Proposition 17.1.1].
Lemma 2.3
Let X be a lcHs. The compact operators are a 2-sided ideal in \({{\mathcal {L}}}(X)\).
To establish the continuity of \(C_t\), for \(t\in [0,1]\), in the Fréchet spaces considered in this paper we will need the following result, [14, Lemma 25].
Lemma 2.4
Let \(X=\cap _{n=1}^\infty X_n\) and \(Y=\cap _{m=1}^\infty Y_m\) be two Fréchet spaces which resp. are the intersection of the sequence of Banach spaces \((X_n,\Vert \cdot \Vert _n)\), for \(n\in {{\mathbb {N}}}\), and of the sequence of Banach spaces \((Y_m,|||\cdot |||_m)\), for \(m\in {{\mathbb {N}}}\), satisfying \(X_{n+1}\subset X_n\) with \(\Vert x\Vert _n\le \Vert x\Vert _{n+1}\) for each \(n\in {{\mathbb {N}}}\) and \(x\in X_{n+1}\) and \(Y_{m+1}\subset Y_m\) with \(|||y|||_m\le |||y|||_{m+1}\) for each \(m\in {{\mathbb {N}}}\) and \(y\in Y_{m+1}\). Suppose that X is dense in \(X_n\) for each \(n\in {{\mathbb {N}}}\). Then a linear operator \(T:X\rightarrow Y\) is continuous if, and only if, for each \(m\in {{\mathbb {N}}}\) there exists \(n\in {{\mathbb {N}}}\) such that the operator T has a unique continuous extension \(T_{n,m}:X_n\rightarrow Y_m\).
The following result, based on [8, Lemma 2.1], will be needed to determine the spectra of \(C_t\), for \(t\in [0,1]\), in the Fréchet spaces considered in this paper.
Lemma 2.5
Let \(X=\cap _{n=1}^\infty X_n\) be a Fréchet space which is the intersection of a sequence of Banach spaces \((X_n,\Vert \cdot \Vert _n)\), for \(n\in {{\mathbb {N}}}\), satisfying \(X_{n+1}\subset X_n\) with \(\Vert x\Vert _n\le \Vert x\Vert _{n+1}\) for each \(n\in {{\mathbb {N}}}\) and \(x\in X_{n+1}\). Let \(T\in {{\mathcal {L}}}(X)\) satisfy the following condition:
(A) For each \(n\in {{\mathbb {N}}}\) there exists \(T_n\in {{\mathcal {L}}}(X_n)\) such that the restriction of \(T_n\) to X (resp. of \(T_n\) to \(X_{n+1}\)) coincides with T (resp. with \(T_{n+1}\)).
Then the following properties are satisfied.
-
(i)
\(\sigma (T;X)\subseteq \cup _{n=1}^\infty \sigma (T_n;X_n)\) and \(\sigma _{pt}(T;X)\subseteq \cap _{n=1}^\infty \sigma _{pt}(T_n;X_n)\).
-
(ii)
If \(\cup _{n=1}^\infty \sigma (T_n;X_n)\subseteq \overline{\sigma (T;X)}\), then \(\sigma ^*(T;X)=\overline{\sigma (T;X)}\).
-
(iii)
If
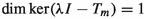 for each \(\lambda \in \cap _{n=1}^\infty \sigma _{pt}(T_n;X_n)\) and \(m\in {{\mathbb {N}}}\), then \(\sigma _{pt}(T;X)=\cap _{n=1}^\infty \sigma _{pt}(T_n;X_n)\).
for each \(\lambda \in \cap _{n=1}^\infty \sigma _{pt}(T_n;X_n)\) and \(m\in {{\mathbb {N}}}\), then \(\sigma _{pt}(T;X)=\cap _{n=1}^\infty \sigma _{pt}(T_n;X_n)\).
Proof
In view of [8, Lemma 2.1] it remains to show the validity of the inclusion \(\sigma _{pt}(T;X)\subseteq \cap _{n=1}^\infty \sigma _{pt}(T_n,X_n)\) in the statement (i) and the identity in (iii).
The inclusion \(\sigma _{pt}(T;X)\subseteq \cap _{n=1}^\infty \sigma _{pt}(T_n;X_n)\) is clear. Indeed, if \((\lambda I-T)x=0\) for some \(x\in X{\setminus }\{0\}\) and \(\lambda \in {{\mathbb {C}}}\), then in view of \(X\subseteq X_n\) and \(T_n|_X=T\), for \(n\in {{\mathbb {N}}}\), (see condition (A)), we have that \(x\in X_n{{\setminus }}\{0\}\) and \((\lambda I-T_n)x=0\) for every \(n\in {{\mathbb {N}}}\). Hence, \(\lambda \in \cap _{n=1}^\infty \sigma _{pt}(T_n;X_n)\).
To establish the validity of (iii), fix \(\lambda \in \cap _{n=1}^\infty \sigma _{pt}(T_n;X_n)\). Then, for each \(n\in {{\mathbb {N}}}\), there exists \(x_n\in X_n{\setminus }\{0\}\) such that \((\lambda I-T_n)x_n=0\). Since \(x_{n+1}\in X_{n+1}\subseteq X_n\), for \(n\in {{\mathbb {N}}}\), condition (A) implies that also \((\lambda I-T_n)x_{n+1}=0\) in \(X_n\) for each \(n\in {{\mathbb {N}}}\). So, for each \(n\in {{\mathbb {N}}}\), we have that \(x_{n+1}=\mu _n x_n\) for some \(\mu _n\in {{\mathbb {C}}}{\setminus }\{0\}\). Therefore, \(x_n=(\prod _{j=1}^{n-1}\mu _j)x_1\), with \(\prod _{j=1}^{n-1}\mu _j\not =0\). Accordingly, \(x_1\in X_n\) for each \(n\in {{\mathbb {N}}}\) and hence, \(x_1\in X\). On the other hand, applying again condition (A), we can conclude that \((\lambda I-T)x_1=(\lambda I-T_1)x_1=0\), i.e., \(\lambda \in \sigma _{pt}(T;X)\). \(\square \)
Fréchet spaces X which satisfy the assumptions of Lemma 2.5 are often called countably normed Fréchet spaces; for the general theory of such spaces see [29], for example.
A Hausdorff locally convex space \((X,\tau )\) is called an (LB)-space if there is a sequence \((X_k)_{k\in {{\mathbb {N}}}}\) of Banach spaces satisfying \(X_k\subseteq X_{k+1}\) continuously for \(k\in {{\mathbb {N}}}\), \(X=\cup _{k=1}^\infty X_k\) and \(\tau \) is the finest locally convex topology on X such that the natural inclusion \(X_k\subset X\) is continuous for each \(k\in {{\mathbb {N}}}\), [44, pp. 290–291]. In this case we write \(X= \mathrm{ind\,}_k X_k\). If, in addition, X is a regular (LB)-space, [36, p. 83], then a set \(B\subset X\) is bounded if and only if there exists \(m\in {{\mathbb {N}}}\) such that \(B\subset X_m\) and B is bounded in the Banach space \(X_m\). Complete (LB)-spaces are regular, [37, Sect. 19.5(5)]. All of the (LB)-spaces of sequences considered in this note will be regular because of the following result, [44, Proposition 25.19(2)].
Lemma 2.6
Let \(X=\mathrm{ind\,}_k X_k\) be an (LB)-space with an increasing union of reflexive Banach spaces \(X=\cup _{k=1}^\infty X_k\) such that each inclusion \(X_k\subseteq X_{k+1}\), for \(k\in {{\mathbb {N}}}\), is continuous. Then X is complete and hence, also regular.
An (LB)-space \(X=\mathrm{ind\,}_k X_k\) is said to be boundedly retractive if for every \(B\in {{\mathcal {B}}}(X)\) there exists \(k\in {{\mathbb {N}}}\) such that B is contained and bounded in \(X_k\), and X and \(X_k\) induce the same topology on B. The (LB)-space X is said to be sequentially retractive if for every null sequence in X there exists \(k\in {{\mathbb {N}}}\) such that the sequence is contained and converges to zero in \(X_k\). Finally, the (LB)-space X is said to be compactly regular if for every compact subset C of X there exists \(k\in {{\mathbb {N}}}\) such that C is compact in \(X_k\). Each of these three notions implies the completeness of X, [57, Corollary 2.8]. Neus [46] proved that all these notions are equivalent even for inductive limits of normed spaces.
In the setting of boundedly retractive (LB)-spaces, the following general statement on the compactness of certain dual operators is valid.
Proposition 2.7
Let X be a lcHs, \(Y=\mathrm{ind\,}_k Y_k\) be a boundedly retractive (LB)-space and \(T\in {{\mathcal {L}}}(X,Y)\) be compact. Then \(T'\in {{\mathcal {L}}}(Y'_\beta , X'_\beta )\) is compact.
Proof
The compactness of T implies that there exists a closed, absolutely convex neighbourhood \({{\mathcal {U}}}\) of 0 in X such that \(T({{\mathcal {U}}})\) is a relatively compact set in Y. So, the closure \(B:=\overline{T({{\mathcal {U}}})}\in {{\mathcal {B}}}(Y)\) of \(T({{\mathcal {U}}})\) is a compact set in Y. But, Y is a boundedly retractive (LB)-space. Accordingly, there exists \(k\in {{\mathbb {N}}}\) such that B is contained and bounded in \(Y_k\), and Y and \(Y_k\) induce the same topology on B. Therefore, B is also a compact set in \(Y_k\) and \(T(X)\subseteq Y_k\). Accordingly, the operator T acts compactly from X into \(Y_k\). Denote by \(T_1\) the operator T when interpreted to be acting from X into \(Y_k\) and by \(i_k\) the continuous inclusion of \(Y_k\) into Y. So, \(T_1\in {{\mathcal {L}}}(X,Y_k)\) is compact and \(T=i_kT_1\). Denote by p the continuous seminorm on X corresponding to \({{\mathcal {U}}}\) and let \(X_p\) denote the normed quotient space \(\left( \frac{X}{\textrm{Ker}p}, p\right) \). Then there exists a unique continuous linear operator S from \(X_p\) into \(Y_k\) such that \(SQ=T_1\), where Q denotes the canonical quotient map from X into \(X_p\) and hence, is an open map. Since \(T_1\in {{\mathcal {L}}}(X,Y_k)\) is compact and \(Q\in {{\mathcal {L}}}(X,X_p)\) is open, the operator \(S\in {{\mathcal {L}}}(X_p, Y_k)\) is necessarily compact. By Schauder’s theorem, [38, Sect. 42(7), p. 202], it follows that \(S'\in {{\mathcal {L}}}(Y'_k, X_p')\) is compact. So, \(T'_1=Q'S'\in {{\mathcal {L}}}(Y'_k,X'_\beta )\) is compact and hence, \(T'=T'_1i_k'\in {{\mathcal {L}}}(Y'_\beta , X'_\beta )\) is compact (cf. Proposition 17.1.1 in [36]). This completes the proof. \(\square \)
A Fréchet space X is said to be quasinormable if for every neighbourhhod \({{\mathcal {U}}}\) of 0 in X there exists a neighbourhhod \({{\mathcal {V}}}\) of 0 in X so that, for every \(\varepsilon > 0\), there exists \(B\in {{\mathcal {B}}}(X)\) satisfying \({{\mathcal {V}}}\subseteq B+\varepsilon {{\mathcal {U}}}\). Thus, every Fréchet-Schwartz space is quasinormable [44, Remark, p. 313]. The strong dual \(X'_\beta \) of a quasinormable Fréchet space X is necessarily a boundedly retractive (LB)-space [18, Theorem]. Thus, the strong dual of any Fréchet-Schwartz space (briefly, (DFS)-space) is a boundedly retractive (LB)-space.
Corollary 2.8
Let X and Y be two Fréchet spaces and \(T\in {{\mathcal {L}}}(X,Y)\). If \(T''\in {{\mathcal {L}}}(X''_\beta , Y''_\beta )\) is compact, then T is compact.
If, in addition, X is quasinormable and T is compact, then \(T''\in {{\mathcal {L}}}(X''_\beta , Y''_\beta )\) is compact.
Proof
Suppose that \(T''\in {{\mathcal {L}}}(X''_\beta , Y''_\beta )\) is compact. Since X, Y are Fréchet spaces, they are isomorphic to their respective natural image in \(X''_\beta \), \(Y''_\beta \) (in which they are closed subspaces). Moreover, the restriction of \(T''\) to X coincides with T and takes its values in \(Y\subseteq Y''_\beta \). Then the compactness of T follows from that of \(T''\).
Suppose that X is quasinormable and that \(T\in {{\mathcal {L}}}(X,Y)\) is compact. Since X is quasinormable, its strong dual \(X'_\beta \) is a boundedly retractive (LB)-space. Moreover, Y being a Fréchet space implies that \(T':Y'_\beta \rightarrow X'_\beta \) is compact, [27, Corollary 9.6.3]. It follows from Proposition 2.7, with \(Y'_\beta \) in place of X and \(X'_\beta \) in place of \(Y=\mathrm{ind\,}_k Y_k\) and \(T'\) in place of T, that \(T''\in {{\mathcal {L}}}(X''_\beta , Y''_\beta )\) is compact. \(\square \)
To identify the spectrum of \(C_t\) acting in the (LB)-spaces arising in this paper we will require the following two results; the first one, i.e. Lemma 2.9, is a direct consequence of Grothendieck’s factorization theorem (see e.g. [44, Theorem 24.33]), and the second one, i.e. Lemma 2.10, is proved in [11, Lemma 5.2].
Lemma 2.9
Let \(X=\mathrm{ind\,}_n X_n\) and \(Y=\mathrm{ind\,}_mY_m\) be two (LB)-spaces with increasing unions of Banach spaces \(X=\cup _{n=1}^\infty X_n\) and \(Y=\cup _{m=1}^\infty Y_m\). Let \(T:X\rightarrow Y\) be a linear map. Then T is continuous (i.e., \(T\in {{\mathcal {L}}}(X,Y)\)) if and only if for each \(n\in {{\mathbb {N}}}\) there exists \(m\in {{\mathbb {N}}}\) such that \(T(X_n)\subseteq Y_m\) and the restriction \(T:X_n\rightarrow Y_m\) is continuous.
Lemma 2.10
Let \(X=\mathrm{ind\,}_k X_k\) be a Hausdorff inductive limit of a sequence of Banach spaces \((X_k,\Vert \cdot \Vert _k)\). Let \(T\in {{\mathcal {L}}}(X)\) satisfy the following condition:
(A\(\prime \)) For each \(k\in {{\mathbb {N}}}\) the restriction \(T_k\) of T to \(X_k\) maps \(X_k\) into itself and \(T_k\in {{\mathcal {L}}}(X_k)\).
Then the following properties are satisfied.
-
(i)
\(\sigma _{pt}(T;X)=\cup _{k=1}^\infty \sigma _{pt}(T_k;X_k)\).
-
(ii)
If \(\cup _{k=m}^\infty \sigma (T_k;X_k)\subseteq \overline{\sigma (T;X)}\) for some \(m\in {{\mathbb {N}}}\), then \(\sigma ^*(T;X)=\overline{\sigma (T;X)}\).
-
(iii)
\(\sigma (T;X)\subseteq \cap _{m\in {{\mathbb {N}}}}\left( \cup _{n=m}^\infty \sigma (T_n;X_n)\right) \).
Another useful fact for our study is the following result.
Lemma 2.11
Let \(T\in {{\mathcal {L}}}(\omega )\). Let X be a Fréchet space or an (LB)-space continuously included in \(\omega \). If \(T(X)\subseteq X\), then \(T\in {{\mathcal {L}}}(X)\).
Proof
The result follows from the closed graph theorem, [44, Theorem 24.31], after recalling that X is ultrabornological, [44, Remark 24.15(c) & Proposition 24.16] and has a web, [44, Corollary 24.29 & Remark 24.36]. So, it is enough to show that the graph of T in X is closed. To do this, we assume that a net \((x_\alpha )_\alpha \subseteq X\) satisfies \(x_\alpha \rightarrow x\) and \(T(x_\alpha )\rightarrow y\) in X. Since the inclusion \(X\subseteq \omega \) is continuous, \(x_\alpha \rightarrow x\) in \(\omega \) and hence, \(T(x_\alpha )\rightarrow T(x)\) in \(\omega \). On the other hand, by the continuity of the inclusion \(X\subseteq \omega \) also \(T(x_\alpha )\rightarrow y\) in \(\omega \). Then \(T(x)=y\). So, (x, y) belongs to the graph of T. This shows that the graph of T is closed. \(\square \)
For X a barrelled lcHs, every bounded subset of \({{\mathcal {L}}}_s(X)\) is equicontinuous, [44, Proposition 23.27]. It is known that every Fréchet space is barrelled, [44, Remark, p. 296], and that every (LB)-space is barrelled, [44, Proposition 24.16].
The operator norm of a Banach space operator \(T\in {{\mathcal {L}}}(X,Y)\) will be denoted by \(\Vert T\Vert _{X\rightarrow Y}\). The Banach spaces \(\ell ^p=\ell ^p({{\mathbb {N}}}_0)\), for \(1\le p<\infty \), with their standard norm \(\Vert \cdot \Vert _p\) are classical. For \(1<p<\infty \) these spaces are reflexive. The spectra of \(C_t\) acting in such spaces are given in the following result; see [58] for \(1<p<\infty \) and also [55, Sect. 8] for \(1\le p<\infty \). Recall from Sect. 1 that
Proposition 2.12
For each \(t\in [0,1)\) the operator \(C_t\in {{\mathcal {L}}}(\ell ^p)\), for \(1\le p<\infty \), is a compact operator satisfying
and
with \(\Vert C_0\Vert _{\ell ^p\rightarrow \ell ^p}=1\). Moreover,
Concerning the classical Cesàro operator \(C_1\) (c.f. (1.3)) in \({{\mathcal {L}}}(\ell ^p)\) we have the following result.
Proposition 2.13
Let \(1<p<\infty \).
-
(i)
The operator \(C_1\in {{\mathcal {L}}}(\ell ^p)\) with \(\Vert C_1\Vert _{\ell ^p\rightarrow \ell ^p}=p'\), where \(\frac{1}{p}+\frac{1}{p'}=1\).
-
(ii)
The spectra of \(C_1\) are given by
$$\begin{aligned} \sigma _{pt}(C_1;\ell ^p)=\emptyset \ \text{ and } \ \sigma (C_1;\ell ^p)=\left\{ z\in {{\mathbb {C}}}:\, \left| z-\frac{p'}{2}\right| \le \frac{p'}{2}\right\} . \end{aligned}$$
Moreover, the range \((C_1-zI)(\ell ^p)\) is not dense in \(\ell ^p\) whenever \(|z-\frac{p'}{2}|<\frac{p'}{2}\).
For part (i) we refer to [34, Theorem 326] and for part (ii) see [30, 40, 54] and the references therein. In particular, \(C_1\) is a not a compact operator.
G. Bennett thoroughly investigated the discrete Cesàro spaces
where \(|x|:=(|x_n|)_{n\in {{\mathbb {N}}}_0}\), which satisfy \(\ell ^p\subseteq ces(p)\) continuously and are reflexive Banach spaces relative to the norm
see, for example, [17], as well as [15, 24, 31, 41] and the references therein. The following result, [26, Proposition 5.6] describes the spectra of \(C_t\) acting in ces(p).
Proposition 2.14
Let \(t\in [0,1)\) and \(1<p<\infty \). The operator \(C_t\in {{\mathcal {L}}}(ces(p))\) is compact and satisfies
Moreover,
The situation for \(C_1\in {{\mathcal {L}}}(ces(p))\) is quite different. Indeed, \(\Vert C_1\Vert _{ces(p)\rightarrow ces(p)}=p'\) and the spectra are given by
for each \(1<p<\infty \); see Theorem 5.1 and its proof in [24]. In particular, \(C_1\) is not a compact operator.
The dual Banach spaces \((ces(p))'\), for \(1<p<\infty \), are rather complicated, [35]. A more transparent isomorphic identification of \((ces(p))'\) is given in Corollary 12.17 of [17]. It is shown there that
is a Banach space for the norm
which is isomorphic to \((ces(p'))'\), where \(p'\) is the conjugate exponent of p. The sequence \({\hat{x}}\) is called the least decreasing majorant of x. The duality is the natural one given by
In particular, \(d_p\) is reflexive for each \(1<p<\infty \). Since \(|x|\le |{\hat{x}}|\), it is clear that \(\Vert x\Vert _p\le \Vert {\hat{x}}\Vert _p=\Vert x\Vert _{d_p}\), for \(x\in d_p\), that is, \(d_p\subseteq \ell ^p\) continuously. So, for all \(1<p<\infty \), we have \(d_p\subseteq \ell ^p\subseteq ces(p)\) with continuous inclusions. The following result is Theorem 6.9 of [26].
Proposition 2.15
Let \(t\in [0,1)\) and \(1<p<\infty \). The operator \(C_t\in {{\mathcal {L}}}(d_p)\) is compact and satisfies
Moreover,
Concerning the operator \(C_1\in {{\mathcal {L}}}(d_p)\), \(1<p<\infty \), it is known that \(\Vert C_1\Vert _{d_p\rightarrow d_p}=p'\) and that its spectra are given by
see Proposition 3.2 and Corollary 3.5 in [19].
3 The operators \(C_t\) acting in \(\omega \)
Given an element \(x=(x_n)_{n\in {{\mathbb {N}}}_0}\in \omega \) we write \(x\ge 0\) if \(x=|x|=(|x_n|)_{n\in {{\mathbb {N}}}_0}\). By \(x\le z\) it is meant that \((z-x)\ge 0\). The sequence space \(\omega \) is a non-normable Fréchet space for the Hausdorff locally convex topology of coordinatewise convergence, which is determined by the increasing sequence of seminorms
for each \(n\in {{\mathbb {N}}}_0\). Observe that \(r_n(x)=r_n(|x|)\le r_n(|y|)=r_n(y)\) whenever \(x,y\in \omega \) satisfy \(|x|\le |y|\). Let \(e_n:=(\delta _{nj})_{j\in {{\mathbb {N}}}_0}\) for each \(n\in {{\mathbb {N}}}_0\) and set \({{\mathcal {E}}}:=\{e_n:\, n\in {{\mathbb {N}}}_0\}\). It is clear from (1.1) that each \(C_t:\omega \rightarrow \omega \) is a linear map which is represented by a lower triangular matrix with respect to the unconditional basis \({{\mathcal {E}}}\) of \(\omega \). Namely,
with main diagonal the positive, decreasing sequence given by
The following properties of \(C_t\) are recorded in [26, Lemma 2.1], except for part (iv).
Lemma 3.1
Let \(t\in [0,1)\).
-
(i)
Each \(C_t\) is a positive operator on \(\omega \),i.e., \(C_tx\ge 0\) whenever \(x\ge 0\).
-
(ii)
Let \(0\le r\le s\le 1\). Then
$$\begin{aligned} 0\le |C_rx|\le C_r|x|\le C_s|x|,\quad x\in \omega . \end{aligned}$$ -
(iii)
For each \(t\in [0,1)\) the identities
$$\begin{aligned} C_te_n=\sum _{k=0}^\infty \frac{t^k}{k+n+1}e_{k+n}\in \ell ^1, \quad n\in {{\mathbb {N}}}_0, \end{aligned}$$and
$$\begin{aligned} C_t(e_n-te_{n+1})=\frac{1}{n+1}e_n,\quad n\in {{\mathbb {N}}}_0, \end{aligned}$$are valid.
-
(iv)
For each \(1<q<\infty \) we have \(d_q\subseteq \ell ^q\subseteq ces(q)\subseteq \omega \) with continuous inclusions.
Proof
(iv) In view of the discussion after (2.6) it remains to establish that \(ces(q)\subseteq \omega \) continuously. Fix \(x\in ces(q)\). Given \(n\in {{\mathbb {N}}}_0\) observe that
It follows from (3.1) that \(r_n(x)\le (n+1)\Vert x\Vert _{ces(q)}\). Since \(n\in {{\mathbb {N}}}_0\) is arbitrary, we can conclude that \(ces(q)\subseteq \omega \) continuously. \(\square \)
The classical Cesàro operator \(C_1:\omega \rightarrow \omega \) is a bicontinuous topological isomorphism (and hence, is not a compact operator) with spectra given by
see [8, p. 285 and Proposition 4.4]. So, we will only consider the case \(t\in [0,1)\).
Let \(t\in [0,1)\) and fix \(n\in {{\mathbb {N}}}_0\). According to (1.1) and (3.1), for each \(x\in \omega \), it is the case that
This implies that \(C_t\in {{\mathcal {L}}}(\omega )\) and that the family of operators \(\{C_t:\, t\in [0,1)\}\) is an equicontinuous subset of \({{\mathcal {L}}}(\omega )\).
Proposition 3.2
For each \(t\in [0,1)\) the operator \(C_t\in {{\mathcal {L}}}(\omega )\) is a bicontinuous isomorphism of \(\omega \) onto itself with inverse operator \((C_t)^{-1}:\omega \rightarrow \omega \) given by
In particular, \(C_t\) is not a compact operator.
Proof
Fix \(t\in [0,1)\). Let \(x\in \omega \) satisfy \(C_tx=0\). Considering the coordinate 0 of \(C_tx=0\) yields \(x_0=0\); see (1.1). The equation for coordinate 1 of \(C_tx=0\) is \(\frac{tx_0+x_1}{2}=0\) (cf. (1.1)) which yields \(x_1=0\). Proceed inductively for successive coordinates reveals that \(x_n=0\) for all \(n\in {{\mathbb {N}}}_0\). Hence, \(C_t\) is injective.
Given \(y\in \omega \) let \(x\in \omega \) be the element on the right-side of (3.5). Direct calculation shows that \(C_tx=y\). Accordingly, \(C_t\) is surjective.
By the open mapping theorem for Fréchet spaces (cf. Corollary 24.29 and Theorem 24.30 in [44]) the operator \(C_t\) is a bicontinuous isomorphism.
Since \(C_t\) is a bicontinuous isomorphism of \(\omega \), which is an infinite dimensional Fréchet space, \(C_t\) cannot be a compact operator. \(\square \)
To determine the spectrum of \(C_t\in {{\mathcal {L}}}(\omega )\) requires some preparation. Define
with the understanding that there exists \(N\in {{\mathbb {N}}}_0\) such that \(x_n\not =0\) for \(n\ge N\) and the limit \(\beta (x)\) exists. Analogously to \(d_p\), for \(1<p<\infty \), define
see [17, 19, 24, 31] and the references therein. Then \(d_1\) is a Banach lattice for the norm \(\Vert x\Vert _{d_1}:=\Vert {\hat{x}}\Vert _1\) and the coordinatewise order. Since \(0\le |x|\le {\hat{x}}\), for \(x\in \ell ^\infty \), it is clear that \(\Vert x\Vert _1\le \Vert x\Vert _{d_1}\) for \(x\in d_1\), that is, \(d_1\subseteq \ell ^1\) with a continuous inclusion. Clearly, \(d_1\subseteq d_p\), for all \(1<p<\infty \), and \(d_1\subseteq \ell ^1\) implies that \(d_1\subseteq \ell ^p\), for all \(1<p<\infty \). Moreover, \(\ell ^p\subseteq ces(p)\) (cf. Section 2) and so also \(d_1\subseteq ces(p)\), for \(1<p<\infty \). All inclusions are continuous. In view of Lemma 3.1(iv) it is clear that \(d_1\subseteq \omega \) and \(\ell ^1\subseteq \omega \) continuously. It is known that \({\mathcal {S}}\subseteq d_1\), [26, Lemma 3.3].
Remark 3.3
Proposition 2.15 is also valid for \(p=1\); see [26, Theorem 6.9].
The following result, [26, Lemma 3.6], will be required.
Lemma 3.4
Let \(t\in [0,1)\) and \(\varphi \) be as in (3.3). For each \(m\in {{\mathbb {N}}}\) define \(x^{[m]}\in \omega \) by
with \(\alpha _m\in {{\mathbb {C}}}{\setminus }\{0\}\) arbitrary, where 1 is in position m. For \(m=0\) define \(x^{[0]}:=\alpha _0(t^n)_{n\in {{\mathbb {N}}}_0}\) with \(\alpha _0\in {{\mathbb {C}}}{\setminus }\{0\}\) arbitrary.
-
(i)
For each \(m\in {{\mathbb {N}}}_0\), the vector \(x^{[m]}\) is the unique solution in \(\omega \) of the equation \(C_tx=\varphi _m x=\frac{1}{m+1}x\) whose m-th coordinate is \(\alpha _m\).
-
(ii)
The vector \(x^{[m]}\in d_1\subseteq \omega \), for each \(m\in {{\mathbb {N}}}_0\).
Remark 3.5
Let \(t\in [0,1)\) and X be any Banach space in \(\{\ell ^1,d_1\}\cup \{\ell ^p, ces(p), d_p:\, 1<p<\infty \}\). For each \(\nu \in \sigma _{pt}(C_t;X)=\Lambda \), it is the case that \(\textrm{dim}\,\textrm{Ker}(\nu I-C_t)=1\). Indeed, \(d_1\subseteq X\); see the discussion prior to Remark 3.3. Given \(\nu \in \Lambda \) there exists \(m\in {{\mathbb {N}}}_0\) such that \(\nu =\varphi _m\). According to Lemma 3.4 the 1-dimensional eigenspace corresponding to \(\nu \in \sigma _{pt}(C_t;\omega )\) is spanned by \(x^{[m]}\) with \(x^{[m]}\in d_1\). The claim is thereby proved.
The next lemma places a restriction on where \(\sigma (C_t;\omega )\) can be located in \({{\mathbb {C}}}\).
Lemma 3.6
Let \(t\in [0,1)\). For each \(\nu \in {{\mathbb {C}}}{\setminus }\Lambda \) the operator \(C_t-\nu I\) is a bicontinuous isomorphism of \(\omega \) onto itself. In particular, \(\sigma (C_t;\omega )\subseteq \Lambda \).
Proof
Fix \(\nu \not \in \Lambda \). Let \((C_t-\nu I)x=0\) for \(x\in \omega \). It follows from (3.2), by equating the coordinate 0 of \(C_tx=\nu x\), that \(x_0=\nu x_0\) and hence, as \(\nu \not =1\), that \(x_0=0\). Equating the coordinate 1 of \(C_tx=\nu x\) yields \(\frac{tx_0+x_1}{2}=\nu x_1\). Since \(x_0=0\) and \(\nu \not =\frac{1}{2}\), it follows that \(x_1=0\). Considering coordinate 2 gives \(\frac{t^2x_0+tx_1+x_2}{3}=\nu x_2\). Then \(x_0=x_1=0\) and \(\nu \not =\frac{1}{3}\) imply \(x_2=0\). Proceed inductively to conclude that \(x=0\), that is, \(C_t-\nu I\) is injective.
To verify the surjectivity of \(C_t-\nu I\) fix \(y\in \omega \). It is required to show that there exists \(x\in \omega \) satisfying \((C_t-\nu I)x=y\). Equating coordinate 0 gives \(x_0-\nu x_0=y_0\), that is, \(x_0=y_0/(1-\nu )\). Considering coordinate 1 yields \(\frac{tx_0}{2}+(\frac{1}{2}-\nu )x_1=y_1\). Substituting for \(x_0\) gives \((\frac{1}{2}-\nu )x_1=y_1-\frac{t}{2(1-\nu )}y_0\), that is,
Next, an examination of coordinate 2 yields \(\frac{t^2}{3}x_0+\frac{t}{3}x_1+(\frac{1}{3}-\nu )x_2=y_2\). Substituting for \(x_0\) and \(x_1\) we can conclude that
Continuing inductively yields
Then \(x\in \omega \) satisfies \((C_t-\nu I)x=y\). Hence, \(C_t-\nu I\) is surjective. \(\square \)
Combining the previous results yields the main result of this section.
Theorem 3.7
For each \(t\in [0,1)\) the spectra of \(C_t\in {{\mathcal {L}}}(\omega )\) are given by
with each eigenvalue being simple, and
The 1-dimensional eigenspace corresponding to the eigenvalue \(1/(m+1)\in \Lambda \) is spanned by \(x^{[m]}\) (cf. (3.8)), for each \(m\in {{\mathbb {N}}}_0\).
Proof
It is clear from Lemma 3.4 that \(\Lambda \subseteq \sigma _{pt}(C_t;\omega )\) and that each point \(1/(m+1)\in \Lambda \) is a simple eigenvalue of \(C_t\), whose corresponding eigenspace is spanned by \(x^{[m]}\), for each \(m\in {{\mathbb {N}}}_0\). Since \(\sigma (C_t;\omega )\subseteq \Lambda \) (cf. Lemma 3.6) and \(\sigma _{pt}(C_t;\omega )\subseteq \sigma (C_t;\omega )\), we can conclude that \(\sigma (C_t;\omega )=\sigma _{pt}(C_t;\omega )=\Lambda \). The containment \(\sigma (C_t;\omega )\subseteq \sigma ^*(C_t;\omega )\) and the fact that \(\sigma ^*(C_t;\omega )\) is a closed set imply that \(0\in \sigma ^*(C_t;\omega )\).
It remains to show that every \(\nu \not \in (\Lambda \cup \{0\})\) belongs to \(\rho ^*(C_t;\omega )\). So, fix \(\nu \not \in (\Lambda \cup \{0\})\). Select \(\delta >0\) such that the distance \(\epsilon \) of \(B(\nu ,\delta )\) to the compact set \(\Lambda \cup \{0\}\) is strictly positive. It follows from \(0\le t<1\) and the identity (3.9) which is coordinate n of \((C_t-\nu I)^{-1}y\), for each \(y\in \omega \), that for any given \(k\in {{\mathbb {N}}}_0\) there exists \(M_k>0\) such that
where \(r_k\) is the seminorm (3.1), with k in place of n. This implies that \(\{(C_t-\mu I)^{-1}\,:\, \mu \in B(\nu ,\delta )\}\) is a bounded set in \({{\mathcal {L}}}_s(\omega )\) and hence, by the barrelledness of \(\omega \), it is an equicontinuous subset of \({{\mathcal {L}}}(\omega )\). Accordingly, \(\nu \in \rho ^*(C_t;\omega )\). \(\square \)
4 \(C_t\) acting in the Fréchet spaces \(\ell (p+)\), \(d(p+)\) and \(ces(p+)\)
Given \(1\le p<\infty \), consider any strictly decreasing sequence \(\{p_k\}_{k\in {{\mathbb {N}}}}\subseteq (p,\infty )\) which satisfies \(p_k\downarrow p\). Then \(X_k:=\ell ^{p_k}\) satisfies \(X_{k+1}\subseteq X_k\) with \(\Vert x\Vert _{\ell ^{p_k}}\le \Vert x\Vert _{\ell ^{p_{k+1}}}\) for each \(k\in {{\mathbb {N}}}\) and \(x\in X_{k+1}\). Moreover, \(X=\cap _{k=1}^\infty X_k\) (i.e., \(\ell (p+):=\cap _{k=1}^\infty \ell ^{p_k}\)) is a Fréchet space of the type given in Lemma 2.5 whose topology is generated by the increasing sequence of norms \(u_k\), for \(k\in {{\mathbb {N}}}\), given by
That is, \(u_k\le u_{k+1}\) for \(k\in {{\mathbb {N}}}\). Moreover, \(p_k>p\) implies that the natural inclusion map \(\ell (p+)\hookrightarrow \ell ^{p_k}\) is continuous for each \(k\in {{\mathbb {N}}}\). Clearly the Banach space \(\ell ^p\subseteq \ell (p+)\) continuously and also \(\ell (p+)\subseteq \omega \) continuously, as \(\ell ^q\subseteq \omega \) continuously, for every \(1\le q<\infty \) (cf. Lemma 3.1(iv)). The space \(\ell (p+)\) is independent of the choice of \(\{p_k\}_{k\in {{\mathbb {N}}}}\).
Changing the Banach spaces, now let \(X_k:=ces(p_k)\), in which case again \(X_{k+1}\subseteq X_k\) with \(\Vert x\Vert _{ces(p_k)}\le \Vert x\Vert _{ces(p_{k+1})}\) for each \(k\in {{\mathbb {N}}}\) and \(x\in X_{k+1}\); see [13, Proposition 3.2(iii)]. Then \(X=\cap _{k=1}^\infty X_k\) (i.e., \(ces(p+):=\cap _{k=1}^\infty ces(p_k)\)) is a Fréchet space of the type given in Lemma 2.5 whose topology is generated by the increasing sequence of norms \(v_k\), for \(k\in {{\mathbb {N}}}\), given by
That is, \(v_k\le v_{k+1}\) for \(k\in {{\mathbb {N}}}\). Again \(ces(p)\subseteq ces(p+)\) (if \(p>1\)) and \(ces(p+)\subseteq \omega \) with both inclusions continuous, where we again use Lemma 3.1(iv). The Fréchet spaces \(ces(p+)\), for \(1\le p<\infty \), have been intensively studied in [9, 14].
Finally, consider the family of Banach spaces \(X_k:=d_{p_k}\), in which case \(X_{k+1}\subseteq X_k\) with \(\Vert x\Vert _{d_{p_k}}\le \Vert x\Vert _{d_{p_{k+1}}}\) for each \(k\in {{\mathbb {N}}}\) and \(x\in X_{k+1}\); see [19, Proposition 5.1(iii)]. So, \(X=\cap _{k=1}^\infty X_k\) (i.e., \(d(p+):=\cap _{k=1}^\infty d_{p_k}\)) is a Fréchet space of the type given in Lemma 2.5 whose topology is generated by the increasing sequence of norms \(w_k\), for \(k\in {{\mathbb {N}}}\), given by
That is, \(w_k\le w_{k+1}\) for \(k\in {{\mathbb {N}}}\). With continuous inclusions we have \(d_p\subseteq d(p+)\subseteq \omega \); see [20, Sect. 4] or, argue as for \(\ell ^p\) and \(\ell (p+)\).
It is known that the canonical vectors \({\mathcal {E}}\) belong to \(\ell (p+)\), \(d(p+)\) and \(ces(p+)\), for \(1\le p<\infty \), and form an unconditional basis in each of these spaces; see [20, Proposition 3.1], [20, Lemma 4.1] and [9, Proposition 3.5(i)], respectively.
In this section we consider the compactness and determine the spectra of \(C_t\) when they act in the Fréchet spaces \(\ell (p+)\), \(d(p+)\) and \(ces(p+)\), for \(1\le p<\infty \). The decreasing sequence \(\{p_k\}_{k\in {{\mathbb {N}}}}\) always has the properties listed above. Crucial for the proofs is the existence of a particular factorization available for \(C_t\) (cf. Proposition 4.4).
The decreasing sequence \(\varphi \) given in (3.3) satisfies \(\Vert \varphi \Vert _\infty =1\). Define the linear map \(D_\varphi :\omega \rightarrow \omega \) by
The diagonal (multiplication) operator \(D_\varphi \in {{\mathcal {L}}}(\omega )\) since, for each \(n\in {{\mathbb {N}}}_0\),
where \(r_n\) is the seminorm (3.1). Define the right-shift operator \(S:\omega \rightarrow \omega \) by
For each \(n\in {{\mathbb {N}}}\) note that \(r_n(Sx)=\max _{0\le k<n}|x_k|\le r_n(x)\) and for \(n=0\) that \(r_0(Sx)=0\le r_0(x)\) for each \(x\in \omega \). So, for every \(n\in {{\mathbb {N}}}_0\), the operator S satisfies
which implies that \(S\in {{\mathcal {L}}}(\omega )\). The following result is Lemma 2.2 in [26].
Lemma 4.1
For each \(t\in [0,1)\) we have the representation
with the series being convergent in \({{\mathcal {L}}}_s(\omega )\). Equivalently,
with the series being convergent in \(\omega \).
Fix \(t\in [0,1)\) and \(x\in \omega \). For each \(n\in {{\mathbb {N}}}_0\) it follows from (4.6) that
Accordingly, the series
is absolutely convergent in the quasicomplete lcHs \({{\mathcal {L}}}_s(\omega )\). In particular, \(R_t\in {{\mathcal {L}}}(\omega )\). Combining this with Lemma 4.1 and the fact that \(D_\varphi \in {{\mathcal {L}}}(\omega )\) yields the following factorization of \(C_t\).
Proposition 4.2
For each \(t\in [0,1)\) the operators \(D_\varphi \), \(R_t\), \(C_t\) belong to \({{\mathcal {L}}}(\omega )\) and
with the series being absolutely convergent in \({{\mathcal {L}}}_s(\omega )\).
Our aim is to to extend Proposition 4.2 to \({{\mathcal {L}}}(X)\) with \(X\in \{\ell (p+),ces(p+),d(p+):\, 1\le p<\infty \}\), to show that \(D_\varphi \in {{\mathcal {L}}}(X)\) is compact and then to apply Lemma 2.3 to conclude that \(C_t\in {{\mathcal {L}}}(X)\) is compact.
Proposition 4.3
Let X be any Fréchet space in \(\{\ell (p+),ces(p+),d(p+)\,:\, 1\le p<\infty \}\). Then \(D_\varphi \) maps X into X and \(D_\varphi \in {{\mathcal {L}}}(X)\) is compact.
Proof
Recall that \(\varphi \in c_0\) with \(\Vert \varphi \Vert _\infty =1\). We consider each of the three possible cases for X. It was shown above that \(D_\varphi \in {{\mathcal {L}}}(\omega )\) and that \(X\subseteq \omega \) continuously.
(a) Suppose that \(X=\ell (p+)\) for some \(1\le p<\infty \). Clearly, \(D_\varphi (X_k)\subseteq X_k\) for each \(k\in {{\mathbb {N}}}\) and so \(D_\varphi \in {{\mathcal {L}}}(X)\); see Lemma 2.11. In the notation of [14] it is clear from (4.4) that \(D_\varphi \) is precisely the multiplication operator \(M_\varphi \) defined there. Such a multiplication operator is compact if and only if \(\varphi \in \ell (\infty -)=\cup _{s>1}\ell ^s\), [14, Proposition 17], which is surely the case as \(\varphi \in \ell ^2\), for example. So, \(D_\varphi \in {{\mathcal {L}}}(\ell (p+))\) is a compact operator.
(b) Suppose that \(X=ces(p+)\) for some \(1\le p<\infty \). It follows from (2.4) that \(D_\varphi (X_k)\subseteq X_k\) for each \(k\in {{\mathbb {N}}}\) and so \(D_\varphi :X\rightarrow X\). Lemma 2.11 yields that \(M_\varphi =D_\varphi \in {{\mathcal {L}}}(ces(p+))\). Moreover, if \(\varphi \in d(\infty -)=\cup _{s>1} d_s\), then \(M_\varphi \) is also compact, [14, Proposition 10]. But, \(\varphi \) is a positive decreasing sequence and so \(\varphi ={\hat{\varphi }}\). Accordingly, by choosing \(s=2\) say, we see that
Hence, \(\varphi \in d_2\subseteq d(\infty -)\) and so \(D_\varphi =M_\varphi \in {{\mathcal {L}}}(ces(p+))\) is indeed compact.
(c) Suppose \(X=d(p+)\) for some \(1\le p<\infty \). Since \(|D_\varphi x|= D_\varphi |x|\le |x|\), for \(x\in \ell ^\infty \), it is clear that \(\widehat{D_\varphi x}\le {\hat{x}}\). Then (2.6) implies that \(D_\varphi (X_k)\subseteq X_k\) for all \(k\in {{\mathbb {N}}}\) and so \(D_\varphi :X\rightarrow X\). Again Lemma 2.11 yields that \(D_\varphi \in {{\mathcal {L}}}(d(p+))\). Note that the operator \(M_{d(p+)}^\varphi \) in [21] is precisely \(D_\varphi :d(p+)\rightarrow d(p+)\). It was verified in (b) above that \(\varphi \in d(\infty -)\) which, together with \(D_\varphi \in {{\mathcal {L}}}(d(p+))\), implies that \(D_\varphi \) is compact, [21, Theorem 4.13(i)]. \(\square \)
Proposition 4.4
Let \(t\in [0,1)\), and X be any Fréchet space in \(\{\ell (p+),ces(p+),d(p+):\, 1\le p<\infty \}\).
-
(i)
The generalized Cesàro operator \(C_t\) maps X into itself and \(C_t\in {{\mathcal {L}}}(X)\).
-
(ii)
The right-shift operator S given by (4.5) maps X into itself and belongs to \( {{\mathcal {L}}}(X)\).
-
(iii)
The operator \(R_t\) given by (4.7) maps X into itself and belongs to \( {{\mathcal {L}}}(X)\), with the series \(\sum _{n=0}^\infty t^nS^n\) being absolutely convergent in \({{\mathcal {L}}}_s(X)\). Moreover,
$$\begin{aligned} C_t=D_\varphi R_t=\sum _{n=0}^\infty t^nD_\varphi S^n. \end{aligned}$$
Proof
(i) Again we consider the three possible cases for X. Fix \(t\in [0,1)\). According to Proposition 3.2 the operator \(C_t\in {{\mathcal {L}}}(\omega )\).
(a) Suppose that \(X=\ell (p+)\) for some \(1\le p<\infty \). Proposition 2.12 implies that \(C_t(X_k)\subseteq X_k\) for all \(k\in {{\mathbb {N}}}\), with \(X_k=\ell ^{p_k}\), and so \(C_t(X)\subseteq X\). In view of Lemma 2.11, with \(T:=C_t\), it follows that \(C_t\in {{\mathcal {L}}}(\ell (p+))\).
(b) Suppose that \(X=ces(p+)\) for some \(1\le p<\infty \). Proposition 2.14 shows that \(C_t(X_k)\subseteq X_k\) for all \(k\in {{\mathbb {N}}}\), with \(X_k=ces(p_k)\), and so \(C_t(X)\subseteq X\). Again, for \(T:=C_t\), Lemma 2.11 implies that \(C_t\in {{\mathcal {L}}}(ces(p+))\).
(c) Suppose that \(X=d(p+)\) for some \(1\le p<\infty \). Proposition 2.15 shows that \(C_t(X_k)\subseteq X_k\) for all \(k\in {{\mathbb {N}}}\), with \(X_k=d_{p_k}\), and so \(C_t(X)\subseteq X\). Yet again, for \(T:=C_t\), Lemma 2.11 implies that \(C_t\in {{\mathcal {L}}}(d(p+))\).
(ii) Again we check the three separate cases for X. Prior to Lemma 4.1 it was shown that \(S\in {{\mathcal {L}}}(\omega )\).
(a) Suppose that \(X=\ell (p+)\) for some \(1\le p<\infty \). Using the fact that the Banach space right-shift operator \(S:\ell ^{p_k}\rightarrow \ell ^{p_k}\) is an isometry, for every \(k\in {{\mathbb {N}}}\), we see that \(S(X)\subseteq X\). It follows that \(S\in {{\mathcal {L}}}(\ell (p+))\); see Lemma 2.11 for \(T:=S\in {{\mathcal {L}}}(\omega )\).
(b) Suppose that \(X=ces(p+)\) for some \(1\le p<\infty \). It is known, for each \(k\in {{\mathbb {N}}}\), that \(S\in {{\mathcal {L}}}(ces(p_k))\) and \(\Vert S\Vert _{ces(p_k)\rightarrow ces(p_k)}\le 1\), [26, Lemma 5.4]. Accordingly, \(S(X)\subseteq X\) and so Lemma 2.11, for \(T:=S\in {{\mathcal {L}}}(\omega )\), implies that \(S\in {{\mathcal {L}}}(ces(p+))\).
(c) Suppose that \(X=d(p+)\) for some \(1\le p<\infty \). Fix \(k\in {{\mathbb {N}}}\). It is known that \(S\in {{\mathcal {L}}}(d_{p_k})\) and
[26, Lemma 6.2]. For \(m=1\) we can conclude that \(S(d_{p_k})\subseteq d_{p_k}\) for \(k\in {{\mathbb {N}}}\), that is, \(S(X)\subseteq X\). So, in view of Lemma 2.11, for \(T:=S\in {{\mathcal {L}}}(\omega )\), it follows that \(S\in {{\mathcal {L}}}(d(p+))\).
(iii) (a) Suppose that \(X=\ell (p+)\) for some \(1\le p<\infty \). Fix \(k\in {{\mathbb {N}}}\) and \(x\in \ell (p+)\subseteq \ell ^{p_k}\). It follows from S being an isometry in \(\ell ^{p_k}\) that \(u_k(S^n x)= u_k(x)\) for all \(n\in {{\mathbb {N}}}_0\) and hence, that
Accordingly, the series \(\sum _{n=0}^\infty t^n S^n x\) is absolutely convergent in the Fréchet space \(\ell (p+)\) for each \(x\in \ell (p+)\). By part (ii) the sequence \(\{\sum _{n=0}^m t^n S^n \}_{m\in {{\mathbb {N}}}_0}\subseteq {{\mathcal {L}}}(\ell (p+))\) and so, by the Banach-Steinhaus theorem (as \(\ell (p+)\) is barrelled), the series \(\sum _{n=0}^\infty t^n S^n\) is absolutely convergent in \({{\mathcal {L}}}_s(\ell (p+))\); its sum is denoted by \(R_t\in {{\mathcal {L}}}(\ell (p+))\).
It has been established that each of the operators \(C_t\), \(D_\varphi \), \(R_t\) belongs to \({{\mathcal {L}}}(\ell (p+))\). The identities \(C_t=D_\varphi R_t=\sum _{n=0}^\infty t^nD_\varphi S^n\) are valid in \({{\mathcal {L}}}(\ell (p+))\) because they are valid in \({{\mathcal {L}}}(\omega )\); see Lemma 4.1 and both (4.7) and (4.8).
(b) Suppose \(X=ces(p+)\) for some \(1\le p<\infty \). Fix \(k\in {{\mathbb {N}}}\) and \(x\in ces(p+)\subseteq ces(p_k)\). Using \(\Vert S^n\Vert _{ces(p_k)\rightarrow ces(p_k)}\le 1\), for all \(n\in {{\mathbb {N}}}_0\) (see the proof of part (ii)(b)), we can argue as in (a) to conclude that
Hence, the series \(\sum _{n=0}^\infty t^n S^n x\) is absolutely convergent in \(ces(p+)\) for each \(x\in ces(p+)\). Then argue as in (a) to deduce that the series \(R_t:=\sum _{n=0}^\infty t^n S^n \) is absolutely convergent in \({{\mathcal {L}}}_s(ces(p+))\), with \(R_t\in {{\mathcal {L}}}(ces(p+))\), and that the identities \(C_t=D_\varphi R_t=\sum _{n=0}^\infty t^nD_\varphi S^n\) are valid in \({{\mathcal {L}}}(ces(p+))\).
(c) Let \(X=d(p+)\) for some \(1\le p<\infty \). Fix \(k\in {{\mathbb {N}}}\) and \(x\in d(p+)\subseteq d_{p_k}\). It follows from (4.9) that
and hence, since \(0\le t<1\), that
Now argue as in (a) to conclude that the series \(R_t:=\sum _{n=0}^\infty t^n S^n\) is absolutely convergent in \({{\mathcal {L}}}_s(d(p+))\), with \(R_t\in {{\mathcal {L}}}(d(p+))\), and that the identities \(C_t=D_\varphi R_t=\sum _{n=0}^\infty t^nD_\varphi S^n\) are valid in \({{\mathcal {L}}}(d(p+))\). \(\square \)
We come to the main result of this section, which should be compared with Proposition 3.2 and Theorem 3.7.
Theorem 4.5
Let \(t\in [0,1)\) and X be any Fréchet space in \(\{\ell (p+), ces(p+),d(p+):\, 1\le p<\infty \}\).
-
(i)
The generalized Cesàro operator \(C_t\in {{\mathcal {L}}}(X)\) is compact.
-
(ii)
The spectra of \(C_t\) are given by
$$\begin{aligned} \sigma _{pt}(C_t;X)=\Lambda \end{aligned}$$(4.10)and
$$\begin{aligned} \sigma ^*(C_t;X)=\sigma (C_t;X)=\Lambda \cup \{0\}. \end{aligned}$$(4.11) -
(iii)
For each \(\lambda \in \sigma _{pt}(C_t;X)\) the subspace \((\lambda I-C_t)(X)\) is closed in X with \(\textrm{codim}\, (\lambda I- C_t)(X)=1\). Moreover, the 1-dimensional eigenspace \(\textrm{Ker}(\frac{1}{m+1}I-C_t)=\textrm{span} (x^{[m]})\), for each \(m\in {{\mathbb {N}}}_0\), with \(x^{[m]}\in d_1\subseteq X\) given by (3.8).
Proof
(i) Since \(D_\varphi \in {{\mathcal {L}}}(X)\) is compact (cf. Proposition 4.3) and \(R_t\in {{\mathcal {L}}}(X)\) (cf. Proposition 4.4(iii)), the compactness of \(C_t\) follows from the factorization \(C_t=D_\varphi R_t\) (cf. Proposition 4.4(iii)) and Lemma 2.3.
(ii) Since \(X\subseteq \omega \), we can conclude from Theorem 3.7 that
Fix \(1\le p<\infty \). Then \(d_1\subseteq \ell ^1\subseteq \ell ^p\subseteq \ell (p+)\). Since \(\ell ^p\subseteq ces(p)\subseteq ces(p+)\) (cf. (1) on p. 2 of [24]), it follows that also \(d_1\subseteq ces(p+)\). Moreover, \(d_1\subseteq d_p\subseteq d(p+)\). So, \(d_1\subseteq X\). Given \(\nu \in \Lambda \) there exists \(m\in {{\mathbb {N}}}_0\) such that \(\nu =\varphi _m\). According to Lemma 3.4 the 1-dimensional eigenspace corresponding to \(\nu \in \sigma _{pt}(C_t;\omega )\) is spanned by \(x^{[m]}\) with \(x^{[m]}\in d_1\). Since \(d_1\subseteq X\), it follows that \(\nu \in \sigma _{pt}(C_t;X)\). So, it has been established that \(\Lambda \subseteq \sigma _{pt}(C_t;X)\). Combined with (4.12) we can conclude that (4.10) is valid.
The spectrum of a compact operator in a lcHs is necessarily a compact subset of \({{\mathbb {C}}}\) (see [27, Theorem 9.10.2], [33, Theorem 4 & Proposition 6]) and it is either a finite set or a countable sequence of non-zero eigenvalues with limit point 0. It follows from part (i) and (4.10) that
The discussion in the first three paragraphs of this section, with the notation from there, shows that \(X=\cap _{k=1}^\infty X_k\) is a Fréchet space of the type given in Lemma 2.5. Setting there \(T:=C_t\in {{\mathcal {L}}}(X)\) and \(T_n:=C_t\in {{\mathcal {L}}}(X_n)\) for \(n\in {{\mathbb {N}}}\) (see Propositions 2.12, 2.14 and 2.15), it is clear that condition (A) is satisfied. Moreover, \(\sigma (T_n;X_n)=\Lambda \cup \{0\}\) for every \(n\in {{\mathbb {N}}}\) (cf. (2.3), (2.5) and (2.7) with \(p_n\) in place of p) and so, via (4.13), we have that
In particular, \(\cup _{n=1}^\infty \sigma (T_n;X_n)\subseteq \overline{\sigma (T;X)}\) and so we can conclude from Lemma 2.5 that (4.11) is valid.
(iii) First observe that \((\nu I-C_t)=\nu (I- \nu ^{-1}C_t)\), for \(\nu \in {{\mathbb {C}}}{\setminus } \{0\}\), with \(\nu ^{-1}C_t\) being a compact operator by part (i). So, by [27, Theorem 9.10.1(i)], the subspace \((\nu I-C_t)(X)\) is closed in X with  for every \(\nu \in \sigma _{pt}(C_t;X)\). But,
for every \(\nu \in \sigma _{pt}(C_t;X)\). But,  for \(\nu \in \sigma _{pt}(C_t;X)\), as observed in the proof of part (ii), where it was also established that \(\textrm{Ker}(\frac{1}{m+1}I -C_t)=\textrm{span}(x^{[m]})\), for each \(m\in {{\mathbb {N}}}_0\). \(\square \)
for \(\nu \in \sigma _{pt}(C_t;X)\), as observed in the proof of part (ii), where it was also established that \(\textrm{Ker}(\frac{1}{m+1}I -C_t)=\textrm{span}(x^{[m]})\), for each \(m\in {{\mathbb {N}}}_0\). \(\square \)
Remark 4.6
(i) The identity (4.10), established in the proof of part (ii) of Theorem 4.5, can also be deduced from Lemma 2.5(ii).
(ii) Let \(t\in [0,1)\) and X be any Fréchet space in \(\{\ell (p+), ces(p+), d(p+)\,:\, 1\le p<\infty \}\). Since \(X\subseteq \omega \) and \(C_t\in {{\mathcal {L}}}(\omega )\) is injective (cf. Lemma 3.6), also \(C_t\in {{\mathcal {L}}}(X)\) is injective. Moreover, as \(C_t\in {{\mathcal {L}}}(X)\) is compact (cf. Theorem 4.5(i)) it cannot be surjective, otherwise it would be an isomorphism thereby implying that \(0\in \rho (C_t;X)\), which is not the case (see (4.11)). Recall that \({\mathcal {E}}\) is a basis for X and, by Lemma 3.1(iii), that the range \(C_t(X)\) is a proper, dense subspace of X. Hence, 0 belongs to the continuous spectrum of \(C_t\). This is in contrast to the situation of \(\omega \), where \(0\in \rho (C_t;\omega )\); see Theorem 3.7.
(iii) Concerning the case when \(t=1\), it is known that \(\sigma _{pt}(C_1;\ell (p+))=\emptyset \) and
for every \(1<p<\infty \), [8, Theorem 2.2]. For \(p=1\), again \(\sigma _{pt}(C_1;\ell (1+))=\emptyset \) whereas
[8, Theorem 2.4]. For the Fréchet space \(ces(p+)\), both (4.14) and (4.15) are also valid (with \(ces(p+)\), resp. with \(ces(1+)\), in place of \(\ell (p+)\), resp. in place of \(\ell (1+)\)), as well as \(\sigma _{pt}(C_1;ces(p+))=\emptyset \) for all \(1\le p<\infty \), [14, Theorem 3]. For the Fréchet space \(d(p+)\), both (4.14) and (4.15) are again valid with \(d(p+)\) (resp. with \(d(1+)\)), in place of \(\ell (p+)\) (resp. of \(\ell (1+)\)), as well as \(\sigma _{pt}(C_1;d(p+))=\emptyset \) for all \(1\le p<\infty \), [21, Theorem 3.2].
5 \(C_t\) acting in the (LB)-spaces \(\ell (p-)\), \(d(p-)\) and \(ces(p-)\)
Given \(1<p\le \infty \), consider any strictly increasing sequence \(\{p_k\}_{k\in {{\mathbb {N}}}}\subseteq (1,p)\) which satisfies \(p_k\uparrow p\). The Banach spaces \(X_k:=\ell ^{p_k}\) satisfy \(X_k\subset X_{k+1}\) with a continuous inclusion, for each \(k\in {{\mathbb {N}}}\), and \(X=\cup _{k=1}^\infty X_k\) is an (LB)-space, necessarily regular by Lemma 2.6. The (LB)-space X is denoted by \(\ell (p-)=\mathrm{ind\,}_k\ell ^{p_k}\). If we set \(X_k:=ces(p_k)\), then again \(X_k\subset X_{k+1}\) for \(k\in {{\mathbb {N}}}\) (see the discussion prior to Proposition 3.3 in [13]) with a continuous inclusion. The (LB)-space \(X:=\cup _{k=1}^\infty X_k\), necessarily regular by Lemma 2.6, is denoted by \(ces(p-):=\mathrm{ind\,}_k ces(p_k)\). Finally, the Banach spaces \(X_k:=d_{p_k}\) satisfy \(X_k\subset X_{k+1}\) with a continuous inclusion, for \(k\in {{\mathbb {N}}}\) (see Propositions 2.7(ii) and 5.1(iii) in [19]). The (LB)-space \(X:=\cup _{k=1}^\infty X_k\), necessarily regular by Lemma 2.6, is denoted by \(d(p-):=\mathrm{ind\,}_k d_{p_k}\). The discussion after (3.7) shows that \(d_1\) is continuously included in each space in \(\{\ell ^p, ces(p), d_p:\,1<p<\infty \}\), from which it follows that \(d_1\subseteq X\) continuously, for each \(X\in \{\ell (p-), ces(p-),d(p-):\, 1<p\le \infty \}\). Indeed, by the definition of the inductive limit topology, \(\ell ^p\subseteq \ell (p-)\) and \(d_p\subseteq d(p-)\) and \(ces(p)\subseteq ces(p-)\) with all inclusions continuous. In all of these (LB)-spaces the canonical vectors \({\mathcal {E}}\) form a Schauder basis. Indeed, concerning \(\ell (p-)\) recall that \({{\mathcal {E}}}\) is a basis for each Banach space \(\ell ^{p_k}\) and the natural inclusion \(\ell ^{p_k}\subseteq \ell (p-)\) is continuous for each \(k\in {{\mathbb {N}}}\). It follows that \({{\mathcal {E}}}\) is a Schauder basis for \(\ell (p-)\). For the (LB)-spaces \(ces(p-)\), resp. \(d(p-)\), see [12, Proposition 2.1], resp. [20, Theorem 4.6]. It follows from [44, Proposition 24.7] together with Lemma 3.1(iv) that \(X\subseteq \omega \) continuously. For further properties of the (LB)-spaces \(\ell (p-)\), \(ces(p-)\) and \(d(p-)\), and operators acting in them, we refer to [12, 20, 21], for example, and the references therein.
For each of the three cases above it is clear that the diagonal (multiplication) operator \(D_\varphi \in {{\mathcal {L}}}(\omega )\) as defined in (4.4) satisfies \(D_\varphi (X_k)\subseteq X_k\) for all \(k\in {{\mathbb {N}}}\) (cf. proof of Proposition 4.3) and so \(D_\varphi (X)\subseteq X\). By Lemma 2.11 it follows that \(D_\varphi \in {{\mathcal {L}}}(X)\). Actually, \(D_\varphi \in {{\mathcal {L}}}(X)\) is a compact operator. For the case \(X=\ell (p-)\), since \(\varphi \in \ell ^2\subseteq \ell (\infty -)\), Proposition 4.5 of [12] implies that \(D_\varphi \in {{\mathcal {L}}}(\ell (p-))\) is compact. Suppose now that \(X:=ces(p-)\). By Proposition 4.2 of [12] it follows that \(D_\varphi \in {{\mathcal {L}}}(ces(p-))\) is compact provided that \({\hat{\varphi }}\in \ell ^t\) for some \(t>q\) (with \(\frac{1}{p}+\frac{1}{q}=1\)). But, it is clear from (3.3) that \({\hat{\varphi }}=\varphi \in \cap _{s>1}\ell ^s\) and so \(D_\varphi \) is a compact operator in \(ces(p-)\). Consider now when \(X:=d(p-)\). Since \({\hat{\varphi }}\in \ell ^2\) and \({\hat{\varphi }}=\varphi \), it follows that \(\varphi \in d_2\subseteq d(\infty -)\) and so Proposition 4.13(ii) of [21] implies that \(D_\varphi \) is a compact operator in \(d(p-)\). So, we have established the following result.
Proposition 5.1
Let X be any (LB)-space in \(\{\ell (p-), ces(p-), d(p-)\,:\, 1<p\le \infty \}\). Then \(D_\varphi \) maps X into itself and \(D_\varphi \in {{\mathcal {L}}}(X)\) is a compact operator.
The following result will also be required.
Proposition 5.2
Let \(t\in [0,1)\) and X be any (LB)-space in \(\{\ell (p-), ces(p-), d(p-)\,:\, 1<p\le \infty \}\).
-
(i)
The right-shift operator S given by (4.5) maps X into X and belongs to \({{\mathcal {L}}}(X)\).
-
(ii)
The generalized Cesàro operator \(C_t\) maps X into X and satisfies \(C_t\in {{\mathcal {L}}}(X)\).
-
(iii)
The operator \(R_t\) given by (4.7) maps X into X and belongs to \({{\mathcal {L}}}(X)\), with the series \(\sum _{n=0}^\infty t^nS^n\) being convergent in \({{\mathcal {L}}}_s(X)\). Moreover,
$$\begin{aligned} C_t=D_\varphi R_t=\sum _{n=0}^\infty t^n D_\varphi S^n. \end{aligned}$$(5.1)
Proof
(i) It was observed in the proof of Proposition 4.4(ii) that \(S\in {{\mathcal {L}}}(\omega )\) as well as \(S(\ell ^{p_k})\subseteq \ell ^{p_k}\) and \(S(ces(p_k))\subseteq ces(p_k)\) and \(S(d_{p_k})\subseteq d_{p_k}\), for each \(k\in {{\mathbb {N}}}\), from which it is clear that \(S(X)\subseteq X\). By Lemma 2.11 it follows that \(S\in {{\mathcal {L}}}(X)\).
(ii) In each of the three cases \(\ell (p-)\), \(ces(p-)\), \(d(p-)\) for X it is clear that \(C_t:\omega \rightarrow \omega \) (cf. (1.1)) satisfies \(C_t(X_k)\subseteq X_k\) for all \(k\in {{\mathbb {N}}}\) (see the proof of Proposition 4.4(i)) and hence, \(C_t(X)\subseteq X\). Since \(C_t\in {{\mathcal {L}}}(\omega )\), via Proposition 3.2, again by Lemma 2.11 we can conclude that \(C_t\in {{\mathcal {L}}}(X)\).
(iii) According to part (i) the sequence \(\{\sum _{n=0}^kt^nS^n\}_{k\in {{\mathbb {N}}}_0}\subseteq {{\mathcal {L}}}(X)\).
Claim. \(\{\sum _{n=0}^kt^nS^n\,:\, k\in {{\mathbb {N}}}_0\}\) is an equicontinuous subset of \({{\mathcal {L}}}(X)\).
Suppose first that \(X=\ell (p-)\) or \(X=ces(p-)\). Since X is barrelled, to establish the Claim it suffices to show, for each \(x\in X\), that
is a bounded subset of \(X=\mathrm{ind\,}_r X_r\). Since X is a regular (LB)-space, the set B(x) will be bounded if there exists \(m\in {{\mathbb {N}}}\) such that \(B(x)\subseteq X_m\) and B(x) is bounded in the Banach space \(X_m\). But, \(x\in X=\cup _{r=1}^\infty X_r\) and so there exists \(m\in {{\mathbb {N}}}\) such that \(x\in X_m\). Since \(S^n\in {{\mathcal {L}}}(X_m)\) for all \(n\in {{\mathbb {N}}}_0\), it is clear that \(B(x)\subseteq X_m\). Moreover, in the proof of Proposition 4.4(ii) it was noted that \(\Vert S\Vert _{X_m\rightarrow X_m}\le 1\) and hence, \(\Vert S^n\Vert _{X_m\rightarrow X_m}\le 1\) for all \(n\in {{\mathbb {N}}}_0\). Accordingly,
which implies that B(x) is a bounded set in \(X_m\). In the event that \(X=d(p-)\), an analogous argument applies except that now \(X_m=d_{p_m}\) and so \(\Vert S^n\Vert _{d_{p_m}\rightarrow d_{p_m}}=(n+1)^{1/p_m}\) for \(n\in {{\mathbb {N}}}_0\); see (4.9). In this case the previous inequality becomes
which implies that B(x) is a bounded set in \(d_{p_m}\) as \(\sum _{n=0}^\infty t^n (n+1)^{1/p_m}<\infty \). The proof of the Claim is thereby complete.
In view of the Claim, to show that the series \(\sum _{n=0}^\infty t^n S^n\) converges in \({{\mathcal {L}}}_s(X)\) it suffices to show that the limit
exists in X for all \(x\in X\) in some dense subset of X. Since \({{\mathcal {E}}}\) is a Schauder basis for X, its linear span \(\textrm{span}\, {{\mathcal {E}}}\) is a dense subspace of X and so it suffices to show that the limit in (5.2) exists for each \(x\in {{\mathcal {E}}}\). Let \(x:=e_r=(0,\ldots , 0,1,0, \ldots )\), for any fixed \(r\in {{\mathbb {N}}}_0\), where 1 is in position r. Then \(S^ne_r=e_{r+n}\) for all \(n\in {{\mathbb {N}}}_0\). Fix \(k\in {{\mathbb {N}}}_0\). It follows that
where 1 is in position r and \(t^k\) is in position \(r+k\). Observe that \(\Vert e_j\Vert _{\ell ^{p_1}}=1\) for \(j\in {{\mathbb {N}}}_0\). Direct calculation via (2.6) shows that \(\Vert e_j\Vert _{d_{p_1}}=(j+1)^{1/p_1}\), for \(j\in {{\mathbb {N}}}_0\), and by Lemma 4.7 in [17], there exists \(K>0\) such that \(\Vert e_j\Vert _{ces(p_1)}\le K\) for all \(j\in {{\mathbb {N}}}_0\). It follows that \(\sum _{j=r}^\infty t^j \Vert e_j\Vert _{\ell ^{p_1}}=\frac{t^r}{(1-t)}\le \frac{1}{(1-t)}\), that \(\sum _{j=r}^\infty t^j \Vert e_j\Vert _{ces(p_1)}\le \frac{Kt^r}{(1-t)}\le \frac{K}{(1-t)}\) and that \(\sum _{j=r}^\infty t^j \Vert e_j\Vert _{d_{p_1}}\le \sum _{j=r}^\infty t^j(j+1)^{1/p_1}<\infty \). Accordingly, the series
with 1 in position r, is absolutely convergent in the Banach space \(X_1\) belonging to \(\{\ell ^{p_1}, ces(p_1), d_{p_1}\}\) and defines an element of \(X_1\), that is, \(y^{[r]}\in X_1\). Since the inclusion \(X_1\subseteq X\) is continuous, the series (5.4) is also convergent to \(y^{[r]}\) in X. For any \(k>r\) we have
being the tail of the absolutely convergent series (5.2). So, the sequence in (5.3) converges to \(y^{[r]}\) in \(X_1\) for \(k\rightarrow \infty \) and hence, also to \(y^{[r]}\) in X. Since \(r\in {{\mathbb {N}}}_0\) is arbitrary, we have proved that the limit in (5.2) exists in X for each \(x\in \textrm{span}\, {{\mathcal {E}}}\) and hence, by the Claim, it exists for every \(x\in X\). Accordingly, the limit operator \(R_t=\lim _{k\rightarrow \infty }\sum _{n=0}^k t^n S^n\) exists in \({{\mathcal {L}}}_s(X)\). Since \(D_\varphi , R_t, C_t\in {{\mathcal {L}}}(X)\) and \(X\subseteq \omega \) continuously, the equality \(C_t=D_\varphi R_t=\sum _{n=0}^\infty t^n D_\varphi S^n\) follows from Proposition 4.2. \(\square \)
The main result of this section is as follows.
Theorem 5.3
Let \(t\in [0,1)\) and X be any (LB)-space in \(\{\ell (p-), ces(p-),d(p-):\, 1<p\le \infty \}\).
-
(i)
The generalized Cesàro operator \(C_t\in {{\mathcal {L}}}(X)\) is compact.
-
(ii)
The spectra of \(C_t\) are given by
$$\begin{aligned} \sigma _{pt}(C_t;X)=\Lambda \end{aligned}$$(5.5)and
$$\begin{aligned} \sigma ^*(C_t;X)=\sigma (C_t;X)=\Lambda \cup \{0\}. \end{aligned}$$(5.6) -
(iii)
For each \(\lambda \in \sigma _{pt}(C_t;X)\) the subspace \((\lambda I-C_t)(X)\) is closed in X with \(\textrm{codim}\, (\lambda I- C_t)(X)=1\). Moreover, the 1-dimensional eigenspace \(\textrm{Ker}(\frac{1}{m+1}I-C_t)=\textrm{span}(x^{[m]})\), for each \(m\in {{\mathbb {N}}}_0\), with \(x^{[m]}\in d_1\subseteq X\) given by (3.8).
Proof
(i) Since \(D_\varphi \in {{\mathcal {L}}}(X)\) is compact (cf. Proposition 5.1) and \(R_t\in {{\mathcal {L}}}(X)\) (cf. Proposition 5.2(iii)), the compactness of \(C_t\in {{\mathcal {L}}}(X)\) follows from the factorization in (5.1) and Lemma 2.3.
(ii) The (LB)-space \(X=\mathrm{ind\,}_k X_k\) is an inductive limit of the type in Lemma 2.10. Moreover, \(T:=C_t\in {{\mathcal {L}}}(X)\) has the property, for each \(k\in {{\mathbb {N}}}\), that the restriction \(T_k\) of T to the Banach space \(X_k\) maps \(X_k\) into itself and satisfies \(T_k\in {{\mathcal {L}}}(X_k)\). That is, T satisfies condition (A\(\prime \)) of Lemma 2.10. Then, by Lemma 2.10(i) it follows that \(\sigma _{pt}(C_t;X)=\cup _{k=1}^\infty \sigma _{pt}(T_k; X_k)=\Lambda \) (cf. Propositions 2.12, 2.14 and 2.15). Since \(C_t\in {{\mathcal {L}}}(X)\) is compact by part (i), the analogous argument used to prove (4.13), now with (4.10) replaced by (5.5), can be used to show that
Moreover, \(\sigma (T_k;X_k)=\sigma (C_t;X_k)=\Lambda \cup \{0\}\) for every \(k\in {{\mathbb {N}}}\) and so, for \(m=1\) say, we note (via (5.7)) that
We can conclude again from Lemma 2.10(ii) that \(\sigma ^*(C_t;X)=\overline{\sigma (C_t;X)}\). Combined with (5.7) this yields (5.6).
(iii) The analogous argument used to prove part (iii) of Theorem 4.5 also applies to establish the given statement. Again, since \(d_1\subseteq X\) (see the introduction to Sect. 5), it follows that \(\textrm{Ker}(\frac{1}{m+1}I-C_t)=\textrm{span}(x^{[m]})\), for each \(m\in {{\mathbb {N}}}_0\). \(\square \)
Remark 5.4
(i) An examination of the arguments given in Remark 4.6 shows that, when suitably adapted, they also apply here to conclude that \(C_t(X)\) is a proper, dense subspace of X. That is, 0 belongs to the continuous spectrum of \(C_t\).
(ii) Concerning \(t=1\), it is known that \(\sigma _{pt}(C_1;ces(p-))=\emptyset \), [12, Proposition 3.1] with
and
[12, Propositions 3.2 and 3.3].
For the (LB)-space \(d(p-)\), both (5.8) and (5.9) are also valid (with \(d(p-)\) in place of \(ces(p-)\)) as well as \(\sigma _{pt}(C_1; d(p-))=\emptyset \), for all \(1<p\le \infty \); see Theorem 3.6 in [21].
The spectrum of \(C_1\) acting in \(\ell (p-)\) is covered by the next result.
Recall that the space \(\ell (p'+)\) is the strong dual of \(\ell (p-)\), [20, Proposition 3.4(i)], and that the dual operator \(C_1'\in {{\mathcal {L}}}(\ell (p'+))\) of \(C_1\in {{\mathcal {L}}}(\ell (p-))\) is given by
see, for instance, [40, p. 123].
Proposition 5.5
Let \(p\in (1,\infty ]\) and let \(p'\in [1,\infty )\) satisfy \(\frac{1}{p}+\frac{1}{p'}=1\).
-
(i)
\(\sigma _{pt}(C_1;\ell (p-))=\emptyset \) and \(\{z\in {{\mathbb {C}}}\,:\, |z-\frac{p'}{2}|<\frac{p'}{2}\}\subseteq \sigma _{pt}(C_1';\ell (p'+))\).
-
(ii)
\(\{0\}\cup \{z\in {{\mathbb {C}}}\,:\, |z-\frac{p'}{2}|<\frac{p'}{2}\}\subseteq \sigma (C_1;\ell (p-))\subseteq \{z\in {{\mathbb {C}}}\,:\, |z-\frac{p'}{2}|\le \frac{p'}{2}\}\).
-
(iii)
\(\sigma ^*(C_1;\ell (p-))=\{z\in {{\mathbb {C}}}\,:\, |z-\frac{p'}{2}|\le \frac{p'}{2}\}=\overline{\sigma (C_1; \ell (p-))}\).
Proof
(i) The first part of (i) follows from Lemma 2.10(i), the definition \(\ell (p-)=\cup _{k=1}^\infty \ell ^{p_k}\) with \(1<p_k\uparrow p\), and the fact that \(\sigma _{pt}(C_1;\ell ^q)=\emptyset \) for every \(1<q<\infty \); see Proposition 2.13(ii).
To establish the second part, fix \(z\in {{\mathbb {C}}}\) with \(|z-\frac{p'}{2}|<\frac{p'}{2}\). Since \(1<p_k\uparrow p\), it follows that \(p'_k\downarrow p'\) and hence, the open disk \(B(\frac{p'}{2},\frac{p'}{2})\subseteq B(\frac{p'_k}{2},\frac{p'_k}{2})\) for every \(k\in {{\mathbb {N}}}\). Accordingly, \(|z-\frac{p'_k}{2}|<\frac{p_k'}{2}\) for all \(k\in {{\mathbb {N}}}\). So, by [40, Theorem 1(b)], for each \(k\ge 1\) there exists \(x_k\in \ell ^{p'_k}{{\setminus }}\{0\}\) such that \(C'_1x_k=z x_k\) with \(x_k=(x_{k,i})_{i\in {{\mathbb {N}}}_0}\) satisfying \(x_{k,i+1}=x_{k,0}\prod _{h=0}^i(1-\frac{1}{z (h+1)})\) for all \(i\in {{\mathbb {N}}}_0\) (see (1) on p. 125 of [40]) for some \(x_{k,0}\in {{\mathbb {C}}}{{\setminus }}\{0\}\). Setting \(x_{k,0}:=1\) for each \(k\in {{\mathbb {N}}}\), it follows that \(x_k=x_{1}=:x\) for all \(k\in {{\mathbb {N}}}\) and hence, \(x\in \cap _{k\in {{\mathbb {N}}}}\ell ^{p'_k}=(\ell (p-))'=\ell (p'+)\). On the other hand, it is clear that \(C_1'x=z x\). This shows the second part of (i).
(ii) To establish the second containment in (ii) we note that an analogous proof as that given for Proposition 3.2 in [12] also applies here. The use of Theorem 3.1 and Lemma 3.1(ii) there needs to be replaced, respectively, with the fact that \(\sigma (C_1;\ell ^q)=\{z\in {{\mathbb {C}}}\,:\, |z-\frac{q'}{2}|\le \frac{q'}{2}\}\) for \(1<q<\infty \) (cf. Proposition 2.13(ii)) and Lemma 2.10(iii).
Concerning the first containment in (ii), observe that \(C_1\) is not surjective on \(\ell (p-)\). Indeed, the element \(y:=(\frac{1-(-1)^{n+1}}{2(n+1)})_{n\in {{\mathbb {N}}}_0}\) belongs to \(\ell ^{p_1}\) with \(\ell ^{p_1}\subseteq \ell (p-)\) and so \(y\in \ell (p-)\). On the other hand, \(x:=C_1^{-1}y=((-1)^n)_{n\in {{\mathbb {N}}}_0}\) belongs to \(\omega \) but, \(x\not \in \ell ^{p_k}\) for every \(k\in {{\mathbb {N}}}\) implies that \(x\not \in \ell (p-)=\cup _{k=1}^\infty \ell ^{p_k}\). Since x is the unique element in \(\omega \) satisfying \(y=C_1x\) (as \(C_1\in {{\mathcal {L}}}(\omega )\) is a bicontinuous isomorphism), it follows that y is not in the range of \(C_1\in {{\mathcal {L}}}(\ell (p-))\) for every \(1<p\le \infty \). In particular, \(0\in \sigma (C_1;\ell (p-))\).
Fix \(\lambda \in {{\mathbb {C}}}{\setminus }\{0\}\). If \(\lambda \in \rho (C_1;\ell (p-))\), then \((\lambda I-C_1)(\ell (p-))=\ell (p-)\). Since \(\ell (p-)\) is dense in \(\ell ^p\), it follows (with the bar denoting the closure in \(\ell ^p\)) that
By Proposition 2.13 we can conclude that \(|\lambda -\frac{p'}{2}|\ge \frac{p'}{2}\). Accordingly, \(|\lambda -\frac{p'}{2}|<\frac{p'}{2}\) implies that \(\lambda \in \sigma (C_1;\ell (p-))\).
(iii) An analogous argument used for the proof of Propostion 3.3 in [12] also applies here. One only needs to replace the use of Proposition 3.2 and Theorem 3.1 there by part (ii) above and Proposition 2.13, respectively. \(\square \)
6 Dynamics of the generalized Cesàro operators \(C_t\)
The aim of this section is to investigate the mean ergodicity and linear dynamics of the operator \(C_t\), for \(t\in [0,1]\), in \(\omega \), in the Fréchet spaces \(\{\ell (p+), ces(p+), d(p+):\, 1\le p<\infty \}\) and in the (LB)-spaces \(\{\ell (p-), ces(p-), d(p-):\, 1<p\le \infty \}\). For the Banach spaces \(\ell ^1\), \(d_1\) and \(\ell ^p\), ces(p), \(d_p\), for \(1<p<\infty \), these results are also new. We also study the compactness, spectra and linear dynamics of the dual operators \(C_t'\).
An operator \(T\in {{\mathcal {L}}}(X)\), with X a lcHs, is called power bounded if \(\{T^n:\, n\in {{\mathbb {N}}}\}\) is an equicontinuous subset of \({{\mathcal {L}}}(X)\). Here \(T^n:= T \circ ...\circ T\) is the composition of T with itself n times. For a Banach space X, this means precisely that \(\sup _{n\in {{\mathbb {N}}}}\Vert T^n\Vert _{X\rightarrow X}<\infty \). Given \(T\in {{\mathcal {L}}}(X)\), its sequence of averages
is called the Cesàro means of T. The operator T is said to be mean ergodic (resp., uniformly mean ergodic) if \((T_{[n]})_{n\in {{\mathbb {N}}}}\) is a convergent sequence in \({{\mathcal {L}}}_s(X)\) (resp., in \({{\mathcal {L}}}_b(X)\)). It follows from (6.1) that
for \(n\ge 2\). Hence, necessarily \(\frac{T^n}{n}\rightarrow 0\) in \({{\mathcal {L}}}_s(X)\) (resp., in \({{\mathcal {L}}}_b(X)\)) as \(n\rightarrow \infty \), whenever T is mean ergodic (resp., uniformly mean ergodic). A relevant text is [39].
Concerning the dynamics of a continuous linear operator T defined on a separable lcHs X, recall that T is said to be hypercyclic if there exists \(x\in X\) whose orbit \(\{T^nx:\, n\in {{\mathbb {N}}}_0\}\) is dense in X. If, for some \(x\in X\), the projective orbit \(\{\lambda T^nx:\, \lambda \in {{\mathbb {C}}},\ n\in {{\mathbb {N}}}_0\}\) is dense in X, then T is called supercyclic. Clearly, any hypercyclic operator is also supercyclic. As general references, we refer to [16, 32].
We begin with a study of the dynamics of generalized Cesàro operators acting in \(\omega \). For this, we will require, for each fixed \(n\in {{\mathbb {N}}}_0\), the combinatorial identity
For the proof we proceed by induction on \(i=0,\ldots ,n\). For \(i=0\) observe that
Assume that (6.2) is valid for some \(0\le i<n\). For \(i+1\) it follows that
Since this is identity (6.2) for \(i+1\), the proof is complete.
Theorem 6.1
Let \(t\in [0,1)\) and \(x^{[0]}:=\alpha _0(t^n)_{n\in {{\mathbb {N}}}_0}\) with \(\alpha _0\in {{\mathbb {C}}}{\setminus }\{0\}\); see (3.8).
-
(i)
The generalized Cesàro operator \(C_t\in {{\mathcal {L}}}(\omega )\) is power bounded and uniformly mean ergodic.
-
(ii)
\(\textrm{Ker}(I-C_t)=\textrm{span}\,\{x^{[0]}\}\) and the range
$$\begin{aligned} (I-C_t)(\omega )=\{x\in \omega :\, x_0=0\}=\overline{\textrm{span}\,\{e_r:\, r\in {{\mathbb {N}}}\}} \end{aligned}$$(6.3)of \((I-C_t)\) is closed in \(\omega \).
-
(iii)
The operator \(C_t\) is not supercyclic in \(\omega \).
Proof
(i) That \(C_t\) is power bounded follows from the barrelledness of \(\omega \) and \(r_n(C_tx)\le r_n(x)\), for \(x\in \omega \) and \(n\in {{\mathbb {N}}}_0\) (cf. (3.4)), which implies, for every \(x\in \omega \), that
Since \(\omega \) is Montel, \(C_t\) is uniformly mean ergodic, [3, Proposition 2.8].
(ii) By part (i) and [5, Theorem 3.5] we can conclude that \((I-C_t)(\omega )\) is closed in \(\omega \) and that
Moreover, Lemma 3.4(i) yields that \(\textrm{Ker}(I-C_t)=\textrm{span}\{x^{[0]}\}\). Since \((C_tx)_0=x_0\) for each \(x\in \omega \) (cf. (1.1)), we have \((I-C_t)(\omega )\subseteq \{x\in \omega :\, x_0=0\}=\overline{\textrm{span}\,\{e_r:\, r\in {{\mathbb {N}}}\}}\). In order to establish (6.3), it remains to show that \(e_r\in (I-C_t)(\omega )\) for each \(r\ge 1\). Observe, via Lemma 3.1(iii), that
Arguing by induction and using (6.5) we can conclude that \(e_r\in (I-C_t)(\omega )\) for each \(r\ge 1\). Indeed, if \(n=0\), then (6.5) yields \((I-C_t)(e_0-te_1)=-te_1\) and hence, \(e_1\in (I-C_t)(\omega )\). Suppose that \(e_n\in (I-C_t)(\omega )\). Then (6.5) implies that \(\frac{n}{n+1}e_n-te_{n+1}= (I-C_t)(e_n-te_{n+1})\in (I-C_t)(\omega )\). Since \(e_n\in (I-C_t)(\omega )\), by the induction hypothesis, it follows that \(e_{n+1}\in (I-C_t)(\omega )\). This completes the proof of (6.3).
(iii) To verify that \(C_t\in {{\mathcal {L}}}(\omega )\) is not supercyclic we proceed as follows. It follows from (6.4), by a duality argument, that \((\omega )'_\beta = \textrm{Ker}(I-C'_t)\oplus (I-C'_t)((\omega )'_\beta )\) and that  , where \(C'_t\in {{\mathcal {L}}}((\omega )'_\beta )\) is the dual operator of \(C_t\). Accordingly, \(1\in \sigma _{pt}(C_t';(\omega )'_\beta )\). On the other hand, a direct calculation shows that the dual operator \(C'_t\in {{\mathcal {L}}}((\omega )'_\beta )\) is given by the transpose matrix of (3.2), that is,
, where \(C'_t\in {{\mathcal {L}}}((\omega )'_\beta )\) is the dual operator of \(C_t\). Accordingly, \(1\in \sigma _{pt}(C_t';(\omega )'_\beta )\). On the other hand, a direct calculation shows that the dual operator \(C'_t\in {{\mathcal {L}}}((\omega )'_\beta )\) is given by the transpose matrix of (3.2), that is,
Recall that \((\omega )'_\beta \) consists of vectors \(z=(z_n)_{n\in {{\mathbb {N}}}_0}\in {{\mathbb {C}}}^{{{\mathbb {N}}}_0}\) with only finitely many non-zero coordinates. Define
It is shown below that
This reveals that \(\Lambda =\{\frac{1}{n+1}:\, n\in {{\mathbb {N}}}_0\}\subseteq \sigma _{pt}(C_t'; (\omega )_\beta ')\). Since \(\sigma (C_t; \omega )=\sigma _{pt}(C_t;\omega )=\Lambda \) (cf. Theorem 3.7), it follows via (2.1) in Corollary 2.2 that also \(\sigma _{pt}(C_t'; (\omega )'_\beta )\subseteq \sigma (C_t'; (\omega )'_\beta )=\Lambda \). So,
In particular, \(C'_t\) has a plenty of eigenvalues which implies that \(C_t\) cannot be supercyclic, [16, Proposition 1.26].
It remains to establish (6.7). Note, for \(n\in {{\mathbb {N}}}_0\) fixed, that \((z^{[n]})_i=0\) if \(i>n\) and \((z^{[n]})_{n-i}=(-1)^i\left( {\begin{array}{c}n\\ i\end{array}}\right) t^i\) for \(i=0,\ldots ,n\). In particular, \(z^{[n]}\in (\omega )'_\beta {\setminus }\{0\}\). For \(i>n\) it is clear that
To verify that \((C'_tz^{[n]})_{n-i}=\frac{1}{n+1}(z^{[n]})_{n-i}\) for \(i=0,\ldots , n\) observe that
where the last equality follows from (6.2). But, as noted above, \((-1)^i\left( {\begin{array}{c}n\\ i\end{array}}\right) t^i=(z^{[n]})_{n-i}\) and so \((C_t'z^{[n]})_{n-i}=\frac{1}{n+1}(z^{[n]})_{n-i}\) for \(i=0,\ldots , n\). The identity (6.7) is thereby established and the proof is complete. \(\square \)
We now turn to the dynamics of generalized Cesàro operators \(C_t\) acting in the other sequence spaces considered in this paper, for which we first need to establish some general results on bounded linear operators acting in lcHs’. Recall that a linear operator \(T:X\rightarrow Y\), with X, Y lcHs’, is said to be bounded if there exists a neighbourhood \({{\mathcal {U}}}\) of \(0\in X\) such that \(T({{\mathcal {U}}})\) is a bounded subset of Y. It is routine to verify that necessarily \(T\in {{\mathcal {L}}}(X,Y)\). A lcHs X is called locally complete if, for each closed, absolutely convex subset \(B\in {{\mathcal {B}}}(X)\), the space \(X_B:=\textrm{span}\, (B)\) equipped with the Minkowski functional \(\Vert \cdot \Vert _B\), [44, p. 47], is a Banach space, whose closed unit ball is B. Such a set B is also called a Banach disc, [36, Sect. 8.3].
Theorem 6.2
Let X be a locally complete lcHs and \(T\in {{\mathcal {L}}}(X)\) be a bounded operator satisfying \(\sigma (T;X)\subseteq \overline{B(0,\delta )}\) for some \(\delta \in (0,1)\). Then \(T^n\rightarrow 0\) in \({{\mathcal {L}}}_b(X)\) as \(n\rightarrow \infty \). In particular, T is both power bounded and uniformly mean ergodic.
Proof
Since T is a bounded operator, there exists a closed, absolutely convex neighbourhood \({{\mathcal {U}}}\) of \(0\in X\) such that \(T({{\mathcal {U}}})\in {{\mathcal {B}}}(X)\). So, we can select a closed, absolutely convex subset \(B\in {{\mathcal {B}}}(X)\) such that \(T({{\mathcal {U}}})\subseteq B\). By the assumptions, \((X_B, \Vert \cdot \Vert _B)\) is a Banach space. Since \(T({{\mathcal {U}}})\subseteq B\), the map \(S:X\rightarrow X_B\) defined by \(Sx:=Tx\) for \(x\in X\), is well defined and it is clearly continuous. Let \(j:X_B\rightarrow X\) denote the canonical inclusion of \(X_B\) into X, i.e., \(j(x):=x\) for \(x\in X_B\). Then \(j\in {{\mathcal {L}}}(X_B, X)\) and \(T=jS\in {{\mathcal {L}}}(X)\). On the other hand \(Sj\in {{\mathcal {L}}}(X_B)\). So, by [33, Proposition 5, p. 199] we have that
Accordingly, \(\sigma (Sj;X_B)=\sigma (T;X)\subseteq \overline{B(0,\delta )}\). This implies that the spectral radius r(Sj) of Sj satisfies \(r(Sj)\le \delta <1\). Since \(r(Sj)=\lim _{n\rightarrow \infty }\left( \Vert (Sj)^n\Vert _{X_B\rightarrow X_B}\right) ^{1/n}\), it follows via standard arguments that \((Sj)^n\rightarrow 0\) in \({{\mathcal {L}}}_b(X_B)\) as \(n\rightarrow \infty \). The claim is that this implies \(T^n\rightarrow 0\) in \({{\mathcal {L}}}_b(X)\) as \(n\rightarrow \infty \). To establish the claim, fix any \(C\in {{\mathcal {B}}}(X)\) and any absolutely convex neighbourhood \({{\mathcal {V}}}\) of \(0\in X\). Then there exist \(\lambda >0\) such that \(C\subseteq \lambda {{\mathcal {U}}}\) and \(\mu >0\) such that \(B\subseteq \mu {{\mathcal {V}}}\). Since B is the unit closed ball of \(X_B\) and \((Sj)^n\rightarrow 0\) in \({{\mathcal {L}}}_b(X_B)\), there exists \(n_0\in {{\mathbb {N}}}\) such that \((Sj)^n(B)\subseteq \frac{1}{\lambda \mu }B\) for all \(n\ge n_0\). So, for each \(n> n_0\), it follows that
This means, with \(W(C,{{\mathcal {V}}}):=\{R\in {{\mathcal {L}}}(X):\, R(C)\subseteq {{\mathcal {V}}}\}\), that \(T^n\in W(C,{{\mathcal {V}}})\) for each \(n>n_0\). Since \(C\in {{\mathcal {B}}}(X)\) and \({{\mathcal {V}}}\) are arbitrary and the sets \(W(C,{{\mathcal {V}}})\) form a basis of neighbourhoods for 0 in \({{\mathcal {L}}}_b(X)\), the claim is proved, i.e., \(T^n\rightarrow 0\) in \({{\mathcal {L}}}_b(X)\) as \(n\rightarrow \infty \). It follows that T is power bounded (clearly) and that \(T_{[n]}\rightarrow 0\) in \({{\mathcal {L}}}_b(X)\) as \(n\rightarrow \infty \) (i.e., T is uniformly mean ergodic). Indeed, let q be any \(\tau _b\)-continuous seminorm. Then (6.1) implies that \(q(T_{[n]})\le \frac{1}{n}\sum _{m=1}^nq(T^m)\) for \(n\in {{\mathbb {N}}}\). Since \(q(T^n)\rightarrow 0\) in \([0,\infty )\), also its arithmetic means \(\frac{1}{n}\sum _{m=1}^nq(T^m)\rightarrow 0\) for \(n\rightarrow \infty \), that is, \(\lim _{n\rightarrow \infty }q(T_{[n]})=0\). So, we can conclude that \(T_{[n]}\rightarrow 0\) in \({{\mathcal {L}}}_b(X)\) for \(n\rightarrow \infty \). \(\square \)
Theorem 6.2 permits us to formulate and prove the following general criterion for power boundedness and uniform mean ergodicity. To state it, recall that a lcHs X is said to be ultrabornological if it is an inductive limit of Banach spaces, [36, Sect. 13.1], [44, p. 283]. For instance, Fréchet spaces, [36, Corollary 13.1.4], and (LB)-spaces are ultrabornological. A lcHs X is called a webbed space if a web can be defined on X. For the definition of a web and the properties of webbed spaces we refer to [36, Sect. 5.2] and [38, Ch. 2.4]. Recall from Sect. 2 that Fréchet spaces and (LB)-spaces are webbed spaces. Moreover, sequentially closed subspaces and quotients of webbed spaces are webbed spaces, [36, Theorem 5.3.1].
For what follows we require the next result concerning algebraic sums in ultrabornological lcHs’ which can be found in [38, Sect. 35.5(4), p. 66].
Proposition 6.3
Let X be an ultrabornological lcHs such that \(X=X_1\oplus X_2\) algebraically with both \(X_1, X_2\subseteq X\) webbed spaces for the topology induced by X. Then \(X_1\) and \(X_2\) are closed subspaces of X and \(X=X_1\oplus X_2\) topologically, i.e., the canonical projections \(P_i:X\rightarrow X_i\) are continuous for \(i=1,2\).
In general compact operators need not be mean ergodic. Just consider \(T=\alpha I\) with \(|\alpha |>1\) in a finite dimensional space.
Theorem 6.4
Let X be a locally complete, webbed and ultrabornological lcHs. Let \(T\in {{\mathcal {L}}}(X)\) be a compact operator such that \(1\in \sigma (T;X)\) with \(\sigma (T;X){\setminus }\{1\}\subseteq \overline{B(0,\delta )}\) for some \(\delta \in (0,1)\) and satisfying \(\textrm{Ker}(I-T)\cap (I-T)(X)=\{0\}\). Then T is both power bounded and uniformly mean ergodic.
Proof
Since \(T\in {{\mathcal {L}}}(X)\) is a compact operator, the following properties hold true: (a) \((I-T)(X)\) is closed in X, (b)  (1 is necessarily an eigenvalue of T as it is an isolated point of \(\sigma (T;X)\) and T is compact), and (c) \(\textrm{codim}\, (I-T)(X)=\textrm{dim}\, \textrm{Ker}(I-T)<\infty \), see, e.g., [27, Theorem 9.10.1]. Since \(\textrm{Ker}(I-T)\cap (I-T)(X)=\{0\}\) by assumption, it follows that \(X=\textrm{Ker}(I-T)\oplus (I-T)(X)\) algebraically. Moreover, \((I-T)(X)\) and \(\textrm{Ker}(I-T)\) are closed complemented subspaces of X and hence, are webbed spaces, [36, Theorem 5.3.1]. So, we can apply Proposition 6.3 to conclude that \(X=\textrm{Ker}(I-T)\oplus (I-T)(X)\) holds topologically.
(1 is necessarily an eigenvalue of T as it is an isolated point of \(\sigma (T;X)\) and T is compact), and (c) \(\textrm{codim}\, (I-T)(X)=\textrm{dim}\, \textrm{Ker}(I-T)<\infty \), see, e.g., [27, Theorem 9.10.1]. Since \(\textrm{Ker}(I-T)\cap (I-T)(X)=\{0\}\) by assumption, it follows that \(X=\textrm{Ker}(I-T)\oplus (I-T)(X)\) algebraically. Moreover, \((I-T)(X)\) and \(\textrm{Ker}(I-T)\) are closed complemented subspaces of X and hence, are webbed spaces, [36, Theorem 5.3.1]. So, we can apply Proposition 6.3 to conclude that \(X=\textrm{Ker}(I-T)\oplus (I-T)(X)\) holds topologically.
Set \(Y:=(I-T)(X)\) and \(S:=T|_Y\). It is routine to verify that \(S(Y)\subseteq Y\) and \(S:Y\rightarrow Y\) is a compact operator. So, \(\sigma (S;Y){{\setminus }}\{0\} =\sigma _{pt}(S;Y)\subseteq \sigma _{pt}(T;X)\subseteq \sigma (T;X)\). But, \(1\not \in \sigma (S;Y)\). Otherwise, there exists \(y\in Y{{\setminus }}\{0\}\) such that \(Sy=y\), i.e., \(Ty=y\) or, equivalently, \((I-T)y=0\). Thus, \(y\in Y\cap \textrm{Ker}(I-T)=(I-T)(X)\cap \textrm{Ker}(I-T)=\{0\}\) and hence, \(y=0\); a contradiction. Hence, \(\sigma (S;Y) \subseteq \sigma (T;X){\setminus }\{1\}\subseteq \overline{B(0,\delta )}\) with \(\delta \in (0,1)\). Since S is compact, it is also bounded and hence, we can apply Theorem 6.2 to conclude that \(S^n\rightarrow 0\) in \({{\mathcal {L}}}_b(Y)\) as \(n\rightarrow \infty \), after noting that the closed subspace Y of X is locally complete.
Denote by \(P:X\rightarrow X\) the continuous projection onto \(\textrm{Ker}(I-T)\) along \((I-T)(X)=Y\), i.e., for each \(z\in X\) there exist unique elements \(x\in \textrm{Ker}(I-T)\) and \(y\in Y\) such that \(z=x+y\) and so \(Pz:=x\). The claim is that \(T^n\rightarrow P\) in \({{\mathcal {L}}}_b(X)\) as \(n\rightarrow \infty \). To establish this fix \(B\in {{\mathcal {B}}}(X)\) and a neighbourhood \({{\mathcal {U}}}\) of \(0\in X\). As \((I-P)\in {{\mathcal {L}}}(X)\), we have that \((I-P)(B)\in {{\mathcal {B}}}(Y)\). Taking into account that \(S^n\rightarrow 0\) in \({{\mathcal {L}}}_b(Y)\) as \(n\rightarrow \infty \), there exists \(n_0\in {{\mathbb {N}}}\) such that \(S^n((I-P)(B))\subseteq {{\mathcal {U}}}\cap Y\) for every \(n\ge n_0\). On the other hand, for each \(z\in X\) we have that \(Pz\in \textrm{Ker}(I-T)\), i.e., \(TPz=Pz\), and hence, \(T^n(Pz)=Pz\) for each \(n\in {{\mathbb {N}}}\). Accordingly, as \(S=T\) on \((I-P)(X)=(I-T)(X)=Y\) we get, for each \(z\in B\) and \(n\ge n_0\), that
where we used the fact that \((I-P)z\in Y\). Since \(z\in B\) is arbitrary, this implies that \(T^n-P\in W(B,{{\mathcal {U}}}):=\{R\in {{\mathcal {L}}}(X):\, R(B)\subseteq {{\mathcal {U}}}\}\) for each \(n\ge n_0\). So, by the arbitrariness of B and \({{\mathcal {U}}}\), the claim is proved. \(\square \)
Remark 6.5
(i) Let X be a sequentially complete lcHs and \(T\in {{\mathcal {L}}}(X)\). If \(\frac{T^n}{n}\rightarrow 0\) in \({{\mathcal {L}}}_s(X)\) as \(n\rightarrow \infty \), then \(\sigma (T;X)\subseteq \overline{B(0,1)}\), [2, Proposition 5.1 & Remark 5.3]; see also [28, Proposition 4.4]. In particular, if T is power bounded, then \(\sigma (T;X)\subseteq \overline{B(0,1)}\). In view of this fact, Theorem 6.4 can be seen as a sort of converse result (observe that every sequentially complete lcHs is locally complete, [44, Corollary 23.14]).
(ii) Theorem 6.2 should also be compared with [6, Theorem 10] in which it is proved, for \(T\in {{\mathcal {L}}}(X)\) with X a prequojection Fréchet space, that \(T^n\rightarrow 0\) in \({{\mathcal {L}}}_b(X)\) as \(n\rightarrow \infty \) if, and only if, \(\sigma (T;X)\subseteq B(0,1)\) and \(\frac{T^n}{n}\rightarrow 0\) in \({{\mathcal {L}}}_b(X)\). Since \(\sigma (C_t;\omega )\not \subseteq B(0,1)\) (as \(1\in \sigma (C_t;\omega )\) but \(1\not \in {B(0,1)}\)) and \(\omega \) is a prequojection Fréchet space, for each \(t\in [0,1)\), it follows that \((C_t)^n\not \rightarrow 0\) in \({{\mathcal {L}}}_b(\omega )\) for \(n\rightarrow \infty \).
Combining Theorem 6.4 with the results in the preceding sections we get the following result.
Theorem 6.6
Let \(t\in [0,1)\). Let X belong to any one of the sets: \(\{d_p,\ell ^p:\, 1\le p<\infty \}\cup \{ces(p):\, 1<p<\infty \}\) or \(\{\ell (p+), ces(p+), d(p+):\, 1\le p<\infty \}\) or \(\{\ell (p-), ces(p-), d(p-):\, 1< p\le \infty \}\). Then \(C_t\in {{\mathcal {L}}}(X)\) is power bounded and uniformly mean ergodic, but not supercyclic.
Proof
From the results of the preceding sections recall that \(C_t\in {{\mathcal {L}}}(X)\) is a compact operator on X and \(\sigma (C_t;X)=\Lambda \cup \{0\}\). Hence, \(\sigma (C_t;X){\setminus }\{1\}\subseteq \overline{B(0,1/2)}\). Moreover, \((I-C_t)(X)\) is also closed in X. Since \(x^{[0]}\in d_1\subseteq X\), we can adapt the arguments in the proof of Theorem 6.1 to argue that \((I-C_t)(X)=\{x\in X:\, x_0=0\}=\overline{\textrm{span}\{e_r:\, r\in {{\mathbb {N}}}\}}\) and \(\textrm{Ker}(I-C_t)=\textrm{span}\, \{x^{[0]}\}\). Hence, \(\textrm{Ker}(I-C_t)\cap (I-C_t)(X)=\{0\}\). So, all the assumptions of Theorem 6.4 (for \(\delta =\frac{1}{2}\) and \(T:=C_t\)) are satisfied. Then we can conclude that \(C_t\) is power bounded and uniformly mean ergodic.
To show that \(C_t:X\rightarrow X\) is not supercyclic we proceed as follows. Since \(C_t\in {{\mathcal {L}}}(X)\) is compact, the operators \(C_t:X\rightarrow X\) and \(C'_t:X'_\beta \rightarrow X'_\beta \) have the same non-zero eigenvalues, [27, Theorem 9.10.2(2)]. Hence, \(\sigma _{pt}(C'_t;X'_\beta )=\sigma _{pt}(C_t;X)=\Lambda \). According to [16, Proposition 1.26] it follows that the operator \(C_t:X\rightarrow X\) cannot be supercyclic. \(\square \)
A first consequence of the results collected above is the following one concerning the dual operators \(C'_t\). First we recall the relevant dual spaces involved. Namely, for \(p, p'\) satisfying \(\frac{1}{p}+\frac{1}{p'}=1\) we have (see Proposition 3.4(i), Proposition 4.3 and Remark 4.4 in [20], respectively):
\(\ell (p-)\simeq (\ell (p'+))'_\beta \) and \((\ell (p-))'_\beta \simeq \ell (p'+)\), for \(1<p\le \infty \);
\(d(p-)\simeq (ces(p'+))'_\beta \) and \((ces(p-))'_\beta \simeq d(p'+)\), for \(1< p\le \infty \);
\(ces(p-)\simeq (d(p'+))'_\beta \) and \(ces(p'+)\simeq (d(p-))'_\beta \), for \(1<p\le \infty \).
Proposition 6.7
Let \(t\in [0,1)\) and X belong to any one of the sets: \(\{d_p,\ell ^p:\, 1\le p<\infty \}\cup \{ces(p):\, 1<p<\infty \}\) or \(\{\ell (p+), ces(p+), d(p+):\, 1\le p<\infty \}\) or \(\{\ell (p-), ces(p-), d(p-):\, 1<p\le \infty \}\).
-
(i)
The dual operator \(C'_t\in {{\mathcal {L}}}(X'_\beta )\) of \(C_t\in {{\mathcal {L}}}(X)\) is compact and is given by
$$\begin{aligned} C'_ty=\left( \sum _{k=i}^\infty \frac{t^{k-i}}{k+1}y_k\right) _{i\in {{\mathbb {N}}}_0},\quad y=(y_k)_{k\in {{\mathbb {N}}}_0}\in X'_\beta . \end{aligned}$$(6.8) -
(ii)
The point spectrum of \(C'_t\in {{\mathcal {L}}}(X'_\beta )\) is given by
$$\begin{aligned} \sigma _{pt}(C'_t;X'_\beta )=\sigma _{pt}(C_t;X)=\Lambda . \end{aligned}$$(6.9)
Each eigenvalue \(\frac{1}{n+1}\), for \(n\in {{\mathbb {N}}}_0\), is simple and its corresponding eigenspace is spanned by
Moreover,
Proof
(i) Recall that \({{\mathcal {E}}}\) is an unconditional basis in \(\ell (p+), ces(p+), d(p+)\), for \(1\le p<\infty \) (cf. Section 4) and an unconditional basis in \(\ell (p-)\), \(ces(p-)\), \(d(p-)\), for \(1<p\le \infty \) (cf. Section 5). Moreover, \({{\mathcal {E}}}\) is also an unconditional basis in the dual Banach spaces \((\ell ^p)'=\ell ^{p'}\) for \(1<p<\infty \), in the dual Banach spaces \((ces(p))'\simeq d_{p'}\) for \(1<p<\infty \), [19], and in the dual Banach spaces \((d_p)'\simeq ces(p')\) for \(1<p<\infty \) (cf. [17, 24]), as well as in \((d_1)'\simeq ces(0)\), [25, Sect. 6]. In view of the description of \(X'_\beta \) (for X non-normable) given prior to this Proposition it follows, for all \(X\not =\ell ^1\), that the linear space \(\text{ span }({{\mathcal {E}}})=(\omega )'\) is dense in \(X'_\beta \). The continuity of \(C'_t:X'_\beta \rightarrow X'_\beta \) then implies that (6.6) can be extended to an inequality for every \(y\in X'_\beta \), that is, (6.8) is valid.
For \(X=\ell ^1\), the linear space \(\text{ span }({{\mathcal {E}}})=(\omega )'\) is not dense in \(X'_\beta =\ell ^\infty \). So, in this case we argue as follows. Define \(Ty:=\left( \sum _{k=i}^\infty \frac{t^{k-i}}{k+1}y_k\right) _{i\in {{\mathbb {N}}}_0}\) for \(y\in \ell ^\infty \), in which case \(T\in {{\mathcal {L}}}(\ell ^\infty )\). Indeed, for \(y\in \ell ^\infty \), note that
Accordingly, \(\Vert T\Vert _{\ell ^\infty \rightarrow \ell ^\infty }\le \frac{1}{1-t}\), that is, \(T\in {{\mathcal {L}}}(\ell ^\infty )\). For each \(x\in \ell ^1\) and \(y\in \ell ^\infty \), a direct calculation yields
which implies that \(T=C'_t\).
For any Fréchet space \(X\in \{\ell (p+), ces(p+), d(p+)\,:\, 1\le p<\infty \}\) and any Banach space \(X\in \{\ell ^1, d_1\}\cup \{\ell ^p, ces(p), d_p\,:\, 1<p<\infty \}\) the operator \(C_t\in {{\mathcal {L}}}(X)\) is compact (cf. Propositions 2.12, 2.14, 2.15 and Remark 3.3 and Theorem 4.5(i)). Accordingly, the dual operator \(C'_t\in {{\mathcal {L}}}(X'_\beta )\) of \(C_t\in {{\mathcal {L}}}(X)\) is compact, [27, Corollary 9.6.3].
For any (LB)-space \(X\in \{\ell (p-), ces(p-), d(p-)\,:\, 1<p\le \infty \}\) the operator \(C_t\in {{\mathcal {L}}}(X)\) is also compact (cf. Theorem 5.3(i)). So, the compactness of \(C_t'\in {{\mathcal {L}}}(X'_\beta )\) follows from Proposition 2.7, after observing that X is a boundedly retractive (LB)-space. Indeed, \(X=\ell (p-)\), for \(1<p\le \infty \), is a boundedly retractive (LB)-space, as it is the strong dual of the quasinormable Fréchet space \(\ell (p'+)\), [45, p. 12]. On the other hand, \(X\in \{ces(p-), d(p-):\, 1<p\le \infty \}\) is a boundedly retractive (LB)-space, as it is a (DFS)-space, [20, Proposition 2.5(ii) & Lemma 4.2(i)].
(ii) It was shown in the proof of Theorem 6.1 that each vector \(z^{[n]}\in (\omega )'_\beta {\setminus }\{0\}\subseteq X'_\beta \) satisfies \(C'_tz^{[n]}=\frac{1}{n+1}z^{[n]}\), for every \(n\in {{\mathbb {N}}}_0\). Accordingly.
Moreover, \(0\not \in \ \sigma _{pt}(C'_t;X'_\beta )\) as \(C'_t\) is injective. To verify this let \(z\in X'_\beta \) satisfy \(C'_tz=0\). By considering the individual coordinates in (6.8) it follows that
that is, \(z=0\) and so indeed \(0\not \in \ \sigma _{pt}(C'_t;X'_\beta )\). The compactness of \(C'_t\in {{\mathcal {L}}}(X'_\beta )\) then implies that
It follows from (2.1) in Corollary 2.2 (with \(T:=C_t\)), from (6.11) and from the fact that \(\sigma _{pt}(C_t;X)=\Lambda \), that (6.9) is valid.
Parts (1) and (2) of [27, Proposition 9.10.2] imply that each eigenvalue of \(C'_t\) is simple, as this is the case for \(C_t\); see Propositions 2.12, 2.14, 2.15 and Remark 3.3 and Theorems 4.5, 5.3, which also include the identities
Setting \(T:=C_t\) it follows from (2.2) in Corollary 2.2, together with (6.12), that
From general theory (cf. Section 2) we also have that
Since (6.9) and (6.11) imply that \(\sigma (C_t';X'_\beta )=\Lambda \cup \{0\}\), we can conclude that
This, together with (6.12), yields \(\sigma ^*(C_t';X'_\beta )=\sigma ^*(C_t;X)= \Lambda \cup \{0\}\). \(\square \)
A consequence of Theorem 6.6 is the next result.
Proposition 6.8
Let \(t\in [0,1)\). Let X belong to any one of the sets: \(\{d_p, \ell ^p\,:\, 1\le p<\infty \}\cup \{ces(p)\,:\, 1<p<\infty \}\) or \(\{\ell (p+), ces(p+), d(p+):\, 1\le p<\infty \}\) or \(\{\ell (p-), ces(p-), d(p-)\,:\, 1<p\le \infty \}\). Then \(C_t'\in {{\mathcal {L}}}(X_\beta ')\) is power bounded and uniformly mean ergodic, but not supercyclic.
Proof
By Theorem 6.6 the operator \(C_t\in {{\mathcal {L}}}(X)\) is power bounded. Since \((C_t')^n=(C_t^n)'\), for every \(n\in {{\mathbb {N}}}_0\), it follows from [38, Sect. 39.3(6)] that also \(C'_t\in {{\mathcal {L}}}(X'_\beta )\) is power bounded. The operator \(C_t\in {{\mathcal {L}}}(X)\) is also uniformly mean ergodic in X, again by Theorem 6.6. Since X is barrelled (hence, quasi-barrelled), Lemma 2.1 in [4] implies that \(C'_t\) is uniformly mean ergodic in \(X'_\beta \). If \(X\not \in \{\ell ^1, d_1\}\), then \(X'_\beta \) is reflexive with \((X'_\beta )'_\beta =X\) (cf. the proof of Proposition 6.7) and hence, \((C'_t)'=C_t\). It follows from (6.9) that \(C''_t=C_t\) has plenty of eigenvalues so that \(C_t'\in {{\mathcal {L}}}(X'_\beta )\) cannot be supercyclic [16, Proposition 1.26]. Finally, suppose that \(X\in \{\ell ^1, d_1\}\). Since \(C_t\) is compact with \(\sigma _{pt}(C_t; X)=\Lambda \) (cf. Proposition 2.12 and Remark 3.3), it follows that \(\sigma _{pt}(C'_t;X'_\beta )=\sigma _{pt}(C_t; X)=\Lambda \); see [27, Proposition 9.10.2(2)]. Schauder’s theorem implies that \(C'_t\in {{\mathcal {L}}}(X'_\beta )\) is also compact and hence, again by Proposition 9.10.2(2) of [27], now applied to \(C'_t\), we can conclude that \(\sigma _{pt}(C''_t;X''_\beta )=\sigma _{pt}(C'_t;X'_\beta )=\Lambda \). So, \(C''_t\in {{\mathcal {L}}}(X''_\beta )\) has plenty of eigenvalues which implies that \(C'_t\) is not supercyclic. \(\square \)
Remark 6.9
The dynamics of \(C_1\in {{\mathcal {L}}}(X)\), with \(X\not \in \{\ell ^1,d_1\}\) belonging to one of the sets in Theorem 6.6, is quite different. Consider first the Banach space case. For \(1<p<\infty \), the operator \(C_1\in {{\mathcal {L}}}(\ell ^p)\) is neither power bounded nor mean ergodic, [5, Proposition 4.2]. Since \(\{z\in {{\mathbb {C}}}\,:\, |z-\frac{p'}{2}|<\frac{p'}{2}\}\subseteq \sigma _{pt}(C_1'; \ell ^{p'})\) with \(\frac{1}{p}+\frac{1}{p'}=1\), [40, Theorem 1(b)], \(C_1\in {{\mathcal {L}}}(\ell ^p)\) cannot be supercyclic, [16, Proposition 1.26]. Similarly, \(C_1\in {{\mathcal {L}}}(ces(p))\), for \(1<p<\infty \), is not mean ergodic, not power bounded and not supercyclic, [13, Proposition 3.7(ii)]. Also, \(C_1\in {{\mathcal {L}}}(d_p)\) is not mean ergodic and not supercyclic, [19, Propositions 3.10 & 3.11]. Since power bounded operators in reflexive Banach spaces are necessarily mean ergodic, [43], \(C_1\) cannot be power bounded in \(d_p\). Turning to Fréchet spaces, for \(1\le p<\infty \) the operator \(C_1\in {{\mathcal {L}}}(\ell (p+))\) is not mean ergodic, not power bounded and not supercyclic, [8, Theorems 2.3 & 2.5], as is the case for \(C_1\in {{\mathcal {L}}}(ces(p+))\), [14, Proposition 5], and for \(C_1\in {{\mathcal {L}}}(d(p+))\), [21, Proposition 3.5]. For (LB)-spaces, with \(1< p\le \infty \), the operator \(C_1\in {{\mathcal {L}}}(ces(p-))\) is not mean ergodic, not power bounded and not supercyclic, [12, Propositions 3.4 & 3.5], as is the case for \(C_1\in {{\mathcal {L}}}(d(p-))\), [21, Proposition 3.8]. Finally, the dynamics of \(C_1\in {{\mathcal {L}}}(\omega )\) is the same as for \(C_t\in {{\mathcal {L}}}(\omega )\), with \(t\in [0,1)\); see Theorem 6.1 above and [8, Proposition 4.3].
The dynamics of \(C_1\) acting in \(\ell (p-)\) is covered by our final result.
Proposition 6.10
Let \(p\in (1,\infty ]\). The Cesàro operator \(C_1\in {{\mathcal {L}}}(\ell (p-))\) is not mean ergodic, not power bounded and not supercyclic.
Proof
In view of Proposition 5.5(i) the proof follows in a similar way to that of [8, Theorem 2.3]. For the sake of completeness, we indicate the details.
By the discussion prior to Proposition 6.7 we know that \((\ell (p-))'_\beta \simeq \ell (p'+)\). Proposition 5.5(i) implies that \(\frac{1+p'}{2}>1\) belongs to \(\sigma _{pt}(C_1';\ell (p'+))\), where \(\frac{1}{p}+\frac{1}{p'}=1\). So, there exists a non-zero vector \(u\in \ell (p'+)\) satisfying \(C_1'(u) =\frac{1+p'}{2}u\). Choose any \(x\in \ell (p-)\) such that \(\langle x,u\rangle \not =0\). Then
This means that the sequence \(\{\frac{1}{n}(C_1)^n(x)\}_{n\in {{\mathbb {N}}}}\subseteq \ell (p-)\) cannot be bounded in \(\ell (p-)\). Accordingly, \(C_1\) is not mean ergodic and not power bounded.
Applying again Proposition 5.5(i), we see that \(C'_1\) has a plenty of eigenvalues. So, \(C_1\) cannot be supercyclic, [16, Proposition 1.26]. \(\square \)
References
Akhmedov, A.M., Başar, F.: On the fine spectrum of the Cesàro operator in \(c_0\). Math. J. Ibaraki Univ. 36, 25–32 (2004)
Albanese, A.A., Mele, C.: Spectra and ergodic properties of multiplication and convolution operators on the space \(\cal{S} (\mathbb{R} )\). Rev. Mat. Complut. 35, 739–762 (2022)
Albanese, A.A., Bonet, J., Ricker, W.J.: Mean ergodic operators in Fréchet spaces. Ann. Acad. Sci. Fenn. Math. 34, 401–436 (2009)
Albanese, A.A., Bonet, J., Ricker, W.J.: Grothendieck spaces with the Dunford–Pettis property. Positivity 14, 145–164 (2010)
Albanese, A.A., Bonet, J., Ricker, W.J.: Convergence of arithmetic means of operators in Fréchet spaces. J. Math. Anal. Appl. 401, 160–173 (2013)
Albanese, A.A., Bonet, J., Ricker, W.J.: Uniform convergence and spectra of operators in a class of Fréchet spaces. Abstr. Appl. Anal. 179027 (2014)
Albanese, A.A., Bonet, J., Ricker, W.J.: Spectrum and compactness of the Cesàro operator on weighted \(\ell _p\) spaces. J. Aust. Math. Soc. 99, 287–314 (2015)
Albanese, A.A., Bonet, J., Ricker, W.J.: The Cesàro operator in the Fréchet spaces \(\ell ^{p+}\) and \(L^{p-}\). Glasgow Math. J. 59, 273–287 (2017)
Albanese, A.A., Bonet, J., Ricker, W.J.: The Fréchet spaces \(ces(p+)\), \(1 \le p\le \infty \). J. Math. Anal. Appl. 458, 1314–1323 (2018)
Albanese, A.A., Bonet, J., Ricker, W.J.: The Cesàro operator in weighted \(\ell _1\) spaces. Math. Nachr. 291, 1015–1048 (2018)
Albanese, A.A., Bonet, J., Ricker, W.J.: The Cesàro operator on Korenblum type spaces of analytic functions. Collect. Math. 69, 263–281 (2018)
Albanese, A.A., Bonet, J., Ricker, W.J.: Linear operators on the (LB)-spaces \(ces(p-)\), \(1<p\le \infty \), Descriptive topology and functional analysis II, Springer, Cham. Proc. Math. Stat. 286, 43–67 (2019)
Albanese, A.A., Bonet, J., Ricker, W.J.: Multiplier and averaging operators in the Banach spaces \(ces(p), 1<p<\infty \). Positivity 23, 177–193 (2019)
Albanese, A.A., Bonet, J., Ricker, W.J.: Operators on the Fréchet sequence spaces \(ces(p+)\), \(1\le p<\infty \), Rev. R. Acad. Cienc. Exactas Fís. Nat. Ser. A Mat. RACSAM 113, 1533–1556 (2019)
Astashkin, S.V., Maligranda, L.: Structure of Cesàro function spaces: a survey, Function Spaces X, pp. 13-40, Banach Center Publ. 102, Polish Acad. Sci. Inst. Math., Warsaw (2014)
Bayart, F., Matheron, E.: Dynamics of Linear Operators, Cambridge Tracts in Mathematics, vol. 179. Cambridge University Press, Cambridge (2009)
Bennett, G.: Factorizing the classical inequalities. Mem. Am. Math. Soc. 120(576), 1–130 (1996)
Bonet, J.: A question of Valdivia on quasinormable Fréchet spaces. Canad. Math. Bull. 34, 301–304 (1991)
Bonet, J., Ricker, W.J.: Operators acting in the dual spaces of discrete Cesàro spaces. Monatsh. Math. 191, 487–512 (2020)
Bonet, J., Ricker, W.J.: Fréchet and (LB) sequence spaces induced by dual Banach spaces of discrete Cesàro spaces. Bull. Belg. Math. Soc. Simon Stevin 28, 1–19 (2021)
Bonet, J., Ricker, W.J.: Operators acting in sequence spaces generated by dual Banach spaces of discrete Cesàro spaces. Funct. Approx. Comment. Math. 64, 109–139 (2021)
Brown, A., Halmos, P.R., Shields, A.L.: Cesàro operators. Acta Sci. Math. (Szeged) 26, 125–137 (1965)
Curbera, G.P., Ricker, W.J.: Spectrum of the Cesàro operator in \(\ell ^p\). Arch. Math. 100, 267–271 (2013)
Curbera, G.P., Ricker, W.J.: Solid extensions of the Cesàro operator on \(\ell ^p\) and \(c_0\). Integr. Equ. Oper. Theory 80, 61–77 (2014)
Curbera, G.P., Ricker, W.J.: The Cesàro operator and unconditional Taylor series in Hardy spaces. Integr. Equ. Oper. Theory 83, 179–195 (2015)
Curbera, G.P., Ricker, W.J.: Fine spectra and compactness of generalized Cesàro operators in Banach lattices in \({\mathbb{C} ^{\mathbb{N} }_0}\). J. Math. Anal. Appl. 507 (2022). ((Article number 125824))
Edwards, R.E.: Functional Analysis. Theory and Applications. Holt, Rinehart and Winston, New York-Chicago-San Francisco (1965)
Fernández, C., Galbis, A., Jordá, E.: Dynamics and spectra of composition operators on the Schwartz space. J. Funct. Anal. 274, 3503–3530 (2018)
Gelfand, I.M., Shilov, G.E.: Generalized Functions; Spaces of Fundamental and Generalized Functions, vol. 2. Academic Press, New York (1968)
González, M.: The fine spectrum of the Cesàro operator in \(\ell ^p\) (\(1<p<\infty \)). Arch. Math. 44, 355–358 (1985)
Grosse-Erdmann, K.-G.: The Blocking Technique, Weighted Mean Operators and Hardy’s Inequality, LNM vol. 1679, Springer, Berlin-Heidelberg (1998)
Grosse-Erdmann, K.-G., Peris Manguillot, A.: Linear Chaos, Universitext. Springer, London (2011)
Grothendieck, A.: Topological Vector Spaces. Gordon and Breach, London (1973)
Hardy, G.H., Littlewood, J.E., Pólya, G.: Inequalities. Cambridge University Press, Cambridge (1934)
Jagers, A.A.: A note on Cesàro sequence spaces. Nieuw. Arch. Wisk. 22, 113–124 (1974)
Jarchow, H.: Locally Convex Spaces. Teubner, Stuttgart (1981)
Köthe, G.: Topological Vector Spaces I, 2nd Rev. Ed., Springer, Berlin-Heidelberg-New York (1983)
Köthe, G.: Topological Vector Spaces II. Springer, Berlin-Heidelberg-New York (1979)
Krengel, U.: Ergodic Theorems. Walter de Gruyter, Berlin (1985)
Leibowitz, G.: Spectra of discrete Cesàro operators. Tamkang J. Math. 3, 123–132 (1972)
Leśnik, K., Maligranda, L.: Abstract Cesàro spaces. Duality. Math. Anal. Appl. 424, 932-951 (2015)
Lin, M.: On the uniform ergodic theorem. Proc. Am. Math. Soc. 43, 337–340 (1974)
Lorch, E.R.: Means of iterated transformations in reflexive vector spaces. Bull. Am. Math. Soc. 45, 945–947 (1939)
Meise, R., Vogt, D.: Introduction to Functional Analysis. Clarendon Press, Oxford (1997)
Metafune, G., Moscatelli, V.B.: On the space \(\ell ^{p+}=\cap _{q>p}\ell ^q\). Math. Nachr. 147, 7–12 (1990)
Neus, H.: Über die Regularitätsbegriffe induktiver lokalkonvexer sequenzen. Manuscripta Math. 25, 135–145 (1978)
Okutoyi, J.I.: On the spectrum of \(C_1\) as an operator on \(bv_0\). J. Aust. Math. Soc. Ser. A 48, 79–86 (1990)
Okutoyi, J.I.: On the spectrum of \(C_1\) as an operator on \(bv\). Commun. Fac. Sci. Univ. Ank. Ser. A1(41), 197–207 (1992)
Pérez Carreras, P., Bonet, J.: Barrelled Locally Convex Spaces, North Holland Math. Studies 131, Amsterdam (1987)
Prouza, L.: The spectrum of the discrete Cesàro operator. Kybernetika 12, 260–267 (1976)
Reade, J.B.: On the spectrum of the Cesàro operator. Bull. Lond. Math. Soc. 17, 263–267 (1985)
Rhaly, Jr, H.C.: Discrete generalized Cesàro operators. Proc. Am. Math. Soc. 86, 405–409 (1982)
Rhaly, Jr, H.C.: Generalized Cesàro matrices. Canad. Math. Bull. 27, 417–422 (1984)
Rhoades, B.E.: Spectra of some Hausdorff operators. Acta Sci. Math. 32, 91–100 (1971)
Sawano, Y., El-Shabrawy, S.R.: Fine spectra of the discrete generalized Cesàro operator on Banach sequence spaces. Monatsh. Math. 192, 185–224 (2020)
Waelbrock, L.: Topological Vector Spaces and Algebras, LNM vol. 230, Springer, Berlin (1971)
Wengenroth, J.: Acyclic inductive spectra of Fréchet spaces. Studia Math. 130, 247–258 (1996)
Yildrim, M., Durna, N.: The spectrum and some subdivisions of the spectrum of discrete generalized Cesàro operators on \(\ell ^p\) (\(1<p<\infty \)). J. Inequal. Appl. 2017(1), 1–13 (2017)
Yildrim, M., Mursaleen, M., Dogan, C.: The spectrum and fine spectrum of the generalized Rhaly–Cesàro matrices on \(c_0\) and \(c\). Oper. Matrices 12(4), 955–975 (2018)
Yosida, K.: Functional Analysis. Springer, Berlin (1980)
Acknowledgements
The research of J. Bonet was partially supported by the project PID2020-119457GB-100 funded by MCIN/AEI/10.13039/501100011033 and by “ERFD A way of making Europe” and by the project GV AICO/2021/170.
Funding
Open access funding provided by Universitá del Salento within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Albanese, A.A., Bonet, J. & Ricker, W.J. Spectral properties of generalized Cesàro operators in sequence spaces. Rev. Real Acad. Cienc. Exactas Fis. Nat. Ser. A-Mat. 117, 140 (2023). https://doi.org/10.1007/s13398-023-01470-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s13398-023-01470-2
Keywords
- Generalized Cesàro operator
- Compactness
- Spectra
- Power boundedness
- Uniform mean ergodicity
- Sequence space
- Fréchet space
- (LB)-space



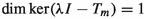 for each
for each