Computing branches and asymptotes of meromorphic functions

Abstract

In this paper, we first summarize the existing algorithms for computing all the generalized asymptotes of a plane algebraic curve implicitly or parametrically defined. From these previous results, we derive a method that allows to easily compute the whole branch and all the generalized asymptotes of a “special” curve defined in n-dimensional space by a parametrization that is not necessarily rational. So, some new concepts and methods are established for this type of curves. The approach is based on the notion of perfect curves introduced from the concepts and results presented in previous papers.

1 Introduction

An asymptote of a curve is a line to which the curve converges. In other words, the curve and its asymptote get infinitely close. Asymptotes have a variety of applications: they are used in big O notation, they are simple approximations to complex equations, they are useful for graphing curves, etc. Graphic means of displaying information are used in all areas of society. They have a complete image, are characterized by symbolism, compactness, relative ease of reading. It is these qualities of graphic images that determine their expanded use. In the near future, more than half of the information presented will have a graphical presentation form. The development of the theoretical foundations of descriptive geometry, engineering graphics, and other related sciences has expanded the methods for obtaining graphic images. Along with manual methods of forming graphic images, compiling project documentation, computer methods are finding wider application. The use of new information technologies provides the creation, editing, storage, replication of graphic images using various software tools.

In this sense the computation of branches and asymptotes as a mathematical tool is very important since curves are essential for engineering, industry, computer aided design (CAD), etc.

For instance there are many applications of engineering curves in industry. The hyperbolic shape for example, finds application in design of cooling towers. Even Mirrors used in long telescopes are hyperbolic in shape. Another type of engineering curve called the archimedean spiral (type of curve in which the moving point is traced out in such a way that movement towards or away from the pole is uniform with vectorial angle from the starting line) has its application in designing and manufacturing of teeth profile of helical gears and profile of cams. Another curve is the cycloid which is used by engineers and designers for designing roller coasters. Even worm gears have cycloidal profile (the ones used in outdoor gears). The head of the tooth of such worm gear is an epicycloid (another engineering curve) and the tooth foot is hypocycloid. While designing objects various types of curves are used.

Mechanical engineers also need mathematical curves. For example, a satellite dish is a basic parabola, a gear has the involute of a circle as its base. These kind of curves are usually not directly supported in CAD systems. They must therefore be drawn using its branches.

There are numerous methods for analysis and synthesis of mechanisms based on geometrical constructions and it is necessary a deepen study of the curves described by a point and the relationship between the geometry of different parts. Many engineering studies are devoted to the study of curves of the tooth profile of gears as well as the coupler path of mechanisms. Then, Geometry plays an important role in many engineering applications, such as engines and mechanisms. The study of curves dates from Ancient Greece, because the first mathematicians of History became interested in them. The Greeks were the first who studied the paths that describe planets in motion but they restricted their mathematics mainly to geometry, and they were primarily concerned with figures which could be obtained from lines and circles (geometric locus). Conics were treated as plane sections of cones (solid locus) and other planar curves like cycloids and spirals were included in their studies although they could not be drawn from lines and circles. Indeed they were known as mechanical curves rather than geometrical curves. In this paper, we have focus the attention in drawing the mechanical curves most used in engineering by using dynamic geometry software; the different cycloid, hypocycloid, epicycloids have been drawn by using the Geogebra software. Some engineering applications of these mechanical curves, planetary gear trains, and the kinematic requirements have been also studied. For some bibliography see for instance [1, 2, 8,9,10,11, 14,15,16], etc.

The asymptotes of an infinity branch (a branch at infinity), B, of a real plane algebraic curve, ${\mathcal {C}}$, reflect the behavior of B at the points with sufficiently large coordinates. In analytic geometry, an asymptote of a curve is a line such that the distance between the curve and the line approaches zero as they tend to infinity. In some contexts, such as algebraic geometry, an asymptote is defined as a line which is tangent to a curve at infinity.

If B can be defined by some explicit equation of the form $y = f(x)$ (or $x = g(y)$), where f (or g) is a continuous function on an infinite interval, it is straightforward to decide whether ${\mathcal {C}}$ has an asymptote at B by analyzing the existence of the limits of certain functions when x tends to $\infty$ (or y tends to $\infty$). Moreover, if these limits can be computed, we may obtain the equation of the asymptote of ${\mathcal {C}}$ at B. However, if this branch B is implicitly defined and its equation cannot be converted into an explicit form, both the decision and the computation of the asymptote of ${\mathcal {C}}$ at B require some other tools. More precisely, an algebraic curve may have more general curves than lines describing the behavior of a branch at the points with sufficiently large coordinates. Intuitively speaking, we say that a curve $\widetilde{{{\mathcal {C}}}}$ is a generalized asymptote (or g-asymptote) of another curve ${\mathcal {C}}$ if the distance between $\widetilde{{{\mathcal {C}}}}$ and ${\mathcal {C}}$ tends to zero as they tend to infinity, and ${\mathcal {C}}$ can not be approached by a new curve of lower degree (see [3,4,5, 7]). This motivates our interest in efficiently computing these generalized asymptotes for a wider variety of varieties such as the curves defined by a not necessarily rational parameterization.

In this paper, we deal with the problem of efficiently computing the asymptotes of meromorphic functions from an open subset of the complex plane onto $\mathbb {C}^n,\,n\ge 1$. We remind that meromorphic functions are functions on an open subset D of $\mathbb {C}$ that are holomorphic on all D except for a set of isolated points, which are poles of the functions. By abuse of notation, and in order to make the article easier for the reader to understand, we will denote by ${{\mathcal {P}}}(t):=(p_1(t),\ldots ,p_n(t))$ these meromorphic functions and we say that the image of ${\mathcal {P}}$ is a special curve  ${\mathcal {C}}$ parametrically defined in n-dimensional space.

The problem of the computation of asymptotes is dealt in previous papers of the third author (see [3,4,5,6,7]) and solved for algebraic rational curves parametrically and implicitly defined. For this purpose, some previous notions as infinity branches (or branches at infinity), approaching curves and perfect curves are introduced. The new goal we solve in this paper consists in working with curves parametrically defined but not necessarily rational. This question is very important in the study of these type of curves because there is no result or concept in this regard.

We have intended the paper to be self-contained. For this reason, we have included Sect. 2, where we review the theory of infinity branches and introduce the notions of convergent branches (that is, branches that get closer as they tend to infinity) and approaching curves (see [3]), and Sect. 3, where we lay down fundamental concepts like perfect curve (a curve of degree d that cannot be approached by any curve of degree less than d) and g-asymptote (a perfect curve that approaches another curve at an infinity branch). In addition, we present the methods that allow to compute the infinity branches of a given curve implicitly and parametrically defined, and a g-asymptote for each of them (see Sects. 3.1, 3.2, 3.2.1).

The main result of the paper is presented in Sect. 4. Here, we develop a method that allows to easily compute all the generalized asymptotes of a curve defined by a parametrization by only determining some simple limits of functions constructed from the given parametrization. The results presented are concerned with plane curves but, as we remark in the paper, they can trivially be adapted for dealing with algebraic curves in n-dimensional space (see Example 6).

Finally, some conclusions, and future work is presented in Sect. 5.

2 Notation and previous results

In this section, we introduce the notion of infinity branch or branch at infinity, convergent branches and approaching curves, and we present some properties which allow us to compare the behavior of two implicit algebraic plane curves at infinity. For more details on these concepts and results, we refer to [4] (see Sects. 3and 4).

We consider an irreducible algebraic affine plane curve ${\mathcal {C}}$ over $\mathbb {C}$ defined by the irreducible polynomial $f(x,y) \in \mathbb {R}[x,y]$. We work over the field of complex numbers $\mathbb {C}$, but ${\mathcal {C}}$ has infinitely many points in the affine plane over $\mathbb {R}$ (see Chapter 7 [13]). The assumption of reality is included because of the nature of the problem, but the theory can be similarly developed for the case of complex non-real curves.

Let ${{\mathcal {C}}}^*$ be its corresponding projective curve, defined by the homogeneous polynomial

$$\begin{aligned} F(x,y,z)=f_d(x,y)+zf_{d-1}(x,y)+z^2f_{d-2}(x,y)+\cdots +z^d f_0 \in \mathbb {R}[x,y,z],\quad \end{aligned}$$

where $d:=\textrm{deg}({{\mathcal {C}}})$ and $f_i(x,y),\,i=0,\ldots ,d$ the homogeneous form of degree i. We assume that (0 : 1 : 0) is not a point at infinity of ${{\mathcal {C}}}^*$ (otherwise, we may consider a projective linear change of coordinates).

In order to get the infinity branches (or branches at infinity) of $\mathcal {C}$, we consider the curve defined by the polynomial $g(y,z)=F(1:y:z)$ and we compute the series expansion for the solutions of $g(y,z)=0$ around $z=0$. We denote by ${\mathbb {C}\ll z\gg }$ e the field of formal Puiseux series. Thus, there exist exactly $\textrm{deg}_{y}(g)$ solutions given by different Puiseux series that can be grouped into conjugacy classes. More precisely, if

$$\begin{aligned} \varphi (z)=m+a_1z^{N_1/N}+a_2z^{N_2/N}+a_3z^{N_3/N} + \cdots \in \mathbb {C}\langle \langle z\rangle \rangle ,\quad a_i\not =0,\, \forall i\in \mathbb {N}, \end{aligned}$$

where $N\in \mathbb {N}$, $N_i\in \mathbb {N},\,\,i\in \mathbb {N}$, and $0<N_1<N_2<\cdots$, $\textrm{gcd}(N,N_1,N_2,\ldots )=1$, is a Puiseux series such that $g(\varphi (z), z)=0$, and $\nu (\varphi )=N$ (i.e., N is the ramification index of $\varphi$), the series

$$\begin{aligned}\varphi _j(z)=m+a_1c_j^{N_1}z^{N_1/N}+a_2c_j^{N_2}z^{N_2/N}+a_3c_j^{N_3}z^{N_3/N} + \cdots \end{aligned}$$

where $c_j^N=1,\,\,j\in \{1,\ldots ,N\}$, are called the conjugates of $\varphi$ (that is, $c_j,\,\,j\in \{1,\ldots ,N\}$ are the $N^{th}$ roots of unity). The set $\{\varphi _1,\ldots , \varphi _N\}$ all the conjugates of $\varphi$ is called the conjugacy class of $\varphi$. It contains $N=\nu (\varphi )$ distinct series which satisfy $g(\varphi _j(z), z)=0,\,j=1,\ldots ,N$.

Since $g(\varphi (z), z)=0$ in some neighborhood of $z=0$ where $\varphi (z)$ converges, there exists $M \in \mathbb {R}^+$ such that $F(1:\varphi (t):t)=g(\varphi (t), t)=0$ for $t\in \mathbb {C}$ and $|t|<M$, which implies that $F(t^{-1}:t^{-1}\varphi (t):1)=f(t^{-1},t^{-1}\varphi (t))=0$, for $t\in \mathbb {C}$ and $0<|t|<M$. We set $t^{-1}=z$, and we obtain that $f(z,r(z))=0$ for $z\in \mathbb {C}$ and $|z|>M^{-1}$ where

$$\begin{aligned} r(z)=z\varphi (z^{-1})=mz+a_1z^{1-N_1/N}+a_2z^{1-N_2/N}+a_3z^{1-N_3/N} + \cdots ,\quad a_i\not =0,\, \forall i\in \mathbb {N} \end{aligned}$$

$N,N_i\in \mathbb {N},\,\,i\in \mathbb {N}$, and $0<N_1<N_2<\cdots$, $\textrm{gcd}(N,N_1,N_2,\ldots )=1$.

Reasoning similarly with the N different series in the conjugacy class, $\varphi _1,\ldots ,\varphi _N$, we get

$$\begin{aligned} r_i(z)=z\varphi _i(z^{-1})=mz+a_1c_i^{N_1}z^{1-N_1/N}+a_2c_i^{N_2}z^{1-N_2/N}+a_3c_i^{N_3}z^{1-N_3/N} + \cdots . \end{aligned}$$

Definition 1

An infinity branch (or branch at infinity) of an affine plane curve ${{\mathcal {C}}}$ associated to the infinity point (or point at infinity) $P=(1:m:0),\,m\in \mathbb {C}$, is a set $B=\bigcup _{j=1}^N L_j$, where $L_j=\{(z,r_j(z))\in \mathbb {C}^2: \,z\in \mathbb {C},\,|z|>M\}$,  $M\in \mathbb {R}^+$, and

$$\begin{aligned} r_j(z)=z\varphi _j(z^{-1})=mz+a_1c_j^{N_1}z^{1-N_1/N}+a_2c_j^{N_2}z^{1-N_2/N}+a_3c_j^{N_3}z^{1-N_3/N} + \cdots \nonumber \\ \end{aligned}$$

(2.1)

where $N, N_i\in \mathbb {N},\,\,i\in \mathbb {N}$, $0<N_1<N_2<\cdots$, and $c_j^N=1,\,\,j\in \{1,\ldots ,N\}$. The subsets $L_1,\ldots ,L_N$ are called the leaves of the infinity branch B.

Remark 1

An infinity branch is uniquely determined from one leaf, up to conjugation.

By abuse of notation, in the following we write $B=\{(z,r(z))\in \mathbb {C}^2: \,z\in \mathbb {C},\,|z|>M\}$ (where $M:=\max \{M_1,\ldots ,M_N\}$). We recall that N is the ramification index of the branch B and we will write $N=\nu (B)$ (the branch B has $\nu (B)$ leaves).

Remark 2

Each infinity branch is associated to a unique infinity point. More precisely, as we stated above, there exists $M \in \mathbb {R}^+$ such that $F(1:\varphi (t):t)=g(\varphi (t), t)=0$ for $|t|<M$, where

$$\begin{aligned} \varphi (z)=m+a_1z^{N_1/N}+a_2z^{N_2/N}+a_3z^{N_3/N} + \cdots \in \mathbb {C}\langle \langle z\rangle \rangle . \end{aligned}$$

Thus, for $t=0$ we get the infinity point $P=(1:\varphi (0):0)=(1:m:0)\in {{\mathcal {C}}}^*.$

Conversely, given an infinity point $P=(1:m:0)$, there must be, at least, one Puiseux solution $\varphi$ such that $\varphi (0)=m$; this solution provides an infinity branch associated to P. In particular, we conclude that every algebraic plane curve has, at least, one infinity branch.

The procedure introduced above allows us to obtain the infinity branches of a curve ${\mathcal {C}}$, under the assumption that $(0:1:0)\notin {{\mathcal {C}}}^*$. However, a curve may have infinity branches, associated to the infinity point (0 : 1 : 0), which can not be constructed in this way. These infinity branches have the form $\{(r(z),z)\in \mathbb {C}^2: \,z\in \mathbb {C},\,|z|>M\}$ and may be obtained by interchanging the variables x and y. See [4] (Definition 3.3) for further details.

In the following, we introduce the notions of convergent branches and approaching curves. Intuitively speaking, two infinity branches converge if they get closer as they tend to infinity. This concept will allow us to analyze whether two curves approach each other.

Definition 2

Two infinity branches, B and $\overline{B}$, are convergent if there exist two leaves $L=\{(z,r(z))\in \mathbb {C}^2:\,z\in \mathbb {C},\,|z|>M\} \subset B$ and $\overline{L}=\{(z,\overline{r}(z))\in \mathbb {C}^2:\,z\in \mathbb {C},\,|z|>\overline{M}\}\subset \overline{B}$ such that $\lim _{z\rightarrow \infty } (\overline{r}(z)-r(z))=0.$ In this case, we say that the leaves L and $\overline{L}$ converge.

The following theorem provides a characterization for the convergence of two infinity branches (see [4]).

Theorem 1

The following statements hold:

• 1. Two leaves $L=\{(z,r(z))\in \mathbb {C}^2:\,z\in \mathbb {C},\,|z|>M\}$ and $\overline{L}=\{(z,\overline{r}(z))\in \mathbb {C}^2:\,z\in \mathbb {C},\,|z|>\overline{M}\}$ are convergent if and only if the terms with non negative exponent in the series r(z) and $\overline{r}(z)$ are the same.

• 2. Two infinity branches B and $\overline{B}$ are convergent if and only if for each leaf $L\subset B$ there exists a leaf $\overline{L}\subset \overline{B}$ convergent with L, and conversely.

• 3. Two convergent infinity branches must be associated to the same infinity point.

This paper is concerned with the study of the asymptotes of a curve. The classical concept of asymptote stands for a line that approaches a given curve when it tends to the infinity. In the following we generalize this idea by claiming that two curves approach each other if they, respectively, have two infinity branches that converge.

Definition 3

Let ${{\mathcal {C}}}$ be an algebraic plane curve with an infinity branch B. We say that a curve ${\overline{{{\mathcal {C}}}}}$ approaches ${{\mathcal {C}}}$ at its infinity branch B if there exists one leaf $L=\{(z,r(z))\in \mathbb {C}^2:\,z\in \mathbb {C},\,|z|>M\}\subset B$ such that $\lim _{z\rightarrow \infty }d((z,r(z)),\overline{{\mathcal {C}}})=0,$ where $d(\cdot ,\cdot )$ represents the euclidean distance.

The following theorem characterize the convergence of two curves at an infinity branch (see [4]).

Theorem 2

Let ${{\mathcal {C}}}$ be a plane algebraic curve with an infinity branch B. A plane algebraic curve ${\overline{{{\mathcal {C}}}}}$ approaches ${{\mathcal {C}}}$ at B if and only if ${\overline{{{\mathcal {C}}}}}$ has an infinity branch, $\overline{B}$, such that B and $\overline{B}$ are convergent.

Obviously, “approaching” is a symmetric concept, that is, ${{\mathcal {C}}}_1$ approaches ${{\mathcal {C}}}_2$ if and only if ${{\mathcal {C}}}_2$ approaches ${{\mathcal {C}}}_1$. When it happens we say that ${{\mathcal {C}}}_1$ and $\mathcal {C}_2$ are approaching curves or that they approach each other. In the next section, we use this concept to generalize the classical notion of asymptote of a curve.

3 Asymptotes of an algebraic curve

Given an algebraic plane curve $\mathcal {C}$ and an infinity branch B, in Sect. 2, we have described how $\mathcal {C}$ can be approached at B by a second curve ${\overline{\mathcal {C}}}$. Now, suppose that $\textrm{deg}({\overline{\mathcal {C}}})<\textrm{deg}(\mathcal {C})$. Then one may say that $\mathcal {C}$ degenerates, since it behaves at infinity as a curve of smaller degree. For instance, a hyperbola is a curve of degree 2 that has two real asymptotes, which implies that the hyperbola degenerates, at infinity, to two lines. Similarly, one can check that every ellipse has two asymptotes, although they are complex lines in this case. However, the asymptotic behavior of a parabola is different, since it cannot be approached at infinity by any line. This motivates the following definition:

Definition 4

An algebraic curve of degree d is a perfect curve if it cannot be approached by any curve of degree less than d.

More properties on perfect curves can be found in [3]. In particular, one has that if a given curve of degree d has an only branch of degree d, then the input curve is perfect. For instance, a curve $\mathcal {C}$ defined by a proper parametrization of the form $(t^{n}, a_{n}t^{n}+a_{n-1}t^{n-1}+\cdots +a_0)$ is always perfect since it has an only branch B given by $(z,r(z))=(z, a_{n}z+a_{n-1}z^{(n-1)/n}+\cdots +a_0)$ and $\textrm{deg}(\mathcal {C})=\textrm{deg}(B)=n$ (see Definition 6 for the degree of a branch).

A curve that is not perfect can be approached by other curves of smaller degree. If these curves are perfect, we call them g-asymptotes. More precisely, we have the following definition.

Definition 5

Let $\mathcal {C}$ be a curve with an infinity branch B. A g-asymptote (generalized asymptote) of $\mathcal {C}$ at B is a perfect curve that approaches $\mathcal {C}$ at B.

The notion of g-asymptote is similar to the classical concept of asymptote. The difference is that a g-asymptote is not necessarily a line, but a perfect curve. Actually, it is a generalization, since every line is a perfect curve (this fact follows from Definition 4). Throughout the paper we refer sometimes to g-asymptote simply as asymptote.

Remark 3

The degree of a g-asymptote is less than or equal to the degree of the curve it approaches. In fact, a g-asymptote of a curve $\mathcal {C}$ at a branch B has minimal degree among all the curves that approach $\mathcal {C}$ at B.

In Sect. 3.1, we show that every infinity branch of a given algebraic plane curve implicitly defined has, at least, one asymptote and we show how to compute it. For this purpose, we rewrite Eq. (2.1) defining a branch B (see Definition 1) as

$$\begin{aligned} r(z)=mz+a_1z^{1-n_1/n}+\cdots +a_kz^{1-n_k/n}+a_{k+1}z^{1-N_{k+1}/N}+\cdots \end{aligned}$$

(3.1)

where $0<N_1<\cdots<N_k\le N<N_{k+1}<\cdots$ and $\textrm{gcd}(N,N_1,\ldots ,N_k)=b$, $N=n \cdot b$, $N_j=n_j\cdot b,\,\,j\in \{1,\ldots ,k\}$. That is, we have simplified the non negative exponents such that $\textrm{gcd}(n,n_1,\ldots ,n_k)=1$. Note that $0<n_1<n_2<\cdots$, and $n_k\le n$, and $N<N_{k+1}$, i.e. the terms $a_jz^{1-N_j/N}$ with $j\ge k+1$ are those which have negative exponent. We denote these terms as $A(z):=\sum _{\ell =k+1}^\infty a_{\ell }z^{-q_{\ell }},$ where $q_{\ell }=1-N_{\ell }/N\in \mathbb {Q}^+,$ $\ell \ge k+1.$

Under these conditions, we introduce the definition of degree of a branch B:

Definition 6

Let $B=\{(z,r(z))\in \mathbb {C}^2: \,z\in \mathbb {C},\,|z|>M\}$ (r(z) is defined in (3.1)) be an infinity branch associated to an infinity point $P=(1:m:0), m\in \mathbb {C}$. We say that n is the degree of B, and we denote it by $\textrm{deg}(B)$.

3.1 Construction of a g-asymptote of a curve implicitly defined

Taking into account Theorems 1 and 2, we have that any curve $\overline{\mathcal {C}}$ approaching $\mathcal {C}$ at B should have an infinity branch $\overline{B}=\{(z,\overline{r}(z))\in \mathbb {C}^2:\,z\in \mathbb {C},\,|z|>\overline{M}\}$ such that the terms with non negative exponent in r(z) and $\overline{r}(z)$ are the same.

In the simplest case, if $A=0$ in the branch B (i.e. there are no terms with negative exponent; see equality (3.1)), we could consider the branch

$$\begin{aligned} \tilde{r}(z)=mz+a_1z^{1-n_1/n}+a_2z^{1-n_2/n}+\cdots +a_kz^{1-n_k/n}, \end{aligned}$$

(3.2)

where $a_1,a_2,\ldots \in \mathbb {C}\setminus \{0\}$, $m\in \mathbb {C}$, $n,n_1,n_2\ldots \in \mathbb {N}$, $\textrm{gcd}(n,n_1,\ldots ,n_k)=1$, and $0<n_1<n_2<\cdots$. Note that $\tilde{r}$ has the same terms with non negative exponent as r, and $\tilde{r}$ does not have terms with negative exponent.

Let $\widetilde{\mathcal {C}}$ be the irreducible plane curve containing the branch $\widetilde{B}=\{(z,\tilde{r}(z))\in \mathbb {C}^2:\,z\in \mathbb {C},\,|z|>\widetilde{M}\}$ (note that $\widetilde{\mathcal {C}}$ is unique since two different algebraic curves have finitely many common points). Observe that

$$\begin{aligned} \widetilde{\mathcal {Q}}(t)=(t^n,mt^n+a_1t^{n-n_1} +\cdots +a_kt^{n-n_k})\in \mathbb {C}[t]^2 \end{aligned}$$

is a polynomial parametrization of $\widetilde{\mathcal {C}}$, and it is proper (see Lemma 3 in [3]). In Theorem 2 in [3], we prove that $\widetilde{\mathcal {C}}$ is a g-asymptote of $\mathcal {C}$ at B.

From these results, we obtain the method presented in [4, 5], that computes g-asymptotes and that is independent of the leaf chosen to define the infinity branch. We assume that we have prepared the input curve $\mathcal {C}$, by means of a suitable projective linear change of coordinates, such that (0 : 1 : 0) is not an infinity point of $\mathcal {C}$.

In the following, we illustrate the method with an example.

Example 1

Let $\mathcal {C}$ be the curve of degree $d=6$ defined by the irreducible polynomial

$$\begin{aligned} f(x,y)= & {} 8y^2x^3+16y^5x-42y^4x+164y^3x^2-71670yx\\{} & {} -34853x^2+20428x+15075y^2x-2213y^3x+196x^3-2530y^2x^2\\{} & {} +13946yx^2-56yx^3-4978y^3-15321y^2+175y^4-197y^5+8y^6 \in \mathbb {R}[x,y]. \end{aligned}$$

First, we have that $f_6(x,y)=y^5(y+2x)$. Hence, the infinity points are $P_1=(1:0:0)$ and $P_2=(1:-2:0).$

We start by analyzing the point $P_1$: there are three infinity branches associated to $P_1$, $B_{1j}=\{(z,r_{1j}(z))\in \mathbb {C}^2:\,z\in \mathbb {C},\,|z|>M_1\}$, $j=1,2,3$, where

$$\begin{aligned} r_{11}(z)= & {} 7/2+7/2I+(-127/8-15/8I) z^{-1}+(2161/16+1189/32I) z^{-2}\\{} & {} + (-6553/4-84517/128I) z^{-3}+\cdots ,\\ r_{12}(z)= & {} 7/2-7/2I+(-127/8+15/8I) z^{-1}+(2161/16-1189/32I) z^{-2}\\{} & {} +(-6553/4+84517/128I) z^{-3} +\cdots \\ r_{13}(z)= & {} 5/24+ 10/3 z^{1/3} {2}^{1/3}- z^{2/3} {2}^{-1/3}+97/3 z^{-1}+ 1289/162 z^{-1/3} 2^{-4/3}+\cdots \end{aligned}$$

(we compute $r_{1j},\,j=1,2,3$ using the algcurves package included in the computer algebra system Maple; in particular we use the command puiseux).

We compute $\tilde{r}_{1j}(z),\,j=1,2,3$, and we have that

$$\begin{aligned}{} & {} \tilde{r}_{11}(z)=7/2+7/2I,\,\quad \tilde{r}_{12}(z)=7/2-7/2I,\, \\{} & {} \quad \tilde{r}_{13}(z)=5/24+10/3 \cdot 2^{1/3}z^{1/3}-2^{-1/3}z^{2/3}. \end{aligned}$$

The parametrizations of the asymptotes $\widetilde{\mathcal {C}}_j,\,j=1,2,3,$ are given by

$$\begin{aligned} \widetilde{\mathcal {Q}}_1(t)= & {} (t,\,7/2+7/2I),\,\quad \widetilde{\mathcal {Q}}_2(t)=(t,\, 7/2-7/2I),\,\\ \widetilde{\mathcal {Q}}_3(t)= & {} (t^3,\, 5/24+10/3 \cdot 2^{1/3}t-2^{-1/3}t^2) \end{aligned}$$

which define two complex lines and the curve defined by the implicit polynomial

$$\begin{aligned} \tilde{f}_3(x,y)= & {} -6912x^2-138240yx+1052800x+8640y^2 \\{} & {} -1800y+125-13824y^3\in \mathbb {R}[x,y] \end{aligned}$$

(one may compute the polynomial defining implicitly $\widetilde{\mathcal {C}}_3$ using for instance the results in [13]; see Chapter 4).

Now, we focus on the point $P_2$: there one infinity branch associated to $P_2$, $B_{2}=\{(z,r_{2}(z))\in \mathbb {C}^2:\,z\in \mathbb {C},\,|z|>M_2\}$, where

$$\begin{aligned} r_{2}(z)=17-2z-261/4 z^{-1}-2241/8 z^{-2}+\cdots . \end{aligned}$$

We compute $\tilde{r}_{2}(z)$, and we have that

$$\begin{aligned} \tilde{r}_{2}(z)=-2z+17. \end{aligned}$$

The parametrization of the asymptote $\widetilde{\mathcal {C}}_4$ is given by

$$\begin{aligned} \widetilde{\mathcal {Q}}_4(t)=(t,\,-2 t+17) \end{aligned}$$

that defines a line implicitly defined by the polynomial

$$\begin{aligned} \tilde{f}_4(x,y)=-2 x+17-y\in \mathbb {R}[x,y]. \end{aligned}$$

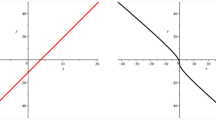
In Fig. 1, we plot the curve $\mathcal {C}$, and the asymptotes $\widetilde{\mathcal {C}}_3$ and $\widetilde{\mathcal {C}}_4$ (the asymptotes $\widetilde{\mathcal {C}}_1$ and $\widetilde{\mathcal {C}}_2$ are complex lines).

Fig. 1

Curve $\mathcal {C}$ (left) and curve and asymptotes (right).

3.2 Construction of a g-asymptote of a curve rationally parametrized

Throughout this paper so far, we have dealt with algebraic plane curves implicitly defined. In this subsection, we present a method to compute infinity branches and g-asymptotes of a plane curve from their parametric (rational) representation (without implicitizing). This method is included in [5] (see Section 5) and it involves the computation of Puiseux series and infinity branches. In Sect. 3.2.1, we develop a new method presented in [7] that allows to easily compute the generalized asymptotes (g-asymptotes) by only determining some simple limits of rational functions constructed from the given parametrization.

Let $\mathcal {C}$ be a plane curve defined by the rational parametrization

$$\begin{aligned} \mathcal {P}(s)=(p_1(s),p_2(s))\in \mathbb {R}(s)^2,\quad p_i(s)=p_{i1}(s)/p_{i2}(s),\quad \textrm{gcd}(p_{i1},p_{i2})=1,\,\,i=1,2. \end{aligned}$$

If $\mathcal {C}^*$ represents the projective curve associated to $\mathcal {C}$, we have that a parametrization of $\mathcal {C}^*$ is given by $\mathcal {P}^*(s)=(p_{1}(s):p_{2}(s):1)$ or, equivalently,

$$\begin{aligned} \mathcal {P}^*(s)=\left( 1:\frac{p_{2}(s)}{p_{1}(s)}:\frac{1}{p_{1}(s)}\right) . \end{aligned}$$

We assume that we have prepared the input curve $\mathcal {C}$, by means of a suitable projective linear change of coordinates (if necessary) such that (0 : 1 : 0) is not a point at infinity of $\mathcal {C}^*$.

In order to compute the g-asymptotes of $\mathcal {C}$, first we need to determine the infinity branches of $\mathcal {C}$. That is, the sets

$$\begin{aligned} B=\{(z, r(z))\in \mathbb {C}^2: \,z\in \mathbb {C},\,|z|>M\},\,\, \text{ where }\,\, r(z)=z\varphi (z^{-1}). \end{aligned}$$

For this purpose, taking into account Definition 1, we have that $f(z,r(z))=F(1:\varphi (z^{-1}):z^{-1})=F(1:\varphi (t):t)=0$ around $t=0$, where $t=z^{-1}$ and F is the polynomial defining implicitly $\mathcal {C}^*$. Observe that in this section, we are given the parametrization $\mathcal {P}^*$ of $\mathcal {C}^*$ and then, $F(\mathcal {P}^*(s))=F\left( 1:{p_{2}(s)}/{p_{1}(s)}:{1}/{p_{1}(s)}\right) =0.$ Thus, intuitively speaking, in order to compute the infinity branches of $\mathcal {C}$, and in particular the series $\varphi$, one needs to rewrite the parametrization $\mathcal {P}^*(s)$ in the form $(1:\varphi (t):t)$ around $t=0$. For this purpose, the idea is to look for a value of the parameter s, say $\ell (t)\in \mathbb {C}\langle \langle t\rangle \rangle$, such that $\mathcal {P}^*(\ell (t))=(1:\varphi (t):t)$ around $t=0$.

Hence, from the above reasoning, we deduce that first, we have to consider the equation $1/p_{1}(s)=t$ (or equivalently, $p_{12}(s)-tp_{11}(s)=0$), and we solve it in the variable s around $t=0$. From Puiseux’s Theorem, there exist solutions $\ell _1(t),\ell _2(t),\ldots ,\ell _k(t)\in \mathbb {C}\langle \langle t\rangle \rangle$ such that, $p_{12}(\ell _i(t))-tp_{11}(\ell _i(t))=0,\,i\in \{1,\ldots ,k\},$ in a neighborhood of $t=0$.

Thus, for each $i\in \{1,\ldots ,k\}$, there exists $M_i\in \mathbb {R}^+$ such that the points $(1:\varphi _{i}(t):t)$ or equivalently, the points $(t^{-1}:t^{-1}\varphi _{i}(t):1)$, where $\varphi _{i}(t)=\frac{p_{2}(\ell _i(t))}{p_{1}(\ell _i(t))},$ are in $\mathcal {C}^*$ for $|t|<M_i$ (note that $\mathcal {P}^*(\ell (t))\in \mathcal {C}^*$ since $\mathcal {P}^*$ is a parametrization of $\mathcal {C}^*$). Observe that $\varphi _{i}(t)$ is a Puiseux series, since $p_{2}(\ell _i(t))$ and $p_{1}(\ell _i(t))$ can be written as Puiseux series and $\mathbb {C}\langle \langle t\rangle \rangle$ is a field.

Finally, we set $z=t^{-1}$. Then, we have that the points $(z,r_{i}(z))$, where $r_{i}(z)=z\varphi _{i}(z^{-1})$, are in $\mathcal {C}$ for $|z|>M_i^{-1}$. Hence, the infinity branches of $\mathcal {C}$ are the sets $B_i=\{(z,r_{i}(z))\in \mathbb {C}^2: \,z\in \mathbb {C},\,|z|>M_i^{-1}\},\quad i\in \{1,\ldots ,k\}.$

Note that the series $\ell _i(t)$ satisfies that $p_1(\ell _i(t))t=1$, for $i\in \{1,\ldots ,k\}$. Then, we have that

$$\begin{aligned} \varphi _{i}(t)=\frac{p_{2}(\ell _i(t))}{p_{1}(\ell _i(t))}=p_2(\ell _i(t))t,\quad r_{i}(z)=z\varphi _{i}(z^{-1})=p_2(\ell _i(z^{-1})). \end{aligned}$$

Once we have the infinity branches, we can compute a g-asymptote for each of them by simply removing the terms with negative exponent from $r_{i}$.

Additionally we note, that some of the solutions $\ell _1(t),\ell _2(t),\ldots ,\ell _k(t)\in \mathbb {C}\langle \langle t\rangle \rangle$ might belong to the same conjugacy class. Thus, we only consider one solution for each of these classes. The output asymptote $\widetilde{\mathcal {C}}$ is independent of the solutions $\ell _1(t),\ell _2(t),\ldots ,\ell _k(t)\in \mathbb {C}\langle \langle t\rangle \rangle$ chosen in step 1, and of the leaf chosen to define the branch B.

In the following example, we consider a parametric plane curve with two real infinity branches. We obtain these branches and compute a g-asymptote for each of them.

Example 2

The plane curve $\mathcal {C}$ introduced in Example 1 turns out to be rational, parametrized by

$$\begin{aligned} \mathcal {P}(s)=\left( \frac{3s^4-s-4+5s^3}{(s-1)s^3(s^2+1)}, \frac{2s^2-7s+2}{(s-1)s^2}\right) \in \mathbb {R}(s)^2. \end{aligned}$$

We compute the asymptotes of $\mathcal {C}$. For this purpose, we determine the solutions of the equation $p_{12}(s)-tp_{11}(s)=0$ around $t=0$. For this purpose, we may use, for instance, the command puiseux included in the package algcurves of the computer algebra system Maple. There are four solutions (up to conjugation) that are given by the Puiseux series

$$\begin{aligned} \ell _1(t)= & {} 1+411/16 t^3+21/2 t^2+3/2+\cdots ,\\ \ell _2(t)= & {} -315/32 t^3+11279/64 I t^3+13/4 t^2-243/16 I t^2-5/4 t+7/4 I t+I+\cdots \\ \ell _3(t)= & {} - 315/32 t^3- 11279/64 I t^3+ 13/4 t^2+ 243/16 I t^2- 5/4 t- 7/4 I t-I+\cdots ,\\ \ell _4(t)= & {} - 17/3 t^2- 42179/7776 2^{1/3}t^{5/3}- 2105/1296 2^{2/3}t^{4/3}+ 1/3 t\\{} & {} + 5/6 2^{1/3}t^{2/3}+2^{2/3}t^{1/3}+\cdots . \end{aligned}$$

Now, we compute

$$\begin{aligned} r_{1}(z)= & {} p_2(\ell _1(z^{-1}))= -2 z+17-261/4 z^{-1}+\cdots \\ r_{2}(z)= & {} p_2(\ell _2(z^{-1}))=7/2-7/2 I-127/8 z^{-1} + 15/8 I z^{-1}+\cdots \\ r_{3}(z)= & {} p_2(\ell _2(z^{-1}))=7/2+7/2 I-127/8 z^{-1} - 15/8 I z^{-1}+\cdots \\ r_{4}(z)= & {} p_2(\ell _2(z^{-1}))=5/24- 2^{-1/3} z^{2/3}+ 10/3\cdot 2^{1/3}z^{1/3}\\{} & {} + 1289/648\cdot 2^{2/3} z^{-1/3}+ 173813/15552\cdot 2^{1/3} z^{-2/3}+\cdots \end{aligned}$$

(we may use, for instance, the command series included in the computer algebra system Maple). The curve has four infinity branches given by $B_i=\{(z,r_{i}(z))\in \mathbb {C}^2: \,z\in \mathbb {C},\,|z|>M\}$ for some $M\in \mathbb {R}^+$ (note that $B_4$ has three leaves).

We obtain $\tilde{r}_{i}(z)$ by removing the terms with negative exponent in $r_{i}(z)$ for $i=1,2,3,4$. We get

$$\begin{aligned} \tilde{r}_{1}(z)= & {} -2 z+17\quad \text { and }\quad \tilde{r}_{2}(z)= 7/2-7/2 I \\ \tilde{r}_{3}(z)= & {} 7/2+7/2 I\quad \text { and }\quad \tilde{r}_{4}(z)= 5/24- 2^{-1/3} z^{2/3}+ 10/3\cdot 2^{1/3}z^{1/3}. \end{aligned}$$

The input curve $\mathcal {C}$ has two complex asymptotes $\widetilde{\mathcal {C}}_i$ at $B_i$ for $i=1,2$ and two real asymptotes $\widetilde{\mathcal {C}}_i$ at $B_i$ for $i=3,4$ that can be polynomially parametrized by (see Fig. 1):

$$\begin{aligned} \widetilde{\mathcal {Q}}_1(t)= & {} (t,\, -2t+17),\quad \widetilde{\mathcal {Q}}_2(t)=(t,\, 7/2-7/2 I),\quad \widetilde{\mathcal {Q}}_3(t)=(t,\, 7/2+7/2 I) \\ \widetilde{\mathcal {Q}}_4(t)= & {} (t^3,\, 5/24+10/3 \cdot 2^{1/3}t-2^{-1/3}t^2). \end{aligned}$$

Compare the output with the output obtained in Example 1.

Remark 4

• 1. When we compute the series ${\ell }_i$, we cannot handle its infinite terms so it must be truncated, which may distort the computation of the series $r_{i}$. However, this distortion may not affect to all the terms in $r_{i}$. In fact, the number of affected terms depends on the number of terms considered in ${\ell }_i$. Nevertheless, note that we do not need to know the full expression of $r_{i}$ but only the terms with non negative exponent. In [5] (Proposition 2), it is proved that one can get the terms with non negative exponent in $r_{i}$ by considering just $2\textrm{deg}(p_1)+1$ terms of $\ell _i$.

• 2. We remind that before to apply the method, the input curve must be prepared such that (0 : 1 : 0) is not a point at infinity. As an alternative, one could apply the algorithm first for ${{\mathcal {P}}}$ and then for ${\overline{\mathcal {P}}}:=(p_2(s),p_1(s))\in \mathbb {R}(s)^2$. In this last case, if we get the asymptote $(h_1,\,h_2)$, we have to undo the necessary change of coordinates and we finally get the asymptote $\widetilde{\mathcal {Q}}(t)=(h_2,\,h_1)$. Some of the asymptotes obtained from $\overline{\mathcal {P}}$ may coincide with others obtained from ${{\mathcal {P}}}$ but some other new asymptotes could appear (those corresponding to vertical asymptotes; see Corollary 1.

3.2.1 New method for the parametric (rational) case

In this subsection, we present an improvement of the method described above, which avoids the computation of infinity branches and Puiseux series (see [7]). We develop this method for the plane case but it can be trivially adapted for dealing with rational curves in n-dimensional space.

In the following we consider a rational plane curve $\mathcal {C}$ defined by the rational parametrization

$$\begin{aligned} \mathcal {P}(s)=(p_1(s),p_2(s))\in \mathbb {R}(s)^2,\quad p_i(s)=p_{i1}(s)/p_{i2}(s),\quad \textrm{gcd}(p_{i1},p_{i2})=1,\,\,i=1,2. \end{aligned}$$

We assume that $\textrm{deg}(p_{i1})\le \textrm{deg}(p_{i2})=d_i,\,i=1,2$ (otherwise, we apply a suitable linear change on the variable t). Thus, we have that $\lim _{s\rightarrow \infty }p_i(s)\ne \infty ,\,i=1,2$ and the infinity branches of $\mathcal {C}$ will be traced when s moves around the different roots of the denominators $p_{12}(s)$ and $p_{22}(s)$. In fact, each of these roots yields an infinity branch. The following theorem shows how to obtain a g-asymptote for each of these branches, by just computing some simple limits of rational functions constructed from ${{\mathcal {P}}}(s)$ (see [7]).

Theorem 3

Let $\mathcal {C}$ be a curve defined by a parametrization

$$\begin{aligned} \mathcal {P}(s)=(p_1(s),p_2(s))\in \mathbb {R}(s)^2,\quad p_i(s)=p_{i1}(s)/p_{i2}(s),\quad \textrm{gcd}(p_{i1},p_{i2})=1,\,\,i=1,2, \end{aligned}$$

where $\textrm{deg}(p_{i1})\le \textrm{deg}(p_{i2})=d_i,\,i=1,2$. Let $\tau \in \mathbb {C}$ be such that $p_{i2}(t)=(t-\tau )^{n_i}\overline{p}_{i2}(t)$ (that is, $\tau \in \mathbb {C}$ is a root of multiplicity $n_i$ of $p_{i2}$) where $\overline{p}_{i2}(\tau )\not =0,\,i=1,2$ (that is, $\tau \in \mathbb {C}$ is not a root of $\overline{p}_{i2}$), and $n_1\ge 1$, and let B be the corresponding infinity branch. A g-asymptote of B is defined by the parametrization

$$\begin{aligned} \widetilde{\mathcal {Q}}(t)=(t^{n_1},\, a_{n_2}t^{n_2}+a_{n_2-1}t^{n_2-1}+\ldots +a_{0}), \end{aligned}$$

where

$$\begin{aligned} \begin{array}{ll} a_{n_2}=\lim _{t\rightarrow \tau }\,\, \displaystyle \frac{p_2(t)}{p_{1}(t)^{n_2/n_1}}&{} \\ a_{n_2-1}=\lim _{t\rightarrow \tau }\, p_1(t)^{1/n_1}f_1(t),\quad &{}f_1(t):=\displaystyle \frac{p_2(t)}{p_{1}(t)^{n_2/n_1}}-a_{n_2} \\ a_{n_2-2}=\lim _{t\rightarrow \tau }\, p_1(t)^{1/n_1}f_2(t),\quad &{}f_2(t):= p_1(t)^{1/n_1}f_1(t)-a_{n_2-1} \\ \qquad \quad \vdots &{} \qquad \quad \vdots \\ a_{n_2-i}=\lim _{t\rightarrow \tau }\, p_1(t)^{1/n_1}f_i(t),\quad &{}f_i(t):= p_1(t)^{1/n_1}f_{i-1}(t)-a_{n_2-(i-1)},\,\,i\in \{2,\ldots ,n_2\}. \\ \end{array} \end{aligned}$$

Remark 5

From the above construction, each root $\tau$ of $p_{12}(t)$ yields an infinity branch and, hence, an infinity point $P^*$ (see Remark 2). Note that the parametrization $\mathcal {P}(t)$ can be expressed as $\mathcal {P}(t)=\left( \frac{q_{11}(t)}{q(t)},\frac{q_{12}(t)}{q(t)}\right)$, where $q(t)=\textrm{lcm}(p_{12}(t),p_{22}(t))$ and $q_{1i}(t)=p_i(t)q(t)$. Now, the corresponding projective curve is parametrized by $\mathcal {P}^*(t)=(q_{11}(t),q_{12}(t),q(t))$ and the infinity point associated to $\tau$ is $P^*=(q_{11}(\tau ):q_{12}(\tau ):0)$.

In the following corollary, we analyze the special case of the vertical and horizontal g-asymptotes, i.e. lines of the form $x-a$ or $y-b$, where $a,b\in \mathbb {C}$ (observe that these asymptotes correspond to branches associated to the infinity points (0 : 1 : 0) and (1 : 0 : 0), respectively). More precisely, we prove that these asymptotes are obtained from the non–common roots of the denominators of the given parametrization. Note that in the practical design of engineering and modeling applications, the rational curves are usually presented by numerical coefficients and ${{\mathcal {P}}}(s)$ mostly satisfies that $\textrm{gcd}(p_{12}, p_{22})=1$.

Corollary 1

Let $\mathcal {C}$ be a curve defined by a parametrization

$$\begin{aligned} \mathcal {P}(s)=(p_1(s),p_2(s))\in \mathbb {R}(s)^2,\quad p_i(s)=p_{i1}(s)/p_{i2}(s),\quad \textrm{gcd}(p_{i1},p_{i2})=1,\,\,i=1,2, \end{aligned}$$

where $\textrm{deg}(p_{i1})\le \textrm{deg}(p_{i2}),\,i=1,2$.

• 1. Let $\tau \in \mathbb {C}$ be such that $p_{12}(t)=(t-\tau )^{n_1}\overline{p}_{12}(t)$ where $p_{22}(\tau )\overline{p}_{12}(\tau )\not =0$, and $n_1\ge 1$. It holds that a g-asymptote of $\mathcal {C}$ corresponding to the infinity point (1 : 0 : 0) is the horizontal line $y-p_{2}(\tau )=0$, defined by the parametrization $\widetilde{\mathcal {Q}}(t)=(t,\, p_{2}(\tau )).$

• 2. Let $\tau \in \mathbb {C}$ be such that $p_{22}(t)=(t-\tau )^{n_2}\overline{p}_{22}(t)$ where $p_{12}(\tau )\overline{p}_{22}(\tau )\not =0$, and $n_2\ge 1$. It holds that a g-asymptote of $\mathcal {C}$ corresponding to the infinity point (0 : 1 : 0) is the vertical line $x-p_{1}(\tau )=0$, defined by the parametrization $\widetilde{\mathcal {Q}}(t)=(p_{1}(\tau ),\, t).$

Remark 6

The previous theorem outputs the parametrization $\widetilde{\mathcal {Q}}(t)=(t^{n_1},\, a_{n_2}t^{n_2}+a_{n_2-1}t^{n_2-1}+\ldots +a_{0}),$ and $n_1\ge n_2$ (otherwise (0 : 1 : 0) is an infinity point of the input curve). Note that the degree of the defined curve is not necessary $n_1$ since ${{\mathcal {Q}}}$ could be improper which is equivalent to $\textrm{gcd}(n_1, n_2,\ldots , n_2-j)\not =0$ for every $j=0,\ldots , n_2-1$ such that $a_{n_2-j}\not =0$. Let us assume that $\textrm{gcd}(n_1, n_2,\ldots , n_2-j)=\beta$ for every $j=0,\ldots , n_2-1$ such that $a_{n_2-j}\not =0$. Then, let $n=n_1/\beta$ and

$$\begin{aligned} {{\mathcal {M}}}(t)={{\mathcal {P}}}(t^{1/\beta })=(t^{n}, a_{n_2}t^{n_2/\beta }+a_{n_2-1}t^{(n_2-1)/\beta }+\ldots +a_{0})\in \mathbb {K}[t]^2 \end{aligned}$$

is a proper reparametrization of ${{\mathcal {Q}}}$. Then we get that the theorem outputs an asymptote since the output curve is perfect (it has an only branch and the degree of the curve which is n is equal to the degree of the branch).

By applying the above results, we can easily obtain all the g-asymptotes of any rational plane curve, as the following example shows.

Example 3

Let $\mathcal {C}$ be the plane curve introduced in Examples 1 and 2 defined by the parametrization

$$\begin{aligned} \mathcal {P}(s)=\left( \frac{3s^4-s-4+5s^3}{(s-1)s^3(s^2+1)}, \frac{2s^2-7s+2}{(s-1)s^2}\right) \in \mathbb {R}(s)^2. \end{aligned}$$

We compute the asymptotes of $\mathcal {C}$ using the new method just presented. For this purpose, we first observe that $p_{12}(s)$ has the roots $\tau _1=1,\,\tau _2=0,\,\tau _3=I,\,\tau _4=-I$, with multiplicities $n_{11}=1$, $n_{12}=3$ and $n_{13}=n_{14}=1$. The multiplicities of these roots in $p_{22}(s)$ are $n_{21}=1$, $n_{22}=2$ and $n_{23}=n_{24}=0$.

For $\tau _1=1,$ we compute

$$\begin{aligned} a_{1}=\lim _{t\rightarrow 1}\,\frac{p_2(t)}{p_{1}(t)}=-2,\qquad a_{0}=\lim _{t\rightarrow 1}\, p_1(t)f_1(t)=17,\quad f_1(t):=\frac{p_2(t)}{p_{1}(t)}-a_{1}. \end{aligned}$$

Then, we obtain the asymptote $\widetilde{\mathcal {C}}_1$, defined by the proper parametrization

$$\begin{aligned} \widetilde{\mathcal {Q}}_1(t)=(t,\, -2t+17). \end{aligned}$$

For $\tau _2=0,$ we compute

$$\begin{aligned} \begin{array}{ll} a_{2}=\lim _{t\rightarrow 2}\,\frac{p_2(t)}{p_{1}(t)^{2}}=2^{-4/3}+I\cdot 2^{-4/3}\,3^{1/2} \\ a_{1}=\lim _{t\rightarrow 2}\, p_1(t)f_1(t)=- 5/3\cdot 2^{1/3}+5/3\cdot I\cdot 2^{1/3}\,3^{1/2},\quad f_1(t):=\frac{p_2(t)}{p_{1}(t)^{2}}-a_{2} \\ a_{0}=\lim _{t\rightarrow 2}\, p_1(t) f_2(t)=\frac{5}{24},\quad f_2(t):=p_1(t)f_{1}(t)-a_{1}. \\ \end{array} \end{aligned}$$

Then, we obtain the asymptote $\widetilde{\mathcal {C}}_2$, defined by the proper parametrization

$$\begin{aligned} \widetilde{\mathcal {Q}}_2(t)=\left( t^3,\, 5/24+(-5/3\cdot 2^{1/3}+5/3\cdot I\cdot 2^{1/3}\,3^{1/2})t+(2^{-4/3}+I\cdot 2^{-4/3}\,3^{1/2})t^2\right) . \end{aligned}$$

Finally for $\tau _3=I,$ and $\tau =-I$ we get the asymptotes $\widetilde{\mathcal {C}}_i,\,i=3,4,$, defined by the proper parametrizations

$$\begin{aligned} \widetilde{\mathcal {Q}}_3(t)=\left( t,\, p_2(I)\right) =\left( t,\, 7/2-7/2 I\right) ,\quad \widetilde{\mathcal {Q}}_4(t)=\left( t,\, p_2(-I)\right) =\left( t,\, 7/2+7/2 I\right) . \end{aligned}$$

See Fig. 1 and compare the output with the output obtained in Example 2. We may check that $\widetilde{\mathcal {Q}}_2(t)$ is a reparametrización of the proper parametrization $\widetilde{\mathcal {Q}}_4(t)$ obtained in Example 2. In fact, note that $\widetilde{\mathcal {Q}}_2(t)= \widetilde{\mathcal {Q}}_4(\xi \,t)$, with $\xi =1/2+I\sqrt{3}/2$ satisfies that $\xi ^3=1$.

Remark 7

The above method allows us to easily obtain all the generalized asymptotes of a rational curve. However, we should compute the roots of the denominators of the parametrization, which may entail certain difficulties if algebraic numbers are involved. This problem is solved using the notion of conjugate points (see Definition 12 in [12]), which help us to overcome this problem. The idea is to collect the points whose coordinates depend algebraically on all the conjugate roots of a same irreducible polynomial (for more details see [12]).

4 The non-rational case: computing branches and asymptotes

Throughout this paper so far, we have dealt with algebraic plane curves implicitly and rational parametrically defined. In this section, we present all the previous concepts introduced before for the case of meromorphic functions. In addition, we present a method to compute infinity branches and g-asymptotes for these type of functions. This method is based on the idea presented in Sect. 3.2.1, where we show how one easily compute the generalized asymptotes by only determining some simple limits of rational functions constructed from the rational functions defining the input parametrization.

We remind that the g-asymptotes of an input curve, $\mathcal {C}$, are perfect curves computed from the infinity branches of $\mathcal {C}$. That is, once one has the branch

$$\begin{aligned} B=\{(z, r(z))\in \mathbb {C}^2: \,z\in \mathbb {C},\,|z|>M\}, \end{aligned}$$

where (see equality 3.1)

$$\begin{aligned} r(z)=mz+a_1z^{1-n_1/n}+\cdots +a_kz^{1-n_k/n}+a_{k+1}z^{1-N_{k+1}/N}+\cdots , \end{aligned}$$

and $0<N_1<\cdots<N_k\le N<N_{k+1}<\cdots$, $\textrm{gcd}(N,N_1,\ldots ,N_k)=b$, $N=n \cdot b$, $N_j=n_j\cdot b,\,\,j\in \{1,\ldots ,k\}$, the asymptote is obtained by considering the terms with non negative exponent in the series r(z). We note that we have simplified the non negative exponents such that $\textrm{gcd}(n,n_1,\ldots ,n_k)=1$, $0<n_1<n_2<\cdots$, and $n_k\le n$. We say that n is the degree of B ($\textrm{deg}(B)$) and N is the ramification index of the branch B ($\nu (B)$).

Additionally, we say that the infinity branch B is associated to the infinity point $P=(1:m:0),\, m\in \mathbb {C}$ and it holds that $f(z,r(z))=0$ for $z\in \mathbb {C},\,|z|>M$ when the curve is implicitly defined. If the curve is defined by the rational parametrization, it holds that

$$\begin{aligned} \lim _{t\rightarrow \tau } \mathcal {P}(t)=\lim _{z\rightarrow \infty } (z, r(z)), \end{aligned}$$

where $\tau$ is a value of t for which ${{\mathcal {P}}}$ is not defined and ${{\mathcal {P}}}^*(\tau )=(1:m:0)$. In the case we are dealing in this section, we do not have an implicit equation so we would use this last characterization.

We also remind that a g-asymptote of $\mathcal {C}$ at B is a perfect curve that approaches $\mathcal {C}$ at B. So, we need to compute a perfect curve approaching the input curve $\mathcal {C}$, then we will get the g-asymptote. For this purpose, we recall that a curve defined by a proper parametrization of the form $(t^{n}, a_{n}t^{n}+a_{n-1}t^{n-1}+\cdots +a_0)$ is always perfect (see Sect. 3). So, our purpose is to compute a curve of this form approaching the input curve $\mathcal {C}$. That is, we impose the condition that

$$\begin{aligned} \lim _{t\rightarrow \tau } \mathcal {P}(t)=\lim _{z\rightarrow \infty } (z^n, a_{n}z^{n}+a_{n-1}z^{n-1}+\cdots +a_0), \end{aligned}$$

where $\tau$ is a value of t for which ${{\mathcal {P}}}$ is not defined.

Using this idea in fact we see how to determine the infinity branches

$$\begin{aligned} B=\{(z, r(z))\in \mathbb {C}^2: \,z\in \mathbb {C},\,|z|>M\}, \end{aligned}$$

where

$$\begin{aligned} r(z)=mz+a_1z^{1-n_1/n}+\cdots +a_kz^{1-n_k/n}+a_{k+1}z^{1-N_{k+1}/N}+\cdots , \end{aligned}$$

and $0<N_1<\cdots<N_k\le N<N_{k+1}<\cdots$. Since we can not compute $\varphi (t)$, in order to compute B, we use the idea presented in Sect. 3.2.1 and we impose the condition

$$\begin{aligned} \lim _{t\rightarrow \tau } \mathcal {P}(t)=\lim _{z\rightarrow \infty } (z, r(z)). \end{aligned}$$

In the following, we deal with meromorphic functions from an open subset of the complex plane onto $\mathbb {C}^n,\,n\ge 1$. We remind that meromorphic functions are functions on an open subset D of $\mathbb {C}$ that are holomorphic on all D except for a set of isolated points, which are poles of the functions. By abuse of notation, we denote by $\mathcal {P}(t):=(p_1(t),\ldots ,p_n(t))$ these meromorphic functions and we say that the image of $\mathcal P$ is a special curve  $\mathcal {C}$ parametrically defined in  n-dimensional space.

We develop the method for $n=2$ but it can be straightforward adapted for dealing with curves in n-dimensional space. Thus, in this section we have a curve $\mathcal {C}$ that is the image of the parametrization

$$\begin{aligned} \mathcal {P}(s)=(p_1(s),p_2(s)),\quad p_i(s)=p_{i1}(s)/p_{i2}(s),\quad \textrm{gcd}(p_{i1},p_{i2})=1,\,\,i=1,2, \end{aligned}$$

where the functions $p_{i}(s),\,i\in \{1,2\}$ are meromorphic on the complex plane.

The different roots of the denominators $p_{i2},\,\i =1,2$ (the poles of the meromorphic functions $p_i(s),\,i=1,2$) yield the infinity branches associated to the infinity points $P=(1:m:0),\, m\in \mathbb {C}$. The following theorem shows how to compute the branches, by just computing some simple limits of some functions constructed from ${{\mathcal {P}}}(s)$. Afterwards, from each of these branches we can easily obtain the g-asymptote.

We assume that we have prepared the input curve $\mathcal {C}$, by means of a suitable projective change of coordinates (if necessary) such that (0 : 1 : 0) is not a point at infinity.

Theorem 4

Let $\mathcal {C}$ be a curve defined by a parametrization

$$\begin{aligned} \mathcal {P}(s)=(p_1(s),p_2(s)),\quad p_i(s)=p_{i1}(s)/p_{i2}(s),\quad \textrm{gcd}(p_{i1},p_{i2})=1,\,\,i=1,2. \end{aligned}$$

Let $\tau \in \mathbb {C}$ be such that $p_{i2}(t)=(t-\tau )^{n_i/m_i}\overline{p}_{i2}(t)$ where $\overline{p}_{i2}(\tau )\not =0,\,i=1,2$, and $n_1/m_1\ge 1$. Let us assume that $p_{i1}(t)=(t-\tau )^{u_i/v_i}\overline{p}_{i1}(t),\,i=1,2$ and $0\le u_1/v_1<n_1/m_1$ and $0\le u_2/v_2\le n_2/m_2$. Let $\gamma :=\textrm{lcm}(m_1,m_2,v_1,v_2)$ and

$$\begin{aligned} \mathcal {M}(s)=\mathcal {P}(s^\gamma )=(\wp _1(s),\wp _2(s)),\quad \wp _i(s)=\wp _{i1}(s)/\wp _{i2}(s),\,\,i=1,2. \end{aligned}$$

Let $\bar{n}_i:=n_i\gamma /m_i-u_i\gamma /v_i,\,i=1,2$. An infinity branch associated to an infinity point $P=(1:m:0), m \in \mathbb {C}$ is given as

$$\begin{aligned} B=\{(z,r(z))\in \mathbb {C}^2: \,z\in \mathbb {C},\,|z|>M\}, \end{aligned}$$

where

$$\begin{aligned} r(z)=a_{\bar{n}_2}z^{\bar{n}_2/\bar{n}_1}+a_{\bar{n}_2-1}z^{(\bar{n}_2-1)/\bar{n}_1}+\ldots +a_{0}+a_{-1}z^{-1/\bar{n}_1}+a_{-2}z^{-2/\bar{n}_1}+\cdots \end{aligned}$$

($m=a_1$), and

$$\begin{aligned} \begin{array}{ll} a_{\bar{n}_2}=\lim \limits _{t\rightarrow \tau }\,\, \displaystyle \frac{\wp _2(t)}{\wp _{1}(t)^{\bar{n}_2/\bar{n}_1}}&{} \\ a_{\bar{n}_2-1}=\lim \limits _{t\rightarrow \tau }\, \wp _1(t)^{1/\bar{n}_1}f_1(t),\quad &{}f_1(t):=\displaystyle \frac{\wp _2(t)}{\wp _{1}(t)^{\bar{n}_2/\bar{n}_1}}-a_{\bar{n}_2} \\ a_{\bar{n}_2-2}=\lim \limits _{t\rightarrow \tau }\, \wp _1(t)^{1/\bar{n}_1}f_2(t),\quad &{}f_2(t):= \wp _1(t)^{1/\bar{n}_1}f_1(t)-a_{\bar{n}_2-1} \\ \qquad \quad \vdots &{} \qquad \quad \vdots \\ a_{\bar{n}_2-i}=\lim \limits _{t\rightarrow \tau }\, \wp _1(t)^{1/\bar{n}_1}f_i(t),\quad &{}f_i(t):= \wp _1(t)^{1/\bar{n}_1}f_{i-1}(t)-a_{\bar{n}_2-(i-1)},\,\, \\ \end{array} \end{aligned}$$

for $i\in \{2,\ldots ,\bar{n}_2,\bar{n}_2+1,\bar{n}_2+2,\cdots \}$.

Proof

We use the equality

$$\begin{aligned} \lim _{t\rightarrow \tau } \mathcal {P}(t)=\lim \limits _{z\rightarrow \infty } (z,r(z)) =\lim \limits _{z\rightarrow \infty } (z^{\bar{n}_1},r(z^{\bar{n}_1})) \end{aligned}$$

for easily obtaining the coefficients, $a_{n_2-i}$ for $i\in \{2,\ldots ,\bar{n}_2,\bar{n}_2+1,\bar{n}_2+2,\cdots \}$. Indeed, we have that

$$\begin{aligned}{} & {} \lim \limits _{t\rightarrow \tau }\,\frac{\wp _2(t)}{\wp _{1}(t)^{\bar{n}_2/\bar{n}_1}}\\{} & {} \quad = \lim _{z\rightarrow \infty }\frac{a_{\bar{n}_2}z^{\bar{n}_2/\bar{n}_1}+a_{\bar{n}_2-1}z^{(\bar{n}_2-1)/\bar{n}_1}+\ldots +a_{0}+a_{-1}z^{-1/\bar{n}_1}+a_{-2}z^{-2/\bar{n}_1} +\cdots }{(z^{\bar{n}_1})^{\bar{n}_2/\bar{n}_1}} = a_{\bar{n}_2},\\{} & {} \lim _{t\rightarrow \tau }\,\frac{\wp _2(t)-a_{\bar{n}_2}\wp _{1}(t)^{\bar{n}_2/\bar{n}_1}}{\wp _{1}(t)^{(\bar{n}_2-1)/\bar{n}_1}}\\{} & {} \quad =\lim _{t\rightarrow \infty }\frac{a_{\bar{n}_2-1}z^{(\bar{n}_2-1)/\bar{n}_1}+\ldots +a_{0}+a_{-1}z^{-1/\bar{n}_1}+a_{-2}z^{-2/\bar{n}_1}+\cdots }{(z^{\bar{n}_1})^{(\bar{n}_2-1)/\bar{n}_1}}=a_{\bar{n}_2-1},\\{} & {} \lim _{t\rightarrow \tau }\,\frac{\wp _2(t)-a_{\bar{n}_2}\wp _{1}(t)^{\bar{n}_2/\bar{n}_1}-a_{\bar{n}_2-1}\wp _{1}(t)^{(\bar{n}_2-1)/\bar{n}_1}}{\wp _{1}(t)^{(\bar{n}_2-2)/\bar{n}_1}}\\{} & {} \quad =\lim _{z\rightarrow \infty }\frac{a_{\bar{n}_2-2}z^{(\bar{n}_2-2)/\bar{n}_1}+\ldots +a_{0}+a_{-1}z^{-1/\bar{n}_1}+a_{-2}z^{-2/\bar{n}_1}+\cdots }{(z^{\bar{n}_1})^{(\bar{n}_2-2)/n_1}}=a_{\bar{n}_2-2} \end{aligned}$$

and, reasoning similarly,

$$\begin{aligned}{} & {} \lim _{t\rightarrow \tau }\,(\wp _2(t)-a_{\bar{n}_2}\wp _{1}(t)^{n_2/n_1}-a_{\bar{n}_2-1}\wp _{1}(t)^{(\bar{n}_2-1)/\bar{n}_1}-\cdots -a_1\wp _{1}(t)^{1/\bar{n}_1})\\{} & {} \quad =\lim _{z \rightarrow \infty } (a_{0}+a_{-1}z^{-1/\bar{n}_1}+a_{-2}z^{-2/\bar{n}_1}+\cdots )=a_{0}. \end{aligned}$$

Additionally, we have that

$$\begin{aligned}{} & {} \lim _{t\rightarrow \tau }\,\frac{\wp _2(t)-a_{\bar{n}_2}\wp _{1}(t)^{n_2/n_1}-a_{\bar{n}_2-1}\wp _{1}(t)^{(\bar{n}_2-1)/\bar{n}_1}-\cdots -a_0}{\wp _1(t)^{-1/n_1}}\\{} & {} \quad =\lim _{z \rightarrow \infty }\frac{a_{-1}z^{-1/\bar{n}_1}+a_{-2}z^{-2/\bar{n}_1}+\cdots }{(z^{n_1})^{-1/n_1}}=a_{-1},\\{} & {} \lim _{t\rightarrow \tau }\,\frac{\wp _2(t)-a_{\bar{n}_2}\wp _{1}(t)^{n_2/n_1}-a_{\bar{n}_2-1}\wp _{1}(t)^{(\bar{n}_2-1)/\bar{n}_1}-\cdots -a_0-a_{-1}z^{-1/\bar{n}_1}}{\wp _1(t)^{-2/n_1}}\\{} & {} \quad =\lim _{z \rightarrow \infty }\frac{a_{-2}z^{-2/\bar{n}_1}+\cdots }{(z^{\bar{n}_1})^{-2/\bar{n}_1}}=a_{-2}, \end{aligned}$$

and, reasoning similarly for $i\ge 3$

$$\begin{aligned}{} & {} \lim _{t\rightarrow \tau }\, \\{} & {} \quad \frac{\wp _2(t)-a_{\bar{n}_2}\wp _{1}(t)^{n_2/n_1}-a_{\bar{n}_2-1}\wp _{1}(t)^{(\bar{n}_2-1)/\bar{n}_1}-\cdots -a_0-a_{-1}z^{-1/\bar{n}_1}-\cdots -a_{-(i-1)}z^{-(i-1)/\bar{n}_1}}{\wp _1(t)^{-i/\bar{n}_1}}\\{} & {} \quad =\lim _{z \rightarrow \infty }\frac{a_{-i}z^{-i/\bar{n}_1}+\cdots }{(z^{n_1})^{-i/n_1}}=a_{-i}. \end{aligned}$$

Finally, we observe that we may write

$$\begin{aligned}{} & {} \frac{\wp _2(t)-a_{\bar{n}_2}\wp _{1}(t)^{\bar{n}_2/\bar{n}_1}}{\wp _{1}(t)^{(\bar{n}_2-1)/\bar{n}_1}}=\wp _1(t)^{1/\bar{n}_1}f_1(t),\\{} & {} f_1(t):=\displaystyle \frac{\wp _2(t)}{\wp _{1}(t)^{\bar{n}_2/\bar{n}_1}}-a_{\bar{n}_2}\\{} & {} \frac{\wp _2(t)-a_{\bar{n}_2}p_{1}(t)^{\bar{n}_2/\bar{n}_1}-a_{\bar{n}_2-1}p_{1}(t)^{(\bar{n}_2-1)/\bar{n}_1}}{\wp _{1}(t)^{(\bar{n}_2-2)/\bar{n}_1}}=\wp _1(t)^{1/\bar{n}_1}f_2(t),\\{} & {} f_2(t):= \wp _1(t)^{1/\bar{n}_1}f_1(t)-a_{\bar{n}_2-1} \end{aligned}$$

and in general,

$$\begin{aligned}{} & {} \frac{\wp _2(t)-a_{\bar{n}_2}\wp _{1}(t)^{n_2/n_1}-a_{\bar{n}_2-1}\wp _{1}(t)^{(\bar{n}_2-1)/\bar{n}_1}-\cdots -a_0-a_{-1}z^{-1/\bar{n}_1}-\cdots -a_{(\bar{n}_2-i+1)}z^{(\bar{n}_2-i+1)/\bar{n}_1}}{\wp _1(t)^{(\bar{n}_2-i)/\bar{n}_1}}\\{} & {} \quad =\wp _1(t)^{1/\bar{n}_1}f_i(t),\quad f_i(t):= \wp _1(t)^{1/\bar{n}_1}f_{i-1}(t)-a_{\bar{n}_2-i+1} \end{aligned}$$

for $i\in \{2,\ldots ,\bar{n}_2,\bar{n}_2+1,\bar{n}_2+2,\cdots \}$. $\square$

Remark 8

Note that $\bar{n}_1$ is not the degree of B but its ramification index. In addition, we observe that since (0 : 1 : 0) is not a point at infinity then $\bar{n}_1\ge \bar{n}_2$.

Remark 9

From the above construction, each root $\tau$ of $p_{12}(t)$ yields an infinity branch and, hence, an infinity point $P=(1:m:0)$ (see Remark 2). Note that the parametrization $\mathcal {M}(t)$ constructed in the previous theorem can be expressed as $\mathcal {M}(t)=\left( \frac{\wp _{11}(t)}{\wp (t)},\frac{\wp _{12}(t)}{\wp (t)}\right)$, where $\wp (t)=\textrm{lcm}(\wp _{12}(t),\wp _{22}(t))$ and $\wp _{1i}(t)=\wp _i(t)\wp (t)$. Now, the corresponding projective curve is parametrized by $\mathcal {M}^*(t)=(\wp _{11}(t),\wp _{12}(t),\wp (t))$ and the infinity point associated to $\tau$ is $P=(\wp _{11}(\tau ):\wp _{12}(\tau ):0)$. Note that $P=(1:\wp _{12}(\tau )/\wp _{11}(\tau ):0)$ if $\wp _{11}(\tau )\not =0$.

From Theorem 4, we easily get the following theorem that allows us to compute the g-asymptote.

Theorem 5

Let $\mathcal {C}$ be a curve defined by a parametrization

$$\begin{aligned} \mathcal {P}(s)=(p_1(s),p_2(s)),\quad p_i(s)=p_{i1}(s)/p_{i2}(s),\quad \textrm{gcd}(p_{i1},p_{i2})=1,\,\,i=1,2. \end{aligned}$$

Let $\tau \in \mathbb {C}$ be such that $p_{i2}(t)=(t-\tau )^{n_i/m_i}\overline{p}_{i2}(t)$ where $\overline{p}_{i2}(\tau )\not =0,\,i=1,2$, and $n_1/m_1\ge 1$, and let B be the corresponding infinity branch. Let us assume that $p_{i1}(t)=(t-\tau )^{u_i/v_i}\overline{p}_{i1}(t),\,i=1,2$ and $0\le u_1/v_1<n_1/m_1$ and $0\le u_2/v_2\le n_2/m_2$. Let $\gamma :=\textrm{lcm}(m_1,m_2,v_1,v_2)$ and

$$\begin{aligned} \mathcal {M}(s)=\mathcal {P}(s^\gamma )=(\wp _1(s),\wp _2(s)),\quad \wp _i(s)=\wp _{i1}(s)/\wp _{i2}(s),\,\,i=1,2. \end{aligned}$$

Let $\bar{n}_i:=n_i\gamma /m_i-u_i\gamma /v_i,\,i=1,2$. A g-asymptote of an infinity branch B associated to an infinity point $P=(1:m:0), m \in \mathbb {C}$ is defined by a proper reparametrization of

$$\begin{aligned} \widetilde{\mathcal {Q}}(t)=(t^{\bar{n}_1},\, a_{\bar{n}_2}t^{\bar{n}_2}+a_{\bar{n}_2-1}t^{\bar{n}_2-1}+\ldots +a_{0}), \end{aligned}$$

($m=a_1$), where

$$\begin{aligned} \begin{array}{ll} a_{\bar{n}_2}=\lim \limits _{t\rightarrow \tau }\,\, \displaystyle \frac{\wp _2(t)}{\wp _{1}(t)^{\bar{n}_2/\bar{n}_1}}&{} \\ a_{\bar{n}_2-1}=\lim \limits _{t\rightarrow \tau }\, \wp _1(t)^{1/\bar{n}_1}f_1(t),\quad &{}f_1(t):=\displaystyle \frac{\wp _2(t)}{\wp _{1}(t)^{\bar{n}_2/\bar{n}_1}}-a_{\bar{n}_2} \\ a_{\bar{n}_2-2}=\lim \limits _{t\rightarrow \tau }\, \wp _1(t)^{1/\bar{n}_1}f_2(t),\quad &{}f_2(t):= \wp _1(t)^{1/\bar{n}_1}f_1(t)-a_{\bar{n}_2-1} \\ \qquad \quad \vdots &{} \qquad \quad \vdots \\ a_{\bar{n}_2-i}=\lim \limits _{t\rightarrow \tau }\, \wp _1(t)^{1/\bar{n}_1}f_i(t),\quad &{}f_i(t):= \wp _1(t)^{1/\bar{n}_1}f_{i-1}(t)-a_{\bar{n}_2-(i-1)},\,\,i\in \{2,\ldots ,\bar{n}_2\}. \\ \end{array} \end{aligned}$$

Proof

We first note that a curve $\widetilde{\mathcal {C}}$ approaching the infinity branch B is given by

$$\begin{aligned} \widetilde{Q}(t)=(t^{\bar{n}_1},\widetilde{r}(t^{\bar{n}_1}))=(t^{\bar{n}_1},\, a_{\bar{n}_2}t^{\bar{n}_2}+a_{\bar{n}_2-1}t^{\bar{n}_2-1}+\ldots +a_{0}), \end{aligned}$$

where $\bar{n}_1\ge \bar{n}_2$ (see Remark 8), and $\widetilde{r}(z)$ can be computed from r(z) by removing the terms with negative exponent (see Theorem 4 and Sect. 3.1). In order to prove that $\widetilde{\mathcal {C}}$ is a g-asymptote, we need to prove that it is a perfect curve. For this purpose, we observe that the degree of $\widetilde{\mathcal {C}}$ is not necessary $\bar{n}_1$ since $\widetilde{Q}$ could be improper which is equivalent to $\textrm{gcd}(\bar{n}_1, \bar{n}_2,\ldots , \bar{n}_2-j)\not =1$ for every $j=0,\ldots , \bar{n}_2-1$ such that $a_{\bar{n}_2-j}\not =0$ (see Remark 8). Let us assume that $\textrm{gcd}(\bar{n}_1, \bar{n}_2,\ldots ,\bar{n}_2-j)=\beta$ for every $j=0,\ldots , \bar{n}_2-1$ such that $a_{\bar{n}_2-j}\not =0$. Then, let we consider the reparametrizatin

$$\begin{aligned} {{\mathcal {M}}}(t)= {{\mathcal {P}}}(t^{1/\beta })=(t^{\bar{n}_1/\beta },\, a_{\bar{n}_2}t^{\bar{n}_2/\beta }+a_{\bar{n}_2-1}t^{(\bar{n}_2-1)/\beta }+\ldots +a_{0}) \end{aligned}$$

is a proper reparametrization of $\widetilde{Q}$ (note that the exponents are natural integers since $\textrm{gcd}(\bar{n}_1, \bar{n}_2,\ldots ,\bar{n}_2-j)=\beta$ for every $j=0,\ldots , \bar{n}_2-1$ such that $a_{\bar{n}_2-j}\not =0$). Then we get that the theorem outputs an asymptote since $\widetilde{\mathcal {C}}$ is perfect (it has an only branch and the degree of the curve $\widetilde{\mathcal {C}}$ which is ${\bar{n}_1/\beta }$, see Remark 8, is equal to the degree of the branch). $\square$

In the following corollaries, we analyze the special case of the vertical and horizontal g-asymptotes, i.e. lines of the form $x-a$ or $y-b$, where $a,b\in \mathbb {C}$ (observe that these asymptotes correspond to branches associated to the infinity points (0 : 1 : 0) and (1 : 0 : 0), respectively). More precisely, we prove that these asymptotes are obtained from the non–common roots of the denominators of the given parametrization. Note that in the practical design of engineering and modeling applications, the curves are usually presented by numerical coefficients and ${{\mathcal {P}}}(s)$ mostly satisfies that $\textrm{gcd}(p_{12}, p_{22})=1$.

Corollary 2

Let $\mathcal {C}$ be a curve defined by a parametrization

$$\begin{aligned} \mathcal {P}(s)=(p_1(s),p_2(s),\quad p_i(s)=p_{i1}(s)/p_{i2}(s),\quad \textrm{gcd}(p_{i1},p_{i2})=1,\,\,i=1,2. \end{aligned}$$

Let $\tau \in \mathbb {C}$ be such that $p_{i2}(t)=(t-\tau )^{n_i/m_i}\overline{p}_{i2}(t)$ where $\overline{p}_{i2}(\tau )\not =0,\,i=1,2$, and $n_1/m_1\ge 1$, and let B be the corresponding infinity branch. Let us assume that $p_{i1}(t)=(t-\tau )^{u_i/v_i}\overline{p}_{i1}(t),\,i=1,2$ and $0\le u_1/v_1<n_1/m_1$ and $0\le u_2/v_2=n_2/m_2$. Let $\gamma :=\textrm{lcm}(m_1,m_2,v_1,v_2)$ and

$$\begin{aligned} \mathcal {M}(s)=\mathcal {P}(s^\gamma )=(\wp _1(s),\wp _2(s)),\quad \wp _i(s)=\wp _{i1}(s)/\wp _{i2}(s),\,\,i=1,2. \end{aligned}$$

Let $\bar{n}_i:=n_i\gamma /m_i-u_i\gamma /v_i,\,i=1,2$. It holds that a g-asymptote of $\mathcal {C}$ corresponding to the infinity point (1 : 0 : 0) is the horizontal line $y-\wp _{2}(\tau )=0$, defined by the parametrization $\widetilde{\mathcal {Q}}(t)=(t,\, \wp _{2}(\tau )).$

Proof

We apply Theorem 3 with $\bar{n}_2=0.$ $\square$

Corollary 3

Let $\mathcal {C}$ be a curve defined by a parametrization

$$\begin{aligned} \mathcal {P}(s)=(p_1(s),p_2(s),\quad p_i(s)=p_{i1}(s)/p_{i2}(s),\quad \textrm{gcd}(p_{i1},p_{i2})=1,\,\,i=1,2. \end{aligned}$$

Let $\tau \in \mathbb {C}$ be such that $p_{i2}(t)=(t-\tau )^{n_i/m_i}\overline{p}_{i2}(t)$ where $\overline{p}_{i2}(\tau )\not =0,\,i=1,2$, and $n_2/m_2\ge 1$, and let B be the corresponding infinity branch. Let us assume that $p_{i1}(t)=(t-\tau )^{u_i/v_i}\overline{p}_{i1}(t),\,i=1,2$ and $0\le u_2/v_2<n_2/m_2$ and $0\le u_1/v_1=n_1/m_1$. Let $\gamma :=\textrm{lcm}(m_1,m_2,v_1,v_2)$ and

$$\begin{aligned} \mathcal {M}(s)=\mathcal {P}(s^\gamma )=(\wp _1(s),\wp _2(s)),\quad \wp _i(s)=\wp _{i1}(s)/\wp _{i2}(s),\,\,i=1,2. \end{aligned}$$

Let $\bar{n}_i:=n_i\gamma /m_i-u_i\gamma /v_i,\,i=1,2$. It holds that a g-asymptote of $\mathcal {C}$ corresponding to the infinity point (0 : 1 : 0) is the vertical line $x-p_{1}(\tau )=0$, defined by the parametrization $\widetilde{\mathcal {Q}}(t)=(\wp _{1}(\tau ),\, t).$

Proof

We apply Corollary 2 to the parametrization $(p_2(s), p_1(s))$ and we get the asymptote defined by the parametrization $(t, p_{1}(\tau ))$. Afterwards, we undo the change of coordinates (see statement 2 in Remark 4). $\square$

In the following we introduce the Algorithm Asymptotes Construction-Parametric Non-Rational Case, which uses the above results for computing the g-asymptotes of a plane curve.

By applying Algorithm Asymptotes Construction-Parametric Non-Rational Case, we can easily obtain all the g-asymptotes of any plane curve, as the following examples show.

Example 4

We consider the curve $\mathcal {C}$ defined by the parametrization

$$\begin{aligned} \mathcal {P}(s)=(p_1(s), p_2(s))=\left( \frac{\,s^{1/2}+1}{\,s^{1/2} \sin (s)}, \frac{s^2+s+5}{\sin (s)}\right) . \end{aligned}$$

We apply the algorithm Asymptotes Construction-Parametric Non-Rational Case.

Step 1::

We observe that $p_{12}(s)$ and $p_{22}(s)$ have the root $\tau =0$, and $p_{i}(s)=p_{i1}/p_{i2},\,i\in \{1,2\}$ are meromorphic functions on the complex plane.

Step 2::

For $\tau =0:$

Step 2.1::

We write

$$\begin{aligned} p_{11}(s)= & {} s^{1/2}+1,\quad p_{12}(s)=s^{3/2}(1-1/6 s^{2}+1/120 s^4-1/5040 s^6+\cdots ) \\ p_{21}(s)= & {} s^2+s+5,\quad p_{22}(s)=s- 1/6 s^3+ 1/120 s^5- 1/5040 s^7+\cdots . \end{aligned}$$

Observe that $p_{i1}(0)\not =0$ for $i=1,2$ and thus, we consider

$$\begin{aligned} \mathcal {M}(s)= & {} \mathcal {P}(s^2)=(\wp _1(s),\wp _2(s))=\left( \frac{s+1}{s \sin (s^2)}, \frac{s^4+s^2+5}{\sin (s^2)}\right) ,\\ \wp _i(s)= & {} \wp _{i1}(s)/\wp _{i2}(s),\,\,i=1,2. \end{aligned}$$

We get that $\bar{n}_1:=3$ and $\bar{n}_2:=2$.

Step 2.2::

We have that

$$\begin{aligned} \begin{array}{ll} a_{2}=\lim _{t\rightarrow 2}\,\frac{p_2(t)}{p_{1}(t)^{2}}=5 &{}\\ a_{1}=\lim _{t\rightarrow 2}\, p_1(t)f_1(t)-10/3,\quad &{}f_1(t):=\frac{p_2(t)}{p_{1}(t)^{2}}-a_{2} \\ a_{0}=\lim _{t\rightarrow 2}\, p_1(t) f_2(t)=8/3,\quad &{}f_2(t):=p_1(t)f_{1}(t)-a_{1}. \\ \end{array} \end{aligned}$$

Step 2.3::

We obtain the asymptote $\widetilde{\mathcal {C}}$, defined by the proper parametrization

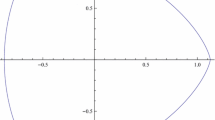
$$\begin{aligned} \widetilde{\mathcal {Q}}(t)=(t^3,\, 5t^2-10/3t+8/3). \end{aligned}$$

Step 3::

We observe that all the roots of $p_{12}(s)$ are also roots of $p_{22}(s)$ (that is, the poles of $p_1$ are the poles of $p_2$), so there are no vertical asymptotes.

Step 4::

The algorithm returns the asymptote $\widetilde{\mathcal {C}}$ of the input curve, $\mathcal {C}$ (see Fig. 2).

Fig. 2

Curve $\mathcal {C}$ (left) and curve and asymptotes (right)

Example 5

We consider the curve $\mathcal {C}$ defined by the parametrization

$$\begin{aligned} \mathcal {P}(s)=(p_1(s), p_2(s))=\left( \frac{\cos (s)-1}{s^{3/2}\sin (s)}, \frac{\sin (s\pi )}{s^{1/2} \sin (s)}\right) . \end{aligned}$$

We apply the algorithm Asymptotes Construction-Parametric Non-Rational Case.

Step 1::

We observe that $p_{12}(s)$ and $p_{22}(s)$ have the root $\tau =0$, and $p_{i}(s)=p_{i1}/p_{i2},\,i\in \{1,2\}$ are meromorphic functions on the complex plane.

Step 2::

For $\tau =0:$

Step 2.1::

We write

$$\begin{aligned}{} & {} p_{12}(s)=s^{5/2}(1-1/6 s^2+1/120s^4-1/5040 s^6+\cdots ) \\{} & {} p_{22}(s)=s^{3/2}(1-1/6 s^2+1/120 s^4-1/5040s^6+\cdots ) \\{} & {} p_{11}(s)s^2(-1/2+1/24s^2-1/720s^4+1/40320s^6+\cdots ) \\{} & {} p_{21}(s)=\pi s (1-1/6s^2\pi ^2+1/120s^4 \pi ^4-1/5040 s^5\pi ^6+\cdots ). \end{aligned}$$

Thus, we consider

$$\begin{aligned} \mathcal {M}(s)= & {} \mathcal {P}(s^2)=(\wp _1(s),\wp _2(s))=\left( \frac{\cos (s^2)-1}{s^3 \sin (s^2)}, \frac{\sin (s^2 \pi )}{s \sin (s^2)}\right) ,\\ \wp _i(s)= & {} \wp _{i1}(s)/\wp _{i2}(s),\,\,i=1,2. \end{aligned}$$

We get that $\bar{n}_1:=1$ and $\bar{n}_2:=1$.

Step 2.2::

We have that

$$\begin{aligned}{} & {} a_{1}=\lim _{t\rightarrow 2}\,\frac{p_2(t)}{p_{1}(t)}=-2\pi ,\\{} & {} a_{0}=\lim _{t\rightarrow 2}\, p_1(t)f_1(t)=0, f_1(t):=\frac{p_2(t)}{p_{1}(t)}-a_{1}. \end{aligned}$$

Step 2.3::

We obtain the asymptote $\widetilde{\mathcal {C}}$, defined by the proper parametrization

$$\begin{aligned} \widetilde{\mathcal {Q}}(t)=(t,\, -2\pi t). \end{aligned}$$

Step 3::

We observe that all the roots of $p_{12}(s)$ are also roots of $p_{22}(s)$ (that is, the the poles of $p_1$ are the poles of $p_2$), so there are no vertical asymptotes.

Step 4::

The algorithm returns the asymptote $\widetilde{\mathcal {C}}$ of the input curve, $\mathcal {C}$ (see Fig. 3).

Fig. 3

Curve $\mathcal {C}$ (left) and curve and asymptotes (right)

Remark 10

The method above described may be straightforward adapted for dealing with algebraic curves in the $n-$dimensional space. For instance, if $n=3$, we have a parametrization $\mathcal {P}(s)=(p_1(s),p_2(s),p_3(s))$ with $p_i(s)=p_{i1}(s)/p_{i2}(s),\,i=1,2,3$ meromorphic functions and $\textrm{gcd}(p_{i1},p_{i2})=1,\,\,i=1,2,3$. Then, the asymptotes are

$$\begin{aligned} \widetilde{\mathcal {Q}}=(t^{n_1},\, a_{n_{2}}t^{n_{2}}+a_{n_{2}-1}t^{n_{2}-1}+\ldots +a_{0},\, b_{m_{2}}t^{m_{2}}+b_{m_{2}-1}t^{m_{2}-1}+\ldots +b_{0}). \end{aligned}$$

These asymptotes can be computed by successively applying the algorithm to each component of ${{\mathcal {P}}}$. Note that as in the planar case, roots $\tau \in \mathbb {C}$ such that $p_{22}(\tau )=p_{32}(\tau )=0\ne p_{12}(\tau )$ could appear (see Step 3 of the algorithm). In this case we must look for asymptotes of the form $\widetilde{\mathcal {M}}=(m_1(t), t^{n}, m_3(t))$ or $\widetilde{\mathcal {M}}=(m_1(t), m_2(t), t^{n})$. Example 6 illustrates these ideas.

Example 6

Let $\mathcal {C}$ be the space curve defined by the parametrization

$$\begin{aligned} \mathcal {P}(s)=(p_1(s), p_2(s))=\left( \frac{(\sqrt{s+1}+2)^{1/4}}{s (1+(\sqrt{s+1}+2)^{3/4})}, \frac{\sqrt{\sqrt{s+1}+2}}{ 1+(\sqrt{s+1}+2)^{3/4}}, \frac{s+3}{\sin (s)}\right) . \end{aligned}$$

We apply the algorithm Asymptotes Construction-Parametric Non-Rational Case for obtaining the different g-asymptotes.

• Step 1: We observe that $p_{12}(s)$ and $p_{32}(s)$ have the root $\tau _1=0$ and $p_{12}(s)$ and $p_{22}(s)$ have the root $\tau _2=\alpha$ where $1+(\,(\alpha +1)^{1/2}+2)^{3/4}=0$. Note that $p_{i}(s)=p_{i1}/p_{i2},\,i\in \{1,2\}$ are meromorphic functions on the complex plane.

• Step 2:

  • $\bullet$ For $\tau _1=0:$

    • Step 2.1: We have that $\bar{n}_{11}=1$ and $\bar{n}_{13}=1$ and $\bar{n}_{12}=0$. Note that $p_{32}(s)=s(1-1/6s^2+1/120s^4-1/5040s^6+\cdots )$ and $p_{i1}(0)\not =0$ for $i=1,2,3$.

    • Step 2.2: We have that

      $$\begin{aligned} \begin{array}{ll} a_{1}=\lim _{t\rightarrow 2}\,\frac{p_3(t)}{p_{1}(t)}=3^{3/4}+3^{3/2} \\ a_{0}=\lim _{t\rightarrow 2}\, p_1(t)f_1(t)=\frac{10\cdot 3^{3/4}+7}{8(1+3^{3/4})},\quad f_1(t):=\frac{p_3(t)}{p_{1}(t)^{2}}-a_{1}. \\ \end{array} \end{aligned}$$

    • Step 2.3: We obtain the asymptote $\widetilde{\mathcal {C}}_1$, defined by the proper parametrization

      $$\begin{aligned} \widetilde{\mathcal {Q}}_1(t)= & {} \left( t,\, p_2(0),\, (3^{3/4}+3^{3/2})t+\frac{10\cdot 3^{3/4}+7}{8(1+3^{3/4})}\right) \\= & {} \left( t,\,\frac{\,3^{1/2}}{1+3^{3/4}},\, (3^{3/4}+3^{3/2})t+\frac{10\cdot 3^{3/4}+7}{8(1+3^{3/4})}\right) . \end{aligned}$$

  • $\bullet$ For $\tau _2=\alpha$ where $1+(\,(\alpha +1)^{1/2}+2)^{3/4}=0:$

    • Step 2.1: We have that $\bar{n}_{11}=1$ and $\bar{n}_{12}=1$ and $\bar{n}_{13}=0$.

    • Step 2.2: We have that

      $$\begin{aligned} \begin{array}{ll} a_{1}=\lim _{t\rightarrow 2}\,\frac{p_2(t)}{p_{1}(t)}=(\,(\alpha +1)^{1/2}+2)^{1/4} \alpha \\ a_{0}=\lim _{t\rightarrow 2}\, p_1(t)f_1(t)=0,\quad f_1(t):=\frac{p_2(t)}{p_{1}(t)^{2}}-a_{1}. \\ \end{array} \end{aligned}$$

    • Step 2.3: We obtain the asymptote $\widetilde{\mathcal {C}}_2$, defined by the proper parametrization

      $$\begin{aligned} \widetilde{\mathcal {Q}}_2(t)= & {} \left( t,\, ((\,(\alpha +1)^{1/2}+2)^{1/4} \alpha )t,\, p_3(\alpha )\right) \\= & {} \left( t,\, ((\,(\alpha +1)^{1/2}+2)^{1/4} \alpha )t,\frac{\alpha +3}{\sin (\alpha )}\right) , \end{aligned}$$

      where $1+(\,(\alpha +1)^{1/2}+2)^{3/4}=0$.

• Step 3: We observe that all the roots of $p_{12}(s)$ are also roots of $p_{22}(s)$ and $p_{23}(s)$ (that is, the poles of $p_1$ are the poles of $p_2$ and $p_3$), so there are no more asymptotes.

• Step 4: The algorithm returns the asymptotes $\widetilde{\mathcal {C}}_i,\,i=1,2$ of the input curve, $\mathcal {C}$

5 Conclusion

The main results of this paper, Theorems 4 and 5, provides a way to determine the branches and the generalized asymptotes of a curve parametrized not necessarily by two rational functions by only computing some simple limits of functions constructed from the given parametrization defined by two meromorphic functions on the complex plane. We remind that a meromorphic function on the complex plane is a function that is holomorphic on all of $\mathbb {C}$ except for a set of isolated points, which are poles of the function. We prove this theorem and we develop an efficient algorithm which determines all the branches and all the g-asymptotes which are obtained from the poles of the functions. As a complement, some corollaries are derived that allow us to obtain the horizontal and vertical asymptotes in an extremely simple way. This technique is proved to work on several illustrative examples.

It is important to stress that this procedure can be trivially applied for dealing with parametrizations of curves in n-dimensional space. Thus, the present paper yields a remarkable improvement of the methodology developed in [5, 7].

As a future work, we aim to extend the notion of g-asymptote to the study of the asymptotic behavior of algebraic surfaces. We look for surfaces which approach a given one of higher degree, when “moving to infinity”, that is, when some of the coordinates take infinitely large values. The ideas introduced in this paper might provide the foundations for efficient methods that allow us to compute those “asymptotic surfaces”.