1 Introduction

Reaction-diffusion systems with cross-diffusion arise in several domains of natural and social sciences: plasma physics, chemical and biological systems, population dynamics, ecology to name but a few. Information about experiments, derivations of models and about different applications one can get for example from [2, 4, 5, 7,8,9,10,11,12]. For convenience we are going to use terminology of population dynamics and speak about “evolution of two species”.

The model system we are interested in reads as the following nonlinear reaction-diffusion system

$$\begin{aligned} \left\{ \begin{array}{lc} u_{t}= (u u_x+\varepsilon _1uv_x+\varepsilon _3vu_x)_x+u(1-u-cv) :=-\frac{\partial }{\partial x}J_1+u(1-u-cv) ,&{} \\ v_{t}=(dvv_x+\varepsilon _4uv_x+\varepsilon _2vu_x)_x+v(a-bu-v):=-\frac{\partial }{\partial x}J_2+v(a-bu-v).&{} \end{array} \right. \end{aligned}$$
(1.1)

The term “cross-diffusion” here means that at least one of the fluxes \(J_i\) has to contain both gradients \(u_x\) and \(v_x\), i.e. either \(\varepsilon _{{1}}\) or \(\varepsilon _{{2}}\) (or both) are different from zero.

This type of systems were first introduced in 1979 in [8]. The basic idea was to model the processes in which one has to take into account not only the random dispersion but also different other factors like environmental conditions, mutually attractive or repulsive (inter-specific) and intra-specific (occurs between individual of the same species) interaction.

All variables and parameters in (1.1) are dimensionless. The scaling was carried out in such a way, that the reaction terms had the most traditional form and with some choice of \(\varepsilon _{i}\) we could return to some special systems important in applications.

In this context \((u,v)= (u(x,t), v(x,t))\) represent the population densities of two species at time t and at point x ; the subscripts denote partial derivatives. We assume that the competitions parameters a, b, c and the self-diffusion parameter d are positives. However, the cross-diffusion parameters \({\varepsilon _{i}}\) may be arbitrary real numbers.

By “pattern” we mean a non-constant stationary solution (u(x), v(x)) of (1.1) which is “stable” in some sense ( we specify it later on); see [3], were one can also find method–motivation about how to introduce different diffusion terms.

In the next two Sections we present (and show the existence) of two different kind of patterns being both non-negative and periodic. The first one we call “one phase”, the second one as “two-phase” pattern. It means that in the first case minima and maxima of u(x) and v(x) are at the same points, whereas in the second case minima of u(x) coincide with maxima of v(x) and vice versa.

We note, that the first type pattern is not typical in competition systems; in fact we have never heard about existence of this sort of phenomenon: probably they are possible in the presence of very special cross-diffusion and reaction only.

2 One–phase periodic patterns

In practice it is important to know what kind of assumptions have to impose such that non - constant stationary solutions of (1.1) exist in the form \((u(x,t), v(x,t))=(u(x),v(x))\). This solution has to satisfy the coupled second order non-linear system of ordinary differential equations (ODE):

$$\begin{aligned} \left\{ \begin{array}{lc} (u {u^\prime } +\varepsilon _1 u {v^\prime }+\varepsilon _3v {u^\prime }) {^\prime }+u(1-u-cv)=0 &{} \\ (dv {v^\prime }+\varepsilon _4u {v^\prime }+\varepsilon _2v {u^\prime }) {^\prime } +v(a-bu-v)=0 &{} \end{array} \right\} (x\in \mathbb {R}), \end{aligned}$$
(2.1)

where the prime \({^\prime } \) denote the derivative with respect to the space variable x.

We would like to show the existence of non-negative periodic (u(x), v(x)). For that we shall find exact solutions.

Of course these patterns do not exist for all parameters: one can say even that the “typical” case is that the solutions of (1.1) goes to constants solutions as t goes to infinity.

One of the main difficulty in the theory of nonlinear reaction-diffusion systems containing parameters is to find the bifurcation surfaces in parameter space (generalization of bifurcation point if one has one parameter) which separate domains with different behavior of solutions.

It turned out, that the exact solutions can help in this respect too: the solution we find have to be physically relevant, non-negative, periodic etc. This will be the case only if the parameters satisfy a rather complicated nonlinear algebraic system of inequalities the solutions of which are domains in parameter space.

In order to show our first result we are looking for stationary non - constant periodic solution (u(x), v(x)) for ode system (2.1) in the following form:

$$\begin{aligned} (u(x),v(x))= (u_0\cos ^2({\omega } x),v_0\cos ^2({\omega } x)), \end{aligned}$$
(2.2)

where \(u_0>0, v_0>0\) are positive constants, \(\omega \in \mathbb {R}\). We call this type of periodic solutions as one-phase solutions because of the maximum and minimum values of the pairs u(x) and v(x) are at the same points.

Substitute (2.2) into the first equation of (2.1). After carrying out the derivatives and using trigonometric identities we obtain an equation in which only the powers of function \(\cos ^2({\omega } x)\) appear. Dividing this equation by \(u_0\cos ^2({\omega } x)\) and collecting the terms containing \(\cos ^2({\omega } x)\) and constants, one gets

$$\begin{aligned} {\left\{ \begin{array}{ll} \left( -8\,\varepsilon _{{1}}{\omega }^{2}v_{{0}}-8\,\varepsilon _{{3}}{\omega }^{2}v_{{0}}-8\,{\omega }^{2}u_{{0}}-cv_{{0}}-u_{{0}} \right) \cos ^{2} \left( \omega \,x \right) + \\ +6\,\varepsilon _{{1}}{\omega }^ {2}v_{{0}}+6\,\varepsilon _{{3}}{\omega }^{2}v_{{0}}+6\,{\omega }^{2}u_{{0}} +1=0. \end{array}\right. } \end{aligned}$$
(2.3)

Similarly, substituting (2.2) into the second equation of (2.1) and simplifying, one has

$$\begin{aligned} {\left\{ \begin{array}{ll} \left( -8\,d{\omega }^{2}v_{{0}}-8\,\varepsilon _{{2}}{\omega }^{2}u_{{0}}- 8\,\varepsilon _{{4}}{\omega }^{2}u_{{0}}-bu_{{0}}-v_{{0}} \right) \ \cos ^{2} \left( \omega \,x \right) + \\ +6\,d{\omega }^{2}v_{{0}}+6 \,\varepsilon _{{2}}{\omega }^{2}u_{{0}}+6\,\varepsilon _{{4}}{\omega }^{2}u_{{0 }}+a=0. \end{array}\right. } \end{aligned}$$
(2.4)

Since the Eqs. (2.3) and (2.4) are satisfied for all \(x\in \mathbb {R}\), the coefficient of \(cos^{2}(\omega x)\) and the constants have to be identically zero. From (2.3) follows that

figure a

From (2.4) we have two more relations:

figure b

The linear combination \(3\cdot (2.5\mathrm{a})+4\cdot (2.5\mathrm{b}) \) provides the following:

$$\begin{aligned} 3\,u_{{0}} +3\,cv_{{0}}=4. \end{aligned}$$
(2.7)

Similarly, the linear combination \(3\cdot (2.6a)+4\cdot (2.6b) \) gives

$$\begin{aligned} 3\,bu_{{0}}+3\,v_{{0}}=4\,a. \end{aligned}$$
(2.8)

Solving the linear system (2.7) and (2.8) for the unknown variables \((u_{0},v_{0})\), we obtain the “amplitude” values :

$$\begin{aligned} u_{{0}}=\frac{4}{3}\,\cdot {\frac{ac-1}{bc-1}} , \ v_{{0}}=\frac{4}{3}\,\cdot {\frac{b-a}{bc-1}}. \end{aligned}$$
(2.9)

After some algebra one can get a formula for \(\omega ^{2} \) expressed by a, b, c,  and \(\varepsilon _{1} + \varepsilon _{3} \) (just substitute \((u_{0},v_{0})\) from (2.9) into (2.5a)). One has

$$\begin{aligned} {\omega }^{2}=\frac{1}{8}\,\cdot {\frac{bc-1}{1-ac- \left( b-a \right) \left( \varepsilon _{{1}}+\varepsilon _{{3}} \right) }}. \end{aligned}$$
(2.10)

It is important to note that the equation (2.5b) is automatically fulfilled when the constants are from (2.9) and (2.10) .

However the two equations in (3.5) are not necessarily satisfied for these parameters. Now we substitute the values \( u_{0},v_{0} \) and \(\omega ^{2} \) from (2.9) and (2.10) into (2.6a). One can write the obtained equality in different forms; we have chosen the possibility to isolate d :

$$\begin{aligned} d=a \left( \varepsilon _{{1}}+\varepsilon _{{3}} \right) +\left( a-\varepsilon _{{2}}-\varepsilon _{{4}}\right) \cdot {\frac{ac-1}{b-a}}. \end{aligned}$$
(2.11)

Again, it is important that the equation (2.6b) is automatically fulfilled when the values from (2.9) , (2.10) and (2.11) are substituted in it!

Remark 1

The relation (2.11) can be considered as an equation of a 7-dim hypersurface P in the 8-dim parameter space. All of our parameters have to stay on it.

There are of course more conditions for existence of the needed exact solutions and we shall consider them. First we formulate the result :

Theorem 1

(Patterns with same phases) Functions

$$\begin{aligned} u(x)=\frac{4}{3}\cdot \frac{ac-1}{bc-1} \cdot \cos ^2({\omega }x),\; v(x)=\frac{4}{3}\cdot \frac{b-a}{bc-1} \cdot \cos ^2({\omega }x) \end{aligned}$$
(2.12)

are exact stationary solutions to (1.1) with parameters \(\omega ^2\) and d given by (2.10) and (2.11).

Now we are going to show that there exist nonempty domains in P where our solutions have physical sense. In fact, these would be the largest ones for parameters \((a,\,b,\,c,\,\varepsilon _{1},\, \varepsilon _{2},\, \varepsilon _{3},\, \varepsilon _{4})\) such that all of the conditions \(u(x)\ge 0\), \(v(x)\ge 0\), \(\omega ^2>0\) and \(d>0\) were fulfilled.

This part of the job isn’t complicated (elementary algebra) but rather labour-intensive if we want to shed some light on the geometric nature of things.

First we introduce four new parameters; this will help us in many senses.

$$\begin{aligned} X=\frac{b}{a},\, Y=ac, \, \varepsilon _{1,3}=\varepsilon _{1}+\varepsilon _{3},\, \varepsilon _{2,4}=\varepsilon _{2}+\varepsilon _{4}. \end{aligned}$$
(2.13)

First we rewrite formulas in (2.9) for \(u_0,v_0\), using parameters (X, Y) and apply the conditions \(u(x)\ge 0\), \(v(x)\ge 0\):

$$\begin{aligned} u_0= \frac{4}{3}\cdot \frac{ac-1}{bc-1} = \frac{4}{3}\cdot \frac{Y-1}{XY-1}>0 \; , \; v_0= \frac{4}{3}\cdot \frac{b-a}{bc-1}= \frac{4}{3}\cdot a\cdot \frac{X-1}{XY-1}>0. \end{aligned}$$
(2.14)

From these we obtain two distinct domains in the reduced parameter space

$$\begin{aligned} \left\{ \begin{array}{cl} &{} D^{(1)}_{1}= \{ (a,X,Y,\varepsilon _{1,3},\varepsilon _{2,4} ) \, \arrowvert \ \, X>1,Y>1,a>0 \},\\ &{} D^{(1)}_{2}= \{ (a,X,Y,\varepsilon _{1,3},\varepsilon _{2,4} ) \, \arrowvert \ \, 0<X<1,0<Y<1,a>0 \}. \end{array} \right\} \end{aligned}$$
(2.15)

Now , in view of (2.13), \(\omega ^2>0\) is equivalent, to

$$\begin{aligned} \omega ^2=\frac{1}{8}\cdot \frac{XY-1}{1-Y-a\cdot \varepsilon _{1,3}\cdot (X-1)}>0. \end{aligned}$$

Because of \({XY-1}>0 \) in \(D^{(1)}_{1}\) and \({XY-1}<0 \) in \(D^{(1)}_{2}\), this condition restrict the domains \(D^{(1)}_{1}\) and \(D^{(1)}_{2}\) into the following two parts

$$\begin{aligned} \left\{ \begin{array}{cl} &{} D^{(2)}_{1}= \{ (a,X,Y,\varepsilon _{1,3},\varepsilon _{2,4} ) \in D^{(1)}_{1} \, \arrowvert \, Y-1<-a\cdot \varepsilon _{1,3}\cdot (X-1) \} \subset D^{(1)}_{1} \\ &{} D^{(2)}_{2}= \{ (a,X,Y,\varepsilon _{1,3},\varepsilon _{2,4} ) \in D^{(1)}_{2} \,\arrowvert \, Y-1>-a\cdot \varepsilon _{1,3}\cdot (X-1) \} \subset D^{(1)}_{2} \end{array} \right\} \end{aligned}$$
(2.16)

From (2.16) we conclude that the inequality \(\varepsilon _{1,3}<0\) holds in all cases.

It is clear from (2.16) that we have a sharp boundary line for the sectors \(D^{(2)}_{1}\) and \(D^{(2)}_{2}\) in the plane (X, Y) which is given by the equation

figure c

This \(Line_1\) goes through the point \((X,Y)=(1,1)\) with positive slope

$$\begin{aligned} m_{1}=-a\cdot \varepsilon _{1,3}>0. \end{aligned}$$
(2.17)

The transformations (2.13) for the parameter \(d>0\) (2.11) gives

$$\begin{aligned} d=a\cdot \varepsilon _{1,3}+(a-\varepsilon _{2,4})\cdot \frac{Y-1}{a\cdot (X-1)}>0. \end{aligned}$$

If we solve this inequality separately in domains \(D^{(1)}_{1}\) and \(D^{(1)}_{2}\) we get two new sectors

$$\begin{aligned} \left\{ \begin{array}{cl} &{} D^{(3)}_{1}= \{ (a,X,Y,\varepsilon _{1,3},\varepsilon _{2,4} ) \in D^{(1)}_{1} \, \arrowvert \, (a-\varepsilon _{2,4})(Y-1)>-a^{2}\,\varepsilon _{1,3}\cdot (X-1) \},\\ &{} D^{(3)}_{2}= \{ (a,X,Y,\varepsilon _{1,3},\varepsilon _{2,4} ) \in D^{(1)}_{2} \,\arrowvert \, (a-\varepsilon _{2,4})(Y-1)<-a^{2}\,\varepsilon _{1,3}\cdot (X-1)\}. \end{array} \right\} \end{aligned}$$
(2.18)

Since \(\varepsilon _{1,3}<0\) is true in all cases, the condition \(a-\varepsilon _{2,4}>0\) is also valid:this follows from inequalities (2.18).

In (X, Y) parameter plane we have another boundary line

figure d

which pass through the point \((X,Y)=(1,1)\) with slope

$$\begin{aligned} m_{2}=-\frac{a^2\cdot \varepsilon _{1,3}}{a-\varepsilon _{2,4}}>0. \end{aligned}$$
(2.19)

Since all of the conditions \(u(x)\ge 0\), \(v(x)\ge 0\), \(\omega ^2>0 \) and \(d>0\) have to be met at the same time, the intersections

$$\begin{aligned} D_{1}= D^{(2)}_{1} \cap D^{(3)}_{1} ,\ D_{2}= D^{(2)}_{2} \cap D^{(3)}_{2} \end{aligned}$$

give the possible final domains of parameters where the non-negative and periodic solutions (2.12) exist. Domains \(D_1\) and \(D_2\) will be nonempty when the slopes of \(Line_{1}\) and \(Line_{2}\) satisfy \(m_2<m_1\) i.e.

$$\begin{aligned} m_{1}-m_{2}=-a\cdot \varepsilon _{1,3}-\Big (\frac{-a^2\cdot \varepsilon _{1,3}}{a-\varepsilon _{2,4}}\Big )= a\cdot \frac{\varepsilon _{1,3}\cdot \varepsilon _{2,4}}{a-\varepsilon _{2,4}}>0. \end{aligned}$$

From this inequality follows that it must be \(\varepsilon _{2,4}<0\), since \(a>0,a-\varepsilon _{2,4}>0\) and \(\varepsilon _{1,3}<0.\)

Summarizing conditions for domains using the original \((a,b,c,\varepsilon _1,\varepsilon _2,\varepsilon _3,\varepsilon _4)\) parameter values with assumptions \(a>0,b>0,c>0,\varepsilon _1+\varepsilon _3<0,\;\varepsilon _2+\varepsilon _4<0 \) one has

$$\begin{aligned} D_{1}={\left\{ \begin{array}{ll} a<b,\;a\cdot c>1,\;\\ a\cdot (a\cdot c-1)<-a\cdot (\varepsilon _1+\varepsilon _3)\cdot (b-a) <(a-\varepsilon _2-\varepsilon _4)\cdot (a\cdot c-1) , \end{array}\right. } \end{aligned}$$
$$\begin{aligned} D_{2}={\left\{ \begin{array}{ll} b<a,\;a\cdot c<1,\;\\ a\cdot (a\cdot c-1)>-a\cdot (\varepsilon _1+\varepsilon _3)\cdot (b-a) >(a-\varepsilon _2-\varepsilon _4)\cdot (a\cdot c-1).\end{array}\right. } \end{aligned}$$

Remark 2

(a) Consider system without cross-diffusion terms when \({\varepsilon _{1}=\varepsilon _{2}=\varepsilon _{3} =\varepsilon _{4}=0} \). This case neither belongs to domain \(D_{1}\) nor domain \(D_{2}\) because of the conditions \(\varepsilon _{1}+\varepsilon _{3}<0\) and \(\varepsilon _{2}+\varepsilon _{4}<0\) are not fulfilled. So in this case there is no periodic solution of type (2.2).

(b) Consider the case \({\varepsilon _{1}=1,\varepsilon _{2}=d,\varepsilon _{3} =\varepsilon _{4}=0}\) ("the tumor growth system") . Parameters neither belongs to domain \(D_{1}\) nor \(D_{2}\) because of the conditions \(\varepsilon _{1}+\varepsilon _{3}=1<0\) and \(\varepsilon _{2}+\varepsilon _{4}=d<0\) are not met. So in this case there is no periodic solution of type (2.2) neither.

For visualization purposes we choose parameter values as \(a =2, b = 4, c =2,d=4,\varepsilon _1 = \varepsilon _2 =1, \varepsilon _3 = -3.5, \varepsilon _4 = -5\) then all requirements are fulfilled which are prescribed at domain \(D_{1}\). Periodic patterns are drawn on left side of Fig. 1 with continuous line for u(x) and dotted line for v(x). On the right side of Fig. 1 we draw the point \(P_{1}\) in domain \(D_{1}\) using coordinate system (\(X=\frac{b}{a},Y=a\cdot c\)). Figure 2 shows patterns and the point \(P_2\) in domain \(D_2\) which corresponds to the parameter values \( a = 2.4, b = 1.4, c =0.07,d=0.2336,\varepsilon _1 =0.2, \varepsilon _2 =0.1, \varepsilon _3 = -3.5, \varepsilon _4 = -7.5\).

Fig. 1
figure 1

Periodic solution (u,v) in the same phases with parameters \(a =2, b = 4, c =2,d=4,\varepsilon _1 = \varepsilon _2 =1, \varepsilon _3 = -3.5, \varepsilon _4 = -5, u_0=4/7, v_0=8/21, \omega =0.6614 \) (on left) and the point \(P_{1}\) in domain \(D_1\) (on right)

Full size image
Fig. 2
figure 2

Periodic solution (u,v) in the same phases with parameters \( a = 2.4, b = 1.4, c =0.07,d=0.2336,\varepsilon _1 =0.2, \varepsilon _2 =0.1, \varepsilon _3 = -3.5, \varepsilon _4 = -7.5, u_0=1.2298, v_0=1.4782, \omega =0.2374 \) (on left) and the point \(P_{2}\) in domain \(D_2\) (on right)

Full size image

As it was mentioned previously, the presence of such kind of distribution of two competing species is not typical but as we see, it is possible: this is a kind of “harmonious cohabitation”. To create such a situation, one has to choose the control parameters in a very delicate way, as it was expected.

Remark 3

Usually (almost always), the diffusion laws are phenomenological (Fick’s, Darcy’s, Newton’s etc.). However new forms can be suggested by new experiments, elementary considerations from physics-mathematics (like the original Morishita 1953 experiment with antlions in different sands+ probability theory, see ([8])). Our solutions are solutions of the Cauchy problem. In practice and in numerical computations the domains are bounded. However the solution can be used in that case too if we take into account Neumann conditions. As it was mentioned above, they describe the final state of the process which could be a one-hump, two-hump etc. Often, if the domain is small, it is even hard to see that the final state is a part of a periodic solution.

As one can see from the next Fig. 3, the cohabitation could be very stable in some sense.

In the definition of “pattern” in ([3]) one asks, beside to be non– constant, also the Liapunov stability of stationary solution. However it is for Cauchy problem on whole line.

If the domain in space is bounded, one has to complete the model (1.1) with boundary conditions, often with homogeneous Neumann condition. We take a new initial condition which is very close to original one but the normal derivative on boundary is different, non zero. In most of cases the solution with this datum will not remain close to the original solution.

However the given pattern can be very stable even with respect to large perturbation if its structure “is not far” from the perturbed one.

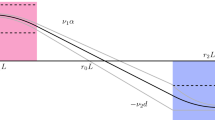
Here we used some multiplicative perturbations like \((1+\varepsilon \cos \omega _1 x ) u(x)\), where, for Figs. 3 and 4, \(\varepsilon =0.2\) and \(\omega _1=25\omega \) so \(\epsilon \) is not necessarily small, u(x) is our solution. One can see that our pattern really stable and the convergence is very fast, almost “in finite time”.

Fig. 3
figure 3

Numeric solutions (u(x,t),v(x,t)) tend to stationary periodic patterns as the time is varying \(t=0, 0.005, 0.01,0.015, 0.02, 0.1 \) where the parameters are \( a = 2, b = 3, c =1.5,d = 1, \varepsilon _1 =1, \varepsilon _2 =1, \varepsilon _3 =-3.5, \varepsilon _4 = -2, u_0=0.7619, v_0=0.3809, \omega =0.9354 \)

Full size image
Fig. 4
figure 4

Numerical solutions (u(x,t),v(x,t)) tends to stationary periodic patterns as time is varying \(t=0, 0.002, 0.005,0.01, 0.5, 10 \) where the parameters are \( a = 2, b = 3, c =0.5,d = 6, \varepsilon _1 =1, \varepsilon _2 =6, \varepsilon _3 = \varepsilon _4 = 0, u_0=1.0667, v_0=1.6, \omega =0.25\)

Full size image

3 Two-phase periodic patterns

In order to find another family of stationary non - constant solution (u(x), v(x)) of (1.1) we are looking for solutions in the form

$$\begin{aligned} (u(x),v(x))= (u_0\cos ^2({\omega } x),v_0\sin ^2({\omega } x)), \end{aligned}$$
(3.1)

where \(u_0>0, v_0>0\) are positive constants and \(\omega \in \mathbb {R}\). We call this type of periodic solutions as they are in opposite phases because of the maximum values of u(x) is at the same places where the minimum values of v(x) and vice versa.

We note that originally the results, like in the case of one–phase one, were obtained in another way. The following derivation is a simpler one, much more transparent.

Substitute (3.1) into the first equation of (2.1). Calculating the derivatives and using trigonometric identities we obtain an equation in which only the powers of \(\cos ^2({\omega } x)\) appear. Dividing this equation by \(u_0\) and collecting terms we have

$$\begin{aligned} {\left\{ \begin{array}{ll} \left( -8\,{\varepsilon _1}\,{\omega }^{2}{v_0}-8\,{\varepsilon _3}\,{\omega }^{2}{ v_0}+8\,{\omega }^{2}{u_0}-c{v_0}+{u_0} \right) \cos ^4 \left( \omega \,x \right) +\\ \left( 6\,{\varepsilon _1}\,{\omega }^{2}{v_0}+10\,{\varepsilon _3}\,{\omega }^{2}{ v_0}-6\,{\omega }^{2}{u_0}+c{v_0}-1 \right) \cos ^2 \left( \omega \,x \right) -2\,{\varepsilon _3}\,{\omega }^{2}{v_0}=0. \end{array}\right. } \end{aligned}$$
(3.2)

Similarly, substitute (3.1) into the second equation of (2.1) and divide by \(v_0\) :

$$\begin{aligned} {\left\{ \begin{array}{ll} \left( 8\,d{\omega }^{2}{v_0}-8\,{\varepsilon _2}\,{\omega }^{2}{u_0}-8\, {\varepsilon _4}\,{\omega }^{2}{u_0}-b{u_0}+{v_0} \right) \cos ^{4} \left( \omega \,x \right) +\\ +\left( -10\,d{\omega }^{2}{ v_0}+10\,{\varepsilon _2}\,{\omega }^{2}{u_0}+6\,{\varepsilon _4}\,{\omega }^{2}{ u_0}+b{u_0}+a-2\,{v_0} \right) \cos ^{2} \left( \omega \,x \right) +\\ +2\,d{\omega }^{2}{v_0}-2\,{\varepsilon _2}\,{\omega }^{2}{u_0}-a+{v_0}=0. \end{array}\right. } \end{aligned}$$
(3.3)

Since equations (3.2) and (3.3) are satisfied for all \(x\in \mathbb {R}\) , all coefficients of powers of \(cos^{2}(\omega x)\) and the constant have to be identically zero. Equality (3.2) gives three equations:

figure e

and equality (3.3) gives three further ones:

figure f

From (3.4c) follows immediately that \(\varepsilon _3=0\), i.e. \(\varepsilon _3\) is missing from the system since \(\omega ^{2}>0\) and \(v_0>0\) is necessary to have periodic pattern.

Substitute \(\varepsilon _3=0\) into (3.4a) and (3.4b), compute the combination \(3\cdot 3.(3.4a)+4\cdot (3.4b) \). We obtain the following simple connection between \(u_0\) and \(v_0\):

$$\begin{aligned} 3\,u_{{0}} +cv_{{0}}=4. \end{aligned}$$
(3.6)

Combination \(5\cdot 5.(3.5a)+4\cdot (3.5b) \) gives

$$\begin{aligned} -16\,{ \varepsilon _4}\,{\omega }^{2}{} { u_0}-b{ u_0}+4\,a-3\,{ v_0}=0. \end{aligned}$$
(3.7)

Other combination \( (3.5b)+5\cdot (3.5c) \) gives

$$\begin{aligned} 6\,{ \varepsilon _4}\,{\omega }^{2}{} { u_0}+b{ u_0}-4\,a+3\,{ v_0}=0. \end{aligned}$$
(3.8)

Add (3.7) and (3.8); the result is

$$\begin{aligned} -10\,{ \varepsilon _4}\,{\omega }^{2}{} { u_0}=0. \end{aligned}$$

One has to have \(\varepsilon _4=0\), i.e. \(\varepsilon _4\) is missing from the system since \(\omega ^{2}>0\) and \(u_0>0\) . Substituting \(\varepsilon _4=0\) into (3.8) we obtain a linear relation between \(u_0\) and \(v_0\) :

$$\begin{aligned} b\,u_{{0}} +3v_{{0}}=4\,a \end{aligned}$$
(3.9)

Solving the linear system (3.6), (3.9) taking as unknowns \((u_{0},v_{0})\) we find the amplitudes:

$$\begin{aligned} u_{{0}}=4\cdot {\frac{a\cdot c-3}{b\cdot c-9}} ,\quad \ v_{{0}}=4\cdot {\frac{b-3\,a}{b\cdot c-9}}. \end{aligned}$$
(3.10)

Substituting \((u_{0},v_{0})\) from (3.10) into (3.4a) and remembering \(\varepsilon _3=0\), we find \(\omega ^{2} \):

$$\begin{aligned} {\omega }^{2}=\frac{1}{8}\cdot {\frac{bc-9-4\cdot (ac-3)}{ac-3- \left( b- 3\,a \right) \varepsilon _{1}}}. \end{aligned}$$
(3.11)

We emphasize that the Eq. (3.4b) is automatically fulfilled when the values from (3.10) and (3.11) are substituted in it.

However the two equations in (3.5) are not satisfied with these parameters and as a consequence of this we have to prescribe, as in the previous Section, for instance the value of the diffusion parameter d. To do this we substitute \( u_{0},v_{0} \) and \(\omega ^{2} \) from (3.10) and from (3.11) into equation (3.5a). Now one can express the parameter d as

$$\begin{aligned} d={\frac{ abc+3\,a-4\,b }{4\,ac-bc-3}}\cdot \varepsilon _1-{\frac{ ac-3 }{3\,a-b}}\cdot \varepsilon _{{2}}+{\frac{ \left( ac-3 \right) \left( abc+3\,a-4\,b \right) }{ \left( 3\,a-b \right) \left( 4\,ac-b c-3 \right) }}. \end{aligned}$$
(3.12)

We emphasize again, that the equation (3.5b) and (3.10) are fulfilled when the constants from (3.10) , (3.11) and (3.12) are substituted in it. Formally (we did not indicated the right parameter domains yet) we have the following

Theorem 2

(Patterns with opposite phases) Functions

$$\begin{aligned} u(x)=4\cdot {\frac{a\, c-3}{b\; c-9}} \cdot \cos ^2({\omega }x),\; v(x)=4\cdot {\frac{b-3\,a}{b\, c-9}} \cdot \sin ^2({\omega }x) \end{aligned}$$
(3.13)

are the exact solutions of (1.1) with parameters \(\omega ^2\) and d given by the formulas in (3.11) and (3.12).

There are several distinct domains of the parameters \((a,\,b,\,c,\,\varepsilon _{1},\, \varepsilon _{2}) \) where all of the conditions \(u(x)\ge 0\), \(v(x)\ge 0\), \(\omega ^2>0\) and \(d>0\) are fulfilled together with \(\varepsilon _{3}=\, \varepsilon _{4}=0\). These domains can be found in analogous way as in Sect. 2.

As an example we consider the model which is close to the so called “tumor growth” system, see ([1, 6]). It can be seen that all the conditions for existence of periodic pattern are met for the following parameters \( a = 2, b = 3, c =0.5,d = 6, \varepsilon _1 =1, \varepsilon _2 =6, \varepsilon _3 = \varepsilon _4 = 0 \).

The next Fig. 4 show how periodic patterns (u(x), v(x)) attract solutions with different initial data. Here we use special (not necessarily small) periodic initial perturbations at time \(t=0 \) and calculate numerically with homogeneous Neumann-boundary conditions on that interval \([-L,L]\). Here \(x=\pm L>0\) are points where the maximal or minimal values of (u(x), v(x)) are attained.