Skip to main content
SpringerLink
Log in

The meshless Kansa method for time-fractional higher order partial differential equations with constant and variable coefficients

  • Original Paper
  • Published:
Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A. Matemáticas Aims and scope Submit manuscript

Abstract

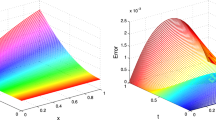
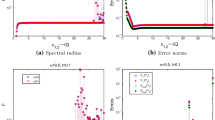
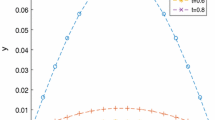
In this work, a meshfree technique based on radial basis functions (RBFs) is proposed for the study of time-fractional higher order partial differential equations (PDEs) of constant and variable coefficients. The RBFs used containing shape parameter, the selection of which is not an easy task and affects stability and accuracy of the results. The required shape parameter has been computed with the help of recently developed algorithm in literature. Computer simulations are performed for six different time-fractional PDEs which features excellent agreement with the exact solutions and earlier works. Approximation quality of the computed solutions are assessed via \(E_{2}\), \(E_{\infty }\) and \(E_{\text {rms}}\) error norms.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12

Similar content being viewed by others

References

  1. Hilfer, R.: Applications of Fractional Calculus in Physics. World Scientific Publishing, River Edge, USA (2000)

    Book  MATH  Google Scholar 

  2. Hilfer, R.: Foundations of fractional dynamics. Fractals 3(3), 549–556 (1995)

    Article  MATH  Google Scholar 

  3. Podlubny, I.: Fractional Differential Equations, p. 198. Academic Press, San Diego, USA (1999)

    MATH  Google Scholar 

  4. Mainardi, F.: Fractional calculus: some basic problems in continuum and statistical mechanics. In: Carpinteri, A., Mainardi, F. (eds.) Fractals and Fractional Calculus in Continuum Mechanics, pp. 291–348. Springer, New York (1997)

    Chapter  Google Scholar 

  5. Fujita, Y.: Cauchy problems of fractional order and stable processes. Japan J. Appl. Math. 7(3), 459–476 (1990)

    Article  MathSciNet  MATH  Google Scholar 

  6. Hilfer, R.: Fractional diffusion based on Riemann–Liouville fractional derivative. J. Phys. Chem. 104, 3914–3917 (2000)

    Article  Google Scholar 

  7. Caputo, M.: Linear models of dissipation whose Q is almost frequency independent, Part II. J. R. Astral. Soc. 13, 529–539 (1967)

    Article  Google Scholar 

  8. Metzler, R., Klafter, J.: Boundary value problems fractional diffusion equations. Phys. A 278, 107–125 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  9. Klafter, J., Blumen, A., Shlesinger, M.F.: Fractal behavior in trapping and reaction: a random walk study. J. Stat. Phys. 36, 561–578 (1984)

    Article  MathSciNet  MATH  Google Scholar 

  10. Agrawal, O.P.: Solution for a fractional diffusion-wave equation defined in a bounded domain. Nonlinear Dyn. 29, 145–155 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  11. Molliq, R.Y., Noorani, M.S.M., Hashim, I.: Variational iteration method for fractional heat- and wave-like equations. Nonlinear Anal. Real World Appl. 10(3), 1854–1869 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  12. Momani, S., Odibat, Z.: Analytical solution of a time-fractional Navier–Stokes equation by Adomian decomposition method. Appl. Math. Comput. 177, 488–494 (2006)

    MathSciNet  MATH  Google Scholar 

  13. El-Ajou, A., Arqub, O.A., Momani, S., Baleanu, D., Alsaedi, A.: A novel expansion iterative method for solving linear partial differential equations of fractional order. Appl. Math. Comput. 257, 119–133 (2015)

    MathSciNet  MATH  Google Scholar 

  14. Oldhan, K.B., Spainer, J.: The Fractional Calculus. Academic Press, New York (1974)

    Google Scholar 

  15. Jafari, H., Dehghan, M., Sayevand, K.: Solving a fourth-order fractional diffusion-wave equation in a bounded domain by decomposition method. Numer. Methods Partial Diff. Eq. 24, 1115–1126 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  16. Golbabai, A., Sayevand, K.: Fractional calculus—a new approach to the analysis of generalized fourth-order diffusion-wave equations. Comp. Math. Appl. 67, 2227–2231 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  17. Appadu, A.R., Djoko, J.K., Gidey, H.H.: Performance of some finite difference methods for a 3D advection-diffusion equation. RACSAM (2017). https://doi.org/10.1007/s13398-017-0414-7

  18. Gomez, H., Colominas, I., Navarrina, F., Casteleiro, M.: A hyperbolic model for convection-diffusion transport problems in CFD: numerical analysis and applications. RACSAM 102(2), 319–334 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  19. Kansa, E.J.: Multiquadrics—a scattered data approximation scheme with application to computation fluid dynamics, II. Solutions to hyperbolic, parabolic, and elliptic partial differential equations. Comput. Math. Appl. 19, 149–161 (1990)

    Article  MathSciNet  Google Scholar 

  20. Dereli, Y.: Solitary wave solutions of the MRLW equation using radial basis functions. Numer. Methods Partial Diff. Eq. 28(1), 235–247 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  21. Fasshauer, G.E.: Meshfree approximation methods with MATLAB, vol. 6. World Scientific, River Edge, NJ, USA (2007)

    MATH  Google Scholar 

  22. Sarra, S.A.: A local radial basis function method for advectiondiffusionreaction equations on complexly shaped domains. Appl. Math. Comput. 218, 9853–9865 (2012)

    MathSciNet  MATH  Google Scholar 

  23. Zhang, H., Guo, C., Su, X., Chen, L.: Shape parameter selection for multi-quadrics function method in solving electromagnetic boundary value problems. COMPEL Int. J. Comput. Math. Electr. Electron. Eng. 35(1), 64–79 (2016)

    Article  Google Scholar 

  24. Haq, S., Uddin, M.: A meshfree interpolation method for the numerical solution of the coupled nonlinear partial differential equations. Eng. Anal. Bound. Elem. 33(3), 399–409 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  25. Haq, S., Uddin, M.: RBFs approximation method for Kawahara equation. Eng. Anal. Bound. Elem. 35, 575–580 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  26. Haq, S., Hussain, M.: Selection of shape parameter in radial basis functions for solution of time-fractional Black–Scholes models. Appl. Math. Comput. 335, 248–263 (2018)

    MathSciNet  Google Scholar 

  27. Hosseini, V.R., Chen, W., Avazzadeh, Z.: Numerical solution of fractional telegraph equation by using radial basis functions. Eng. Anal. Bound. Elem. 38, 31–38 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  28. Uddin, M., Haq, S.: RBF approximation method for time fractional partial differential equations. Comm. Nonlinear Sci. Numer. Simul. 16(11), 4208–4214 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  29. Huang, H.T., Li, Z.C.: Effective condition number and super-convergence of the Trefftz method coupled with high order FEM for singularity problems. Eng. Anal. Bound. Elem. 30(4), 270–283 (2006)

    Article  MATH  Google Scholar 

  30. Li, Z.C., Huang, H.T., Wei, Y., Cheng, A.H.D.: Effective condition number for numerical partial differential equations. Science Press, Beijing (2003)

    Google Scholar 

  31. Reutskiy, S.Y., Lin, J.: A semi-analytic collocation method for space fractional parabolic PDE. Int. J. Comput. Math. 95(6–7), 1326–1339 (2018)

    Article  MathSciNet  Google Scholar 

  32. Lin, J., Reutskiy, S.Y., Lu, J.: A novel meshless method for fully nonlinear advection–diffusion–reaction problems to model transfer in anisotropic media. Appl. Math. Comput. 339, 459–476 (2018)

    Article  MathSciNet  Google Scholar 

  33. Lin, J., Lamichhane, A.R., Chen, C.S., Lu, J.: The adaptive algorithm for the selection of sources of the method of fundamental solutions. Engrg. Anal. Bound. Elem. 95, 154–159 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  34. Hussain, M., Haq, S., Ghafoor, A.: Meshless spectral method for solution of time-fractional coupled KdV equations. Appl. Math. Comput. 341, 321–334 (2019)

    MathSciNet  Google Scholar 

  35. Saadatmandi, A., Dehghan, M., Azizi, M.-R.: The Sinc–Legendre collocation method for a class of fractional convection–diffusion equations with variable coefficients. Commun. Nonlin. Sci. Numer. Simulat. 17, 4125–4136 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  36. Siddiqi, S.S., Arshed, S.: Numerical solution of time-fractional fourth-order partial differential equations. Int. J. Comput. Math. 92, 1496–1518 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  37. Tariq, H., Akram, G.: Quintic spline technique for time fractional fourth-order partial differential equation. Numer. Methods Partial Differ. Eq. 33(2), 445–466 (2017)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The authors are thankful to the anonymous reviewers for their constructive comments that have improved quality of the current work. Second author acknowledges the support of GIK Institute for his Ph.D. studies.

Author information

Authors and Affiliations

  1. Faculty of Engineering Sciences, GIK Institute, Topi-, 23640, KPK, Pakistan

    Sirajul Haq & Manzoor Hussain

Authors
  1. Sirajul Haq
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Manzoor Hussain
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Manzoor Hussain.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Haq, S., Hussain, M. The meshless Kansa method for time-fractional higher order partial differential equations with constant and variable coefficients. RACSAM 113, 1935–1954 (2019). https://doi.org/10.1007/s13398-018-0593-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s13398-018-0593-x

Keywords

Mathematics Subject Classification

Search

Navigation