Introduction

The development of models for analysing mathematical activity has been one of the topics that have produced most interest in Mathematics Education. The researchers who have been devoted to this question can be divided into two large groups: those who have proposed general models for the analysis of mathematical activity, and those who have chosen to propose models for a specific type of mathematical activity. In the first group, there are those who develop theoretical constructs to analyse mathematical activity within the framework of the theories of Mathematics Education (e.g., Brousseau, 2002; Chevallard, 1992; Kuzniak, 2011, among others). In the second group, we find those who focus on specific activities, such as the use of semiotic representations (Duval, 2017), problem solving (Liljedahl & Santos-Trigo, 2019), visualisation (Presmeg, 2006), and also mathematical modelling. On the last of these, the specialised literature has included research on the different ways of structuring modelling cycles (see Borromeo, 2006) as well as the different perspectives on this process in the teaching and learning of mathematics (see Abassian et al., 2020).

Although some research into networking between a general theoretical framework and a theoretical model focused on the analysis of a specific type of mathematical activity has been carried out (see Pino-Fan et al., 2017, for the process of representation; Campo-Meneses & García-García, 2021; and Rodríguez-Nieto, 2021, for the process of connection), it is interesting to extend the study of how these different types of analysis of mathematical activity (i.e., general and specific frameworks) may complement each other. In the present study, a general theoretical framework of mathematical activity and a specific framework for the mathematical modelling process are complemented. Therefore, this research is relevant to the field and addresses a networking of two theories which, as far as we know, has not previously been proposed with these specific theoretical frameworks.

Currently there is a broad consensus on the importance of including mathematical modelling in school curricula, and on the development of the competencies linked to this process (Kaiser, 2020). It is considered that this incorporation helps students to improve their understanding of mathematics, providing real contexts for its learning, and therefore contributing to the development of different mathematical competencies, among other benefits (Blum, 2011). However, what has not yet been agreed on is specifically how to incorporate mathematical modelling into the curriculum, since there is no consensus on the objectives of the process and the theoretical justification for the design and implementation of its teaching. This situation stems from the diversity of approaches to mathematical modelling that have been proposed (Borromeo, 2013).

Among the specific frameworks for the analysis of mathematical activity in modeling, one of the remarkable approaches within the educational community is the Mathematical Modelling Cycle from a Cognitive Perspective (MMCCP), proposed by Borromeo (2007a). As regards general frameworks for the analysis of mathematical activity, one key reference is the onto-semiotic approach (OSA) (Godino, 2002; Godino et al., 2007), a theoretical model of mathematical cognition and instruction that provides conceptual and methodological tools to pose and deal with research problems in Mathematics Education. While the MMCCP has an impact in the European research community and has also been worked by Hispanic researchers (see Borromeo, 2018), the OSA, in addition to its European impact, has a substantial impact in the Hispanic academic worldFootnote 1, and has also been worked in the Australasian context (see, Claudia et al., 2021; Rudi et al., 2020; among others).

Taking into account the impact of the theoretical frameworks mentioned above, and the authors’ expertise in their use (since the first and third authors have experience in using the MMCCP, and the second and third authors in the use of the OSA), in this paper we address the following research question: To what extent does the application of the onto-semiotic tools complement the analysis from a cognitive perspective of a mathematical modelling process? In order to address this issue, we used the tools provided by the OSA to analyse the complexity of the mathematical activity involved in the MMCCP, and we followed a methodology that is very similar to that used in the networking of theories (Bikner-Ahsbahs & Prediger, 2010, 2014) to understand the potential complementarities between the analyses performed with the two theoretical frameworks considered in this study.

We consider that answering this question is relevant for Mathematics Education research in two scopes: on the one hand, because it will allow both a better understanding and refinement of the MMCCP, and the theoretical development of the OSA through a connection between the modelling process and the tools provided by this framework; on the other hand, because it is related to the current interest of reflecting on the networking of theories — in this case, between a general and a specific framework — and it is in line with the work developed by Vergel et al. (2021).

Theoretical framework

In this section, we describe the two theoretical frameworks considered for this study.

Mathematical modelling

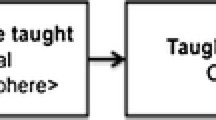
Despite differences with respect to the positions on mathematical modelling, there is a relative consensus that this process consists of a transition between the real world and the mathematical world, when solving real context problems. Although different models have been proposed for this transition, here we choose the MMCCP proposed by Borromeo (2007a), as shown in Fig. 1. This cycle, based on that developed by Blum and Leiß (2007a), explains the phases that an individual goes through in order to solve a modelling problem.

Fig. 1
figure 1

adapted from Borromeo, 2018, p. 15)

Mathematical modelling cycle from a cognitive perspective (

Full size image

In terms of what is described by Borromeo (2011, 2018), the real situation is understood as a problem taken from reality, and that may be represented in written form (textual statement), visual form (pictures), or a mixture of the two (text and pictures). The mental representation of the situation is generated from understanding of the task, mental reconstruction of the problem, and the associations the individual makes with the proposed situation. To obtain a real model, the mental image the individual has formed based on the problem must be simplified and structured, and it may include external representations (diagrams, figures, etc.). As in a modelling problem not all the data necessary for its resolution are always given, the individual’s extra-mathematical knowledge plays an important role when working with the available information, adding some considerations to the context of the situation according to personal experience. The mathematical model takes into account the mathematical objects which allow the real situation presented to be explained (Abassian et al., 2020), and it will be the product of the mathematisation (translation into mathematical language) of the real model and the contributions of the individual’s extra-mathematical knowledge. From the mathematical work with the mathematical model, mathematical results are obtained that, after being interpreted in the real situation context, will allow real results to be obtained. Finally, the validation of the real results — comparison of the triad real results ↔ mental representation of the situation ↔ real model — should lead to an adequate answer to the proposed problem.

The competence in Mathematical modelling is present throughout this entire cycle. It consists of being able to work (construct, critically analyse, evaluate) with mathematical models and to take into account adequately elements from the extra-mathematical domain, as the phases of the modelling cycle progress (Niss & Højgaard, 2019). This competence is carried out through different mathematical modelling sub-competencies (numbered on the right side of Fig. 1), which enable transition between these phases (see Maaß, 2006).

Example of a modelling problem and the analysis of its resolution using the MMCCP

In the Bales of straw problem (proposed by Blum and Leiß, 2007b), students are required to calculate the height of a mountain of bales of straw from a picture (see Fig. 2). This problem has been used by Borromeo (2011, 2018) to exemplify the MMCCP. We chose this problem for analysis in this study precisely because it is a paradigmatic example used to illustrate this modelling cycle.

Fig. 2
figure 2

adapted from Borromeo, 2007b, p. 2084)

The Bales of straw problem (

Full size image

Table 1 analyses the resolution of the Bales of straw problem from the perspective of the MMCCP.

Table 1 Analysis of the Bales of straw problem using the MMCCP (
Full size table

Onto-semiotic approach

The OSA considers that mathematical activity aims to solve problems. As a result of a process of problematisation, the subject or the institution assumes the task of solving a problem (proposed by someone else or created by oneself), through carrying out mathematical practices — any action or manifestation, linguistic or otherwise, carried out by somebody to solve mathematical problems, to communicate the solution to other people, or to validate and generalise that solution to other contexts and problems (Godino & Batanero, 1998). In order to carry out them and to interpret whether their results are satisfactory, it is necessary, in addition to considering the problem itself, to bring into operation other mathematical objects, which emerge from these mathematical practices. Indeed, in the resolution of the problem, it is necessary to use different languages (verbal, symbolic, etc.), which are the ostensive part of a series of definitions, propositions, and procedures that intervene in the elaboration of arguments that allow the problem to be solved. Consequently, when a subject performs and evaluates a sequence of mathematical practices, he/she activates a cluster made up of problem situations, languages, definitions, propositions, procedures, and arguments articulated in what the OSA terms a configuration of primary objects (Font et al., 2013). These networks of objects that intervene and emerge are called epistemic configurations when they are considered from an institutional perspective, and cognitive configurations when they are considered from a personal perspective.

The mathematical objects that intervene in the mathematical practices and those that emerge from them may be considered from the perspective of the following ways of being/existing, which are grouped into facets or dual dimensions (see Font & Contreras, 2008; Font et al., 2013): extensive–intensive, expression–content, personal–institutional, ostensive–non-ostensive, and unitary–systemic.

Problem solving is achieved through the articulation of sequences of practices. Such sequences take place in time and are often considered as processes. In particular, the use and/or the emergence of the primary objects of the configuration (problems, languages, definitions, propositions, procedures, and arguments) takes place through the respective mathematical processes of communication, problematisation, definition, enunciation, elaboration of procedures (algorithmisation, routinisation, etc.), and argumentation (applying the process-product duality). Meanwhile, the dualities described above give rise to the following processes: institutionalisation – personalisation, generalisation – particularisation, analysis/decomposition – synthesis/reification, materialisation/concretion – idealisation/abstraction, expression/representation – meaning.

This list of processes derived from the typology of primary objects and dual facets used as tools to analyse mathematical activity in the OSA, while contemplating some of the processes considered as important in mathematical activity, is not intended to include all the processes involved in that activity. This is because, among other reasons, some of the most important processes, such as problem solving and mathematical modelling, are hyper or mega processes rather than just mere processes (Godino et al., 2007), since they involve more elementary processes, such as representation, argumentation, idealisation, and generalisation.

In the OSA (Godino et al., 2009), it is considered that both mathematical practices and the instructional process are regulated, among other things, by epistemic norms (which regulate mathematical practices and contents, in correspondence with the mathematical discourse that can be developed in an institution), mediational norms (which regulate the resources — time or artefacts — used in practices), interactional norms (which regulate the modes of interaction between the individuals involved in mathematical practices or the instructional process), and ecological norms (external aspects — curricular guidelines, educational policies, etc. — which condition practices in lessons). In this study, we focused on epistemic norms, and in particular the meta-mathematical ones which regulate the practices carried out in a modelling process.

The theoretical tools just described allow for analysis of mathematical activity in which firstly, temporal analysis of the mathematical practices carried out to solve a certain problem is performed; then the configuration of primary objects that intervene in those practices is analysed (which provides information on the elements or parts of this mathematical activity), and finally analysis in terms of processes is carried out again, to complete the analysis in terms of practices (which provides information on the temporal dynamics of mathematical activity). Meanwhile, the normative analysis allows us to describe the norms that regulate this mathematical activity. In the next section, we illustrate this way of analysing the mathematical activity using the resolution of the Bales of straw problem. Due to the lack of space, other types of analysis, applying other tools provided by the OSA, are excluded; for instance, plotting the semiotic functions that interlink the primary objects which intervene in mathematical practices (e.g., Breda et al., 2021), or the metacognitive configurations (e.g., Gusmão, 2006).

Example of a modelling problem and the analysis of its resolution using the OSA

The following analysis only considers the first mathematical model mentioned in Table 1 (due to a lack of space), that is, the multiple addition of heights. Firstly, we described our resolution of the problem as a mathematical narration. The solver began by reading the problem, which requires the calculation of the height of a mountain of bales of straw. For this, presumably, he/she estimated the height of a woman (approximately 1.7 m), then compared this height visually with the diameter of a bale, concluding that it would be somewhat smaller (approximately 1.5 m). Looking at the picture, he/she noticed that there are five rows of bales in total, of which the even ones are smaller in size (three quarters of the calculated diameter) than the odd ones, due to the way the bales are stacked and fit together. In order to calculate the total height of the mountain, he/she could have represented the situation as a diagram where the five rows are shown (Fig. 3a), and assigned lengths to the diameters of each row (Fig. 3b). Thus, the total height of the mountain of bales would be equal to the sum of each of the rows of bales (6.75 m).

Fig. 3
figure 3

Representations of the situation through a diagram of rows (a), and with the lengths of the diameters of each row (b)

Full size image

Secondly, based on the mathematical narration mentioned above, we identified the following mathematical practices (P) that can be performed to solve the task:

  • P1: Read the task.

  • P2: Estimate the height of the woman.

  • P3: Make a visual comparison between the height of the woman and the height of the bale, to estimate its diameter.

  • P4: Make an iconic representation of the situation.

  • P5: Calculate the portion of the height of the even rows that does not fit with the height of the odd rows, using a visual comparison.

  • P6: Perform the calculations to arrive at the total height.

  • P7: Assess whether the solution makes sense in the context of the problem.

Thirdly, since mathematical modelling is considered within the OSA as a mega process, we identified the processes involved in each of the practices listed above, and the objects that emerge from these practices. As a result, in Table 2 we present the analysis of the problem using the tools provided by the OSA, including the mathematical practices (first column), processes (second column), and objects (third column) that intervene to solve the problem.

Table 2 Analysis of the Bales of straw problem using the tools provided by the OSA
Full size table

Fourthly, from the analysis in Table 2, we identified that some epistemic (metamathematical) norms that govern the modelling activity also emerge. They are indicated below, according to the mathematical practice they are related with:

  • Norm 1: Minimise the amount of information, replacing it with signs and figures (principle of simplification) [Practice 4].

  • Norm 2: Make a representation that maintains the structure of the problem statement (iconic representation, diagram), and the information necessary to solve it [Practice 4].

  • Norm 3: The representation can be drawn by hand or using a graphic software [Practice 4].

  • Norm 4: The problem may have approximate, non-exact solutions [Practice 5].

  • Norm 5: The solution must make sense in the real world, as it is a real context problem [Practice 7].

Concerning this last norm, two considerations must be made: (a) the results must exist in reality (for example, a negative height should be discarded in this context), and (b) the results must be reasonable, as determined by triangulating with other context information (for example, a height of 250 m or 30 cm would not be reasonable), or by searching for context information on the Internet or in other sources.

If there are different resolutions of the problem (with different mathematical practices, processes, or objects), a new norm appears (Norm 6), which consists of assessing which solution is best suited to answering the problem, taking into account several questions such as: What do I need the answer for? Is it consistent with the problem context? What are the mathematical aspects involved? (Among others).

Methodology

The study we developed is principally reflective on theory, and in it we aimed to compare analysis of mathematical activity from the perspective of the two theoretical frameworks mentioned above, in order to understand how the onto-semiotic tools complement the MMCCP. To this end, we followed a method that is very similar to that used in the networking of theories, particularly the one used in works of networking between a general theoretical framework and a theoretical model focused on the analysis of a specific type of mathematical activity (e.g., for the process of representation, see Pino-Fan et al., 2017; and for the process of connection, see Campo-Meneses & García-García, 2021; Rodríguez-Nieto, 2021).

Networking of theories

In a first step, we explained the two theoretical frameworks to each other, in order to ensure that all three of us have a good understanding of both. The way in which the two frameworks understand both the specific mathematical activity of modelling and mathematical activity in general was explained above (see ‘Theoretical framework’).

Various authors have shown an interest in determining the aspects that characterise a theory, in order to clarify it and compare it to others (see Bikner-Ahsbahs & Prediger, 2010, 2014). According to Radford (2008), the essential elements of a theory include paradigmatic principles, methods, and research questions. The principles of each theory imply that a position is adopted (either explicitly or implicitly) on the nature of mathematical objects. The second step allowed us to find concordances and differences between the theoretical frameworks, and also provided a first general idea of how they could be coordinated. This second step was essential in order to be able to continue to the following ones, since, on the one hand, an initial comparison between the constructs used in the two approaches to analyse mathematical activity made certain concordances evident, and, on the other hand, we concluded that the different positions concerning the nature of mathematical objects were not so decisive as to make it pointless to continue seeking for connections between them (see ‘Concordances and differences between the theoretical frameworks’).

Once this first comparison between the two theoretical frameworks was made, one of the basic principles of the networking of theories was applied: Ensure that the work of establishing connections is as accurate as possible. In accordance with this principle, since modelling should clearly be the topic, the third step was to select a specific task from this type of mathematical activity, thus we chose a paradigmatic task which is used to illustrate the MMCCP (the Bales of straw problem in Fig. 2). Since its expert solution and analysis were taken from Borromeo (2011, 2018), we made our own expert solution of the problem and then applied the tools provided by the OSA for its analysis (as described in ‘Example of a modelling problem and the analysis of its resolution using the OSA’).

In a fourth step, the problem in question was given to two groups of prospective mathematics teachers to solve it, in order to use their mathematical strategies and models which could emerge from its resolution to illustrate — in the following steps — how the analysis tools of both frameworks (MMCCP and OSA) are applied to a real protocol of a modelling task. Therefore, in the fifth step, the different resolutions obtained were grouped together and analysed using the two approaches as follows: The first and third authors carried out the analysis in accordance with the MMCCP, while the second and third authors complemented and deepened that analysis using the tools provided by the OSA (as mentioned in the third step). Finally, the sixth step, which was carried out jointly by all of us, focused on determining the contributions made by the analysis of modelling activity using the tools provided by the OSA to that of the MMCCP, and vice versa.

Stage of implementation

At this stage, the Bales of straw problem was given to two groups of prospective mathematics teachers from two universities in Barcelona (Spain). These were intentional samples (according to our access possibilities and their willingness to participate) in different training contexts. The first group, with 60 prospective primary school teachers (at undergraduate level), was in the context of a problem-solving module. The second group, with 20 prospective secondary school teachers (taking a teacher training master’s degree), was in the context of a mathematical modelling module.

The dynamics with the two groups was: First, they were introduced to general aspects of mathematical modelling; second, the problem was posed for them to solve it in teams, and they were asked to write down all their procedures; third, they presented their results to the whole group, and then discussed the strategies used by each team; and finally, the MMCCP was presented to them, exemplifying it with the resolution from Table 1. In line with what Blum (2011) proposes, the teacher in charge of the activity (the first author) tried to intervene as little as possible with the participants during the modelling task. Their written production was collected, and the explanations of their resolutions were recorded in audio.

Results

In this section, we detail the results of the comparison between the two theoretical frameworks and of their application to the analysis of the modelling problem.

Concordances and differences between the theoretical frameworks

As mentioned in the second step of the methodology, we carried out a first analysis of the concordances and differences between the MMCCP and the OSA. This comparison was organised around the essential elements of a theory according to Radford (2008), as mentioned in ‘Networking of theories’.

Specific cognitive approach versus broad approach

On the one hand, the MMCCP is situated on cognitive bases and the aim is to study the mental processes that occur in the specific mathematical activity of modelling (Borromeo, 2018). On the other hand, the OSA assumes a broad conception of Didactics as a discipline, considering that the descriptive, explanatory, and predictive questions that belong to scientific knowledge must be addressed, as too must the prescriptive and evaluative questions which belong to technological knowledge. According to the OSA, Didactics must provide results that allow the suitable action of a portion of reality, namely, teaching and learning mathematics in different contexts in which these take place. For this, it must take into account the following types of problem areas and their interactions: epistemological, ontological, semiotic-cognitive, educational-instructional, ecological, and optimisation of the instructional process. Some of the tools developed to respond to these problem areas are those used in ‘Example of a modelling problem and the analysis of its resolution using the OSA’.

Principles

Regarding the nature of mathematical objects, although there is not a clear position in the MMCCP, a realistic-empiricist type of position can be inferred, which considers that mathematics describes (models) the true structure of reality (see Borromeo, 2011; Kaiser-Messner, 1993). The principle assumed by the MMCCP is that the importance of mathematics must be presented to students within a teaching-learning process that encourages the authentic problem solving (Kaiser-Messner, 1993) which involve a modelling process, since mathematics is not a rigid formula and it is used daily in almost all professional areas (Borromeo, 2011).

In contrast, the OSA (Font et al., 2013) assumes a constructivist–conventionalist position, which is opposed to realist theses in the philosophy of mathematics: Mathematical statements do not describe any kind of reality (either ideal or natural) that exists prior to the constructive activity of a mathematician. The type of existence of definition–concepts, propositions, and procedures of epistemic configurations is that which conventional rules have, because actually they are used as such despite being presented as descriptions of mathematical objects whose existence is independent of people.

In the OSA, the didactic suitability of a teaching–learning process is understood as the degree to which it (or a part of it) meets certain characteristics that allow it to be qualified as suitable (optimal or adequate) to achieve the adaptation between the personal meaning achieved by the students (learning) and the intended or implemented institutional meanings (teaching), taking into account the circumstances and available resources (environment). It is thus a multidimensional construct divided into partial suitability types (epistemic, cognitive, interactional, affective, mediational, and ecological suitability) and each of these, into components and indicators (Breda, 2020; Breda & Lima, 2016). One of the components of epistemic suitability is the ‘richness of processes’, understood in the sense that the instructional process proposes a sequence of tasks that encourage students to carry out relevant processes of mathematical activity (problem solving, modelling, connections, argumentation, etc.). Furthermore, one of the components of ecological suitability is the ‘intra- and interdisciplinary connections’, that is, the sequence of tasks encourages the contents to be related to other mathematical contents (connection of advanced mathematics with the mathematics of the curriculum, and connection between different mathematical contents included in the curriculum), and/or with contents from other disciplines (extra-mathematical context and/or with contents from other subjects of the educational stage). So, enhancing modelling is considered in the OSA as an aspect that improves the suitability of the instructional process (Sala et al., 2017); therefore, both theoretical approaches coincide in the importance of incorporating this process into the teaching and learning of mathematics.

Modelling

The MMCCP has a very specific and well-developed proposal concerning the modelling process (as explained in ‘Mathematical modelling’). In contrast, although it considers modelling as a mega process, the OSA does not have a detailed proposal for the subprocesses that conform it.

Concordance of methods

The method used by the MMCCP analyses the mathematical activity carried out by the subject during the modelling process, and in this way identifies the phases of the cycle he/she goes through (or not). Now, this mathematical activity is analysed from the position of an observer who knows the mathematical rules that regulate the mathematical practice and, therefore, can give a meaning (or not) to the observed student behaviour. So, this way of analysing mathematical activity by the MMCCP partially coincides with the one used by the OSA for the same purpose. In other words, in the modelling cycle, what is actually applied is a semiotic-cognitive perspective, rather than just a cognitive perspective. This concordance in the way of analysing the mathematical activity is what allows the complementarity of the two approaches.

Concordance of research questions

The research questions posed in the studies on the teaching and learning of mathematical modelling from the teacher’s point of view have mainly focused on two aspects:

  • Effective or adequate teaching of mathematical modelling in the classroom or laboratory.

  • The development, optimisation, and evaluation of mathematical modelling in initial and continuous teacher training (Borromeo, 2018).

More specifically, the following are some of the questions posed to research from the aforementioned modelling cycle:

  • What influence do mathematical thinking styles have on the modelling process in mathematics classes where sequences of extra-mathematical context tasks are posed? (Borromeo, 2007a).

  • What phases or stages can be reconstructed in the individual modelling processes? What modelling patterns or preferences can be identified on the part of the students? Are there preferences for certain phases, stages, or procedures on the part of the teachers? (Borromeo, 2011).

The following types of problems are intended to be answered by the OSA (Godino et al., 2019):

  • Epistemological problem: How does mathematics emerge and develop?

  • Ontological problem: What is a mathematical object? What types of objects are involved in mathematical activity?

  • Semiotic-cognitive problem: What does it mean to know a mathematical object? What does the object O mean to a subject, at a certain moment and in certain circumstances?

  • Educational-instructional problem: What is teaching? What is learning? How are they related?

  • Ecological problem: What factors and norms condition and support the development of instructional processes?

  • Learning optimisation problem (Didactic Suitability Criteria): What kind of actions and resources should be implemented in the instructional processes to optimise the mathematical learning?

We conclude that the research question posed from the MMCCP can be framed within some of the problematic areas addressed by the OSA or in the intersection of some of them. In other words, the tools developed by the OSA to resolve these problematic areas can also be very useful in answering the questions posed from the referenced mathematical modelling cycle.

Analysis of the prospective teachers’ modelling processes using the MMCCP and the OSA

In this subsection, we present the analyses on the implementation of a modelling task with prospective mathematics teachers, from the perspective of the two theoretical frameworks considered in this study. After both implementations, the productions were collected and two of them were chosen (based on the authors’ criteria) to be analysed, on the basis of (a) the clarity in the resolution of the problem and (b) the use of different mathematical models in their resolution (estimation of measurements and trigonometric ratios). These analyses were performed in accordance with the theoretical dispositions of each framework for the analysis of mathematical activity (as described in ‘Example of a modelling problem and the analysis of its resolution using the MMCCP’ and ‘Example of a modelling problem and the analysis of its resolution using the OSA’).

Mathematical model: estimation of measurements (type A strategy)

The subjects were three prospective primary school teachers, who initially worked on their real model (see Table 3), assigning an undetermined height (x) to each bale, and determined the total height of the mountain as the product of the number of rows and the height of each bale (5x).

Table 3 Initial production and transcription of the resolution using the estimation of measurements
Full size table

The group assumed that this answer may be very obvious, and then discussed its plausibility. They considered this first answer incorrect, as seen from their production (see Table 3). On reflection, they considered the relevance of taking into account that the bales are stacked, and not just balanced on each other, in addition to the fact that the height of the mountain should be given by a numerical result. They thus reformulated their resolution (see Table 4) and estimated the height of each bale as 1.5 m (making it equal to the height they estimated for the woman), with a total of one-third of each bale fitting into the rows below and above (0.25 m per side). In this way, they determined the total height of the mountain as the sum of the four rows of stacked bales (4 × 1.25 m) plus the last complete ball of straw (1.5 m). Now, this group considered their resolution to be correct.

Table 4 Final production and transcription of the solution using the estimation of measurements
Full size table

Table 5 presents the analysis of the modelling process applying both theoretical frameworks, for the resolution of the problem according to the mathematical model (type A strategy). By state, we mean the phase of the modelling process that represents an input/output of a portion of mathematical activity which is analysed.

Table 5 Analysis of the modelling process applying both frameworks, for the type A strategy
Full size table

Mathematical model: trigonometric ratios (type B strategy)

The subject was a prospective secondary school teacher, who simplified the mountain of bales as an equilateral triangle whose vertices are at the centres of the circumferences at the edges of the figure, assigning each side the value of four diameters (4d) (Fig. 4a). Then, she traced the height of the triangle and extracted a right-angle triangle from the figure, assigning values to its interior angles (Fig. 4b), and determining that the value of the height would be calculated by applying the cosine (Fig. 4c).

Fig. 4
figure 4

Production of the resolution using trigonometric ratios in three steps (a), (b), and (c)

Full size image

Table 6 presents the analysis of the modelling process applying both theoretical frameworks, for the resolution of the problem according to the mathematical model — type B strategy.

Table 6 Analysis of the modelling process applying both frameworks, for the type B strategy
Full size table

Comments on the implementation

Regarding the intervention with the prospective primary school teachers, who organised themselves into teams of three to five members each, they basically solved the problem according to the mathematical models described in Table 1. Most of them used the estimation and addition of heights (or a variant of this), and although there were attempts by some groups to solve it using the Pythagorean theorem, this did not materialise in their written production. However, when the subjects asked for ideas on how to approach the problem, it was made clear to them that there may be more than one way to solve it. This fact represented the introduction of a new epistemic norm (in addition to the six detailed in ‘Example of a modelling problem and the analysis of its resolution using the OSA’): The problem does not have a single solution. A common mistake that was evident in these groups was related to the transition between the phases: mental representation of the situation ↔ real model ↔ mathematical model. In terms of the modelling cycle considered, this refers to the sub-competences of simplifying and subsequent mathematising, which was manifested by not considering the stacking of the bales to be a determining factor in order to obtain the height of the mountain. Concerning the answers of the groups, the real results for the height of the mountain varied (between 4.8 and 8.5 m) depending on the height they estimated for the woman pictured (between 1.5 and 1.7 m; extra-mathematical knowledge), so the estimation procedure was an essential element to solving the problem for them. During the discussion with these groups, the different results obtained were compared, although the participants did not question the characteristics of the task presented, assuming it to be a real problem.

Regarding the intervention with the prospective secondary school teachers, who worked individually or in pairs, they took into account both the estimation model and the Pythagorean model, in addition to the one based on the use of trigonometric ratios. Unlike the previous case, the stacking of the bales was not an inconvenience when moving from the mental representation of the situation to the mathematical model since, as they worked with the mathematical models of the Pythagorean theorem and the trigonometric ratios, they only considered the sections of the real model which do not fit between the rows. However, their production included algebraic expressions to represent the height of the mountain, using a function of the radius or diameter of each bale as a variable, and they did not provide a real numerical quantity. In this sense, the sub-competence of interpreting the mathematical results as real results was not in evidence. This was due, in part, to the fact that they did not consider the estimation procedure of the height of the woman or of the diameter of each bale, in order to express a specific numerical result. During the discussion with these groups, there were participants who questioned the problem and its realistic quality, in terms that the statement did not oblige in-depth contemplation of the plausibility of the result obtained, due to the multiplicity of answers that can be obtained from the problem. That is, if the result is very small or very large, the need to study its plausibility will appear; but if the result is 7, 8, or 9 m for the height, for example, the task does not require an analysis of its plausibility. In other words, the problem statement does not make it easy to follow the Norm 5; but in their opinion, a change in the problem such as ‘establish if the bales can be placed into a barn of X height’ actually would force compliance with this norm.

It seems reasonable to conclude that the level of mathematical knowledge of the subjects determines the resolution strategy to be used (choice of a mathematical model) and the results obtained (mathematical results → real results). Although all the participants — due to their previous school training — should have had sufficient mathematical knowledge to solve the problem using the three models (estimation of measurements, Pythagorean theorem, or trigonometric ratios), the prospective primary school teachers mainly opted for the estimation of measurements, while the prospective secondary school teachers considered the three models, in particular the one based on trigonometric ratios, which was not considered within the analysis from the modelling cycle (see Table 1).

The lower level of mathematical knowledge on the part of prospective primary school teachers was also evident, as stated above, in the difficulties they had in simplifying the mental representation of the situation to construct a real model and its subsequent mathematisation into a mathematical model. Now, a question that arises is whether only the mathematical knowledge of the subjects was the determining factor in the choice of the strategy (mathematical model) for solving a problem. It could be argued that the prospective primary school teachers were mentally placed in a primary classroom (either as teachers or as students), that is, in a context where only the procedure of estimation would make sense.

Regarding the results of the problem, the prospective primary school teachers answered with real results (with greater or lesser success) to the situation, while the prospective secondary school teachers did not offer the interpretation of mathematical results — obtained from the work with the mathematical model — in real results, in order to give a specific answer to the problem. One possible explanation for this discrepancy in the answers is that the prospective primary school teachers live in a world of more elementary mathematics, where the processes of abstraction and generalisation are not as deep as those that are present in the prospective secondary school teachers, who live a more advanced mathematics, where the processes of abstraction and generalisation may have several levels of depth.

This kind of findings is related to some of the ones reported by Verschaffel and collaborators in studies with primary and secondary mathematics teachers (see Chen et al., 2011; Van Dooren et al., 2002, 2003; Verschaffel et al., 1997; among others). However, as an opinion beyond this explanation, it is plausible to suppose that the problem statement does not oblige the solver to find real results, just as the prospective secondary school teachers stated in the discussion of the problem.

Theoretical discussion

We can now answer the question posed in this paper: To what extent does the application of the onto-semiotic tools complement the analysis from a cognitive perspective of a mathematical modelling process? Our main conclusion here is that we have identified some concordances and complementarities between these two ways of analysing the mathematical activity involved in the modelling process, which we detail below.

In Tables 5 and 6, the columns summarise the analysis of the mathematical activity carried out by the prospective mathematics teachers with the tools provided by the OSA (as in Table 2), whereas the shaded rows correspond to the phases (see Table 1) and transitions (see Fig. 1) of the MMCCP. While the level of detail in the two methods differs, Tables 5 and 6 make it clear that they are complementary methods. This complementarity is due to the fact that the more detailed analysis carried out with the tools provided by the OSA allows us to zoom in on the mathematical activity that underlies the phases and transitions of the MMCCP. This zoom in allows us to see these phases and transitions as an iceberg formed by a conglomerate of mathematical practices, processes, norms, and primary objects (activated in these practices). In turn, the phases and transitions of the MMCCP provide an initial structure (scheme) for the analysis carried out following the OSA model (as seen in Tables 5 and 6), and allow us to group together (in fact, to encapsulate) the mathematical practices (with the processes and primary objects activated in them) performed in each of the phases and transitions of the cycle.

The analysis carried out by following the OSA model highlights an important aspect, that is, the plot of norms that regulate the modelling processes. It is important since, in order to make students proficient in Modelling, a teacher must be aware of the existence of these norms and must ensure that they are established in the instructional process involving the modelling. This significant role of the epistemic (mathematical and metamathematical) norms in the modelling process is not, to our knowledge, explicitly included as part of the MMCCP.

Another relevant element is that this more detailed analysis allows the explanation of why a specific transition of the MMCCP cannot be performed by a solver of this task (as occurred with some groups in this implementation).

Although the application of the OSA allows to discover the mathematical activity plot that underlies the modelling cycle, we consider that there are two aspects to take into account when applying a general theoretical framework for the analysis of mathematical activity.

The first aspect is that, since there is no agreement or paradigm in the area on how to make an analysis of mathematical activity, it is plausible to think that perhaps another theoretical framework could complement the MMCCP even more. As stated at the introduction, the particular choice of the MMCCP and the OSA is justified by our expertise in their use. Thereby, one aspect to be discussed is whether the answer we give to the question ‘To what extent does the application of the onto-semiotic tools complement the analysis from a cognitive perspective of a mathematical modelling process?’ is a more relevant contribution than the one obtained by analysing this same modelling cycle from other general theoretical frameworks of mathematical activity (e.g., Cosmes & Montoya, 2021, from the Mathematical Working Spaces theory). Another discussion within this first aspect, is the comparison between the results of this research with the analyses of the modelling process carried out from the perspective of other frameworks that have used modelling cycles other than the MMCCP, and that have enriched them with analysis tools of mathematical activity that go beyond modelling activity. For instance, the analysis carried out by Niss and Blum (2020), or the research developed by Galbraith and Stillman (2006), which presents a framework for identifying students’ blockages during transitions in the modelling process, based on a more detailed analysis of mathematical and metacognitive activity involved in these transitions. This first aspect is part of a theoretical discussion that we are working on, but that would require a specific article.

The second aspect is that, once a general theoretical framework has been selected, its theoretical constructs should be useful to capture the complexity of mathematical activity, and also be reasonably easy to apply. For instance, if the theoretical framework distinguishes between the constructs ‘proposition’ and ‘procedure’, it should be easy to identify when we are referring to a ‘proposition’ or a ‘procedure’. In other words, a researcher who masters the tools provided by the OSA could be able to make analyses quite similar to those presented in Tables 5 and 6. However, our experience in applying these tools on the analysis of mathematical activity has made us evident that it is not always an easy task. On this fact, several reflections have been within the OSA, and the conclusion is that the problem is not as much the constructs developed for the analysis of mathematical activity (e.g., procedure, proposition, norm), but rather it is a problem of the philosophy of mathematics, in the sense that mathematics is presented as a descriptive discourse of a certain reality (whether Platonic or empiricist) when, in terms of the OSA, its deep nature is to be conventional. This would explain why, for instance, a ‘proposition’ becomes a ‘procedure’ (e.g., the derivatives product rule) or vice versa, as appropriate (there is a deeper discussion in Font et al., 2013).

Conclusions

The analysis of the modelling process, expanded with the tools provided by the OSA, is important because it can help us to design didactic proposals to implement modelling in the classroom. According to the analyses presented (see Tables 2, 5, and 6), no processes, for example, such as the generalisation of patterns, are evident, which could be achieved if the specification that there are five rows was omitted, and only the picture (Fig. 2) was presented with the three rows visible, so that the student can conclude the formation pattern of the rows in the mountain. Another process to which this analysis can contribute is that of validation (in Practice 7 from Table 2), where the detail shows — regardless of the result for the height of the mountain (either 7, 8, or 9 m) — the process in question would be the same, since it is only determined by the verification of the method of resolution (mathematical model → mathematical results). When identifying the primary objects involved in the validation process, especially the procedure and the argument, we observe that the discussion on the reasonableness of the result (mathematical results → real results) is only mediated by the choice of an estimated height in the real context, and does not play a determining role in answering this particular problem. Due to the problematisation process being closely linked to the validation of the results, the richness of this last process could be improved by modifying the situation context, for example, if the height of the mountain is required in order to store the bales in a barn of specific dimensions.

Following this line of helping to improve the didactic design, the analysis carried out with the tools provided by the OSA allows us to see the configuration of primary objects that intervene in the solving process. The analysis of these configurations provides information concerning the anatomy of the solution to the problem posed (see Badillo et al., 2015; Malaspina & Font, 2010; Malaspina et al., 2019), in addition to making it possible to create new problems, among other aspects, through variation of those initially proposed or directly, in such a way that a certain (or several) primary object(s) must be used in their solution.

The detailed analysis provided by the OSA can also be very useful for the development and evaluation of modelling sub-competencies, as mentioned when we commented on the production of the prospective mathematics teachers. Indeed, this analysis can be used to specify which practice, object, or process is (or is not) evidence of the sub-competence that it is intended to develop or evaluate, and it can be particularly useful to offer detailed feedback to the student.

Finally, we stress that this article is also a contribution to the networking of theories, because it illustrates how a networking can be made between two theories of different levels — in this case, a general theory for the analysis of mathematical activity (OSA) and a theoretical framework for the analysis of the specific mathematical activity of modelling (MMCCP). This approach results in an integrated proposal of the two theories for the analysis of the mathematical activity of interest to the specific theory, in this case, the modelling process.