Topological methods in moduli theory

Abstract

One of the main themes of this long article is the study of projective varieties which are K(H,1)’s, i.e. classifying spaces BH for some discrete group H. After recalling the basic properties of such classifying spaces, an important class of such varieties is introduced, the one of Bagnera–de Franchis varieties, the quotients of an Abelian variety by the free action of a cyclic group. Moduli spaces of Abelian varieties and of algebraic curves enter into the picture as examples of rational K(H,1)’s, through Teichmüller theory. The main trhust of the paper is to show how in the case of K(H,1)’s the study of moduli spaces and deformation classes can be achieved through by now classical results concerning regularity of classifying maps. The Inoue type varieties of Bauer and Catanese are introduced and studied as a key example, and new results are shown. Motivated from this study, the moduli spaces of algebraic varieties, and especially of algebraic curves with a group of automorphisms of a given topological type are studied in detail, following new results by the author, Michael Lönne and Fabio Perroni. Finally, the action of the absolute Galois group on the moduli spaces of such K(H,1) varieties is studied. In the case of surfaces isogenous to a product, it is shown how this yields a faifhtul action on the set of connected components of the moduli space: for each Galois automorphism of order different from 2 there is an algebraic surface S such that the Galois conjugate surface of S has fundamental group not isomorphic to the one of S.

1 Introduction

The interaction of algebraic geometry and topology has been such, in the last three centuries, that it is often difficult to say when does a result belong to one discipline or to the other, the archetypical example being the Bézout theorem, first conceived through a process of geometrical degeneration (algebraic hypersurfaces degenerating to union of hyperplanes), and later clarified through topology and through algebra.

This ‘caveat’ is meant to warn the reader that a more appropriate title for the present survey article could be: ‘Some topological methods in moduli theory, and from the personal viewpoint, taste and understanding of the author’. In fact, many topics are treated, some classical and some very recent, but with a choice converging towards some well defined research interests.

I considered for some time the tempting and appealing title ‘How can the angel of topology live happily with the devil of abstract algebra’, paraphrasing the motto by Hermann Weyl.¹

The latter title would have matched with my personal philosophical point of view: while it is reasonable that researchers in mathematics develop with enthusiasm and dedication new promising mathematical tools and theories, it is important then that the accumulated knowledge and cultural wealth (the instance of topology in the twentieth century being a major one) be not lost afterwards. This wealth must indeed not only be invested and exploited, but also further developed by addressing problems in other fields, problems which often raise new and fascinating questions. In more down to earth words, the main body of the article is meant to be an invitation for algebraic geometers to use more classical topology. This invitation is not new, see for istance the work of Atiyah and Bott on the moduli spaces of vector bundles on curves [15]; but explains the structure of the article which is, in a sense, that of a protracted colloquium talk, and where we hope that also topologists, for which many of these notions are well known, will get new kicks coming from algebraic geometry, and especially moduli theory.

In this article we mostly consider moduli theory as the fine part of classification theory of complex varieties: and we want to show how in some lucky cases topology helps also for the fine classification, allowing the study of the structure of moduli spaces: as we have done quite concretely in several papers [30–33, 35–37].

We have already warned the reader about the inhomogeneity of the level assumed in the text: usually many sections start with very elementary arguments but, at a certain point, when we deal with current problems, the required knowledge may raise considerably.

Let us try to summarize the logical thread of the article.

Algebraic topology flourished from some of its applications (such as Brouwer’s fixed point theorem, or the theorem of Borsuk–Ulam) inferring the non existence of certain continuous maps from the observation that their existence would imply the existence of homomorphisms satisfying algebraic properties which are manifestly impossible to be verified.

Conversely, the theory of fibre bundles and homotopy theory give a topological incarnation of a group G through its classifying space BG. The theory of classifying spaces translates then group homomorphisms into continuous maps to classifying spaces. For instance, in algebraic geometry, the theory of Albanese varieties can be understood as dealing with the case where G is free abelian and the classifying maps are holomorphic.

For more general G, an important question is the one of the regularity of these classifying maps, such as harmonicity, addressed by Eells and Sampson, and their complex analyticity addressed by Siu and others. These questions, which were at the forefront of mathematical research in the last 40 years, have powerful applications to moduli theory.

After a general introduction directed towards a broader public, starting with classical theorems by Zeuthen-Segre and Lefschetz, proceeding to classifying spaces and their properties, I shall concentrate on some classes of projective varieties which are classifying spaces for some group, providing several explicit examples. I discuss then locally symmetric varieties, and at a certain length the quotients of Abelian varieties by a cyclic group acting freely, which are here called Bagnera–De Franchis varieties.

At this point the article becomes instructional, and oriented towards graduate students, and several important topics, like orbifold fundamental groups, Teichmüller spaces, moduli spaces of curves, group cohomology and homology are treated in detail (and a new proof of a classical theorem of Hopf is sketched).

Then some applications are given to concrete problems in moduli theory, in particular a new construction of surfaces with $p_g=q=1$ is given.

The next section is devoted to a preparation for the rigidity and quasi-rigidity properties of projective varieties which are classifying spaces (meaning that their moduli spaces are completely determined by their topology); in the section are recalled the by now classical results of Eells and Sampson, and Siu’s results about complex analyticity of harmonic maps, with particular emphasis on bounded domains and locally symmetric varieties.

Other more elementary results, based on Hodge theory, the theorem of Castelnuovo-De Franchis, and on the explicit constructions of classifying spaces are explained in detail because of their importance for Kähler manifolds. We then briefly discuss Kodaira’s problem and Voisin’s counterexamples, then we dwell on fundamental groups of projective varieties, and on the Shafarevich conjecture.

Afterwards we deal with several concrete investigations of moduli spaces, which in fact lead to some group theoretical questions, and to the investigation of moduli spaces of varieties with symmetries.

Some key examples are: varieties isogenous to a product, and the Inoue-type varieties introduced in recent work with Ingrid Bauer: for these the moduli space is determined by the topological type. I shall present new results and open questions concerning this class of varieties.

In the final part, after recalling basic results on complex moduli theory, we shall also illustrate the concept of symmetry marked varieties and their moduli, discussing the several reasons why it is interesting to consider moduli spaces of triples $(X,G,\alpha )$ where X is a projective variety, G is a finite group, and $\alpha$ is an effective action of G on X. If X is the canonical model of a variety of general type, then G is acting linearly on some pluricanonical model, and we have a moduli space which is a finite covering of a closed subspace ${\mathfrak {M}}^G$ of the moduli space.

In the case of curves we show how this investigation is related to the description of the singular locus of the moduli space ${\mathfrak {M}}_g$ (for instance of its irreducible components, see [129]), and of its compactification $\overline{{\mathfrak {M}}_g}$ (see [113]).

In the case of surfaces there is another occurrence of Murphy’s law, as shown in my joint work with Ingrid Bauer [33]: the deformation equivalence for minimal models S and for canonical models differs drastically (nodal Burniat surfaces being the easiest example). This shows how appropriate it is to work with Gieseker’s moduli space of canonical models of surfaces.

In the case of curves, there are interesting relations with topology. Moduli spaces ${\mathfrak {M}}_g (G)$ of curves with a group G of automorphisms of a fixed topological type have a description by Teichmüller theory, which naturally leads to conjecture genus stabilization for rational homology groups. I will then describe two equivalent descriptions of the irreducible components of ${\mathfrak {M}}_g (G)$, surveying known irreducibility results for some special groups. A new fine homological invariant was introduced in our joint work with Lönne and Perroni: it allows to prove genus stabilization in the ramified case, extending a beautiful theorem due to Livingston [272] and Dunfield and Thurston [141], who dealt with the easier unramified case.

Another important application is the following one, in the direction of arithmetic: in the 60’s Serre [336] showed that there exists a field automorphism $\sigma$ in the absolute Galois group $Gal(\bar{{\mathbb {Q}}} / {\mathbb {Q}})$, and a variety X defined over a number field, such that X and the Galois conjugate variety $X^{\sigma }$ have non isomorphic fundamental groups, in particular they are not homeomorphic.

In a joint paper with I. Bauer and F. Grunewald we proved a strong sharpening of this phenomenon discovered by Serre, namely, that if $\sigma$ is not in the conjugacy class of the complex conjugation then there exists a surface (isogenous to a product) X such that X and the Galois conjugate variety $X^{\sigma }$ have non isomorphic fundamental groups.

In the end we finish with an extremely quick mention of several interesting topics which we do not have the time to describe properly, among these, the stabilization results for the cohomology of moduli spaces and of arithmetic varieties.

2 Prehistory and beyond

The following discovery belongs to the 19-th century: consider the complex projective plane ${\mathbb {P}}^2$ and two general homogeneous polynomials $F, G \in {\mathbb {C}}[x_0,x_1,x_2]$ of the same degree d. Then F, G determine a linear pencil of curves $C_{\lambda } , \ \forall \lambda = (\lambda _0, \lambda _1) \in {\mathbb {P}}^1$,

$$\begin{aligned} C_{\lambda } := \left\{ x = (x_0,x_1,x_2) \in {\mathbb {P}}^2 | \lambda _0 F(x) + \lambda _1 G(x) = 0 \right\} \!. \end{aligned}$$

One sees that the curve $C_{\lambda }$ is singular for exactly $\mu = 3 (d-1)^2$ values of $\lambda$, as can be verified by an elementary argument which we now sketch.

In fact, x is a singular point of some $C_{\lambda }$ iff the following system of three homogeneous linear equations in $\lambda = ( \lambda _0, \lambda _1)$ has a nontrivial solution:

$$\begin{aligned} \lambda _0 \frac{\partial F}{\partial x_i} (x) + \lambda _1 \frac{\partial G}{\partial x_i} (x) = 0, \quad \forall i = 0,1,2. \end{aligned}$$

By generality of F, G we may assume that the curves $C_0 : = \{x | F(x) = 0\}$ and $C_1 : = \{x | G(x) = 0\}$ are smooth and intersect transversally (i.e., with distinct tangents) in $d^2$ distinct points; hence if a curve of the pencil $C_{\lambda }$ has a singular point x, then we may assume that for this point we have $F(x) \ne 0 \ne G(x)$, and then $\lambda$ is uniquely determined.

If now $\frac{\partial F}{\partial x_0}$ and $\frac{\partial G}{\partial x_0}$ do not vanish simultaneously in x, then the above system has a nontrivial solution if and only if

$$\begin{aligned} \left[ \frac{\partial G}{\partial x_0} \cdot \frac{\partial F}{\partial x_i } - \frac{\partial F}{\partial x_0} \cdot \frac{\partial G}{\partial x_i }\right] (x)= 0, \quad i=1,2. \end{aligned}$$

By the theorem of Bézout (see [369]) the above two equations have $( 2 (d-1))^2 = 4 (d-1)^2$ solutions, including among these the $(d-1)^2$ solutions of the system of two equations $\frac{\partial F}{\partial x_0}(x) = \frac{\partial G}{\partial x_0} (x) = 0$.

One sees that, for F, G general, there are no common solutions of the system

$$\begin{aligned} \frac{\partial F}{\partial x_0}(x) = \frac{\partial G}{\partial x_0} (x) = \left[ \frac{\partial G}{\partial x_1} \cdot \frac{\partial F}{\partial x_2 } - \frac{\partial F}{\partial x_1} \cdot \frac{\partial G}{\partial x_2 }\right] (x)= 0, \end{aligned}$$

hence the solutions of the above system are indeed

$$\begin{aligned} 3 (d-1)^2 = 4 (d-1)^2 - (d-1)^2 . \end{aligned}$$

It was found indeed that, rewriting $\mu = 3 (d-1)^2 = d^2 + 2d (d-3)+ 3$, the above formula generalizes to a beautiful formula, valid for any smooth algebraic surface S, and which is the content of the so-called theorem of Zeuthen-Segre; this goes as follows: observe in fact that $d^2$ is the number of points where the curves of the pencil meet, while the genus g of a plane curve of degree d equals $\frac{ (d-1)(d-2)}{2}$.

Theorem 1

(Zeuthen-Segre, classical) Let S be a smooth projective surface, and let $C_{\lambda } , \ \lambda \in {\mathbb {P}}^1$ be a linear pencil of curves of genus g which meet transversally in $\delta$ distinct points. If $\mu$ is the number of singular curves in the pencil (counted with multiplicity), then

$$\begin{aligned} \mu - \delta - 2 (2g-2) = I + 4, \end{aligned}$$

where the integer I is an invariant of the algebraic surface, called Zeuthen-Segre invariant.

Here, the integer $\delta$ equals the self-intersection number $C^2$ of the curve C, while in modern terms the number $2 g -2 = C^2 + K_S \cdot C$, $K_S$ being the divisor (zeros minus poles) of a rational differential 2-form.

In particular, our previous calculation shows that for ${\mathbb {P}}^2$ the invariant $I = -1$.

The interesting part of the discovery is that the integer $I + 4$ is not only an algebraic invariant, but is indeed a topological invariant.

Indeed, for a compact topological space X which can be written as the disjoint union of locally closed sets $X_i, \ i = 1, \ldots r,$ homeomorphic to an Euclidean space ${\mathbb {R}}^{n_i}$, one can define

$$\begin{aligned} e(X) := \sum _i^r (-1)^{n_i}, \end{aligned}$$

and indeed this definition is compatible with the more abstract definition

$$\begin{aligned} e(X) = \sum _{j=0}^{\dim (X)} (-1)^j {{\mathrm{\text {rank}}}}H_j(X, {\mathbb {Z}}). \end{aligned}$$

For example, the plane ${\mathbb {P}}^2 = {\mathbb {P}}^2_{{\mathbb {C}}}$ is obtained from a point attaching ${\mathbb {C}}= {\mathbb {R}}^2$ and then ${\mathbb {C}}^2 = {\mathbb {R}}^4$, hence $e({\mathbb {P}}^2) = 3$ and we verify that $e({\mathbb {P}}^2) = I + 4$.

While for an algebraic curve C of genus g its topological Euler–Poincaré characteristic, for short Euler number, equals $e(C) = 2 - 2g$, since C is obtained as the disjoint union of one point, 2g arcs, and a 2-disk (think of the topological realization as the quotient of a polygon with 4 g sides).

The Euler Poincaré characteristic is multiplicative for products:

$$\begin{aligned} e (X \times Y ) = e (X) \cdot e (Y), \end{aligned}$$

and more generally for fibre bundles (a concept we shall introduce in the next section), and accordingly there is a generalization of the theorem of Zeuthen-Segre:

Theorem 2

(Zeuthen-Segre, modern) Let S be a smooth compact complex surface, and let $f : S \rightarrow B$ be a fibration onto a projective curve B of genus b (i.e., the fibres $f^{-1}(P)$, $P \in B$, are connected), and denote by g the genus of the smooth fibres of f. Then

$$\begin{aligned} e(S) = (2b- 2 )(2g-2) + \mu , \end{aligned}$$

where $\mu \ge 0$, and $\mu = 0$ if and only if all the fibres of f are either smooth or, in the case where $g=1$, a multiple of a smooth curve of genus 1.

The technique of studying linear pencils turned out to be an invaluable tool for the study of the topology of projective varieties. In fact, Solomon Lefschetz in the beginning of the 20-th century was able to describe the relation holding between a smooth projective variety $X \subset {\mathbb {P}}^N$ of dimension n and its hyperplane section $W = X \cap H$, where H is a general linear subspace of codimension 1, a hyperplane.

The work of Lefschetz deeply impressed the Italian algebraic geometer Guido Castelnuovo, who came to the conclusion that algebraic geometry could no longer be carried over without the new emerging techniques, and convinced Oscar Zariski to go on setting the building of algebraic geometry on a more solid basis. The report of Zariski [379] had a big influence and the results of Lefschetz were reproven and vastly extended by several authors: they say essentially that homology and homotopy groups of real dimension smaller than the complex dimension n of X are the same for X ands its hyperplane section W.

In my opinion the nicest proofs of the theorems of Lefschetz are those given much later by Andreotti and Frankel [4, 5].

Theorem 3

Let X be a smooth projective variety of complex dimension n, let $W = X \cap H$ be a smooth hyperplane section of X, and let further $Y = W \cap H'$ be a smooth hyperplane section of W.

First Lefschetz’ theorem: the natural homomorphism $H_i (W, {\mathbb {Z}}) \rightarrow H_i (X, {\mathbb {Z}})$ is bijective for $i < n-1$, and surjective for $i = n-1$; the same is true for the natural homomorphisms of homotopy groups $\pi _i (W) \rightarrow \pi _i (X)$ (the results hold more generally, see [288], p. 41, even if X is singular and W contains the singular locus of X).

Second Lefschetz’ theorem: The kernel of $H_{n-1} (W, {\mathbb {Z}}) \rightarrow H_{n-1} (X, {\mathbb {Z}})$ is the subgroup ${{\mathrm{\text {Van}}}}H_{n-1} (W, {\mathbb {Z}})$ generated by the vanishing cycles, i.e., those cycles which are mapped to 0 when W tends to a singular hyperplane section $W_{\lambda }$ in a pencil of hyperplane sections of X.

Generalized Zeuthen-Segre theorem: if $\mu$ is the number of singular hyperplane sections in a general linear pencil of hyperplane sections of X, then

$$\begin{aligned} e(X) = 2 e(W) - e(Y) + (-1)^n \mu . \end{aligned}$$

Third Lefschetz’ theorem or Hard Lefschetz’ theorem:

The first theorem and the universal coefficients theorem imply for the cohomology groups that $H^i (X, {\mathbb {Z}}) \rightarrow H^i (W, {\mathbb {Z}})$ is bijective for $i < n-1$, while $H^{n-1} (X, {\mathbb {Z}}) \rightarrow H^{n-1} (W, {\mathbb {Z}})$ is injective. Defining ${{\mathrm{\text {Inv}}}}H_{n-1} (W, {\mathbb {Z}})$ as the Poincaré dual of the image of $H^{n-1} (X, {\mathbb {Z}})$, then we have a direct sum decomposition (orthogonal for the cup product) after tensoring with ${\mathbb {Q}}$:

$$\begin{aligned} H_{n-1} (W, {\mathbb {Q}}) = {{\mathrm{\text {Inv}}}}H_{n-1} (W, {\mathbb {Q}}) \oplus {{\mathrm{\text {Van}}}}H_{n-1} (W, {\mathbb {Q}}). \end{aligned}$$

Equivalently, the operator L given by cup product with the cohomology class $h \in H^2 (X, {\mathbb {Z}})$ of a hyperplane, $L :H^i (X, {\mathbb {Z}}) \rightarrow H^{i+2} (X, {\mathbb {Z}})$, induces an isomorphism

$$\begin{aligned} L^j :H^{n-j} (X, {\mathbb {Q}}) \rightarrow H^{n+j} (X, {\mathbb {Q}}), \quad \forall j \le n. \end{aligned}$$

Not only the theorems of Lefschetz play an important role for our particular purposes, but we feel that we should also spend a few words sketching how they lead to some very interesting and still widely open conjectures, the Hartshorne conjectures (see [210]).

Assume now that the smooth projective variety $X \subset {\mathbb {P}}^N$ is the complete intersection of $N-n$ hypersurfaces (this means the the sheaf ${\mathcal {I}}_X$ of ideals of functions vanishing on X is generated by polynomials $F_1, \ldots , F_c$, $c : = N - n$ being the codimension of X). Then the theorems of Lefschetz² imply that the homology groups of X equal those of ${\mathbb {P}}^N$ for $i \le n-1$ (recall that $H_i({\mathbb {P}}^N, {\mathbb {Z}}) = 0$ for i odd, while $H_i({\mathbb {P}}^N, {\mathbb {Z}}) = {\mathbb {Z}}$ for $i \le 2N$, i even). Similarly holds true for the homotopy groups, and we recall that, since ${\mathbb {P}}^N = S^{2N+1} / S^1$, then $\pi _i ({\mathbb {P}}^N) = 0$ for $i \le 2N, i \ne 0,2$.

It was an interesting discovery by Barth (see [22–24, 174] for the following and related results) that a similar (but weaker) result holds true for each smooth subvariety of ${\mathbb {P}}^N$, provided the codimension $c = N - n$ of X is smaller than the dimension.

Theorem 4

(Barth–Larsen) Let X be a smooth subvariety of dimension n in ${\mathbb {P}}^N$: then the homomorphisms

$$\begin{aligned} H_i (X, {\mathbb {Z}}) \rightarrow H_i ({\mathbb {P}}^N, {\mathbb {Z}}) , \quad \pi _i (X) \rightarrow \pi _i ({\mathbb {P}}^N) \end{aligned}$$

are bijective for $i \le n - c \Leftrightarrow i < 2n - N + 1$, and surjective for $i = n - c + 1 = 2n - N + 1$.

Observe that, if $N= n+1$, then the above result yields exactly the one of Lefschetz, hence the theorem is sharp in this trivial case (but much weaker for complete intersections of higher codimension). The case of the Segre embedding $X := {\mathbb {P}}^1 \times {\mathbb {P}}^2 \rightarrow {\mathbb {P}}^5$ is a case which shows how the theorem is sharp since $({\mathbb {Z}})^2 \cong H_2 (X, {\mathbb {Z}}) \rightarrow H_2 ({\mathbb {P}}^8, {\mathbb {Z}}) \cong {\mathbb {Z}}$ is surjective but not bijective.

The reader might wonder why the theorem of Barth and Larsen is a generalization of the theorem of Lefschetz. First of all, while Barth used originally methods of holomorphic convexity in complex analysis (somehow reminiscent of Morse theory in the real case) Hartshorne showed [210] how the third Lefschetz Theorem implies the result of Barth for cohomology with coefficients in ${\mathbb {Q}}$. Moreover a strong similarity with the Lefschetz situation follows from the fact that one may view it (as shown by Badescu, see [18]) as an application of the classical Lefschetz theorem to the intersection

$$\begin{aligned} ( X \times {\mathbb {P}}^N) \cap \Delta \cong X, \end{aligned}$$

where $\Delta \subset {\mathbb {P}}^N \times {\mathbb {P}}^N$ is the diagonal. In turn, an idea of Deligne [133, 175] shows that the diagonal $\Delta \subset {\mathbb {P}}^N \times {\mathbb {P}}^N$ behaves ‘like’ a complete intersection, essentially because, under the standard birational map ${\mathbb {P}}^N \times {\mathbb {P}}^N \dashrightarrow {\mathbb {P}}^{2N}$, it maps to a linear subspace of ${\mathbb {P}}^{2N}$.

The philosophy is then that smooth subvarieties of small codimension behave like complete intersections. This could be no accident if the well known Hartshorne conjecture [210] were true.

Conjecture 5

(On subvarieties of small codimension, Hartshorne) Let X be a smooth subvariety of dimension n in ${\mathbb {P}}^N$, and assume that the dimension is bigger than twice the codimension, $n > 2 (N-n)$: then X is a complete intersection.

While the conjecture says nothing in the case of curves and surfaces and is trivial in the case where $n \le 4$, since a codimension 1 subvariety is defined by a single equation, it starts to have meaning for $n \ge 5$ and $c = N - n \ge 2$.

In the case where $c = N - n = 2$, then by a result of Serre one knows (see [154], p. 143, also for a general survey of the Hartshorne conjecture for codimension 2 subvarieties) that X is the zero set of a section s of a rank 2 holomorphic vector bundle V on ${\mathbb {P}}^N$ (observe that in this codimension one has that ${{\mathrm{\text {Pic}}}}(X) \cong {{\mathrm{\text {Pic}}}}({\mathbb {P}}^N)$, so that X satisfies the condition of being subcanonical: this means that $\omega _X = {\mathcal {O}}_X(d)$ for some d): in the case $c=2$ the conjecture by Hartshorne is then equivalent to the conjecture

Conjecture 6

(On vector bundles of rank 2 on projective space, Hartshorne) Let V be a rank 2 vector bundle on ${\mathbb {P}}^N$, and assume that $N \ge 7$: then V is a direct sum of line bundles.

The major evidence for the conjecture on subvarieties of small codimension comes from the concept of positivity of vector bundles ([175], also [267]). In fact, many construction methods of subvarieties X of small codimension involve a realization of X as the locus where a vector bundle map drops rank to an integer r, and X becomes singular if there are points of X in the locus $\Sigma$ where the rank drops further down to $(r-1)$.

The expected dimension of $\Sigma$ is positive in the range of Hartshorne’s conjecture, but nevertheless this is not sufficient to show that $\Sigma \cap X$ is non empty.

Hartshorne’s Conjecture 5 is related to projections: in fact, for each projective variety $X \subset {\mathbb {P}}^N$ there exists a linear projection ${\mathbb {P}}^N \dashrightarrow {\mathbb {P}}^{2n+1}$ whose restriction to X yields an embedding $X \subset {\mathbb {P}}^{2n+1}$: in other words, an embedding where the codimension is equal to the dimenion n plus 1. The condition of being embedded as a subvariety where the codimension is smaller or equal than the dimension is already a restriction (for instance, not all curves are plane curves, and smooth surfaces in ${\mathbb {P}}^3$ are simply connected by Lefschetz’s theorem), and the smaller the codimension gets, the stronger the restrictions are (as shown by Theorem 4).

Speaking now in more technical terms, a necessary condition for X to be a complete intersection is that the sheaf of ideals ${\mathcal {I}}_X$ be arithmetically Cohen-Macaulay (ACM, for short), which means that all higher cohomology groups $H^i({\mathbb {P}}^N, {\mathcal {I}}_X(d)) = 0$ vanish for $n \ge i >0$ and $\forall d \in {\mathbb {Z}}$. In view of the exact sequence

$$\begin{aligned} 0 \rightarrow {\mathcal {I}}_X \rightarrow {\mathcal {O}}_{{\mathbb {P}}^N} \rightarrow {\mathcal {O}}_X \rightarrow 0 \end{aligned}$$

the CM condition amounts to two conditions:

• (1) X is projectively normal, i.e., the linear system cut on X by polynomials of degree d is complete ( $H^0({\mathbb {P}}^N, {\mathcal {O}}_{{\mathbb {P}}^N}(d) ) \rightarrow H^0 ({\mathcal {O}}_X(d))$ is surjective for all $d \ge 0$)

• (2) $H^i(X , {\mathcal {O}}_X(d)) = 0$ for all $d \in {\mathbb {Z}}$, and for all $0 < i < n = \dim (X)$.

In the case where X has codimension 2, and $N \ge 6$ (see [154], cor. 4.2, p. 165), the condition of being a complete intersection is equivalent to projective normality.

Linear normality is the case $d = 1$ and means that X is not obtained as the projection of a non-degenerate variety from a higher dimensional projective space ${\mathbb {P}}^{N+1}$. This part of Hartshorne’s conjecture is the only one which has been verified: a smooth subvariety with $n \ge 2 c -1 = 2 (N-n) -1$ is linearly normal (theorem of Zak [378]).

For higher d, one considers the so-called formal neighbourhood of X: denoting by $N_X^{\vee } : = {\mathcal {I}}_X / {\mathcal {I}}_X^2$ the conormal bundle of X, one sees that, in order to show projective normality, in view of the exact sequence

$$\begin{aligned} 0 \rightarrow {\mathcal {I}}_X^{m+1}(d) \rightarrow {\mathcal {I}}_X^m (d)\rightarrow Sym^m \left( N_X^{\vee }\right) (d) \cong \left( {\mathcal {I}}_X^m / {\mathcal {I}}_X^{m+1}\right) (d) \rightarrow 0, \end{aligned}$$

a crucial role is played by the cohomology groups

$$\begin{aligned} H^q( Sym^m ( N_X^{\vee })(d))). \end{aligned}$$

We refer the reader to [323] for a discussion of more general Nakano type vanishing statements of the form $H^q( Sym^m ( N_X^{\vee })(d) \otimes \Omega ^p_X)$ (these could be implied by very strong curvature properties on the normal bundle, see also [267]).

Observe finally that the theorems of Lefschetz have been also extended to the case of singular varieties (see [172, 184]), but we shall not need to refer to these extensions in the present paper.

3 Algebraic topology: non existence and existence of continuous maps

The first famous achievements of algebraic topology were based on functoriality, which was used to infer the nonexistence of certain continuous maps.

The Brouwer’s fixed point theorem says that every continuous self map $f : D^n \rightarrow D^n$, where $D^n = \{ x \in {\mathbb {R}}^n | |x| \le 1\}$ is the unit disk, has a fixed point. The argument is by contradiction: otherwise, letting $\phi (x)$ be the intersection of the boundary $S^{n-1}$ of $D^n$ with the half line stemming from f (x) in the direction of x, $\phi$ would be a continuous map

$$\begin{aligned} \phi : D^n \rightarrow S^{n-1}, \quad s.t. \ \phi |_{S^{n-1}} = {{\mathrm{\text {Id}}}}_{S^{n-1}}. \end{aligned}$$

The key point is to show that the reduced³ homology group $H_{n-1} ({S^{n-1}} , {\mathbb {Z}}) \cong {\mathbb {Z}}$, while $H_{n-1} (D^n , {\mathbb {Z}}) = 0$, the disc being contractible; after that, denoting by $\iota : S^{n-1} \rightarrow D^n$ the inclusion, functoriality of homology groups, since $\phi \circ \iota = {{\mathrm{\text {Id}}}}_{S^{n-1}}$, would imply $0 = H_{n-1} ( \phi ) \circ H_{n-1} ( \iota )= H_{n-1} ( {{\mathrm{\text {Id}}}}_{S^{n-1}}) = {{\mathrm{\text {Id}}}}_{{\mathbb {Z}}}$, the desired contradiction.

Also well known is the Borsuk–Ulam theorem, asserting that there is no odd continuous function $F : S^n \rightarrow S^m$ for $n > m$ (odd means that $F ( -x) = - F(x)$).

Here there are two ingredients, the main one being the cohomology algebra, and its contravariant functoriality: to any continuous map $f : X \rightarrow Y$ there corresponds an algebra homomorphism

$$\begin{aligned} f^* : H^* (Y, R) = \oplus _{i=0}^{\dim (Y)} H^i (Y, R) \rightarrow H^* (X, R), \end{aligned}$$

for any ring R of coefficients.

In our case one takes as $X : = {\mathbb {P}}^n_{{\mathbb {R}}} = S^n /\{\pm 1\}$, similarly $Y : = {\mathbb {P}}^m_{{\mathbb {R}}} = S^m /\{\pm 1\}$ and lets f be the continuus map induced by F. One needs to show that, choosing $R = {\mathbb {Z}}/ 2 {\mathbb {Z}}$, then the cohomology algebra of real projective space is a truncated polynomial algebra, namely:

$$\begin{aligned} H^* ( {\mathbb {P}}^n_{{\mathbb {R}}}, {\mathbb {Z}}/ 2 {\mathbb {Z}}) \cong ( {\mathbb {Z}}/ 2 {\mathbb {Z}}) [\xi _n] / (\xi _n^{n+1}). \end{aligned}$$

The other ingredient consists in showing that

$$\begin{aligned} f^* ([\xi _m]) = [\xi _n], \end{aligned}$$

$[\xi _m]$ denoting the residue class in the quotient algebra.

One gets then the desired contradiction since, if $n > m$,

$$\begin{aligned} 0 = f^*(0) = f^* ([\xi _m]^{m+1}) = f^* ([\xi _m])^{m+1} = [\xi _n]^{m+1} \ne 0. \end{aligned}$$

Notice that up to now we have mainly used that f is a continuous map $f : ={\mathbb {P}}^n_{{\mathbb {R}}} \rightarrow {\mathbb {P}}^m_{{\mathbb {R}}},$ while precisely in order to obtain that $f^* ([\xi _m]) = [\xi _n]$ we must make use of the hypothesis that f is induced by an odd function F.

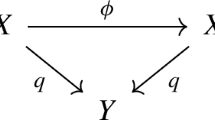
This property can be interpreted as the property that one has a commutative diagram

$$\begin{aligned} \begin{matrix} S^n &{} \rightarrow &{} S^m \\ \downarrow &{} &{} \downarrow \\ {\mathbb {P}}^n_{{\mathbb {R}}}&{}\rightarrow &{} {\mathbb {P}}^m_{{\mathbb {R}}} \end{matrix} \end{aligned}$$

which exhibits the two sheeted covering of ${\mathbb {P}}^n_{{\mathbb {R}}}$ by $S^n$ as the pull-back of the analogous two sheeted cover for ${\mathbb {P}}^m_{{\mathbb {R}}}$. Now, as we shall digress soon, any such two sheeted covering is given by a homomorphism of $H_1(X, {\mathbb {Z}}/ 2 {\mathbb {Z}}) \rightarrow {\mathbb {Z}}/ 2 {\mathbb {Z}}$, i.e., by an element in $H^1(X, {\mathbb {Z}}/ 2 {\mathbb {Z}})$, and this element is trivial if and only if the covering is trivial (that is, homeomorphic to $X \times ( {\mathbb {Z}}/ 2 {\mathbb {Z}})$, in other words a disconnected cover).

This shows that the pull back of the cover, which is nontrivial, corresponds to $f^* ([\xi _m])$ and is nontrivial, hence $f^* ([\xi _m]) = [\xi _n]$.

As we saw already in the first section, algebraic topology attaches to a good topological space homology groups $H_i (X, R)$, which are covariantly functorial, a cohomology algebra $H^* (X, R)$ which is contravariantly functorial, and these groups can be calculated, by virtue of the Mayer Vietoris exact sequence and of excision (see any textbook), by chopping the space in smaller pieces. In particular, these groups vanish when $i > dim (X)$. But to X are also attached the homotopy groups $\pi _i(X)$. The common feature is that homotopic maps induce the same homomorphisms on homology, cohomology, and homotopy.

We are, for our purposes, more interested in the more mysterious homotopy groups, which, while not necessarily vanishing for $i > dim (X)$, enjoy however a fundamental property.

Recall the definition due to Whitney and Steenrod [350] of a fibre bundle. In the words of Steenrod, the notion of a fibre bundle is a weakening of the notion of a product, since a product $X \times Y$ has two continuous projections $p_X : X \times Y \rightarrow X$, and $p_Y : X \times Y \rightarrow Y$, while a fibre bundle E over B with fibre F has only one projection, $p = p_B : E \rightarrow B$ and its similarity to a product lies in the fact that for each point $x \in B$ there is an open set U containing x, and a homeomorphism $p_B^{-1} (U) \cong U \times F$ compatible with both projections onto U.

The fundamental property of fibre bundles is that there is a long exact sequence of homotopy groups

$$\begin{aligned} \cdots \rightarrow \pi _i(F) \rightarrow \pi _i(E) \rightarrow \pi _i(B ) \rightarrow \pi _{i-1}(F ) \rightarrow \pi _{i-1}(E ) \rightarrow \pi _{i-1}(B ) \rightarrow \cdots \end{aligned}$$

where one should observe that $\pi _i (X)$ is a group for $i \ge 1$, an abelian group for $i \ge 2$, and for $i=0$ is just the set of arc-connected components of X (we assume the spaces to be good, that is, locally arcwise connected, semilocally simply connected, see [189], and, most of the times, connected).

The special case where the fibre F has the discrete topology is the case of a covering space, which is called the universal covering if moreover $\pi _1(E)$ is trivial.

Special mention deserves the following more special case.

Definition 7

Assume that E is arcwise connected, contractible (hence all homotopy groups $\pi _i(E)$ are trivial), and that the fibre F is discrete, so that all the higher homotopy groups $\pi _i(B ) = 0$ for $i \ge 2$, while $\pi _1(B ) \cong \pi _0(F) = F$. Then one says that B is a classifying space $K(\pi , 1)$ for the group $\pi = \pi _1(B )$.

In general, given a group $\pi$, a CW complex B is said to be a $K(\pi , 1)$ if $\pi _i(B ) = 0$ for $i \ge 2$, while $\pi _1(B ) \cong \pi$.

Example 8

The easiest examples are the following ones, where (2) is a case where we have a complex projective variety (see Sect. 3 for more such examples):

• (1) the real torus $T^n : = {\mathbb {R}}^n / {\mathbb {Z}}^n$ is a classifying space $K ({\mathbb {Z}}^n, 1)$ for the group $\pi = {\mathbb {Z}}^n$;

• (2) a complex projective curve C of genus $g \ge 2$ is a classifying space $K (\pi _g, 1)$, since by the uniformization theorem its universal covering is the Poincaré upper half plane ${\mathcal {H}}: = \{ z \in {\mathbb {C}}| Im (z) > 0 \}$ and its fundamental group $\pi _1(C)$ is isomorphic to the group

  $$\begin{aligned} \pi _g : = \langle \alpha _1, \beta _1, \ldots \alpha _g,\beta _g | \Pi _1^g [ \alpha _i, \beta _i] = 1\rangle , \end{aligned}$$

  quotient of a free group with 2g generators by the normal subgroup generated by the relation $\Pi _1^g [ \alpha _i, \beta _i]$;

• (3) a classifying space $K ({\mathbb {Z}}/ 2 {\mathbb {Z}}, 1)$ is given by the inductive limit ${\mathbb {P}}^{\infty }_{{\mathbb {R}}} : = \lim _{n \rightarrow \infty } {\mathbb {P}}^n_{{\mathbb {R}}}$. To show this, it suffices to show that $S^{ \infty } : = \lim _{n \rightarrow \infty } S^n$ is contractible or, equivalently, that the identity map is homotopic to a constant map. We do this as follows:⁴ let $\sigma : {\mathbb {R}}^{ \infty } \rightarrow {\mathbb {R}}^{ \infty }$ be the shift operator, and first define a homotopy of the identity map of ${\mathbb {R}}^{ \infty } {\setminus } \{ 0 \}$ to the constant map with value $e_1$. The needed homotopy is the composition of two homotopies:

  $$\begin{aligned}&F (t,v) : = (1-t) v + t \sigma (v),\quad 0 \le t \le 1 , \\&F (t,v) := (2-t) \sigma (v) + (t-1) e_1, \ \quad 1 \le t \le 2, \quad \forall v \in {\mathbb {R}}^{ \infty } . \end{aligned}$$

  Then we simply project the homotopy from ${\mathbb {R}}^{ \infty } {\setminus } \{ 0 \}$ to $S^{ \infty }$ considering $\frac{F(t,v)}{| F(t,v)|}$.

These classifying spaces, although not unique, are unique up to homotopy-equivalence (we use the notation $X \sim _{h.e.} Y$ to denote homotopy equivalence: this means that there exist continuous maps $f : X \rightarrow Y, \ g : Y \rightarrow X$ such that both compositions $f\circ g$ and $g \circ f$ are homotopic to the identity).

Therefore, given two classifying spaces for the same group, they not only do have the same homotopy groups, but also the same homology and cohomology groups. Thus the following definition is well posed.

Definition 9

Let $\Gamma$ be a finitely presented group, and let $B\Gamma$ be a classifying space for $\Gamma$: then the homology and cohomology groups and algebra of $\Gamma$ are defined as

$$\begin{aligned} H_i (\Gamma , {\mathbb {Z}}) : = H_i ( B \Gamma , {\mathbb {Z}}), \ H^i (\Gamma , {\mathbb {Z}}) : = H^i ( B \Gamma , {\mathbb {Z}}), \ H^* (\Gamma , {\mathbb {Z}}) : = H^*( B \Gamma , {\mathbb {Z}}), \end{aligned}$$

and similarly for other rings of coefficients instead of ${\mathbb {Z}}$.

Remark 10

The concept of a classifying space BG is indeed more general: the group G could also be a Lie group, and then, if EG is a contractible space over which G has a free (continuous) action, then one defines $BG : = EG / G$.

The typical example is the simplest compact Lie group $G = S^1$: then, keeping in mind that $S^1 = \{ z \in {\mathbb {C}}| |z| = 1 \}$, we take as EG the space

$$\begin{aligned} E S^1 : = S ({\mathbb {C}}^{\infty }) = lim_{n \rightarrow \infty } S ({\mathbb {C}}^{n}) = lim_{n \rightarrow \infty } \left\{ w \in {\mathbb {C}}^{n} | |w| = 1 \right\} . \end{aligned}$$

Classifying spaces, even if often quite difficult to construct explicitly, are very important because they guarantee the existence of continuous maps! We have more precisely the following (cf. [349], Theorem 9, p. 427, and Theorem 11, p. 428)

Theorem 11

Let Y be a ‘nice’ topological space, i.e., Y is homotopy-equivalent to a CW-complex, and let X be a nice space which is a $K (\pi , 1)$ space: then, choosing base points $y_0 \in Y, x_0 \in X$, one has a bijective correspondence

$$\begin{aligned} \left[ (Y, y_0 ), (X, x_0 )\right] \cong {{\mathrm{\text {Hom}}}}(\pi _1(Y, y_0), \pi _1(X, x_0)),\quad [f] \mapsto \pi _1 (f) , \end{aligned}$$

where $[ (Y, y_0 ), (X, x_0 )]$ denotes the set of homotopy classes [f] of continuous maps $f : Y \rightarrow X$ such that $f(y_0 ) = x_0$ (and where the homotopies F(y, t) are also required to satisfy $F(y_0,t) = x_0, \ \forall t \in [0,1]$).

In particular, the free homotopy classes [Y, X] of continuous maps are in bijective correspondence with the conjugacy classes of homomorphisms ${{\mathrm{\text {Hom}}}}(\pi _1(Y, y_0), \pi )$ (conjugation is here inner conjugation by ${{\mathrm{\text {Inn}}}}(\pi )$ on the target).

Observe that, quite generally, the universal covering $E _{\pi }$ of a classifying space $B \pi : = K (\pi , 1)$ associates (by the lifting property) to a continuous map $f : Y \rightarrow B \pi$ a $\pi _1(Y)$-equivariant map $\tilde{f}$

$$\begin{aligned} \tilde{f} : \tilde{Y} \rightarrow E _{\pi }, \end{aligned}$$

where the action of $\pi _1(Y)$ on $E _{\pi }$ is determined by the homomorphism $\varphi : = \pi _1(f) : \pi _1(Y) \rightarrow \pi = \pi _1 (B \pi )$.

Moreover, any $\varphi : \pi _1(Y) \rightarrow \pi = \pi _1 (B \pi )$ determines a fibre bundle $E_{\varphi }$ over Y with fibre $E _{\pi }$:

$$\begin{aligned} E_{\varphi } : = ( \tilde{Y} \times E _{\pi } ) / \pi _1(Y) \rightarrow Y = ( \tilde{Y} ) / \pi _1(Y) = Y, \end{aligned}$$

where the action of $\gamma \in \pi _1(Y)$ is as follows: $\gamma (y' , v) = (\gamma (y'), \varphi (\gamma ) (v))$.

While topology deals with continuous maps, when dealing with manifolds more regularity is wished for. For instance, when we choose for Y a differentiable manifold M, and the group $\pi$ is abelian and torsion free, say $\pi = {\mathbb {Z}}^r$, then a more precise incarnation of the above theorem is given by the De Rham theory.

In fact, a homomorphism $\varphi : \pi _1(Y) \rightarrow {\mathbb {Z}}^r$ factors through the Abelianization $H_1 (Y, {\mathbb {Z}})$ of the fundamental group. Since $H^1 (Y, {\mathbb {Z}})= {{\mathrm{\text {Hom}}}}( H_1 (Y, {\mathbb {Z}}), {\mathbb {Z}})$, $\varphi$ is equivalent to giving an element in

$$\begin{aligned} \varphi \in H^1 (Y, {\mathbb {Z}})^r \subset H^1 (Y, {\mathbb {R}})^r \cong H^1_{DR} (Y, {\mathbb {R}})^r, \end{aligned}$$

where $H^1_{DR} (Y, {\mathbb {R}})$ is the quotient space of the space of closed differentiable 1-forms modulo exact 1-forms.

In this case the classifying space is a real torus

$$\begin{aligned} T_r : = {\mathbb {R}}^r / {\mathbb {Z}}^r. \end{aligned}$$

Observe however that to give $\varphi : \pi _1(Y) \rightarrow {\mathbb {Z}}^r$ it is equivalent to give its r components $\varphi _i , i = 1, \ldots , r$, which are homomorphisms into ${\mathbb {Z}}$, and giving a map to $T_r : = {\mathbb {R}}^r / {\mathbb {Z}}^r$ is equivalent to giving r maps to $T_1 : = {\mathbb {R}}/ {\mathbb {Z}}$: hence we may restrict ourselves to consider the case $r=1$.

Let us sketch the basic idea of the previous Theorem 11 in this special case. Let us assume that Y is a cell complex, and define as usual $Y^j$ to be its j-th skeleton, the union of all the cells of dimension $i \le j$.

Since the fundamental group of Y is generated by the free group $F : = \pi _1 (Y^1)$, we get a homomorphism $\Phi : F \rightarrow {\mathbb {Z}}$ inducing $\varphi$. For each 1-cell $\gamma \cong S^1$ we send $\gamma \rightarrow S^1$ according to the map $z \in S^1 \mapsto z^m \in S^1$, where $m = \Phi (\gamma )$.

In this way we get a continuous map $f^1 : Y^1 \rightarrow S^1$, and we want to extend it inductively to $Y^j$ for each j. Now, assume that f is already defined on Z, and that you are attaching an n-cell to Z, according to a continuous map $\psi : \partial (D^n)= S^{n-1} \rightarrow Z$. In order to extend f to $Z \cup _{\psi } D^n$ it suffices to extend the map $f \circ {\psi }$ to the interior of the disk $D^n$. This is possible once the map $f \circ {\psi } : S^{n-1} \rightarrow S^1$ is homotopic to a constant map. Now, for $n=2$, this condition holds by assumption: since ${\psi } (S^1)$ yields a relation for $\pi _1(Y)$, therefore its image under $\phi$ must be equal to zero.

For higher n, $n \ge 3$, it suffices to observe that a continuous map $h : S^{n-1} \rightarrow S^{1}$ extends to the interior always: since $S^{n-1}$ is simply connected, and $S^1= {\mathbb {R}}/ {\mathbb {Z}}$, h lifts to a continuous map $h' : S^{n-1} \rightarrow {\mathbb {R}}$, and we can extend $h'$ to $D^n$ by setting

$$\begin{aligned} h' (x) : = |x| h' \left( \frac{x}{|x|}\right) , \quad \forall x \ne 0,\quad \ h'(0) : = 0. \end{aligned}$$

(h is then the composition of $h'$ with the projection ${\mathbb {R}}\rightarrow {\mathbb {R}}/ {\mathbb {Z}}= S^1$).

In general, when both Y and the classifying space X ( as $T_1$ here) are differentiable manifolds, then each continuous map $f : Y \rightarrow X$ is homotopic to a differentiable map $f'$. Take in fact $X \subset {\mathbb {R}}^N$ and observe that the implicit function theorem implies that there is a tubular neighbourhood $X \subset {\mathcal {T}}_X \subset {\mathbb {R}}^N$ diffeomorphic to a tubular neighbourhood of X embedded as the 0-section of the normal bundle $N_X$ of the embedding $X \subset {\mathbb {R}}^N$.

Therefore, approximating the function $f : Y \rightarrow {\mathbb {R}}^N$ by a differentiable function $f''$ with values in ${\mathcal {T}}_X$, we can use the bundle projection $N_X \rightarrow X$ to project $f''$ to a differentiable function $f' : Y \rightarrow X$, and similarly we can project the natural homotopy between f and $f''$, $f(y) + t f'' (y)$ to obtain a homotopy between f and $f'$.

Once we have a differentiable map $f' : Y \rightarrow T_1 = {\mathbb {R}}/ {\mathbb {Z}}$, we simply take the lift $\tilde{f'} : \tilde{Y} \rightarrow {\mathbb {R}}$, and the differential $d \tilde{f'}$ descends to a closed differential form $\eta$ on Y such that its integral over a closed loop $\gamma$ is just $\phi (\gamma )$.

We obtain the

Proposition 12

Let Y be a differentiable manifold, and let X be a differentiable manifold that is a $K (\pi , 1)$ space: then, choosing base points $y_0 \in Y, x_0 \in X$, one has a bijective correspondence

$$\begin{aligned}{}[ (Y, y_0 ), (X, x_0 )]^{diff} \cong {{\mathrm{\text {Hom}}}}(\pi _1(Y), \pi ),\quad [f] \mapsto \pi _1 (f) , \end{aligned}$$

where $[ (Y, y_0 ), (X, x_0 )] ^{diff}$ denotes the set of differential homotopy classes [f] of differentiable maps $f : Y \rightarrow X$ such that $f(y_0 ) = x_0$.

In the case where X is a torus $T^r = {\mathbb {R}}^r / {\mathbb {Z}}^r$, then f is obtained as the projection onto $T^r$ of

$$\begin{aligned} \tilde{\phi } (y) : = \int _{y_0}^y (\eta _1, \ldots , \eta _r), \eta _j \in H^1 (Y, {\mathbb {Z}}) \subset H^1_{DR} (Y, {\mathbb {R}}). \end{aligned}$$

Remark 13

In the previous proposition, $\eta _j$ is indeed a closed 1-form, representing a certain De Rham cohomology class with integral periods ( i.e., $\int _{\gamma } \eta _j = \varphi (\gamma ) \in {\mathbb {Z}}$, $\forall \gamma \in \pi _1 (Y)$). Therefore f is defined by $\int _{y_0}^y (\eta _1, \ldots , \eta _r) \text { mod}({\mathbb {Z}}^r)$. Moreover, changing $\eta _j$ with another form $\eta _j + d F_j$ in the same cohomology class, one finds a homotopic map, since $\int _{y_0}^y (\eta _j + t dF_j)= \int _{y_0}^y (\eta _j ) + t( F_j(y) - F_j (y_0))$.

Before we dwell into a review of results concerning higher regularity of the classifying maps, we consider in the next section the basic examples of projective varieties that are classifying spaces.

4 Projective varieties which are $K(\pi , 1)$

The following are the easiest examples of projective varieties which are $K(\pi ,1)$’s.

(1) Projective curves C of genus $g \ge 2$.

By the Uniformization theorem, these have the Poincaré upper half plane ${\mathcal {H}}: =\{ z \in {\mathbb {C}}| Im (z) > 0 \}$ as universal covering, hence they are compact quotients $C = {\mathcal {H}}/\Gamma$, where $\Gamma \subset {\mathbb {P}}SL (2, {\mathbb {R}})$ is a discrete subgroup isomorphic to the fundamental group of C, $\pi _1(C) \cong \pi _g$. Here

$$\begin{aligned} \pi _g : = \langle \alpha _1, \beta _1, \ldots \alpha _g,\beta _g | \Pi _1^g [ \alpha _i, \beta _i] = 1\rangle \end{aligned}$$

contains no elements of finite order. Hence, given a faithful action of $\pi _g$ on ${\mathcal {H}}$, it follows that necessarily $\Gamma$ acts freely on ${\mathcal {H}}$. Moreover, the quotient must be compact, otherwise C would be homotopically equivalent to a bouquet of circles, hence $H_2(C, {\mathbb {Z}}) = 0$, a contradiction, since $H_2(C, {\mathbb {Z}}) \cong H_2(\pi _g, {\mathbb {Z}}) \cong {\mathbb {Z}}$, as one sees taking the standard realization of a classifying space for $\pi _g$ by glueing the 2g sides of a polygon in the usual pattern.

Moreover, the complex orientation of C induces a standard generator [C] of $H_2(C, {\mathbb {Z}}) \cong {\mathbb {Z}}$, the so-called fundamental class.

(2) AV : = Abelian varieties.

More generally, a complex torus $X = {\mathbb {C}}^g / \Lambda$, where $\Lambda$ is a discrete subgroup of maximal rank (isomorphic then to ${\mathbb {Z}}^{2g}$), is a Kähler classifying space $K ({\mathbb {Z}}^{2g},1)$, the Kähler metric being induced by the translation invariant Euclidean metric $\frac{i}{2} \sum _1^g dz_j \otimes d \overline{ z_j}$.

For $g=1$ one gets in this way all projective curves of genus $g=1$; but, for $g > 1$, X is in general not projective: it is projective, and called then an Abelian variety, if it satisfies the Riemann bilinear relations. These amount to the existence of a positive definite Hermitian form H on ${\mathbb {C}}^g$ whose imaginary part A ( i.e., $H = S + i A$), takes integer values on $\Lambda \times \Lambda$. In modern terms, there exists a positive line bundle L on X, with Chern class $A \in H^2 (X, {\mathbb {Z}}) = H^2 (\Lambda , {\mathbb {Z}}) = \wedge ^2 ({{\mathrm{\text {Hom}}}}(\Lambda , {\mathbb {Z}}))$, whose curvature form, equal to H, is positive (the existence of a positive line bundle on a compact complex manifold X implies that X is projective algebraic, by Kodaira’s theorem, [247]).

We shall indeed see (82) that Abelian varieties are exactly the projective $K(\pi , 1)$ varieties, for which $\pi$ is an abelian group.

(3) LSM : = Locally symmetric manifolds.

These are the quotients of a bounded symmetric domain ${\mathcal {D}}$ by a cocompact discrete subgroup $\Gamma \subset Aut ({\mathcal {D}})$ acting freely. Recall that a bounded symmetric domain ${\mathcal {D}}$ is a bounded domain ${\mathcal {D}}\subset \subset {\mathbb {C}}^n$ such that its group $Aut ({\mathcal {D}})$ of biholomorphisms contains for each point $p \in {\mathcal {D}}$, a holomorphic automorphism $\sigma _p$ such that $\sigma _p (p)= p$, and such that the derivative of $\sigma _p$ at p is equal to $- Id$. This property implies that $\sigma$ is an involution (i.e., it has order 2), and that $Aut ({\mathcal {D}})^0$ (the connected component of the identity) is transitive on ${\mathcal {D}}$, and one can write ${\mathcal {D}}= G/K$, where G is a connected Lie group, and K is a maximal compact subgroup.

The two important properties are:

(3.1) ${\mathcal {D}}$ splits uniquely as the product of irreducible bounded symmetric domains.

(3.2) each such ${\mathcal {D}}$ is contractible, since there is a Lie subalgebra ${\mathcal {L}}$ of the Lie algebra ${\mathfrak {G}}$ of G such that the exponential map is a homeomorphism ${\mathcal {L}}\cong {\mathcal {D}}$. Hence X is a classifying space for the group $\Gamma \cong \pi _1(X)$.

Bounded symmetric domains were classified by Elie Cartan [77], and there is only a finite number of them (up to isomorphism) for each dimension n.

Recall the notation for the irreducible domains:

• (i) $I_{n,p}$ is the domain ${\mathcal {D}}= \{ Z \in Mat (n,p, \mathbb {C}) : {\mathrm {I}}_p - ^tZ \cdot \overline{Z} > 0 \}$.

• (ii) $II_{n}$ is the intersection of the domain $I_{n,n}$ with the subspace of skew symmetric matrices.

• (iii) $III_{n}$ is instead the intersection of the domain $I_{n,n}$ with the subspace of symmetric matrices.

• (iv) The Cartan–Harish Chandra realization of a domain of type $IV_{n}$ in $\mathbb {C}^{n}$ is the subset ${\mathcal {D}}$ defined by the inequalities (compare [213], p. 527)

  $$\begin{aligned}&|z_1^2 + z_2^2 + \cdots + z_n^2 | < 1 , \\&1 + | z_1^2 + z_2^2 + \cdots + z_n^2 |^2 - 2\left( |z_1|^2 + |z_2|^2 + \cdots + |z_n|^2 \right) > 0. \end{aligned}$$

• (v) ${\mathcal {D}}_{16}$ is the exceptional domain of dimension $d=16$.

• (vi) ${\mathcal {D}}_{27}$ is the exceptional domain of dimension $d=27$.

We refer the reader to [213], Theorem 7.1, p. 383 and exercise D, pp. 526–527, and [329] p. 525 for a list of these irreducible bounded symmetric domains, and a description of all of them as homogeneous spaces G / K. In this context the domains are also called Hermitian symmetric spaces of non compact type. Each of these is contained in the so-called compact dual, which is a Hermitian symmetric spaces of compact type.

The easiest example is, for type I, the Grassmann manifold. For type IV, the compact dual of ${\mathcal {D}}$ is the hyperquadric $Q^n \subset \mathbb {P}^{n+1}$ defined by the polynomial $\sum _{j=0}^{n-1} X_j^2 - X_n^2 - X_{n+1}^2$. Notice that ${\mathrm {SO}}_0(n,2) \subset {\mathrm {Aut}}(Q^n)$. The Borel embedding $j : {\mathcal {D}}\rightarrow Q^n$ is given by

$$\begin{aligned} j(z_1,\ldots ,z_n) = [2z_1 : 2z_2 : \cdots : 2z_n : \mathrm {i}(\Lambda - 1) : \Lambda + 1 ], \end{aligned}$$

where $\Lambda := z_1^2 + \cdots + z_n^2$. The map j identifies the domain ${\mathcal {D}}$ with the ${\mathrm {SO}}_0(n,2)$-orbit of the point $[0:0:\cdots :1:\mathrm {i}] \in Q^n$, i.e. ${\mathcal {D}}\cong {\mathrm {SO}}_0(n,2)/{\mathrm {SO}}(n)\times {\mathrm {SO}}(2)$.

Among the bounded symmetric domains are the so called bounded symmetric domains of tube type, those which are biholomorphic to a tube domain, a generalized Siegel upper half-space

$$\begin{aligned} T_{{\mathcal {C}}} = \mathbb {V} \oplus \sqrt{-}1 {\mathcal {C}}\end{aligned}$$

where $\mathbb {V}$ is a real vector space and ${\mathcal {C}}\subset \mathbb {V}$ is a symmetric cone, i.e., a self dual homogeneous convex cone containing no full lines.

In the case of type III domains, the tube domain is Siegel’s upper half space:

$$\begin{aligned} {\mathcal {H}}_g : = \left\{ \tau \in {{\mathrm{\text {Mat}}}}(g,g,{\mathbb {C}})| \tau = \ ^t\tau , {{\mathrm{\text {Im}}}}(\tau ) > 0 \right\} , \end{aligned}$$

a generalisation of the upper half-plane of Poincaré.

Borel proved in [57] that for each bounded symmetric domain ${\mathcal {D}}$ there exists a compact free quotient $X = {\mathcal {D}}/ \Gamma$, called a compact Clifford–Klein form of the symmetric domain ${\mathcal {D}}$.

A classical result of Hano (see [207] Theorem IV, p. 886, and Lemma 6.2, p. 317 of [292]) asserts that a bounded homogeneous domain that is the universal cover of a compact complex manifold is symmetric.

(4) A particular, but very explicit case of locally symmetric manifolds is given by the VIP : = Varieties isogenous to a product.

These were studied in [96], and they are defined as quotients

$$\begin{aligned} X = (C_1 \times C_2 \times \cdots \times C_n) / G \end{aligned}$$

of the product of projective curves $C_j$ of respective genera $g_j \ge 2$ by the action of a finite group G acting freely on the product.

In this case the fundamental group of X is not so mysterious and fits into an exact sequence

$$\begin{aligned} 1 \rightarrow \pi _1 (C_1 \times C_2 \times \cdots \times C_n) \cong \pi _{g_1} \times \cdots \times \pi _{g_n} \rightarrow \pi _1 (X) \rightarrow G \rightarrow 1. \end{aligned}$$

Such varieties are said to be of the unmixed type if the group G does not permute the factors, i.e., there are actions of G on each curve such that

$$\begin{aligned} \gamma (x_1, \ldots , x_n ) = ( \gamma x_1, \ldots , \gamma x_n ) , \forall \gamma \in G. \end{aligned}$$

Equivalently, each individual subgroup $\pi _{g_j}$ is normal in $\pi _1 (X)$.

(5) Kodaira fibrations $f : S \rightarrow B$.

Here S is a smooth projective surface and all the fibres of f are smooth curves of genus $g \ge 2$, in particular f is a differentiable fibre bundle. Unlike the examples above, where $C= (C_1 \times C_2) / G \rightarrow C_2 / G$ is a holomorphic fibre bundle with fibre $C_1$ if G acts freely on $C_2$, the second defining property for Kodaira fibrations is that the fibres are not all biholomorphic to each other.

These Kodaira fibred surfaces S are very interesting topological objects: they were constructed by Kodaira [251] as a counterexample to the conjecture that the index (of the cup product in middle cohomology) would be multiplicative for fibre bundles. In fact, for curves the pairing $H^1(C, {\mathbb {Z}}) \times H^1(C, {\mathbb {Z}}) \rightarrow H^2(C, {\mathbb {Z}}) \cong {\mathbb {Z}}$ is skew symmetric, hence it has index zero; while Kodaira showed that the index of the cup product $H^2(S, {\mathbb {Z}}) \times H^2(S, {\mathbb {Z}}) \rightarrow H^4(S, {\mathbb {Z}}) \cong {\mathbb {Z}}$ is strictly positive.

The fundamental group of S fits obviously into an exact sequence:

$$\begin{aligned} 1 \rightarrow \pi _{g} \rightarrow \pi _1 (S) \rightarrow \pi _{b} \rightarrow 1, \end{aligned}$$

where g is the fibre genus and b is the genus of the base curve B, and it is known that $b \ge 2$, $g \ge 3$ (see [109], also for more constructions and a thorough discussion of their moduli spaces).

By simultaneous uniformization ([40]) the universal covering $\tilde{S}$ of a Kodaira fibred surface S is biholomorphic to a bounded domain in ${\mathbb {C}}^2$ (fibred over the unit disk $\Delta : = \{ z \in {\mathbb {C}}| |z| < 1\}$ with fibres isomorphic to $\Delta$), which is not homogeneous.

(6) Hyperelliptic surfaces: these are the quotients of a complex torus of dimension 2 by a finite group G acting freely, and in such away that the quotient is not again a complex torus.

These surfaces were classified by Bagnera and de Franchis ([19], see also [21, 156]) and they are obtained as quotients $(E_1 \times E_2)/G$ where $E_1, E_2$ are two elliptic curves, and G is an abelian group acting on $E_1$ by translations, and on $E_2$ effectively and in such a way that $E_2/G \cong {\mathbb {P}}^1$.

(7) In higher dimension we define the Generalized Hyperelliptic Varieties (GHV) as quotients A / G of an Abelian Variety A by a finite group G acting freely, and with the property that G is not a subgroup of the group of translations. Without loss of generality one can then assume that G contains no translations, since the subgroup $G_T$ of translations in G would be a normal subgroup, and if we denote $G' = G/G_T$, then $A/G = A' / G'$, where $A'$ is the Abelian variety $A' : = A/G_T$.

We propose instead the name Bagnera–de Franchis (BdF) Varieties for those quotients $X = A/G$ were G contains no translations, and G is a cyclic group of order m, with generator g (observe that, when A has dimension $n=2$, the two notions coincide, thanks to the classification result of Bagnera and De Franchis [19]).

A concrete description of such Bagnera–De Franchis varieties shall be given in the following section.

We end this section giving an example of a projective variety which is not a $K(\pi ,1)$, thus showing that the property of being a projective classifying space is lost after taking hyperplane sections.

Proposition 14

Let $n \ge 3$, and consider $X = C_1 \times \cdots \times C_n$, the product of n projective curves $C_i$ of respective genera $g_i \ge 1$. Let $X \subset {\mathbb {P}}^N$ be a projective embedding, and let S be a smooth surface, obtained taking the complete intersection of X with $n-2$ hypersurfaces. Then $\pi _2 (S) \ne 0$, in particular, S is not a projective classifying space.

Proof

By the theorem of Lefschetz $\pi _1(S) \cong \pi _1(X)$, hence the universal covering $\tilde{S}$ of S is a closed complex submanifold of $\tilde{X} = {\mathbb {C}}^r \times {\mathbb {H}}^{n-r}$. Hence $\tilde{S}$ is a Stein manifold, therefore (see [4]) it has the homotopy type of a CW complex of real dimension $\le 2$.

Since $\pi _1 (\tilde{S}) = 0$, we claim that $H_2 (\tilde{S}, {\mathbb {Z}}) = \pi _2 (\tilde{S}) = \pi _2 (S) \ne 0$ (the first isomorphism follows from the theorem of Hurewicz).

Otherwise, all homology and homotopy groups of $\tilde{S}$ would be trivial and $\tilde{S}$ would be contractible, S would be a $K(\pi ,1)$, hence $H^* (S, {\mathbb {Z}}) = H^* (\pi _1(S), {\mathbb {Z}}) = H^* (X, {\mathbb {Z}})$. This is a contradiction, since $H^{2n} (X, {\mathbb {Z}}) \ne 0, \ H^{2n} (S, {\mathbb {Z}}) = 0$, by our hypothesis that $n \ge 3$. $\square$

5 A trip around Bagnera–de Franchis varieties and group actions on Abelian varieties

5.1 Bagnera–de Franchis varieties

Let A / G be a Generalized Hyperelliptic Variety. An easy observation is that any $g \in G$ is induced by an affine transformation $x \mapsto \alpha x + b$ on the universal cover, hence it does not have a fixed point on $A = V/ \Lambda$ if and only if there is no solution of the equation

$$\begin{aligned}&\exists x \in V , \ g (x) \equiv x \ (\text { mod}\,\, \Lambda )\\&\quad \Leftrightarrow \exists x \in V, \lambda \in \Lambda , \ (\alpha - {{\mathrm{\text {Id}}}}) x = \lambda - b. \end{aligned}$$

This remark implies that 1 must be an eigenvalue of $\alpha$ for all non trivial transformations $g \in G$.

Since $\alpha \in GL (\Lambda ) \cong GL (2n, {\mathbb {Z}})$, the eigenspace $V_1 = Ker ( \alpha - {{\mathrm{\text {Id}}}})$ is a complex subspace defined over ${\mathbb {Q}}$, hence we have an Abelian subvariety

$$\begin{aligned} A_1 \subset A, A_1 := V_1 / \Lambda _1, \quad \Lambda _1 : = (V_1 \cap \Lambda ). \end{aligned}$$

While what we said up to now was valid for any complex torus, we replace this assumption by the stronger assumption that A is an Abelian variety. This assumption allows us to invoke Poincaré’ s complete reducibility theorem, so that we can split

$$\begin{aligned} V = V_1 \oplus V_2, \ V_2 : = (V_1)^{\perp },\quad A_2 : = V_2 / \Lambda _2, \quad \Lambda _2 : = (V_2 \cap \Lambda ). \end{aligned}$$

We get then an isogeny $A_1 \times A_2 \rightarrow A,$ with kernel $T: = \Lambda / ( \Lambda _1 \oplus \Lambda _2)$. Observe that $T \cap A_j = \{ 0 \}, j=1,2$.

In view of the splitting $V = V_1 \oplus V_2$, we can write, after a change of the origin in the affine space $V_2$,

$$\begin{aligned} \alpha (v_1 + v_2) = v_1 + \alpha _2 v_2, g(v) = v_1 + b_1 + \alpha _2 v_2,\quad b_1 \in V_1, b_1 \notin \Lambda . \end{aligned}$$

If $\alpha _2$ has order equal to m, then necessarily the image of $b_1$ has order exactly m in A, by virtue of our assumption that G contains no translations. In other words, $b_1$ induces a translation on $A_1$ of order exactly m.

Now, g lifts naturally to $A_1 \times A_2$, by

$$\begin{aligned} g (a_1, a_2) = (a_1 + [b_1], \alpha _2 a_2), \end{aligned}$$

where $[b_1]$ is the class of $b_1$ in $A_1$.

We reach the conclusion that $X = A /G = ((A_1 \times A_2)/ T) /G$, where T is the finite group of translations $T = \Lambda / ( \Lambda _1 \oplus \Lambda _2)$.

Conversely, given such an automorphism g of $A_1 \times A_2$, it descends to $A : = (A_1 \times A_2)/ T$ if and only if the linear part of g sends T to T.

Denote now by $T_j$ the (isomorphic) image of $T \rightarrow A_j$: then $T \subset T_1 \times T_2$ is the graph of an isomorphism $\phi : T_1 \rightarrow T_2$, hence the condition which allows g to descend to A is that:

$$\begin{aligned} (**) ({{\mathrm{\text {Id}}}}\times \alpha _2) (T)= & {} T \Leftrightarrow \alpha _2 \circ \phi = \phi \Leftrightarrow \\ \Leftrightarrow ( \alpha _2 - {{\mathrm{\text {Id}}}}) \circ \phi= & {} 0 \Leftrightarrow ( \alpha _2 - {{\mathrm{\text {Id}}}}) T_2 = 0. \end{aligned}$$

We are in the position to illustrate the standard example, before we give the more general more complete description of BdF varieties.

The basic example is the one where $m=2$, hence $\alpha _2$ is scalar multiplication by $-1$. Then $\phi = - \phi$ implies that $T_2, T_1$ are 2-torsion subgroups. Then also $2 [b_1] = 0$ implies that $[b_1]$ is a 2-torsion element. However $[b_1]$ cannot belong to $T_1$, else $g : A \rightarrow A$ would be induced by

$$\begin{aligned} (a_1, a_2 ) \mapsto ( a_1 + [b_1], \alpha _2 a_2) \equiv ( a_1, \alpha _2 a_2 - \phi ([b_1]) ) \ (mod \ T), \end{aligned}$$

which has a fixed point on A.

We conclude that the standard example of Bagnera–de Franchis Varieties of order $m=2$ is the following:

$$\begin{aligned} X= & {} A / g, \quad \mathrm{where} \ A : = (A_1 \times A_2 )/ T , \quad \mathrm{and} \ \\ T= & {} \left\{ (t_1, \phi (t_1))\right\} , T_j \subset A_j[2] , \phi : T_1 \cong T_2, \beta _1 \in A_1[2] {\setminus } T_1,\\ g : A\rightarrow & {} A, \quad \ g(a_1, a_2) = (a_1 + \beta _1, - a_2). \end{aligned}$$

In order to conclude appropriately the above discussion, we give some useful definition.

Definition 15

We define first a Bagnera–de Franchis manifold (resp.: variety) of product type as a quotient $X= A/G$ where $A = A_1 \times A_2$, $A_1, A_2$ are complex tori (resp.: Abelian Varieties), and $G \cong {\mathbb {Z}}/m$ is a cyclic group operating freely on A, generated by an automorphism of the form

$$\begin{aligned} g (a_1, a_2 ) = ( a_1 + \beta _1, \alpha _2 (a_2)), \end{aligned}$$

where $\beta _1 \in A_1[m]$ is an element of order exactly m, and similarly $\alpha _2 : A_2 \rightarrow A_2$ is a linear automorphism of order exactly m without 1 as eigenvalue (these conditions guarantee that the action is free). If moreover all eigenvalues of $\alpha _2$ are primitive m-th roots of 1, we shall say that $X= A/G$ is a primary Bagnera–de Franchis manifold.

We have the following proposition, giving a characterization of Bagnera- De Franchis varieties.

Proposition 16

Every Bagnera–de Franchis variety $X= A/G$, where $G \cong {\mathbb {Z}}/m$ contains no translations, is the quotient of a Bagnera–de Franchis variety of product type, $(A_1 \times A_2)/ G$ by any finite subgroup T of $A_1 \times A_2$ which satisfies the following properties:

• (1) T is the graph of an isomorphism between two respective subgroups $T_1 \subset A_1, T_2 \subset A_2,$

• (2) $(\alpha _2 - {{\mathrm{\text {Id}}}}) T_2 = 0$

• (3) if $g (a_1, a_2 ) = ( a_1 + \beta _1, \alpha _2 (a_2)),$ then the subgroup of order m generated by $\beta _1$ intersects $T_1$ only in $\{0\}$.

In particular, we may write X as the quotient $X = (A_1 \times A_2)/ (G \times T)$ by the abelian group $G \times T$.

5.2 Actions of a finite group on an Abelian variety

Assume that we have the action of a finite group G on a complex torus $A = V / \Lambda$. Since every holomorphic map between complex tori lifts to a complex affine map of the respective universal covers, we can attach to the group G the group of affine transformations $\Gamma$ which fits into the exact sequence:

$$\begin{aligned} 0 \rightarrow \Lambda \rightarrow \Gamma \rightarrow G \rightarrow 1. \end{aligned}$$

$\Gamma$ consists of all affine transformations of V which lift transformations of the group G.

Define now $G^0$ to be the subgroup of G consisting of all the translations in G.

Proposition 17

The abstract group $\Gamma$ determines an exact sequence

$$\begin{aligned} 0 \rightarrow \Lambda ' \rightarrow \Gamma \rightarrow G' \rightarrow 1 \end{aligned}$$

such that $\Lambda ' \subset \Lambda$, $\Lambda '$ is a lattice in V, $\Lambda ' / \Lambda = G^0$, $G' \subset Aut (V/ \Lambda ')$ contains no translations.

Proof

It is clear that $V = \Lambda \otimes _{{\mathbb {Z}}} {\mathbb {R}}$ as a real vector space, and we denote by $V_{{\mathbb {Q}}}: = \Lambda \otimes {\mathbb {Q}}$. Consider the homomorphism $\alpha _L$ associating to an affine transformation its linear part, and let

$$\begin{aligned}&\Lambda ' := \ker ( \alpha _L : \Gamma \rightarrow {{\mathrm{\text {GL}}}}(V_{{\mathbb {Q}}}) \subset {{\mathrm{\text {GL}}}}(V)) ,\\&\overline{G}_1 := {{\mathrm{\text {Im}}}}( \alpha _L : \Gamma \rightarrow {{\mathrm{\text {GL}}}}(V_{{\mathbb {Q}}})). \end{aligned}$$

$\Lambda '$ is a subgroup of the group of translations in V, hence it is obviously Abelian, and maps isomorphically onto a lattice of V which contains $\Lambda$. We shall identify this lattice with $\Lambda '$, writing with shorthand notation $\Lambda ' \subset V$.

In turn $V = \Lambda ' \otimes _{{\mathbb {Z}}} {\mathbb {R}}$, and, if $G' : = \Gamma / \Lambda '$, then $G' \cong \overline{G}_1$ and we have the exact sequence

$$\begin{aligned} 0 \rightarrow \Lambda ' \rightarrow \Gamma \rightarrow G' \rightarrow 1, \end{aligned}$$

yielding an embedding $G' \subset GL(\Lambda ')$.

There remains to show that $\Lambda '$ is determined by $\Gamma$ as an abstract group, independently of the exact sequence we started with. In fact, one property of $\Lambda '$ is that it is a maximal abelian subgroup, normal and of finite index.

Assume that $\Lambda ''$ has the same property: then their intersection $\Lambda ^0 : = \Lambda ' \cap \Lambda ''$ is a normal subgroup of finite index, in particular $\Lambda ^0 \otimes _{{\mathbb {Z}}} {\mathbb {R}}= \Lambda ' \otimes _{{\mathbb {Z}}} {\mathbb {R}}= V$; hence $\Lambda '' \subset \ker ( \alpha _L : \Gamma \rightarrow {{\mathrm{\text {GL}}}}(V))= \Lambda '$, where $\alpha _L$ is induced by conjugation on $\Lambda ^0$ By maximality $\Lambda ' = \Lambda ''$. $\square$

In the case where A is an Abelian variety, we can say a little bit more about the affine representation of the group $\Gamma$.

Lemma 18

Let A an Abelian variety, and let G be a finite group of automorphisms. Then there is a positive integer r such that the group $\Gamma$ of affine transformations which are lifts of transformations in G satisfies

$$\begin{aligned} \Gamma \subset Aff \left( \frac{1}{r} \Lambda \right) . \end{aligned}$$

In other words, we can write any transformation $g \in G$ as induced by the affine transformation of V: $v \mapsto \alpha (v) + \frac{\lambda }{r}, \lambda \in \Lambda$.

Proof

Let L be an ample divisor class on A. Since G is finite, there is a G-invariant such class L (simply replace L by $\sum _{g\in G} g^* (L') = : L'$).

We can further assume that the class of L is not only G-invariant , but also indivisible. There is a homomorphism $\phi _L : A \rightarrow A^{\vee }$, such that $\phi _L(a) : = T_a^* L - L \in Pic^0(A) = A^{\vee }$, and where $T_a$ is the translation by a, $v \mapsto v + a$.

Let $K_L : = \ker (\Phi _L)$, which is a finite group, and denote by r its exponent (hence, $r K_L = 0$ and $K_L \subset (\frac{1}{r} \Lambda )/ \Lambda$).

Represent now L by a line bundle whose cocycle is in Appell-Humbert normal form $f_{\lambda } (z) = \rho (\lambda ) exp ( \pi H(z,\lambda ) + \frac{\pi }{2} H (\lambda , \lambda ))$, and write a transformation $g\in G$ as induced by $v \mapsto \alpha (v) + b$. The condition that the Chern class of L is G-invariant implies that the Hermitian form H on V is left invariant by $\alpha$ (i.e., we have a group of isometries of V for the metric given by the Hermitian form H).

Hence also the translation part leaves L invariant, therefore the class of b lies in $K_L \subset (\frac{1}{r} \Lambda )/ \Lambda$. $\square$

Observe now that, given an affine group $\Gamma \subset Aff ( \Lambda \otimes _{{\mathbb {Z}}} {\mathbb {R}})$ as above, in order to obtain the structure of a complex torus on $V / \Lambda '$, we must give a complex structure on V which makes the action of $G' \cong \overline{G}_1$ complex linear.

In order to study the moduli spaces of the associated complex manifolds, we introduce therefore a further invariant, called Hodge type, according to the following definition.

Definition 19

• (i) Given a faithful representation $G \rightarrow Aut (\Lambda )$, where $\Lambda$ is a free abelian group of even rank 2n, a G- Hodge decomposition is a G-invariant decomposition

  $$\begin{aligned} \Lambda \otimes {\mathbb {C}}= H^{1,0} \oplus H^{0,1}, \quad H^{0,1} = \overline{H^{1,0}}. \end{aligned}$$

• (ii) Write $\Lambda \otimes {\mathbb {C}}$ as the sum of isotypical components

  $$\begin{aligned} \Lambda \otimes {\mathbb {C}}= \oplus _{\chi \in {{\mathrm{\text {Irr}}}}(G)} U_{ \chi }. \end{aligned}$$

Write also $U_{ \chi } = W_{ \chi } \otimes M_{ \chi }$, where $W_{ \chi }$ is the irreducible representation corresponding to the character $\chi$, and $M_{ \chi }$ is a trivial representation whose dimension is denoted $n_{ \chi }$.

Write accordingly $V : = H^{1,0} = \oplus _{\chi \in {{\mathrm{\text {Irr}}}}(G)} V_{ \chi },$ where $V_{ \chi } = W_{ \chi } \otimes M^{1,0}_{ \chi }$.

Then the Hodge type of the decomposition is the datum of the dimensions

$$\begin{aligned} \nu ( \chi ): = dim_{{\mathbb {C}}} M^{1,0}_{ \chi } \end{aligned}$$

corresponding to the Hodge summands for non real representations (observe in fact that one must have: $\nu ( \chi ) + \nu ( \bar{\chi }) = \dim ( M_{ \chi })$).

Remark 20

Given a faithful representation $G \rightarrow Aut (\Lambda )$, where $\Lambda$ is a free abelian group of even rank 2n, all the G-Hodge decompositions of a fixed Hodge type are parametrized by an open set in a product of Grassmannians. Since, for a non real irreducible representation $\chi$ one may simply choose $M^{1,0}_{ \chi }$ to be a complex subspace of dimension $\nu ( \chi )$ of $M_{ \chi }$, and for $M_{ \chi } = \overline{M_{ \chi }}$, one simply chooses a complex subspace $M^{1,0}_{ \chi }$ of middle dimension. Then the open condition is just that (since $M^{0,1}_{ \chi } : = \overline{M^{1,0}_{ \chi } }$) we want

$$\begin{aligned} M_{ \chi } = M^{1,0}_{ \chi } \oplus M^{0,1}_{ \chi }, \end{aligned}$$

or, equivalently, $M_{ \chi } = M^{1,0}_{ \chi } \oplus \overline{M^{1,0}_{\bar{ \chi }} }$.

5.3 The general case where G is Abelian

Assume now that G is Abelian, and consider the linear representation

$$\begin{aligned} \rho : G \rightarrow {{\mathrm{\text {GL}}}}(V). \end{aligned}$$

We get a splitting

$$\begin{aligned} V = \oplus _{\chi \in G^{\vee }} V_{\chi } = \oplus _{\chi \in {\mathcal {X}}} V_{\chi }, \end{aligned}$$

where $G^{\vee } : = Hom (G, {\mathbb {C}}^*) = \{ \chi : G \rightarrow {\mathbb {C}}^* \}$ is the dual group of characters of G, $V_{\chi }$ is the $\chi$-eigenspace of G ( for each $v \in V_{\chi }$, $\rho (g) (v) = \chi (g) v$), and ${\mathcal {X}}$ is the set of characters $\chi$ such that $V_{\chi } \ne 0$.

Proposition 21

Assume that an abelian group G acts on a complex torus $X : = V / \Lambda$.

Then the isomorphism class of the group $\Gamma$ of affine transformations which are lifts of transformations in G determines the real affine type of the action of $\Gamma$ on $V = ( \Lambda \otimes {\mathbb {R}})$, in particular the above exact sequence determines the action of G up to a real affine isomorphism of $A= ( \Lambda \otimes {\mathbb {R}})/ \Lambda$.

Proof

By Proposition 17 we may reduce ourselves to the case where G contains no translations.

Step (I): let us first treat the case where G is cyclic, generated by an element $g'$ of order m.

Then we claim that the power $g^m$ of a lift g of $g'$ determines the affine type of the transformation g.

In fact, if $g(v) = \alpha v + b$, V splits according to the eigenspaces of the linear map $\alpha$, which has order exactly m, and we can write $V = V_1 \oplus V_2$, where $V_1 = \ker ( \alpha - Id)$.

Then $g (v_1 + v_2) = (v_1 + b_1 ) + (\alpha _2 (v_2) + b_2)$, and choosing as the origin in the affine space $V_2$ the unique fixed point of $g_2 : = v_2 \mapsto \alpha _2 (v_2) + b_2$, we reach the normal form $g (v_1 + v_2) = (v_1 + b_1 ) + \alpha _2 (v_2)$. Now, $g^m(v_1 + v_2) = (v_1 + m b_1 ) + v_2$, hence $g^m$ determines $b_1$, and therefore also the normal form of g.

Step (II): split $V = \oplus _{\chi } V_{\chi }$ according the the characters of G, and choose, for each $\chi$, an element $g_{\chi }$ whose image under $\chi$ generates $\chi (G) \subset {\mathbb {C}}^*$.

For each $\chi$, as in step I, choose as origin in the affine space $V_{\chi }$ a fixed point for $g_{\chi }$.

Let now g be an arbitrary element in G: then g acts on $V_{\chi }$ by $v \mapsto \chi (g) v + b_{\chi }$.

We only need to show that $b_{\chi }$ is uniquely determined.

This is clear, by step I, if $\chi (g) =1$. Else, there is an integer r such that $\chi (g g_{\chi }^r) =1$, hence the affine action of $g g_{\chi }^r$ on $V_{\chi }$ is uniquely determined, therefore also the one of g. $\square$

Remark 22

If G is a general group, we can write $V = \oplus _{\rho } V_{\rho }$ where $V_{\rho }$ is irreducible (but the same irreducible representation may occur more than once) and let $H_{\rho }$ be a subgroup such that $\rho (H_{\rho } ) = \rho (G)$. Argueing as in step II above, the theorem holds for G if one can prove that the affine action of $H_{\rho }$ on $V_{\rho }$ is uniquely determined up to affine conjugation.

I.e., it suffices to prove the result when V is irreducible and $G \subset Aut (V)$.

Remark 23

In the papers [35, 37] we claimed the validity of Proposition 21 for any finite group G, but the proof was incorrect. Does the result hold for any finite group G, at least in the case of an Abelian variety A? We leave this question open, hoping to return on it.

In the case of generalized hyperelliptic varieties, we require the condition that the action of G is free: this implies the following condition

$$\begin{aligned} (1) \ \forall g \in G, \exists \chi \in {\mathcal {X}}, \quad \chi (g) = 1, \Leftrightarrow \cup _{\chi \in {\mathcal {X}}} \ker (\chi ) = G, \end{aligned}$$

while we may assume that G contains no translations, i.e., that $\rho$ is injective (equivalently , ${\mathcal {X}}$ spans $G^{\vee }$).

With the above in mind, we pass to investigate in more detail the case where G is cyclic, the case where the quotient variety shall be called a Bagnera–de Franchis variety.

5.4 Bagnera–de Franchis varieties of small dimension

In view of the characterization given in Proposition 16, we can see a Bagnera–de Franchis variety as the quotient of one of product type, since the actions of T and g commute (by the property that $\alpha _2 \circ \phi = \phi$).

Dealing with appropriate choices of T is the easy part, since, as we saw, the points $t_2$ of $T_2$ satisfy the property $\alpha _2 (t_2) = t_2$. It suffices to choose $T_2 \subset A_2[*]:= \ker (\alpha _2 - {{\mathrm{\text {Id}}}}_{A_2})$, which is a finite subgroup of $A_2$, and then to pick an isomorphism $\psi : T_2 \rightarrow T_1 \subset A_1$, such that $T_1 : = Im (\psi ) \cap \langle \beta _1 \rangle = \{ 0\}$.

Let us then restrict ourselves to consider Bagnera–de Franchis varieties of product type.

We show now how to further reduce to the investigation of primary Bagnera–de Franchis varieties.

In fact, in the case of a BdF variety of product type, $\Lambda _2$ is a G -module, hence a module over the group ring

$$\begin{aligned} R : = R(m) : = {\mathbb {Z}}[G] \cong {\mathbb {Z}}[x] / (x^m - 1). \end{aligned}$$

This ring is in general far from being an integral domain, since indeed it can be written as a direct sum of cyclotomic rings, which are the integral domains defined as

$$\begin{aligned} R_m: = {\mathbb {Z}}[x] / P_m(x). \end{aligned}$$

Here $P_m(x)$ is the m-th cyclotomic polynomial

$$\begin{aligned} P_m(x) = \Pi _{0 < j < m, (m,j)=1} (x - \epsilon ^j), \end{aligned}$$

where $\epsilon = \exp ( 2 \pi i /m)$.

Then

$$\begin{aligned} R (m) = \oplus _ { k | m} R_k. \end{aligned}$$

The following elementary lemma, together with the splitting of the vector space V as a direct sum of eigenspaces for g, yields a decomposition of $A_2$ as a direct product $A_2 = \oplus _{ k | m} A_{2,k}$ of G-invariant Abelian subvarieties $A_{2,k}$ on which g acts with eigenvalues of order precisely k.

Lemma 24

Assume that M is a module over a ring $R = \oplus _k R_k$.

Then M splits uniquely as a direct sum $M = \oplus _k M_k$ such that $M_k$ is an $R_k$-module, and the R-module structure is obtained through the projection $R \rightarrow R_k$.

Proof

We can write the identity in R as a sum of idempotents $1 = \Sigma _k e_k$, where $e_k$ is the identity of $R_k$, and $e_k e_j = 0$ for $j \ne k$.

Then each element $w \in M$ can be written as

$$\begin{aligned} w = 1 w = ( \Sigma _k e_k) w = \Sigma _k e_k w = : \Sigma _k w_k. \end{aligned}$$

Hence $M_k$ is defined as $e_k M$. $\square$

In the situation where we have a primary Bagnera–de Franchis variety $\Lambda _2$ is a module over the integral domain $R : = R_m: = {\mathbb {Z}}[x] / P_m(x)$,

Since $\Lambda _2$ is a projective module, a classical result (see [290], lemmas 1.5 and 1.6) is that $\Lambda _2$ splits as the direct sum $\Lambda _2 = R^r \oplus I$ of a free module with an ideal $I \subset R$, and it is indeed free if the class number $h(R)=1$ (to see for which integers m this occurs, see the table in [370], p. 353). To give a complex structure to $A_2 : = (\Lambda _2 \otimes _{{\mathbb {Z}}} {\mathbb {R}})/ \Lambda _2$ it suffices to give a decomposition $\Lambda _2 \otimes _{{\mathbb {Z}}} {\mathbb {C}}= V \oplus \bar{V},$ such that the action of x is holomorphic, which is equivalent to asking that V is a direct sum of eigenspaces $V_{\lambda }$, for $\lambda = \epsilon ^j$ a primitive m-th root of unity.

Writing $U: = \Lambda _2 \otimes _{{\mathbb {Z}}} {\mathbb {C}}= \oplus U_{\lambda }$, the desired decomposition is obtained by choosing, for each eigenvalue $\lambda$, a decomposition $U_{\lambda } = U_{\lambda }^{1,0} \oplus U_{\lambda }^{0,1}$ such that $\overline{U_{\lambda }^{1,0}} = U^{0,1}_{\bar{\lambda }}$.

The simplest case (see [89] for more details) is the one where $I =0, r=1$, hence $\dim (U_{\lambda } ) = 1$, so that we have only a finite number of complex structures, depending on the choice of the $\varphi (m)/2$ indices j such that $U_{\epsilon ^j} = U^{1,0}_{\epsilon ^j}$.

The above discussion does however leave open the following question (see [265] for some partial results), which should have an affirmative answer (in the sense that each family of complex structures should contain some Abelian variety).

Question: when is then the complex torus $A_2$ an Abelian variety?

Observe that the classification in small dimension is possible thanks to the observation that the ${\mathbb {Z}}$-rank of R (or of any ideal $I \subset R$) cannot exceed the real dimension of $A_2$: in other words we have

$$\begin{aligned} \varphi (m) \le 2 (n-1), \end{aligned}$$

where $\varphi (m)$ is the Euler function, which is multiplicative for relatively prime numbers, and satisfies $\varphi (p^r) = (p-1) p^{r-1}$ when p is a prime number.

For instance, when $n \le 3$, then $\varphi (m) \le 4$, and $\varphi (p^r) \le 4$ iff $p=3, 5 , r=1$, or $p=2, r \le 3$.

Observe that the case $m=2$ was completely described, in view of Proposition 16, hence we may assume that $m \ge 3$ and ask for the classification for the Bagnera–de Franchis varieties (or manifolds) of order m.

Assuming then $m \ge 3$, if $n \le 3$, it is only possible to have $m = 3,4,6, \varphi (m)= 2$, or $m = 5,8,10,12, \varphi (m)= 4$. The classification is then made easier by the fact that, in the above range for m, R is a P.I.D., hence every torsion free module is free. In particular $\Lambda _2$ is a free R-module.

The classification for $n = 4$, since we must have $\varphi (m) \le 6$, is going to include also the case $m=7, 9$.

We are not aware of literature dedicated to a precise classification of Bagnera–de Franchis varieties, or generalised hyperelliptic varieties, at least in dimension $>$3 (see however [264, 357] for results in dimension 3). Observe that the hypothesis that G is a finite group allows to find a G-invariant Hermitian metric on V, hence the affine group $\Gamma$ extension of $\Lambda$ by G is a Bieberbach group, and in each dimension we have only a finite number of those.

We end this section mentioning some elementary results which are useful to locate the BdF varieties in the classification theory of algebraic varieties.

Proposition 25

The Albanese variety of a Bagnera–de Franchis variety $X = A/G$ is the quotient $A_1 / (T_1 + \langle \beta _1\rangle )$.

Proof

Observe that the Albanese variety $H^0(\Omega ^1_X)^{\vee }/ Im (H_1(X, {\mathbb {Z}}))$ of $X = A/G$ is a quotient of the vector space $V_1$ by the image of the fundamental group of X (actually of its abelianization, the first homology group $H_1(X, {\mathbb {Z}})$): since the dual of $V_1$ is the space of G-invariant forms on A, $H^0(\Omega ^1_A)^G \cong H^0(\Omega ^1_X)$.

We also observe that there is a well defined map $X \rightarrow A_1 / (T_1 + \langle \langle \beta _1 \rangle \rangle )$, since $T_1$ is the first projection of T. The image of the fundamental group of X contains the image of $\Lambda$, which is precisely the extension of $\Lambda _1$ by the image of T, namely $T_1$. Since we have the exact sequence

$$\begin{aligned} 1 \rightarrow \Lambda = \pi _1 (A) \rightarrow \pi _1 (X) \rightarrow G \rightarrow 1 \end{aligned}$$

the image of the fundamental group of X is generated by the image of $\Lambda$ and by the image of the transformation g, which however acts on $A_1$ by translation by $\beta _1 =$ $[b_1]$. $\square$

Remark 26

Unlike the case of complex dimension $n=2$, there are Bagnera–de Franchis varieties $X = A/G$ with trivial canonical divisor, for instance some examples are given by:

• (1) any BdF variety which is standard (i.e., $m=2$) and is such that $A_2$ has even dimension has trivial canonical divisor, as well as

• (2) some BdF varieties $X = A/G = (A_1 \times A_2) / (T \times G)$ whose associated product type BdF variety $Y = (A_1 \times A_2) / G$ is primary and elementary (meaning that $\Lambda _2 \cong R_m$). For instance, when $m=p$ is an odd prime, there is a primary and elementary BdF variety with trivial canonical divisor if and only if, given the set of integers $\{ 1,2, \ldots , [\frac{p-1}{2}] \}$, there is a partition of it into two sets whose respective sums are the same: for $m=7$, it suffices to choose the partition $\{ 1,2\} \cup \{3\}$. This partition yields the sets $\{1,2,4\}$ and $\{3,5,6\}$, which determine $V= H^{1,0}$ as $V = H^{1,0} : = U_1 \oplus U_2 \oplus U_4$. Whereas, for $m = 17$, there are many choices, consisting of the union of two doubletons of the form $\{ j, 9 - j\}$.

We do not further consider the question of determining exactly the case where the divisor $K_X$ is trivial, also because this question can be asked also for the more general case where the action of G is not free (see [316] for a classification in dimension $n=3$).

6 Orbifold fundamental groups and rational $K(\pi , 1)$’s

6.1 Orbifold fundamental group of an action

In the previous section we have considered quotients $X = A/G$ of a complex torus $A = V / \Lambda$ by the free action of a finite group G. In this case the affine group $\Gamma$ fitting into the exact sequence

$$\begin{aligned} 1 \rightarrow \Lambda = \pi _1 (A) \rightarrow \Gamma \rightarrow G \rightarrow 1 \end{aligned}$$

equals $\pi _1 (X)$.

We have also seen that we have the same exact sequence in the more general case where the action of G is no longer free, and that the group $\Gamma$ determines in general the affine action of $\Gamma$ on the real affine space V (resp. on the rational affine space $\Lambda \otimes {\mathbb {Q}}$) and that, once the Hodge type of V is fixed, these varieties are parametrized by a connected complex manifold.

In the case where the action of G is no longer free, we would like to remember the group $\Gamma$, in view of its importance, even if it is no longer a ‘bona fide’ fundamental group. This can be done through a more general correspondence which associates to the pair of X and the group action of G a group $\Gamma$ which is called the orbifold fundamental group and can be defined in many ways (see [96, 135]). Here is one.

Definition 27

Let Z be a ‘good’ topological space, i.e., arcwise connected and semi-locally 1-connected, so that there exists the universal cover ${\mathcal {D}}$ of Z. Then we have $Z = {\mathcal {D}}/ \pi$ where $\pi : = \pi _1 (Z)$; denote $p : {\mathcal {D}}\rightarrow Z$ the quotient projection.

Assume now that a group G acts properly discontinuously on Z, and set $X : = Z/ G$. Then we define the orbifold fundamental group of the quotient of Z by G as the group of all the possible liftings of the action of G on ${\mathcal {D}}$, more precisely:

$$\begin{aligned} \pi _1^{orb} ( Z, G): = \left\{ \gamma : {\mathcal {D}}\rightarrow {\mathcal {D}}| \exists g \in G, \quad s.t. \ p \circ \gamma = g \circ p \right\} \end{aligned}$$

Remark 28

(1) We obtain an exact sequence, called orbifold fundamental group exact sequence,

$$\begin{aligned} (***) \ 1 \rightarrow \pi _1 (Z) \rightarrow \pi _1^{orb} ( Z, G) \rightarrow G \rightarrow 1 \end{aligned}$$

since for each $g \in G$ we have a lifting $\gamma$ of g, because ${\mathcal {D}}$ is the universal cover, so its associated subgroup is the identity, hence the lifting property is ensured. Moreover the lifting is uniquely determined, given base points $z_0 \in Z, y_0 \in {\mathcal {D}}$, with $p(y_0) = z_0$, by the choice of $y \in p^{-1} (\{ z_0\})$ with $\gamma (y_0) = y$.

(2) In the case where the action of G is free, then $\pi _1^{orb} ( Z, G) = \pi _1 ( Z/G) = \pi _1( X)$.

(3) If G acts properly discontinuously on Z, then $\Gamma : = \pi _1^{orb} ( Z, G)$ acts also properly discontinuously on ${\mathcal {D}}$: in fact the defining property that, for each compact $K \subset {\mathcal {D}}$, $\Gamma (K,K) : = \{ \gamma | \gamma (K) \cap K \ne \emptyset \}$ is finite, follows since p(K) is compact, and since $\pi$ acts properly discontinuously.

(4) If the space Z is a $K ( \pi , 1)$, i.e., a classifying space $Z = B \pi$, then (***) determines the topological type of the G-action. The group $\Gamma$ acts by conjugation on $\pi$, and this yields an homomorphism $G \rightarrow {{\mathrm{\text {Out}}}}(\pi ) = {{\mathrm{\text {Aut}}}}(\pi ) / {{\mathrm{\text {Inn}}}}(\pi )$, and we just have to recall that the topological action of $\gamma \in \Gamma$ is determined by its action on $\pi$, taken up to ${{\mathrm{\text {Inn}}}}(\pi )$ if we do not keep track of the base point.

In fact there is a bijection between homotopy classes of self maps of Z and homomorphisms of $\pi$, taken of course up to inner conjugation (inner conjugation is the effect of changing the base point, and if we do not insist on taking pointed spaces, i.e., pairs $(Z,z_0)$ the action of a continuous map on the fundamental group is only determined up to inner conjugation). Clearly a homeomorphism $\varphi : Z \rightarrow Z$ yields then an associated element $\pi _1 (\varphi ) \in {{\mathrm{\text {Out}}}}(\pi )$.

(5) Even if not useful for computations, one can still interpret the exact sequence (***) as an exact sequence for the fundamental groups of a tower of covering spaces, using the standard construction for equivariant cohomology that we shall discuss later.

Just let $BG = EG / G$ be a classifying space, and consider the free product action of G on $Z \times EG$.

Then we have a tower of covering spaces

$$\begin{aligned} ({\mathcal {D}}\times EG) \rightarrow ( Z \times EG) \rightarrow ( Z \times EG)/ G, \end{aligned}$$

where ${\mathcal {D}}\times EG$ is simply connected, and is the universal cover of $Y : = ( Z \times EG)/ G$, such that $\pi _1 (Y) \cong \pi _1^{orb} ( Z, G)$.

Of course, the above definitions seem apparently unrelated to the fundamental group of X, however we can take the maximal open set $U' \subset {\mathcal {D}}$ where $\Gamma : = \pi _1^{orb} ( Z, G)$ acts freely. Indeed $U' = p^{-1} (U)$, where U is the open set $U : = Z \setminus \{ z | G_z : = Stab (z) \ne \{ {{\mathrm{\text {Id}}}}_G\} \}$.

The conclusion is that $U' / \Gamma = U / G =: U'' \subset X$, hence we get exact sequences

$$\begin{aligned}&1 \rightarrow \pi _1 (U) \rightarrow \pi _1 (U'') \rightarrow G \rightarrow 1, \\&1 \rightarrow \pi _1 (U') \rightarrow \pi _1 (U'') \rightarrow \Gamma \rightarrow 1. \end{aligned}$$

We make now the hypothesis that ${\mathcal {D}}$, hence also Z, X are normal complex spaces, in particular they are locally contractible, and that the actions are holomorphic: then we have surjections

$$\begin{aligned} \pi _1 (U'') \rightarrow \pi _1 (X), \ \pi _1 (U) \rightarrow \pi _1 (Z), \end{aligned}$$

moreover $\pi _1 (U') \rightarrow \pi _1 ({\mathcal {D}}) = \{1\}$, and finally we get

$$\begin{aligned} \pi _1(Z) = \pi _1 (U) / \pi _1 (U'), \ \pi _1^{orb} ( Z, G) \rightarrow \pi _1(X) \rightarrow 0. \end{aligned}$$

Example 29

Assume that Z, X are smooth complex curves $Z = C$, $X = C'$. Then for each point $p_i \in X {\setminus } U''$ we get the conjugate $\gamma _i \in \pi _1(U'')$ of a circle around the point $p_i$, and we have $\ker ( \pi _1(U'') \rightarrow \pi _1(X)) = \langle \langle \{ \gamma _i \} \rangle \rangle$, i.e., the kernel is normally generated by these loops.

Each of these loops $\gamma _i$ maps to an element $c_i \in G$, and we denote by $m_i$ the order of the element $(c_i)$ in the group G. Then $\gamma _i ^{m_i} \in \pi _1 (U)$, and it is the conjugate of small circle around a point of $Z {\setminus } U$, hence it maps to zero in $\pi _1(Z)$. One can see that in this case

$$\begin{aligned} \pi _1^{orb} ( Z, G) = \pi _1(U'') / \langle \langle \left\{ \gamma _i ^{m_i}\right\} \rangle \rangle \end{aligned}$$

and the kernel of the natural surjection onto $\pi _1(X)$ is normally generated by the $\gamma _i$’s.

This means that, if the genus of $X = C'$ is equal to $g'$, then the orbifold fundamental group is isomorphic to the abstract group

$$\begin{aligned}&\pi _{g',m_1, \ldots ,\,m_d} :=\langle \alpha _1, \beta _1, \ldots , \alpha _{g'},\beta _{g'}, \gamma _1, \ldots , \gamma _d | \Pi _1^d \gamma _j \Pi _1^{g'} [ \alpha _i, \beta _i] = 1,\\&\gamma _1^{m_1} = \cdots = \gamma _d^{m_d} =1 \rangle . \end{aligned}$$

And the orbifold exact sequence is an extension, called Nielsen extension, of type

$$\begin{aligned} (NE) \ 1 \rightarrow \pi _g \rightarrow \pi _{g',m_1, \ldots ,\, m_d} \rightarrow G \rightarrow 1. \end{aligned}$$

A similar description holds in general (see [96], definition 4.4 and proposition 4.5, pp. 25–26 ), at least when Z is a complex manifold.

Remark 30

The notion of orbifold fundamental group has turned out to be quite useful also in real algebraic geometry, where one considers the action of complex conjugation on a real algebraic variety (see [97] for example).

6.2 Rational $K(\pi ,1)$’s: basic examples

An important role is also played by complex Rational $K(\pi ,1)$’s, i.e., quasi projective varieties (or complex spaces) Z such that

$$\begin{aligned} Z = {\mathcal {D}}/ \pi , \end{aligned}$$

where ${\mathcal {D}}$ is a contractible manifold (or complex space) and the action of $\pi$ on ${\mathcal {D}}$ is properly discontinuous but not necessarily free.

While for a $K(\pi ,1)$ we have $H^* (\pi , {\mathbb {Z}}) \cong H^* (Z, {\mathbb {Z}})$, $H_* (\pi , {\mathbb {Z}}) \cong H_* (Z, {\mathbb {Z}})$, for a rational $K(\pi ,1)$, as a consequence of Proposition 46 and of the spectral sequence of Theorem 62, we have $H^* (\pi , {\mathbb {Q}}) \cong H^* (Z, {\mathbb {Q}})$ and therefore also $H_* (\pi , {\mathbb {Q}}) \cong H_* (Z, {\mathbb {Q}})$.

Typical examples of such rational $K(\pi ,1)$’s are:

• (1) quotients of a bounded symmetric domain ${\mathcal {D}}$ by a subgroup $\Gamma \subset {{\mathrm{\text {Aut}}}}({\mathcal {D}})$ which is acting properly discontinuously (equivalently, $\Gamma$ is discrete); especially noteworthy are the case where $\Gamma$ is cocompact, meaning that $X = {\mathcal {D}}/\Gamma$ is compact, and the finite volume case where the volume of X via the invariant volume form for ${\mathcal {D}}$ is finite.

• (2) the moduli space of principally polarized Abelian Varieties, which is an important special case of the above examples;

• (3) the moduli space of curves ${\mathcal {M}}_g$.

For the first example the property is clear (we observed already that such a domain ${\mathcal {D}}$ is contractible).

For the second example it suffices to observe that the moduli space of Abelian Varieties of dimension g, and with a polarization of type $(d_1, d_2, \ldots , d_g)$ is the quotient of Siegel’s upper half space

$$\begin{aligned} {\mathcal {H}}_g : = \left\{ \tau \in {{\mathrm{\text {Mat}}}}(g,g,{\mathbb {C}})| \tau = ^t \tau , {{\mathrm{\text {Im}}}}(\tau ) > 0 \right\} , \end{aligned}$$

which is biholomorphic to a bounded symmetric domain of type III in E. Cartan’s classification [77], by the properly discontinuous action of the group

$$\begin{aligned} {{\mathrm{\text {Sp}}}}(D, {\mathbb {Z}}) : = \left\{ M \in Mat(2g, {\mathbb {Z}})| ^t M D M = D \right\} \!, \end{aligned}$$

where

$$\begin{aligned} D' : = {{\mathrm{\text {diag}}}}(d_1, d_2, \ldots , d_g), D: = \begin{pmatrix} 0 &{}\quad D' \\ - D' &{}\quad 0 \end{pmatrix} \end{aligned}$$

and,

$$\begin{aligned} M: = \left( \begin{matrix} \alpha &{}\quad \beta \\ \gamma &{}\quad \delta \end{matrix}\right) , \ \ \tau \mapsto - D' (D' \alpha - \tau \gamma )^{-1} ( D' \beta - \tau \delta ). \end{aligned}$$

In fact, these Abelian varieties are quotients ${\mathbb {C}}^g / \Lambda$, where $\Lambda$ is generated by the columns of the matrices $D, - \tau ,$ and the Hermitian form associated to the real matrix $\mathfrak {I}m (\tau )^{-1}$ has imaginary part which takes integral values on $\Lambda \times \Lambda$, and its associated antisymmetric matrix in the chosen basis is equal to D.

The quotient ${\mathcal {A}}_{g,D'} : = {\mathcal {H}}_g / {{\mathrm{\text {Sp}}}}(D, {\mathbb {Z}})$ is not compact, but of finite volume, and there exist several compactifications which are projective algebraic varieties (see [163, 176, 311]).

6.3 The moduli space of curves

The most useful (and first fully successful) approach to the moduli space of curves of genus g is to view it as a quotient

$$\begin{aligned} (**) \ {\mathfrak {M}}_g = {\mathcal {T}}_g / {\mathcal {M}}ap _g \end{aligned}$$

of a connected complex manifold ${\mathcal {T}}_g$ of dimension $3g-3 +a(g)$, called Teichmüller space, by the properly discontinuous action of the Mapping class group ${\mathcal {M}}ap _g$ (here $a (0) = 3, a(1) = 1, a(g)= 0, \forall g \ge 2$ is the complex dimension of the group of automorphisms of a curve of genus g). A key result (see [217, 237, 356]) is the

Theorem 31

Teichmüller space ${\mathcal {T}}_g$ is diffeomorphic to a ball, and the action of ${\mathcal {M}}ap _g$ is properly discontinuous.

Denoting as usual by $\pi _g$ the fundamental group of a compact complex curve C of genus g, we have in fact a more concrete description of the mapping class group (see [9, 10, 44, 45, 125, 165, 212, 220] for general results on braid and mapping class groups):

$$\begin{aligned} (M) \ {\mathcal {M}}ap _g \cong {{\mathrm{\text {Out}}}}^+ (\pi _g). \end{aligned}$$

The above superscript $^+$ refers to the orientation preserving property.

There is a simple algebraic way to describe the orientation preserving property: any automorphism of a group induces an automorphism of its abelianization, and any inner automorphism acts trivially.

Hence ${{\mathrm{\text {Out}}}}(G)$ acts on $G^{ab}$, in our particular case ${{\mathrm{\text {Out}}}}(\pi _g)$ acts on $\pi _g^{ab} \cong {\mathbb {Z}}^{2g}$, and ${{\mathrm{\text {Out}}}}^+ (\pi _g) \subset {{\mathrm{\text {Out}}}}(\pi _g)$ is the inverse image of $SL (2g, {\mathbb {Z}})$.

The above isomorphism (M) is of course related to the fact that C is a $K (\pi _g,1)$, as soon as $g \ge 1$.

As we already discussed, there is a bijection between homotopy classes of self maps of C and endomorphisms of $\pi _g$, taken up to inner conjugation. Clearly a homeomorphism $\varphi : C \rightarrow C$ yields then an associated element $\pi _1 (\varphi ) \in {{\mathrm{\text {Out}}}}(\pi _g)$.

Such a homeomorphism acts then on the second homology group $H_2 (C, {\mathbb {Z}}) \cong {\mathbb {Z}}[C]$, where the generator [C] corresponds to the orientation associated to the complex structure; the condition $H_2 (\varphi ) = +1$ that $\varphi$ is orientation-preserving translates into the above algebraic condition on $\psi : = \pi _1 (\varphi )$. That the induced action $\psi ^{ab}$ on the Abelianization $\pi _1(C)^{ab} \cong \pi _g^{ab} \cong {\mathbb {Z}}^{2g}$ satisfies: $\wedge ^{2g} (\psi ^{ab})$ acts as the identity on $\wedge ^{2g} ( {\mathbb {Z}}^{2g} ) \cong {\mathbb {Z}}$.

In other words, the image of the product of commutators $\epsilon : = \Pi _j [\alpha _j, \beta _j]$ is sent to a conjugate of $\epsilon$.

Turning now to the definition of the Teichmüller space ${\mathcal {T}}_g$, we observe that it is somehow conceptually easier to give the definition of Teichmüller space for more general manifolds.

6.4 Teichmüller space

Let M be an oriented real differentiable manifold of real dimension 2n, for simplicity let’s assume that M is compact.

Ehresmann [149] defined an almost complex structure on M as the structure of a complex vector bundle on the real tangent bundle $TM_{{\mathbb {R}}}$: namely, the action of $\sqrt{-1}$ on $TM_{{\mathbb {R}}}$ is provided by an endomorphism

$$\begin{aligned} J : TM_{{\mathbb {R}}} \rightarrow TM_{{\mathbb {R}}}, \quad \mathrm{with }\,\ J^2 = - Id. \end{aligned}$$

Equivalently, as done for the complex tori, one gives the decomposition of the complexified tangent bundle $TM_{{\mathbb {C}}} : = TM_{{\mathbb {R}}} \otimes _{{\mathbb {R}}}{\mathbb {C}}$ as the direct sum of the i, respectively $-i$ eigenbundles:

$$\begin{aligned} TM_{{\mathbb {C}}} = TM^{1,0} \oplus TM^{0,1}\quad \mathrm{where}\,\, TM^{0,1} = \overline{TM^{1,0} }. \end{aligned}$$

The space ${\mathcal {A}}{\mathcal {C}}(M)$ of almost complex structures, once $TM_{{\mathbb {R}}}$ (hence all associated bundles) is endowed with a Riemannian metric, is a subset of the Fréchet space $H^0 (M, {\mathcal {C}}^{\infty } (End (TM_{{\mathbb {R}}}) ))$ .

A closed subspace of ${\mathcal {A}}{\mathcal {C}}(M)$ consists of the set ${\mathcal {C}}(M)$ of complex structures: these are the almost complex structures for which there are at each point x local holomorphic coordinates, i.e., ${\mathbb {C}}$-valued functions $z_1, \ldots , z_n$ whose differentials span the dual $(TM^{1,0}_y)^{\vee }$ of $TM^{1,0}_y$ for each point y in a neighbourhood of x.

In general, the splitting

$$\begin{aligned} TM_{{\mathbb {C}}}^{\vee } = (TM^{1,0})^{\vee } \oplus (TM^{0,1})^{\vee } \end{aligned}$$

yields a decomposition of exterior differentiation of functions as $df = \partial f + \bar{\partial } f$, and a function is said to be holomorphic if its differential is complex linear, i.e., $\bar{\partial } f = 0$.

This decomposition $d= \partial + \bar{\partial }$ extends to higher degree differential forms.

The theorem of Newlander and Nirenberg [312], first proven by Eckmann and Frölicher in the real analytic case [144] characterizes the complex structures through an explicit equation:

Theorem 32

(Newlander–Nirenberg) An almost complex structure J yields the structure of a complex manifold if and only if it is integrable, which means $\bar{\partial } ^2 = 0.$

Obviously the group of oriented diffeomorphisms of M acts on the space of complex structures, hence one can define in few words some basic concepts.

Definition 33

Let ${\mathcal {D}}iff ^+ (M)$ be the group of orientation preserving diffeomorphisms of M , and let ${\mathcal {C}}(M)$ be the space of complex structures on M. Let ${\mathcal {D}}iff ^0 (M) \subset {\mathcal {D}}iff ^+ (M)$ be the connected component of the identity, the so called subgroup of diffeomorphisms which are isotopic to the identity.

Then Dehn [132] defined the mapping class group of M as

$$\begin{aligned} {\mathcal {M}}ap (M) : = {\mathcal {D}}iff ^+ (M) / {\mathcal {D}}iff ^0 (M), \end{aligned}$$

while the Teichmüller space of M, respectively the moduli space of complex structures on M are defined as

$$\begin{aligned} {\mathcal {T}}(M) : = {\mathcal {C}}(M) / {\mathcal {D}}iff ^0 (M), \quad {\mathfrak {M}} (M) : = {\mathcal {C}}(M) / {\mathcal {D}}iff ^+ (M). \end{aligned}$$

From these definitions follows that

$$\begin{aligned} \ {\mathfrak {M}} (M) = {\mathcal {T}}(M) / {\mathcal {M}}ap (M). \end{aligned}$$

The simplest examples here are two: complex tori and compact complex curves. In the case of tori a connected component of Teichmüller space (see [100] and also [103]) is an open set ${\mathcal {T}}_n$ of the complex Grassmann Manifold Gr(n, 2n), image of the open set of matrices

$$\begin{aligned} \left\{ \Omega \in {{\mathrm{\text {Mat}}}}(2n,n; {\mathbb {C}}) \ | \ i^n det (\Omega \overline{\Omega }) > 0 \right\} . \end{aligned}$$

This parametrization is very explicit: if we consider a fixed lattice $\Lambda \cong {\mathbb {Z}}^{2n}$, to each matrix $\Omega$ as above we associate the subspace of ${\mathbb {C}}^{2n} \cong \Lambda \otimes {\mathbb {C}}$ given as

$$\begin{aligned} V = \Omega {\mathbb {C}}^{n}, \end{aligned}$$

so that $V \in Gr(n,2n)$ and $\Lambda \otimes {\mathbb {C}}\cong V \oplus \bar{V}$.

Finally, to $\Omega$ we associate the torus

$$\begin{aligned} Y_V : = V / p_V (\Lambda ) = (\Lambda \otimes {\mathbb {C}})/ (\Lambda \oplus \bar{V} ), \end{aligned}$$

$p_V : V \oplus \bar{V} \rightarrow V$ being the projection onto the first addendum.

It was observed however by Kodaira and Spencer already in their first article on deformation theory ([248], and volume II of Kodaira’s collected works) that the mapping class group $SL ( 2n, {\mathbb {Z}})$ does not act properly discontinuously on ${\mathcal {T}}_n$.

The case of compact complex curves C is instead the one which was originally considered by Teichmüller.

In this case, if the genus g is at least 2, the Teichmüller space ${\mathcal {T}}_g$ is a bounded domain, diffeomorphic to a ball, contained in the vector space of quadratic differentials $H^0 ( C, {\mathcal {O}}_C ( 2 K_C)) \cong {\mathbb {C}}^{3g-3}$ on a fixed such curve C.

In fact, for each other complex structure on the oriented 2-manifold M underlying C we obtain a complex curve $C'$, and there is a unique extremal quasi-conformal map $f : C \rightarrow C'$, i.e., a map such that the Beltrami distortion $\mu _f : = \bar{\partial } f / \partial f$ has minimal norm (see for instance [217] or [8]).

The fact that the Teichmüller space ${\mathcal {T}}_g$ is diffeomorphic to a ball (see [356] for a simple proof) is responsible for the fact that the moduli space of curves ${\mathfrak {M}}_g$ is a rational $K(\pi , 1)$.

6.5 Singularities of $\mathfrak M_g$, I

Teichmüller’s theorem says that, for $g \ge 2$, $\mathcal {T}_g \subset {\mathbb {C}}^{3g-3}$ is an open subset diffeomorphic to a ball. Moreover ${{\mathcal {M}}ap}_g \cong {{\mathcal {M}}ap}(C)$ acts properly discontinuously on $\mathcal {T}_g$, but not freely.

The lack of freeness of this action is responsible of the fact that $\mathfrak M_g$ is a singular complex space (it is quasi-projective by the results of Mumford and Gieseker, see [302, 304]).

Therefore one has to understand when a class of complex structure C on the manifold M is fixed by an element $\gamma \in {\mathcal {M}}ap_g$. Since $\gamma$ is represented by the class of an orientation preserving diffeomorphism $\varphi : M \rightarrow M$, it is not difficult to see that this situation means that the diffeomorphism $\varphi$ carries the given complex structure to itself, or, in other words, the differential of $\varphi$ preserves the splitting of the complexified tangent bundle of M, $TM_{{\mathbb {C}}} = TM^{1,0} \oplus TM^{0,1}$.

This is then equivalent to $\bar{\partial } \varphi = 0$, i.e., $\varphi$ is a biholomorphic map, i.e., $\varphi \in {{\mathrm{\text {Aut}}}}(C)$.

Conversely, let $\gamma \in {{\mathrm{\text {Aut}}}}(C)$ be a nontrivial automorphism. Consider then the graph of $\gamma$, $\Gamma _{\gamma } \subset C \times C$, and intersect it with the diagonal $\Delta \subset C \times C$: their intersection number must be a nonnegative integer, because intersection points of complex subvarieties carry always a positive local intersection multiplicity.

This argument was used by Lefschetz to prove the following

Lemma 34

(Lefschetz’ lemma) If we have an automorphism $\gamma \in {{\mathrm{\text {Aut}}}}(C)$ of a projective curve of genus $g \ge 2$, then $\gamma$ is homotopic to the identity iff it is the identity:

$$\begin{aligned} \gamma \underset{h}{\sim } Id_C \Leftrightarrow \gamma =Id_C. \end{aligned}$$

Proof

The self intersection of the diagonal $\Delta ^2$ equals the degree of the tangent bundle to C, which is $2 - 2g$. If $\gamma$ is homotopic to the identity, then $\Gamma _{\gamma } \cdot \Delta = 2- 2g < 0$, and this is only possible if $\Gamma _{\gamma }= \Delta$, i.e., iff $\gamma =id_C$. $\square$

In particular, since C is a classifying space $B \pi _g$ for the group $\pi _g$, $\gamma :C \rightarrow C \,$ is such that the homotopy class of $\gamma$ is determined by the conjugacy class of $\pi _1(\gamma ) :\pi _1(C,y_0) \rightarrow \pi _1(C, \gamma \cdot y_0).$ Hence we get an injective group homomorphism

$$\begin{aligned} \rho _C :{{\mathrm{\text {Aut}}}}(C) \rightarrow \frac{\mathrm{Aut}(\pi _g)}{\mathrm{Inn}(\pi _g)}=\mathrm{Out}(\pi _g). \end{aligned}$$

Actually, since a holomorphic map is orientation preserving, we have that $\rho _C : {{\mathrm{\text {Aut}}}}(C) \rightarrow \mathrm{Out}^+(\pi _g)=\mathrm{Map}_g \cong \frac{\mathrm{{\mathcal {D}}iff}^+(C)}{\mathrm{{\mathcal {D}}iff}^0(C)}$.

The conclusion is then that curves with a nontrivial group of automorphisms ${{\mathrm{\text {Aut}}}}(C) \ne \{ Id_C\}$ correspond to points of ${\mathcal {T}}_g$ with a non trivial stabilizer for the action of ${\mathcal {M}}ap_g$.

Remark 35

There is of course the possibility that the action of ${\mathcal {M}}ap_g$ is not effective, i.e., there is a normal subgroup acting trivially on ${\mathcal {T}}_g$. This happens exactly in genus $g=2$, where every curve is hyperelliptic and the normal subgroup of order 2 generated by the hyperelliptic involution is exactly the kernel of the action.

The famous theorem of Hurwitz gives a precise upper bound $| {{\mathrm{\text {Aut}}}}(C) | \le 84 (g-1)$ for the cardinality of the stabilizer ${{\mathrm{\text {Aut}}}}(C)$ of C (that this is finite follows also by the proper discontinuity of the action).

Now, coming to ${{\mathrm{\text {Sing}}}}( \mathfrak M_g)$, we get that $\mathfrak M_g$ is locally analytically isomorphic to a quotient ‘singularity’ ${\mathbb {C}}^{3g-3} / {{\mathrm{\text {Aut}}}}(C)$ (indeed, as we shall see, to the quotient singularity of $H^1 (\Theta _C) / Aut (C)$ at the origin).

Now, given a quotient singularity ${\mathbb {C}}^{n} / G$, where G is a finite group, then by a well known lemma by H. Cartan [78] we may assume that G acts linearly, and then a famous theorem by Chevalley [124] and Shephard and Todd [338] says that the quotient ${\mathbb {C}}^{n} / G$ is smooth if and only if the action of $G \subset GL (n, {\mathbb {C}})$ is generated by pseudo-reflections, i.e., matrices which are diagonalizable with $(n-1)$ eigenvalues equal to 1, and the last one a root of unity.

Theorem 36

Let $G \subset GL (n, {\mathbb {C}})$, let $G^{pr}$ be the normal subgroup of G generated by pseudo reflections, and let $G^q$ be the factor group. Then

• (1) the quotient ${\mathbb {C}}^{n} / G^{pr}$ is smooth,

• (2) We have a factorization of the quotient map ${\mathbb {C}}^{n} \rightarrow {\mathbb {C}}^{n} / G$ as ${\mathbb {C}}^{n} \rightarrow ({\mathbb {C}}^{n} / G^{pr} ) \cong {\mathbb {C}}^{n} \rightarrow {\mathbb {C}}^{n} / G^q$ and ${\mathbb {C}}^{n} / G$ is singular if $G \ne G^{pr}$.

This result is particularly interesting in this situation, since the only pseudo-reflection occurs for the case of the hyperelliptic involution in genus $g=3$.

Teichmüller theory can be further applied in order to analyse the fixed loci of finite subgroups G of the mapping class group (see [96, 237, 356])

Theorem 37

(Refined Nielsen realization) Let $G \subset {\mathcal {M}}ap_g$ be a finite subgroup. Then $Fix(G) \subset {\mathcal {T}}_g$ is a non empty complex manifold, diffeomorphic to a ball.

Remark 38

(1) The name Nielsen realization comes from the fact that Nielsen [313–315] conjectured that any topological action of a finite group G on a Riemann surface could be realized as a group of biholomorphic automorphisms if and only if the action would yield an embedding $\rho : G \rightarrow {\mathcal {M}}ap_g$.

(2) The question can be reduced to a question of algebra, by the following observation.

The group $\pi _g$, for $g \ge 2$, has trivial centre: in fact, two commuting hyperbolic transformations in ${\mathbb {P}}SL(2, {\mathbb {R}})$ can be simultaneously written as Möbius transformations of the form $z \mapsto \lambda z, z \mapsto \mu z$, hence if the first transformation were in the centre of $\pi _g \subset {\mathbb {P}}SL(2, {\mathbb {R}})$, the group $\pi _g$ would be abelian, a contradiction.

Then $\pi _g \cong Inn (\pi _g)$ and from the exact sequence

$$\begin{aligned} 1 \rightarrow \pi _g \cong Inn (\pi _g) \rightarrow {{\mathrm{\text {Aut}}}}(\pi _g ) \rightarrow {{\mathrm{\text {Out}}}}(\pi _g) \rightarrow 1 \end{aligned}$$

and an injective homomorphism $\rho : G \rightarrow {\mathcal {M}}ap_g = {{\mathrm{\text {Out}}}}^+ (\pi _g)$ one can pull-back an extension⁵

$$\begin{aligned} 1 \rightarrow \pi _g \rightarrow \hat{G} \rightarrow G \rightarrow 1. \end{aligned}$$

(4) The main question is to show that the group $\hat{G}$ is isomorphic to an orbifold fundamental group of the form $\pi _{g', m_1, \ldots , m_d}$. Because then we have a Nielsen extension, and the epimorphism $\mu : \pi _{g', m_1, \ldots , m_d} \rightarrow G \rightarrow 1$ combined with Riemann’s existence theorem finds for us a curve C over which G acts with the given topological type: such a curve C is given by the ramified covering of a curve $C'$ of genus $g'$, branched on d points $y_1, \ldots , y_d$ and with monodromy $\mu$.

(5) Since $\pi _g$ is torsion free (hyperbolic elements in ${\mathbb {P}}SL(2, {\mathbb {R}})$ have infinite order), we see that the branch points correspond to conjugacy classes of cyclic subgroups of finite order in $\hat{G}$, and that their order $m_i$ in $\hat{G}$ equals the order of their image in G.

In turn, the question can be reduced to showing that there is a differentiable action of the group G on the curve C inducing the topological action $\rho$. There is the following

Lemma 39

Given $\rho : G \rightarrow Map_g = {\mathcal {D}}iff^+(C) / {\mathcal {D}}iff^0(C)$, if there is a homomorphism $\psi : G \rightarrow {\mathcal {D}}iff^+(C)$ whose projection to $Map_g$ is $\rho$, then there is a complex curve with a G action of topological type $\rho$.

Proof

In fact, by Cartan’s lemma [78], at each fixed point $x \in C$, there are local coordinates such that in these coordinates the action of the stabilizer $G_x$ of x is linear (in particular, if we assume that the action of G is orientation preserving, then $G_x \subset SO(2, {\mathbb {R}})$, and $G_x$ is a cyclic group of rotations).

Therefore, for each $\gamma \in G$, $\gamma \ne 1_G$, the set of fixed points $Fix (\gamma )$, which is closed, is either discrete (hence finite), or it consists of a discrete set plus a set (the points $x \in Fix (\gamma )$ where the derivative is the identity) which is open and closed. Since C is connected, the only possible alternative is that, for $\gamma \ne 1_G$, the set of fixed points $Fix (\gamma )$ is finite.

Now, it is easy to see that the quotient $C/G = : C'$ is a smooth Riemann surface and we can take a complex structure on $C'$ and lift it to C, so that $C' = C/G$ as complex curves. $\square$

Remark 40

In general Marković has proven that the mapping class group cannot be realized, as hoped by Thurston, as a subgroup of the group of diffeomorphisms of a Riemann surface of genus g. There are other recent results concerning non finite groups (see [41]).

Remark 41

(1) It is interesting to observe that one can view the orbifold fundamental group, in the case of curves, as the quotient of a bona fide fundamental group.

Let TC be the tangent bundle of the complex curve, and assume that G has a differentiable action on C, so that G acts on TC, preserving the zero section. We can further assume, by averaging a Riemannian metric on TC, that G preserves the sphere bundle of TC,

$$\begin{aligned} SC : = \left\{ v \in TC | |v| = 1\right\} . \end{aligned}$$

Since each stabilizer $G_x$ is a cyclic group of rotations, the conclusion is that G acts on SC by a free action, and we get an exact sequence

$$\begin{aligned} (Seifert) \ 1 \rightarrow \pi _1(SC) \rightarrow \pi _1(SC/G ) \rightarrow G \rightarrow 1. \end{aligned}$$

It is well known (see e.g. [105]) that the fundamental group of the fibre bundle SC is a central extension

$$\begin{aligned} 1 \rightarrow {\mathbb {Z}}\rightarrow \pi _1(SC) \rightarrow \pi _g \rightarrow 1, \end{aligned}$$

and is the quotient of the direct product ${\mathbb {Z}}\times {\mathbb {F}}_{2g}$ by the subgroup normally generated by the relation

$$\begin{aligned} c^{2g-2} \Pi _1^{g} [ \alpha _i, \beta _i] = 1, \end{aligned}$$

where c is a generator of the central subgroup $\langle c \rangle \cong {\mathbb {Z}}$.

Taking the quotient by the subgroup $\langle c \rangle$ generated by c one obtains the orbifold group exact sequence. The fibration $SC/G \rightarrow C' = C/G$ is a so-called Seifert fibration, with fibres all homemorphic to $S^1$, but the fibres over the branch points $y_j$ are multiple of multiplicity $m_j$.

Now, an injection $G \rightarrow {{\mathrm{\text {Out}}}}^+(\pi _g)$ determines an action of G on $\pi _1(SC)$ (sending c to itself), an extension of the type we denoted (Seifert), and a topological action on the classifying space SC.

(2) The main point of the proof of the Nielsen realization is however based on analysis, and, more precisely, on the construction of a Morse function f on ${\mathcal {T}}_g$ of class $C^1$ which is G-invariant, strictly convex and proper, and therefore has only one minimum.

The unique minimum must be G-invariant, hence we get a point C in Fix(G) . Since the function is strictly convex and proper, it does not have other critical points, and it has only one minimum: therefore Morse theory tells that ${\mathcal {T}}_g$ is diffeomorphic to a ball.

Now, in turn, the locus Fix(G) is a non empty submanifold, and the group G acts nontrivially on the normal bundle of Fix(G) in ${\mathcal {T}}_g$.

The same analysis applies to the restriction of the Morse function to any connected component Y of Fix(G) . The function has exactly one critical point D, which is an absolute minimum on Y, hence Y is also diffeomorphic to a ball.

To show that Fix(G) is connected it suffices to show that $C=D$, i.e., that D is also a critical point on the whole space ${\mathcal {T}}_g$. But the derivative of f at D is a G-invariant linear functional, vanishing on the subspace of G-invariants: therefore the derivative of f at D is zero.

Hence $Fix(G) =Y$, as well as ${\mathcal {T}}_g$, is diffeomorphic to a ball.

(3) It may happen that Fix(G) may be also the fixed locus for a bigger subgroup $H \subset {\mathcal {M}}ap_g$. We shall see examples later in Examples 189, 190. To determine when this happens is an interesting question, fully answered by Cornalba in the case where G is a cyclic group of prime order [127] (this result is the key to understanding the structure of the singular locus ${{\mathrm{\text {Sing}}}}( \mathfrak M_g)$).

A partial answer to the question whether G is not a full subgroup (i.e., $\exists H \supset G$, $Fix(H) = Fix(G)$ was given by several authors, who clarified the orbifold fundamental groups associated to the quotients $C \rightarrow C/G \rightarrow C/H$ [275, 327, 343].

6.6 Group cohomology and equivariant cohomology

The roots of group cohomology go back to Jacobi and to the study of periodic meromorphic functions as quotients of quasi-periodic holomorphic functions; these functions, which can more generally be taken as vector-valued functions $s : {\mathbb {C}}^n \rightarrow {\mathbb {C}}^m$, are solutions to the functional equation

$$\begin{aligned} s(x + \gamma ) = f_{\gamma }(x) s(x), \end{aligned}$$

where $\Lambda \subset {\mathbb {C}}^n$ is a discrete subgroup, $\forall \gamma \in \Lambda \subset {\mathbb {C}}^n, x \in {\mathbb {C}}^n, f_{\gamma } : {\mathbb {C}}^n \rightarrow {{\mathrm{\text {GL}}}}(m, {\mathbb {C}}),$ and clearly $f_{\gamma }$ satisfies then the cocycle condition

$$\begin{aligned} f_{\gamma + \gamma ' }(x) = f_{\gamma }(x + \gamma ' ) f_{\gamma '}(x), \quad \forall \gamma , \gamma ' \in \Lambda , \quad \forall x \in {\mathbb {C}}^n. \end{aligned}$$

Later on, the ideas of Jacobi were generalised through the concept of vector bundles, since the cocycle $f_{\gamma } (x)$ can be used to constructing a vector bundle on the quotient manifold ${\mathbb {C}}^n / \Lambda$ taking a quotient of the trivial bundle ${\mathbb {C}}^n \times {\mathbb {C}}^m \rightarrow {\mathbb {C}}^n$ by the relation

$$\begin{aligned} (x,v) \sim ( x + \gamma , f_{\gamma }(x) v), \end{aligned}$$

and the cocycle relation just says that the above is an equivalence relation. The main difficulty classically consisted in simplifying as much as possible the form of these cocycles, replacing $f_{\gamma }(x)$ by an equivalent one $\phi (x + \gamma ) f_{\gamma }(x) \phi (x)^{-1}$, for $\phi : {\mathbb {C}}^n \rightarrow {{\mathrm{\text {GL}}}}(m, {\mathbb {C}})$.

The construction can be vastly generalized by viewing any bundle on a classifying space $Y = B \Gamma$, quotient of a contractible space $X = E \Gamma$, as the quotient of the trivial bundle $X \times F$ by an action which covers the given action of G on X, hence such that there exists $f_{\gamma }: X \rightarrow Homeo (F)$ with

$$\begin{aligned} \gamma (x, v) = ( \gamma (x), f_{\gamma }(x)(v) ) \Rightarrow \forall \gamma , \gamma ' , \forall x \in X, \ f_{\gamma ' \gamma }(x) = f_{\gamma '}(\gamma (x)) f_{\gamma }(x). \end{aligned}$$

As remarked by David Mumford [309], classical mathematics led to concrete understanding of 1-cocycles and 2-cocycles, hence of first and second cohomology groups. But the general machinery of higher cohomology groups is harder to understand concretely.

As always in mathematics, good general definitions help to understand what one is doing, but explicit calculations remain often a hard task. Let us concentrate first on the special case where we look at the singular cohomology groups of a classifying space.

In the case of a classifying space $B \Gamma$, we know that for each ring of coefficients R,

$$\begin{aligned} H^* (\Gamma , R) = H^*( B \Gamma , R), \end{aligned}$$

and for this it suffices indeed that

$$\begin{aligned} H^* (\Gamma , {\mathbb {Z}}) = H^*( B \Gamma , {\mathbb {Z}}). \end{aligned}$$

Which side of the equation is the easier one to get hold of? The answer depends of course on our knowledge of the group $\Gamma$ and of the classifying space $B \Gamma$, which is determined only up to homotopy equivalence.

For instance, we saw that an incarnation of $B ({\mathbb {Z}}/ 2)$ is given by the inductive limit ${\mathbb {P}}^{\infty }_{{\mathbb {R}}} : = \lim _{n \rightarrow \infty } {\mathbb {P}}^n_{{\mathbb {R}}}$.

A topologist would just observe that ${\mathbb {P}}^{\infty }_{{\mathbb {R}}}$ is a CW-complex obtained adding a cell $\sigma _n$ in each dimension n, and with boundary map

$$\begin{aligned} \partial ( \sigma _{2n}) = 2 \sigma _{2n-1}, \quad \partial ( \sigma _{2n-1}) = 0 \cdot \sigma _{2n-2}, \quad \forall n \ge 1. \end{aligned}$$

Therefore $H_{2i}( {\mathbb {Z}}/ 2, {\mathbb {Z}}) = 0, H_{2i-1}( {\mathbb {Z}}/ 2, {\mathbb {Z}}) = {\mathbb {Z}}/ 2, \forall i \ge 1,$ and taking the dual complex of cellular cochains one gets:

$$\begin{aligned} H^{2i}( {\mathbb {Z}}/ 2, {\mathbb {Z}}) = {\mathbb {Z}}/ 2, H^{2i-1}( {\mathbb {Z}}/ 2, {\mathbb {Z}}) = 0, \forall i \ge 1. \end{aligned}$$

There are two important ways how this special calculation generalizes:

• (i) a completely general construction of a CW complex which is a classifying space $B \Gamma$ for a finitely presented group $\Gamma$,

• (ii) a completely algebraic definition of group cohomology.

• (i): In fact, assume we are given a finite presentation of $\Gamma$ as

  $$\begin{aligned} \Gamma = \langle x_1, \ldots , x_n | R_1(x), \ldots R_m (x) \rangle , \end{aligned}$$

which means that $\Gamma$ is isomorphic to the quotient of the free group ${\mathbb {F}}_n$ with generators $x_1, \ldots , x_n$ by the minimal normal subgroup R containing the words $R_j \in {\mathbb {F}}_n$ (R is called the subgroup of relations, and it is said to be normally generated by the relations $R_j$).

Then the standard construction of the 2-skeleton of $B\Gamma$ is the CW-complex $B\Gamma ^2$, of dimension two, which is obtained by attaching, to a bouquet of n circles (which correspond to the generators $x_1, \ldots , x_n$), m 2-cells whose respective boundary is the closed path corresponding to the word $R_j, \forall j=1, \ldots , m$.

For instance,

$$\begin{aligned} {\mathbb {Z}}/ 2 = {\mathbb {Z}}/ ( 2 {\mathbb {Z}})= \langle \langle x_1 | x_1^2 \rangle \rangle , \end{aligned}$$

and the above procedure produces ${\mathbb {P}}^2_{{\mathbb {R}}}$ as 2-skeleton.

However, the universal cover of ${\mathbb {P}}^2_{{\mathbb {R}}}$ is the sphere $S^2$, which has a homotopy group $\pi _2 (S^2) \cong {\mathbb {Z}}$, and we know that the higher ($i \ge 2$) homotopy groups $\pi _i (X)$ of a space equal the ones of its universal cover. Then a 3-cell is attached to ${\mathbb {P}}^2_{{\mathbb {R}}}$, obtaining ${\mathbb {P}}^3_{{\mathbb {R}}}$, and one continues to attach cells in order to kill all the homotopy groups. The same is done more generally to obtain $B\Gamma$ from the CW-complex $B\Gamma ^2$: 3-cells are attached in order to kill the second homotopy groups, and one then obtains $B\Gamma ^3$; one obtains then $B\Gamma ^4$ adding 4-cells in order to kill $\pi _3(B\Gamma ^3)$, and so on.

The disadvantage of this construction is that from the third step onwards it is no longer so explicit, since calculating homotopy groups is difficult.

An easy but important remark used in the proof of a theorem of Gromov (see [91, 196]) is that when the group $\pi$ has few relations, which more precisely means here $n \ge m + 2$, then necessarily there is an integer b with $0 \le b \le m$ such that the rank of $H^1 (B \pi , {\mathbb {Z}})$ equals $n-m +b$, while ${{\mathrm{\text {rank}}}}(H^2 (B \pi , {\mathbb {Z}})) \le b:$ since by the above construction $H_2 (B \pi ^2, {\mathbb {Z}})$ is the kernel of a linear map $\partial : {\mathbb {Z}}^m \rightarrow H_1 (B \pi ^1, {\mathbb {Z}}) = {\mathbb {Z}}^n$, whose rank is denoted by $m-b$, and we have a surjection $H_2 (B \pi ^2, {\mathbb {Z}}) \rightarrow H_2 (B \pi , {\mathbb {Z}})$.

Hence, if we consider the cup product bilinear map

$$\begin{aligned} \cup : H^1 (B \pi , {\mathbb {Z}}) \times H^1 (B \pi , {\mathbb {Z}}) \rightarrow H^2 (B \pi , {\mathbb {Z}}), \end{aligned}$$

for each $\psi \in H^1 (B \pi , {\mathbb {Z}})$ the linear map $\phi \mapsto \psi \cup \phi$ has a kernel of rank $\ge n-m \ge 2$. This means that each element $\psi \in H^1 (B \pi , {\mathbb {Z}})$ is contained in an isotropic subspace (for the cup product map) of rank at least 2.

It follows that if the fundamental group of a space X, $\Gamma : = \pi _1(X)$ admits a surjection onto $\pi$, then the induced classifying continuous map $\phi : X \rightarrow B \pi$ (see 11) has the property

• that its induced homomorphism on first cohomology

  $$\begin{aligned} H^1 (\phi ) : H^1 (B \pi , {\mathbb {Z}}) \rightarrow H^1 (X, {\mathbb {Z}}) \end{aligned}$$

  is injective (since $H_1 (\phi ) : H_1 (X, {\mathbb {Z}}) \rightarrow H_1 (B \pi , {\mathbb {Z}})$ is surjective)

• the image W of $H^1 (\phi )$ is such that each element $w \in W$ is contained in an isotropic subspace of rank $\ge 2$.

We shall explain Gromov’s theorem, for the case where X is a Kähler manifold, in the next section.

But let us return to the algebraic point of view (see for instance [223], pp. 355–362, also [63]).

(ii): Assume now that G is a group, so that we have the group algebra ${\mathcal {A}}: = {\mathbb {Z}}[G]$. Recall the functorial definition of group cohomology and of group homology, which gives a high brow explanation for a rather concrete definition we shall give later.

Definition 42

Consider the category of modules M over the group ring ${\mathcal {A}}: = {\mathbb {Z}}[G]$ (i.e., of abelian groups over which there is an action of G, also called G-modules).

Then there are two functors, the functor of invariants

$$\begin{aligned} M \mapsto M^G : = \{ w \in M | g(w) = w \quad \forall g \in G \} = \cap _{g \in G } \ker (g-Id), \end{aligned}$$

associating to each module M the submodule of elements which are left fixed by the action of G, and the functor of co-invariants

$$\begin{aligned} M \mapsto M_G : =M / ( \Sigma _{g \in G } Im (g-Id)), \end{aligned}$$

associating to each module M the minimal quotient module on which the action of G becomes trivial.

Both $M^G$ and $M_G$ are trivial G-modules, and one defines the cohomology groups $H^i(G,M)$ as the derived functors of the functor of invariants, while the homology groups $H_i(G,M)$ are the derived functors of the functor of co-invariants.

The relation of these concepts to homological algebra is furnished by the following elementary lemma.

Lemma 43

Let ${\mathbb {Z}}$ be the trivial G-module, i.e., we consider the abelian group ${\mathbb {Z}}$ with module structure such that every $g \in G$ acts as the identity.

Then we have canonical isomorphisms

$$\begin{aligned} {{\mathrm{\text {Hom}}}}_{{\mathbb {Z}}[G]} ( {\mathbb {Z}}, M) \cong M^G , \quad M \otimes _{{\mathbb {Z}}[G]} {\mathbb {Z}}\cong M_G, \end{aligned}$$

given by the homomorphisms $f \mapsto f(1)$, respectively $w \otimes n \mapsto [ n w]$.

In particular, we have

$$\begin{aligned} H^i(G,M) = Ext^i_{{\mathbb {Z}}[G]} ( {\mathbb {Z}}, M), \quad H_i(G,M) = Tor_i^{{\mathbb {Z}}[G]} ( {\mathbb {Z}}, M). \end{aligned}$$

We illustrate now the meaning of the above abstract definition for the case of group cohomology.

One can construct an explicit free resolution (a projective resolution would indeed suffice) for the trivial ${\mathcal {A}}$-module $M = {\mathbb {Z}}$

$$\begin{aligned} \cdots L_n \rightarrow L_{n-1} \rightarrow \cdots \rightarrow L_1 \rightarrow L_0 \rightarrow {\mathbb {Z}}\rightarrow 0. \end{aligned}$$

Then for each ${\mathcal {A}}$-module M the cohomology groups $H^n (G, M)$ are computed as the cohomology groups of the complex

$$\begin{aligned} {{\mathrm{\text {Hom}}}}(L_0, M) \rightarrow {{\mathrm{\text {Hom}}}}(L_1, M) \rightarrow \cdots \rightarrow {{\mathrm{\text {Hom}}}}(L_{n-1}, M) \rightarrow {{\mathrm{\text {Hom}}}}(L_n, M) \rightarrow \cdots . \end{aligned}$$

While the homology groups are calculated as the homology groups of the complex

$$\begin{aligned} \cdots \rightarrow M \otimes _{{\mathbb {Z}}[G]} L_{i+1} \rightarrow M \otimes _{{\mathbb {Z}}[G]} L_{i} \rightarrow M \otimes _{{\mathbb {Z}}[G]} L_{i-1} \rightarrow \cdots . \end{aligned}$$

For instance, if G is a cyclic group of order m, then ${\mathcal {A}}= {\mathbb {Z}}[x]/ (x^m - 1)$ and the free resolution of ${\mathbb {Z}}$ is given by free modules of rank one: the homomorphisms are the augmentation $\epsilon : L_0 \rightarrow {\mathbb {Z}}$ (defined by setting $\epsilon (\Sigma _g a_g \cdot g ) : = \Sigma _g a_g$) and the scalar multiplications:

$$\begin{aligned} ( x-1) : L_{2n+1} \rightarrow L_{2n}, \ ( 1 + x \cdots + x^{m-1}) : L_{2n+2} \rightarrow L_{2n+ 1}, \end{aligned}$$

in view of the fact that $(x-1)( 1 + x \cdots + x^{m-1}) = x^m -1 \equiv 0 \in {\mathcal {A}}$.

The case $m=2$ we saw before is a very special case, since then ${\mathcal {A}}= {\mathbb {Z}}\oplus {\mathbb {Z}}x$, with $x^2 = 1$, hence on the trivial module ${\mathbb {Z}}= {{\mathrm{\text {Hom}}}}_{{\mathbb {Z}}[G]} ( {\mathbb {Z}}[G], {\mathbb {Z}})$ $(1-x)$ acts as multiplication by 0, $1 + x$ acts as multiplication by 2. But the same pattern happens for all m: $(1-x)$ acts as multiplication by 0, $1 + x \cdots + x^{m-1}$ acts as multiplication by m.

In particular, the homology groups can be calculated as

$$\begin{aligned} H_{2i}({\mathbb {Z}}/m, {\mathbb {Z}}) = 0, i \ge 1, \quad H_{2i+1}({\mathbb {Z}}/m, {\mathbb {Z}}) \cong {\mathbb {Z}}/m, \quad i \ge 0. \end{aligned}$$

For more general groups there is a general complex, called the bar-complex, which yields a resolution of the ${\mathcal {A}}$-module ${\mathbb {Z}}$.

It is easier to first give the concrete definition of the cohomology groups (see also [180]).

Definition 44

Given a group G and a ${\mathcal {A}}: = {\mathbb {Z}}[G]$-module M, one defines the group of i-cochains with values in M as:

$$\begin{aligned} C^i (G, M) : = \{ f : G^{i+1} \rightarrow M| f (\gamma g_0, \ldots , \gamma g_i) = \gamma f ( g_0, \ldots , g_i) \quad \forall \gamma \in G \}, \end{aligned}$$

and the differential $d_i : C^i (G, M) \rightarrow C^{i+1} (G, M)$ through the familiar formula

$$\begin{aligned} df ( g_0, \ldots , g_{i+1} ) : = \Sigma _0^{i+1} (-1)^j f ( g_0, \ldots , \hat{g_j} ,\ldots , g_{i+1} ). \end{aligned}$$

Then the groups $H^i (G, M)$ are defined as the cohomology groups of the complex of cochains, that is,

$$\begin{aligned} H^i (G, M) = \ker (d_i) / Im (d_{i-1}). \end{aligned}$$

Remark 45

(1) In group theory one gives a different, but equivalent formula, obtained by considering a cochain as a function of i instead of $i+1$ variables, as follows:

$$\begin{aligned} \varphi ( g_1, \ldots , g_i) : = f (1, g_1, g_1 g_2, \ldots , g_1 g_2 \ldots g_i). \end{aligned}$$

One observes in fact that, in view of equivariance of f with respect to left translation on G, giving f is equivalent to giving $\varphi$.

Then the formula for the differential becomes asymmetrical

$$\begin{aligned} d \varphi ( g_1, \ldots , g_{i+1})= & {} g_1 \varphi ( g_2, \ldots , g_{i+1}) - \varphi ( g_1 g_2, g_3, \ldots , g_{i+1})\\&+\, \varphi ( g_1, g_2 g_3, \ldots , g_{i+1}) \ldots (-1)^i \varphi ( g_1, g_2, g_3, \ldots , g_{i}). \end{aligned}$$

(2) The second formula is more reminiscent of the classical formulae, and indeed, for $i=0$, yields

$$\begin{aligned} H^0(G, M)= & {} \left\{ x \in M | g x - x = 0 \quad \forall g \in G \right\} = M^G, \\ Z^1(G, M)= & {} \left\{ \varphi = \varphi (g) | g _1 \varphi (g_2) - \varphi (g_1 g_2 ) + \varphi (g_1) = 0 \quad \forall g_1, g_2 \in G \right\} ,\\ B^1(G, M)= & {} \left\{ \varphi = \varphi (g) | \exists x \in M , \varphi (g)\right. \\= & {} \left. g x - x \right\} , \ H^1(G, M) = Z^1(G, M) / B^1(G, M). \end{aligned}$$

(3) Hence, if M is a trivial G-module, then $B^1(G, M) =0$ and $H^1(G, M) = {{\mathrm{\text {Hom}}}}(G, M)$.

We have been mainly interested in the case of ${\mathbb {Z}}$-coefficients, however if we look at coefficients in a field k, we have:

Proposition 46

Let G be a finite group, and let k be a field such that the characteristic of k does not divide |G|. Then

$$\begin{aligned} H^i(G, k) = 0 \quad \forall i \ge 1. \end{aligned}$$

Proof

If M is a k[G]-module, we observe first that

$$\begin{aligned} M^G \cong Hom_{{\mathbb {Z}}[G]} ({\mathbb {Z}}, M) \cong Hom_{k[G]} (k , M), \end{aligned}$$

and then that the functor $M \mapsto M^G$ is exact, because $M^G$ is a direct summand of M (averaging $v \mapsto \frac{1}{|G|} \sum _{g \in G} gv$ yields a projector with image $M^G$). Hence $H^i(G, M) = 0 \ \forall i \ge 1$. $\square$

6.7 Group homology, Hopf’s theorem, Schur multipliers

To give some explicit formula in order to calculate homology groups, we need to describe the bar-complex, which gives a resolution of the trivial module ${\mathbb {Z}}$.

In order to relate it to the previous formulae for group cohomology, we should preliminary observe that the group algebra ${\mathbb {Z}}[G]$ can be thought of as the subalgebra of the space of functions $a: G \rightarrow {\mathbb {Z}}$ generated by the characteristic functions of elements of G (so that $g \in {\mathbb {Z}}[G]$ is the function such that $g(x) = 1$ for $x=g$, else $g(x) = 0, x\ne g$. As well known, multiplication on the group algebra corresponds to convolution of the corresponding functions, $f_1 * f_2 (x) = \int _G f_1 (x y^{-1} ) f_2 (y) dy$.

It is then clear that the tensor product ${\mathbb {Z}}[G] \otimes _{{\mathbb {Z}}} M$ yields a space of M-valued functions on G (all of them, if the group G is finite), and we get a space of ${\mathbb {Z}}$-valued functions on the i-th Cartesian product $G^{i+1}$ by considering the $(i+1)$-fold tensor product

$$\begin{aligned} C_i : = {\mathbb {Z}}[G] \otimes _{{\mathbb {Z}}} {\mathbb {Z}}[G] \otimes \cdots \otimes _{{\mathbb {Z}}} {\mathbb {Z}}[G], \end{aligned}$$

with ${\mathbb {Z}}[G]$-module structure given by

$$\begin{aligned} g (x_0 \otimes \cdots \otimes x_i ): = g (x_0) \otimes \cdots \otimes x_i. \end{aligned}$$

Definition 47

The bar-complex of a group G is the homology complex given by the free ${\mathbb {Z}}[G]$-modules $C_i$ (a basis is given by

$$\begin{aligned} \left\{ (g_1, \ldots , g_i) : = 1 \otimes g_1 \otimes \cdots \otimes g_i \right\} ) \end{aligned}$$

and with differential $d_i : C_i \rightarrow C_{i-1}$ (obtained by dualizing the previously considered differential for functions), defined by

The augmentation map $\epsilon : C_0 = {\mathbb {Z}}[G] \rightarrow {\mathbb {Z}}$ shows then the the bar-complex is a free resolution of the trivial ${\mathbb {Z}}[G]$-module ${\mathbb {Z}}$.

As a consequence, the homology groups $H_n(G, {\mathbb {Z}})$ are then the homology groups of the complex $( C_n \otimes _{{\mathbb {Z}}[G]} {\mathbb {Z}}, d_n)$, and one notices that, since ${\mathbb {Z}}[G] \otimes _{{\mathbb {Z}}[G]} {\mathbb {Z}}\cong {\mathbb {Z}}$, (observe in fact that $g\otimes 1 = 1 \otimes g 1 = 1 \otimes 1$), then $C_n \otimes _{{\mathbb {Z}}[G]} {\mathbb {Z}}$ is a trivial ${\mathbb {Z}}[G]$-module and a free ${\mathbb {Z}}$-module with basis $\{ (g_1, \ldots , g_n) \}$.

The algebraic definition yields the expected result for $i=1$.

Corollary 48

$H_1(G, {\mathbb {Z}}) = G^{ab} = G / [G,G]$, [G, G] being as usual the subgroup generated by commutators.

Proof

First argument, from algebra: we have

$$\begin{aligned} \oplus _{g_1, g_2 \in G} {\mathbb {Z}}(g_1, g_2) \rightarrow \oplus _{g \in G} {\mathbb {Z}}g \rightarrow {\mathbb {Z}}\end{aligned}$$

but the second homomorphism is zero, hence

$$\begin{aligned} H_1(G, {\mathbb {Z}}) = ( \oplus _{g \in G} {\mathbb {Z}}g ) / \langle g_2 - g_1 g_2 + g_1 \rangle = G^{ab}, \end{aligned}$$

since we have then the equivalence relation $g_1 g_2 \equiv g_1 + g_2$.

Second argument, from topology: $H_1(X, {\mathbb {Z}})$ is the abelianization of the fundamental group, so we just apply this to the case of $X = BG$, since $\pi _1 (BG) \cong G$. $\square$

The machinery of algebraic topology is also useful in order to show the following ‘duality’ statement.

Theorem 49

If G is a finite group there is an isomorphism between the group $H_2(G, {\mathbb {Z}})$ and the group of ‘Schur multipliers’ $H^2 (G, {\mathbb {C}}^*)$.

Proof

Let us consider the exact sequence of groups

$$\begin{aligned} 0 \rightarrow {\mathbb {Z}}\rightarrow {\mathbb {C}}\rightarrow {\mathbb {C}}^* \rightarrow 1, \end{aligned}$$

and use that $H^i(G, {\mathbb {C}}) = 0$ for $i \ge 1$ (see [223]).

Hence we have an isomorphism $H^2 (G, {\mathbb {C}}^*) \cong H^3 (G, {\mathbb {Z}})$.

Now, by the universal coefficient formula, the torsion subgroup of $H_n(X, {\mathbb {Z}})$ equals the torsion subgroup of $H^{n+1}(X, {\mathbb {Z}})$. Apply this observation to the case $X = BG$, $n=2$, remarking that the groups $H^i(G, {\mathbb {Z}})$, hence also the groups $H_i(G, {\mathbb {Z}})$, are torsion abelian groups for $i \ge 1$. Indeed, $H^i(G, {\mathbb {R}}) = H^i(BG, {\mathbb {R}}) = H^i(EG, {\mathbb {R}})^G = 0$). $\square$

The calculation of the above group $H_2(G, {\mathbb {Z}})$ was achieved by Hopf [215], and we shall sketch the underlying topological idea.

Theorem 50

(Hopf) Assume that we have a presentation of a group G as the quotient $G = F/R$ of a free group. Then

$$\begin{aligned} H_2(G, {\mathbb {Z}}) = ( [F,F] \cap R) / [F,R]. \end{aligned}$$

Proof

(Sketch)

Proof I (currently fashionable argument)

To the exact sequence of groups

$$\begin{aligned} 1 \rightarrow R \rightarrow F \rightarrow G \rightarrow 1 \end{aligned}$$

there correspond continuous maps of classifying spaces. These maps are only well defined up to homotopy, and using a small trick we can arrange the corresponding maps to be the standard inclusion of a fibre into a fibre bundle.

More precisely, let $BG = EG /G$ be a classifying space for G, and $BF = EF/F$ be a classifying space for F: since the group is free, BF shall be a bouquet of circles. Moreover, since R is a subgroup of F, its classifying space BR is a covering of BF, indeed it is $BR = EF /R$, and is a CW-complex of dimension 1 (whence, the theorem of Nielsen that a subgroup R of a free group F is also free).

The surjection $F \rightarrow G$ yields an action of F on EG, which restricts to a trivial action of R.

We use the construction of equivariant cohomology to obtain a new classifying space

$$\begin{aligned} B'F : = (EF \times EG) / F. \end{aligned}$$

The projection of the product $(EF \times EG) \rightarrow EG$ yields a fibre bundle $(EF \times EG)/ F \rightarrow EG/ G$ with fibre EF / R.

Hence an associated sequence of continuous maps

$$\begin{aligned} BR = EF/R \rightarrow (EF \times EG)/ F = B'F \rightarrow EG/ G = BG, \end{aligned}$$

associated to the fibre bundle $B'F \rightarrow BG$ and with 1-dimensional fibre BR.

We obtain associated maps of first homology groups

$$\begin{aligned} H_1(BR, {\mathbb {Z}}) = R / [R,R] \rightarrow H_1(BF, {\mathbb {Z}}) = F / [F,F] \rightarrow H_1(BG, {\mathbb {Z}}) = G / [G,G], \end{aligned}$$

and since $BR, B'F$ have vanishing i-th homology groups for $i \ge 2$, application of the Serre spectral sequence for fibre bundles [336] shows that we have the exact sequence

$$\begin{aligned} 0 \rightarrow H_2(G, {\mathbb {Z}}) \rightarrow H_1(BR, {\mathbb {Z}})_F = (R / [R,R])_F \rightarrow F / [F,F] \rightarrow G / [G,G] \rightarrow 0. \end{aligned}$$

In the above exact sequence appears the group of co-invariants $(R / [R,R])_F$, which is the quotient of R / [R, R] by the relations of the form $frf^{-1} = r, \ \forall f \in F, \ r \in R$, or, equivalently, by the subgroup [F, R] generated by the commutators $frf^{-1} r^{-1}$. In other words,

$$\begin{aligned} (R / [R,R])_F = R / [F,R]. \end{aligned}$$

Now, from the exact sequences

$$\begin{aligned} (*) \ 0 \rightarrow H_2(G, {\mathbb {Z}}) \rightarrow R / [F,R] \rightarrow {\mathcal {K}}\rightarrow 0 \end{aligned}$$

and

$$\begin{aligned} 0 \rightarrow {\mathcal {K}}\rightarrow F / [F,F] \rightarrow G / [G,G] \rightarrow 0, \end{aligned}$$

since $\ker (F \rightarrow G / [G,G] ) = R [F,F]$, we infer that

$$\begin{aligned} {\mathcal {K}}= (R [F,F]) / [F,F] = R / ( R \cap [F,F]), \end{aligned}$$

where the last equality follows from the third isomorphism theorem for groups.

Since $[F,R] \subset ( R \cap [F,F])$, Hopf’s theorem follows from (*) above.

Proof II (direct argument): follows from the following lemma, since the kernel of $R / [F,R] \rightarrow F / [F,F]$ clearly equals $( R \cap [F,F]) / [F,R]$. $\square$

The relation between algebra and geometry in Hopf’s theorem is further explained in lemma 2.5 of [116].

Lemma 51

Let BG be a CW-complex which is a classifying space for the group $G = F / R$, such that

• (i) its 1-skeleton $BG^1$ has all the 1-cells in bijective correspondence with a set of generators of F,

• (ii) its 2-skeleton $BG^2$ has all the 2-cells in bijective correspondence with a set of generators of R (hence R / [R, R] is isomorphic to the relative homology group $H_2(BG^2, BG^1, {\mathbb {Z}})$).

Then the following exact sequence of relative homology

$$\begin{aligned} 0 \rightarrow H_2(BG, {\mathbb {Z}}) \rightarrow H_2(BG, BG^1, {\mathbb {Z}}) \rightarrow H_1(BG^1, {\mathbb {Z}}) \rightarrow H_1(BG, {\mathbb {Z}}) \rightarrow 0 \end{aligned}$$

is isomorphic to

$$\begin{aligned} 0 \rightarrow ( [F,F] \cap R) / [F,R] \rightarrow R / [F,R] \rightarrow F / [F,F] \rightarrow G / [G,G] \rightarrow 0. \end{aligned}$$

Proof

(Sketch) The main point is to show that the obvious surjection

$$\begin{aligned} H_2(BG^2, BG^1, {\mathbb {Z}}) \rightarrow H_2(BG, BG^1, {\mathbb {Z}}) \end{aligned}$$

reads out algebraically as the surjection $R / [R,R] \rightarrow R / [F,R]$.

In order to explain this, assume that $\{r_j | j \in J\}$ is a system of free generators of R. Now, $BG^3$ is obtained attaching 3-cells in order to kill the second homotopy group of $BG^2$ which, in turn, by Hurewicz’ theorem, is the second homology group of its universal cover $\tilde{BG^2}$. But it is then easy to see that generators for $H_2(\tilde{BG^2}, {\mathbb {Z}})$ are obtained applying the covering transformations of $G = F/R$ to the 2-cells corresponding to the elements $\{r_j | j \in J\}$. One can then show that the boundaries of these 3-cells yield relations on R / [R, R] which are exactly those of the form $[a,r_j]$, for $a \in F$. $\square$

Example 52

For a finite cyclic group $G = {\mathbb {Z}}/ m$, $F= {\mathbb {Z}}$, hence $[F,F] = 0$, $H_2 ( {\mathbb {Z}}/ m, {\mathbb {Z}}) =0$ and the result fits with previous calculations.

The spectral sequence argument is however more powerful, and yields a much more general result (see [372] and references therein).

Theorem 53

(Lyndon–Hochshild–Serre spectral sequence) Let H be any group, and R a normal subgroup, and let $G = H / R$ be the factor group.

Assume that A is an H-module, so that $A_H$ and $A^H$ are G-modules. Then there are converging first quadrant spectral sequences

$$\begin{aligned} E^2_{p,q}= & {} H_p (G ; H_q (R, A)) \Rightarrow H_{p+q}(H, A) \\ E_2^{p,q}= & {} H^p (G ; H^q (R, A)) \Rightarrow H^{p+q}(H, A) \end{aligned}$$

Example 54

Assume that the group H is a metacyclic group, i.e., we have an exact sequence

$$\begin{aligned} 1 \rightarrow R \cong {\mathbb {Z}}/n \rightarrow H \rightarrow G \cong {\mathbb {Z}}/m \rightarrow 1. \end{aligned}$$

As previously remarked, $H_2 ({\mathbb {Z}}/n, {\mathbb {Z}}) =0$, $H_1 ({\mathbb {Z}}/n, {\mathbb {Z}}) ={\mathbb {Z}}/n$, while $H_0 ({\mathbb {Z}}/n, {\mathbb {Z}})$ is the trivial ${\mathbb {Z}}/m$-module ${\mathbb {Z}}$. Hence the spectral sequence has many zeros, and reveals an exact sequence

$$\begin{aligned} {\mathbb {Z}}/m \rightarrow H_1 ( {\mathbb {Z}}/m, {\mathbb {Z}}/n) \rightarrow H_2 (H, {\mathbb {Z}}) \rightarrow 0. \end{aligned}$$

Let x be a generator of $R \cong {\mathbb {Z}}/n$, and y a generator of $G \cong {\mathbb {Z}}/m$, which we shall identify to one of its lifts to H (the order of y may be assumed to be equal to m if and only if the exact sequence splits, or, as one says H is split metacyclic).

Now, conjugation by y sends x to $x^a$, where $(a,n) = 1$, and we have also $a^m \equiv 1 \ ( mod \ n)$. Hence the $G= {\mathbb {Z}}/m$-structure of $R \cong {\mathbb {Z}}/n$, is described by $y (b) = ab \in {\mathbb {Z}}/n$.

Tensoring R with the bar-complex of G we find

$$\begin{aligned} \oplus _{g_1, g_2 \in G} ({\mathbb {Z}}/n (g_1, g_2)) \rightarrow \oplus _{g \in G} ({\mathbb {Z}}/n) g \rightarrow {\mathbb {Z}}/n \end{aligned}$$

where however the last homomorphism is no longer the zero map, and its image is just the image of multiplication by $(a-1)$, i.e.,

$$\begin{aligned} (a-1) ({\mathbb {Z}}/n) = (n, a-1) {\mathbb {Z}}/ n {\mathbb {Z}}. \end{aligned}$$

In fact ${\mathbb {Z}}/ n \cong {\mathbb {Z}}[G] \otimes _{ {\mathbb {Z}}[G] } {\mathbb {Z}}/n$, with $y^i \cdot 1 \equiv a^i \in {\mathbb {Z}}/n$. Therefore we obtain that $H_1 ( G, {\mathbb {Z}}/n)$ is the quotient of the kernel of multiplication by $(a-1)$, inside the direct sum $\oplus _{g \in G} ({\mathbb {Z}}/n) g$, by the subgroup generated by $g_1 g_2 \equiv g_1 + g_1(1) g_2$.

Writing the elements in G multiplicatively, $g_1 = y^i, g_2 = y^j$, we get the relations

$$\begin{aligned} y^{i+j} \equiv y^i + a^i y^j. \end{aligned}$$

For $i=0$ we get thus $y^0 = 0$, and then inductively we find the equivalent relations

$$\begin{aligned} y^i = ( 1 + \cdots + a^{i-1} )y, \quad \forall 1 \le i \le m-1, \ 0 = y^m = ( 1 + \cdots + a^{m-1} )y. \end{aligned}$$

Hence $H_1 ( G, {\mathbb {Z}}/n) \subset {\mathbb {Z}}/(n, r)$, where we set $r : = ( 1 + \dots + a^{m-1} ) = (a^m -1)/(a-1)$, is the kernel of multiplication by $(a-1)$, hence it is cyclic of order

$$\begin{aligned} d: = \frac{1}{n}(n,a-1)(n,r). \end{aligned}$$

The conclusion is that $H_2 (H, {\mathbb {Z}})$ is a cokernel of ${\mathbb {Z}}/m \rightarrow {\mathbb {Z}}/d$.

Edmonds shows in [146], with a smart trick, that the map ${\mathbb {Z}}/m \rightarrow {\mathbb {Z}}/d$ is the zero map when we have a split metacyclic extension, hence $H_2 (H, {\mathbb {Z}}) \cong {\mathbb {Z}}/d$ in this case. We shall show how to make the computation directly using Hopf’s theorem: this has the advantage of writing an explicit generator inside R / [F, R], a fact which shall be proven useful in the sequel.

6.8 Calculating $H_2(G, {\mathbb {Z}})$ via combinatorial group theory

We treat again the case of a split metacyclic group H.

$H = F /R$, where F is a free group on two generators x, y, and the subgroup R of relations is normally generated by

$$\begin{aligned} \xi : = x^n, \quad \eta : = y^m,\quad \zeta : = x^a y x^{-1} y^{-1}, \end{aligned}$$

with $(a,n)=1$, $a^m \equiv 1 ( \mathrm{mod}\ n)$.

Since R is the fundamental group of the Cayley graph of H, whose vertices corresponding to the elements of

$$\begin{aligned} H = \left\{ x^i y^j | 0 \le i \le n-1, 0 \le j \le m-1 \right\} , \end{aligned}$$

and R is a free group on $mn+1$ generators.

We use now the Reidemeister-Schreier algorithm (see [276]), which shows that a basis of R is given by:

and where $[b] \in \{ 0, \ldots , n-1\}$ is the unique positive representative of the residue class of b in ${\mathbb {Z}}/ n$.

We want to calculate $H_2(G, {\mathbb {Z}})$ as the kernel of $R / [F,R] \rightarrow {\mathcal {K}}\rightarrow 0$, keeping in mind that, since $F^{ab} = F / [F,F]$ is the free abelian group on generators X, Y, then ${\mathcal {K}}= ker ( F^{ab} \rightarrow G ^{ab} )$ is generated by the images of $\xi , \eta , \zeta$ in $F^{ab}$, i.e., n X, m Y, $(a-1) X$.

We conclude that ${\mathcal {K}}$ is a free abelian group with basis $(n, a-1) X, m Y,$ and contains the free abelian group with basis n X, m Y.

Our trick is then to observe that $\xi \mapsto nX, \ \eta = \eta _0 \mapsto mY$, hence $H_2(G, {\mathbb {Z}})$ is the kernel of the surjection

$$\begin{aligned} Q: = (R / [F,R])/ ({\mathbb {Z}}\xi + {\mathbb {Z}}\eta )) \rightarrow {\mathcal {K}}/ ( {\mathbb {Z}}(nX) \oplus {\mathbb {Z}}(mY)) = (n, a-1) {\mathbb {Z}}/ n {\mathbb {Z}}\rightarrow 0. \end{aligned}$$

This shall simplify our calculations considerably.

Observe that R / [F, R], since $[R,R] \subset [F,R]$, is a quotient of $R^{ab}$. $R^{ab}$ is a free abelian group on generators $\Xi , \Xi _{i,j}, \Theta _i$, which are the respective images of the elements $\xi , \xi _{i,j}, \eta _i$.

Thus R / [F, R], is the quotient of $R^{ab}$ by the relations of the form

$$\begin{aligned} r \sim f r f^{-1},\quad r \in R,\quad f \in F. \end{aligned}$$

Down to earth, each generator is put to be equivalent to its conjugate by x, respectively its conjugate by y.

Conjugation by x clearly sends $\eta _i$ to $\eta _{i+1}$, for all $i < n-1$, while $x \eta _{n-1} x^{-1} = x^n y^m x^{-n}= \xi \eta \xi ^{-1}$, thus in the abelianization we get $\Theta _i = \Theta , \forall i$, and in our further quotient Q the classes of the $\Theta _i$’s are all zero.

Conjugation of $\xi _{i,j}$ by x makes

$$\begin{aligned} \xi _{i,j} \sim x x^i y^j x y^{-j} x^ { - [i + a^j]} x^{-1} = x^{i+1} y^j x y^{-j} x^ { - 1- [i + a^j]} = \xi _{i+1,j} \quad \mathrm{or}\quad \xi _{i+1,j} \xi ^{-1}, \end{aligned}$$

hence the classes of $\Xi _{i,j}$ and of $\Xi _{i+1,j}$ are the same. Therefore the class of $\Xi _{i,j}$ is always equal to the one of $\Xi _{0,j}$.

Conjugation by $y^j$ of $\xi = x^n$ yields that the class of $y^j x^n y^{-j}$ is trivial. But, observing that the class of $x^n = \xi$ and all its conjugates is trivial, we can consider the exponents of powers of x as just residue classes modulo n, and avoid to use the square brackets. Then

$$\begin{aligned} y^j x^n y^{-j}= & {} (y^j x y^{-j})^n \sim (y^j x y^{-j} x^{- a^j} ) ( x^{a^j}y^j x y^{-j} x^{- 2 a^j} )\\&\cdots ( x^{(n-1)a^j}y^j x y^{-j} x^{- n a^j} ), \end{aligned}$$

which means that the class of $n \Xi _{0,j} = 0$. We denote by $Z_j$ the class of $\Xi _{0,j}$. Hence $n Z_j = 0$, and Q is generated by the classes $Z_j$.

In the calculation of conjugation by y on $\Xi _{0,j}$ we observe that

$$\begin{aligned} \xi _{i,j} \sim y y^j x y^{-j} x^ { - [ a^j]} y^{-1} = (y^{j+1} x y^{-j-1} x^ { - [a^{j+1}]}) x^ { [a^{j+1}]} y x^ { - [ a^j]} y^{-1}. \end{aligned}$$

Hence

$$\begin{aligned} Z_j \sim y Z_j y^{-1}= & {} Z_{j+1} x^ { a^{j+1}} y x^ { - a^j} y^{-1} \!=\! Z_{j+1} x^ { a^{j+1}} y x y ^{-1} x^ { - a^j -a} x^ { a^j +a} y x^ { - a^j - 1} y^{-1}\\= & {} Z_{j+1} Z_1^k x^ { a^{j+1}+ ka } y x^ { - a^j -k} y ^{-1}. \end{aligned}$$

For $k = - a^j$ we obtained the desired relation

$$\begin{aligned} Z_j = Z_{j+1} Z_1^{ - a^j} \Leftrightarrow Z_{j+1} = Z_j Z_1^{ a^j}, \end{aligned}$$

which can be written additively as

$$\begin{aligned} y^{i+1} \equiv y^i + a^i y. \end{aligned}$$

The conclusion is that we have a cyclic group whose order is $d: = \frac{1}{n}(n, a-1)(n,r)$ and with generator $\frac{n}{(n, a-1)} Z_1$, where $Z_1$ is the class of $\xi _{0,1} = y x y^{-1 } x ^{ - a}$.

6.9 Sheaves and cohomology on quotients, linearizations

The method of the bar-complex apparently settles the problem of calculating the cohomology groups of a K(G, 1) space, and also to calculate the cohomology groups $H^n (X, {\mathbb {Q}})$ for a rational K(G, 1) space X, except that one must have a good knowledge of the group G, for instance a finite presentation does not always suffice.

More generally, Grothendieck [199] approached the question of calculating the cohomology of a quotient $Y = X / G$ where X is not necessarily contractible. Using sheaf theory, one can reach a higher generality, considering G-linearized sheaves, i.e. sheaves ${\mathcal {F}}$ on X with a lifting of the action of G to ${\mathcal {F}}$ (this is the analogue to taking cohomology groups on non trivial G-modules).

Since this concept is very useful in algebraic geometry, and lies at the heart of some important calculations, we shall try now to briefly explain it, following Mumford’s treatment ([303], appendix to section 2, pp. 22–24, section 7, pp. 65–74, section 12, pp. 108–122).

The following is the basic example we have in mind, where we consider two formally different cases:

• (1) X is a projective variety, G is a finite group acting on X with the property that for each point x the orbit G x is contained in an affine open subset of X (this property holds if there is an ample divisor H whose linear equivalence class is fixed by G), or

• (2) X is a complex space, G acts properly discontinuously on X (in case where the quotient X / G is a projective variety, we can apply the G.A.G.A. principle by which there is an equivalence of categories between coherent algebraic sheaves and coherent holomorphic sheaves).

Assume that we have a vector bundle V on a quotient variety X / G. Denote by $p : X \rightarrow X/G$ the quotient map and take the fibre product $p^*(V) : = V \times _{X/G} X$. We consider the action of G on $V \times X$, which is trivial on the factor V, and the given one on X. In this way the action of G extends to the pull back $p^*(V) =V \times _{X/G} X$ of V, and the sections of V on X / G are exactly seen to be the G-invariant sections of $p^*(V)$.

Now, a main goal is to construct interesting varieties as quotient varieties X / G, and then study line bundles on them; the following result is quite useful for this purpose.

Proposition 55

Let $Y = X/G$ be a quotient algebraic variety, $p : X \rightarrow Y$ the quotient map.

• (1) Then there is a functor between (the category of) line bundles ${\mathcal {L}}'$ on Y and (the category of) G-linearized line bundles ${\mathcal {L}}$ on X, associating to ${\mathcal {L}}'$ its pull back $p^* ({\mathcal {L}}')$. The functor ${\mathcal {L}}\mapsto p_*({\mathcal {L}})^G$ is a right inverse to the previous one, and $p_*({\mathcal {L}})^G$ is invertible if the action is free, or if both X and Y are smooth.⁶

• (2) Given a line bundle ${\mathcal {L}}$ on X, it admits a G-linearization if and only if there is a Cartier divisor D on X which is G-invariant and such that ${\mathcal {L}}\cong {\mathcal {O}}_X(D)$ (observe that ${\mathcal {O}}_X(D)= \{ f \in {\mathbb {C}}(X) | div(f) + D \ge 0\}$ has an obvious G-linearization).

• (3) A necessary condition for the existence of a linearization is that

  $$\begin{aligned} \forall g \in G,\quad g^* ( {\mathcal {L}}) \cong {\mathcal {L}}. \end{aligned}$$

  If this condition holds, defining the Thetagroup of ${\mathcal {L}}$ as:

  $$\begin{aligned} \Theta ({\mathcal {L}}, G) : = \left\{ (\psi , g ) | g \in G,\quad \psi : g^* ( {\mathcal {L}}) \cong {\mathcal {L}}\ \mathrm{isomorphism} \right\} \!, \end{aligned}$$

  there is an exact sequence

  $$\begin{aligned} 1 \rightarrow {\mathbb {C}}^* \rightarrow \Theta ({\mathcal {L}}, G) \rightarrow G \rightarrow 1. \end{aligned}$$

The splittings of the above sequence correspond to the G-linearizations of ${\mathcal {L}}$.

If the sequence splits, the linearizations are a principal homogeneous space over the dual group ${{\mathrm{\text {Hom}}}}(G, {\mathbb {C}}^*) = : G^*$ of G (namely, each linearization is obtained from a fixed one by multiplying with an arbitrary element in $G^*$).

Proof

In (1), the case where G acts freely is trivial in the holomorphic context, and taken care of by proposition 2, p. 70 of [303] in the algebraic context.

For (2) and (3) we refer to [302], section 3, chapter 1, and [85], lemmas 4–6.

We only provide an argument for the last statement in (1), for which we do not know of a precise reference. The question is local, hence we may assume that P is a smooth point of X, and that G is equal to the stabilizer of P, hence it is a finite group. The invertible sheaf is locally isomorphic to ${\mathcal {O}}_X$, except that this isomorphism does not respect the linearization. The G-linearization of ${\mathcal {L}}$ corresponds then locally to a character $\chi : G \rightarrow {\mathbb {C}}^*$. In particular, there exists an integer m such that the induced linearization on ${\mathcal {L}}^{\otimes m}$ corresponds to the trivial character on ${\mathcal {O}}_X$.

Let R be the ramification divisor of the quotient map $p : X \rightarrow Y = X/G$, and let $X^0 : = X {\setminus } Sing(R)$, which is G-invariant. Set $Y^0 : = p (X^0 )$.

Step I: $p_*({\mathcal {L}})^G$ is invertible on $Y^0$.

This is clear on the open set which is the complement of the branch set p(R). At the points of R which are smooth points, then the G action can be linearized locally, and it is a pseudoreflection; so in this case the action of G involves only the last variable, hence the result follows from the dimension 1 case, where every torsion free module is locally free.

Step II. Let ${\mathcal {M}}: = p_*({\mathcal {L}})^G$. We claim that ${\mathcal {M}}$ is invertible at every point.

Pick a point y not in $Y^0$ and a local holomorphic Stein neighbourhood U of y, say biholomorphic to a ball. Then $U^0 : = U \cap Y^0$ has vanishing homology groups $H^i(U^0 , {\mathbb {Z}})$ for $i=1,2$. By the exponential sequence $H^1(U^0 , {\mathcal {O}}^*_Y) \cong H^1(U^0 , {\mathcal {O}}_Y)$, which is a vector space hence has no torsion elements except the trivial one. Since ${\mathcal {M}}^{\otimes m}$ is trivial on $U^0$, we conclude that ${\mathcal {M}}$ is trivial on $U^0$. By Hartogs’ theorem there is then an isomorphism between G-invariant sections of ${\mathcal {L}}$ on $p^{-1} (U)$ and sections of ${\mathcal {O}}_Y$ on U. $\square$

Thus, the question of the existence of a linearization is reduced to the algebraic question of the splitting of the central extension given by the Theta group. This question is addressed by group cohomology theory, as follows (see [223]).

Proposition 56

An exact sequence of groups

$$\begin{aligned} 1 \rightarrow M \rightarrow \Gamma \rightarrow G \rightarrow 1, \end{aligned}$$

where M is abelian, is called an extension. Conjugation by lifts of elements of G makes M a G-module. Each choice of a lift $e_{g} \in \Gamma$ for every element $g \in G$ determines a 2-cocycle

$$\begin{aligned} \psi (g_1,g_2) : = e_{g_1} e_{g_2} e_{g_1g_2}^{-1}. \end{aligned}$$

The cohomology class $[\psi ] \in H^2(G, M)$ is independent of the choice of lifts, and in this way $H^2(G, M)$ is in bijection with the set of strict isomorphism classes of extensions $1 \rightarrow M \rightarrow \Gamma ' \rightarrow G \rightarrow 1$ (i.e., one takes isomorphisms inducing the identity on M and G). Whereas isomorphism classes of extensions $1 \rightarrow M' \rightarrow \Gamma ' \rightarrow G \rightarrow 1$ (they should only induce the identity on G) are classified by isomorphism classes of pairs $(M', \psi ')$.

In particular, we have that the extension is a direct product $M \times G$ if and only if M is a trivial G-module (equivalenty, M is in the centre of $\Gamma$) and the class $[\psi ] \in H^2(G, M)$ is trivial.

Corollary 57

Let ${\mathcal {L}}$ be an invertible sheaf whose class in Pic(X) is G-invariant. Then the necessary and sufficient condition for the existence of a linearization is the triviality of the extension class $[\psi ] \in H^2(G, {\mathbb {C}}^*)$ of the Thetagroup $\Theta (G, {\mathcal {L}})$.

The group $H^2(G, {\mathbb {C}}^*)$ is the group of Schur multipliers (see again [223], p. 369) , which for a finite group is, as we saw in Theorem 49, another incarnation of the second homology group $H_2(G, {\mathbb {Z}})$. It occurs naturally when we have a projective representation of a group G. Since, from a homomorphism $G \rightarrow {\mathbb {P}}GL(r, {\mathbb {C}})$ one can pull back the central extension

$$\begin{aligned} 1 \rightarrow {\mathbb {C}}^* \rightarrow GL(r, {\mathbb {C}}) \rightarrow {\mathbb {P}}GL(r, {\mathbb {C}}) \rightarrow 1 \Rightarrow 1 \rightarrow {\mathbb {C}}^* \rightarrow \hat{G} \rightarrow G\rightarrow 1, \end{aligned}$$

and the extension class $[\psi ] \in H^2(G, {\mathbb {C}}^*)$ is the obstruction to lifting the projective representation to a linear representation $G \rightarrow GL(r, {\mathbb {C}})$.

It is an important remark that, if the group G is finite, and $n = ord (G)$, then the cocycles take value in the group of roots of unity $\mu _n : = \{ z \in {\mathbb {C}}^* | z^n = 1 \}$.

Example 58

Let E be an elliptic curve, with the point O as the origin,and let G be the group of 2-torsion points $G : = E[2]$ acting by translation on E. The divisor class of 2 O is never represented by a G-invariant divisor, since all the G-orbits consist of 4 points, and the degree of 2O is not divisible by 4. Hence, ${\mathcal {L}}: = {\mathcal {O}}_E (2O)$ does not admit a G-linearization. However, we have a projective representation on ${\mathbb {P}}^1 = {\mathbb {P}}(H^0( {\mathcal {O}}_E (2O))$, where each non zero element $\eta _1$ of the group fixes 2 divisors: the sum of the two points corresponding to $\pm \eta _1/2$, and its translate by another point $\eta _2 \in E[2]$.

The two group generators yield two linear transformations, which act on $V = {\mathbb {C}}x_0 \oplus {\mathbb {C}}x_1$ as follows:

$$\begin{aligned} \eta _1(x_0) = x_1,\quad \eta _1(x_1) = x_0,\quad \eta _2 (x_j) = (-1)^j x_j. \end{aligned}$$

The linear group generated is however $D_4$, since

$$\begin{aligned} \eta _1\eta _2 (x_0) = x_1,\quad \eta _1\eta _2 (x_1) = - x_0. \end{aligned}$$

Example 59

The previous example is indeed a special case of the Heisenberg extension, and V generalizes to the Stone von Neumann representation associated to an abelian group G, which is nothing else than the space $V : = L^2 (G, {\mathbb {C}})$ of square integrable functions on G (see [221, 303]).

G acts on $V = L^2 (G, {\mathbb {C}})$ by translation $f (x) \mapsto f (x - g)$, $G^*$ acts by multiplication with the given character $f (x) \mapsto f (x) \cdot \chi ( x))$, and the commutator $[g, \chi ]$ acts by the scalar multiplication with the constant $\chi (g)$.

The Heisenberg group is the group of automorphisms of V generated by $G, G^*$ and by ${\mathbb {C}}^*$ acting by scalar multiplication, and there is a central extension

$$\begin{aligned} 1 \rightarrow {\mathbb {C}}^* \rightarrow Heis(G) \rightarrow G \times G^* \rightarrow 1, \end{aligned}$$

whose class is classified by the ${\mathbb {C}}^*$-valued bilinear form $(g, \chi ) \mapsto \chi (g)$, an element of

$$\begin{aligned} \wedge ^2 ( Hom ( G \times G^*, {\mathbb {C}}^*)) \subset H^2 ( G \times G^*, {\mathbb {C}}^*). \end{aligned}$$

The relation with Abelian varieties $A = V / \Lambda$ is through the Thetagroup associated to an ample divisor L.

In fact, since by the theorem of Frobenius the alternating form $c_1(L) \in H^2(A, {\mathbb {Z}}) \cong \wedge ^2 ( Hom (\Lambda , {\mathbb {Z}}))$ admits, in a suitable basis for $\Lambda$, the normal form

$$\begin{aligned}&D: = \begin{pmatrix} 0 &{}\quad D' \\ - D' &{}\quad 0 \end{pmatrix}\\&D' : = {{\mathrm{\text {diag}}}}(d_1, d_2, \ldots , d_g), d_1| d_2 | \ldots | d_g. \end{aligned}$$

The key property is that, if one sets $G : = {\mathbb {Z}}^g/ D' {\mathbb {Z}}^g$, then L is invariant exactly for the translations in $( G \times G^*) \cong ( G \times G ) \subset A$, and the Thetagroup of L is just isomorphic to the Heisenberg group Heis(G).

The nice part of the story is the following useful result, which was used by Atiyah in the case of elliptic curves, to study vector bundles over these [12].

Proposition 60

Let G be a finite abelian group, and let $V : = L^2 (G, {\mathbb {C}})$ be the Stone-von Neumann representation. Then $V \otimes V^{\vee }$ is a representation of $( G \times G^*)$ and splits as the direct sum of all the characters of $( G \times G^*)$, taken with multiplicity one.

Proof

Since the centre ${\mathbb {C}}^*$ of the Heisenberg group Heis(G) acts trivially on $V \otimes V^{\vee }$, $V \otimes V^{\vee }$ is a representation of $( G \times G^*)$. Observe that $( G \times G^*)$ is equal to its group of characters, and its cardinality equals to the dimension of $V \otimes V^{\vee }$, hence it shall suffice, and it will be useful for applications, to write for each character an explicit eigenvector.

We shall use the notation g, h, k for elements of G, and the notation $\chi , \eta , \xi$ for elements in the dual group. Observe that V has two bases, one given by $\{ g \in G\}$, and the other given by the characters $\{ \chi \in G^* \}$. In fact, the Fourier transform yields an isomorphism of the vector spaces $V : = L^2 (G, {\mathbb {C}})$ and $W : = L^2 (G^*, {\mathbb {C}})$

$$\begin{aligned} {\mathcal {F}}(f) := \hat{f},\quad \hat{f}(\chi ) : = \int f(g) ( \chi , g) dg. \end{aligned}$$

The action of $h \in G$ on V sends $f(g) \mapsto f (g-h)$, hence for the characteristic functions in ${\mathbb {C}}[G]$, $g \mapsto g + h$. While $\eta \in G^*$ sends $f \mapsto f \cdot \eta$, hence $\chi \mapsto \chi + \eta$, where we use the additive notation also for the group of characters.

Restricting V to the finite Heisenberg group which is a central extension of $G \times G^*$ by $\mu _n$, we get a unitary representation, hence we identify $V^{\vee }$ with $\bar{V}$. This said, a basis of $V \otimes \bar{V}$ is given by the set $\{ g \otimes \bar{\chi }\}$.

Given a vector $\sum _{g, \chi } a_{g, \chi } (g \otimes \bar{\chi } )$the action by $h \in G$ sends it to

$$\begin{aligned} \sum _{g, \chi } (\chi , h) a_{g -h, \chi } (g \otimes \bar{\chi } ), \end{aligned}$$

while the one by $\eta \in G^*$ sends it to

$$\begin{aligned} \sum _{g, \chi } (\eta , g) a_{g, \chi - \eta } (g \otimes \bar{\chi } ). \end{aligned}$$

Hence one verifies right away that

$$\begin{aligned} F_{k, \xi } : = \sum _{g, \chi } ( \chi - \xi , g - k) (g \otimes \bar{\chi } ) \end{aligned}$$

is an eigenvector with eigenvalue $(\xi , h) (\eta , k)$ for $(h, \eta ) \in ( G \times G^*)$. $\square$

Remark 61

The explicit calculation reproduced above is based on the fact that the Fourier transform does not commute with the action of the Heisenberg group: the action of G on V corresponds to the action of $G = (G^*)^*$ on W, while the action of $G^*$ on W corresponds to the multiplication of functions $f(g) \in V$ with the conjugate $\bar{\chi }$ of the character $\chi$.

In the next subsection we shall give an explicit example where the Heisenberg group is used for a geometrical construction. Now let us return to the general discussion of cohomology of G-linearized sheaves.

In the special case where the action is free there is an isomorphism between the category of G-linearized sheaves ${\mathcal {F}}$ on X, and sheaves ${\mathcal {F}}^G$ on the quotient Y; we have then

Theorem 62

(Grothendieck [199]) Let $Y = X / G$, where G acts freely on X, and let ${\mathcal {F}}$ be a G-linearized sheaf on X, let ${\mathcal {F}}^G$ be the G-invariant direct image on Y.

Then there is a spectral sequence converging to a suitable graded quotient of $H^{p+q}(Y, {\mathcal {F}}^G)$ and with $E_1$ term equal to $H^p (G, H^q(X, {\mathcal {F}}))$; we write then as a shorthand notation:

$$\begin{aligned} H^p (G, H^q(X, {\mathcal {F}})) \Rightarrow H^{p+q}(Y, {\mathcal {F}}^G). \end{aligned}$$

The underlying idea is simple, once one knows (see [79, 214]) that there is a spectral sequence for the derived functors of a composition of two functors: in fact one takes here the functor ${\mathcal {F}}\mapsto H^0(X, {\mathcal {F}})^G$, which is manifestly the composition of two functors ${\mathcal {F}}\mapsto H^0(X, {\mathcal {F}})$ and $A \mapsto A^G$, but also the composition of two other functors, since $H^0(X, {\mathcal {F}})^G = H^0(Y, {\mathcal {F}}^G)$.

The main trouble is that the functor ${\mathcal {F}}\mapsto {\mathcal {F}}^G$ is no longer exact if we drop the hypothesis that the action is free.

A particular case is of course the one where ${\mathcal {F}}$ is the constant sheaf ${\mathbb {Z}}$: in the case where the action is not free one has in the calculation to keep track of stabilizers $G_x$ of points $x \in X$, or, even better, to keep track of fixed loci of subgroups $H \subset G$.

Since this bookkeeping is in some situations too difficult or sometimes also of not so much use, Borel [56] proposed (in a way which is similar in spirit to the one of Grothendieck) to consider a generalization of the cohomology of the quotient (see [173] for a nice account of the theory and its applications in algebraic geometry).

Definition 63

Let G be a Lie group acting on a space X, and let $BG = EG / G$ be a classifying space for G. Here we do not need to specify whether G acts on the left or on the right, since for each left action $(g,x) \mapsto gx$ there is the mirror action $xg : = g^{-1} x$.

Letting R be an arbitrary ring of coefficients, the equivariant cohomology of X with respect to the action of G is defined in one of the following equivalent ways.

• (1) Assume that G acts on both spaces X and EG from the left: then we have the diagonal action $g (e,x) : = (ge, gx)$ and

  $$\begin{aligned} H^i_G(X, R): = H^i ((EG \times X)/ G, R). \end{aligned}$$

• (2) (as in [173]) Assume without loss of generality that G acts on X from the left, and on EG from the right: then

  $$\begin{aligned} H^i_G(X, R): = H^i (EG \times ^G X, R), \end{aligned}$$

where the space $EG \times ^G X$ is defined to be the quotient of the Cartesian product $EG \times X$ by the relation

$$\begin{aligned} (e \cdot g, x) \sim ( e, g \cdot x). \end{aligned}$$

Remark 64

Observe that, in the special case where X is a point, and G is discrete, we reobtain the cohomology group $H^i (G , R)$.

Example 65

The consideration of arbitrary Lie groups is rather natural, for instance if $G = {\mathbb {C}}^*$, then $BG = {\mathbb {P}}^{\infty }_{{\mathbb {C}}} = ( {\mathbb {C}}^{\infty } {\setminus } \{0\} )/ {\mathbb {C}}^{*}$.

Similarly the infinite Grassmannian ${\mathcal {G}}r (n, {\mathbb {C}}^{\infty } )$ is a classifying space for ${{\mathrm{\text {GL}}}}(n, {\mathbb {C}})$, it is a quotient (cf. [291]) of the Stiefel manifold of frames

$$\begin{aligned} {\mathcal {S}}t (n, {\mathbb {C}}^{\infty } ) : = \{ (v_1, \ldots , v_n ) | v_i \in {\mathbb {C}}^{\infty }, {{\mathrm{\text {rank}}}}\langle v_1, \ldots , v_n \rangle = n\}. \end{aligned}$$

Clearly the universal vector subbundle on the Grassmannian is obtained as the invariant direct image of a ${{\mathrm{\text {GL}}}}(n, {\mathbb {C}})$- linearised vector bundle on the Stiefel manifold.

The names change a little bit: instead of a linearized vector bundle one talks here of G-equivariant vector bundles, and there is a theory of equivariant characteristic classes, i.e., these classes are equivariant for morphisms of G-spaces (spaces with a G-action).

Rather than dwelling more on abstract definitions and general properties, I prefer at this stage to mention the most important issues of G-linearized bundles for geometric rational $K (\pi , 1)$’s.

6.10 Hodge bundles of weight = 1

(1) Hodge bundle for families of Abelian varieties

Consider the family of Abelian Varieties of dimension g, and with a polarization of type $D' \sim (d_1, d_2, \ldots , d_g)$ over Siegel’s upper half space

$$\begin{aligned} {\mathcal {H}}_g : = \left\{ \tau \in {{\mathrm{\text {Mat}}}}(g,g,{\mathbb {C}})| \tau = ^t \tau , {{\mathrm{\text {Im}}}}(\tau ) > 0 \right\} \!. \end{aligned}$$

The family is given by the quotient of the trivial bundle $H : = {\mathcal {H}}_g \times {\mathbb {C}}^g$ by the action of $\lambda \in {\mathbb {Z}}^{2g}$ acting by

$$\begin{aligned} (\tau , z) \mapsto ( \tau , z + (D', - \tau ) \lambda ). \end{aligned}$$

The local system corresponding to the first cohomology groups of the fibres is the ${{\mathrm{\text {Sp}}}}(D, {\mathbb {Z}})$-linearized local system (bundle with fibre ${\mathbb {Z}}^{2g}$) on $H_{{\mathbb {Z}}} : = {\mathcal {H}}_g \times {\mathbb {Z}}^{2g}$, with the obvious action of ${{\mathrm{\text {Sp}}}}(D, {\mathbb {Z}})$

$$\begin{aligned}&M \in {{\mathrm{\text {Sp}}}}(D, {\mathbb {Z}}) , \quad M ( \tau , \lambda ) = ( M (\tau ) , M \lambda ),\\&M:= \begin{pmatrix} \alpha &{}\quad \beta \\ \gamma &{}\quad \delta \end{pmatrix} , \ \quad M ( \tau ) = - D' (D' \alpha - \tau \gamma )^{-1} ( D' \beta - \tau \delta ). \end{aligned}$$

Obviously $H_{{\mathbb {Z}}} \otimes _{{\mathbb {Z}}} {\mathbb {C}}$ splits as $H^{1,0} \oplus H^{0,1}$ and the above vector bundle H equals $H^{1,0}$ and is called the Hodge bundle.

Stacks are nowadays the language in order to be able to treat the above local system and the Hodge bundle as living over the quotient moduli space ${\mathcal {A}}_{g,D'} : = {\mathcal {H}}_g / {{\mathrm{\text {Sp}}}}(D, {\mathbb {Z}})$.

(2) Hodge Bundle for families of curves

Over Teichmüller space we have a universal family of curves, which we shall denote by $p_g : {\mathcal {C}}_g \rightarrow {\mathcal {T}}_g$.

The reason is the following: letting M be here a compact oriented Riemann surface of genus g, and ${\mathcal {C}}(M)$ the space of complex structures on M, it is clear that there is a universal tautological family of complex structures parametrized by ${\mathcal {C}}(M)$, and with total space

$$\begin{aligned} {\mathfrak {U}}_{ {\mathcal {C}}(M)} : = M \times {\mathcal {C}}(M), \end{aligned}$$

on which the group ${\mathcal {D}}iff ^+ (M)$ naturally acts, in particular ${\mathcal {D}}iff ^0(M)$.

A rather simple consequence of the Lefschetz’ Lemma 34 is that ${\mathcal {D}}iff ^0(M)$ acts freely on ${\mathcal {C}}(M)$: in fact Lefschetz’ Lemma 34 implies that for each complex structure C on M the group of biholomorphisms Aut(C) contains no automorphism (other than the identity) which is homotopic to the identity, hence a fortiori no one that is differentiably isotopic to the identity.

We have the local system $H_{{\mathbb {Z}}} : = {\mathcal {R}}^1 (p_g)_* ({\mathbb {Z}})$, and again

$$\begin{aligned} H_{{\mathbb {Z}}} \otimes _{{\mathbb {Z}}} {\mathbb {C}}= H^{1,0} \oplus H^{0,1}, \ \quad H^{1,0} : = (p_g)_* \left( \Omega ^1_{ {\mathcal {C}}_g |T_g}\right) \!. \end{aligned}$$

$H : = H^{1,0}$ is called the Hodge bundle, and it is indeed the pull back of the Hodge bundle on ${\mathcal {A}}_g$ by the Torelli map, or period map, which associates to a complex structure C the Jacobian variety ${{\mathrm{\text {Jac}}}}(C) : = H^{1,0}(C) ^{\vee } / H_1 (M, {\mathbb {Z}})$.

The i-th Chern class of the Hodge bundle yield some cohomology classes which Mumford [304, 307] denoted as the $\lambda _i$-class (while the notation $\lambda$-class is reserved for $\lambda _1$).

Other classes, which play a crucial role in Mumford’s conjecture ([307], see also theorem 233), are the classes ${\mathcal {K}}_i$, defined as

$$\begin{aligned} {\mathcal {K}}_i : = (p_g)_* (K^{i+1}), \quad \ K : = c_1 \left( \Omega ^1_{ {\mathcal {C}}_g |{\mathcal {T}}_g}\right) . \end{aligned}$$

6.11 A surface in a Bagnera–De Franchis threefold

We want to describe here a construction given in joint work with Ingrid Bauer and Frapporti [37] of a surface S with an ample canonical divisor $K_S$, and with $K_S^2 = 6$, $p_g : = h^0({\mathcal {O}}_S(K_S)) = 1, \ q : = h^0(\Omega ^1_S)=1$.

Let $A_1$ be an elliptic curve, and let $A_2$ be an Abelian surface with a line bundle $L_2$ yielding a polarization of type (1, 2) (i.e., the elementary divisors for the Chern class of $L_2$ are $d_1 = 1, d_2 = 2$). Take as $L_1$ the line bundle ${\mathcal {O}}_{A_1} ( 2 O)$, and let L be the line bundle on $A' : = A_1 \times A_2$ obtained as the exterior tensor product of $L_1$ and $L_2$, so that

$$\begin{aligned} H^0 (A', L) = H^0 (A_1, L_1) \otimes H^0 (A_2, L_2). \end{aligned}$$

Moreover, we choose the origin in $A_2$ so that the space of sections $H^0 (A_2, L_2)$ consists only of even sections (hence, we shall no longer be free to further change the origin by an arbitrary translation).

We want to take a Bagnera–De Franchis threefold $X: = A/ G$, where $A = (A_1 \times A_2) / T$, and $G \cong T \cong {\mathbb {Z}}/2$, and have a surface $S \subset X$ which is the quotient of a $G\times T$ invariant $D \in |L|$, so that $S^2 = \frac{1}{4} D^2 = 6$.

We write as usual $A_1 = {\mathbb {C}}/ {\mathbb {Z}}\oplus {\mathbb {Z}}\tau$, and we let $A_2 = {\mathbb {C}}^2 / \Lambda _2$, with $\lambda _1,\lambda _2, \lambda _3, \lambda _4$ a basis of $\Lambda _2$ on which the Chern class of $L_2$ is in Frobenius normal form. We let then

$$\begin{aligned}&G := \{ Id, g \}, \quad \ g (a_1 + a_2 ) : = a_1 + \tau /2 - a_2 + \lambda _2 / 2,\quad \forall a_1 \in A_1,\quad a_2 \in A_2\nonumber \\ \end{aligned}$$

(66)

$$\begin{aligned}&T := ( {\mathbb {Z}}/2 ) ( 1/2 + \lambda _4 / 2) \subset A = (A_1 \times A_2). \end{aligned}$$

(67)

Now, $G \times T$ surjects onto the group of two torsion points $A_1[2]$ of the elliptic curve (by the homomorphism associating to an affine transformation its translation vector) and also on the subgroup $( {\mathbb {Z}}/2 ) ( \lambda _2 / 2) \oplus ( {\mathbb {Z}}/2 ) ( \lambda _4 / 2) \subset A_1[2]$, and both $H^0 (A_1, L_1)$ and $H^0 (A_2, L_2)$ are the Stone–von Neumann representation of the Heisenberg group which is a central ${\mathbb {Z}}/2$ extension of $G \times T$.

By Proposition 60, since in this case (recall the notation $A = V / \Lambda$), we have $V \cong \bar{V}$ (the only roots of unity occurring are just $\pm 1$), we conclude that there are exactly 4 divisors in |L|, invariant by $a_1 + a_2 \mapsto a_1 - a_2$, and by $a_1 + a_2 \mapsto a_1 + \tau /2 + a_2 + \lambda _2 / 2$, and $a_1 + a_2 \mapsto a_1 + 1 /2 + a_2 + \lambda _4 / 2$.

Hence these four divisors descend to give four surfaces $S \subset X$.

This construction is used in [37] to prove the following.

Theorem 68

Let S be a surface of general type with invariants $K_S^2 = 6$, $p_g =q = 1$ such that there exists an unramified double cover $\hat{S} \rightarrow S$ with $q ( \hat{S} ) = 3$, and such that the Albanese morphism $\hat{\alpha } : \hat{S} \rightarrow A$ is birational onto it image Z, a divisor in A with $Z^3 = 12$.

Then the canonical model of $\hat{S}$ is isomorphic to Z, and the canonical model of S is isomorphic to $Y = Z / ({\mathbb {Z}}/2)$, which a divisor in a Bagnera–De Franchis threefold $X: = A/ G$, where $A = (A_1 \times A_2) / T$, $G \cong T \cong {\mathbb {Z}}/2$, and where the action is as in (66, 67).

These surfaces exist, have an irreducible four dimensional moduli space, and their Albanese map $\alpha : S \rightarrow A_1 = A_1/ A_1[2]$ has general fibre a non hyperelliptic curve of genus $g=3$.

Proof

By assumption the Albanese map $\hat{\alpha } : \hat{S} \rightarrow A$ is birational onto Z, and we have $K_{ \hat{S}}^2 = 12 = K_Z^2$, since by adjunction ${\mathcal {O}}_Z(Z)$ is the dualizing sheaf of Z (so Z restricts to the canonical divisor $K_Z$ of Z).

We argue similarly to [35], Step 4 of theorem 0.5, p. 31. Denote by W the canonical model of $\hat{S}$, and observe that by adjunction (see loc. cit.) we have $K_W = \hat{\alpha }^* (K_Z ) - {\mathfrak {U}}$, where ${\mathfrak {U}}$ is an effective ${\mathbb {Q}}$-Cartier divisor.

We observe now that $K_Z$ is ample (by adjunction, since Z is ample) and $K_W$ is also ample, hence we have an inequality,

$$\begin{aligned} 12 = K_W^2 = (\hat{\alpha }^* (K_Z ) - {\mathfrak {U}})^2 = K_Z^2 - (\hat{\alpha }^* (K_Z ) \cdot {\mathfrak {U}}) - (K_W \cdot {\mathfrak {U}}) \ge K_Z^2 = 12, \end{aligned}$$

and since both terms are equal to 12, we conclude that ${\mathfrak {U}}= 0$, which means that $K_Z$ pulls back to $K_W$ hence W is isomorphic to Z. We have a covering involution $\iota : \hat{S} \rightarrow \hat{S}$, such that $S = \hat{S} / \iota$. Since the action of ${\mathbb {Z}}/2$ is free on $\hat{S}$, ${\mathbb {Z}}/2$ also acts freely on Z.

Since $Z^3 = 12$, Z is a divisor of type (1, 1, 2) in A. The covering involution $\iota : \hat{S} \rightarrow \hat{S}$ can be lifted to an involution g of A, which we write as an affine transformation $g (a) = \alpha a + \beta$.

We have Abelian subvarieties $A_1 = \ker (\alpha - Id)$, $A_2 = \ker (\alpha + Id)$, and since the irregularity of S equals 1, $A_1$ has dimension 1, and $A_2$ has dimension 2.

We observe preliminarly that g is fixed point free: since otherwise the fixed point locus would be non empty of dimension one, so it would intersect the ample divisor Z, contradicting that $\iota : Z \rightarrow Z$ acts freely.

Therefore $Y = Z / \iota$ is a divisor in the Bagnera–De Franchis threefold $X = A / G$, where G is the group of order two generated by g.

We can then write (using the notation introduced in Proposition 16) the Abelian threefold A as $A' / T$, and since $\beta _1 \notin T_1$ we have only two possible cases.

• Case (0) : $T = 0$.

• Case (1) : $T \cong {\mathbb {Z}}/2$.

We further observe that since the divisor Z is g-invariant, its polarization is $\alpha$ invariant, in particular its Chern class $c \in \wedge ^2 ( {{\mathrm{\text {Hom}}}}(\Lambda , {\mathbb {Z}}))$, where $A = V / \Lambda$.

Since $T = \Lambda / ( \Lambda _1 \oplus \Lambda _2)$, c pulls back to

$$\begin{aligned} c' \in \wedge ^2 ( {{\mathrm{\text {Hom}}}}( \Lambda _1 \oplus \Lambda _2, {\mathbb {Z}})) = \wedge ^2 ( \Lambda _1^{\vee }) \oplus \wedge ^2 ( \Lambda _2^{\vee }) \oplus (\Lambda _1^{\vee })\otimes (\Lambda _2^{\vee }), \end{aligned}$$

and by invariance $c' = (c'_1 \oplus c'_2 ) \in \wedge ^2 ( \Lambda _1^{\vee }) \oplus \wedge ^2 ( \Lambda _2^{\vee })$.

So Case 0) bifurcates in the cases:

• Case (0-I) $c'_1$ is of type (1), $c'_2$ is of type (1, 2).

• Case (0-II) $c'_1$ is of type (2), $c'_2$ is of type (1, 1).

Both cases can be discarded, since they lead to the same contradiction. Set $D: = Z$: then D is the divisor of zeros on $A = A_1 \times A_2$ of a section of a line bundle L which is an exterior tensor product of $L_1$ and $L_2$. Since

$$\begin{aligned} H^0 (A, L) = H^0 (A_1, L_1) \otimes H^0 (A_2, L_2), \end{aligned}$$

and $H^0 (A_1, L_1)$ has dimension one in case (0-I), while $H^0 (A_2, L_2)$ has dimension one in case (0-II), we conclude that D is a reducible divisor, a contradiction, since D is smooth and connected.

In case (1), we denote $A' : = A_1 \times A_2$, and we let D be the inverse image of Z inside $A'$. Again D is smooth and connected, since $\pi _1(\hat{S})$ surjects onto $\Lambda$. Now $D^2 = 24$, so the Pfaffian of $c'$ equals 4, and there are a priori several possibilities.

• Case (1-I) $c'_1$ is of type (1).

• Case (1-II) $c'_2$ is of type (1, 1).

• Case (1-III) $c'_1$ is of type (2), $c'_2$ is of type (1, 2).

• Cases (1-I) and (1-II) can be excluded as case (0), since then D would be reducible.

We are then left only with case (1-III), and we may, without loss of generality, assume that $H^0 (A_1, L_1)= H^0 (A_1, {\mathcal {O}}_{A_1} (2 O))$, and assume that we have chosen the origin so that all the sections of $H^0 (A_2, L_2)$ are even.

We have $A = A' / T$, and we may write the generator of T as $t_1 \oplus t_2$, and write $g (a_1 + a_2 ) = (a_1 + \beta _1) + ( a_2 - \beta _2)$.

By the description of Bagnera–De Franchis varieties given in Sect. 5.1 we have that $t_1$ and $\beta _1$ are a basis of the group of 2 torsion points of the elliptic curve $A_1$.

Now our divisor D, since all sections of $L_2$ are even, is $G \times T$ invariant if and only if it is invariant by T and by translation by $\beta$.

This condition however implies that translation by $\beta _2$ of $L_2$ is isomorphic to $L_2$, and similarly for $t_2$. It follows that $\beta _2, t_2$ are basis of the kernel $K_2$ of the map $\phi _{L_2}: A_2 \rightarrow Pic^0 (A_2)$, associating to y the tensor product of the translation of $L_2$ by y with the inverse of $L_1$.

The isomorphism of $G \times T$ with both $K_1 : = A_1 [2]$ and $K_2$ allows to identify both $H^0 (A_1, L_1)$ and $H^0 (A_2, L_2)$ with the Stone von Neumann representation $L^2 ( T)$: observe in fact that there is only one alternating function $(G \times T) \rightarrow {\mathbb {Z}}/2$, independent of the chosen basis.

Therefore, there are exactly 4 invariant divisors in the linear system |L|.

Explicitly, if $H^0 (A_1, L_1)$ has basis $x_0, x_1$ and $H^0 (A_2, L_2)$ has basis $y_0, y_1$, then the invariant divisors correspond to the four eigenvectors

$$\begin{aligned} x_0 y_0 + x_1 y_1,\quad x_0 y_0 - x_1 y_1,\quad x_0 y_1 + x_1 y_0,\quad x_0 y_1 - x_1 y_0. \end{aligned}$$

To prove irreducibility of the above family of surfaces, it suffices to show that all the four invariant divisors occur in the same connected family.

To this purpose, we just observe that the monodromy of the family of elliptic curves $E_{\tau } : = {\mathbb {C}}/ ( {\mathbb {Z}}\oplus {\mathbb {Z}}\tau )$ on the upperhalf plane has the effect that a transformation in $SL ( 2 , {\mathbb {Z}})$ acts on the subgroup $E_{\tau } [2]$ of points of 2-torsion by its image matrix in $GL ( 2 , {\mathbb {Z}}/2)$, and in turn the effect on the Stone von Neumann representation is the one of twisting it by a character of $E_{\tau } [2]$.

This concludes the proof that the moduli space is irreducible of dimension 4, since the moduli space of elliptic curves, respectively the moduli space of Abelian surfaces with a polarization of type (1, 2), are irreducible, of respective dimensions 1, 3. The final assertion is a consequence of the fact that $Alb(S) = A_1 / (T_1 + \langle \langle \beta _1 \rangle \rangle )$, so that the fibres of the Albanese map are just divisors in $A_2$ of type (1, 2). Their self intersection equals $4 = 2 (g-1)$, hence $g=3$.

In order to establish that the general fibre of the Albanese map is non hyperelliptic, it suffices to prove the following lemma.

Lemma 69

Let $A_2$ be an Abelian surface, endowed with a divisor L of type (1, 2), so that there is an isogeny of degree two $f : A_2 \rightarrow A'$ onto a principally polarised Abelian surface, with kernel generated by a point t of 2-torsion, and such that $L = f^*(\Theta )$. Then the only curves $C \in |L|$ that are hyperelliptic are contained in the pull backs of a translate of $\Theta$ by a point of order 2 for a suitable such isogeny $f : A_2 \rightarrow A'$. In particular, the general curve $C \in |L|$ is not hyperelliptic.

Proof

Let $C \in |L|$, and consider $D : = f_* (C) \in | 2 \Theta |$. There are two cases.

Case (I): $C + t = C$. Then $D = 2 B$, where B has genus 2, so that $C = f^* (B)$, hence, since $2B \equiv 2 \Theta$, B is a translate of $\Theta$ by a point of order 2. There are exactly two such curves, and for them $C \rightarrow B$ is étale.

Case (II): $C + t \ne C$. Then $C \rightarrow D$ is birational, $f^* (D) = C \cup (C + t)$. Now, $C+t$ is also linearly equivalent to L, hence $C \cap (C+t)$ meet in the 4 base points of the pencil |L|. Hence D has two double points and geometric genus equal to 3. These double points are the intersection points of $\Theta$ and a translate by a point of order 2, and are points of 2-torsion.

The sections of $H^0({\mathcal {O}}_{A'} (2 \Theta ))$ are all even and $| 2 \Theta |$ is the pull-back of the space of hyperplane sections of the Kummer surface ${\mathcal {K}}\subset {\mathbb {P}}^3$, the quotient ${\mathcal {K}}= A' / \{\pm 1\}$.

Therefore the image $E'$ of each such curve D lies in the pencil of planes through 2 nodes of ${\mathcal {K}}$.

$E'$ is a plane quartic, hence $E'$ has geometric genus 1, and we conclude that C admits an involution $\sigma$ with quotient an elliptic curve E (normalization of $E'$), and the double cover is branched in 4 points.

Assume that C is hyperelliptic, and denote by h the hyperelliptic involution, which lies in the centre of Aut(C). Hence we have $({\mathbb {Z}}/2)^2$ acting on C, with quotient ${\mathbb {P}}^1$. We easily see that there are exactly six branch points, two being the branch points of $C/h \rightarrow {\mathbb {P}}^1$, four being the branch points of $E \rightarrow {\mathbb {P}}^1$. It follows that there is an étale quotient $C \rightarrow B$ , where B is the genus 2 curve, double cover of ${\mathbb {P}}^1$ branched on the six points.

Now, the inclusion $C \subset A_2$ and the degree 2 map $C \rightarrow B$ induces a degree two isogeny $A_2 \rightarrow J(B)$, and C is the pull back of the Theta divisor of J(B), thus it cannot be a general curve.

                              QED for the lemma. $\square$

Definition 70

Let us call a surface S as in Theorem 68 a Sicilian surface with $q=p_g=1$.

Observe that the fundamental group of S is isomorphic to the fundamental group $\Gamma$ of X, and that $\Gamma$, fitting into the exact sequence

$$\begin{aligned} 1 \rightarrow \Lambda \rightarrow \Gamma \rightarrow G = {\mathbb {Z}}/2 \rightarrow 1, \end{aligned}$$

is generated by the union of the set $\{ g , t\},$ where

$$\begin{aligned} g ( v_1 + v_2 )= & {} v_1 + \tau / 2 - v_2 + \lambda _2 / 2 \\ t ( v_1 + v_2 )= & {} v_1 + 1 / 2 + v_2 + \lambda _4 / 2 \end{aligned}$$

with the set of translations by the elements of a basis $\lambda _1, \lambda _2, \lambda _3, \lambda _4$ of $\Lambda _2$.

It is therefore a semidirect product of ${\mathbb {Z}}^5 = \Lambda _2 \oplus {\mathbb {Z}}t$ with the infinite cyclic group generated by g: conjugation by g acts as $-1$ on $\Lambda _2$, and it sends $t \mapsto t - \lambda _4$ (hence $2 t - \lambda _4$ is an eigenvector for the eigenvalue 1).

We shall now give a topological characterization of Sicilian surfaces with $q=p_g=1$, following the lines of [222].

Observe in this respect that X is a $K(\Gamma , 1)$ space, so that its cohomology and homology are just group cohomology, respectively homology, of the group $\Gamma$.

Corollary 71

A Sicilian surface S with $q=p_g=1$ is characterized by the following properties:

• (1) $K_S^2 = 6$

• (2) $\chi (S) = 1$

• (3) $\pi _1(S) \cong \Gamma$, where $\Gamma$ is as above,

• (4) the classifying map $f : S \rightarrow X$, where X is the Bagnera–De Franchis threefold which is a classifying space for $\Gamma$, has the property that $f_* [S] : = Y$ satisfies $Y^3=6$.

In particular, any surface homotopically equivalent to a Sicilian surface is a Sicilian surface, and we get a connected component of the moduli space of surfaces of general type which is stable under the action of the absolute Galois group.⁷

Proof

Since $\pi _1(S) \cong \Gamma$, first of all $q(S) =1$, hence also $p_g(S) = 1$. By the same token there is a double étale cover $\hat{S} \rightarrow S$ such that $q(\hat{S} ) = 3$, and the Albanese image of $\hat{S}$, counted with multiplicity, is the inverse image Z of Y, therefore $Z^3 = 12$. From this, it follows that $\hat{S} \rightarrow Z$ is birational, since the class of Z is indivisible.

We may now apply the previous theorem in order to obtain the classification.

Observe finally that the condition $(\hat{\alpha }_* \hat{S})^3 = 12$ is not only a topological condition, it is also invariant under Galois autorphisms. $\square$

7 Regularity of classifying maps and fundamental groups of projective varieties

7.1 Harmonic maps

Given a continuous map $f : M \rightarrow N$ of differentiable manifolds, we can approximate it, as already partly explained, by a differentiable one, homotopic to the previous one. Indeed, as we already explained, we may assume that $N \subset {\mathbb {R}}^n, M \subset {\mathbb {R}}^m$ and, by a partition of unity argument, that M is an open set in ${\mathbb {R}}^h$. Convolution approximates then f by a differentiable function $F_1$ with values in a tubular neighbourhood T (N) of N, and then the implicit function theorem applied to the normal bundle provides a differentiable retraction $r : T(N) \rightarrow N$. Then $F : = r \circ F_1$ is the required approximation, and the same retraction provides a homotopy between f and F (the homotopy between f and $F_1$ being obvious).

If however M, N are algebraic varieties, and algebraic topology tells us about the existence of a continuous map f as above, we would wish for more regularity, possibly holomorphicity of the homotopic map F.

Now, Wirtinger’s theorem (see [306]) characterises complex submanifolds as area minimizing ones, so the first idea is to try to deform a differentiable mapping f until it minimizes some functional.

We may take the Riemannian structure inherited form the chosen embedding, and assume that $(M, g_M), (N, g_N)$ are Riemannian manifolds.

If we assume that M is compact, then one defines the Energy ${\mathcal {E}}(f)$ of the map as the integral:

$$\begin{aligned} {\mathcal {E}}(f) : = 1/2 \int _M |Df|^2 d\mu _M, \end{aligned}$$

where Df is the derivative of the differentiable map f, $d \mu _M$ is the volume element on M, and |Df| is just its norm as a differentiable section of a bundle endowed with a metric:

$$\begin{aligned} Df \in H^0 (M, {\mathcal {C}}^{\infty }(TM^{\vee } \otimes f^* (TN))). \end{aligned}$$

Remark 72

• (1) in more concrete terms, the integral in local coordinates has the form

  $$\begin{aligned} {\mathcal {E}}(f) : = 1/2 \int _M \Sigma _{\alpha ,\beta , i,j} \left[ (g_N)_{\alpha ,\beta } \frac{ \partial f_{\alpha }}{\partial x_i} \frac{ \partial f_{\beta }}{\partial x_j} (g_M)^{-1}_{i,j}\right] \sqrt{det (g_{ij})}. \end{aligned}$$

• (2) Linear algebra shows that, once we identify TM, TN with their dual bundles via the Riemannian metrics, $|Df|^2 = Tr ( (Df)^{\vee } \circ Df )$, hence we integrate over M the sum of the eigenvalues of the endomorphism $(Df)^{\vee } \circ Df : TM \rightarrow TM$.

• (3) The first variation of the energy function vanishes precisely when f is a harmonic map, i.e., $\Delta (f) = 0$, where $\Delta (f) : = Tr (\nabla (Df)),$ $\nabla$ being the connection on $TM^{\vee } \otimes f^* (TN)$ induced by the Levi-Civita connections on M and N.

• (4) The energy functional enters also in the study of geodesics and Morse theory (see [288])

These notions were introduced by Eells and Sampson in the seminal paper [147], which used the heat flow

$$\begin{aligned} \frac{\partial f_t}{\partial t} = \Delta (f) \end{aligned}$$

in order to find extremals for the energy functional. These curves in the space of maps are (as explained in [147]) the analogue of gradient lines in Morse theory, and the energy functional decreases on these lines.

The obvious advantage of the flow method with respect to discrete convergence procedures (‘direct methods of the calculus of variations’) is that here it is clear that all the maps are homotopic to each other!⁸

The next theorem is one of the most important results, first obtained in [147]

Theorem 73

(Eells–Sampson) Let M, N be compact Riemannian manifolds, and assume that the sectional curvature ${\mathcal {K}}_N$ of N is semi-negative (${\mathcal {K}}_N \le 0$): then every continuous map $f_0 : M \rightarrow N$ is homotopic to a harmonic map $f : M \rightarrow N$. Moreover the equation $\Delta (f) = 0$ implies, in case where M, N are real analytic manifolds, the real analyticity of f.

Remark 74

Observe that, in the case where N has strictly negative sectional curvature, Hartmann [209] proved the unicity of the harmonic map in each homotopy class.

Not only the condition about the curvature is necessary for the existence of a harmonic representative in each homotopy class, but moreover it constitutes the main source of connections with the concept of classifying spaces, in view of the classical (see [76, 288]) theorem of Cartan–Hadamard establishing a deep link between curvature and topology.

Theorem 75

(Cartan–Hadamard) Suppose that N is a complete Riemannian manifold, with semi-negative (${\mathcal {K}}_N \le 0$) sectional curvature: then the universal covering $\tilde{N}$ is diffeomorphic to an Euclidean space, more precisely given any two points there is a unique geodesic joining them.

Remark 76

The reader will notice that the hypotheses of Theorem 73 and of Hartmann’s theorem apply naturally to two projective curves M, N of the same genus $g \ge 2$, taken with the metric of constant curvature $-1$ provided by the uniformization theorem: then one may take for $f_0$ a diffeomorphism, and apply the result, obtaining a unique harmonic map f which Samson [330] shows to be also a diffeomorphism. The result obtained is that to the harmonic map f one associates a quadratic differential $\eta _f \in H^0 ( \Omega _M^{\otimes 2})= H^0 ({\mathcal {O}}_M ( 2 K))$, and that $\eta _f$ determines the isomorphism class of N. This result constitutes another approach to Teichmüller space ${\mathcal {T}}_g$.

Thus in complex dimension 1 one cannot hope for a stronger result, to have a holomorphic map rather than just a harmonic one. The surprise comes from the fact that, with suitable assumptions, the hope can be realized in higher dimensions, with a small proviso: given a complex manifold X, one can define the conjugate manifold $\bar{X}$ as the same differentiable manifold, but where in the decomposition $TX \otimes _{{\mathbb {R}}} {\mathbb {C}}= T^{(1,0)} \oplus T^{(0,1)}$ the roles of $T^{(1,0)}$ and $T^{(0,1)}$ are interchanged (this amounts, in case where X is an algebraic variety, to replacing the defining polynomial equations by polynomials obtained from the previous ones by applying complex conjugation to the coefficients, i.e., replacing each $P(x_0, \ldots , x_N)$ by $\overline{P(\overline{x_0}, \ldots , \overline{x_N})}$).

In this case the identity map, viewed as a map $\iota : X \rightarrow \bar{X}$ is no longer holomorphic, but antiholomorphic. Assume now that we have a harmonic map $f : Y \rightarrow X$: then also $\iota \circ f$ shall be harmonic, but a theorem implying that f must be holomorphic then necessarily implies that there is a complex isomorphism between X and $\bar{X}$. Unfortunately, this is not the case, as one sees, already in the case of elliptic curves; but then one may restrict the hope to proving that f is either holomorphic or antiholomorphic.

A breakthrough in this direction was obtained by Siu [344] who proved several results, that we shall discuss in the next sections.

7.2 Kähler manifolds and some archetypal theorem

The assumption that a complex manifold X is a Kähler manifold is that there exists a Hermitian metric on the tangent bundle $T^{(1,0)}$ whose associated (1, 1) form $\xi$ is closed. In local coordinates the metric is given by

$$\begin{aligned} h = \Sigma _{i,j} g_{i,j} d z_i d\bar{z_j }, \quad \mathrm{with}\quad \ d \xi = 0,\quad \xi : = ( \Sigma _{i,j} g_{i,j} d z_i \wedge d\bar{z_j } ). \end{aligned}$$

Hodge theory shows that the cohomology of a compact Kähler manifold X has a Hodge–Kähler decomposition, where $H^{p,q}$ is the space of harmonic forms of type (p, q), which are in particular d-closed (and $d^*$-closed):

$$\begin{aligned} H^m (X, {\mathbb {C}}) = \oplus _{p,q \ge 0, p+q = m} H^{p,q} , \quad H^{q,p} = \overline{H^{p,q} } ,\quad H^{p,q} \cong H^q (X, \Omega ^p_X). \end{aligned}$$

We give just an elementary application of the above theorem, a characterization of complex tori (see [90, 103, 110] for other characterizations)

Theorem 77

Let X be a cKM, i.e., a compact Kähler manifold X, of dimension n. Then X is a complex torus if and only if it has the same integral cohomology algebra of a complex torus, i.e. $H^*(X, {\mathbb {Z}}) \cong \wedge ^* H^1(X, {\mathbb {Z}})$. Equivalently, if and only if $H^*(X, {\mathbb {C}}) \cong \wedge ^* H^1(X, {\mathbb {C}})$ and $H^{2n}(X, {\mathbb {Z}}) \cong \wedge ^{2n}H^1(X, {\mathbb {Z}})$

Proof

Since $H^{2n}(X, {\mathbb {Z}}) \cong {\mathbb {Z}}$, it follows that $H^1(X, {\mathbb {Z}})$ is free of rank equal to 2n, therefore $dim_{{\mathbb {C}}} (H^{1,0}) = n$. We consider then, chosen a base point $x_0 \in X$, the Albanese map

$$\begin{aligned} a_X : X \rightarrow {{\mathrm{\text {Alb}}}}(X) : = H^0(\Omega ^1_X)^{\vee } / {{\mathrm{\text {Hom}}}}(H^1(X, {\mathbb {Z}}), {\mathbb {Z}}), \quad x \mapsto \int _{x_0}^x. \end{aligned}$$

Therefore we have a map between X and the complex torus $T : = {{\mathrm{\text {Alb}}}}(X)$, which induces an isomorphism of first cohomology groups, and has degree 1, in view of the isomorphism

$$\begin{aligned} H^{2n}(X, {\mathbb {Z}}) \cong \Lambda ^{2n}(H^1(X, {\mathbb {Z}})) \cong H^{2n}(T, {\mathbb {Z}}). \end{aligned}$$

In view of the normality of X, it suffices to show that $a_X$ is finite. Let Y be a subvariety of X of dimension $m >0$ mapping to a point: then the cohomology (or homology class, in view of Poincaré duality) class of Y is trivial, since the cohomology algebra of X and T are isomorphic. But since X is Kähler, if $\xi$ is the Kähler form, $\int _Y \xi ^m >0$, a contradiction, since this integral depends only (by the closedness of $\xi$) on the homology class of Y. $\square$

One can conjecture that a stronger theorem holds, namely

Conjecture 78

Let X be a cKM, i.e., a compact Kähler manifold X, of dimension n. Then X is a complex torus if and only if it has the same rational cohomology algebra of a complex torus, i.e. $H^*(X, {\mathbb {Q}}) \cong \wedge ^* H^1(X, {\mathbb {Q}})$. Equivalently, if and only if $H^*(X, {\mathbb {C}}) \cong \wedge ^* H^1(X, {\mathbb {C}})$.

Remark 79

Observe that $H^*(X, {\mathbb {Q}}) \cong \wedge ^* H^1(X, {\mathbb {Q}}) \Leftrightarrow H^*(X, {\mathbb {C}}) \cong \wedge ^* H^1(X, {\mathbb {C}})$ by virtue of the universal coefficients theorem.

The same argument of the previous Theorem 77 yields that, since $H^{2n}(X, {\mathbb {Z}}) \cong {\mathbb {Z}}$, $dim_{{\mathbb {C}}} (H^{1,0}) = n$ and the Albanese map

$$\begin{aligned} a_X : X \rightarrow A: = {{\mathrm{\text {Alb}}}}(X) : = H^0(\Omega ^1_X)^{\vee } / {{\mathrm{\text {Hom}}}}(H^1(X, {\mathbb {Z}}), {\mathbb {Z}}), \ x \mapsto \int _{x_0}^x \end{aligned}$$

is finite, and it suffices to show that it is unramified (étale), since we have an isomorphism $H^1(X, {\mathbb {Z}}) \cong H^1(A, {\mathbb {Z}})$.

One sets therefore R to be the ramification divisor of $a_X$, and $B = {a_X}_* (R)$ the branch divisor.

There are two cases:

• Case (i) B is an ample divisor, and A and X are projective.

• Case (ii) : B is non ample, thus, by a result of Ueno [358] there is a subtorus $A_0 \subset A$ such that B is the pull-back of an ample divisor on $A/A_0$.

• Case (ii) can be reduced, via Ueno’s fibration to case (i), which is the crucial one.

Since we have an isomorphism of rational cohomology groups, and Poincaré duality holds, we get that ${a_X}_*$ and $a_X^*$ are, in each degree, isomorphisms with rational coefficients.

The first question is to show that the canonical divisor, which is just the ramification divisor R, is an ample divisor.

Then to observe that the vanishing of the topological Euler Poincaré characteristic e(X) and of the Euler Poincaré characteristics $\chi (\Omega ^i_X) = 0$ for all i implies (using Riemann Roch?) that the first Chern class of X is zero, thus obtaining a contradiction to the ampleness of $K_X$.

This step works at least in dimension $n=2$, since then we have the Noether formula $e(X) + K_X^2 = 12 \chi ({\mathcal {O}}_X)$, hence we obtain $K_X^2 = 0$.

Added in proof: Will Sawin observed that case i) does not occur for varieties of general type, since for these, by a result of Popa and Schnell, holomorphic 1- forms always have zeros. Instead, Debarre, Jiang and Lahoz showed that case ii) leads to the occurrence of certain iterated torus bundles, so that only a proper modification of our conjecture can be true.

Remark 80

Of course the hypothesis that X is Kähler is crucial: there are several examples, due to Blanchard, Calabi, and Sommese [46–48, 69, 348], of complex manifolds which are diffeomorphic to a complex torus but are not complex tori: indeed $K_X$ is not linearly equivalent to a trivial divisor (see [99] for references to the cited papers , and [110] for partial results on the question whether a compact complex manifold with trivial canonical divisor, which is diffeomorphic to a torus, is indeed biholomorphic to a complex torus).

The previous Theorem 77 allows a simple generalization which illustrates well the use of topological methods in moduli theory.

Theorem 81

Let $X = A/G$ be a Generalized Hyperelliptic manifold of complex dimension n and assume that Y is a compact Kähler Manifold satisfying the following properties:

• (1) $\pi _1(Y) \cong \pi _1(X) \cong \Gamma$

• (2) $H^{2n}(Y, {\mathbb {Z}}) \cong H^{2n}(\Gamma , {\mathbb {Z}})$ via the natural homomorphism of cohomology groups induced by the continuous map of Y to the classifying space $X = B \Gamma$, associated to the homomorphism $\pi _1(Y) \cong \pi _1(X) \cong \Gamma$.

• (3) $H^{i}(Y, {\mathbb {C}}) \cong H^{i}(\Gamma , {\mathbb {C}}) \ \forall i$ via the natural homomorphism analogous to the one defined in (2).

Then

• (1) Y is a Generalized Hyperelliptic manifold $Y = A' / G$,

• (2) if G is abelian, then Y is (real) affinely equivalent to X, and moreover

• (3) Y is a complex deformation of X if and only if X and Y have the same Hodge type.

Proof

Without loss of generality, we may assume that G contains no translations.

Since $\Gamma = \pi _1(X)$, we have an exact sequence $1\rightarrow \Lambda \rightarrow \Gamma \rightarrow G \rightarrow 0$, and we let W be the unramified covering of Y corresponding to the surjection $\pi _1(Y) \cong \Gamma \rightarrow G$.

Then the Albanese variety $A'$ of W has dimension n, and the group G acts on $A'$.

Main claim: G acts freely on $A'$.

This follows since, otherwise, there is an element $g' \in G {\setminus }{1_G}$ and a lift g of $g'$ in $\Gamma$ such that a positive power $g^m$ of g equals the neutral element $1_{\Gamma }$ (see Step I of the proof of Proposition 21). But then $g'$ would not act freely on A.

Now the Albanese map $W \rightarrow A'$ induces a holomorphic map $f : Y \rightarrow A'/G$, and we know that $A'/G$ is a classifying space with $\pi _1(A'/G) \cong \Gamma$. By our hypothesis f induces an isomorphism of cohomology groups and has degree equal to 1. The same argument as in Theorem 77 shows that f is an isomorphism. Therefore Y is also a Generalized Hyperelliptic manifold of complex dimension n.

For the second assertion, we simply apply Proposition 21, stating that the exact sequence $1\rightarrow \Lambda \rightarrow \Gamma \rightarrow G \rightarrow 0$ determines, when G is abelian, the real affine type of the action of $\Gamma$.

The last assertion is a direct consequence of Remark 20. $\square$

The following is one more characterization of complex tori and Abelian varieties.

Corollary 82

Let Z be a projective variety. Then Z is a projective $K(\pi , 1)$ with $\pi$ an abelian group $\Leftrightarrow$ Z is an Abelian variety. Similarly, if Z is a cKM, Z is a $K(\pi , 1)$ with $\pi$ abelian $\Leftrightarrow$ Z is a complex torus.

Proof

Since $\pi$ is finitely generated, we can write $\pi = {\mathbb {Z}}^m \oplus T$, where T is a finite abelian group. The subgroup ${\mathbb {Z}}^m$ is the fundamental group of a Galois cover $W \rightarrow Z$ with group T. In this case m must be even $m=2n$, by the Kähler assumption, and since $H^* (W, {\mathbb {Z}}) = H^* ({\mathbb {Z}}^{2n}, {\mathbb {Z}})$, we obtain that $n = dim_{{\mathbb {C}}} (W) = dim_{{\mathbb {C}}} (Z)$ and we can apply Theorem 77 to infer that W is a complex torus.

Now, $Z = W / T$, where T is abelian, and T acts trivially by conjugation on $\pi _1(W) \cong {\mathbb {Z}}^{2n}$. Hence T is a group of translations, and we obtain that Z is a complex torus. Moreover, since the fundamental group of a torus is torsion free, we can actually conclude that $T=0$. $\square$

7.3 Siu’s results on harmonic maps

The result by Siu that is the simplest to state is the following

Theorem 83

(I) Assume that $f : M \rightarrow N$ is a harmonic map between two compact Kähler manifolds and that the curvature tensor of N is strongly negative. Assume further that the real rank of the derivative Df is at least 4 in some point of M. Then f is either holomorphic or antiholomorphic.

(II) In particular, if $\dim _{{\mathbb {C}}} (N) \ge 2$ and M is homotopy equivalent to N, then M is either biholomorphic or antibiholomorphic to N.

From Theorem 83 follows an important consequence.

Corollary 84

Assume that $f : M \rightarrow N$ is a continuous map between two compact Kähler manifolds and that the curvature tensor of N is strongly negative. Assume further that there is a $j \ge 4$ such that $H_j(f, {\mathbb {Z}}) \ne 0$: then f is homotopic to a map F which is either holomorphic or antiholomorphic.

Proof

f is homotopic to a harmonic map F. One needs to show that at some point the real rank of the derivative DF is at least 4. If it were not so, then by Sard’s lemma the image $Y : = F(M)$ would be a subanalytic compact set of Hausdorff dimension at most 3.

Lemma 85

Let Y be a subanalytic compact set, or just a compact set of Hausdorff dimension at most h. Then $H_i(Y, {\mathbb {Z}}) = 0$ for $i \ge h+1$.

The lemma then implies $H_i(Y, {\mathbb {Z}}) = 0, \ \forall i \ge 4$, contradicting the existence of an $i \ge 4$ such that $H_i(f, {\mathbb {Z}}) \ne 0$ .

First proof of the lemma: Y is a finite union of locally closed submanifolds of dimension $\le h$, by the results of [42]. Using the exact sequence of Borel-Moore homology (see [59]) relating the homology of $Y = U \cup F$, where Y is the union of a closed set F with an open subset U, and induction on the number of such locally closed sets, we obtain that $H_i(Y, {\mathbb {Z}}) = 0$ for $i \ge h + 1$.

Second proof of the lemma: Y is a compact of Hausdorff dimension at most h. By theorem VII 3 of [219], page 104, follows that the dimension of Y is at most h. In turn, using theorem 2’ , p. 362 of [1], it follows (take A ibidem to be a point P ) that $H_i(Y, {\mathbb {Z}}) = H_i(Y, P , {\mathbb {Z}}) = 0$ for $i \ge h+1$.

Remark 86

(1) The hypothesis that the rank of the differential should be at least 4 at some point is needed for instance to avoid that the image of F is a complex projective curve C contained inside a projective variety N with such a strongly negative Kähler metric. Because in this case f could be the composition of a holomorphic map $g : M \rightarrow C'$ to a curve $C'$ of the same genus as C, but not isomorphic to C, composed with a diffeomorphism between $C'$ and C.

(2) Part II of Theorem 83 follows clearly from part I: because, as we have seen, the homotopy equivalence between M and N is realised by a harmonic map $f : M \rightarrow N$. From part I of the theorem one knows that f is holomorphic or antiholomorphic (in short, one says that f is dianalytic). W.l.o.g. let us assume that f is holomorphic (replacing possibly N by $\bar{N}$). There remains only to prove that f is biholomorphic. The argument is almost the same as the one used in the archetypal Theorem 77.

Step 1: f is a finite map; otherwise, since f is proper, there would be a complex curve C such that f(C) is a point. But in a Kähler manifold the homology class in dimension 2m of a subvariety of complex dimension m, here C, is never trivial. On the other hand, since f is a homotopy equivalence, and f(C) is a point, this class must be zero.

Step 2: f is a map of degree one since f induces an isomorphism between the last non zero homology groups of M, N respectively. If $n = \dim _{{\mathbb {C}}} N, m = \dim _{{\mathbb {C}}} M$, then these groups are $H_{2m}(M, {\mathbb {Z}})$, respectively $H_{2n}(N, {\mathbb {Z}})$; hence $n=m$ and

$$\begin{aligned} H_{2m} (f) : H_{2m}(M, {\mathbb {Z}}) \cong {\mathbb {Z}}[M] \rightarrow H_{2m}(N, {\mathbb {Z}}) \cong {\mathbb {Z}}[N] \end{aligned}$$

is an isomorphism.

Step 3: f is holomorphic, finite and of degree 1.Therefore there are open subsets whose complements are Zariski closed such that $f : U \rightarrow V \subset N$ is an isomorphism. Then the inverse of f is defined on V , the complement of a complex analytic set, and by the Riemann extension theorem (normality of smooth varieties) the inverse extends to N, showing that f is biholomorphic.

(3) We have sketched the above argument since it appears over and over in the application of homotopy equivalence to proving isomorphism of complex projective (or just Kähler) manifolds. Instead, the proof of part I is based on the Bochner–Nakano formula, which was later further generalised by Siu [346], and is too technical to be fully discussed here.

Let us try however to describe precisely the main hypothesis of strong negativity of the curvature, which is a stronger condition than the strict negativity of the sectional curvature.

As we already mentioned, the assumption that N is a Kähler manifold is that there exists a Hermitian metric on the tangent bundle $T^{(1,0)}$ whose associated (1, 1) form is closed. In local coordinates the metric is given by

$$\begin{aligned} \Sigma _{i,j} g_{i,j} d z_i d\bar{z_j }, \quad \mathrm{with} \quad d ( \Sigma _{i,j} g_{i,j} d z_i \wedge d\bar{z_j } ) = 0. \end{aligned}$$

The curvature tensor is a (1, 1) form with values in $(T^{(1,0)}) ^{\vee } \otimes T^{(1,0)}$, and using the Hermitian metric to identify $(T^{(1,0)}) ^{\vee } \cong \overline{T^{(1,0)}} = T^{(0,1)}$, and their conjugates $( (T^{(0,1)}) ^{\vee } = \overline{(T^{(0,1)}) } \cong T^{(1,0)}$ ) we write as usual the curvature tensor as a section R of

$$\begin{aligned} (T^{(1,0)}) ^{\vee } \otimes (T^{(0,1)}) ^{\vee } \otimes (T^{(1,0)}) ^{\vee } \otimes (T^{(0,1)}) ^{\vee }. \end{aligned}$$

Then seminegativity of the sectional curvature is equivalent to

$$\begin{aligned} - R \left( \xi \wedge \bar{\eta } - \eta \wedge \bar{\xi }, \overline{\xi \wedge \bar{\eta } - \eta \wedge \bar{\xi }}\right) \le 0, \end{aligned}$$

for all pairs of complex tangent vectors $\xi , \eta$ (here one uses the isomorphism $T^{(1,0)} \cong TN$, and one sees that the expression depends only on the real span of the two vectors $\xi , \eta$).

Strong negativity means instead that

$$\begin{aligned} - R \left( \xi \wedge \bar{\eta } - \zeta \wedge \bar{\theta }, \overline{ \xi \wedge \bar{\eta } - \zeta \wedge \bar{\theta }}\right) < 0 , \end{aligned}$$

for all 4-tuples of complex tangent vectors $\xi , \eta , \zeta , \theta$.

The geometrical meaning is the following (see [2], p. 71): the sectional curvature is a quadratic form on $\wedge ^2 (TN)$, and as such it extends to the complexified bundle $\wedge ^2 (TN) \otimes {\mathbb {C}}$ as a Hermitian form. Then strong negativity in the sense of Siu is also called negativity of the Hermitian sectional curvature $R (v,w, \bar{v}, \bar{w})$ for all vectors $v,w \in (TN) \otimes {\mathbb {C}}$.

Then a reformulation of the result of Siu [344] and Sampson [331] is the following:

Theorem 87

Let M be a compact Kähler manifold, and N a Riemannian manifold with semi-negative Hermitian sectional curvature. Then every harmonic map $f : M \rightarrow N$ is pluri-harmonic.

Now, examples of varieties N with a strongly negative curvature are the balls in ${\mathbb {C}}^n$, i.e., the BSD of type $I_{n,1}$; Siu finds out that ([344], see also [70]) for the irreducible bounded symmetric domains of type

$$\begin{aligned} I_{p,q},\quad \mathrm{for} \ p q \ge 2, \ II_n,\quad \forall n \ge 3, III_n,\quad \forall n \ge 2,IV_n,\quad \forall n \ge 3, \end{aligned}$$

the metric is not strongly negative, but just very strongly seminegative, where very strong negativity simply means negativity of the curvature as a Hermitian form on $T^{1,0} \otimes T^{0,1}= T^{1,0} \otimes \overline{T^{0,1}}$.

Indeed, the bulk of the calculations is to see that there is an upper bound for the nullity of the Hermitian sectional curvature, i.e. for the rank of the real subbundles of TM where the Hermitian sectional curvature restricts identically to zero (in Siu’s notation, then one considers always the case where very strongly seminegativity holds, and 2-negative means strongly negative, adequately negative means that the nullity cannot be maximal).

Hence Siu derives several results,

Theorem 88

(Siu) Suppose that M, N are compact Kähler manifolds and the curvature tensor of N is negative of order k. Assume that $f : M \rightarrow N$ is a harmonic map such that, $\exists i \ge 2k$ such that $H_{i}(f , {\mathbb {Z}}) \ne 0$. Then f is either holomorphic or antiholomorphic.

Theorem 89

(Siu) Suppose that M is a compact Kähler manifold and N is a locally symmetric manifold ${\mathcal {D}}/\Gamma$, where ${\mathcal {D}}$ is an irreducible bounded symmetric domain of one of the following types:

$$\begin{aligned} I_{p,q},\quad \mathrm{for}\quad \ pq \ge 2, \ II_n,\quad \forall n \ge 3, III_n,\quad \forall n \ge 2,IV_n,\quad \forall n \ge 3. \end{aligned}$$

Assume that $f : M \rightarrow N$ is a harmonic map such that, $n : = dim_{{\mathbb {C}}} N$, $H_{2n}(f , {\mathbb {Z}}) \ne 0$. Then f is either holomorphic or antiholomorphic.

In particular, if M is a compact Kähler manifold homotopically equivalent to N as above, then either $M \cong N$ or $M \cong \bar{N}$.

The most general result is ([2], p. 80, theorems 6.13–15):

Theorem 90

(Siu) Suppose that M is a compact Kähler manifold and N is a locally Hermitian symmetric space ${\mathcal {D}}/ \Gamma = G/K$, where the irreducible decomposition of ${\mathcal {D}}$ contains no dimension 1 factors.

• (1) Assume that $f : M \rightarrow N$ is a harmonic map such that, $n : = dim_{{\mathbb {C}}} N$, $H_{2n}(f , {\mathbb {Z}}) \ne 0$. Then f is holomorphic for some invariant complex structure on G / K.

• (2) Assume that M is homotopically equivalent to N: then f is biholomorphic to G / K for some invariant complex structure on G / K.

Remark 91

A few words are needed to explain the formulation ‘for some invariant complex structure on G / K’. In the case where ${\mathcal {D}}$ is irreducible, we can just take the conjugate complex structure. But if ${\mathcal {D}}= {\mathcal {D}}_1 \times \cdots \times {\mathcal {D}}_l$, one can just take the conjugate complex structure on a subset ${\mathcal {I}}$ of the indices $j \in \{ 1, \ldots , l\}$.

7.4 Hodge theory and existence of maps to curves

Siu also used harmonic theory in order to construct holomorphic maps from Kähler manifolds to projective curves. The first result in this direction was the theorem of [347], also obtained by Jost and Yau (see [239] and also [228] for other results).

Theorem 92

(Siu) Assume that a compact Kähler manifold X is such that there is a surjection $\phi : \pi _1(X) \rightarrow \pi _g$, where $g\ge 2$ and, as usual, $\pi _g$ is the fundamental group of a projective curve of genus g. Then there is a projective curve C of genus $g' \ge g$ and a fibration $f : X \rightarrow C$ (i.e., the fibres of f are connected) such that $\phi$ factors through $\pi _1 (f)$.

In this case the homomorphism leads to a harmonic map to a curve, and one has to show that the Stein factorization yields a map to some Riemann surface which is holomorphic for some complex structure on the target.

In this case it can be seen more directly how the Kähler assumption, which boils down to Kähler identities, is used.

Recall that Hodge theory shows that the cohomology of a compact Kähler manifold X has a Hodge–Kähler decomposition, where $H^{p,q}$ is the space of harmonic forms of type (p, q):

$$\begin{aligned} H^m (X, {\mathbb {C}}) = \oplus _{p,q \ge 0, p+q = m} H^{p,q} , \quad H^{q,p} = \overline{H^{p,q} } ,\quad H^{p,q} \cong H^q (X, \Omega ^p_X). \end{aligned}$$

The Hodge–Kähler decomposition theorem has a long story, revived by Griffths in [192, 193], and was proven by Picard in special cases. It entails the following consequence:

Holomorphic forms are closed, i.e., $\eta \in H^0 (X, \Omega ^p_X) \Rightarrow d \eta = 0$.

At the turn of last century this fact was then used by Castelnuovo and de Franchis [80, 130]:

Theorem 93

(Castelnuovo–de Franchis) Assume that X is a compact Kähler manifold, $\eta _1 , \eta _2 \in H^0 (X, \Omega ^1_X)$ are ${\mathbb {C}}$-linearly independent, and the wedge product $\eta _1 \wedge \eta _2$ is d-exact. Then $\eta _1 \wedge \eta _2 \equiv 0$ and there exists a fibration $f : X \rightarrow C$ such that $\eta _1, \eta _2 \in f^* H^0 ( C, \Omega ^1_C)$. In particular, C has genus $g \ge 2$.

Even if the proof is well known, let us point out that the first assertion follows from the Hodge–Kähler decomposition, while $\eta _1 \wedge \eta _2 \equiv 0$ implies the existence of a non constant rational function $\varphi$ such that $\eta _2 = \varphi \eta _1$. This shows that the foliation defined by the two holomorphic forms has Zariski closed leaves, and the rest follows then rather directly taking the Stein factorization of the rational map $\varphi : X \rightarrow {\mathbb {P}}^1$.

Now, the above result, which is holomorphic in nature, combined with the Hodge decomposition, produces results which are topological in nature (they actually only depend on the cohomology algebra structure of $H^*(X, {\mathbb {C}})$).

To explain this in the most elementary case, we start from the following simple observation. If two linear independent vectors in the first cohomology group $H^1 (X, {\mathbb {C}})$ of a Kähler manifold have wedge product which is trivial in cohomology, and we represent them as $\eta _1 + \overline{\omega _1}, \eta _2 + \overline{\omega _2},$ for $\eta _1 , \eta _2 , \omega _1, \omega _2 \in H^0 (X, \Omega ^1_X)$, then by the Hodge decomposition and the first assertion of the theorem of Castelnuovo–de Franchis

$$\begin{aligned} (\eta _1 + \overline{\omega _1}) \wedge ( \eta _2 + \overline{\omega _2}) = 0 \in H^2 (X, {\mathbb {C}}) \end{aligned}$$

implies

$$\begin{aligned} \eta _1 \wedge \eta _2 \equiv 0 , \quad \omega _1 \wedge \omega _2 \equiv 0. \end{aligned}$$

We can apply Castelnuovo–de Franchis unless $\eta _1 , \eta _2$ are ${\mathbb {C}}$-linearly dependent, and similarly $\omega _1 , \omega _2$. W.l.o.g. we may assume $\eta _2 \equiv 0$ and $\omega _1 \equiv 0$. But then $\eta _1 \wedge \overline{\omega _2} = 0$ implies that the Hodge norm

$$\begin{aligned} \int _X (\eta _1 \wedge \overline{\omega _2}) \wedge \overline{(\eta _1 \wedge \overline{\omega _2}) } \wedge \xi ^{n-2}= 0, \end{aligned}$$

where $\xi$ is here the Kähler form. A simple trick is to observe that

$$\begin{aligned} 0 = \int _X \left( \eta _1 \wedge \overline{\omega _2} \right) \wedge \overline{(\eta _1 \wedge \overline{\omega _2}) } \wedge \xi ^{n-2}= - \int _X \left( \eta _1 \wedge \omega _2\right) \wedge \overline{(\eta _1 \wedge \omega _2}) \wedge \xi ^{n-2}, \end{aligned}$$

therefore the same integral yields that the Hodge norm of $\eta _1 \wedge \omega _2$ is zero, hence $\eta _1 \wedge \omega _2 \equiv 0;$ the final conclusion is that we can in any case apply Castelnuovo-de Franchis and find a map to a projective curve C of genus $g \ge 2$.

More precisely, one gets the following theorem [87]:

Theorem 94

(Isotropic subspace theorem) On a compact Kähler manifold X there is a bijection between isomorphism classes of fibrations $f : X \rightarrow C$ to a projective curve of genus $g\ge 2$, and real subspaces $V \subset H^1 (X, {\mathbb {C}})$ (‘real’ means that V is self conjugate, $\overline{V} = V$) which have dimension 2g and are of the form $V = U \oplus \bar{U}$, where U is a maximal isotropic subspace for the wedge product

$$\begin{aligned} H^1 (X, {\mathbb {C}}) \times H^1 (X, {\mathbb {C}}) \rightarrow H^2 (X, {\mathbb {C}}). \end{aligned}$$

It is interesting that the above result implies the following theorem of Gromov [196], which in turn obviously implies theorem 92 of Siu (see [25, 197] for related results).

Theorem 95

(Gromov’s few relations theorem) Let X be a compact Kähler manifold and assume that there exists a surjection of its fundamental group

$$\begin{aligned} \Gamma : = \pi _1 (X) \rightarrow G = \langle x_1, \ldots , x_n | R_1(x), \ldots , R_m (x) \rangle , \end{aligned}$$

onto a finitely presented group that has ‘few relations’, more precisely where $n \ge m-2$. Then there exists a fibration $f : X \rightarrow C$, onto a projective curve C of genus $g \ge \frac{1}{2} (n-m)$.

If moreover $\pi _1 (X) \cong G$, then the first cohomology group $H^1 (X, {\mathbb {C}})$ equals $f^* H^1 (C, {\mathbb {C}})$.

Proof

We saw in a Sect. 6.6 that if the fundamental group of X, $\Gamma : = \pi _1(X)$ admits a surjection onto G, then the induced classifying continuous map $\phi : X \rightarrow B G$ has the properties that its induced action on first cohomology

$$\begin{aligned} H^1 (\phi ) : H^1 (B G, {\mathbb {C}}) \rightarrow H^1 (X, {\mathbb {C}}) \end{aligned}$$

is injective and the image W of $H^1 (\phi )$ is such that each element $w \in W$ is contained in an isotropic subspace of rank $\ge n-m$.

Hence it follows immediately that there is an isotropic subspace of dimension $\ge n-m$ and a fibration onto a curve of genus $g \ge n-m$.

For the second assertion, let U be a maximal isotropic subspace contained in $W = H^1 (X, {\mathbb {C}})$: then there exists a fibration $f : X \rightarrow C$, onto a projective curve C of genus $g \ge 2$ such that $f^* H^1 (C, {\mathbb {C}}) = U \oplus \bar{U}$. We are done unless $U \oplus \bar{U} \ne H^1 (X, {\mathbb {C}})$.

But in this case we know that $W = H^1 (X, {\mathbb {C}})$ is the union of such proper subspaces $U \oplus \bar{U}$.

These however are of the form $f^* H^1 (C, {\mathbb {Z}}) \otimes {\mathbb {C}}$, hence they are a countable number; by Baire’s theorem their union cannot be the whole ${\mathbb {C}}$-vector space $W = H^1$ $(X, {\mathbb {C}})$. $\square$

Not only one sees clearly how the Kähler hypothesis is used, but indeed Kato [233] and Pontecorvo [324] showed how the results are indeed false without the Kähler assumption, using twistor spaces of algebraic surfaces which are ${\mathbb {P}}^1$-bundles over a projective curve C of genus $g \ge 2$. A simpler example was then found by Kotschick ([2], ex. 2.16, p. 28): a primary Kodaira surface (an elliptic bundle over an elliptic curve, with $b_1(X) = 3, b_2(X) = 4$).

We do not mention in detail generalisations of the Castelnuovo–de Franchis theory to higher dimensional targets (see [87, 190, 191, 342]), since these shall not be used in the sequel.

We want however to mention another result ([106], see also [102] for a weaker result) which again, like the isotropic subspace theorem, determines explicitly the genus of the target curve (a result which is clearly useful for classification and moduli problems).

Theorem 96

Let X be a compact Kähler manifold, and let $f : X \rightarrow C$ be a fibration onto a projective curve C, of genus g, and assume that there are exactly r fibres which are multiple with multiplicities $m_1, \ldots m_r \ge 2$. Then f induces an orbifold fundamental group exact sequence

$$\begin{aligned} \pi _1 (F) \rightarrow \pi _1 (X) \rightarrow \pi _1 (g; m_1, \ldots m_r) \rightarrow 0, \end{aligned}$$

where F is a smooth fibre of f, and

$$\begin{aligned}&\pi _1 (g; m_1, \ldots m_r) \\&\quad := \ \langle \alpha _1, \beta _1, \ldots , \alpha _g, \beta _g, \gamma _1, \ldots \gamma _r | \ \ \Pi _1^g [\alpha _j, \beta _j] \Pi _1^r \gamma _i = \gamma _1^{m_1}= \cdots = \gamma _r^{m_r} = 1\rangle . \end{aligned}$$

Conversely, let X be a compact Kähler manifold and let $(g, m_1, \dots m_r)$ be a hyperbolic type, i.e., assume that $2g-2 + \Sigma _i (1 - \frac{1}{m_i} ) > 0$.

Then each epimorphism $\phi : \pi _1 (X) \rightarrow \pi _1 (g; m_1, \ldots m_r)$ with finitely generated kernel is obtained from a fibration $f : X \rightarrow C$ of type $(g; m_1, \ldots m_r)$.

7.5 Restrictions on fundamental groups of projective varieties

A very interesting (and still largely unanswered) question posed by Serre [335] is:

Question 97

(Serre)

• (1) Which are the projective groups, i.e., the groups $\pi$ which occur as fundamental groups $\pi = \pi _1(X)$ of a complex projective manifold?

• (2) Which are the Kähler groups, i.e., the groups $\pi$ which occur as fundamental groups $\pi = \pi _1(X)$ of a compact Kähler manifold?

Remark 98

• (i) Serre himself proved (see [337]) that the answer to the first question is positive for every finite group. In this chapter we shall only limit ourselves to mention some examples and results to give a general idea, especially about the use of harmonic maps, referring the reader to the book [2], entirely dedicated to this subject.

• (ii) For question (1), in view of the Lefschetz hyperplane section Theorem 3, the class of projective groups $\pi$ is exactly the class of groups which occur as fundamental groups $\pi = \pi _1(X)$ of a complex projective smooth surface.

• (iii) if $\pi$ and $\pi '$ are projective (resp. Kähler), the same is true for the Cartesian product (take $X \times X'$).

The first obvious restriction for a group $\Gamma$ to be a Kähler group (only a priori the class of Kähler groups is a larger class than the one of projective groups) is that their first Betti number $b_1$ (rank of the abelianization $\Gamma ^{ab} = \Gamma / [ \Gamma , \Gamma ]$) is even; since if $\Gamma = \pi _1(X)$, then $\Gamma ^{ab} = H_1(X, {\mathbb {Z}})$, and $H_1(X, {\mathbb {Z}}) \otimes {\mathbb {C}}$ has even dimension by the Hodge–Kähler decomposition.

A more general restriction is that the fundamental group $\Gamma$ of a compact differentiable manifold M must be finitely presented: since by Morse theory (see [288]) M is homotopically equivalent to a finite CW-complex (M is obtained attaching finitely many cells of dimension $\le \dim _{{\mathbb {R}}} (M)$).

Conversely (see [333], p. 180),

Theorem 99

Any finitely presented group $\Gamma$ is the fundamental group of a compact oriented 4-manifold.

Recall for this the

Definition 100

(Connected sum) Given two differentiable manifolds $M_1, M_2$ of the same dimension n, take respective points $P_i \in M_i, i=1,2$ and respective open neighbourhoods $B_i$ which are diffeomorphic to balls, and with smooth boundary $\partial B_i \cong S^{n-1}$. Glueing together the two manifolds with boundary $M_i {\setminus } B_i, \partial B_i$ we obtain a manifold $M_1 \sharp M_2$, which is denoted by the connected sum of $M_1, M_2$ and whose diffeomorphism class is independent of the choices made in the construction. Also, if $M_1, M_2$ are oriented, the same holds for $M_1 \sharp M_2$, provided the diffeomorphisms $\partial B_i \cong S^{n-1}$ are chosen to be orientation preserving.

Definition 101

(Free product) If $\Gamma , \Gamma '$ are finitely presented groups,

$$\begin{aligned} \Gamma = \langle x_1, \ldots , x_n | R_1(x), \ldots , R_m (x) \rangle , \Gamma ' = \langle y_1, \ldots , y_h | R'_1(y), \ldots , R'_k (y) \rangle , \end{aligned}$$

their free product is the finitely presented group

$$\begin{aligned} \Gamma * \Gamma ' = \langle x_1, \ldots , x_n , y_1, \ldots , y_h | R_1(x), \ldots , R_m (x), R'_1(y), \ldots , R'_k (y) \rangle . \end{aligned}$$

Idea for the proof of theorem 99: By the van Kampen theorem, the fundamental group of the union $X = X_1 \cup X_2$ of two open sets with connected intersection $X_1 \cap X_2$ is the quotient of the free product $\pi _1 (X_1 ) * \pi _1 (X_2)$ by the relations $i_1 (\gamma ) = i_2(\gamma ), \forall \gamma \in \pi _1 (X_1 \cap X_2)$, where $i_j : \pi _1 (X_1 \cap X_2) \rightarrow \pi _1 (X_j)$ is induced by the natural inclusion $(X_1 \cap X_2) \subset X_j$.

Now, assume that $\Gamma$ has a finite presentation

$$\begin{aligned} \Gamma = \langle x_1, \ldots , x_n | R_1(x), \ldots , R_m (x) \rangle . \end{aligned}$$

Then one considers the connected sum of n copies of $S^1 \times S^3$, which has then fundamental group equal to a free group ${\mathbb {F}}_n = \langle \langle x_1, \ldots , x_n \rangle \rangle$.

Realizing the relations $R_j(x)$ as loops connecting the base point to m disjoint embedded circles (i.e., diffeomorphic to $S^1$), one can perform the so called surgery replacing tubular neighbourhoods of these circles, which are diffeomorphic to $S^1 \times B^3$, and have boundary $S^1 \times S^2$, each by the manifold with boundary $B^2 \times S^2$. These manifolds are simply connected, hence by van Kampen we introduce the relation $R_j(x) = 1$, and finally one obtains a M with fundamental group $\cong \Gamma$.

There are no more restrictions, other than finite presentability, if one requires that $\Gamma$ be the fundamental group of a compact complex manifold, as shown by Taubes [351], or if one requires that $\Gamma$ be the fundamental group of a compact symplectic 4-manifold, as shown by Gompf [182]. Notice however that, by the main results of Kodaira’s surface classification (see [21]), the fundamental groups of complex non projective surfaces form a very restricted class, in particular either their Betti number $b_1$ is equal to 1, or they sit in an exact sequence of the form

$$\begin{aligned} 1 \rightarrow {\mathbb {Z}}\rightarrow \Gamma \rightarrow \pi _g \rightarrow 1. \end{aligned}$$

In fact Taubes builds on the method of Seifert and Threlfall in order to construct a compact complex manifold X with $\pi _1 (X) = \Gamma$. He takes a (differentiable) 4-manifold M with $\pi _1(M) = \Gamma$ and then, taking the connected sum with a suitable number of copies of the complex projective plane with opposed orientation, he achieves that M allows a metric with anti self dual Weyl tensor. This condition on the metric of M, by a theorem of Atiyah, Hitchin and Singer [14] makes the twistor space Tw(M) a complex manifold (not just an almost complex manifold). Note that (see [268], especially page 366) the twistor space Tw(M) of an oriented Riemannian 4-manifold is an $S^2$-bundle over M, such that the fibre over $P\in M$ equals the sphere bundle of the rank 3 vector subbundle $\Lambda ^+ \subset \Lambda ^2 (TM)$. Here $\Lambda ^2 (TM) = \Lambda ^+ \oplus \Lambda ^-$ is the eigenspace decomposition for the $*$-operator $* : \Lambda ^2 (TM) \rightarrow \Lambda ^2 (TM)$, such that $*^{2} = 1$.

The fact that Tw(M) is an $S^2$-bundle over M is of course responsible of the isomorphism $\pi _1 (Tw(M)) \cong \pi _1(M)$.

Returning to Serre’s question, a first result was given by Johnson and Rees [225], which was later extended by other authors [7, 196]:

Theorem 102

(Johnson–Rees) Let $\Gamma _1 , \Gamma _2$ be two finitely presented groups admitting some non trivial finite quotient. Then the free product $\Gamma _1 * \Gamma _2$ cannot be the fundamental group of a normal projective variety. More generally, this holds for any direct product $H \times (\Gamma _1 * \Gamma _2)$.

The idea of proof is to use the fact that the first cohomology group $H^1(X, {\mathbb {C}})$ carries a nondegenerate skew-symmetric form, obtained simply from the cup product in 1-dimensional cohomology multiplied with the $(n-1)$-th power of the Kähler class.

An obvious observation is that the crucial hypothesis is projectivity. In fact, if we take a quasi-projective variety, then the theorem does not hold true: it suffices to take as X the complement of d points in a projective curve of genus g, and then $\pi _1(X) \cong {\mathbb {F}}_{2g + d -1}$ is a free group. This is not just a curve phenomenon: already Zariski showed that if C is a plane sextic with equation $Q_2(x)^3 - G_3(X)^2=0$, where $Q_2, G_3$ are generic forms of respective degrees 2, 3, then $\pi _1 ({\mathbb {P}}^2 {\setminus } C) \cong {\mathbb {Z}}/2 * {\mathbb {Z}}/3$.

One important ingredient for the theorem of Johnson and Rees is the Kurosh subgroup theorem, according to which $\Gamma _1 * \Gamma _2$ would have a finite index subgroup of the form ${\mathbb {Z}}* K$, which would therefore also be the fundamental group of a projective variety. Another proof is based on the construction of a flat bundle E corresponding to a homomorphism ${\mathbb {Z}}* K \rightarrow \{\pm 1\}$ with some cohomology group $H^i(X, E)$ of odd dimension, contradicting the extension of Hodge theory to flat rank 1 bundles (see [181]).

Arapura, Bressler and Ramachandran answer in particular one question raised by Johnson and Rees, namely they show [7]:

Theorem 103

(Arapura, Bressler and Ramachandran) If X is a compact Kähler manifold, then its universal cover $\tilde{X}$ has only one end. And $\pi _1(X)$ cannot be a free product amalgamated by a finite subgroup.

Here, the ends of a non compact topological space $X'$ are just the limit, as the compact subset K gets larger, of the connected components of the complement set $X' {\setminus } K$.

The theorem of Johnson and Rees admits the following consequence

Corollary 104

(Johnson–Rees) Let $X_1, X_2$ be smooth projective manifolds of dimension $n \ge 2$ with non zero first Betti number, or more generally with the property that $\pi _1(X_j)$ has a non trivial finite quotient. Then $X_1 \sharp X_2$ cannot be homeomorphic to a projective manifold.

It is interesting to observe that the previous result was extended by Donaldson [138] also to the case where $X_1, X_2$ are simply connected smooth projective surfaces. One could believe that the combination of the two results implies tout court that the connected sum $X_1 \sharp X_2$ of two projective manifolds of dimension at least two cannot be homeomorphic to a projective manifold. This is unfortunately not clear (at least to the author), because of a deep result by Toledo [354], giving a negative answer to another question posed by Serre

Theorem 105

(Toledo) There exist projective manifolds X whose fundamental group $G : = \pi _1(X)$ is not residually finite.

This means that the natural homomorphism of $G : = \pi _1(X)$ into its profinite completion $\hat{G}$ is not injective $\widehat{\pi _1(X) }$ is also called the algebraic fundamental group and denoted by $\pi _1 (X)^{alg}$.

The profinite completion is defined as the following inverse limit

$$\begin{aligned} \hat{G} : = \lim _{K < G, } G/K, \end{aligned}$$

where K runs through the set of normal subgroups of finite index.

Even the following question does not have yet a positive answer.

Question 106

Does there exist a projective manifold X such that $G = \pi _1 (X) \ne 0$, while $\hat{G} = : \pi _1 (X)^{alg} = 0$? ( $\pi _1(X)$ would then be an infinite group).

If the answer were negative, then the hypothesis in Corollary 104 would be that $X_1, X_2$ are not simply connected.

Concluding this section, it is clear how the results of Siu (and Mostow [300]), can be used to obtain restrictions for Kähler groups.

For instance, using the above mentioned techniques of classifying spaces and harmonic maps, plus some Lie theoretic arguments, Carlson and Toledo [75], while giving alternative proofs of the results of Siu, prove:

Theorem 107

(Carlson–Toledo) If X is a compact Kähler manifold, then its fundamental group $\pi _1(X)$ cannot be isomorphic to a discrete subgroup $\Gamma < SO(1,n)$ such that ${\mathcal {D}}/ \Gamma$ be compact, where ${\mathcal {D}}$ is the hyperbolic space SO(1, n) / SO(n).

Similar in spirit is the following theorem of Simpson [341], for which we recall that a lattice $\Gamma$ contained in a Lie group G is a discrete subgroup such that $G / \Gamma$ has finite volume, and that a reductive Lie group is of Hodge type if it has a compact Cartan subgroup.

Theorem 108

(Simpson) If X is a compact Kähler manifold, its fundamental group $\pi _1(X)$ cannot be isomorphic to a lattice $\Gamma$ contained in a simple Lie group not of Hodge type.

For more information on Kähler groups (fundamental group of a cKM X), we refer to the book [2], to the survey article by Campana [72] and to [73].

7.6 Kähler versus projective, Kodaira’s problem and Voisin’s negative answer

Many of the restrictions for a group $\Gamma$ to be a projective group (fundamental group of a projective variety X) are indeed restrictions to be a Kähler group. For long time, it was not clear which was the topological difference between projective smooth varieties and compact Kähler manifolds. Even more, there was a question by Kodaira whether any compact Kähler manifold X would be a deformation (or even a direct deformation) of a projective manifold Y, according to the following well known definition.

Definition 109

• (1) Given two compact complex manifolds Y, X, Y is a direct deformation of X if there is a smooth proper and connected family $p: {\mathcal {X}}\rightarrow B$, where B is a smooth connected complex curve, such that X and Y isomorphic to some fibres of p.

• (2) We say instead that Y is deformation equivalent to X if Y is equivalent to X for the equivalence relation generated by the (symmetric) relation of direct deformation.

Indeed, Kodaira proved:

Theorem 110

(Kodaira [249]) Every compact Kähler surface is a deformation of a projective manifold.

It was for a long time suspected that Kodaira’s question, although true in many important cases (tori, surfaces), would be in general false. The counterexamples by Claire Voisin were based on topological ideas, namely on the integrality of some multilinear algebra structures on the cohomology of projective varieties.

To explain this, recall that a Kähler form $\xi$ on a Kähler manifold X determines the Lefschetz operator on forms of type (p, q):

$$\begin{aligned} L : {\mathcal {A}}^{p,q} \rightarrow {\mathcal {A}}^{p+1,q+1},\quad L (\phi ) : = \xi \wedge \phi \end{aligned}$$

whose adjoint

$$\begin{aligned} \Lambda : = L^* : {\mathcal {A}}^{p,q} \rightarrow {\mathcal {A}}^{p-1,q-1} \end{aligned}$$

is given by $\Lambda = w * L *$ where

$$\begin{aligned}&w := \sum _{p,q} (-1)^{p-q} \pi _{p,q},\quad (Weil),\\&c:= \sum _{p,q} (i)^{p-q} \pi _{p,q},\quad \, (Chern-Weil), \end{aligned}$$

are the Weil and Chern–Weil operators respectively. Here $\pi _{p,q}$ is the projector onto the space of forms of type (p, q).

These operators satisfy the commutation relations:

• (1) $[ L, w ] = [L, c] = [\Lambda , w] = [\Lambda , c ] = 0$

• (2) $\ B := [L, \Lambda ] = \sum (p+q -n)\pi _{p,q},$

• (3) $[L, B] = -2L$.

In this way the bigraded algebra of differential forms is a representation of the Lie Algebra $sl(2, {{\mathbb {C}}})$, which has the basis:

$$\begin{aligned} b= & {} \left( \begin{array}{c@{\quad }c} -1 &{} 0\\ 0 &{} 1 \end{array} \right) \!,\\ l= & {} \left( \begin{array}{c@{\quad }c} 0 &{} 0\\ 1 &{} 0 \end{array} \right) \!,\\ \lambda= & {} \left( \begin{array}{c@{\quad }c} 0 &{} 1\\ 0 &{} 0 \end{array} \right) \!, \end{aligned}$$

and with Lie bracket given by

$$\begin{aligned} b= & {} [l, \lambda ],\\ -2l= & {} [l,b],\\ 2 \lambda= & {} [\lambda , b]. \end{aligned}$$

For finite dimensional representations of $sl(2, {{\mathbb {C}}})$ one has the following structural result.

Proposition 111

Let $\rho : sl(2, {{\mathbb {C}}}) \longrightarrow End(W)$ be a representation of $sl(2, {{\mathbb {C}}})$, $dim(W) < \infty$, and set $L := \rho (l)$, $\Lambda := \rho (\lambda )$, $B := \rho (b)$. Then we have:

• (1) $W = \oplus _{\nu \in {\mathbb {Z}}} W_{\nu }$ is a finite direct sum, where $W_{\nu }$ is the eigenspace of B with eigenvalue $\nu$.

• (2) $L(W_{\nu }) \subset W_{\nu +2}$, $\Lambda (W_{\nu }) \subset W_{\nu -2}$.

• (3) Let $P = \{w \ | \ \Lambda w =0\}$, be the space of primitive vectors, then we have a direct sum decomposition

  $$\begin{aligned} W = \oplus _{r \in {{\mathbb {N}}}} L^r (P). \end{aligned}$$

• (4) Moreover, the irreducible representations of $sl(2, {{\mathbb {C}}})$ are isomorphic to $S^m({{\mathbb {C}}}^2)$, where $S^m({{\mathbb {C}}}^2)$ is the m-th symmetric power of the natural representation of $SL(2, {{\mathbb {C}}})$ on ${{\mathbb {C}}}^2$ (i.e., the space of homogeneneous polynomials of degree m).

• (5) Let $P_{\mu } := P \cap W_{\mu }$: then $P_{\mu } =0$ for $\mu >0$ and

  $$\begin{aligned} P = \oplus _{\mu \in {\mathbb {Z}}, \ \mu \le 0} P_{\mu }. \end{aligned}$$

• (6) $L^r : P_{-m} \longrightarrow W_{-m +2r}$ is injective for $r \le m$ and zero for $r >m$.

• (7) $L^r: W_{-r} \longrightarrow W_r$ is an isomorphism $\forall r$, and

  $$\begin{aligned} W_{\mu } = \oplus _{r \in {{\mathbb {N}}}, \ r \ge \mu } L^r(P_{\mu - 2r}). \end{aligned}$$

On a compact Kähler manifold the projectors $\pi _{p,q}$ commute with the Laplace operator, so that the components $\psi _{p,q}$ of a harmonic form $\psi$ are again harmonic, hence the operators $L, \Lambda ,\dots$ preserve the finite dimensional subspace ${\mathcal {H}}$ of harmonic forms, and one can apply the above Proposition 111. The following theorem goes often after the name of Lefschetz decomposition, and is essential in order to prove the third Lefschetz theorem (see 3).

Theorem 112

• (i) Let $(X, \xi )$ be a compact Kähler manifold. Then $\Delta$ commutes with the operators $*$, $\partial$, $\overline{\partial }$, $\partial ^*$, $\overline{\partial }^*$, L, $\Lambda$.

• (ii) In particular, a k- form $\eta = \sum _{p+q = k} \eta _{p,q}$ is harmonic if and only if all the $\eta _{p,q}$’s are harmonic.

• (iii) Hence there is the so-called Hodge Decomposition of the de Rham cohomology:

  $$\begin{aligned} \oplus _k H^k_{DR} (X, {\mathbb {C}}) \cong \oplus _k{{\mathcal {H}}}^k(X, {{\mathbb {C}}}) = \oplus _{p.q} {{\mathcal {H}}}^{p,q}, \end{aligned}$$

  where ${{\mathcal {H}}}^{p,q}$ is the space of the harmonic Forms of Type (p, q),

• (iv) Hodge Symmetry holds true, i.e., we have ${{\mathcal {H}}}^{p,q}= \overline{ {{\mathcal {H}}}^{q,p}}$.

• (v) There is a canonical isomorphism ${{\mathcal {H}}}^{p,q} \cong H^q ( X, \Omega _X^p)$.

• (vi) The Lefschetz operators $L, \Lambda$ make ${\mathcal {H}}$ a representation of ${\mathfrak {s}} {\mathfrak {l}} (2, {{\mathbb {C}}})$ ⁹, with eigenspaces $H_{\mu } : = \oplus _{ p+q = \mu + n} {{\mathcal {H}}}^{p,q}$, and the space $P^{p,q}$ of primitive forms of type (p, q) allows a decomposition

  $$\begin{aligned} {\mathcal {H}}^{p,q} = \oplus _{r \in {{\mathbb {N}}}, \ r \ge \mu = p + q - n} L^r(P_{p-r, q-r}), \end{aligned}$$

  where $P^{p,q}= 0$ for $p + q > n$.

Moreover, the Hermitian product on $P^{p,q}$ given by

$$\begin{aligned} \langle \eta , \eta \rangle : = i^{n-2pq} L^{(n-p-q)}(\eta \wedge \overline{\eta }) \end{aligned}$$

is positive definite.

Now, a projective manifold is a compact Kähler manifold when endowed with the Fubini-Study metric

$$\begin{aligned} - \frac{1}{2 \pi i} \partial \overline{\partial } log \left( \sum | z_i|^2\right) \!. \end{aligned}$$

This is the Chern class $c_1 ({\mathcal {L}})$ where ${\mathcal {L}}$ is the line bundle ${\mathcal {O}}_X(1)$.

Kodaira’s embedding theorem characterizes projective manifolds as those compact Kähler manifolds which admit a Kähler metric whose associated form is integral, i.e., it is the first Chern class of a positive line bundle.

Definition 113

Let M be a compact differentiable manifold of real even dimension $dim_{{\mathbb {R}}}(M) = 2n$.

• (1) M is said to admit a real polarized Hodge structure if there exists a real closed two form $\xi$ and a Hodge decomposition of its cohomology algebra (i.e., as in iii of Theorem 112) such that the operators $L (\psi ) : = \xi \wedge \psi$, and $\Lambda : w * L *$ satisfy properties (iv), (v) and (vi) of Theorem 112.

• (2) M is said to admit an integral polarized Hodge structure if one can take $\xi$ as above in $H^2(M, {\mathbb {Z}})$.

Thus the differentiable manifolds underlying a complex Kähler manifolds admit a real polarized Hodge structure, while those underlying a complex projective manifold admit an integral polarized Hodge structure.

Voisin showed that these properties can distinguish between Kähler and projective manifolds. We need here perhaps to recall once more that deformation equivalent complex manifolds are diffeomorphic.

Theorem 114

(Voisin [364]) In any complex dimension $n \ge 4$ there exist compact Kähler manifolds which are not homotopically equivalent to a complex projective manifold.

The construction is not so complicated: taking a complex torus T with an appropriate endomorphism $\varphi$, and blowing up $T \times T$ along four subtori

$$\begin{aligned} T \times \{0\}, \{0\} \times T, \Delta _T, \Gamma _{\varphi }, \end{aligned}$$

where $\Delta _T$ is the diagonal, and $\Gamma _{\varphi }$ is the graph of $\varphi$, one obtains the desired Kähler manifold X.

The crucial property is the following lemma

Lemma 115

(Voisin [364]) Assume that the characteristic polynomial f of $\varphi$, a monic integral polynomial, has all eigenvalues of multiplicity 1, none of them is real, and moreover the Galois group of its splittiing field is the symmetric group ${\mathcal {S}}_{2n}$.

Then T is not an Abelian variety.

We refer to the original paper for details of the construction and proof. However, since our X is obviously bimeromorphic to the torus $T \times T$ , which is a deformation of a projective manifold, later Voisin went on to prove a stronger result in [365].

Theorem 116

(Voisin [365]) In any complex dimension $n \ge 10$ there exist compact Kähler manifolds such that no compact smooth bimeromorphic model $X'$ of X is homotopically equivalent to a complex projective manifold. Indeed, no such model $X'$ has the same rational cohomology ring of a projective manifold.

That the rational cohomology ring was the essential topological invariant of Kähler manifolds, had been found already some 30 years before by Deligne, Griffiths, Morgan, and Sullivan  [134], using Sullivan’s theory of rational homotopy theory and minimal models of graded differential algebras (see [195] for a thourough introduction, and for some of the notation that we shall introduce here without explanation).

Theorem 117

Let X, Y be compact complex manifolds, which are either Kähler, or such that the $d d^c$ lemma holds for them (as for instance it happens when X is bimeromorphic to a cKM).

• (1) Then the real homotopy type of X is determined by its real cohomology ring $H^*(X, {\mathbb {R}})$ , and similarly the effect of every holomorphic map $f : X \rightarrow Y$ on real homotopy types is a formal consequence of the induced homomorphism of real cohomology rings $f^* : H^*(Y, {\mathbb {R}}) \rightarrow H^*(X, {\mathbb {R}})$.

• (2) If moreover X is simply connected, then the graded Lie algebra of real homotopy groups $\pi _*(X) \otimes _{{\mathbb {Z}}}{\mathbb {R}}$ depends only on the cohomology ring $H^*(X, {\mathbb {R}})$. In particular, all Massey products of any order are zero over ${\mathbb {Q}}$.

• (3) If instead X is not simply connected, then the real form of the canonical tower of nilpotent quotients of $\pi _1(X)$ (the real form is obtained by taking $\otimes _{{\mathbb {Z}}}{\mathbb {R}}$ of graded pieces and extension maps) is completely determined by $H^1(X, {\mathbb {R}})$ and the cup product map

  $$\begin{aligned} H^1(X, {\mathbb {R}}) \times H^1(X, {\mathbb {R}})\rightarrow H^2(X, {\mathbb {R}}). \end{aligned}$$

The article [134] contains several proofs, according to the taste of the several authors.

A basic property of compact Kähler manifolds which plays here a key role is the following lemma, also called principle of the two types in [194].

Lemma 118

($d d^c$-Lemma) Let $\phi$ be a differential form such that

• (1) $\partial \phi = \overline{\partial } \phi = 0$ (equivalently, $d \phi = d^c \phi = 0$, where $d^c$ is the real operator $-i ( \partial - \overline{\partial } )$),

• (2) $d (\phi ) = 0$ (or $d^c (\phi ) = 0$), then

• (3) there exists $\psi$ such that $\phi =\partial \overline{\partial } \psi$ (equivalently, there exists $\psi$ such that $\phi = d d^c (\psi )$).

One can see the relation of the above lemma with the vanishing of Massey products, which we now define in the simplest case.

Definition 119

Let X be a topological space, and let $a,b,c \in H^i(X , R)$ be cohomology classes such that

$$\begin{aligned} a \cup b = b \cup c = 0, \end{aligned}$$

where R is any ring of coefficients.

Then the triple Massey product $\langle {a,b,c}\rangle$ is defined as follows: take cocycle representatives $a', b', c'$ for a, b, c,  respectively, and cochains $x,y \in C^{2i-1}(X, R)$ such that

$$\begin{aligned} dx = a' \cup b', dy = b' \cup c'. \end{aligned}$$

Then $\langle {a,b,c}\rangle$ is the class of

$$\begin{aligned} a' \cup y + (-1)^{i+1} x \cup c' \end{aligned}$$

inside

$$\begin{aligned} H^{3i -1}(X, R) / (a \cup H^{2i -1}(X, R)+ H^{2i -1}(X, R)\cup c). \end{aligned}$$

Concerning the choice of the ring R of coefficients: if we take X a cKM, and $R = {\mathbb {R}}$, or $R= {\mathbb {Q}}$, then these Massey products vanish, as stated in [134].

Instead things are different for torsion coefficients, as shown by Torsten Ekedahl [150].

Theorem 120

• (i) There exist a smooth complex projective surface X and $a,b,c \in H^1( X, {\mathbb {Z}}/l)$ such that $a \cup b = b \cup c = 0,$ but $\langle {a,b,c}\rangle \ne 0$.

• (ii) Let $X \rightarrow {\mathbb {P}}^6$ be an embedding and let Y be the blow up of ${\mathbb {P}}^6$ along X.

Then there exist $a'',b'',c'' \in H^3( X, {\mathbb {Z}}/l)$ such that $a'' \cup b'' = b'' \cup c'' = 0,$ but $\langle {a'',b'',c''}\rangle \ne 0$.

Remark 121

• (1) As already mentioned, Theorem 112 is an essential ingredient in the proof of the third Lefschetz theorem. Indeed, for a smooth hyperplane section $W = H \cap X$ of a projective variety X, the cup product with the hyperplane class $h \in H^2(X, {\mathbb {Z}})$ corresponds at the level of forms to the operator L given by wedge product with $\xi$, the first Chern form of ${\mathcal {O}}_X(H)$.

• (2) Most Kähler manifolds, for instance a general complex torus, do not admit any nontrivial analytic subvariety (nontrivial means: different from X or from a point). Whereas for projective varieties X of dimension $n \ge 2$ one can take hyperplane sections successively and obtain a surface S with $\pi _1(S) \cong \pi _1(X)$. Hence the well known fact that the set of fundamental groups of smooth projective varieties is just the set of fundamental groups of smooth algebraic surfaces.

• (3) As explained in the book by Shafarevich [337], the same idea was used by J.P. Serre to show that any finite group G occurs as the fundamental group of a smooth projective surface S. Serre considers the regular representation on the Cartesian product of Y indexed by G, which we denote as usual by $Y^G$, and where for instance $Y = {\mathbb {P}}^m$ is a simply connected projective variety of dimension $m \ge 3$. The quotient $X: = (Y^G)/G$ is singular on the image of the big diagonal, which however has codimension at least m. Cutting X with an appropriate number of general hyperplanes one obtains a surface S with $\pi _1(S) \cong G$.

• (4) Serre’s result is used in Ekedahl’s theorem: Ekedahl shows the existence of a group G of order $l^5$ such that there is a principal fibration $K(G,1) \rightarrow K(({\mathbb {Z}}/l)^3,1)$ with fibre a $K(({\mathbb {Z}}/l)^2,1)$; moreover he deduces the existence of elements a, b, c as desired from the fact that there is some CW complex with non zero triple Massey product.

Then the blow up of ${\mathbb {P}}^6$ along a surface X with $\pi _1(X) \cong G$ is used to obtain an example with classes in the third cohomology group $H^3(Y, {\mathbb {Z}}/l)$.

7.7 The Shafarevich conjecture

One of the many reasons of the beauty of the theory of curves is given by the uniformization theorem, stating that any complex manifold C of dimension 1 which is not of special type (i.e., not ${\mathbb {P}}^1$, ${\mathbb {C}}$, ${\mathbb {C}}^*$, or an elliptic curve) has as universal covering the unit disk ${\mathbb {B}}_1 = \{ z \in {\mathbb {C}}| |z| < 1 \}$, which is biholomorphic to the upper half plane ${\mathbb {H}}= \{ z \in {\mathbb {C}}|Im (z) > 0 \}$.

In other terms, the universal cover is either ${\mathbb {P}}^1$, ${\mathbb {C}}$, or ${\mathbb {H}}$ according to the sign of the curvature of a metric with constant curvature (positive, zero or negative).

In higher dimensions there are simply connected projective varieties that have a positive dimensional moduli space: already in the case of surfaces, e.g., smooth surfaces in ${\mathbb {P}}^3$, of degree at least 3, there is an uncountable family of pairwise non isomorphic varieties.

So, if there is some analogy, it must be a weaker one, and the first possible direction is to relate somehow Kodaira dimension with curvature.

In the case where the canonical divisor $K_X$ is ample, there is the theorem of Aubin and Yau (see [16, 376]) showing the existence, on a projective manifold with ample canonical divisor $K_X$, of a Kähler–Einstein metric, i.e. a Kähler metric $\omega$ such that

$$\begin{aligned} Ric (\omega ) = - \omega . \end{aligned}$$

This theorem is partly the right substitute for the uniformization theorem in dimension $n >1$, but the Kähler–Einstein condition, i.e. the existence of a Kähler metric $\omega$ such that

$$\begin{aligned} Ric (\omega ) = c \omega , \end{aligned}$$

forces $K_X$ ample if $c <0$, $K_X$ trivial if $c=0$, and $- K_X$ ample if $c >0$.

In the case where $K_X$ is trivial, Yau showed the existence of a Kähler–Einstein metric in [376], while the existence of such a metric on Fano manifolds (those with ample anticanonical divisor $- K_X$) has only recently been settled, under a stability assumption (see [122, 123, 352]).

In the general case, one is looking for suitable metrics on singular varieties, but we shall not dwell on this here, since we are focusing on topological aspects: we refer for instance to [162] (see also [204]). Once more, however, curvature influences topology: Yau showed in fact [375] that, for a projective manifold with ample canonical divisor $K_X$, the famous Yau inequality is valid

$$\begin{aligned} K_X^n \le \frac{2(n + 1)}{n} K_X^{n-2} c_2 (X), \end{aligned}$$

equality holding if and only if the universal cover $\widetilde{X}$ is the unit ball ${\mathbb {B}}_n$ in ${\mathbb {C}}^n$.

The second possible direction is to investigate properties of the universal covering $\tilde{X}$ of a projective variety. For instance, one analogue of projective curves of genus $g \ge 2$, whose universal cover is the unit ball ${\mathbb {B}}_1 \subset {\mathbb {C}}$, is given by the compact complex manifolds X whose universal covering $\tilde{X}$ is biholomorphic to a bounded domain $\Omega \subset {\mathbb {C}}^n$.

Necessarily such a manifold X is projective and has ample canonical divisor $K_X$ (see [246, 247], Theorem 8.4 p. 144, where the Bergman metric is used, while the method of Poincaré series is used in [340], Theorem 3 p. 117 , see also [255], Chapter 5).

Moreover, it is known, by a theorem of Siegel ([339], cf. also [242], Theorem 6.2), that $\Omega$ must be holomorphically convex, indeed a Stein domain. We recall these concepts (see for instance [6, 185]).

Definition 122

A complex space X is said to be a Stein complex space if and only if one of the following equivalent conditions hold:

• (1S) X is a closed analytic subspace of ${\mathbb {C}}^N$, for some N,

• (2S) for any coherent analytic sheaf ${\mathcal {F}}$, we have $H^j(X, {\mathcal {F}}) = 0$, for all $j \ge 1$,

• (3S) X coincides with the maximal spectrum $Spec^m(Hol_X)$ of its algebra of global holomorphic functions $Hol_X : = H^0(X, {\mathcal {O}}_X)$, where $Spec^m(Hol_X)$ is the subspace of $Spec(Hol_X)$ consisting of the maximal ideals.

• (4S) Global holomorphic functions separate points and X possesses a ${\mathcal {C}}^{\infty }$ strictly plurisubharmonic exhaustion function, i.e., there is a real valued proper function $f : X \rightarrow {\mathbb {R}}$ such that the Levi form ${\mathcal {L}}(f) : = i \partial \overline{\partial } f$ is strictly positive definite on the Zariski tangent space of each point.

A complex space is said to be holomorphically convex if and only if one of the following equivalent conditions hold:

• (1HC) For each compact K, its envelope of holomorphy $K' : = \{ x \in X | |f(x)| \le max_K |f|\}$ is also compact

• (2HC) X admits a proper holomorphic map $s : X \rightarrow \Sigma$ to a complex Stein space (this map is called Steinification, or Cartan–Remmert reduction), which induces an isomorphism of function algebras $s^* : Hol_{\Sigma } \rightarrow Hol_X$.

• (3HC) X admits a real valued twice differentiable proper function $f : X \rightarrow {\mathbb {R}}$ and a compact $K \subset X$ such that

  • (3i) there is a number $c \in {\mathbb {R}}$ with $f^{-1} (( - \infty , c]) \subset K$

  • (3ii) the Levi form ${\mathcal {L}}(f) : = i \partial \overline{\partial } f$ is semipositive definite and strictly positive definite outside K.

Finally, a complex space X is Stein manifold iff it is holomorphically convex and global holomorphic functions separate points.

Now, a compact complex manifold (or space) is by definition holomorphically convex, so this notion captures two extreme behaviours of the universal covers we just described: bounded domains in ${\mathbb {C}}^n$, and compact manifolds. In his book [337] Shafarevich answered the following

Shafarevich’s question: is the universal covering $\tilde{X}$ of a projective variety X, or of a compact Kähler manifold X, holomorphically convex?

Remark 123

The answer is negative for a compact complex manifold that is not Kähler, since for instance Hopf surfaces $X = ({\mathbb {C}}^2 {\setminus } \{0\})/ {\mathbb {Z}}$ have ${\mathbb {C}}^2 {\setminus } \{0\}$ as universal cover, which is not Stein since it has the same algebra of holomorphic functions as the larger affine space ${\mathbb {C}}^2$.

Observe that all the $K(\pi , 1)$ projective manifolds we have considered so far satisfy the Shafarevich property, since their universal covering is either ${\mathbb {C}}^n$ or a bounded domain in ${\mathbb {C}}^n$ (this holds also for Kodaira fibred surfaces, by Bers’ simultaneous uniformization, [40]).

An interesting question concerns projective varieties whose universal cover is a bounded domain ${\mathcal {D}}$ in ${\mathbb {C}}^n$. In this case the group $Aut ({\mathcal {D}})$ contains an infinite cocompact subgroup, so it is natural to look first at domains which have a big group of automorphisms, especially at bounded homogeneous domains, i.e., bounded domains such that the group ${\mathrm {Aut}}(\Omega )$ of biholomorphisms of $\Omega$ acts transitively.

But, as already mentioned, a classical result of J. Hano (see [207] Theorem IV, p. 886, and Lemma 6.2, p. 317 of [292]) asserts that a bounded homogeneous domain that covers a compact complex manifold is a bounded symmetric domain.

These naturally occur as such universal covers: Borel proved in [57] that for each bounded symmetric domain there exists a compact free quotient $X = \Omega / \Gamma$, called a Hermitian locally symmetric projective manifold (these were also called compact Clifford-Klein forms of the symmetric domain $\Omega$).

By taking finite ramified coverings of such locally symmetric varieties, and blow ups of points of the latter, we easily obtain many examples which are holomorphically convex but not Stein. But if we blow up some subvariety $Y \subset X$ of positive dimension some care has to be taken: what is the inverse image of Y in the universal cover $\tilde{X}$? It depends on the image of $\pi _1(Y)$ inside $\pi _1(X)$: if the image is finite, then we obtain a disjoint union of compact varieties, else the connected components of the inverse image are not compact.

A more general discussion leads to the following definition.

Definition 124

Assume that the Shafarevich property holds for a compact Kähler manifold: then the fundamental group $\pi _1(X)$ acts properly discontinuously on $\tilde{X}$ and on its Steinification $\Sigma$, hence one has a quotient complex space of $\Sigma$ which is holomorphically dominated by X:

$$\begin{aligned} Shaf(X) : = \Sigma / \pi _1(X) , shaf_X: X= \tilde{X} / \pi _1(X) \rightarrow Shaf(X) = \Sigma / \pi _1(X). \end{aligned}$$

Shaf(X) is then called the Shafarevich variety of X, and $shaf_X$ is called the Shafarevich morphism. They are characterized by the following universal property:

a subvariety $Y \subset X$ is mapped to a point in Shaf(X) if and only if, letting $Y^n$ be the normalization of Y, the image of $\pi _1(Y^n) \rightarrow \pi _1(X)$ is finite.

So, a first attempt towards the question was in the 90’s to verify the existence of the Shafarevich morphism $shaf_X$.

A weaker result was shown by Kollár [254] and by Campana [71]: we borrow here the version of Kóllar, which we find more clearly formulated.

Theorem 125

Let X be a normal projective variety: then X admits a rational Shafarevich map $shaf_X: X \dashrightarrow Shaf(X)$, with the following properties:

• (1) $shaf_X$ has connected fibres

• (2) there are countably many subvarieties $D_i \subset X$ such that for every subvariety $Y \subset X$, $Y \nsubseteq \cup _i D_i$, $shaf_X (Y)$ is a point if and only if, letting $Y^n$ be the normalization of Y, the image of $\pi _1(Y^n) \rightarrow \pi _1(X)$ is finite.

Moreover, the above properties determine Shaf(X) up to birational equivalence.

Remark 126

(1) A subtle point concerning the definition of Shafarevich morphism is the one of passing to the normalization of a subvariety Y. In fact, the normalization $Y^n$ has a holomorphic map to X since X is normal, and the fibre product $Y^n \times _X \tilde{X}$ has a holomorphic map to $\tilde{X}$. If the image of $\pi _1(Y^n) \rightarrow \pi _1(X)$ is finite, this fibre product consists of a (possibly infinite) Galois unramified covering of $Y^n$ whose components are compact.

If $\tilde{X}$ is holomorphically convex, then these components map to points in the Steinification $\Sigma$.

(2) Consider the following special situation: X is a smooth rational surface, and Y is a curve of geometric genus zero with a node. Then the normalization is ${\mathbb {P}}^1$ and the Shafarevich map should contract $Y^n$.

Assume however that $\pi _1(Y) \cong {\mathbb {Z}}$ injects into $\pi _1(X)$: then the inverse image of Y in $\tilde{X}$ consists of an infinite chain of ${\mathbb {P}}^1$’s, which should be contracted by the Steinification morphism, hence this map would not be proper. The existence of a curve satisfying these two properties would then give a negative answer to the Shafarevich question.

(3) In other words, the Shafarevich property implies that:

(***) if $\pi _1(Y^n) \rightarrow \pi _1(X)$ has finite image , then also $\pi _1(Y) \rightarrow \pi _1(X)$ has finite image.

So, we can define a subvariety to be Shafarevich bad if

(SB) $\pi _1(Y^n) \rightarrow \pi _1(X)$ has finite image , but $\pi _1(Y) \rightarrow \pi _1(X)$ has infinite image.

The rough philosophy of the existence of a rational Shafarevich map is thus that Shafarevich bad subvarieties do not move in families which fill the whole X, but they are contained in a countable union of subvarieties $D_i$ (one has indeed to take into account also finite union of subvarieties, for instance two ${\mathbb {P}}^1$’s crossing transversally in 2 points: these are called by Kollár ‘normal cycles’).

But still, could they exist, giving a negative answer to the Shafarevich question?

Potential counterexampes were proposed by Bogomolov and Katzarkov [49], considering fibred surfaces $f : X \rightarrow B$. Indeed, for each projective surface, after blowing up a finite number of points, we can always obtain such a fibration.

Assume that $f : X \rightarrow B$ is a fibration of hyperbolic type: then, passing to a finite unramified covering of X and passing to a finite covering of the base B, we may assume that the fibration does not have multiple fibres.

Then (see Theorem 96) the surjection $\pi _1(X) \rightarrow \pi _1(B)$ induces an infinite unramified covering

$$\begin{aligned} \hat{f} : \hat{X} \rightarrow \hat{B} : = {\mathbb {H}}= {\mathbb {B}}_1, \end{aligned}$$

and we shall say that this fibration is obtained by opening the base.

If instead $f : X \rightarrow B$ is a fibration of parabolic type, we get an infinite unramified covering

$$\begin{aligned} \hat{f} : \hat{X} \rightarrow \hat{B} : = {\mathbb {C}}. \end{aligned}$$

In the elliptic case, $B= {\mathbb {P}}^1$ and we set $\hat{X} : = X, \hat{B} : = B$.

Now, the Shafarevich question has a positive answer if the fundamental group of $\hat{X}$, the image of the fundamental group of a general fibre F inside $\pi _1(X)$, is finite.

Assume instead that this image is infinite and look at components of the singular fibres: we are interested to see whether we find some Shafarevich bad cycles. For this, it is important to describe the fundamental group $\pi _1(\hat{X} )$ as a quotient of $\pi _g = \pi _1 (F)$, where F is a general fibre, and g is its genus.

Observe preliminarily that we may assume that there are singular fibres, else either we have a Kodaira fibration, or an isotrivial fibration (see [285]) so that, denoting by $B^*$ the complement of the critical locus of $\hat{f}$, the fundamental group of $B^*$ is a free group.

For each singular fibre $F_t, t \in B$, a neighbourhood of $F_t$ is retractible to $F_t$, and because of this we have a continuous map $F \rightarrow F_t$.

The group of local vanishing cycles is defined as the kernel of $\pi _1(F )\rightarrow \pi _1(F_t)$,and denoted by $Van_t$.

Then we obtain a description of $\pi _1(\hat{X} )$ as

$$\begin{aligned} \pi _1(\hat{X} ) = \pi _g / \langle \langle \cup _t \{ Van_t \} \rangle \rangle , \end{aligned}$$

where $\langle \langle M \rangle \rangle$ denotes the subgroup normally generated by M.

Bogomolov and Katzarkov consider the situation where the fibre singularities are exactly nodes, and then for each node p there is a vanishing cycle $van_p$ on the nearby smooth fibre. In this case we divide by the subgroup normally generated by the vanishing cycles $van_p$.

Their first trick is now to replace the original fibration by the pull back via a map $\varphi : B' \rightarrow B$ which is ramified at each critical value t of multiplicity N.

In this way they obtain a surface $X'$ which is singular, with singular points q of type $A_{N-1}$, i.e., with local equation $z^N = xy$. Since these are quotient singularities ${\mathbb {C}}^2 / ({\mathbb {Z}}/N)$, they have local fundamental group $\pi _{1, loc} (X'{\setminus } \{q\}) = {\mathbb {Z}}/N$.

As a second step, they construct another surface $S_N$ such that the image of $\pi _1(S_N)$ has finite index inside $\pi _1 (X' {\setminus } Sing(X'))$.

They show (lemma 2.7 and theorem 2.3 of loc. cit.) the following.

Proposition 127

The Bogomolov–Katzarkov procedure constructs a new fibred surface $S_N$ such that, if we open the base of the fibration, we get a surface $\hat{S_N}$ such that

$$\begin{aligned} \pi _1(\hat{S_N} ) = \pi _g / \langle \langle \cup _p \{ van_p^N \} \rangle \rangle . \end{aligned}$$

In this way they propose to construct counterexamples to the Shafarevich question (with non residually finite fundamental group), provide certain group theoretic questions have an affirmative answer.

Remark 128

We want to point out a topological consequence of the Shafarevich property, for simplicity we consider only the case of a projective surface X with infinite fundamental group.

Assume that $\tilde{X}$ is holomorphically convex, and let $s : \tilde{X} \rightarrow \Sigma$ the Cartan–Remmert reduction morphism, where $\Sigma$ is Stein and simply connected. If $dim (\Sigma ) = 1,$ then $\Sigma$ is contractible, otherwise we know [4] that $\Sigma$ is homotopy equivalent to a CW complex of real dimension 2.

In the first case we have a fibration with compact fibres of complex dimension 1, in the second case we have a discrete set such that the fibre has complex dimension 1, and the conclusion is that:

if a projective surface with infinite fundamental group satisfies the Shafarevich property, then $\tilde{X}$ is homotopy equivalent to a CW complex of real dimension at most 2.

To my knowledge, even this topological corollary of the Shafarevich property is yet unproven.

On the other hand, the main assertion of the Shafarevich property is that the quotient of $\tilde{X}$ by the equivalence relation which contracts to points the compact analytic subspaces of $\tilde{X}$ is not only a complex space, but a Stein space. This means that one has to produce a lot of holomorphic functions on $\tilde{X}$, in order to embed the quotient as a closed analytic subspace in some ${\mathbb {C}}^N$.

There are positive results, which answer the Shafarevich question in affirmative provided the fundamental group of X satisfies certain properties, related somehow to some of the themes treated in this article, which is the existence of certain homomorphisms to fundamental groups of classifying spaces, and to the theory of harmonic maps. To give a very very simple idea, an easy result in this directions is that $\tilde{X}$ is a Stein manifold if the Albanese morphism $\alpha : X \rightarrow A : = Alb(X)$ is a finite covering.

Now, since there has been a series of results in this direction,we refer to the introduction and bibliography in the most recent one [160] for some history of the problem and for more information concerning previous results, especially the first ones due to Jost and Zuo (for instance, [198, 229–231]) and other ones.

We want however to directly cite some previous results due to Katzarkov and Ramachandran [234], respectively to Eyssidieux [159] (see also [161] for a general introduction) which are simpler to state. We only want to recall that a reductive representation is one whose image group is reductive, i.e., all of its representations are semi-simple, or completely reducible (any invariant subspace $W \subset V$has an invariant complement).

Theorem 129

(Katzarkov–Ramachandran) Let X be a normal Kähler compact surface, and $X' \rightarrow X$ an unramified cover with Galois group $\Gamma$ (so $X = X' / \Gamma$). If $\Gamma$ does not contain ${\mathbb {Z}}$ as a finite index subgroup and it admits an almost faithful (i.e., with finite kernel) Zariski dense representation in a connected reductive complex Lie group, then $X'$ is holomorphically convex.

Theorem 130

(Eyssidieux) Let X be a smooth projective variety, consider a homomorphism $\rho : \pi _1(X) \rightarrow G$, and let $\tilde{X}_{\rho } : = \tilde{X}/ ker (\rho )$ be the connected unramified covering of X associated to $ker (\rho )$.

• (1) If $G = {{\mathrm{\text {GL}}}}(n, {\mathbb {C}})$ and $\rho$ is a reductive representation, then there is a relative Shafarevich morphism

  $$\begin{aligned} shaf_{\rho } : X \rightarrow Shaf_{\rho }(X) \end{aligned}$$

  to a normal projective variety, satisfying the universal property that for each normal variety Z mapping to X, its image in $Shaf_{\rho }(X)$ is a point if and only if the image of $\pi _1(Z) \rightarrow \pi _1(X)$ is finite. Moreover, the connected components of the fibres of $\tilde{X}_{\rho } \rightarrow Shaf_{\rho }(X)$ are compact.

• (2) Let M be a quasi compact and absolute constructible (i.e., it remains constructible after the action of each $\sigma \in Aut({\mathbb {C}})$) set of conjugacy classes of reductive linear representations of $\pi _1(X)$, and let $H_M$ be the intersection of the respective kernels. Then $\tilde{X}_M : = \tilde{X}/ H_M$ is holomorphically convex.

The main result of [160] consists of two parts, the first one being the following:

Theorem 131

(Eyssidieux–Katzarkov–Pantev–Ramachandran) Let X be a smooth projective variety, and let G be a reductive algebraic group defined over ${\mathbb {Q}}$. Consider the Betti character scheme $M : = M_B (X, B)$ such that, for a ${\mathbb {C}}$-algebra A of finite type, the set of A-valued points $M(A) = M( Spec(A))$ parametrizes the representations

$$\begin{aligned} (*) \ \ \rho : \pi _1(X) \rightarrow G(A). \end{aligned}$$

• (1) Denote by $\tilde{H}_M^{\infty }$ the kernel of all such representations: then the associated Galois connected unramified covering $\tilde{X}_M^{\infty }$ is holomorphically convex.

• (2) there is a non-increasing family of normal subgroups $\tilde{H}_M^{k}$ (obviously containing $\tilde{H}_M^{\infty }$), which correspond to homomorphisms $\rho : \pi _1(X) \rightarrow G(A)$, with the property that A is an Artinian local ${\mathbb {C}}$-algebra, and that the Zariski closure of the image has k-step unipotent radical.

Then the associated Galois connected unramified covering $\tilde{X}_M^{k}$ is holomorphically convex.

7.8 Strong and weak rigidity for projective $K(\pi , 1)$ manifolds

We want here to see how the moduli problem is solved for many projective $K(\pi , 1)$ manifolds, which were mentioned in Sect. 3. However, we want here not to be entangled in the technical discussion whether a variety of moduli exists, and, if so, which properties does it have. So, we use the notion of deformation equivalence introduced by Kodaira and Spencer.

Definition 132

(Rigidity)

• (1) Let X be a projective manifold: then we say that X is strongly rigid if, for each projective manifold Y homotopy equivalent to X, then Y is isomorphic to X or to the complex conjugate variety $\bar{X}$ ($X \cong Y$ or $\bar{X} \cong Y$).

• (2) We say instead that X is weakly rigid if, for each other projective manifold Y homotopy equivalent to X, then either Y is direct deformation of X, or Y is direct deformation of $\bar{X}$ (see 109).

• (3) We say instead that X is quasi rigid if, for each other projective manifold Y homotopy equivalent to X, then either Y is deformation equivalent to X, or Y is deformation equivalent to $\bar{X}$ (recall that deformation equivalence is the equivalence relation generated by the relation of direct deformation).

Remark 133

• (a) This is the intuitive meaning of the above definition: assume that there is a moduli space ${\mathfrak {M}}$, whose points correspond to isomorphism classes of certain varieties, and such that for each flat family $p: {\mathcal {X}}\rightarrow B$ the natural map $B \rightarrow {\mathfrak {M}}$ associating to $b \in B$ the isomorphism class of the fibre $X_b : = p^{-1} (b)$ is holomorphic. Then to be a direct deformation of each other means to belong to the same irreducible component of the moduli space ${\mathfrak {M}}$, while being deformation equivalent means to belong to the same connected component of the moduli space ${\mathfrak {M}}$.

• (b) The same definition can be given in the category of compact Kähler manifolds, or in the category of compact complex manifolds.

• (c) Of course, if $p: {\mathcal {X}}\rightarrow B$ is a smooth proper family with base B a smooth connected complex manifold, then all the fibres $X_b$ are direct deformation equivalent.

• (d) We shall need in the sequel some more technical generalization of these notions, which amount, given a product of varieties $X_1 \times X_2 \times \cdots \times X_h$, to take the complex conjugate of a certain number of factors.

Definition 134

Let X be a projective manifold: then we say that X is strongly * rigid if, for each other projective manifold Y homotopy equivalent to X, then Y is isomorphic to X or to another projective variety Z obtained by X as follows: there is a Galois unramified covering $X'$ of X ( thus $X = X' / G$) which splits as a product

$$\begin{aligned} X' = X'_1 \times X'_2 \times \cdots \times X'_h. \end{aligned}$$

Set then, after having fixed a subset ${\mathcal {J}}\subset \{1, \ldots , h\}$: $Z' _j : = \overline{ X'_j }$ for $j \in {\mathcal {J}}$, and $Z'_j : = X'_j$ for $j \notin {\mathcal {J}}$. Consider then the action of G on $Z' = (Z'_1 \times Z'_2 \times \cdots \times Z'_h)$, and let $Z : = Z' / G$.

Replacing the word: ‘isomorphic’ by ‘direct deformation equivalent’, resp. ‘deformation equivalent’, we define the notion of weakly * rigid, resp. quasi * rigid.

• (1) The first example, the one of projective curves, was essentially already discussed: we have the universal family

  $$\begin{aligned} p_g: {\mathcal {C}}_g \rightarrow {\mathcal {T}}_g, \end{aligned}$$

  hence, according to the above definition, projective curves are weakly rigid (and in a stronger way, since we do not need to allow for complex conjugation, as the complex conjugate $\bar{C}$ is a direct deformation of C).

• (2) Complex tori are weakly rigid in the category of compact Kähler manifolds, since any manifold with the same integral cohomology of a complex torus is a complex torus (Theorem 77).

Moreover, complex tori are parametrized by an open set ${\mathcal {T}}_n$ of the complex Grassmann Manifold Gr(n, 2n), image of the open set of matrices $\{ \Omega \in Mat(2n,n; {\mathbb {C}}) \ | i^n det (\Omega \overline{\Omega }) > 0 \},$ as follows: we consider a fixed lattice $\Gamma \cong {\mathbb {Z}}^{2n}$, and to each matrix $\Omega$ as above we associate the subspace

$$\begin{aligned} V = \Omega {\mathbb {C}}^{n}, \end{aligned}$$

so that $V \in Gr(n,2n)$ and $\Gamma \otimes {\mathbb {C}}\cong V \oplus \bar{V}$.

Finally, to $\Omega$ we associate the torus $Y_V : = V / p_V (\Gamma )$, $p_V : V \oplus \bar{V} \rightarrow V$ being the projection onto the first addendum.

As it was shown in [100] (cf. also [103]) ${\mathcal {T}}_n$ is a connected component of Teichmüller space.

• (3) Complex tori are not quasi rigid in the category of compact complex manifolds. Sommese generalized some construction by Blanchard and Calabi, obtaining [348] that the space of complex structures on a six dimensional real torus is not connected.

• (4) Abelian varieties are quasi rigid, but not weakly rigid. In fact, we saw that all the Abelian varieties of dimension g admitting a polarization of type $D'$ are contained in a family over ${\mathcal {H}}_g$. Moreover, products $E_1 \times \cdots \times E_g$ of elliptic curves admit polarizations of each possible type.

• (5) Locally symmetric manifolds ${\mathcal {D}}/ \Gamma$ where ${\mathcal {D}}$ is irreducible of dimension $> 1$ are strongly rigid by Siu’s theorem 90.

• (6) Locally symmetric manifolds ${\mathcal {D}}/ \Gamma$ with the property that ${\mathcal {D}}$ does not have any irreducible factor of dimension 1 are strongly * rigid by Siu’s theorem 90.

• (7) Varieties isogenous to a product (VIP) are weakly * rigid in all dimensions, according to Theorem 136, that we are going to state soon (see below). They are weakly rigid in dimension $n=2$ only if we require the homotopy equivalence to be orientation preserving.

• (8) Among the VIP’s, the strongly * rigid are exactly the quotients $X = (C_1 \times C_2 \times \cdots \times C_n)/ G$ where G not only acts freely, but satisfies the following property. Denote by $G^0 \subset G$ (see [96] for more details) the subgroup which does not permute the factors, and observe that

  $$\begin{aligned} G^0 \subset {{\mathrm{\text {Aut}}}}(C_1) \times {{\mathrm{\text {Aut}}}}(C_2 )\times \cdots \times {{\mathrm{\text {Aut}}}}(C_n). \end{aligned}$$

  Then $G^0$ operates on each curve $C_i$, and the required condition is that this action is rigid, more precisely we want : $C_i / G^0 \cong {\mathbb {P}}^1$ and the quotient map $p_i : C_i \rightarrow C_i / G^0 \cong {\mathbb {P}}^1$ is branched in three points (we shall also say that we have then a triangle curve).

Again, in dimension $n=2$ we get some strongly rigid surfaces, which have been called (ibidem) Beauville surfaces. We propose therefore to call Beauville varieties the strongly * rigid VIP’s.

• (9) Hyperelliptic surfaces are weakly rigid, as classically known, see below for a more general result.

• (10) It is unclear, as we shall see, whether Kodaira fibred surfaces are weakly * rigid, however any surface homotopically equivalent to a Kodaira fibred surface is also a Kodaira fibred surface. Indeed a stronger result, with a similar method to the one of [96] was shown by Kotschick (see [258] and Theorem 138 below), after some partial results by Jost and Yau.

• (11) Generalized hyperelliptic varieties X are a class of varieties for which a weaker property holds. Namely, if Y is a compact Kähler manifold which is homotopy equivalent to X (one can relax this assumption a bit, obtaining stronger results), then Y is the quotient of ${\mathbb {C}}^n$ by an affine action of $\Gamma : = \pi _1 (X) \cong \pi _1 (Y)$ which, using Proposition 150, can be shown to have the same real affine type as the action yielding X as a quotient. But the Hodge type could be different, except in special cases where weak rigidity holds.

The following (see [96, 98]) is the main result concerning surfaces isogenous to a product, and is a stronger result than weak * rigidity.

Theorem 135

(a) A projective smooth surface S is isogenous to a product of two curves of respective genera $g_1, g_2 \ge 2$ , if and only if the following two conditions are satisfied:

• (1) there is an exact sequence

  $$\begin{aligned} 1 \rightarrow \pi _{g_1} \times \pi _{g_2} \rightarrow \pi = \pi _1(S) \rightarrow G \rightarrow 1, \end{aligned}$$

  where G is a finite group and where $\pi _{g_i}$ denotes the fundamental group of a projective curve of genus $g_i \ge 2$;

• (2) $e(S) (= c_2(S)) = \frac{4}{|G|} (g_1-1)(g_2-1)$. (b) Write $S = (C_1 \times C_2) / G$. Any surface X with the same topological Euler number and the same fundamental group as S is diffeomorphic to S and is also isogenous to a product. There is a smooth proper family with connected smooth base manifold T, $p : {\mathcal {X}}\rightarrow T$ having two fibres respectively isomorphic to X, and Y, where Y is one of the 4 surfaces $S = (C_1 \times C_2) / G$, $S_{+-} : = (\overline{C_1} \times C_2) / G$, $\bar{S }= (\overline{C_1} \times \overline{C_2} ) / G$, $S_{-+} : = (C_1 \times \overline{C_2} ) / G = \overline{ S_{+-} }$.

(c) The corresponding subset of the moduli space of surfaces of general type $\mathfrak {M}^{top}_S = \mathfrak {M}^{diff}_S$, corresponding to surfaces orientedly homeomorphic, resp. orientedly diffeomorphic to S, is either irreducible and connected or it contains two connected components which are exchanged by complex conjugation.

In particular, if $S'$ is orientedly diffeomorphic to S, then $S'$ is deformation equivalent to S or to $\bar{S}$.

Idea of the proof

$\Gamma : = \pi _1 (S)$ admits a subgroup $\Gamma '$ of index d such that $\Gamma ' \cong (\pi _{g_1} \times \pi _{g_2})$. Let $S'$ be the associated unramified covering of S. Then application of the isotropic subspace theorem or of Theorem 96 yields a pair of holomorphic maps $f_j : S' \rightarrow C_j$, hence a holomorphic map

$$\begin{aligned} F : = f_1 \times f_2 : S' \rightarrow C'_1 \times C'_2. \end{aligned}$$

Then the fibres of $f_1$ have genus $h_2 \ge g_2$, hence by the Zeuthen Segre formula (2) $e(S') \ge 4 (h_2 -1 ) (g_1 - 1)$, equality holding if and only if all the fibres are smooth.

But $e(S') = 4 (g_1-1)(g_2-1) \le 4 (h_2 -1 ) (g_1 - 1)$, so $h_2= g_2$, all the fibres are smooth hence isomorphic to $C'_2$; therefore F is an isomorphism.

The second assertion follows from the refined Nielsen realization theorem, Theorem 37, considering the action of the index two subgroup $G^0$ of G. Notice that if a group, here $G^0$, acts on a curve C, then it also acts on the complex conjugate curve, thus $G^0 \subset {{\mathrm{\text {Aut}}}}(C) \Rightarrow G^0 \subset {{\mathrm{\text {Aut}}}}(\bar{C})$. But since complex conjugation is orientation reversing, these two actions are conjugate by ${{\mathrm{\text {Out}}}}(\pi _g)$, not necessarily by ${\mathcal {M}}ap_g = {{\mathrm{\text {Out}}}}^+ (\pi _g)$.

Recall now that the exact sequence

$$\begin{aligned} 1 \rightarrow \pi _{g_1} \times \pi _{g_2} \rightarrow \Gamma ^0 \rightarrow G^0 \rightarrow 1 \end{aligned}$$

yields two injective homomorphisms $\rho _j : G^0 \rightarrow Out (\pi _{g_j} )$ for $j=1,2$. Now, we choose the isomorphism $\pi _1 (C_j) \cong \pi _{g_j}$ in such a way that it is orientation preserving. The isomorphism $\pi _1(X) \cong \pi _1(S)$, and the realization $X = (C'_1 \times C'_2) / G$ then gives an isomorphism $\phi _j : \pi _1 (C'_j) \cong \pi _{g_j}$. If this isomorphism is orientation preserving, then the two actions of $G^0$ on $C_j, C'_j$ are deformation of each other by the refined Nielsen realization. If instead this isomorphism is orientation reversing, then we replace $C_j$ by $\overline{C_j}$ and now the two actions are conjugate by ${\mathcal {M}}ap_g$, so we can apply the refined Nielsen realisation theorem to $\overline{C_j}, C'_j$. Finally, in the case where the homeomorphism of X with S is orientation preserving, then either both $\phi _1, \phi _2$ are orientation preserving, or they are both orientation reversing. Then X is a deformation either of S or of $\bar{S}$. $\square$

The first part of the following theorem is instead a small improvement of theorem 7.1 of [96], the second part is theorem 7.7 ibidem, and relies on the results of Mok [294, 295].

Theorem 136

• (1) Let Y be a projective variety of dimension n with $K_Y$ ample and that $\Gamma : = \pi _1 (Y)$ admits a subgroup $\Gamma '$ of index d such that

  $$\begin{aligned} \Gamma ' \cong \pi _{g_1} \times \pi _{g_2} \times \cdots \times \pi _{g_n}, \ g_i \ge 2 \quad \forall i, \end{aligned}$$

  and moreover $H^{2n} (\Gamma , {\mathbb {Z}}) \rightarrow H^{2n} ( Y, {\mathbb {Z}})$ is an isomorphism. Then Y is a variety isogenous to a product.

• (2) Let X be projective variety with universal covering the polydisk ${\mathcal {H}}^n$, and let Y be a projective variety of dimension n with $K_Y$ ample and such that $\pi _1 (Y) \cong \Gamma : = \pi _1 (X)$, and assume that $H^{2n} (\Gamma , {\mathbb {Z}}) \rightarrow H^{2n} ( Y, {\mathbb {Z}})$ is an isomorphism. Then also Y has ${\mathcal {H}}^n$ as universal covering (hence we have a representation of Y as a quotient $Y = {\mathcal {H}}^n / \Gamma$).

• (3) In particular X is weakly * rigid, and strongly * rigid if the action of $\Gamma$ is irreducible (this means that there is no finite index subgroup $\Gamma ' < \Gamma$ and an isomorphism ${\mathcal {H}}^n \cong {\mathcal {H}}^m \times {\mathcal {H}}^{n-m}$ such that

  $$\begin{aligned} \Gamma ' = \Gamma ' _1 \times \Gamma ' _2, \ \ \Gamma ' _1 \subset {{\mathrm{\text {Aut}}}}( {\mathcal {H}}^m ), \ \Gamma ' _2 \subset {{\mathrm{\text {Aut}}}}( {\mathcal {H}}^{n-m}). \end{aligned}$$

Proof of (1): As in the previous theorem we take the associated unramified covering $Y'$ of Y associated to $\Gamma '$, and with the same argument we produce a holomorphic map

$$\begin{aligned} F : Y' \rightarrow Z : = C_1 \times C_2 \times \cdots \times C_n. \end{aligned}$$

We claim that F is an isomorphism. Indeed, by the assumption $H^{2n} (\Gamma , {\mathbb {Z}}) \cong H^{2n} ( Y, {\mathbb {Z}})$ follows that $H^{2n} (\Gamma ', {\mathbb {Z}}) \cong H^{2n} ( Y', {\mathbb {Z}})$, hence F has degree 1 and is a birational morphism. Let R be the ramification divisor of F, so that $K_{Y'} = F^* ( K_Z) + R$. Now, since F is birational we have $H^0( m K_{Y'} ) \cong H^0 (m K_Z)$, for all $m \ge 0$. This implies for the corresponding linear systems of divisors:

$$\begin{aligned} | m K_{Y'} | = F^* (|m K_Z| ) + m R. \end{aligned}$$

For $m >> 0$ this shows that $K_{Y'}$ cannot be ample, contradicting the ampleness of $K_Y$. $\square$

Remark 137

Part (2) of the above theorem is shown in [96], while part (3) follows by the same argument given in the proof of Theorem 135 in the case where X is isogenous to a product. We omit the proof of (3) in general.

Theorem 138

(Kotschick) Assume that S is a compact Kähler surface, and that

• (i) its fundamental group sits into an exact sequence, where $g,b \ge 2$:

  $$\begin{aligned} 1 \rightarrow \pi _g \rightarrow \pi _1(S) \rightarrow \pi _b \rightarrow 1 \end{aligned}$$

• (ii) $e(S) = 4 (b-1) ( g-1)$.

Then S has a smooth holomorphic fibration $f : S \rightarrow B$, where B is a projective curve of genus b, and where all the fibres are smooth projective curves of genus g. f is a Kodaira fibration if and only if the associated homomorphism $\rho : \pi _b \rightarrow {\mathcal {M}}ap_g$ has image of infinite order, else it is a surface isogenous to a product of unmixed type and where the action on the first curve is free.

Proof

By Theorem 96 the above exact sequence yields a fibration $f : S \rightarrow B$ such that there is a surjection $\pi _1(F) \rightarrow \pi _g$, where F is a smooth fibre. Hence, denoting by h the genus of F, we conclude that $h \ge g$, and again we can use the Zeuthen–Segre formula to conclude that $h = g$ and that all fibres are smooth. So F is a smooth fibration. Let $C' \rightarrow C$ be the unramified covering associated to $\ker (\rho )$: then the pull back family $S' \rightarrow C'$ has a topological trivialization, hence is a pull back of the universal family ${\mathcal {C}}_g \rightarrow {\mathcal {T}}_g$ for an appropriate holomorphic map $\varphi : C' \rightarrow {\mathcal {T}}_g$.

If $\ker (\rho )$ has finite index, then $C'$ is compact and, since Teichmüller space is a bounded domain in ${\mathbb {C}}^{3g-3}$, the holomorphic map is constant. Therefore $S'$ is a product $C' \times C_2$ and, denoting by $G : = {{\mathrm{\text {Im}}}}(\rho )$, $S = (C' \times C_2)$, and we get exactly the surfaces isogenous to a product such that the action of G on the curve $C'$ is free.

If instead $G : = {{\mathrm{\text {Im}}}}(\rho )$ is infinite, then the map of $C'$ into Teichmüller space is not constant, since the isotropy group of a point corresponding to a curve F is, as we saw, equal to the group of automorphisms of F (which is finite). Therefore, in this case, we have a Kodaira fibration. $\square$

Remark 139

Jost and Yau [226] proved a weaker result, that a deformation of the original examples by Kodaira of Kodaira fibrations are again Kodaira fibrations. In our joint paper with Rollenske [109] we gave examples of Kodaira fibred surfaces which are rigid, and we also described the irreducible connected components of the moduli space corresponding to the subclass of those surfaces which admit two different Kodaira fibrations.

Question 140

Are Kodaira fibred surfaces weakly * rigid?

Let us explain why one can ask this question: a Kodaira fibration $f : S \rightarrow B$ yields a holomorphic map $\varphi : B \rightarrow {\mathfrak {M}}_g$. The unramified covering $B'$ associated to $\ker (\rho )$, $\rho : \pi _1 (B) \rightarrow {\mathcal {M}}ap_g$ admits then a holomorphic map $\varphi ' : B' \rightarrow {\mathcal {T}}_g$ which lifts $\varphi$. If ${\mathfrak {M}}_g$ were a classifying space the homomorphism $\rho$ would determine the homotopy class of $\varphi$. A generalization of the cited theorems of Eells and Samson and of Hartmann ([147, 209], see theorem 73)would then show that in each class there is a unique harmonic representative, thus proving that, fixed the complex structure on B, there is a unique holomorphic representative, if any. This might help to describe the locus thus obtained in ${\mathcal {T}}_b$ (the set of maps $\varphi ' : B' \rightarrow {\mathcal {T}}_g$ that are $\rho$-equivariant).

But indeed, our knowledge of Kodaira fibrations is still scanty, for instance the following questions are still open.

Question 141

• (1) Given an exact sequence $1 \rightarrow \pi _g \rightarrow \pi \rightarrow \pi _b \rightarrow 1$ where $g \ge 3$, $b \ge 2$, does there exist a Kodaira fibred surface S with fundamental group $\pi$?

• (2) (Le Brun’s question, see [109]) : are there Kodaira fibred surfaces with slope $c_1^2 / c_2 > 8/3$?

• (3) Are there surfaces admitting three different Kodaira fibrations?

A brief comment on question (1) above. The given exact sequence determines, via conjugation of lifts, a homomorphism $\rho : \pi _b \rightarrow {{\mathrm{\text {Out}}}}^+ (\pi _g) = Map_g$. If the image G of $\rho$ is finite, then $\pi$ is the fundamental group of a surface isogenous to a product, and the answer is positive, as we previously explained.

Case (II) : $\rho$ is injective, hence (as $\pi _b$ has no nontrivial elements of finite order) $G = Im (\rho )$ acts freely on Teichmüller space ${\mathcal {T}}_g$, and $M : = {\mathcal {T}}_g/G$ is a classifying space for $\pi _b$. There is a differentiable map of a curve of genus b into M, and the question is whether one can deform it to obtain a harmonic or holomorphic map.

Case (III) : $\rho$ is not injective. This case is the most frequent one, since, given a Kodaira fibred surface $f : S \rightarrow B$, for each surjection $F : B' \rightarrow B$, the pull-back $S' : = S \times _B B'$ is again a Kodaira fibration and $\rho '$ factors as the composition of the surjection $\pi _1(B') \rightarrow \pi _1(B)$ with $\rho : \pi _1(B) \rightarrow Map_g$.

It is interesting to observe, via an elementary calculation, that the slope $K^2_S / e(S) > 2$ can only decrease for a branched covering $B' \rightarrow B$, and that it tends to 2 if moreover the weight of the branch divisor $\beta : = \sum (1 - 1/m_i)$ tends to $\infty$.

Similar phenomena ($ker (\rho ) \ne 0$, and the slope decreases) occur if we take general hypersurface sections of large degree $B \subset {\mathfrak {M}}_g^*$ in the Satake compactification of the moduli space ${\mathfrak {M}}_g$ which intersect neither the boundary $\partial \ {\mathfrak {M}}_g^* = {\mathfrak {M}}_g^* \setminus {\mathfrak {M}}_g$ nor the locus of curves with automorphisms (both have codimension at least 2).

7.9 Can we work with locally symmetric varieties?

As we shall see in the sequel, Abelian varieties and curves are simpler objects to work with, because explicit constructions may be performed via bilinear algebra in the former case, and via ramified coverings in the latter. For locally symmetric varieties, the constructions are more difficult, hence rigidity results are not enough to decide in concrete cases whether a given variety is locally symmetric.

Recently, as a consequence of the theorem of Aubin and Yau on the existence of a Kähler–Einstein metric on projective varieties with ample canonical divisor $K_X$, there have been several simple explicit criteria which guarantee that a projective variety with ample canonical divisor $K_X$ is locally symmetric (see [117, 118, 362, 377]).

A difficult question which remains open is the one of studying actions of a finite group G on them, and especially of describing the G-invariant divisors.

8 Inoue type varieties

While a couple of hundreds examples are known today of families of minimal surfaces of general type with geometric genus $p_g (S) : = \dim H^0({\mathcal {O}}_S(K_S)) = 0$ (observe that for these surfaces $1 \le K_S^2 \le 9$), for the value $K_S^2= 7$ there are only two examples known (cf. [121, 222]), and for a long time only one family of such surfaces was known, the one constructed by Masahisa Inoue (cf. [222]).

The attempt to prove that Inoue surfaces form a connected component of the moduli space of surfaces of general type proved to be successful [35], and was based on a weak rigidity result: the topological type of an Inoue surface determines an irreducible connected component of the moduli space (a phenomenon similar to the one which was observed in several papers, as [30, 31, 36, 119]).

The starting point was the calculation of the fundamental group of an Inoue surface with $p_g = 0$ and $K_S^2 =7$: it sits in an extension ($\pi _g$ being as usual the fundamental group of a projective curve of genus g):

$$\begin{aligned} 1 \rightarrow \pi _{5} \times \mathbb {Z}^4 \rightarrow \pi _1(S) \rightarrow (\mathbb {Z}/2\mathbb {Z})^5 \rightarrow 1. \end{aligned}$$

This extension is given geometrically, i.e., stems from the observation [35] that an Inoue surface S admits an unramified $({\mathbb {Z}}/ 2{\mathbb {Z}})^5$—Galois covering $\hat{S}$ which is an ample divisor in $E_1 \times E_2 \times D$, where $E_1, E_2$ are elliptic curves and D is a projective curve of genus 5; while Inoue described $\hat{S}$ as a complete intersection of two non ample divisors in the product $E_1 \times E_2 \times E_3 \times E_4$ of four elliptic curves.

It turned out that the ideas needed to treat this special family of Inoue surfaces could be put in a rather general framework, valid in all dimensions, setting then the stage for the investigation and search for a new class of varieties, which we proposed to call Inoue-type varieties.

Definition 142

([35]) Define a complex projective manifold X to be an Inoue-type manifold if

• (1) $dim (X) \ge 2$;

• (2) there is a finite group G and an unramified G-covering $\hat{X} \rightarrow X$, (hence $X = \hat{X} / G$) such that

• (3) $\hat{X}$ is an ample divisor inside a $K(\Gamma , 1)$-projective manifold Z, (hence by the theorems of Lefschetz, see Theorem 3, $\pi _1 ( \hat{X}) \cong \pi _1 (Z) \cong \Gamma$) and moreover

• (4) the action of G on $\hat{X}$ yields a faithful action on $\pi _1 ( \hat{X}) \cong \Gamma$: in other words the exact sequence

  $$\begin{aligned} 1 \rightarrow \Gamma \cong \pi _1 ( \hat{X}) \rightarrow \pi _1 ( X) \rightarrow G \rightarrow 1 \end{aligned}$$

  gives an injection $G \rightarrow {{\mathrm{\text {Out}}}}(\Gamma )$, defined by conjugation by lifts of elements of G;

• (5) the action of G on $\hat{X}$ is induced by an action of G on Z.

Similarly one defines the notion of an Inoue-type variety, by requiring the same properties for a variety X with canonical singularities.

Example 143

Indeed, the examples of Inoue, which also allow him to find another description of the surfaces constructed by Burniat [65], are based on products of curves, and there the group G is a ${\mathbb {Z}}/2$-vector space.

In fact things can be done more algebraically (as in [36]). If we take a $({\mathbb {Z}}/2)^3$-covering of ${\mathbb {P}}^1$ branched on 4 points, it has equations in ${\mathbb {P}}^3$:

$$\begin{aligned} x_1^2 + x_2^2 + x_3^2 = 0, \quad x_0^2 - a_2 x_2^2 - a_3 x_3^2 = 0, \end{aligned}$$

the group $G \cong ({\mathbb {Z}}/2)^3$ is the group of transformations $x_i \mapsto \pm x_i$, the quotient is

$$\begin{aligned} {\mathbb {P}}^1 = \left\{ y \in {\mathbb {P}}^3 | y_1+ y_2 + y_3 = 0, \ y_0 - a_2 y_2 - a_3 y_3 = 0\right\} \!, \end{aligned}$$

and the branch points are the 4 points $y_i = 0, i = 0,1,2,3$.

The group G, if we see the elliptic curve as ${\mathbb {C}}/({\mathbb {Z}}+ {\mathbb {Z}}\tau )$, is the group of affine transformations

$$\begin{aligned}{}[z] \mapsto \pm [z] + \frac{1}{2} ( a + b \tau ),\quad \ a,b \in \{ 0,1\}, \end{aligned}$$

with linear coefficient $\pm 1$ and translation vector a point of 2-torsion.

Algebra becomes easier than theta functions if one takes several square (or cubic) roots: for instance 3 square roots define a curve of genus 5 in ${\mathbb {P}}^4$:

$$\begin{aligned} x_1^2 + x_2^2 + x_3^2 = 0, \quad x_0^2 - a_2 x_2^2 - a_3 x_3^2 = 0,\quad x_4^2 - b_2 x_2^2 - b_3 x_3^2 = 0. \end{aligned}$$

One can take more generally a $({\mathbb {Z}}/2)^n$ covering of ${\mathbb {P}}^1$ branched on $n+1$ points, which is a curve of genus $g = 2^{n-2} (n-3) + 1$, or curves corresponding to similar Kummer coverings ($({\mathbb {Z}}/m)^n$ coverings of ${\mathbb {P}}^1$ branched on $n+1$ points).

The above definition of Inoue type manifold, although imposing a strong restriction on X, is too general, and in order to get weak rigidity type results it is convenient to impose restrictions on the fundamental group $\Gamma$ of Z, for instance the most interesting case is the one where Z is a product of Abelian varieties, curves, and other locally symmetric varieties with ample canonical bundle.

Definition 144

We shall say that an Inoue-type manifold X is

• (1) a special Inoue type manifold if moreover

  $$\begin{aligned} Z = (A_1 \times \cdots \times A_r) \times (C_1 \times \cdots \times C_h) \times (M_1 \times \cdots \times M_s) \end{aligned}$$

  where each $A_i$ is an Abelian variety, each $C_j$ is a curve of genus $g_j \ge 2$, and $M_i$ is a compact quotient of an irreducible bounded symmetric domain of dimension at least 2 by a torsion free subgroup;

• (2) a classical Inoue type manifold if moreover $Z = (A_1 \times \cdots \times A_r) \times (C_1 \times \cdots \times C_h)$ where each $A_i$ is an Abelian variety, each $C_j$ is a curve of genus $g_j \ge 2$;

• (3) a special Inoue type manifold is said to be diagonal if moreover:

  • (I) the action of G on $\hat{X}$ is induced by a diagonal action on Z, i.e.,

    $$\begin{aligned} G \subset \prod _{i=1}^r {{\mathrm{\text {Aut}}}}(A_i) \times \prod _{j=1}^h{{\mathrm{\text {Aut}}}}(C_j) \times \prod _{l=1}^s{{\mathrm{\text {Aut}}}}(M_l) \end{aligned}$$

    (145)

    and furthermore:

  • (II) the faithful action on $\pi _1 ( \hat{X}) \cong \Gamma$, induced by conjugation by lifts of elements of G in the exact sequence

    $$\begin{aligned} 1 \rightarrow \Gamma = \Pi _{i=1}^r (\Lambda _i) \times \Pi _{j=1}^h (\pi _{g_j}) \times \Pi _{l=1}^s (\pi _1 (M_l)) \rightarrow \pi _1 ( X) \rightarrow G \rightarrow 1 \end{aligned}$$

    (146)

    (observe that each factor $\Lambda _i$, resp. $\pi _{g_j}, \pi _1 (M_l)$ is a normal subgroup), satisfies the Schur property

    $$\begin{aligned} (SP) \ \ \ \ {{\mathrm{\text {Hom}}}}(V_i, V_j)^{G} = 0,\quad \forall i \ne j. \end{aligned}$$

    Here $V_j : = \Lambda _j\otimes {\mathbb {Q}}$ and, in order that the Schur property holds, it suffices for instance to verify that for each $\Lambda _i$ there is a subgroup $H_i$ of G for which ${{\mathrm{\text {Hom}}}}(V_i, V_j)^{H_i} = 0, \forall j \ne i$.

The Schur property (SP) plays an important role in order to show that an Abelian variety with such a G-action on its fundamental group must split as a product.

Before stating the main general result of [35] we need the following definition, which was already used in 77 for the characterization of complex tori among Kähler manifolds.

Definition 147

Let Y, $Y'$ be two projective manifolds with isomorphic fundamental groups. We identify the respective fundamental groups $\pi _1(Y) = \pi _1(Y') = \Gamma$. Then we say that the condition (SAME HOMOLOGY) is satisfied for Y and $Y'$ if there is an isomorphism $\Psi : H_*(Y', {\mathbb {Z}}) \cong H_*(Y, {\mathbb {Z}})$ of homology groups which is compatible with the homomorphisms

$$\begin{aligned} u :H_*(Y, {\mathbb {Z}}) \rightarrow H_*(\Gamma , {\mathbb {Z}}),\quad u' :H_*(Y', {\mathbb {Z}}) \rightarrow H_*(\Gamma , {\mathbb {Z}}), \end{aligned}$$

i.e., $\Psi$ satisfies $u \circ \Psi = u'$.

We can now state the following

Theorem 148

Let X be a diagonal special Inoue type manifold, and let $X'$ be a projective manifold with $K_{X'}$ nef and with the same fundamental group as X, which moreover either

(A) is homotopically equivalent to X;

or satisfies the following weaker property:

(B) let $\hat{X'}$ be the corresponding unramified covering of $X'$. Then $\hat{X}$ and $\hat{X}'$ satisfy the condition (SAME HOMOLOGY).

Setting $W : = \hat{X'}$, we have that

(1) $X'= W / G$ where W admits a generically finite morphism $f : W \rightarrow Z'$, and where $Z'$ is also a $K(\Gamma , 1)$ projective manifold, of the form $Z' = (A'_1 \times \cdots \times A'_r) \times (C'_1 \times \cdots \times C'_h) \times (M'_1 \times \cdots \times M'_s)$.

Moreover here $M'_i$ is either $M_i$ or its complex conjugate, and the product decomposition corresponds to the product decomposition (146) of the fundamental group of Z.

The image cohomology class $f_*([W])$ corresponds, up to sign, to the cohomology class of $\hat{X}$.

(2) The morphism f is finite if $n = \dim X$ is odd, and it is generically injective if

(**) the cohomology class of $\hat{X}$ (in $H^* (Z, {\mathbb {Z}})$) is indivisible, or if every strictly submultiple cohomology class cannot be represented by an effective G-invariant divisor on any pair $\mathrm{(}Z', G\mathrm{)}$ homotopically equivalent to (Z, G).

(3) f is an embedding if moreover $K_{X'}$ is ample,

(*) every such divisor W of $Z'$ is ample, and

(***) $\ \ \ K_{X'}^n = K_{X}^n$.¹⁰

In particular, if $K_{X'}$ is ample and (*), (**) and (***) hold, also $X'$ is a diagonal SIT (special Inoue type) manifold.

A similar conclusion holds under the alternative assumption that the homotopy equivalence sends the canonical class of W to that of $\hat{X}$: then $X'$ is a minimal resolution of a diagonal SIT (special Inoue type) variety.

Hypothesis (A) in Theorem 148 is used to derive the conclusion that also $W : = \hat{X'}$ admits a holomorphic map $f'$ to a complex manifold $Z'$ with the same structure as Z, while hypotheses (B) and following ensure that the morphism is birational onto its image, and the class of the image divisor $f' (\hat{X'} )$ corresponds to $\pm$ that of $\hat{X}$ under the identification

$$\begin{aligned} H_*(Z' , {\mathbb {Z}}) \cong H_*(\Gamma , {\mathbb {Z}}) \cong H_*(Z , {\mathbb {Z}}). \end{aligned}$$

Since $K_{X'}$ is ample, one uses (***) to conclude that $f'$ is an isomorphism with its image.

The next question which the theorem leaves open is weak * rigidity, for which several ingredients should come into play: the Hodge type, a fine analysis of the structure of the action of G on Z, the problem of existence of hypersurfaces on which G acts freely and the study of the family of such invariant effective divisors, in particular whether the family has a connected base.

We have restricted ourselves to special Inoue type manifolds in order to be able to use the regularity results for classifying maps discussed in the previous section (the diagonality assumption is only a simplifying assumption).

Let us now sketch the proof of Theorem 148.

Proof of Theorem 148

Step 1 The first step consists in showing that $W : = \hat{X'}$ admits a holomorphic mapping to a manifold $Z'$ of the above type $Z' = (A'_1 \times \cdots \times A'_r) \times (C'_1 \times \cdots \times C'_h) \times (M'_1 \times \cdots \times M'_s)$, where $M'_i$ is either $M_i$ or its complex conjugate.

First of all, by the results of Siu and others ([101, 106, 344, 345], Theorem 5.14) cited in Sect. 6, W admits a holomorphic map to a product manifold of the desired type

$$\begin{aligned} Z_2'\times Z'_3 = (C'_1 \times \cdots \times C'_h) \times (M'_1 \times \cdots \times M'_s). \end{aligned}$$

Look now at the Albanese variety ${{\mathrm{\text {Alb}}}}(W)$ of the Kähler manifold W, whose fundamental group is the quotient of the Abelianization of $\Gamma = \pi _1 (Z)$ by its torsion subgroup. Write the fundamental group of ${{\mathrm{\text {Alb}}}}(W)$ as the first homology group of $A \times Z_2 \times Z_3$, i.e., as

$$\begin{aligned} H_1 ( {{\mathrm{\text {Alb}}}}(W)) = \Lambda \oplus H_1 ( Z_2, {\mathbb {Z}}) \oplus (H_1 ( Z_3, {\mathbb {Z}})/ Torsion), \end{aligned}$$

(${{\mathrm{\text {Alb}}}}(Z_2)$ is the product of Jacobians $J : = ({{\mathrm{\text {Jac}}}}(C_1) \times \cdots \times {{\mathrm{\text {Jac}}}}(C_h))$).

Since however, by the universal property, ${{\mathrm{\text {Alb}}}}(W)$ has a holomorphic map to

$$\begin{aligned} B' : = {{\mathrm{\text {Alb}}}}(Z'_2) \times {{\mathrm{\text {Alb}}}}(Z'_3), \end{aligned}$$

inducing a splitting of the lattice $H_1 ({{\mathrm{\text {Alb}}}}(W), {\mathbb {Z}}) = \Lambda \oplus H_1 (B', {\mathbb {Z}})$, it follows that ${{\mathrm{\text {Alb}}}}(W)$ splits as $A' \times B'$.

Now, we want to show that the Abelian variety $A'$ (W is assumed to be a projective manifold) splits as desired. This is in turn a consequence of assumption (3) in Definition 144. In fact, the group G acts on the Abelian variety $A'$ as a group of biholomorphisms, hence it acts on $\Lambda \otimes {\mathbb {R}}$ commuting with multiplication by $\sqrt{-1}$. Hence multiplication by $\sqrt{-1}$ is an isomorphism of G representations, and then (3) implies that $\Lambda _i\otimes {\mathbb {R}}$ is stable by multiplication by $\sqrt{-1}$; whence $\Lambda _i\otimes {\mathbb {R}}$ generates a subtorus $A'_i$. Finally, $A'$ splits because $\Lambda$ is the direct sum of the sublattices $\Lambda _i$. We are through with the proof of step 1.

Step 2 Consider now the holomorphic map $f :W \rightarrow Z'$. We shall show that the image $W' : = f (W)$ is indeed a divisor in $Z'$. For this we use the assumption (SAME HOMOLOGY) and, in fact, the claim is an immediate consequence of the following lemma.

Lemma 149

Assume that W is a Kähler manifold, such that

• (i) there is an isomorphism of fundamental groups $\pi _1 (W) = \pi _1 (\hat{X})= \Gamma$, where $\hat{X}$ is a smooth ample divisor in a $K(\Gamma , 1)$ complex projective manifold Z;

• (ii) there exists a holomorphic map $f : W \rightarrow Z'$, where $Z'$ is another $K(\Gamma , 1)$ complex manifold, such that $f_* : \pi _1 (W) \rightarrow \pi _1 (Z') = \Gamma$ is an isomorphism, and moreover

• (iii) (SAME HOMOLOGY) there is an isomorphism $\Psi : H_*( W, {\mathbb {Z}}) \cong H_*(\hat{X}, {\mathbb {Z}})$ of homology groups which is compatible with the homomorphisms

  $$\begin{aligned} u :H_*(\hat{X}, {\mathbb {Z}}) \rightarrow H_*(\Gamma , {\mathbb {Z}}) ,\quad u' :H_*( W, {\mathbb {Z}}) \rightarrow H_*(\Gamma , {\mathbb {Z}}) , \end{aligned}$$

  i.e., we have $u \circ \Psi = u'$.

Then f is a generically finite morphism of W into $Z'$, and the cohomology class $f_* ([W])$ in

$$\begin{aligned} H^*(Z', {\mathbb {Z}}) = H^*(Z, {\mathbb {Z}}) =H^*(\Gamma , {\mathbb {Z}}) \end{aligned}$$

corresponds to $\pm 1$ the one of $\hat{X}$.

Proof of the Lemma

We can identify the homology groups of W and $\hat{X}$ under $\Psi : H_*(W, {\mathbb {Z}}) \cong H_*(\hat{X}, {\mathbb {Z}})$, and then the image in the homology groups of $H_*(Z', {\mathbb {Z}}) = H_*(Z, {\mathbb {Z}}) =H_*(\Gamma , {\mathbb {Z}})$ is the same.

We apply the above consideration to the fundamental classes of the oriented manifolds W and $\hat{X}$, which are generators of the infinite cyclic top degree homology groups $H_{2n}(W, {\mathbb {Z}})$, respectively $H_{2n}( \hat{X}, {\mathbb {Z}})$.

This implies a fortiori that $f :W \rightarrow Z'$ is generically finite: since then the homology class $f_* ([W])$ (which we identify to a cohomology class by virtue of Poincaré duality) equals the class of $\hat{X}$, up to sign. $\square$

Step 3 We claim that $f :W \rightarrow Z'$ is generically 1-1 onto its image $W'$.

Let d be the degree of $f :W \rightarrow W'$.

Then $f_* ([W]) = d [W']$, hence if the class of $\hat{X}$ is indivisible, then obviously $d=1$.

Otherwise, observe that the divisor $W'$ is an effective G-invariant divisor and use our assumption (**).

Step 4 Here we are going to prove that f is an embedding under the additional hypotheses that $K_X^n =K_{X'}^n$ and that $W'$ is ample, as well as $K_{X'}$.

We established that f is birational onto its image $W'$, hence it is a desingularization of $W'$.

We use now adjunction. We claim that, since (by our assumption on $K_{X'}$) $K_W$ is nef, there exists an effective divisor ${\mathfrak {U}}$, called the adjunction divisor, such that

$$\begin{aligned} K_W = f^* (K_{Z'} + W') - {\mathfrak {U}}. \end{aligned}$$

This can be shown by taking the Stein factorization

$$\begin{aligned} p \circ h :W \rightarrow W^N \rightarrow W', \end{aligned}$$

where $W^N$ is the normalization of $W'$.

Let ${\mathcal {C}}$ be the conductor ideal $\mathcal {H}om (p_*{\mathcal {O}}_{W^N}, {\mathcal {O}}_{W'} )$ viewed as an ideal ${\mathcal {C}}\subset {\mathcal {O}}_{W^N}$; then the Zariski canonical divisor of $W^N$ satisfies

$$\begin{aligned} K_{W^N} = p^* (K_{W'}) - C = p^* (K_{Z'} + W') - C \end{aligned}$$

where C is the Weil divisor associated to the conductor ideal (the equality on the Gorenstein locus of $W^N$ is shown for instance in [83], then it suffices to take the direct image from the open set to the whole of $W^N$).

In turn, we would have in general $K_W = h^* (K_{W^N } ) - {\mathfrak {B}}$, with ${\mathfrak {B}}$ not necessarily effective; but, by Lemma 2.5 of [128], see also Lemma 3.39 of [257], and since $- {\mathfrak {B}}$ is h-nef, we conclude that ${\mathfrak {B}}$ is effective. We establish the claim by setting ${\mathfrak {U}} : = {\mathfrak {B}} + h^* C$.

Observe that, under the isomorphism of homology groups, $f^* (K_{Z'} + W')$ corresponds to $(K_{Z} + \hat{X})|_{\hat{X}}= K_{\hat{X}}$, in particular we have

$$\begin{aligned} K_{\hat{X}}^n = f^* (K_{Z'} + W')^n = (K_W + {\mathfrak {U}})^n . \end{aligned}$$

If we assume that $K_W$ is ample, then $(K_W + {\mathfrak {U}})^n \ge (K_W)^n$, equality holding if and only if ${\mathfrak {U}} = 0$.

Under assumption (**), it follows that

$$\begin{aligned} K_{\hat{X}}^n = |G| K_X^n = |G| K_{X'}^n= K_W^n, \end{aligned}$$

hence ${\mathfrak {U}} = 0$. Since however $K_W$ is ample, it follows that f is an embedding.

If instead we assume that $K_W$ has the same class as $f^* (K_{Z'} + W')$, we conclude first that necessarily ${\mathfrak {B}} =0$, and then we get that $C= 0$.

Hence $W'$ is normal and has canonical singularities.

Step 5 Finally, the group G acts on W, preserving the direct summands of its fundamental group $\Gamma$. Hence, G acts on the curve-factors, and on the locally symmetric factors.

By assumption, moreover, it sends the summand $\Lambda _i$ to itself, hence we get a well defined linear action on each Abelian variety $A'_i$, so that we have a diagonal linear action of G on $A'$.

Since however the image of W generates $A'$, we can extend the action of G on W to a compatible affine action on $A'$. In the case where G is abelian¹¹, we can show that the real affine type of the action on $A'$ is uniquely determined. This is taken care of by the following lemma.

Lemma 150

Given a diagonal special Inoue type manifold, if G is abelian, the real affine type of the action of G on the Abelian variety $A = (A_1 \times \cdots \times A_r )$ is determined by the fundamental group exact sequence

$$\begin{aligned} 1 \rightarrow \Gamma = \Pi _{i=1}^r (\Lambda _i) \times \Pi _{j=1}^h (\pi _{g_j}) \times \Pi _{l=1}^s (\pi _1 (M_l)) \rightarrow \pi _1 ( X) \rightarrow G \rightarrow 1. \end{aligned}$$

Proof

Define as before $\Lambda : = \Pi _{i=1}^r \Lambda _i = \pi _1 (A)$; moreover, since all the summands on the left hand side are normal in $\pi _1 ( X)$, set

$$\begin{aligned} \overline{G} : = \pi _1 ( X) / (( \Pi _{j=1}^h \pi _{g_j} ) \times (\Pi _{l=1}^s \pi _1 (M_l) )). \end{aligned}$$

Observe now that X is the quotient of its universal covering

$$\begin{aligned} \tilde{X} = {\mathbb {C}}^m \times \prod _{j=1}^h\mathbb {H}_j \times \prod _{l=1}^s\mathcal {D}_l \end{aligned}$$

by its fundamental group, acting diagonally (here $\mathbb {H}_j$ is a copy of Poincaré’s upper half plane, while $\mathcal {D}_l$ is an irreducible bounded symmetric domain of dimension at least two), hence we obtain that $\overline{G}$ acts on ${\mathbb {C}}^m$ as a group of affine transformations.

This action yields a homomorphism

$$\begin{aligned} \alpha : \overline{G} \twoheadrightarrow {{\mathrm{\text {Im}}}}(\alpha ) =: \hat{G} \subset {{\mathrm{\text {Aff}}}}(m, {\mathbb {C}}): \end{aligned}$$

let ${\mathcal {K}}$ the kernel of $\alpha$, and let

$$\begin{aligned} \overline{G}_1 : = \ker ( \alpha _L : \overline{G} \rightarrow {{\mathrm{\text {GL}}}}(m, {\mathbb {C}})). \end{aligned}$$

$\overline{G}_1$ is obviously Abelian, and contains $\Lambda$, and maps onto a lattice $\Lambda ' \subset \hat{G}$.

Since $\Lambda$ injects into $\Lambda '$, $\Lambda \cap {\mathcal {K}}= 0$, whence ${\mathcal {K}}$ injects into G, therefore ${\mathcal {K}}$ is a torsion subgroup; since $\Lambda '$ is free, we obtain

$$\begin{aligned} \overline{G}_1 = \Lambda ' \oplus {\mathcal {K}}, \end{aligned}$$

and we finally get

$$\begin{aligned} {\mathcal {K}}= {{\mathrm{\text {Tors}}}}(\overline{G}_1 ), \ \ \hat{G} = \overline{G} / {{\mathrm{\text {Tors}}}}(\overline{G}_1 ). \end{aligned}$$

Since our action is diagonal, we can write $\Lambda ' = \oplus _{i=1}^r \Lambda '_i$, and the linear action of the group $G_2 : = G / {\mathcal {K}}$ preserves the summands.

Since $\hat{G} \subset {{\mathrm{\text {Aff}}}}(\Lambda ' \otimes {\mathbb {R}})$, we can now apply Proposition 21 to it.

This shows that the affine group $\hat{G}$ is uniquely determined.

Finally, using the image groups $G_{2,i}$ of $G_2$ inside ${{\mathrm{\text {GL}}}}( \Lambda '_i)$, we can define uniquely groups of affine transformations of $A_i$ which fully determine the diagonal action of G on A (up to real affine automorphisms of each $A_i$).

The proof of Theorem 148 is now completed. $\square$

In order to obtain weak rigidity results, one has to use, as an invariant for group actions on tori and Abelian varieties, the Hodge type, introduced in Definition 19 (see also Remark 20).

Remark 151

In the previous theorem special assumptions are needed in order to guarantee that for each manifod $X'$ homotopy equivalent to X the classifying holomorphic map $f : \hat{X' } \rightarrow Z'$ be birational onto its image, and indeed an embedding.

However, there is the possibility that an Inoue type variety deforms to one for which f is a covering of finite degree. This situation should be analyzed and the singularities of the image of f described in detail, so as to lead to a generalization of the theory of Inoue type varieties, including ‘multiple’ Inoue type varieties (those for which f has degree at least two).

The study of moduli spaces of Inoue type varieties, and their connected and irreducible components, relies very much on the study of moduli spaces of varieties X endowed with the action of a finite group G: and it is for us a strong motivation to pursue this line of research.

This topic will occupy a central role in the following sections, first in general, and then in the special case of algebraic curves.

9 Moduli spaces of surfaces and higher dimensional varieties

Teichmüller theory works out quite fine in the case of projective curves, as well as other approaches, like Geometric Invariant Theory (see [178, 179, 302, 304]), which provides a quasi-projective moduli space ${\mathfrak {M}}_g$ endowed with a natural compactification $\overline{{\mathfrak {M}}_g}$ (this is a coarse moduli space for the so-called moduli stable projective curves: these are the reduced curves with at most nodes as singularities, such that their group of automorphisms is finite).

In higher dimensions one has a fully satisfactory theory of ‘local moduli’ for compact complex manifolds or spaces, but there are difficulties with the global theory.

So, let us start from the local theory, developed by Kodaira and Spencer, and culminating in the results of Kuranishi and Grauert.

9.1 Kodaira–Spencer–Kuranishi theory

While describing complex structures as integrable almost complex structures (see Theorem 32), it is convenient to view an almost complex structure as a differentiable (0, 1)-form with values in the dual of the cotangent bundle $(TY^{1,0})^{\vee }$.

This representation leads to the Kodaira–Spencer–Kuranishi theory of local deformations, addressing precisely the study of the small deformations of a complex manifold $Y = (M, J_0)$.

In this theory, complex structures correspond to closed such forms which, by Dolbeault’s theorem, determine a cohomology class in $H^1 ( \Theta _Y)$, where $\Theta _Y$ is the sheaf of holomorphic sections of the holomorphic tangent bundle $TY^{1,0}$.

We shall use here unambiguously the double notation $TM^{0,1} = TY^{0,1}$, $TM^{1,0} = TY^{1,0}$ to refer to the splitting of the complexified tangent bundle determined by the complex structure $J_0$.

$J_0$ is a point in ${\mathcal {C}}(M)$, and a neighbourhood in the space of almost complex structures corresponds to a distribution of subspaces which are globally defined as graphs of an endomorphism

$$\begin{aligned} \phi : TM^{0,1} \rightarrow TM^{1,0}, \end{aligned}$$

called a small variation of almost complex structure, since one then defines

$$\begin{aligned} TM^{0,1}_{\phi } : = \{ (u, \phi (u))| \ u \in TM^{0,1} \} \subset TM^{0,1} \oplus TM^{1,0}. \end{aligned}$$

In terms of the old $\bar{\partial }$ operator, the new one is simply obtained by considering

$$\begin{aligned} \bar{\partial }_{\phi } : = \bar{\partial } + \phi , \end{aligned}$$

and the integrability condition is given by the Maurer–Cartan equation

$$\begin{aligned} (MC) \ \ \bar{\partial } (\phi ) + \frac{1}{2} [ \phi , \phi ] = 0. \end{aligned}$$

Observe that, since our original complex structure $J_0$ corresponds to $\phi = 0$, the derivative of the above equation at $\phi = 0$ is simply

$$\begin{aligned} \bar{\partial } (\phi )= 0, \end{aligned}$$

hence the tangent space to the space of complex structures consists of the space of $\bar{\partial }$-closed forms of type (0, 1) and with values in the bundle $TM^{1,0}$.

One can restrict oneself (see e.g. [114]) to consider only the class of such forms $\phi$ in the Dolbeault cohomology group

$$\begin{aligned} H^1 (\Theta _Y): = ker ( \bar{\partial } ) / Im ( \bar{\partial }), \end{aligned}$$

by looking at the action of the group of diffeomorphisms which are exponentials of global vector fields on M.

Representing these cohomology classes by harmonic forms, the integrability equation becomes easier to solve via the following Kuranishi equation.

Let $\eta _1, \ldots , \eta _m \in H^1 (\Theta _Y)$ be a basis for the space of harmonic (0,1)-forms with values in $TM^{1,0}$, and set $t : =(t_1, \ldots , t_m) \in {\mathbb {C}}^m$, so that $t \mapsto \sum _i t_i \eta _i$ establishes an isomorphism ${\mathbb {C}}^m \cong H^1 (\Theta _Y)$.

Then the Kuranishi slice is obtained by associating to t the unique power series solution of the following equation:

$$\begin{aligned} \phi (t) = \sum _i t_i \eta _i + \frac{1}{2} \bar{\partial }^* G [ \phi (t), \phi (t)], \end{aligned}$$

satisfying moreover $\phi (t) = \sum _i t_i \eta _i +$ higher order terms (G denotes here the Green operator).

The upshot is that for these forms $\phi (t)$ the integrability equation simplifies drastically; the result is summarized in the following definition.

Definition 152

The Kuranishi space $\mathfrak B (Y)$ is defined as the germ of complex subspace of $H^1 (\Theta _Y)$ defined by $\{ t \in {\mathbb {C}}^m | \ H [ \phi (t), \phi (t)] = 0 \}$, where H is the harmonic projector onto the space $H^2 (\Theta _Y)$ of harmonic forms of type (0, 2) and with values in $TM^{1,0}$.

Kuranishi space $\mathfrak B (Y)$ parametrizes the set of small variations of almost complex structure $\phi (t)$ which are integrable. Hence over $\mathfrak B (Y)$ we have a family of complex structures which deform the complex structure of Y.

It follows then that the Kuranishi space $\mathfrak B (Y)$ surjects onto the germ of the Teichmüller space at the point corresponding to the given complex structure $Y = (M, J_0)$.

It fails badly in general to be a homeomorphism (see [86, 114]): for instance Teichmüller space, in the case of the Hirzebruch Segre surface ${\mathbb {F}}_{2n}$ (blow up of the cone onto the rational normal curve of degree 2n), consists of $n+1$ points $p_0, p_2, \ldots ,p_{2n}$, such that the open sets are exactly the sets $\{ p_{2i} | i \le k\}$.

But a first consequence is that Teichmüller space is locally connected by holomorphic arcs, hence the determination of the connected components of ${\mathcal {C}}(M)$, respectively of ${\mathcal {T}}(M)$, can be done using the original definition of deformation equivalence, given by Kodaira and Spencer [248] (see Definition 109).

One can define deformations not only for complex manifolds, but also for complex spaces.

Definition 153

(1) A deformation of a compact complex space X is a pair consisting of

(1.1) a flat proper morphism $\pi : {\mathcal {X}}\rightarrow T$ between connected complex spaces (i.e., $\pi ^* : {\mathcal {O}}_{T,t} \rightarrow {\mathcal {O}}_{{\mathcal {X}},x}$ is a flat ring extension for each x with $\pi (x) = t$)

(1.2) an isomorphism $\psi : X \cong \pi ^{-1}(t_0) : = X_0$ of X with a fibre $X_0$ of $\pi$.

(2.1) A small deformation is the germ $\pi : ({\mathcal {X}}, X_0) \rightarrow (T, t_0)$ of a deformation.

(2.2) Given a deformation $\pi : {\mathcal {X}}\rightarrow T$ and a morphism $f : T' \rightarrow T$ with $f (t'_0) = t_0$, the pull-back $f^* ({\mathcal {X}})$ is the fibre product ${\mathcal {X}}': = {\mathcal {X}}\times _T T'$ endowed with the projection onto the second factor $T'$ (then $X \cong X'_0$).

(3.1) A small deformation $\pi : {\mathcal {X}}\rightarrow T$ is said to be versal or complete if every small deformation $\pi : {\mathcal {X}}' \rightarrow T'$ is obtained from it via pull back; it is said to be semi-universal if the differential of $f : T' \rightarrow T$ at $t'_0$ is uniquely determined, and universal if the morphism f is uniquely determined.

(4) Two compact complex manifolds X, Y are said to be directly deformation equivalent if there are

(4i) a deformation $\pi : {\mathcal {X}}\rightarrow T$ of X with T irreducible and where all the fibres are smooth, and

(4ii) an isomorphism $\psi ' : Y \cong \pi ^{-1}(t_1) = : X_1$ of Y with a fibre $X_1$ of $\pi$.

Remark 154

The technical assumption of flatness replaces, for families of spaces, the condition on $\pi$ to be a submersion, necessary in order that the fibres be smooth manifolds.

Let’s however come back to the case of complex manifolds, observing that in a small deformation of a compact complex manifold one can shrink the base T and assume that all the fibres are smooth.

We can now state the results of Kuranishi and Wavrik [259, 260, 371] in the language of deformation theory.

Theorem 155

(Kuranishi) Let Y be a compact complex manifold: then

• (I) the Kuranishi family $\pi : ({\mathcal {Y}}, Y_0) \rightarrow (\mathfrak B (Y), 0)$ of Y is semiuniversal.

• (II) $(\mathfrak B (Y), 0)$ is unique up to (non canonical) isomorphism, and is a germ of analytic subspace of the vector space $H^1 (Y, \Theta _Y)$, inverse image of the origin under a local holomorphic map (called Kuranishi map)

  $$\begin{aligned} k : H^1 (Y, \Theta _Y) \rightarrow H^2 (Y, \Theta _Y) \end{aligned}$$

  whose differential vanishes at the origin. Moreover the quadratic term in the Taylor development of k is given by the bilinear map $H^1 (Y, \Theta _Y) \times H^1 (Y, \Theta _Y) \rightarrow H^2 (Y, \Theta _Y)$, called Schouten bracket, which is the composition of cup product followed by Lie bracket of vector fields.

• (III) The Kuranishi family is a versal deformation of $Y_t$ for $t \in \mathfrak B (Y)$.

• (IV) The Kuranishi family is universal if $H^0 (Y, \Theta _Y)= 0$.

• (V) (Wavrik) The Kuranishi family is universal if $\mathfrak B (Y)$ is reduced and $h^0 (Y_t, \Theta _{Y_t})$ $:= \mathrm{dim}\ H^0 (Y_t, \Theta _{Y_t})$ is constant for $t \in \mathfrak B (Y)$ in a suitable neighbourhood of 0.

The Kodaira Spencer map, defined soon below, is to be thought as the derivative of a family of complex structures.

Definition 156

The Kodaira Spencer map of a family $\pi : ({\mathcal {Y}}, Y_0) \rightarrow (T, t_0)$ of complex manifolds having a smooth base T is defined as follows: consider the cotangent bundle sequence of the fibration

$$\begin{aligned} 0 \rightarrow \pi ^* (\Omega ^1_T) \rightarrow \Omega ^1_{{\mathcal {Y}}} \rightarrow \Omega ^1_{{\mathcal {Y}}| T} \rightarrow 0, \end{aligned}$$

and the direct image sequence of the dual sequence of bundles,

$$\begin{aligned} 0 \rightarrow \pi _* (\Theta _{{\mathcal {Y}}| T}) \rightarrow \pi _* (\Theta _{{\mathcal {Y}}}) \rightarrow \Theta _T \rightarrow {\mathcal {R}}^1 \pi _* (\Theta _{{\mathcal {Y}}| T}). \end{aligned}$$

Evaluation at the point $t_0$ yields a map $\rho$ of the tangent space to T at $t_0$ into $H^1 (Y_0, \Theta _{Y_0})$, which is the derivative of the variation of complex structure.

The Kodaira Spencer map and the implicit functions theorem allow to determine the Kuranishi space and the Kuranishi family in many cases.

Corollary 157

Let Y be a compact complex manifold and assume that we have a family $\pi : ({\mathcal {Y}}, Y_0) \rightarrow (T, t_0)$ with smooth base T, such that $Y \cong Y_0$, and such that the Kodaira Spencer map $\rho _{t_0}$ surjects onto $H^1 (Y, \Theta _Y)$.

Then the Kuranishi space $\mathfrak B (Y)$ is smooth and there is a submanifold $T' \subset T$ which maps isomorphically to $\mathfrak B (Y)$; hence the Kuranishi family is the restriction of $\pi$ to $T'$.

The key point is that, by versality of the Kuranishi family, there is a morphism $f : T \rightarrow \mathfrak B (Y)$ inducing $\pi$ as a pull back, and $\rho$ is the derivative of f: then one uses the implicit functions theorem.

This approach clearly works only if Y is unobstructed, which simply means that $\mathfrak B (Y)$ is smooth. In general it is difficult to describe the obstruction map, and even calculating the quadratic term is nontrivial (see [216] for an interesting example).

Even if it is difficult to calculate the obstruction map, Kuranishi theory gives a lower bound for the ‘number of moduli’ of Y, since it shows that $\mathfrak B (Y)$ has dimension $\ge h^1 (Y, \Theta _Y) - h^2 (Y, \Theta _Y)$. In the case of curves $H^2 (Y, \Theta _Y) = 0$, hence curves are unobstructed; in the case of a surface S

$$\begin{aligned} \mathrm{dim} \mathfrak B (S ) \ge h^1 ( \Theta _S) - h^2 ( \Theta _S) = - \chi ( \Theta _S) + h^0 ( \Theta _S) = 10 \chi ({\mathcal {O}}_S) - 2 K^2_S + h^0 ( \Theta _S). \end{aligned}$$

The above is the Enriques inequality ([157], see also [155], and [126] for an improvement: observe that Max Noether postulated equality), proved by Kuranishi in all cases and also for non algebraic surfaces.

9.2 Kuranishi and Teichmüller

Ideally, we would like to have that Teichmüller space, up to now only defined as a topological space, is indeed a complex space, locally isomorphic to Kuranishi space.

In fact, we already remarked that there is a locally surjective continuous map of $\mathfrak B (Y)$ to the germ ${\mathcal {T}}(M)_Y$ of ${\mathcal {T}}(M)$ at the point corresponding to the complex structure yielding Y. For curves this map is a local homeomorphism, and this fact provides a complex structure on Teichmüller space.

Whether this holds in general is related to the following definition.

Definition 158

A compact complex manifold Y is said to be rigidified if $Aut(Y) \cap {\mathcal {D}}iff ^0(Y) = \{ Id_Y \}$.

A compact complex manifold Y is said to be cohomologically rigidified if $Aut(Y) \rightarrow Aut (H^* (Y, {\mathbb {Z}}))$ is injective, and rationally cohomologically rigidified if $Aut(Y) \rightarrow Aut (H^* (Y, {\mathbb {Q}}))$ is injective.

Remark 159

We refer to [68] for the proof that surfaces of general type with $q \ge 3$ are cohomologically rigidified, and for examples showing that there are rigidified surfaces of general type which are not cohomologically rigidified.

In fact, it is clear that there is a universal tautological family of complex structures parametrized by ${\mathcal {C}}(M)$ (the closed subspace ${\mathcal {C}}(M)$ of ${\mathcal {A}}{\mathcal {C}}(M)$ consisting of the set of complex structures on M), and with total space

$$\begin{aligned} {\mathfrak {U}}_{ {\mathcal {C}}(M)} : = M \times {\mathcal {C}}(M), \end{aligned}$$

on which the group ${\mathcal {D}}iff ^+ (M)$ naturally acts, in particular ${\mathcal {D}}iff ^0(M)$.

The main observation is that ${\mathcal {D}}iff ^0(M)$ acts freely on ${\mathcal {C}}(M)$ if and only if for each complex structure Y on M the group of biholomorphisms Aut(Y) contains no nontrivial automorphism which is differentiably isotopic to the identity. Thus, the condition of being rigidified implies that the tautological family of complex structures descends to a universal family of complex structures on Teichmüller space:

$$\begin{aligned} {\mathfrak {U}}_{ {\mathcal {T}}(M)} : = (M \times {\mathcal {C}}(M)) / {\mathcal {D}}iff ^0(M) \rightarrow {\mathcal {C}}(M)) / {\mathcal {D}}iff ^0(M) = {\mathcal {T}}(M), \end{aligned}$$

on which the mapping class group acts.

Fix now a complex structure yielding a compact complex manifold Y, and compare with the Kuranishi family

$$\begin{aligned} {\mathcal {Y}}\rightarrow \mathfrak B (Y). \end{aligned}$$

Now, we already remarked that there is a locally surjective continuous map of $\mathfrak B (Y)$ to the germ ${\mathcal {T}}(M)_Y$ of ${\mathcal {T}}(M)$ at the point corresponding to the complex structure yielding Y.

The following was observed in [114].

Remark 160

If

• (1) the Kuranishi family is universal at any point

• (2) $\mathfrak B (Y) \rightarrow {\mathcal {T}}(M)_Y$ is injective (it is then a local homeomorphism at every point)

then Teichmüller space has a natural structure of complex space.

In many cases (for instance, complex tori) Kuranishi and Teichmüller space coincide, in spite of the fact that the manifolds are not rigidified. For instance we showed in [114]:

Proposition 161

• (1) The continuous map $\pi :\mathfrak B (Y) \rightarrow {\mathcal {T}}(M)_Y$ is a local homeomorphism between Kuranishi space and Teichmüller space if there is an injective continuous map $f :\mathfrak B (Y) \rightarrow Z$, where Z is Hausdorff, which factors through $\pi$.

• (2) Assume that Y is a compact Kähler manifold and that the local period map f is injective: then $\pi :\mathfrak B (Y) \rightarrow {\mathcal {T}}(M)_Y$ is a local homeomorphism.

• (3) In particular, this holds if Y is Kähler with trivial or torsion canonical divisor.

Remark 162

• (1) The condition of being rigidified implies the condition $H^0 (\Theta _Y)=0$ (else there is a positive dimensional Lie group of biholomorphic self maps), and is obviously implied by the condition of being cohomologically rigidified.

• (2) By the cited Lefschetz’ lemma compact curves of genus $g \ge 2$ are rationally cohomologically rigidified, and it is an interesting question whether compact complex manifolds of general type are rigidified (see [67] and [68] for recent progresses).

• (3) One can dispense with many assumptions, at the cost of having a more complicated result. For instance, Meersseman shows in [284], explaining the situation via classical examples of [81], that one can take a quotient of the several Kuranishi families (using their semi-universality), obtaining, as analogues of Teichmüller spaces, respectively moduli spaces, an analytic Teichmüller groupoid, respectively a Riemann groupoid, both independent up to analytic Morita equivalence of the chosen countable disjoint union of Kuranishi spaces. These lead to some stacks called by the author ‘analytic Artin stack’ (see [11] and [164] as a reference on Artin stacks).

9.3 Varieties with singularities

For higher dimensional varieties moduli theory works better if one considers varieties with moderate singularities, rather than smooth ones (see [256]), as we shall illustrate in the next sections for the case of algebraic surfaces.

The Kuranishi theory does indeed extend perfectly to all compact complex spaces, and Kuranishi’s theorem was generalized by Grauert (see [186, 187], see also [334] for the algebraic analogue).

Theorem 163

Grauert’s Kuranishi type theorem for complex spaces. Let X be a compact complex space: then

• (I) there is a semiuniversal deformation $\pi : ({\mathcal {X}}, X_0) \rightarrow (T, t_0)$ of X, i.e., a deformation such that every small deformation $\pi ' : ({\mathcal {X}}', X'_0) \rightarrow (T', t'_0)$ is the pull-back of $\pi$ for an appropriate morphism $f : (T', t'_0) \rightarrow (T, t_0)$ whose differential at $t'_0$ is uniquely determined.

• (II) $(T, t_0)$ is unique up to isomorphism, and is a germ of analytic subspace of the vector space ${\mathbb {T}}^1$ of first order deformations.

$(T, t_0)$ is the inverse image of the origin under a local holomorphic map (called Kuranishi map)

$$\begin{aligned} k : {\mathbb {T}}^1 \rightarrow {\mathbb {T}}^2 \end{aligned}$$

to the finite dimensional vector space ${\mathbb {T}}^2$ (called obstruction space), and whose differential vanishes at the origin (the point corresponding to the point $t_0$).

If X is reduced, or if the singularities of X are local complete intersection singularities, then ${\mathbb {T}}^1 = \mathrm{Ext }^1 (\Omega ^1_X, {\mathcal {O}}_X )$.

If the singularities of X are local complete intersection singularities, then ${\mathbb {T}}^2 = \mathrm{Ext }^2 (\Omega ^1_X, {\mathcal {O}}_X)$.

Indeed, the singularities which occur for the canonical models of varieties of general type are called canonical singularities and are somehow tractable (see [326]); nevertheless the study of their deformations may present highly nontrivial problems.

For this reason, we restrict now ourselves to the case of complex dimension two, where these singularities are easier to describe.

10 Moduli spaces of surfaces of general type

10.1 Canonical models of surfaces of general type.

The classification theory of algebraic varieties proposes to classify the birational equivalence classes of projective varieties.

Now, in the birational class of a non ruled projective surface there is, by the theorem of Castelnuovo (see e.g. [55]), a unique (up to isomorphism) minimal model S (concretely, minimal means that S contains no ($-$1)-curves, i.e., curves E such that $E \cong {\mathbb {P}}^1$, and with $E^2=-1$).

We shall assume from now on that S is a smooth minimal (projective) surface of general type: this is equivalent (see [55]) to the two conditions:

(*) $K_S^2 > 0$ and $K_S$ is nef, where as well known, a divisor D is said to be nef if, for each irreducible curve C, we have $D \cdot C \ge 0$.

It is very important that, as shown by Kodaira [250], the class of non minimal surfaces is stable by small deformation; on the other hand, a small deformation of a minimal algebraic surface of general type is again minimal (see prop. 5.5 of [21]). Therefore, the class of minimal algebraic surfaces of general type is stable by deformation in the large.

Even if the canonical divisor $K_S$ is nef, it does not however need to be an ample divisor, indeed

The canonical divisor $K_S$ of a minimal surface of general type S is ample iff there does not exist an irreducible curve C on S with $K\cdot C=0$ $\Leftrightarrow$ there is no ($-$2)-curve C on S, i.e., a curve such that $C\cong {\mathbb {P}}^1$, and $C^2=-2$.

The number of ($-$2)-curves is bounded by the rank of the Neron Severi lattice $NS(S) \subset H^2(S, {\mathbb {Z}})/ Torsion$ of S (NS(S) is the image of $Pic(S) = H^1 ({\mathcal {O}}^*_S)$ inside $H^2(S, {\mathbb {Z}})/ Torsion$, and, by Lefschetz’ (1,1) theorem, it is the intersection with the Hodge summand $H^{1,1}$); the ($-$2)-curves can be contracted by a contraction $\pi :S \rightarrow X$, where X is a normal surface which is called the canonical model of S.

The singularities of X are called Rational Double Points (also called Du Val or Kleinian singularities, see [142]), and X is a Gorenstein variety , i.e. (see [211]) the dualizing sheaf $\omega _X$ is invertible, and the associated Cartier divisor $K_X$, called again canonical divisor, is ample and such that $\pi ^* ( K_X) = K_S$.

X is also the projective spectrum (set of homogeneous prime ideals) of the canonical ring

$$\begin{aligned} {\mathcal {R}}(S) : = {\mathcal {R}}(S,K_S) : = \bigoplus _{m \ge 0}H^0 ({\mathcal {O}}_S (mK_S). \end{aligned}$$

This definition generalizes to any dimension, since for a variety of general type (one for which there is a pluricanonical map which is birational onto its image) the canonical ring is a finitely generated graded ring, as was proven by Birkar, Cascini, Hacon, and McKernan [43]. And one defines a canonical model as a variety with canonical singularities and with ample canonical divisor $K_X$.

More concretely, the canonical model of a surface of general type is directly obtained as the image, for $m \ge 5$, of the m-th pluricanonical map of S (associated to the sections in $H^0 ({\mathcal {O}}_S (mK_S))$) as shown by Bombieri [54] (extended to any characteristic by Ekedahl [151], and in [93, 94]).

Theorem 164

(Bombieri) Let S be a minimal surface of general type, and consider the m-th pluricanonical map $\varphi _m$ of S (associated to the linear system $|mK_S|$) for $m\ge 5$, or for $m=4$ when $K^2_S \ge 2$.

Then $\varphi _m$ is a birational morphism whose image is isomorphic to the canonical model X, embedded by its m-th pluricanonical map.

Corollary 165

Bombieri [55] Minimal surfaces S of general type with given topological invariants $e(S), b^+(S)$ (here, $b^+(S)$ is the positivity of the intersetion form on $H^2(S, {\mathbb {Z}})$, and the pair of topological invariants is equivalent to the pair of holomorphic invariants $K^2_S, \chi (S) := \chi ({\mathcal {O}}_S)$) are ‘bounded’, i.e., they belong to a finite number of families having a connected base.

In particular, for fixed Euler number and positivity $e(S), b^+(S)$ we have a finite number of differentiable and topological types.

In fact, one can deduce from here effective upper bounds for the number of these families, hence for the types (see [88, 92]); see [273] for recent work on lower bounds and references to other recent and less recent results.

Results in the style of Bombieri have been recently obtained by Hacon and Mckernan [205], and from these one obtains (non explicit) boundedness results for the varieties of general type with fixed invariants $K^n_X, \chi (X)$ .

10.2 The Gieseker moduli space

When one deals with projective varieties or projective subschemes the most natural parametrization, from the point of view of deformation theory, is given by the Hilbert scheme, introduced by Grothendieck [200].

For instance, in the case of surfaces of general type with fixed invariants $\chi (S) = a$ and $K^2_S = b$, their 5-canonical models $X_5$ are surfaces with Rational Double Points as singularities and of degree 25 b in a fixed projective space ${\mathbb {P}}^N$, where $N + 1 = P_5: = h^0 (5 K_S) = \chi (S) + 10 K^2_S = a + 10 b$.

The Hilbert polynomial of $X_5$ is the polynomial

$$\begin{aligned} P (m) := h^0 (5 m K_S) = a + \frac{1}{2}( 5 m -1) 5 m b. \end{aligned}$$

Grothendieck [200] showed that, given a Hilbert polynomial (see [211]), there is

• (i) an integer d and

• (ii) a subscheme ${\mathcal {H}}= {\mathcal {H}}_P$ of the Grassmannian of codimension P(d)- subspaces of $H^0 ({\mathbb {P}}^N, {\mathcal {O}}_{{\mathbb {P}}^N} (d))$, called Hilbert scheme, such that

• (iii) ${\mathcal {H}}$ parametrizes the degree d graded pieces $H^0 ({\mathcal {I}}_{\Sigma }(d))$ of the homogeneous ideals of all the subschemes $\Sigma \subset {\mathbb {P}}^N$ having the given Hilbert polynomial P.

The Hilbert point of $\Sigma$ is the Plücker point

$$\begin{aligned} \Lambda ^{P(d)} (r_{\Sigma }^{\vee }) \in {\mathbb {P}}(H^0 ({\mathbb {P}}^N, {\mathcal {O}}_{{\mathbb {P}}^N} (d))^{\vee } ) \end{aligned}$$

where $r_{\Sigma }$ is the restriction homomorphism (surjective for d large)

$$\begin{aligned} r_{\Sigma } : H^0 ({\mathbb {P}}^N, {\mathcal {O}}_{{\mathbb {P}}^N} (d)) \rightarrow H^0 (\Sigma , {\mathcal {O}}_{\Sigma } (d)). \end{aligned}$$

Inside ${\mathcal {H}}$ one has the open sets

$$\begin{aligned} {\mathcal {H}}^* = \{ \Sigma | \Sigma \mathrm{\ is \ smooth} \} \subset {\mathcal {H}}^0, \end{aligned}$$

where

$$\begin{aligned} {\mathcal {H}}^0 : = \{ \Sigma | \Sigma \mathrm{\ is\ reduced \ with \ only \ rational \ Gorenstein \ singularities } \}. \end{aligned}$$

Gieseker showed in [177], replacing the 5-canonical embeddding by an m-canonical embedding with much higher m, the following

Theorem 166

(Gieseker) The moduli space of canonical models of surfaces of general type with invariants $\chi , K^2$ exists as a quasi-projective scheme

$$\begin{aligned} {\mathfrak {M}}_{\chi , K^2}^{can} \end{aligned}$$

which is called the Gieseker moduli space.

Similar theorems hold also for higher dimensional varieties, see [256, 361], for the most recent developments, but we do not state here the results, which are more complicated and technical.

10.3 Components of moduli spaces and deformation equivalence

We mentioned previously that the relation of deformation equivalence is a good general substitute for the condition that two manifolds belong to the same connected (resp.: irreducible) component of the moduli space.

Things get rather complicated and sometimes pathological in higher dimension, especially since, even for varieties of general type, there can be three models, smooth, terminal, and canonical model, and the latter are singular.

In the case of surfaces of general type things still work out fine (up to a certain extent), since the main issue is to compare the deformations of minimal models versus the ones of canonical models.

We have then the following theorem.

Theorem 167

Given two minimal surfaces of general type $S, S'$ and their respective canonical models $X, X'$, then

S and $S'$ are deformation equivalent $\Leftrightarrow$ X and $X'$ are deformation equivalent $\Leftrightarrow$ X and $X'$ yield two points in the same connected component of the Gieseker moduli space.

One idea behind the proof is the observation that, in order to analyse deformation equivalence, one may restrict oneself to the case of families parametrized by a base T with $dim (T) = 1$: since two points in a complex space $T \subset {\mathbb {C}}^n$ (or in an algebraic variety) belong to the same irreducible component of T if and only if they belong to an irreducible curve $T ' \subset T$. And one may further reduce to the case where T is smooth simply by taking the normalization $T^0 \rightarrow T_{red} \rightarrow T$ of the reduction $T_{red}$ of T, and taking the pull-back of the family to $T^0$.

A less trivial result which is used is the so-called simultaneous resolution of singularities (cf. [60–62, 353])

Theorem 168

(Simultaneous resolution according to Brieskorn and Tjurina) Let $T : = {\mathbb {C}}^{\tau }$ be the basis of the semiuniversal deformation of a Rational Double Point (X, 0). Then there exists a ramified Galois cover $T' \rightarrow T$, with $T'$ smooth $T' \cong {\mathbb {C}}^{\tau }$ such that the pull-back ${\mathcal {X}}' : = {\mathcal {X}}\times _T T'$ admits a simultaneous resolution of singularities $p : {\mathcal {S}}' \rightarrow {\mathcal {X}}'$ (i.e., p is bimeromorphic, all the fibres of the composition ${\mathcal {S}}' \rightarrow {\mathcal {X}}' \rightarrow T'$ are smooth, and the fibre over $t' = 0$ is equal to the minimal resolution of singularities of (X, 0)).

Another important observation is that the local analytic structure of the Gieseker moduli space is determined by the action of the group of automorphisms of X on the Kuranishi space of X.

Remark 169

Let X be the canonical model of a minimal surface of general type S with invariants $\chi , K^2$. The isomorphism class of X defines a point $[X] \in {\mathfrak {M}}_{\chi , K^2}^{can}$.

Then the germ of complex space $({\mathfrak {M}}_{\chi , K^2}^{can},{[X]})$ is analytically isomorphic to the quotient ${\mathfrak {B}} (X) / Aut (X)$ of the Kuranishi space of X by the finite group $Aut (X) = Aut (S)$.

Let S be a minimal surface of general type and let X be its canonical model. To avoid confusion between the corresponding Kuranishi spaces, denote by ${{\mathrm{\text {Def}}}}(S)$ the Kuranishi space for S, respectively ${{\mathrm{\text {Def}}}}(X)$ the Kuranishi space of X.

Burns and Wahl [66], inspired by [13] explained the relation holding between ${{\mathrm{\text {Def}}}}(S)$ and ${{\mathrm{\text {Def}}}}(X)$.

Theorem 170

(Burns–Wahl) Assume that $K_S$ is not ample and let $\pi :S \rightarrow X$ be the canonical morphism.

Denote by ${\mathcal {L}}_X$ the space of local deformations of the singularities of X (Cartesian product of the corresponding Kuranishi spaces) and by ${\mathcal {L}}_S$ the space of deformations of a neighbourhood of the exceptional locus $Exc ( \pi )$ of $\pi$. Then ${{\mathrm{\text {Def}}}}(S)$ is realized as the fibre product associated to the Cartesian diagram

where $\nu$ is the number of rational $(-2)$-curves in S, and $\lambda$ is a Galois covering with Galois group $W := \oplus _{i=1}^r W_i$, the direct sum of the Weyl groups $W_i$ of the singular points of X (these are generated by reflections, hence yield a smooth quotient, see [124]).

An immediate consequence is the following

Corollary 171

(Burns–Wahl)

• (1) $\psi :{{\mathrm{\text {Def}}}}(S) \rightarrow {{\mathrm{\text {Def}}}}(X)$ is a finite morphism, in particular, $\psi$ is surjective.

• (2) If the derivative of ${{\mathrm{\text {Def}}}}(X) \rightarrow {\mathcal {L}}_X$ is not surjective (i.e., the singularities of X cannot be independently smoothened by the first order infinitesimal deformations of X), then ${{\mathrm{\text {Def}}}}(S)$ is singular.

In the next section we shall see the role played by automorphisms.

10.4 Automorphisms and canonical models

Assume that G is a group with a faithful action on a complex manifold Y: then G acts naturally on the sheaves associated to $\Omega ^1$, hence we have a linear representation of G on the vector spaces that are the cohomology groups of such sheaves: for instance G acts linearly on $H^q (\Omega ^p_Y)$, and also on the vector spaces $H^0 ( (\Omega ^n_Y)^{\otimes m}) = H^0 ({\mathcal {O}}_Y (mK_Y))$, hence on the canonical ring

$$\begin{aligned} {\mathcal {R}}(Y) : ={\mathcal {R}}(Y,K_Y) : = \bigoplus _{m \ge 0}H^0 ({\mathcal {O}}_Y (mK_Y)). \end{aligned}$$

If Y is a variety of general type, then G acts linearly on the vector space $H^0 ({\mathcal {O}}_Y (mK_Y))$, hence linearly on the m-th pluricanonical image $Y_m$, which is an algebraic variety bimeromorphic to Y. Hence G is isomorphic to a subgroup of the algebraic group $Aut (Y_m)$. Matsumura [283] used the structure theorem for linear algebraic groups (see [218]) to show that, if G were infinite, then $Aut (Y_m)$ would contain a non trivial Cartan subgroup (${\mathbb {C}}$ or ${\mathbb {C}}^*$), hence Y would be uniruled: a contradiction. Hence we have the (already mentioned) theorem:

Theorem 172

(Matsumura) The automorphism group of a variety Y of general type is finite.

The above considerations apply now to the m-th pluricanonical image X of a variety Y of general type.

I.e., we have an embedded variety $X \subset {\mathbb {P}}(V)$ and a linear representation of a finite group G on the vector space V, such that X is G-invariant (for Y of general type one has $V := V_m : = H^0 ({\mathcal {O}}_Y (mK_Y))$).

Now, since we work over ${\mathbb {C}}$, the vector space V splits uniquely, up to permutation of the summands, as a direct sum of irreducible representations

$$\begin{aligned} (**) \ \ V_m = \bigoplus _{\rho \in Irr (G)} W_{\rho }^{n(\rho )}. \end{aligned}$$

We come now to the basic notion of a family of G-automorphisms (this notion shall be further explained in the next section).

Definition 173

A family of G-automorphisms is a triple

$$\begin{aligned} ((p :{\mathcal {X}}\rightarrow T), G, \alpha ) \end{aligned}$$

where:

• (1) $(p :{\mathcal {X}}\rightarrow T)$ is a flat family in a given category (a smooth family for the case of minimal models of surfaces of general type)

• (2) G is a (finite) group

• (3) $\alpha :G \times {\mathcal {X}}\rightarrow {\mathcal {X}}$ yields a biregular action $G \rightarrow Aut ({\mathcal {X}})$, which is compatible with the projection p and with the trivial action of G on the base T (i.e., $p(\alpha (g,x)) = p(x) , \ \forall g \in G, x \in {\mathcal {X}}$).

As a shorthand notation, one may also write g(x) instead of $\alpha (g,x)$, and by abuse of notation say that the family of automorphisms is a deformation of the pair $(X_t,G)$ instead of the triple $(X_t,G, \alpha _t)$.

The following then holds.

Proposition 174

• (1) A family of automorphisms of manifolds of general type (not necessarily minimal models) induces a family of automorphisms of canonical models.

• (2) A family of automorphisms of canonical models induces, if the basis T is connected, a constant decomposition type $(**)$ for $V_m (t)$.

• (3) A family of automorphisms of smooth complex manifolds admits a differentiable trivialization, i.e., in a neighbourhood of $t_0 \in T$, a diffeomorphism as a family with $( S_0 \times T, p_T, \alpha _0 \times Id_T)$; in other words, with the trivial family for which $g (y,t) = (g(y),t)$.

We refer to [114] for a sketchy proof, let us just observe that if we have a continuous family of finite dimensional representations, the multiplicity of an irreducible summand is a locally constant function on the parameter space T (being given by the scalar product of the respective trace functions, it is an integer valued continuous function, hence locally constant).

Let us then consider the case of a family of canonical models of varieties of general type: by 2) above, and shrinking the base in order to make the addendum ${\mathcal {R}}(p)_m = p_* ({\mathcal {O}}_{{\mathcal {S}}} (mK))$ free, we get an embedding of the family

$$\begin{aligned} ({\mathfrak {X}}, G) \hookrightarrow T \times \left( {\mathbb {P}}\left( V_m = \bigoplus _{\rho \in Irr (G)} W_{\rho }^{n(\rho )} \right) , G\right) . \end{aligned}$$

In other words, all the canonical models $X_t$ are contained in a fixed projective space, where also the action of G is fixed.

Now, the canonical model $X_t$ is left invariant by the action of G if and only if its Hilbert point is fixed by G. Hence, we get a closed subset ${\mathcal {H}}_0 (\chi , K^2)^G$ of the Hilbert scheme ${\mathcal {H}}^0 (\chi , K^2)$

$$\begin{aligned} {\mathcal {H}}_0 (\chi , K^2)^G: = \left\{ X | \omega _X \cong {\mathcal {O}}_X(1),\quad X \quad {is \, normal,} \quad \gamma (X) = X \quad \forall \gamma \in G\right\} . \end{aligned}$$

For instance in the case of surfaces one has the following theorem (see [256, 360, 361] and references therein for results on moduli spaces of canonically polarized varieties in higher dimension).

Theorem 175

The surfaces of general type which admit an action of a given pluricanonical type $(**)$ i.e., with a fixed irreducible G- decomposition of their canonical ring, form a closed subvariety $({\mathfrak {M}}_{\chi , K^2}^{can})^{G, (**)}$ of the moduli space ${\mathfrak {M}}_{\chi , K^2}^{can}$.

Remark 176

The situation for the minimal models of surfaces of general type is different, because then the subset of the moduli space where one has a fixed differentiable type is not closed, as showed in [33].

The puzzling phenomenon which we discovered in joint work with Ingrid Bauer [32, 33], on the moduli spaces of Burniat surfaces) is that deformations of automorphisms differ for canonical and for minimal models.

More precisely, let S be a minimal surface of general type and let X be its canonical model. Denote by ${{\mathrm{\text {Def}}}}(S)$, resp. ${{\mathrm{\text {Def}}}}(X)$, the base of the Kuranishi family of S, resp. of X.

Assume now that we have $1 \ne G \le {{\mathrm{\text {Aut}}}}(S) = {{\mathrm{\text {Aut}}}}(X)$.

Then we can consider the Kuranishi space of G-invariant deformations of S, denoted by ${{\mathrm{\text {Def}}}}(S,G)$, and respectively consider ${{\mathrm{\text {Def}}}}(X,G)$; we have a natural map ${{\mathrm{\text {Def}}}}(S,G) \rightarrow {{\mathrm{\text {Def}}}}(X,G)$.

We indeed show in [33] that this map needs not be surjective, even if surjectivity would seem plausible; we have the following result:

Theorem 177

The deformations of nodal Burniat surfaces with $K^2_S =4$ to extended Burniat surfaces with $K^2_S =4$ yield examples where ${{\mathrm{\text {Def}}}}(S,({\mathbb {Z}}/2{\mathbb {Z}})^2) \rightarrow {{\mathrm{\text {Def}}}}(X,({\mathbb {Z}}/2{\mathbb {Z}})^2)$ is not surjective.

Moreover, whereas for the canonical model we have:

$$\begin{aligned} {{\mathrm{\text {Def}}}}(X,({\mathbb {Z}}/2{\mathbb {Z}})^2) = {{\mathrm{\text {Def}}}}(X), \end{aligned}$$

for the minimal models we have

$$\begin{aligned} {{\mathrm{\text {Def}}}}(S,({\mathbb {Z}}/2{\mathbb {Z}})^2) \subsetneq {{\mathrm{\text {Def}}}}(S) \end{aligned}$$

and indeed the subset ${{\mathrm{\text {Def}}}}(S,({\mathbb {Z}}/2{\mathbb {Z}})^2)$ corresponds to the locus of nodal Burniat surfaces.

The moduli space of pairs (S, G) of an extended (or nodal) smooth projective and minimal Burniat surface S with $K^2_S =4$, taken together with its canonical $G: = ({\mathbb {Z}}/2{\mathbb {Z}})^2$-action, is disconnected; but its image in the Gieseker moduli space is a connected open set.

10.5 Kuranishi subspaces for automorphisms of a fixed type

Proposition 174 is quite useful when one analyses the deformations of a given G-action, say on a compact complex manifold: it tells us that we have to look at the complex structures for which the given differentiable action is holomorphic. Hence we derive (see [86]):

Proposition 178

Consider a fixed action of a finite group G on a compact complex manifold X. Then we obtain a closed subset Def(X, G) of the Kuranishi space, corresponding to deformations which preserve the given action, and yielding a maximal family of deformations of the G-action.

The subset Def(X, G) is the intersection $Def(X) \cap H^1(\Theta _X)^G$.

Remark 179

• (1) The proof is based on the well known and already cited Cartan’s lemma ([78]), that the action of a finite group in an analytic neighbourhood of a fixed point can be linearized. The proof and the result extend also to encompass compact complex spaces.

• (2) The above proposition is, as we shall now show in the example of projective curves, quite apt to estimate the dimension of the subspace $Def(X,G) \subset Def(X)$. For instance, if Def(X) is smooth, then the dimension of Def(X, G) is just equal to $dim (H^1(\Theta _X)^G)$.

We want to show how to calculate the tangent space to the Kuranishi space of G-invariant deformations in some cases.

To do this, assume that X is smooth, and that there is a normal crossing divisor $D = \cup _i D_i$ such that

• (1) $D_i$ is a smooth divisor

• (2) the $D_i$ ’s intersect transversally

• (3) there is a cyclic sugbroup $G_i \subset G$ such that $D_i = Fix (G_i)$

• (4) the stabilizer on the smooth locus of $D_{i_1} \cap D_{i_2} \cap \cdots \cap D_{i_k}$ equals $G_{i_1} \oplus G_{i_2} \oplus \cdots \oplus G_{i_k}$.

Then, setting $Y : = X/G$, Y is smooth and the branch divisor B is a normal crossing divisor $B = \cup _i B_i$.

Define as usual the sheaf of logarithmic forms $\Omega ^1_X ( \log D_1, \ldots ,\log D_h)$, as the sheaf generated by $\Omega ^1_X$, and by the logarithmic derivatives of the equations $s_i$ of the divisors $D_i$, define $\Theta _Y (- \log D_1, \ldots ,- \log D_h)$ as the dual sheaf (this sheaf can also be more generally defined as the sheaf of derivations carrying the ideal sheaf of D to itself). We have then the following proposition.

Proposition 180

Let $p : X \rightarrow Y = X/G$ the quotient projection. Then $p_* ( \Theta _X) = \Theta _Y (- \log B_1, \ldots ,- \log B_h)$.

In particular, $H^i (\Theta _X ) = H^i (\Theta _Y (- \log B_1, \ldots ,- \log B_h))$.

Idea of proof

The basic idea of the proof is the calculation one does in dimension $n=1$ (and is the same one to be done at the generic point of the divisor $D_i$, which maps to $B_i$).

Namely, assume that the local quotient map is given by $w = z^m$, the action being given by $z \mapsto \epsilon z$, $\epsilon$ being a primitive m-th root of unity. It follows that $dz \mapsto \epsilon dz$, and, dually, $(\partial / \partial z) \mapsto \epsilon ^{-1} (\partial / \partial z)$.

In particular,

$$\begin{aligned} d log(z) = dz/z = (1/m) dw/w \quad \,{and} \quad z (\partial / \partial z) = m w (\partial / \partial w) \end{aligned}$$

are invariant.

Then a vector field

$$\begin{aligned} \theta = f(z) \partial / \partial z = f(z)/z (z \partial / \partial z ) = f(z)/z m w (\partial / \partial w) \end{aligned}$$

is invariant if and only if f(z) / z is invariant, hence if and only if $f (z)/ z = F(w)$, where F(w) is holomorphic. $\square$

For instance, in the case of algebraic curves, where Def(X) is smooth, the dimension of Def (X, G) equals the dimension of

$$\begin{aligned} H^1 (\Theta _Y (- \log B_1, \ldots ,- \log B_d))= H^1 (\Theta _Y (- y_1, \ldots ,- y_d)). \end{aligned}$$

Let $g'$ be the genus of Y, and observe that this vector space is Serre dual to $H^0 ( 2 K_Y + y_1+ \cdots + y_d))$. By Riemann-Roch its dimension equals $3 g' -3 + d$ whenever $3 g' -3 + d \ge 0$ (in fact $H^0 (\Theta _Y (- y_1, \ldots ,- y_d))= 0$ when $2 - 2g' - d < 0$).

Calculations with the above sheaves are the appropriate ones to calculate the deformations of ramified coverings, see for instance [32, 82, 95, 317], and especially [33].

The main problem with the group of automorphisms on minimal models of surfaces (see [114]) is that a limit of isomorphisms need not be an isomorphism¹², it can be for instance a Dehn twist on a vanishing cycle (see also [106, 332]).

11 Moduli spaces of symmetry marked varieties

11.1 Moduli marked varieties

We give now the definition of a symmetry marked variety for projective varieties, but one can similarly give the same definition for complex or Kähler manifolds; to understand the concept of a marking, it suffices to consider a cyclic group acting on a variety X. A marking consists in this case of the choice of a generator for the group acting on X. The marking is very important when we have several actions of a group G on some projective varieties, and we want to consider the diagonal action of G on their product.

Definition 181

• (1) A G-marked (projective) variety is a triple $(X, G, \eta )$ where X is a projective variety, G is a group and $\eta :G \rightarrow {{\mathrm{\text {Aut}}}}(X)$ is an injective homomorphism;

• (2) equivalently, a marked variety is a triple $(X, G, \alpha )$ where $\alpha :X \times G \rightarrow X$ is a faithful action of the group G on X.

• (3) Two marked varieties $(X,G, \alpha )$, $(X',G, \alpha ')$ are said to be isomorphic if there is an isomorphism $f :X \rightarrow X'$transporting the action $\alpha :X \times G \rightarrow X$ into the action $\alpha ' :X' \times G \rightarrow X'$, i.e., such that

  $$\begin{aligned} f \circ \alpha = \alpha ' \circ ( f \times {{\mathrm{\text {id}}}}) \Leftrightarrow \eta ' = Ad(f) \circ \eta , \ \ Ad (f) (\phi ) : = f \phi f^{-1}. \end{aligned}$$

• (4) If G is a subset of ${{\mathrm{\text {Aut}}}}(X)$, then the natural marked variety is the triple (X, G, i), where $i :G \rightarrow {{\mathrm{\text {Aut}}}}(X)$ is the inclusion map, and it shall sometimes be denoted simply by the pair (X, G).

• (5) A marked curve $(D,G, \eta )$ consisting of a smooth projective curve of genus g and a faithful action of the group G on D is said to be a marked triangle curve of genus g if $D / G \cong {\mathbb {P}}^1$ and the quotient morphism $p :D \rightarrow D / G \cong {\mathbb {P}}^1$ is branched in three points.

Remark 182

Observe that:

• (1) we have a natural action of ${{\mathrm{\text {Aut}}}}(G)$ on G-marked varieties, namely, if $\psi \in Aut (G)$,

  $$\begin{aligned} \psi (X,G,\eta ) : = (X, G, \eta \circ \psi ^{-1}). \end{aligned}$$

  The corresponding equivalence class of a G-marked variety is defined to be a G-(unmarked) variety.

• (2) the action of the group ${{\mathrm{\text {Inn}}}}(G)$ of inner automorphisms does not change the isomorphism class of $(X,G,\eta )$ since, for $\gamma \in G$, we may set $f : = \eta (\gamma )$, $\psi : = Ad (\gamma )$, and then $\eta \circ \psi = Ad(f) \circ \eta$, since $\eta ( \psi (g)) = \eta ( \gamma g \gamma ^{-1} ) = \eta ( \gamma ) \eta ( g ) (\eta (\gamma )^{-1} ) = Ad(f) (\eta (g))$.

• (3) In the case where $G = {{\mathrm{\text {Aut}}}}(X)$, we see that ${{\mathrm{\text {Out}}}}(G)$ acts simply transitively on the isomorphism classes of the ${{\mathrm{\text {Aut}}}}(G)$-orbit of $(X,G,\eta )$.

In the spirit of the above concept we have already given, in the previous section, the definition of a family of G-automorphisms (we shall also speak of a family of G-marked varieties).

The local deformation theory of a G-marked variety X, at least in the case where the group G is finite, is simply given by the fixed locus ${{\mathrm{\text {Def}}}}(X)^G$ of the natural G -action on the Kuranishi space ${{\mathrm{\text {Def}}}}(X)$. As we mentioned previously (see 177), one encounters difficulties, when X has dimension at least 2, to use the Kuranishi approach for a global theory of moduli of G-marked minimal models.

But we have a moduli space of G-marked varieties in the case of curves of genus $g \ge 2$ and in the case of canonical models of surfaces of general type, and similarly also for canonical models in higher dimension.

In fact, one considers again a fixed linear representation space for the group G, the associated projective action,

$$\begin{aligned} \left( {\mathbb {P}}\left( V_m = \bigoplus _{\rho \in Irr (G)} W_{\rho }^{n(\rho )} \right) \!, G\right) . \end{aligned}$$

and a locally closed subset of the Hilbert scheme

$$\begin{aligned}&{\mathcal {H}}_{can} (\chi , K^2)^G \subset {\mathcal {H}}^0 (\chi , K^2)\\&{\mathcal {H}}_{can} (\chi , K^2)^{G}:= \left\{ X | \omega _X \cong {\mathcal {O}}_X(1), \gamma (X) = X \quad \forall \gamma \in G,\right. \\&\qquad \left. \quad X\quad {is \, normal, \, with \, canonical \, singularities\ } \right\} . \end{aligned}$$

In this case one divides the above subset by the subgroup

$$\begin{aligned} {\mathcal {C}}(G) \subset GL (V_m) \end{aligned}$$

which is the centralizer of $G \subset GL (V_m)$.

Remark 183

(1) Assume in fact that there is an isomorphism of the marked varieties (X, G) and $(X', G)$ (here the marking is furnished by an m-th pluricanonical embedding of $X, X' \hookrightarrow {\mathbb {P}}( V_m)$, and by the fixed action $\rho : G \hookrightarrow GL (V_m)$).

Then there is an isomorphism $f : X \cong X'$ with $f \circ \gamma = \gamma \circ f$ $\forall \gamma \in G$. Now, f induces a linear map of $V_m$ which we denote by the same symbol: hence we can write the previous condition as

$$\begin{aligned} f \circ \gamma \circ f^{-1} = \gamma , \ \forall \gamma \in G \Leftrightarrow f \in {\mathcal {C}}(G). \end{aligned}$$

(2) By Schur’s lemma ${\mathcal {C}}(G) = \Pi _{\rho \in Irr (G)} GL (n(\rho ), {\mathbb {C}})$ is a reductive group.

(3) Observe that, since the dimension of $V_m$ is determined by the holomorphic invariants of X, then there is only a finite number of possible representation types for the action of G on $V_m$.

(4) Assume moreover that $X, X'$ are isomorphic varieties: then there is such a linear isomorphism $f : V_m \rightarrow V_m$ sending X to $X'$.

The variety $X'$ has therefore two G-markings, the marking $\eta ' : G \rightarrow Aut (X')$ provided by the pluricanonical embeddding $X' \hookrightarrow {\mathbb {P}}( V_m)$, and another one given, in an evident notation, by $Ad (f) \circ \eta$.

Therefore $Aut (X')$ contains two subgroups, $G : = Im (\eta ')$, and $G ' : = Im ( Ad (f) \circ \eta )$. $G = G'$ if and only if f lies in the normalizer ${\mathcal {N}}_G$ of G.

(5) This happens if G is a full subgroup (this means that $G = Aut (X')$). In general f will just belong to the normalizer ${\mathcal {N}}_{X'}$ of $Aut (X')$, and ${\mathcal {N}}_G$ shall just be the finite index subgroup of ${\mathcal {N}}_{X'}$ which stabilises, via conjugation, the subgroup G.

(6) In other words, we define the marked moduli space (of a fixed representation type) as the quotient

$$\begin{aligned} \mathfrak M[G] : = {\mathcal {H}}_{can} \left( \chi , K^2\right) ^G / {\mathcal {C}}_G. \end{aligned}$$

Then the forgetful map from the marked moduli space to the moduli space $\mathfrak M[G] \rightarrow \mathfrak M$, which factors through the quotient $\mathfrak M(G)$ by ${\mathcal {N}}_G / {\mathcal {C}}_G$, yields finite maps $\mathfrak M[G] \rightarrow \mathfrak M(G) \rightarrow \mathfrak M^G$.

We omit here technical details in higher dimension, which have been treated by Binru Li in his Bayreuth Ph.D. Thesis (in preparation).

Observe that the action of Out (G) does not need to respect the representation type.

Let us see now how the picture works in the case of curves: this case is already very enlightening and intriguing.

11.2 Moduli of curves with automorphisms

There are several ‘moduli spaces’ of curves with automorphisms. First of all, given a finite group G, we define a subset ${\mathfrak {M}}_{g,G}$ of the moduli space ${\mathfrak {M}}_g$ of smooth curves of genus $g>1$: ${\mathfrak {M}}_{g,G}$ is the locus of the curves that admit an effective action by the group G. It turns out that ${\mathfrak {M}}_{g,G}$ is a Zariski closed algebraic subset.

In order to understand the irreducible components of ${\mathfrak {M}}_{g,G}$ we have seen that Teichmüller theory plays an important role: it shows the connectedness, given an injective homomorphism $\rho :G \rightarrow Map_g$, of the locus

$$\begin{aligned} {\mathcal {T}}_{g, \rho } : = Fix ( \rho (G)). \end{aligned}$$

Its image ${\mathfrak {M}}_{g, \rho }$ in ${\mathfrak {M}}_{g,G}$ is a Zariski closed irreducible subset (as observed in [115]). Recall that to a curve C of genus g with an action by G we can associate several discrete invariants that are constant under deformation.

The first is the above topological type of the G-action: it is a homomorphism $\rho :G \rightarrow Map_g$, which is well-defined up to inner conjugation (induced by different choices of an isomorphism $Map (C) \cong Map_g$).

We immediately see that the locus ${\mathfrak {M}}_{g, \rho }$ is first of all determined by the subgroup $\rho (G)$ and not by the marking. Moreover, this locus remains the same not only if we change $\rho$ modulo the action by $\mathrm{Aut}(G)$, but also if we change $\rho$ by the adjoint action by $\mathrm{Map}_g$.

Definition 184

• (1) The moduli space of G-marked curves of a certain topological type $\rho$ is the quotient of the Teichmüller submanifold ${\mathcal {T}}_{g, \rho }$ by the centralizer subgroup ${\mathcal {C}}_{\rho (G)}$ of the subgroup $\rho (G)$ of the mapping class group. We get a normal complex space which we shall denote $\mathfrak M_g[\rho ]$. $\mathfrak M_g[\rho ] = {\mathcal {T}}_{g, \rho } / {\mathcal {C}}_{\rho (G)}$ is a finite covering of a Zariski closed subset of the usual moduli space (its image $\mathfrak M_{g, \rho }$), therefore it is quasi-projective, by the theorem of Grauert and Remmert.

• (2) Defining $\mathfrak M_g(\rho )$ as the quotient of ${\mathcal {T}}_{g, \rho }$ by the normalizer ${\mathcal {N}}_{\rho (G)}$ of $\rho (G)$, we call it the moduli space of curves with a G-action of a given topological type. It is again a normal quasi-projective variety.

Remark 185

• (1) If we consider $G' : = \rho (G)$ as a subgroup $G' \subset Map_g$, then we get a natural $G'$-marking for any $C \in Fix(G') = {\mathcal {T}}_{g, \rho }$.

• (2) As we said, $Fix(G') = {\mathcal {T}}_{g, \rho }$ is independent of the chosen marking, moreover the projection $Fix(G') = {\mathcal {T}}_{g, \rho } \rightarrow \mathfrak M_{g, \rho }$ factors through a finite map $\mathfrak M_g(\rho ) \rightarrow \mathfrak M_{g, \rho }$.

The next question is whether $\mathfrak M_g(\rho )$ maps 1-1 into the moduli space of curves. This is not the case, as we shall easily see. Hence we give the following definition.

Definition 186

Let $G \subset Map_g$ be a finite group, and let C represent a point in Fix(G). Then we have a natural inclusion $G \rightarrow A_C : = Aut (C)$, and C is a fixed point for the subgroup $A_C \subset Map_g$: $A_C$ is indeed the stabilizer of the point C in $Map_g$, so that locally (at the point of $\mathfrak M_g$ corresponding to C) we get a complex analytic isomorphism $\mathfrak M_g = {\mathcal {T}}_g / A_C.$

We define $H_G : = \cap _{ C \in Fix(G)} A_C$ and we shall say that G is a full subgroup if $G = H_G$. Equivalently, $H_G$ is the largest subgroup H such that $Fix(H) = Fix (G)$.

This implies that $H_G$ is a full subgroup.

Remark 187

The above definition shows that the map ${\mathcal {T}}_{g, \rho } \rightarrow \mathfrak M_{g, \rho }$ factors through $\mathfrak M_g (H_G) : = {\mathcal {T}}_{g, \rho } / {\mathcal {N}}_{H_G}$, hence we restrict our attention only to full subgroups.

Proposition 188

If H is a full subgroup $H \subset Map_g$, and $\rho : H \subset Map_g$ is the inclusion homomorphism, then $\mathfrak M_g (\rho )$ is the normalization of $\mathfrak M_{g, \rho }$.

Proof

Recall that $\mathfrak M_g (H) = Fix (H) / {\mathcal {N}}_H$, and that for a general curve $C \in Fix (H)$ we have $A_C = H$.

Assume then that $C = \gamma (C')$, and that both $C, C' \in Fix (H)$. Then $\gamma A_C \gamma ^{-1} = A_C$, hence for C general $\gamma \in {\mathcal {N}}_H$.

This means that the finite surjective morphism $\varphi : \mathfrak M_g (H) \rightarrow \mathfrak M_{g, H}$ is generically bijective; $\mathfrak M_g (H)$ is a normal variety, being locally the quotient of a smooth variety by a finite group: hence $\varphi$ is the normalization morphism and $\mathfrak M_g (H)$ is the normalization of $\mathfrak M_{g, H}$. $\square$

Next we investigate when the natural morphism $\mathfrak M_g (H) \rightarrow \mathfrak M_{g, H}$ is not injective. In order that this be the case, we have already seen that we must pick up a curve C such that $H \subset A_C \ne H$. Now, let $C'$ be another point of Fix (H) which has the same image in the moduli space: this means that $C'$ is in the orbit of C so there is an element $\gamma \in Map_g$ carrying $C'$ to C.

By conjugation $\gamma$ sends H to another subgroup $H'$ of $A_C$. We can assume that $H \ne H'$, else $\gamma$ lies in the normalizer $N_H$ and we have the same point in $\mathfrak M_g (H)$. Hence the points of $\mathfrak M_g (H)$ that have the same image as C correspond to the subset of subgroups $H' \subset A_C$ which are conjugate to H by the action of some $\gamma \in Map_g$.

Example 189

Consider the genus 2 curve C birational to the affine curve with equation $y^2 = (x^6-1)$. Its canonical ring is generated by $x_0, x_1, y$ and is the quotient ${\mathbb {C}}[x_0, x_1, y] / (y^2 - x_1^6 + x_0^6)$.

Its group of automorphisms is generated (as a group of projective transformations) by $a (x_0, x_1, y) : = (x_0, \epsilon x_1, y)$ where $\epsilon$ is a primitive sixth root of 1, and by $b (x_0, x_1, y) : = (x_1, x_0, i y)$. a has order 6, b has order 4, the square $b^2$ is the hyperelliptic involution $h (x_0, x_1, y) : = (x_0, x_1, -y)$.

We have

$$\begin{aligned} b \circ a \circ b^{-1} = a^{-1}, \end{aligned}$$

a formula which implies the (known) fact that the hyperelliptic involution lies in the centre of the group $A_C = Aut (C)$ .

Taking as H the cyclic subgroup generated by b, the space Fix (H) has dimension equal to 1 since $C \rightarrow C/H = {\mathbb {P}}^1$ is branched in 4 points. The quotient of $A_C = Aut (C)$ by $b^2$ is the dihedral group $D_6$, and we see that H is conjugate to 6 different subgroups of $A_C$.

Of course an important question in order to understand the locus in $\mathfrak M_g$ of curves with automorphisms is the determination of all the non full subgroups $G \ne H_G$.

For instance Cornalba [127] answered this question for cyclic groups of prime order, thereby obtaining a full determination of the irreducible components of $Sing (\mathfrak M_g)$. In fact, for $g \ge 4$, the locus $Sing (\mathfrak M_g)$ is the locus of curves admitting a nontrivial automorphism, so this locus is the locus of curves admitting a nontrivial automorphism of prime order. In this case, as we shall see in the next subsection, the topological type is easily determined. We omit to state Cornalba’s result in detail: it amounts in fact to a list of all non full such subgroups of prime order. We limit ourselves to indicate the simplest example of such a situation.

Example 190

Consider the genus $g = \frac{p-1}{2}$ curve C, birational to the affine curve with equation $z^p = (x^2-1)$, where p is an odd prime number. Letting H be the cyclic group generated by the automorphisms $(x,z) \mapsto (x, \epsilon z)$, where $\epsilon$ is a primitive p-th root of unity, we see that the quotient morphism $C \rightarrow C / H \cong {\mathbb {P}}^1$ corresponds to the inclusion of fields ${\mathbb {C}}(x) \hookrightarrow {\mathbb {C}}(C)$. The quotient map is branched on the three points $x = 1, -1 , \infty$, so that Fix (H) consists of just a point (the above curve C).

An easy inspection of the above equation shows that the curve C is hyperelliptic, with involution $h : (x,z) \mapsto (-x, z)$ which is hyperelliptic since ${\mathbb {C}}(C)^h = {\mathbb {C}}(z)$. In this case the locus Fix(H) is contained in the hyperelliptic locus, and therefore it is not an irreducible component of $Sing (\mathfrak M_g)$.

11.3 Numerical and homological invariants of group actions on curves

As already mentioned, given an effective action of a finite group G on C, we set $C':=C/G$, $g':=g(C')$, and we have the quotient morphism $p:C \rightarrow C/G=: C'$, a G-cover.

The geometry of p encodes several numerical invariants that are constant on $M_{g,\rho }(G)$: first of all the genus $g'$ of $C'$, then the number d of branch points $y_1, \ldots , y_d \in C'$.

We call the set $B=\{ y_1, \ldots , y_d\}$ the branch locus, and for each $y_i$ we denote by $m_i$ the multiplicity of $y_i$ (the greatest number dividing the divisor $p^{*} (y_i)$). We choose an ordering of B such that $m_1 \le \cdots \le m_d$.

These numerical invariants $g', d, m_1 \le \cdots \le m_d$ form the so-called primary numerical type.

$p :C\rightarrow C'$ is determined (Riemann’s existence theorem) by the monodromy, a surjective homomorphism:

$$\begin{aligned} \mu :\pi _1(C'{\setminus } B) \rightarrow G. \end{aligned}$$

We have:

$$\begin{aligned} \pi _1(C' {\setminus } B) \cong \Pi _{g', d}:= \langle \gamma _1, \ldots , \gamma _d, \alpha _1, \beta _1 , \ldots , \alpha _{g'}, \beta _{g'} | \prod _{i=1}^d \gamma _i \prod _{j=1}^{g'} [\alpha _j, \beta _j]=1 \rangle . \end{aligned}$$

We set then $c_i : = \mu (\gamma _i)$, $a_j : = \mu (\alpha _j)$, $b_j : = \mu (\beta _j)$, thus obtaining a Hurwitz generating vector, i.e. a vector

$$\begin{aligned} v : = (c_1, \ldots , c_d, a_1, b_1, \ldots , a_{g'}, b_{g'}) \in G^{d+2g'} \end{aligned}$$

s.t.

• G is generated by the entries $c_1, \ldots , c_d, a_1, b_1, \ldots , a_{g'}, b_{g'}$,

• $c_i \not = 1_G$, $\forall i$, and

• $\prod _{i=1}^d c_i \prod _{j=1}^{g'}[a_j,b_j]=1$.

We see that the monodromy $\mu$ is completely equivalent, once an isomorphism $\pi _1(C' {\setminus } B) \cong \Pi _{g', d}$ is chosen, to the datum of a Hurwitz generating vector (we also call the sequence $c_1, \ldots ,c_d, a_1, b_1, \ldots , a_{g'}, b_{g'}$ of the vector’s coordinates a Hurwitz generating system).

A second numerical invariant of these components of ${\mathfrak {M}}_{g} (G)$ is obtained from the monodromy $\mu :\pi _1(C'{\setminus }\{ y_1, \ldots , y_d\})\rightarrow G$ of the restriction of p to $p^{-1}(C'{\setminus } \{ y_1, \ldots , y_d \})$, and is called the $\nu$-type or Nielsen function of the covering.

The Nielsen function $\nu$ is a function defined on the set of conjugacy classes in G which, for each conjugacy class $\mathcal {C}$ in G, counts the number $\nu ({\mathcal {C}})$ of local monodromies $c_1, \ldots , c_d$ which belong to $\mathcal {C}$ (observe that the numbers $m_1 \le \cdots \le m_d$ are just the orders of the local monodromies).

Observe in fact that the generators $\gamma _j$ are well defined only up to conjugation in the group $\pi _1(C'{\setminus }\{ y_1, \ldots , y_d\})$, hence the local monodromies are well defined only up to conjugation in the group G.

We have already observed that the irreducible closed algebraic sets $M_{g,\rho }(G)$ depend only upon what we call the ‘unmarked topological type’, which is defined as the conjugacy class of the subgroup $\rho (G)$ inside $Map_g$. This concept remains however still mysterious, due to the complicated nature of the group $Map_g$. Therefore one tries to use more geometry to get a grasp on the topological type.

The following is immediate by Riemann’s existence theorem and the irreducibility of the moduli space ${\mathfrak {M}}_{g',d}$ of d-pointed curves of genus $g'$. Given $g'$ and d, the unmarked topological types whose primary numerical type is of the form $g', d, m_1, \ldots , m_d$ are in bijection with the quotient of the set of the corresponding monodromies $\mu$ modulo the actions by Aut(G) and by $Map(g',d)$.

Here $Map(g',d)$ is the full mapping class group of genus $g'$ and d unordered points.

Thus Riemann’s existence theorem shows that the components of the moduli space

$$\begin{aligned} {\mathfrak {M}} (G): = \cup _g {\mathfrak {M}}_g (G) \end{aligned}$$

with numerical invariants $g', d$ correspond to the following quotient set.

Definition 191

$$\begin{aligned} {\mathcal {A}}(g',d,G) : = \mathrm{Epi}(\Pi _{g',d}, G)/\mathrm{Map}_{g',d}\times \mathrm{Aut}(G). \end{aligned}$$

Thus a first step toward the general problem consists in finding a fine invariant that distinguishes these orbits.

In the paper [115] we introduced a new homological invariant $\hat{\epsilon }$ for G-actions on smooth curves (and showed that, in the case where G is the dihedral group $D_n$ of order 2n, $\hat{\epsilon }$ is a fine invariant since it distinguishes the different unmarked topological types).

This invariant generalizes the classical homological invariant in the unramified case.

Definition 192

Let $p:C \rightarrow C/G=: C'$ be unramified, so that $d=0$ and we have a monodromy $\mu :\pi _1(C')\rightarrow G$.

Since $C'$ is a classifying space for the group $\pi _{g'}$, we obtain a continuous map

$$\begin{aligned} m : C' \rightarrow BG, \ \pi _1(m) = \mu . \end{aligned}$$

Moreover, $H_2(C', {\mathbb {Z}})$ has a natural generator $[C']$, the fundamental class of $C'$ determined by the orientation induced by the complex structure of $C'$.

The homological invariant of the G-marked action is then defined as:

$$\begin{aligned} \epsilon : = H_2(m) ([C']) \in H_2(BG, {\mathbb {Z}}) = H_2(G, {\mathbb {Z}}). \end{aligned}$$

If we forget the marking we have to take $\epsilon$ as an element in $H_2(G, {\mathbb {Z}})/ Aut(G)$.

Proposition 193

Assume that a finite group G has a fixed point free action on a curve of genus $g \ge 3$.

Let $p:C \rightarrow C/G=: C'$ be the quotient map and pick an isomorphism $\pi _1(C') \cong \pi _{g'}$. Let $\mu : \pi _{g'} \rightarrow G$ be the surjection corresponding to the monodromy of p, and denote by $a_i : = \mu (\alpha _i), b_j : = \mu (\beta _j), \ i,j = 1, \ldots , g'$.

Assume that we have a realization $G = F /R$ of the group G as the quotient of a free group F, and that $\widehat{a_i}, \widehat{b_j}$ are lifts of $a_i, b_j$ to F.

Then the homological invariant $\epsilon$ of the covering is the image of

$$\begin{aligned} \epsilon ' = \prod _1^{g'}[\widehat{a_i}, \widehat{b_i}] \in [F,F] \cap R \end{aligned}$$

into $H_2(G, {\mathbb {Z}}) = ([F,F] \cap R) / [F,R]$.

Proof

$C'$ is obtained attaching a 2-cell D to a bouquet of circles, with boundary $\partial D$ mapping to $\prod _1^{g'}[\alpha _i, \beta _i]$.

Similarly the 2-skeleton $BG^2$ of BG is obtained from a bouquet of circles, with fundamental group $\cong F$, attaching 2-cells according to the relations in R. Since $\prod _1^{g'}[{a_i}, {b_i}] = 1$ in $\pi _{g'}$, the relation $\prod _1^{g'}[\widehat{a_i}, \widehat{b_i}]$ is a product of elements of R. In this way m is defined on D, and the image of the fundamental class of $C'$ is the image of D, which is a sum of 2-cells whose boundary is exactly the loop $\epsilon '$. If we write $\epsilon$ as a sum of 2-cells, we get an element in $H_2(BG^2, BG^1,{\mathbb {Z}})$: but since $\epsilon$ is a product of commutators, the boundary of the corresponding 2-chain is indeed zero, so we get an element in $H_2(BG, {\mathbb {Z}}) = H_2(G, {\mathbb {Z}})$. $\square$

11.4 The refined homology invariant in the ramified case

Assume now that $p : C \rightarrow C/G$ is ramified. Then we define H to be the minimal normal subgroup of G generated by the local monodromies $c_1, \ldots , c_d$ $\Leftrightarrow$ H is the (normal) subgroup generated by the transformations $\gamma \in G$ which have some fixed point.

We have therefore a factorization of p

$$\begin{aligned} C \rightarrow C'' : = C/H \rightarrow C' : = C/G \end{aligned}$$

where $C'' \rightarrow C'$ is an unramified G / H-cover, and where $C \rightarrow C''$ is totally ramified.

The refined homology invariant includes and extends two invariants that have been studied in the literature, and were already mentioned: the $\nu$-type (or Nielsen type) of the cover (also called shape in [170]) and the class in the second homology group $H_2(G/H, {\mathbb {Z}})$ corresponding to the unramified cover $p' :C''= C/H \rightarrow C'$.

The construction of the invariant $\hat{\epsilon }$ is similar in spirit to the procedure used in the unramified case. But we achieve a little less in the ‘branched’ case of a non-free action. In this case we are only able to associate, to two given actions with the same $\nu$-type, an invariant in a quotient group of $H_2(G,{\mathbb {Z}})$ which is the ‘difference’ of the respective $\hat{\epsilon }$-invariants. Here is the way we do it.

Let $\Sigma$ be the Riemann surface (with boundary) obtained from $C'$ after removing open discs $\Delta _i$ around each of the branch points.

Take generators $\gamma _1, \ldots , \gamma _d$ formed by a simple path going from the base point $y_0$ to a point $z_i$ on the circle bounding the open discs $\Delta _i$, and by the circle $\partial \Delta _i$.

Fix then a CW-decomposition of $\Sigma$ as follows. The 0-skeleton $\Sigma ^0$ consists of the point $y_0$ and of the points $z_i$, $i=1, \ldots , d$. The 1-skeleton $\Sigma ^1$ is given by the geometric basis $\alpha _1, \ldots , \beta _{g'}, \gamma _1, \ldots , \gamma _d$ and the 2-skeleton $\Sigma ^2$ consists of one cell.

The restriction $p_\Sigma$ of $p:C \rightarrow C'$ to $p^{-1}(\Sigma )$ is an unramified G-covering of $\Sigma$ and hence corresponds to a continuous map $Bp_\Sigma :\Sigma \rightarrow BG$, well defined up to homotopy. Let $Bp_1 :\Sigma \rightarrow BG$ be a cellular approximation of $Bp_\Sigma$. Since $Bp_1$ can be regarded as a map of pairs $Bp_1 :(\Sigma , \partial \Sigma )\rightarrow (BG,BG^1)$, the push-forward of the fundamental (orientation) class $[\Sigma , \partial \Sigma ]$ gives an element

$$\begin{aligned} {Bp_1}_* [\Sigma , \partial \Sigma ] \in H_2(BG,BG^1)=\frac{R}{[F,R]}. \end{aligned}$$

This element depends on the chosen cellular approximation $Bp_1$ of $Bp_\Sigma$, but its image in a quotient group which we denote by $K_\Gamma$ does not depend on the chosen cellular approximation, as shown in [116]. The main idea to define this quotient group is that a homotopy between two 1-cellular approximations can also be made cellular, hence the difference in relative homology is the sum of boundaries of cylinders; and if we have a cylinder ${\mathcal {C}}$ with upper circle a, lower circle c (with the same orientation), and meridian b, then the boundary of the corresponding 2-cell is

$$\begin{aligned} \partial {\mathcal {C}}= a b c^{-1} b^{-1}. \end{aligned}$$

Definition 194

(1) For any finite group G, let F be the free group generated by the elements of G and let $R\trianglelefteq F$ be the subgroup of relations, that is $G=F/R$.

Denote by $\hat{g}\in F$ the generator corresponding to $g\in G$.

For any $\Gamma \subset G$, union of non trivial conjugacy classes, let $G_\Gamma$ be the quotient group of F by the minimal normal subgroup $R_{\Gamma }$ generated by [F, R] and by the elements $\hat{a}\hat{b}\hat{c}^{-1}\hat{b}^{-1}\in F$, for any $a, c \in \Gamma$, $b\in G$, such that $b^{-1} ab=c$.

(2) Define instead

$$\begin{aligned} K_\Gamma = R / R_{\Gamma } \subset G_\Gamma = F / R_{\Gamma }, \end{aligned}$$

a central subgroup of $G_\Gamma$. We have thus a central extension

$$\begin{aligned} 1 \rightarrow K_\Gamma \rightarrow G_\Gamma \rightarrow G \rightarrow 1. \end{aligned}$$

(3) Define

$$\begin{aligned} H_{2,\Gamma }(G)=\ker \left( G_\Gamma \rightarrow G\times G_\Gamma ^{ab} \right) \!. \end{aligned}$$

Notice that

$$\begin{aligned} H_2(G,{\mathbb {Z}})\cong \frac{R\cap [F,F]}{[F,R]} \cong \ker \left( \frac{F}{[F,R]} \rightarrow G\times G^{ab}_\emptyset \right) \!. \end{aligned}$$

Remark 195

In particular, when $\Gamma = \emptyset$, $H_{2,\Gamma }(G)\cong H_2(G, {\mathbb {Z}})$.

By [115, Lemma 3.12] we have that the morphism

$$\begin{aligned} R\cap [F,F] \rightarrow \frac{R}{R_\Gamma }, \quad r \mapsto rR_\Gamma \end{aligned}$$

induces a surjective group homomorphism

$$\begin{aligned} H_2(G,{\mathbb {Z}}) \rightarrow H_{2, \Gamma }(G). \end{aligned}$$

Now, to a given G-cover $p:C \rightarrow C'$ we associate the set $\Gamma$ of the local monodromies, i.e., of the elements of G which can be geometrically described as those which (i) stabilize some point x of C and (ii) act on the tangent space at x by a rotation of angle $\frac{2\pi }{m}$ where m is the order of the stabilizer at x.

In terms of the notation that we have previously introduced $\Gamma =\Gamma _v$ is simply the union of the conjugacy classes of the $c_i$’s.

Definition 196

The tautological lift $\hat{v}$ of v is the vector:

$$\begin{aligned} \left( \widehat{c_1}, \ldots , \widehat{c_d}; \widehat{a_1}, \widehat{b_1}, \ldots , \widehat{a_{g'}}, \widehat{b_{g'}}\right) \!. \end{aligned}$$

Finally, define $\epsilon (v)$ as the class in $K_{\Gamma }$ of

$$\begin{aligned} \prod _1^d\widehat{c_j} \cdot \prod _1^{g'}\left[ \widehat{a_i}, \widehat{b_i}\right] \!. \end{aligned}$$

It turns out that the image of $\epsilon (v)$ in $K_{\Gamma } /_{Inn(G)}$ is invariant under the action of $Map(g',d)$, as shown in [115].

Moreover the $\nu$-type of a Hurwitz monodromy vector v can be deduced from $\epsilon (v)$, as it is essentially the image of $\epsilon (v)$ in the abelianized group $G_{\Gamma }^{ab}$.

Proposition 197

Let v be a Hurwitz generating vector and let $\Gamma _v\subset G$ be the union of the conjugacy classes of the $c_j$’s , $j\le d$. The abelianization $G_{\Gamma _v}^{ab}$ of $G_{\Gamma _v}$ can be described as follows:

$$\begin{aligned} G_{\Gamma _v}^{ab}\cong \left( \bigoplus _{\mathcal {C}\subset \Gamma _v}{\mathbb {Z}}\langle \mathcal {C} \rangle \right) \oplus \left( \bigoplus _{g\in G{\setminus } \Gamma _v}{\mathbb {Z}}\langle g \rangle \, \right) \!, \end{aligned}$$

where $\mathcal {C}$ denotes a conjugacy class of G.

Moreover the Nielsen function $\nu (v)$ coincides with the vector whose $\mathcal {C}$-components are the corresponding components of the image of $\epsilon (v)\in G_{\Gamma _v}$ in $G_{\Gamma _v}^{ab}$.

11.5 Genus stabilization of components of moduli spaces of curves with G-symmetry

In order to take into account also the automorphism group Aut(G), one has to consider

$$\begin{aligned} K^\cup : = {\coprod }_\Gamma K_{\Gamma }, \end{aligned}$$

the disjoint union of all the $K_{\Gamma }$’s. Now, the group Aut(G) acts on $K^\cup$ and we get a map

$$\begin{aligned} \hat{\epsilon }:{\mathcal {A}}(g',d,G) \rightarrow (K^\cup )/_{Aut(G)} \end{aligned}$$

which is induced by $v\mapsto \epsilon (v)$.

Next, one has to observe that the Nielsen functions of coverings have to satisfy a necessary condition, consequence of the relation

$$\begin{aligned} \prod _{i=1}^d c_i \prod _{j=1}^{g'}[a_j,b_j]=1. \end{aligned}$$

Definition 198

An element

$$\begin{aligned} \nu = (n_{\mathcal {C}})_\mathcal {C} \in \bigoplus _{\mathcal {C}\not = \{ 1 \}}{\mathbb {N}}\langle \mathcal {C}\rangle \end{aligned}$$

is admissible if the following equality holds in the ${\mathbb {Z}}$-module $G^{ab}$:

$$\begin{aligned} \sum _\mathcal {C} n_{\mathcal {C}} \cdot [\mathcal {C}] =0 \end{aligned}$$

(here $[{\mathcal {C}}]$ denotes the image element of ${\mathcal {C}}$ in the abelianization $G^{ab}$).

The main result of [116] is the following ‘genus stabilization’ theorem.

Theorem 199

There is an integer h such that for $g' > h$

$$\begin{aligned} \hat{\epsilon }:{\mathcal {A}}(g',d,G) \rightarrow (K^\cup )/_{Aut(G)} \end{aligned}$$

induces a bijection onto the set of admissible classes of refined homology invariants.

In particular, if $g' > h$, and we have two Hurwitz generating systems $v_1, v_2$ having the same Nielsen function, they are equivalent if and only if the ‘difference’ $\hat{\epsilon } (v_1) \hat{\epsilon } (v_2) ^{-1} \in H_{2, \Gamma }(G)$ is trivial.

The above result extends a nice theorem of Livingston [272], Dunfield and Thurston [141] in the unramifed case, where also the statement is simpler.

Theorem 200

For $g' > > 0$

$$\begin{aligned} \hat{\epsilon }:{\mathcal {A}}(g',0, G) \rightarrow H_2(G, {\mathbb {Z}}) /_{Aut(G)} \end{aligned}$$

is a bijection.

Remark 201

Unfortunately the integer h in Theorem 199, which depends on the group G, is not explicit.

A key concept used in the proof is the concept of genus stabilization of a covering, which we now briefly explain.

Definition 202

Consider a group action of G on a projective curve C, and let $C \rightarrow C' = C/G$ the quotient morphism, with monodromy

$$\begin{aligned} \mu :\pi _1(C'{\setminus } B) \rightarrow G \end{aligned}$$

(here B is as usual the branch locus). Then the first genus stabilization of the differentiable covering is defined geometrically by simply adding a handle to the curve $C'$, on which the covering is trivial.

Algebraically, given the monodromy homomorphism

$$\begin{aligned} \mu : \pi _1(C' {\setminus } B) \cong \Pi _{g', d}:= & {} \langle \gamma _1, \ldots , \gamma _d, \alpha _1, \beta _1 , \ldots , \alpha _{g'}, \beta _{g'} |\\&\times \prod _{i=1}^d \gamma _i \prod _{j=1}^{g'} [\alpha _j, \beta _j]=1 \rangle \rightarrow G, \end{aligned}$$

we simply extend $\mu$ to $\mu ^1 :\Pi _{g'+1, d} \rightarrow G$ setting

$$\begin{aligned} \mu ^1 (\alpha _{g' + 1 }) = \mu ^1 ( \beta _{g' + 1} ) = 1_G. \end{aligned}$$

In terms of Hurwitz vectors and Hurwitz generating systems, we replace the vector

$$\begin{aligned} v : = (c_1, \ldots , c_d, a_1, b_1, \ldots , a_{g'}, b_{g'}) \in G^{d+2g'} \end{aligned}$$

by

$$\begin{aligned} v^1 : = (c_1, \ldots , c_d, a_1, b_1, \ldots , a_{g'}, b_{g'}, 1,1) \in G^{d+2g'+ 2}. \end{aligned}$$

The operation of first genus stabilization generates then an equivalence relation among monodromies (equivalently, Hurwitz generating systems), called stable equivalence.

The most important step in the proof, the geometric understanding of the invariant $\epsilon \in H_2(G, {\mathbb {Z}})$ was obtained by Livingston [272].

Theorem 203

Two monodromies $\mu _1$, $\mu _2$ are stably equivalent if and only if they have the same invariant $\epsilon \in H_2(G, {\mathbb {Z}})$.

A purely algebraic proof of Livingston’s theorem was given by Zimmermann [380], while a nice sketch of proof was given by Dunfield and Thurston [141].

Idea of proof

Since one direction is clear (the map to BG is homotopically trivial on the handle that one adds to $C'$), one has to show that two coverings are stably equivalent if their invariant is the same.

The first idea is then to interpret second homology as bordism: given two maps of two curves $C'_1, C'_2 \rightarrow BG$, they have the same invariant in $H_2(G, {\mathbb {Z}})$ (image of the fundamental classes $[C'_1],[ C'_2 ]$) if and only if there is a 3-manifold W with boundary $\partial W = C'_1 - C'_2$, and a continuous map $f :W \rightarrow BG$ which extends the two maps defined on the boundary $\partial W = C'_1 - C'_2$.

Assume now that there is relative Morse function for $(W, \partial W )$, and that one first adds all the 1-handles (for the critical points of negativity 1) and then all the 2-handles.

Assume that at level t we have a curve $C'_t$, to which we add a 1-handle. Then the genus of $C'_t$ grows by 1, and the monodromy is trivial on the meridian $\alpha$ (image of the generator of the fundamental group of the cylinder we are attaching).

Pick now a simple loop $\beta '$ meeting $\alpha$ transversally in one point with intersection number 1: since the monodromy $\mu$ is surjective, there is a simple loop $\gamma$ disjoint from $\alpha$ and $\beta '$ with $\mu (\gamma ) = \mu (\beta ')$. Replacing $\beta '$ by $\beta := \beta ' \gamma ^{-1}$, we obtain that the monodromy is trivial on the two simple loops $\alpha$ and $\beta$. A suitable neighbourhood of $\alpha \cup \beta$ is then a handle that is added to $C'_t$, and with trivial monodromy. This shows that at each critical value of the Morse function we pass from one monodromy to a stably equivalent one (for the case of a 2-handle, repeat the same argument replacing the Morse function F by its opposite $-F$). $\square$

11.6 Classification results for certain concrete groups

The first result in this direction was obtained by Nielsen [313] who proved that $\nu$ determines $\rho$ if G is cyclic (in fact in this case $H_2(G, {\mathbb {Z}}) = 0$!).

In the cyclic case the Nielsen function for $G = {\mathbb {Z}}/n$ is simply a function $\nu : ({\mathbb {Z}}/n) {\setminus } \{0\} \rightarrow {\mathbb {N}}$, and admissibility here simply means that

$$\begin{aligned} \sum _i i \cdot \nu (i) \equiv 0 \ ( mod \ n). \end{aligned}$$

The class of $\nu$ is just the equivalence class for the equivalence relation $\nu (i) \sim \nu _r ( i)$, $\forall r \in ({\mathbb {Z}}/n)^*$, where $\nu _r (i) : = \nu ( r i)$, $\forall i \in ({\mathbb {Z}}/n)$.

From the refined Nielsen realization theorem of [96] (37) it follows that the components of ${\mathfrak {M}}_g ({\mathbb {Z}}/n)$ are in bijection with the classes of Nielsen functions (see also [113] for an elementary proof).

Example 204

For instance, in the case $n=3$, the components of ${\mathfrak {M}}_g ({\mathbb {Z}}/3)$ correspond to triples of integers $g', a , b \in {\mathbb {N}}$ such that $a \equiv b \ ( mod \ 3),$ and $g-1 = 3 (g'-1) + a + b$ ($a : = \nu (1), b : = \nu (2)$).

For $g'=0$ we have, if we assume $a \le b$ (we can do this by changing the generator of ${\mathbb {Z}}/3$), $b = a + 3 r, r \in {\mathbb {N}}$, and $2a + 3r = g+2$, thus $a \equiv -(g-1) \ (mod \ 3)$, and $2a \le g+2$.

In the case where $g'=0$, two such components $N_a$ ( labelled by a as above) have images which do not intersect in ${\mathfrak {M}}_g$ as soon as $g \ge 5$.

Otherwise we would have two ${\mathbb {Z}}/3$-quotient morphisms $p_1, p_2 : C \rightarrow {\mathbb {P}}^1$ and a birational map $C \rightarrow C'' \subset {\mathbb {P}}^1 \times {\mathbb {P}}^1$. Then C would be the normalization of a curve of arithmetic genus 4, so $g \le 4$.

The genus $g'$ and the Nielsen class (which refine the primary numerical type), and the homological invariant $h \in H_2 (G/H,{\mathbb {Z}})$ (here H is again the subgroup generated by the local monodromies) determine the connected components of ${\mathfrak {M}}_g (G)$ under some restrictions: for instance when G is abelian or when G acts freely and is the semi-direct product of two finite cyclic groups (as it follows by combining results from [96, 113, 145, 146]).

Theorem 205

(Edmonds) $\nu$ and $h \in H_2 (G/H,{\mathbb {Z}})$ determine $\rho$ for G abelian. Moreover, if G is split-metacyclic and the action is free, then h determines $\rho$.

However, in general, these invariants are not enough to distinguish unmarked topological types, as one can see already for non-free $D_n$-actions (see [115]). Already for dihedral groups, one needs the refined homological invariant $\hat{\epsilon }$.

Theorem 206

([115]) For the dihedral group $G=D_n$ the connected components of the moduli space ${\mathfrak {M}}_g (D_n)$ are in bijection, via the map $\hat{\epsilon }$, with the admissible classes of refined homology invariants.

Remark 207

In this case, the classification is simple: two monodromies with the same Nielsen function differ by an element in $H_{2, \Gamma }(D_n)$, which is a quotient of $H_{2}(D_n, {\mathbb {Z}})$. This last group is 0 if n is odd, and $\cong {\mathbb {Z}}/2$ for n even.

More precisely: $H_{2,\Gamma }(D_n)=\{0\}$ if and only if

• n is odd or

• n is even and $\Gamma$ contains some reflection or

• n is even and $\Gamma$ contains the non-trivial central element.

In the remaining cases, $H_{2,\Gamma }(D_n)={\mathbb {Z}}/2{\mathbb {Z}}$.

The above result completes the classification of the unmarked topological types for $G = D_n$, begun in [112]; moreover this result entails the classification of the irreducible components of the loci ${\mathfrak {M}}_{g,D_n}$ (see the appendix to [115]).

It is an interesting question: for which groups G does the refined homology invariant $\hat{\epsilon }$ determine the connected components of ${\mathfrak {M}}_g (G)$?

In view of Edmonds’ result in the unramified case, it is reasonable to expect a positive answer for split metacyclic groups (work in progress by Sascha Weigl) or for some more general metacyclic or metaabelian groups.

As mentioned in [141], p. 499, the group $G = {\mathbb {P}}SL(2, {\mathbb {F}}_{13})$ shows that, for $g'=2$, in the unramified case there are different components with trivial homology invariant $\epsilon \in H_2(G,{\mathbb {Z}})$: these topological types of coverings are therefore stably equivalent but not equivalent.

11.7 $Sing({\mathfrak {M}}_g)$ II: loci of curves with automorphisms in ${\mathfrak {M}}_g$

Several authors independently found restrictions in order that a finite subgroup H of $Map_g$ be a not full subgroup (Singerman [343], Ries [327], and Magaard, Shaska, Shpectorov, and Völklein [275])

We refer to lemma 4.1 of [275] for the proof of the following result.

Theorem 208

(MSSV) Suppose $H \subset G \subset Map_g$ and assume $Z : = Fix (H) = Fix (G) \subset {\mathcal {T}}_g$, with H a proper subgroup of G, and let $C\in Z$. Then

$$\begin{aligned} \delta : = dim (Z) \le 3. \end{aligned}$$

(I) if $\delta = 3$, then H has index 2 in G, and $C \rightarrow C/G$ is covering of ${\mathbb {P}}^1$ branched on six points, $P_1, \ldots , P_6$, and with branching indices all equal to 2. Moreover the subgroup H corresponds to the unique genus two double cover of ${\mathbb {P}}^1$ branched on the six points, $P_1, \ldots , P_6$ (by Galois theory, intermediate covers correspond to subgroups of G bijectively).

(II) If $\delta = 2$, then H has index 2 in G, and $C \rightarrow C/G$ is covering of ${\mathbb {P}}^1$ branched on five points, $P_1, \ldots , P_5$, and with branching indices $2,2,2,2,c_5$ (where obviously $c_5 \ge 2$). Moreover the subgroup H corresponds to a genus one double cover of ${\mathbb {P}}^1$ branched on four of the points $P_1, \ldots , P_5$ which have branching index 2.

(III) If $\delta = 1$, then there are three possibilities.

(III-a) H has index 2 in G, and $C \rightarrow C/G$ is covering of ${\mathbb {P}}^1$ branched on four points $P_1, \ldots , P_4$, with branching indices $2,2,2, 2 d_4$, where $d_4 > 1$. Moreover the subgroup H corresponds to the unique genus one double cover of ${\mathbb {P}}^1$ branched on the four points, $P_1, \ldots , P_4$.

(III-b) H has index 2 in G, and $C \rightarrow C/G$ is covering of ${\mathbb {P}}^1$ branched on four points, $P_1, \ldots , P_4$, with branching indices $2,2,c_3, c_4$, where $2 \le c_3 \le c_4 > 2$. Moreover the subgroup H corresponds to a genus zero double cover of ${\mathbb {P}}^1$ branched on two points whose branching index equals 2.

(III-c) H is normal in G, $G/H \cong ({\mathbb {Z}}/2)^2$, moreover $C \rightarrow C/G$ is covering of ${\mathbb {P}}^1$ branched on four points, $P_1, \ldots , P_4$, with branching indices $2,2,2, c_4$, where $c_4 > 2$. Moreover the subgroup H corresponds to the unique genus zero cover of ${\mathbb {P}}^1$ with group $({\mathbb {Z}}/2)^2$ branched on the three points $P_1, P_2, P_3$ whose branching index equals 2.

The main point in the theorem above is a calculation via the Hurwitz formula, showing that the normalizer of H in G is nontrivial; from this follows the classification of the singular locus of ${\mathfrak {M}}_g$, due to Cornalba, and which we do not reproduce here (see [127], and also [113] for a slightly different proof).

11.8 Stable curves and their automorphisms, $Sing (\overline{{\mathfrak {M}}_g}$)

The compactification of the moduli space of curves ${\mathfrak {M}}_g$ is given by the moduli space $\overline{{\mathfrak {M}}_g}$ of stable curves of genus g (see [136, 179, 304]).

Definition 209

A stable curve of genus $g \ge 2$ is a reduced and connected projective curve C, not necessarily irreducible, whose singularities are only nodes, such that

• (1) the dualizing sheaf $\omega _C$ has degree $2g-2$

• (2) its group of automorphisms Aut(C) is finite (equivalently, each smooth irreducible component $D \subset C$ of genus zero intersects $C {\setminus } D$ in at least 3 points).

Again the Kuranishi family Def(C) of a stable curve is smooth of dimension $3g-3$, and the locus of stable curves which admit a given G-action forms a smooth submanifold of Def(C).

Hence again the singular locus of $\overline{{\mathfrak {M}}_g}$ corresponds to loci of curves with automorphisms which do not form a divisor.

Example 210

We say that C has an elliptic tail if we can write $C = C_1 \cup E$, where E is a smooth curve of genus 1 intersecting $C_1$ in only one point P.

In this case C has always an automorphism $\gamma$ of order 2: $\gamma$ is the identity on $C_1$, and, if we choose P as the origin of the elliptic curve (E, P), $\gamma$ is simply multiplication by $-1$.

An easy calculation shows that such curves with an elliptic tail form a divisor inside $\overline{{\mathfrak {M}}_g}$.

We refer to [113] (the second part) for the explicit determination of the loci of stable curves admitting an action by a cyclic group of prime order, especially those contained in the boundary $\partial \overline{{\mathfrak {M}}_g}$. From this follows the description of the singular locus $Sing (\overline{{\mathfrak {M}}_g})$, which we do not reproduce here.

An interesting question is to describe similar loci also for other groups.

As mentioned, there are irreducible loci which are contained in the boundary, while other ones are the closures of irreducible loci in ${\mathfrak {M}}_g$. But it is possible that some loci which are disjoint in ${{\mathfrak {M}}_g}$ have closures that meet in $\overline{{\mathfrak {M}}_g}$.

We end this section with an explicit example, due to Antonio F. Costa, Milagros Izquierdo, and Hugo Parlier (cf. [129]), but we give a different proof. We refer to the notation of Example 204 in the following theorem.

Theorem 211

The strata $N_a$ and $N_{3+a}$ of ${\mathfrak {M}}_g({\mathbb {Z}}/3)$ fulfill:

• (i) $N_a \cap N_{3+a} = \emptyset$

• (ii) $\overline{N_a} \cap \overline{N_{3+a}} \ne \emptyset$ in $\overline{{\mathfrak {M}}_g}$.

Proof

By the fact that inside Kuranishi space the locus of curves with a given action of a group G is a smooth manifold, hence locally irreducible, one sees right away that these strata must intersect in a point corresponding to a curve with at least two different automorphisms of order 3. A natural choice is to take a stable curve with an action of $({\mathbb {Z}}/3)^2$.

The simplest choice is to take first the Fermat cubic

$$\begin{aligned} F : = \left\{ (x_0, x_1, x_2) | x_0^3 + x_1^3 + x_2^3 = 0\right\} \end{aligned}$$

with the action of $(u,v) \in ({\mathbb {Z}}/3)^2$

$$\begin{aligned} (x_0, x_1, x_2) \mapsto (x_0, \epsilon ^u x_1, \epsilon ^v x_2). \end{aligned}$$

We let then C be a $({\mathbb {Z}}/3)$-covering of the projective line, of genus $g-3$ and with $\nu (1) = a$. Denote by $\psi$ the covering automorphism and take a point $p \in C$ which is not a ramification point: then glue the three points $\psi ^v (p), \ v \in {\mathbb {Z}}/3,$ with the three points $(1,0, - \epsilon ^v)$. In this way we get a stable curve D of genus g, and with an action of $({\mathbb {Z}}/3)^2$.

We have two actions of ${\mathbb {Z}}/3$ on D, the first induced by the action of (0, 1) on F and of $\psi$ on C, and the second induced by the action of (1, 1) on F and $\psi$ on C (it is immediate to observe that the glueing is respected by the action).

Now, for the first action of the generator $\bar{1} \in {\mathbb {Z}}/3$ on F, the fixed points are the points $x_2=0$, with local coordinate $t = \frac{x_2}{x_0}$, such that $t \mapsto \epsilon t$, while for the second action the fixed points are the points $x_0=0$, with local coordinate $t = \frac{x_0}{x_1}$, such that $t \mapsto \epsilon ^2 t$.

Hence the same curve has two automorphisms of order 3, the first with $\nu (1) = a + 3$, the second with $\nu (1) = a$. As easily shown (cf. [113]), since, for any of these two actions of ${\mathbb {Z}}/3$, the nodes are not fixed, then there exists a smoothing for both actions of ${\mathbb {Z}}/3$ on the curve D. This shows that the strata $N_a$ and $N_{a+3}$ have D in their closure. $\square$

11.9 Branch stabilization and relation with other approaches

When $g'=0$ our $G_\Gamma$ is related to the group $\widehat{G}$ defined in [170] (Appendix), where the authors give a proof of a theorem by Conway and Parker. Roughly speaking the theorem says that: if the Schur multiplier M(G) (which is isomorphic to $H_2(G,{\mathbb {Z}}$)) is generated by commutators, then the $\nu$-type is a fine stable invariant, when $g'=0$.

Theorem 212

(Conway–Parker, loc.cit.) In the case $g'=0$, let $G = F / R$ where F is free, and assume that $H_2(G,{\mathbb {Z}}) \cong \frac{[F,F]\cap R}{[F,R]}$ is generated by commutators. Then there is an integer N such that if the numerical function $\nu$ takes values $\ge N$, then there is only one equivalence class with the given numerical function $\nu$.

Michael Lönne, Fabio Perroni and myself have been able to extend this result in the following way:

Theorem 213

Assume that $g'=0$, or more generally that the union $\Gamma$ of nontrivial conjugacy classes of G generates G.

Then there exists an integer N, depending on $\Gamma$, such that if two Hurwitz generating systems v, w satisfy $\nu (v) \ge N \chi _{\Gamma }, \nu (w) \ge N \chi _{\Gamma }$, where $\chi _{\Gamma }$ is the characteristic function of the set of conjugacy classes corresponding to $\Gamma$, the Nielsen functions $\nu (v)$ and $\nu (w)$ are equivalent $\Leftrightarrow$ v is equivalent to w and they yield the same point in ${\mathcal {A}}(g',d, G)$.

It is still an open question how to extend the previous result without the condition that $\Gamma$ generates G.

Similar results have been obtained by Kulikov and Kharlamov [240], who use geometric arguments for the construction of semigroups similar to the ones constructed by Fried and Völklein, while a purely algebraic construction of a group similar to our group $K_{\Gamma }$ can be found in work of Moravec on unramified Brauer groups ([297]).

11.10 Miller’s description of the second homology of a group and developments

Clair Miller found ([286]) another nice description of the second homology group $H_2(G, {\mathbb {Z}})$, as follows.

Definition 214

Let $\langle G, G \rangle$ be the free group on all pairs $\langle x, y \rangle$ with $x,y \in G$.

Then there is a natural surjection of $\langle G, G \rangle$ onto the commutator subgroup [G, G] sending $\langle x, y \rangle$ to the commutator [x, y].

Denote as in [286] by Z (G) the kernel of this surjection (it might have been better to denote it by $Z (\langle G, G \rangle )$), and then denote by B (G) (it might have been better to denote it by $B (\langle G, G \rangle )$) the normal subgroup of Z (G) normally generated by the following elements

• (1) $\langle x, y \rangle$

• (2) $\langle x, y \rangle \langle y, x \rangle$

• (3) $\langle z, xy \rangle \langle y^x, z^x \rangle \langle x, z \rangle$, where $y^x : = x y x^{-1}$,

• (4) $\langle z^x, y^x \rangle \langle x, [y,z] \rangle \langle y, z \rangle$.

Theorem 215

(Miller) There is a canonical isomorphism $Z(G) / B(G) \cong H_2(G, {\mathbb {Z}})$.

Clearly we have then an exact sequence

$$\begin{aligned} 0 \rightarrow H_2(G, {\mathbb {Z}}) \cong Z(G) / B(G) \rightarrow \langle G, G \rangle \rightarrow [G, G] \rightarrow 0 \end{aligned}$$

which corresponds to the previously seen

$$\begin{aligned} 0 \rightarrow H_2(G, {\mathbb {Z}}) = (R \cap [F,F] ) / [F,R] \rightarrow [F,F] / [F,R] \rightarrow [G, G] \rightarrow 0. \end{aligned}$$

The relations by Miller were later slightly modified by Moravec [297] in a more symmetric fashion as follows:

• (1) $\langle g,g \rangle \sim 1$

• (2) $\langle g_1 g_2, h \rangle \sim \langle g_2^{g_1}, h^{ g_1} \rangle \langle g_1 , h \rangle$

• (3) $\langle g, h_1 h_2 \rangle \sim \langle g , h_1 \rangle \langle g^{h_1}, h_2^{ h_1} \rangle$.

In the case where we consider also a finite union $\Gamma$ of conjugacy classes, Moravec defined the following group

Definition 216

(Moravec)

$$\begin{aligned} G \wedge _{\Gamma } G = \langle G, G \rangle / B_{\Gamma }, \end{aligned}$$

where $B_{\Gamma }$ is defined by the previous relation (1), (2), (3) and by the further relation

$$\begin{aligned} (4) \ \langle g,k \rangle \sim 1, \quad \forall k \in \Gamma . \end{aligned}$$

The definition by Moravec and the one given in [116] are related, as the following easy proposition shows.

Proposition 217

There is an exact sequence

$$\begin{aligned} 0 \rightarrow H_{2, \Gamma } (G, {\mathbb {Z}}) \rightarrow G \wedge _{\Gamma } G \rightarrow [G, G] \rightarrow 0. \end{aligned}$$

Another important source of interest for these quotient groups of $H_2(G, {\mathbb {Z}})$ comes from rationality questions.

In general, the stable cohomology of a finite group G, or more generally of an algebraic group G, is obtained in the following way.

Let V be a finite dimensional representation of G, and let U be an open set of V where G acts freely: then U / G is considered as an algebraic approximation to a classifying space for G, and one can take the limit over such representations (V and $V'$ begin smaller than their direct sum) of the cohomology groups of U / G. The same can of course be done also for homology groups and Chow groups (see [355]).

The groups that are thus obtained are important to study the problem of rationality of the quotients V / G, or of their stable rationality (X is said to be stably rational if there is an integer n such that $X \times {\mathbb {P}}^n$ is rational).

We refer to [20, 50, 51, 297] and the literature cited there for more details.

12 Connected components of moduli spaces and the action of the absolute Galois group

Let X be a complex projective variety: let us quickly recall the notion of a conjugate variety.

Remark 218

• (1) $\phi \in Aut ({\mathbb {C}})$ acts on ${\mathbb {C}}[z_0, \ldots z_n]$, by sending $P (z) = \sum _{i =0}^n \ a_i z ^i \mapsto \phi (P) (z) : = \sum _{i =0}^n \ \phi (a_i) z ^i$.

• (2) Let X be as above a projective variety

  $$\begin{aligned} X \subset {\mathbb {P}}^n_{\mathbb {C}}, X : = \{ z | f_i(z) = 0 \quad \forall i \}. \end{aligned}$$

The action of $\phi$ extends coordinatewise to ${\mathbb {P}}^n_{\mathbb {C}}$, and carries X to another variety, denoted $X^{\phi }$, and called the conjugate variety. Since $f_i(z) = 0$ implies $\phi (f_i)(\phi (z) )= 0$, we see that

$$\begin{aligned} X^{\phi } = \left\{ w | \phi (f_i)(w) = 0 \quad \forall i \right\} . \end{aligned}$$

If $\phi$ is complex conjugation, then it is clear that the variety $X^{\phi }$ that we obtain is diffeomorphic to X; but, in general, what happens when $\phi$ is not continuous?

Observe that, by the theorem of Steiniz, one has a surjection $Aut ({\mathbb {C}}) \rightarrow Gal(\bar{{\mathbb {Q}}} /{\mathbb {Q}})$, and by specialization the heart of the question concerns the action of $Gal(\bar{{\mathbb {Q}}} /{\mathbb {Q}})$ on varieties X defined over $\bar{{\mathbb {Q}}}$.

For curves, since in general the dimensions of spaces of differential forms of a fixed degree and without poles are the same for $X^{\phi }$ and X, we shall obtain a curve of the same genus, hence $X^{\phi }$ and X are diffeomorphic.

12.1 Galois conjugates of projective classifying spaces

General questions of which the first is answered in the positive in most concrete cases, and the second is answered in the negative in many cases, as we shall see, are the following.

Question 219

Assume that X is a projective $K (\pi , 1)$, and assume $\phi \in Aut ({\mathbb {C}})$.

• (A) Is then the conjugate variety $X^{\phi }$ still a classifying space $K (\pi ', 1)$?

• (B) Is then $\pi _1 ( X^{\phi } ) \cong \pi \cong \pi _1 (X)$?

Since $\phi$ is never continuous, there would be no reason to expect a positive answer to both questions (A) and (B), except that Grothendieck showed [201], see also [202].

Theorem 220

Conjugate varieties $X, X^{\phi }$ have isomorphic algebraic fundamental groups

$$\begin{aligned} \pi _1(X)^{alg} \cong \pi _1(X^{\phi } )^{alg}, \end{aligned}$$

where $\pi _1(X)^{alg}$ is the profinite completion of the topological fundamental group $\pi _1(X)$.

We recall once more that the profinite completion of a group G is the inverse limit

$$\begin{aligned} {\hat{G}} = lim_{K\unlhd _f G} (G/K), \end{aligned}$$

of the factor groups G / K, K being a normal subgroup of finite index in G; and since finite index subgroups of the fundamental group correspond to finite unramified (étale) covers, Grothendieck [201] defined in this way the algebraic fundamental group for varieties over other fields than the complex numbers, and also for more general schemes.

The main point of the proof of the above theorem is that if we have $f : Y \rightarrow X$ which is étale, also the Galois conjugate $f^{\phi } : Y^{\phi } \rightarrow X^{\phi }$ is étale ($f^{\phi }$ is just defined taking the Galois conjugate of the graph of f, a subvariety of $Y \times X$).

Since Galois conjugation gives an isomorphism of natural cohomology groups, which respects the cup product, as for instance the Dolbeault cohomology groups $H^p(\Omega ^q_X)$, we obtain interesting consequences in the direction of question A) above. Recall the following definition.

Definition 221

Two varieties X, Y are said to be isogenous if there exist a third variety Z, and étale finite morphisms $f_X : Z \rightarrow X$, $f_Y : Z \rightarrow Y$.

Remark 222

It is obvious that if X is isogenous to Y, then $X^{\phi }$ is isogenous to $Y^{\phi }$.

Theorem 223

• (i) If X is an Abelian variety, or isogenous to an Abelian variety, the same holds for any Galois conjugate $X^{\phi }$.

• (ii) If S is a Kodaira fibred surface, then any Galois conjugate $S^{\phi }$ is also Kodaira fibred.

• (iii) If X is isogenous to a product of curves, the same holds for any Galois conjugate $X^{\phi }$.

Proof

(i) X is an Abelian variety if and only it is a projective variety and there is a morphism $X \times X \rightarrow X$, $(x,y) \mapsto (x \cdot y^{-1})$, which makes X a group (see [303], it follows indeed that the group is commutative). This property holds for X if and only if it holds for $X^{\phi }$.

(ii) The hypothesis is that there is $f : S \rightarrow B$ such that all the fibres are smooth and not all isomorphic: obviously the same property holds, after Galois conjugation, for $f^{\phi } : S^{\phi } \rightarrow B^{\phi }$.

(iii) It suffices to show that the Galois conjugate of a product of curves is a product of curves. But since $X^{\phi } \times Y^{\phi } = (X \times Y) ^{\phi }$ and the Galois conjugate of a curve C of genus g is again a curve of the same genus g, the statement follows. $\square$

Proceeding with other projective $K(\pi , 1)$’s, the question becomes more subtle and we have to appeal to a famous theorem by Kazhdan on arithmetic varieties (see [117, 118, 235, 236, 287, 362]).

Theorem 224

Assume that X is a projective manifold with $K_X$ ample, and that the universal covering $\tilde{X}$ is a bounded symmetric domain.

Let $\tau \in {\mathrm {Aut}}(\mathbb {C})$ be an automorphism of $\mathbb {C}$.

Then the conjugate variety $X^{\tau }$ has universal covering $\tilde{X^{\tau }} \cong \tilde{X}$.

Simpler proofs follow from recent results obtained together with Antonio Di Scala, and based on the Aubin–Yau theorem and the results of Berger [39]. These results yield a precise characterization of varieties possessing a bounded symmetric domain as universal cover, and can be rather useful in view of the fact that our knowledge and classification of these fundamental groups is not so explicit.

To state them in detail would require some space, hence we just mention the simplest result (see [117]).

Theorem 225

Let X be a compact complex manifold of dimension n with $K_X$ ample.

Then the following two conditions (1) and (1’), resp. (2) and (2’) are equivalent:

• (1) X admits a slope zero tensor $0 \ne \psi \in H^0(S^{mn}(\Omega ^1_X)(-m K_X) )$, (for some positive integer m);

• (1’) $X \cong \Omega / \Gamma$ , where $\Omega$ is a bounded symmetric domain of tube type and $\Gamma$ is a cocompact discrete subgroup of ${\mathrm {Aut}}(\Omega )$ acting freely.

• (2) X admits a semi special tensor $0 \ne \phi \in H^0(S^n(\Omega ^1_X)(-K_X) \otimes \eta )$, where $\eta$ is a 2-torsion invertible sheaf, such that there is a point $p\in X$ for which the corresponding hypersurface $F_p : = \{\phi _p = 0 \}\subset {\mathbb {P}}(TX_p)$ is reduced.

• (2’) The universal cover of X is a polydisk.

Moreover, in case (1), the degrees and the multiplicities of the irreducible factors of the polynomial $\psi _p$ determine uniquely the universal covering $\widetilde{X}=\Omega$.

12.2 Connected components of Gieseker’s moduli space

For the sake of simplicity we shall describe in this and the next subsection the action of the absolute Galois group on the set of connected components of the moduli space of surfaces of general type. We first recall the situation concerning these components.

As we saw, all 5-canonical models of surfaces of general type with invariants $K^2$, $\chi$ occur in a big family parametrized by an open set of the Hilbert scheme ${\mathcal {H}}^0$ parametrizing subschemes with Hilbert polynomial $P (m)= \chi + \frac{1}{2}( 5 m -1) 5 m K^2 ,$ namely the open set

$$\begin{aligned} {\mathcal {H}}^0 (\chi , K^2) : = \left\{ \Sigma | \Sigma \mathrm{\ is\ reduced \ with \ only \ R.D.P. 's \ as \ singularities \ }\right\} \!. \end{aligned}$$

We shall however, for the sake of brevity, talk about connected components ${\mathcal {N}}$ of the Gieseker moduli space $\mathfrak M_{a,b}$ even if these do not really parametrize families of canonical models.

We refer to [108] for a more ample discussion of the basic ideas which we are going to sketch here.

$\mathfrak M_{a,b}$ has a finite number of connected components, and these parametrize the deformation classes of surfaces of general type with numerical invariants $\chi (S) = a, K^2_S = b$. By the classical theorem of Ehresmann [148], deformation equivalent varieties are diffeomorphic, and moreover, via a diffeomorphism carrying the canonical class to the canonical class.

Hence, fixed the two numerical invariants $\chi (S) = a, K^2_S = b$, which are determined by the topology of S (indeed, by the Betti numbers $b_i(S)$ of S and by $b^+:=$ positivity of the intersection form on $H^2(S, {\mathbb {R}})$), we have a finite number of differentiable types.

For some time the following question was open: whether two surfaces which are orientedly diffeomorphic would belong to the same connected component of the moduli space.

I conjectured (in [232]) that the answer should be negative, on the basis of some families of simply connected surfaces of general type constructed in [82] and later investigated in [84, 104] and [111]: these were shown to be homeomorphic by the results of Freedman (see [166, 167]), and it was then relatively easy to show then [85] that there were many connected components of the moduli space corresponding to homeomorphic but non diffeomorphic surfaces. It looked like the situation should be similar even if one would fix the diffeomorphism type.

Friedman and Morgan instead made the ‘speculation’ that the answer to the DEF = DIFF question should be positive (1987) (see [168]), motivated by the new examples of homeomorphic but not diffeomorphic surfaces discovered by Donaldson (see [138] and [139] for a survey on this topic).

The question was finally answered in the negative, and in every possible way ([26, 98, 104, 239, 278]).

Theorem 226

(Manetti ’98, Kharlamov–Kulikov 2001, C. 2001, C.-Wajnryb 2004, Bauer–C.-Grunewald 2005)

The Friedman–Morgan speculation does not hold true and the DEF = DIFF question has a negative answer.

In my joint work with Wajnryb [104] the DEF = DIFF question was shown to have a negative answer also for simply connected surfaces (indeed for some of the families of surfaces constructed in [82]).

I refer to [106] for a rather comprehensive treatment of the above questions (and to [3, 17, 100, 107, 111] for the symplectic point of view, [37, 137] for the special case of geometric genus $p_g=$ 0).

12.3 Arithmetic of moduli spaces and faithful actions of the absolute Galois group

A basic remark is that all the schemes involved in the construction of the Gieseker moduli space are defined by equations involving only ${\mathbb {Z}}$-coefficients, since the defining equation of the Hilbert scheme is a rank condition for a multiplication map (see for instance [188]), and similarly the condition $\omega _{\Sigma }^{ \otimes 5} \cong {\mathcal {O}}_{\Sigma }(1)$ is also closed (see [303]) and defined over ${\mathbb {Z}}$.

It follows that the absolute Galois group $Gal (\overline{{\mathbb {Q}}}, {\mathbb {Q}})$ acts on the Gieseker moduli space $\mathfrak M_{a,b}$. In particular, it acts on the set of its irreducible components, and on the set of its connected components.

After an incomplete initial attempt in [28] in joint work with Ingrid Bauer and Fritz Grunewald, we were able in [29] to show:

Theorem 227

The absolute Galois group $Gal(\bar{{\mathbb {Q}}} /{\mathbb {Q}})$ acts faithfully on the set of connected components of the Gieseker moduli space of surfaces of general type,

$$\begin{aligned} \mathfrak M : = \cup _{x,y \in {\mathbb {N}}, x,y \ge 1} \mathfrak M_{x,y}. \end{aligned}$$

Another result in a similar direction had been obtained by Easton and Vakil [143] using abelian coverings of the plane branched on union of lines.

Theorem 228

The absolute Galois group $Gal(\bar{{\mathbb {Q}}} /{\mathbb {Q}})$ acts faithfully on the set of irreducible components of the Gieseker moduli space of surfaces of general type,

$$\begin{aligned} \mathfrak M : = \cup _{x,y \in {\mathbb {N}}, x,y \ge 1} \mathfrak M_{x,y}. \end{aligned}$$

The main ingredients for the proof of Theorem 227 are the following ones.

• (1) Define, for any complex number $a \in {\mathbb {C}}{\setminus } \{ -2g,0,1, \ldots , 2g-1 \}$, $C_a$ as the hyperelliptic curve of genus $g \ge 3$ which is the smooth complete model of the affine curve of equation

  $$\begin{aligned} w^2 = (z-a) (z + 2g) \Pi _{i=0}^{2g-1} (z-i). \end{aligned}$$

  Consider then two complex numbers a, b such that $a \in {\mathbb {C}}\setminus {\mathbb {Q}}$: then $C_a \cong C_b$ if and only if $a = b$.

• (2) If $a \in \bar{{\mathbb {Q}}}$, then by Belyi’s theorem [38] there is a morphism $f_a : C_a \rightarrow {\mathbb {P}}^1$ which is branched only on three points, $0,1,\infty$.

• (3) The normal closure $D_a$ of $f_a$ yields a triangle curve, i.e., a curve $D_a$ with the action of a finite group $G_a$ such that $D_a / G_a \cong {\mathbb {P}}^1$, and $D_a \rightarrow {\mathbb {P}}^1$ is branched only on three points.

• (4) Take surfaces isogenous to a product $S = (D_a \times D')/G_a$ where the action of $G_a$ on $D'$ is free. Denote by ${\mathcal {N}}_a$ the union of connected components parametrizing such surfaces.

• (5) Take all the possible twists of the $G_a$-action on $D_a \times D'$ via an automorphism $\psi \in Aut (G_a)$ (i.e., given the action $(x,y) \mapsto (\gamma x, \gamma y)$, consider all the actions of the form

  $$\begin{aligned} (x,y) \mapsto (\gamma x, \psi (\gamma ) y). \end{aligned}$$

  One observes that, for each $\psi$ as above, we get more connected components in ${\mathcal {N}}_a$.

• (6) Find by an explicit calculation (using (4) and (5)) that the subgroup of $Gal(\bar{{\mathbb {Q}}} /{\mathbb {Q}})$ acting trivially on the set of connected components of the moduli space would be a normal and abelian subgroup.

• (7) Finally, this contradicts a known theorem (cf. [169]).

Remark 229

An interesting remark of a referee is that the meaning of the above theorem could be further elaborated as a parallel of the Drinfend theory of Galois representation, built on the theorem of Belyi (see [140]). We leave this as a future task.

12.4 Change of fundamental group

Jean Pierre Serre proved in the 60’s [336] the existence of a field automorphism $\phi \in Gal(\bar{{\mathbb {Q}}} /{\mathbb {Q}})$, and a variety X defined over $\bar{{\mathbb {Q}}}$ such that X and the Galois conjugate variety $X^{\phi }$ have non isomorphic fundamental groups.

In [29] this phenomenon is vastly generalized, thus answering question B) in the negative.

Theorem 230

If $\sigma \in Gal(\bar{{\mathbb {Q}}} /{\mathbb {Q}})$ is not in the conjugacy class of complex conjugation, then there exists a surface isogenous to a product X such that X and the Galois conjugate surface $X^{\sigma }$ have non-isomorphic fundamental groups.

Since the argument for the above theorem is not constructive, let us observe that, in work in collaboration with Bauer and Grunewald [27, 29], we discovered wide classes of explicit algebraic surfaces isogenous to a product for which the same phenomenon holds.

By the strong rigidity of locally symmetric spaces $X = {\mathcal {D}}/ \Gamma$ whose universal covering ${\mathcal {D}}$ is an irreducible bounded symmetric domain of dimension $\ge 2$, similar phenomena should also occur in this case.

Remark 231

Further developments have been announced in [183] by Gonzaléz-Diez and Jaikin-Zapirain: for instance the faithfulness of the action of the absolute Galois group on the discrete set of the moduli space corresponding to Beauville surfaces, and the extension of Theorem 230 to all automorphisms $\sigma$ different from complex conjugation.

13 Stabilization results for the homology of moduli spaces of curves and Abelian varieties

We have seen that the moduli space of curves is a rational $K(\pi ,1)$, since it can be written as a quotient of the Teichmüller space $\mathcal {T}_g$ of a closed oriented real 2-manifold M of genus g

$$\begin{aligned} \mathfrak {M}_g = \mathcal {T}_g / Map_g , \quad {\mathcal {T}}_g := \mathcal {C}S(M)/\mathrm{Diff}^0(M), \ \end{aligned}$$

As a corollary, and as we saw, the rational cohomology of the moduli space is calculated by group cohomology:

$$\begin{aligned} H^*(\mathfrak {M}_g, {\mathbb {Q}}) \cong H^*(\mathrm{Map}_g, {\mathbb {Q}}). \end{aligned}$$

Harer showed, using the concept of genus stabilization that we have already introduced in Sect. 10, that these cohomology groups stabilize with g; indeed, stabilization furnishes an inclusion of a space which is homotopically equivalent to $\mathfrak {M}_g$ inside $\mathfrak {M}_{g+1}$ (alternatively, one may say that $Map_g \rightarrow Map_{g+1}$, by letting the operation be trivial on the added handle).

Theorem 232

(Harer [208]) Let $\mathrm{Map}_{g,r}^s$ be the mapping class group of an orientable surface F of genus g with r boundary components and s punctures. Then, for $g\ge 3k-1$, $H_k(\mathrm{Map}_{g,r}^s , {\mathbb {Z}})$ is independent of g and r as long as $r>0$, for $g\ge 3k$, $H_k(\mathrm{Map}_{g,r}^s, {\mathbb {Q}})$ is independent of g and r for every r, and for $g\ge 3k+1$, $H_k(\mathrm{Map}_{g,r}^s , {\mathbb {Z}})$ is independent of g and r for every r.

The ring structure of the cohomology of the “stable mapping class group” is described by a conjecture of Mumford [307], that has been proven by Madsen and Weiss [274].

Theorem 233

(Mumford’s conjecture) The stable cohomology of the moduli space of curves is a polynomial algebra

$$\begin{aligned} H^* ( Map_{\infty } , {\mathbb {Q}}) = {\mathbb {Q}}[ {\mathcal {K}}_1, {\mathcal {K}}_2, \ldots ] \end{aligned}$$

where the class ${\mathcal {K}}_i$ is the direct image $(p_g)_* (K^{i+1})$ of the $(i+1)$-th power of the relative canonical divisor of the universal family of curves.

These results paralleled earlier results of Borel [58] and Charney and Lee [120] on the cohomology of arithmetic varieties, such as the moduli space of Abelian varieties and some partial compactifications of them.

For instance, in the case of the moduli space of Abelian varieties we have the following theorem by Borel.

Theorem 234

(Borel) The stable cohomology of the moduli space of Abelian varieties is a polynomial algebra

$$\begin{aligned} H^* ( {\mathcal {A}}_{\infty } , {\mathbb {Q}}) = {\mathbb {Q}}[ \lambda _1, \lambda _3, \lambda _5 \ldots ] \end{aligned}$$

where the class $\lambda _i$ is the i-th Chern class of the universal bundle $H^{1,0}$.

The theme of homology (cohomology-) stabilization is indeed a very general one, which has been recently revived through the work of several authors, also in other contexts ( see for instance [131, 153, 158, 203]).

It would take too long to dwell here on this topic, which would deserve a whole survey article devoted to it.

13.1 Epilogue

There are many other interesting topics which are very tightly related to the main theme of this article.

For instance, there is a relation between symmetric differentials and the fundamental group ([52, 53, 64, 241]).

Brunebarbe, Klingler and Totaro showed indeed in [64] that some ‘linearity’ property of the fundamental group entails the existence of nontrivial symmetric differentials.

Theorem 235

Let X be a compact Kähler manifold, and let k be any field.

Assume that there is a representation

$$\begin{aligned} \rho : \pi _1(X) \rightarrow GL (r, k) \end{aligned}$$

with infinite image.

Then the symmetric algebra of X is nontrivial,

$$\begin{aligned} \oplus _{m\ge 0} H^0 ( S^m (\Omega ^1_X)) \ne {\mathbb {C}}. \end{aligned}$$

Another very interesting topic is Gromov’s h-principle, for which we refer the reader to [152], and [74]. Perhaps not only the author is tired at this point.