Second derivative of high-order accuracy methods for the numerical integration of stiff initial value problems

Abstract

In Mitsui (Sci Eng Rev Doshisha Univ Jpn 51(3):181–190, 2010) the author introduced a new class of discrete variable methods known as look-ahead linear multistep methods (LALMMs) which consist of a pair of predictor-corrector (PC), including a function value at one more step beyond the present step for the numerical solution of ordinary differential equations. Two-step family of Look-Ahead linear multistep methods of fourth-order pair were derived and shown to be A($\theta$)-stable in Mitsui and Yakubu (Sci Eng Rev Doshisha Univ Jpn 52(3):181–188, 2011). The derived integration methods are of low orders and unfortunately cannot cope with stiff systems of ordinary differential equations. In this paper we extend the concept adopted in Mitsui and Yakubu (Sci Eng Rev Doshisha Univ Jpn 52(3):181–188, 2011) to construct second-derivative of high-order accuracy methods with off-step points which behave essentially like one-step methods. The resulting integration methods are A-stable, convergent, with large regions of absolute stability, suitable for stiff systems of ordinary differential equations. Numerical comparisons of the new methods have been made and enormous gains in efficiency are achieved.

1 Introduction

We present second-derivative of high-order accuracy methods for the numerical integration of stiff systems of initial-value problems (IVPs) in ordinary differential equations (ODEs) given by

$$\begin{aligned} \frac{dy}{dx}=f(x,y(x)), y(x_0 )=y_0 , \quad a\,\le x\,\le b, \end{aligned}$$

(1.1)

on the finite interval [a, b]. Supposing f is continuous and satisfies $\left| {f(x,y)-f(x,\bar{y})} \right| \le L\left| {y-\bar{y}} \right|$ on $[a,\,b]\times (-\infty ,\,\infty )$ guarantees the existence of a unique solution y(x)$\in$C$^{1}$[a, b]. We shall assume that y has continuous derivatives on [a, b] of any order required. Of the many numerical integration methods available for the solution of (1.1) most of them have specific advantages so that they are chosen for special types of problems. Several of them have a general applicability that has made them popular in a wide variety of problems. There exists, however, a class of equations which present considerable difficulty in their solution and for which there does not seem to be a simple and accurate method available for their solution, since most of the methods are of low orders and are not A-stable, hence they are not suitable for such differential equations. In this paper we introduce second-derivative of high-order accuracy methods with off-step points designed for the numerical integration of such systems of initial value problems. Although several authors have studied methods with second derivative terms, for example, see [7, 16, 21, 22, 26–28]. Further, some of the methods considered for the solution of (1.1) were derived on the basis that the required function evaluations are to be done only at the grid points (discrete points) which is typically of discrete variable methods [18] (Euler method, Runge-Kutta methods, Picard method, etc.). However, in the years between 1960 and 1970 many authors introduced some off-grid points in their methods with the hope of generalizing the two traditional numerical integration methods (Runge-Kutta methods and linear multistep methods) as a result of the barrier theorems of Dahlquist [11], for example see [3, 4, 13, 14]. In this report, we consider methods that are A-stable suitable for generating the solution of stiff initial value problems at both grid and off-grid points simultaneously within the interval of integration. These methods are derived by introducing one extra intermediate off-grid point in between the usual grid points and include some of the collocation points as interpolation points.

The motivation The motivation for the study of the block second-derivative of high-order accuracy methods is that construction of A-stable multi-derivative methods of higher orders are possible, which are suitable for solving stiff systems. Secondly, block methods generally preserve the traditional advantage of one-step methods of being self-starting and of permitting easy change of step length during integration, see [19]. Thirdly, their advantage over Runge-Kutta methods lies in the fact that they are very inexpensive in terms of number of function evaluations per step. The effectiveness of this class of methods for the treatment of ODEs is shown on the basis of their attractive properties and the efficient technique to deal with a wide range of stiff test problems.

Definition 1.1

A numerical method is said to be A-stable if its region of absolute stability contains the whole of the complex left hand-half plane (Dahlquist [11]). Alternatively, a numerical method is called A-stable if all the solution of (1.1) tend to zero as $n\rightarrow \infty$, when the method is applied with fixed positive h to any differential equation of the form dy/dx =$\lambda$y, where $\lambda$ is a complex constant with negative real part.

Definition 1.2

Let $Y_m$and $F_m$ be defined by $Y_m =( {y_n ,y_{n+1} ,\ldots ,y_{n+r-1} })^T,F_m =( {f_n ,f_{n+1} ,\ldots ,f_{n+r-1} })^T.$

Then a general k-block, r-point block method is a matrix of finite difference equation of the form

$$\begin{aligned} Y_m =\sum \limits _{i=0}^k {A_i } Y_{m-i} +h\sum \limits _{i=0}^k {B_i } F_{m-1} , \end{aligned}$$

(1.2)

where all the A$_{i}$’s and B$_{i}$’s are properly chosen $r\times r$ matrix coefficients and m = 0,1,2,..., represents the block number, n = mr is the first step number of the m$^\mathrm{th}$ block and r is the proposed block size [10].

Assumption 1.1

In the ODEs (1.1), the function f belongs to $C^1$-class, and therefore, satisfies the Lipschitz condition with the constant L. That is, if the estimation

$$\begin{aligned} \left\| {f(x,y)-f(x,\tilde{y})} \right\| \le L\left\| {y-\tilde{y}} \right\| \end{aligned}$$

holds, L is called the Lipschitz constant.

Definition 1.3

A solution y(x) of (1.1) is said to be stable if given any $\in >0$ there is $\delta >0$ such that any other solution $\hat{y}(x)$ of (1.1) satisfies

$$\begin{aligned} \left| {y(a)-} \right. \left. {\hat{y}(a)} \right| \le \delta \end{aligned}$$

(1.3a)

also satisfies

$$\begin{aligned} \left| {y(x)-} \right. \left. {\hat{y}(x)} \right| \le \in \end{aligned}$$

(1.3b)

for all $x>a$.

The solution y(x) is asymptotically stable if in addition to (1.3b) $\left| {y(x)-} \right. \left. {\hat{y}(x)} \right| \rightarrow 0$ as $x\rightarrow \infty .$

2 Derivation principle of the second-derivative of high-order methods

In this section, our objective is to describe the derivation principle of the second-derivative high-order accuracy methods with off-step points for the direct integration of stiff systems of initial value problems of the form (1.1). In order to obtain such highly stable methods we seek an approximate solution to the exact solution of (1.1) by the interpolant of the form

$$\begin{aligned} y( x)=\phi _0 +\phi _1 x+\phi _2 x^2+\cdots +\phi _{p-1} x^{p-1}=\sum \limits _{i=0}^{p-1} {\phi _i } x^i, \end{aligned}$$

(2.1)

which is twice continuously differentiable function of y(x). We set the sum p = r+s+t where r denotes the number of interpolation points used and $s >$ 0, $t >$ 0 are distinct collocation points. Interpolating y(x) in (2.1) at the points {$x_{n+j}$}, and collocating ${y}'(x)$ and ${y}''(x)$ at the points {$c_{n+j}$} we have the following system of equations:

$$\begin{aligned} y(x_{n+j} )=y_{n+j} , \qquad (j=0,1,\ldots ,r-1), \end{aligned}$$

(2.2)

$$\begin{aligned} {y}'(c_{n+j} )=f_{n+j} ,\qquad (j=0,1,\ldots ,s-1), \end{aligned}$$

(2.3)

$$\begin{aligned} {y}''(c_{n+j} )=g_{n+j} , \qquad (j=0,1,\ldots ,t-1). \end{aligned}$$

(2.4)

From Eqs. (2.2)–(2.4) we obtain the continuous multistep collocation method of the form:

$$\begin{aligned} y(x)=\sum \limits _{j=0}^{r-1} {\phi _j (x)} y_{n+j} +h\sum \limits _{j=0}^{s-1} {\psi _j } (x)f_{n+j} +h^2\sum \limits _{j=0}^{t-1} {\omega _j } (x)g_{n+j} \end{aligned}$$

(2.5)

where

$$\begin{aligned} y_{n+j} \approx y( {x_n +jh}), \quad f_{n+j} \equiv f( {x_n +jh,y( {x_n +jh})})\text { and }g_{n+j} \equiv \frac{df( {x,y( x)})}{dx}\left| {\begin{array}{l} x=x_{n+j} \\ y=y_{n+j} \\ \end{array}} \right. . \end{aligned}$$

Here $\phi _j (x)$, $\psi _j (x)$ and $\omega _j (x)$ are parameters of the method which are to be determined. They are assumed polynomials of the form

$$\begin{aligned} \phi _j (x)=\sum \limits _{i=0}^{p-1} {\phi _{j,i+1} } x^i, \quad h\psi _j (x)=\sum \limits _{i=0}^{p-1} {h\psi _{j,i+1} } x^i \text { and }h^2\omega _j (x)=\sum \limits _{i=0}^{p-1} {h^2\omega _{j,i+1} } x^i.\nonumber \\ \end{aligned}$$

(2.6)

The numerical constant coefficients $\phi _{j,i+1}$,$\psi _{j,i+1}$ and $\omega _{j,i+1}$ in (2.6) are to be determined. They are selected so that accurate approximations of well behaved problems are obtained efficiently. Actual evaluations of the constant coefficients $\phi _{j,i+1}$, $\psi _{j,i+1}$ and $\omega _{j,i+1}$ are carried out with a computer algebra system, for example Maple software package.

In the second-derivative methods, we see that, in addition to the computation of the f-values of the usual standard multistep methods, the modified methods involve computing g-values, where g is defined in (2.5). According to [8] the second-derivative methods can be practical if the costs of evaluating $\varvec{g}$ are comparable to those in evaluating $\varvec{f}$, and can even be more efficient than the standard methods if the number of function evaluations is fewer.

3 An eighth order second-derivative of high-order accuracy method

The parameters of the first second-derivative method can now be obtain by considering the multistep collocation method (2.5), set $\xi =(x-x_n )$ and introduce the intermediate off-step points in between the usual grid points which are respectively denoted by, u = $\frac{1}{2}$ and v = $\frac{3}{2}$. These points are carefully chosen to guarantee the zero stability of the block second-derivative of high-order accuracy method see [12]. Thus, expanding (2.5) we have the following continuous scheme:

$$\begin{aligned} \begin{array}{l} y(x)=\phi _0 (x)y_n +\phi _1 (x)y_{n+1} +\phi _2 (x)y_{n+2} +h[\psi _0 (x)f_n +\psi _1 (x)f_{n+1} +\psi _2 (x)f_{n+2} ] \\ \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad + h^2[\omega _0 (x)g_n +\omega _1 (x)g_{n+1} +\omega _2 (x)g_{n+2} ] \\ \end{array}\nonumber \\ \end{aligned}$$

(3.1)

where

$$\begin{aligned}&\phi _0 (x)=\left[ {\frac{24\xi ^8-207h\xi ^7+713h^2\xi ^6-1233h^3\xi ^5+1083h^4\xi ^4-396h^5\xi ^3+16h^8}{16h^8}} \right] ,\\&\phi _1 (x)=\left[ {\frac{-3\xi ^8+24h\xi ^7-76h^2\xi ^6+120h^3\xi ^5-96h^4\xi ^4+32h^5\xi ^3}{h^8}} \right] ,\\&\phi _2 (x)=\left[ {\frac{24\xi ^8-177h\xi ^7+503h^2\xi ^6-687h^3\xi ^5+453h^4\xi ^4-116h^5\xi ^3}{16h^8}} \right] ,\\&\psi _0 (x)=\left[ {\frac{9\xi ^8-79h\xi ^7+279h^2\xi ^6-501h^3\xi ^5+468h^4\xi ^4-192h^5\xi ^3+16h^7\xi }{16h^7}} \right] ,\\&\psi _1 (x)=\left[ {\frac{-\xi ^7+7h\xi ^6-18h^2\xi ^5+20h^3\xi ^4-8h^4\xi ^3}{h^6}} \right] ,\\&\psi _2 (x)=\left[ {\frac{-9\xi ^8+65h\xi ^7-181h^2\xi ^6+243h^3\xi ^5-158h^4\xi ^4+40h^5\xi ^3}{16h^7}} \right] ,\\&\omega _0 (x)=\left[ {\frac{\xi ^8-9h\xi ^7+33h^2\xi ^6-63h^3\xi ^5+66h^4\xi ^4-36h^5\xi ^3+8h^6\xi ^2}{16h^6}} \right] ,\\&\omega _1 (x)=\left[ {\frac{-\xi ^8+8h\xi ^7-25h^2\xi ^6+38h^3\xi ^5-28h^4\xi ^4+8h^5\xi ^3}{2h^6}} \right] ,\\&\omega _2 (x)=\left[ {\frac{\xi ^8-7h\xi ^7+19h^2\xi ^6-25h^3\xi ^5+16h^4\xi ^4-4h^5\xi ^3}{16h^6}} \right] . \end{aligned}$$

Evaluating the continuous scheme y(x) in (3.1) at the points $x=x_{n+u}$ and $x_{n+v}$ we obtain the first and third members in the block (3.2). Differentiating the continuous scheme in (3.1) once and evaluate at the points, $x=x_{n+u}$,$x_{n+v}$ again, then solve simultaneously for the values of $y_{n+1}$ and $y_{n+2}$ to complete the first block Second-Derivative of high-order accuracy method, consisting of four members in a block as follows:

$$\begin{aligned} y_{n+u}= & {} \frac{675}{2048}y_n +\frac{1512}{2048}y_{n+1} -\frac{139}{2048}y_{n+2} +\frac{h}{4096}\left[ {351f_n -864f_{n+1} +93f_{n+2} } \right] \nonumber \\&+\frac{h^2}{4096}\left[ {27g_n +216g_{n+1} -9g_{n+2} } \right] \end{aligned}$$

(3.2)

$$\begin{aligned} y_{n+1}= & {} \frac{67}{64}y_n -\frac{3}{64}y_{n+2} +\frac{h}{1728}\left[ {405f_n +1024f_{n+u} +432f_{n+1} +29f_{n+2} } \right] \\&+\frac{h^2}{1 728}\left[ {27g_n -3g_{n+2} } \right] \end{aligned}$$

$$\begin{aligned} y_{n+v}= & {} -\frac{139}{2048}y_n +\frac{1512}{2048}y_{n+1} +\frac{675}{2048}y_{n+2} +\frac{h}{4096}\left[ {-93f_n +864f_{n+1} -351f_{n+2} } \right] \\&+\frac{h^2}{4096}\left[ {-9g_n +216g_{n+1} +27g_{n+2} } \right] \end{aligned}$$

$$\begin{aligned} y_{n+2}= & {} \frac{3}{67}y_n +\frac{64}{67}y_{n+1} +\frac{h}{1809}[29f_n +432f_{n+1} +1024f_{n+v} +405f_{n+2} ]\\&+ \frac{h^2}{1809}[3g_n -27g_{n+2} ]\,\,. \end{aligned}$$

3.1 An eleventh order second-derivative of high-order accuracy method

For the 2$^{nd}$ second-derivative high-order accuracy method, we similarly introduce three intermediate off-step points in between the usual grid points and denote them by u = $\frac{1}{2}$, v = $\frac{3}{2}$ and w =$\frac{5}{2}$. Again, these points are carefully chosen to guarantee the zero stability of the block second-derivative high order method, see [12]. Hence expanding (2.5) we obtain the continuous scheme of the form,

$$\begin{aligned} \begin{array}{l} y(x)=\phi _0 (x)y_n +\phi _1 (x)y_{n+1} +\phi _2 (x)y_{n+2} +\phi _3 (x)y_{n+3}\\ \quad \quad \quad + h\left[ {\psi _0 (x)f_n +\psi _1 (x)f_{n+1} +\psi _2 (x)f_{n+2} +\psi _3 (x)f_{n+3} } \right] \\ \quad \quad \quad + h^2\left[ {\omega _0 (x)g_n +\omega _1 (x)g_{n+1} +\omega _2 (x)g_{n+2} +\omega _3 (x)g_{n+3} } \right] \\ \end{array} \end{aligned}$$

(3.3)

where

$$\begin{aligned} \phi _0 (x)=\left[ {\frac{{\begin{array}{l} -103\xi ^{11}+1821h\xi ^{10}-13935h^2\xi ^9+60345h^3\xi ^8-162057h^4\xi ^7+\\ 277335h^5\xi ^6-297221h^6\xi ^5+184515h^7\xi ^4-51996h^8\xi ^3+1296h^{11}\\ \end{array}}}{1296h^{11}}} \right] , \end{aligned}$$

$$\begin{aligned}&\phi _1 (x)=\left[ {\frac{{\begin{array}{l} 9\xi ^{11}-150h\xi ^{10}+1070h^2\xi ^9-4260h^3\xi ^8+10341h^4\xi ^7 \\ -15670h^5\xi ^6+14508h^6\xi ^5-7560h^7\xi ^4+1728h^8\xi ^3 \\ \end{array}}}{16h^{11}}} \right] ,\\&\phi _2 (x)=\left[ {\frac{{\begin{array}{l} -9\xi ^{11}+147h\xi ^{10}-1025h^2\xi ^9+3975h^3\xi ^8-9351h^4\xi ^7 \\ +13625h^5\xi ^6-11979h^6\xi ^5+5805h^7\xi ^4-1188h^8\xi ^3 \\ \end{array}}}{16h^{11}}} \right] ,\\&\phi _3 (x)=\left[ {\frac{{\begin{array}{l} 103\xi ^{11}-1578h\xi ^{10}+10290h^2\xi ^9-37260h^3\xi ^8+81867h^4\xi ^7 \\ -111690h^5\xi ^6+92372h^6\xi ^5-42360h^7\xi ^4+8256h^8\xi ^3 \\ \end{array}}}{1296h^{11}}} \right] ,\\&\psi _0 (x)=\left[ {\frac{{\begin{array}{l} -11\xi ^{11}+196h\xi ^{10}-1515h^2\xi ^9+6648h^3\xi ^8-18177h^4\xi ^7+31908h^5\xi ^6 \\ -35521h^6\xi ^5+23456h^7\xi ^4-7416h^8\xi ^3+432h^{10}\xi \\ \end{array}}}{432h^{10}}} \right] ,\\&\psi _1 (x)=\left[ {\frac{{\begin{array}{l} 3\xi ^{11}-49h\xi ^{10}+340h^2\xi ^9-1302h^3\xi ^8+2987h^4\xi ^7 \\ -4157h^5\xi ^6+3366h^6\xi ^5-1404h^7\xi ^4+216h^8\xi ^3 \\ \end{array}}}{16h^{10}}} \right] ,\\&\psi _2 (x)=\left[ {\frac{{\begin{array}{l} 3\xi ^{11}-50h\xi ^{10}+355h^2\xi ^9-1398h^3\xi ^8+3329h^4\xi ^7 \\ -4894h^5\xi ^6+4329h^6\xi ^5-2106h^7\xi ^4+432h^8\xi ^3 \\ \end{array}}}{16h^{10}}} \right] ,\\&\psi _3 (x)=\left[ {\frac{{\begin{array}{l} -11\xi ^{11}+167h\xi ^{10}-1080h^2\xi ^9+3882h^3\xi ^8-8475h^4\xi ^7 \\ +11499h^5\xi ^6-9466h^6\xi ^5+4324h^7\xi ^4-840h^8\xi ^3 \\ \end{array}}}{432h^{10}}} \right] ,\\&\omega _0 (x)=\left[ {\frac{{\begin{array}{l} -\xi ^{11}+18h\xi ^{10}-141h^2\xi ^9+630h^3\xi ^8-1767h^4\xi ^7+3222h^5\xi ^6 \\ -3815h^6\xi ^5+2826h^7\xi ^4-1188h^8\xi ^3+216h^9\xi ^2 \\ \end{array}}}{432h^9}} \right] ,\\&\omega _1 (x)=\left[ {\frac{{\begin{array}{l} \xi ^{11}-17h\xi ^{10}+124h^2\xi ^9-506h^3\xi ^8+1261h^4\xi ^7 \\ -1961h^5\xi ^6+1854h^6\xi ^5-972h^7\xi ^4+216h^8\xi ^3 \\ \end{array}}}{16h^9}} \right] ,\\&\omega _2 (x)=\left[ {\frac{{\begin{array}{l} -\xi ^{11}+16h\xi ^{10}-109h^2\xi ^9+412h^3\xi ^8-943h^4\xi ^7 \\ +1336h^5\xi ^6-1143h^6\xi ^5+540h^7\xi ^4-108h^8\xi ^3 \\ \end{array}}}{16h^9}} \right] ,\\&\omega _3 (x)=\left[ {\frac{{\begin{array}{l} \xi ^{11}-15h\xi ^{10}+96h^2\xi ^9-342h^3\xi ^8+741h^4\xi ^7 \\ -999h^5\xi ^6+818h^6\xi ^5-372h^7\xi ^4+72h^8\xi ^3 \\ \end{array}}}{432h^9}} \right] . \end{aligned}$$

Evaluating the continuous scheme (3.3) and its first derivative as done in (3.1) at the points {$x=x_{n+u}$,$x_{n+v}$ and $x_{n+w}$} where {u =$\frac{1}{2}$, v =$\frac{3}{2}$ and w = $\frac{5}{2}$} we obtain the block method (3.4) as follows:

$$\begin{aligned} \begin{array}{ll} y_{n+u} =\frac{24125}{98304}y_n +\frac{37125}{32768}y_{n+1} -\frac{13375}{32768}y_{n+2} +\frac{2929}{98304}y_{n+3}\\ \qquad \qquad +\frac{h}{32768}[1875f_n -3375f_{n+1} +4875f_{n+2} -295f_{n+3} ] \\ \qquad \qquad +\frac{h^2}{32768}[125g_n +3375g_{n+1} -1125g_{n+2} +25g_{n+3} ] \\ \end{array} \end{aligned}$$

(3.4)

$$\begin{aligned}&y_{n+1} =\frac{3079}{1377}y_n -\frac{69}{51}y_{n+2} +\frac{161}{1377}y_{n+3}\\&\qquad \qquad +\frac{h}{11475}[5375f_n +16384f_{n+u} +11475f_{n+1} +5675f_{n+2} -409f_{n+3} ] \\&\qquad \qquad +\frac{h^2}{11475}[325g_n +2025g_{n+1} -1425g_{n+2} +35g_{n+3} ] \end{aligned}$$

$$\begin{aligned}&y_{n+v} =-\frac{383}{32768}y_n +\frac{16767}{32768}y_{n+1} +\frac{16767}{32768}y_{n+2} -\frac{383}{32768}y_{n+3}\\&\qquad \qquad +\frac{h}{32768}[-111f_n +5103f_{n+1} -5103f_{n+2} +111f_{n+3} ] \\&\qquad \qquad +\frac{h^2}{32768}[-9g_n +729g_{n+1} +729g_{n+2} -9g_{n+3} ] \end{aligned}$$

$$\begin{aligned}&y_{n+2} =\frac{-31}{6561}y_n +\frac{6561}{6561}y_{n+1} +\frac{31}{6561}y_{n+3}\\&\qquad \qquad +\frac{h}{32805}[-41f_n +8019f_{n+1} +16384f_{n+v} +8019f_{n+2} -41f_{n+3} ] \\&\qquad \qquad +\frac{h^2}{32805}[-3g_n +729g_{n+1} -729g_{n+2} +3g_{n+3} ] \end{aligned}$$

$$\begin{aligned}&y_{n+w} =\frac{2929}{98304}y_n -\frac{13375}{32768}y_{n+1} +\frac{37125}{32768}y_{n+2} +\frac{24125}{98304}y_{n+3}\\&\qquad \qquad +\frac{h}{32768}[295f_n -4875f_{n+1} +3375f_{n+2} -1875f_{n+3} ] \\&\qquad \qquad +\frac{h^2}{32768}[25g_n -1125g_{n+1} +3375g_{n+2} +125g_{n+3} ] \end{aligned}$$

$$\begin{aligned}&y_{n+3} =\frac{-161}{3079}y_n +\frac{1863}{3079}y_{n+1} +\frac{1377}{3079}y_{n+2}\\&\qquad \qquad +\frac{h}{76975}[-1227f_n +17025f_{n+1} +34425f_{n+2} +49152f_{n+5/2} +16125f_{n+3} ] \\&\qquad \qquad +\frac{h^2}{76975}[-105g_n +4275g_{n+1} -6075g_{n+2} -975g_{n+3} ] \end{aligned}$$

4 Analysis of the second-derivative of high-order accuracy methods

4.1 Order, consistency, zero-stability and convergence of the SDH methods

With the multistep collocation method (2.5) we associate the linear difference operator $\ell$ defined by

$$\begin{aligned} \ell \,[y(x);h]=\sum \limits _{j=0}^r {\phi _j (x)y(x+jh)} +h\sum \limits _{j=0}^s {\psi _j } (x){y}'(x+jh)+h^2\sum \limits _{j=0}^t {\omega _j } (x){y}''(x+jh) \end{aligned}$$

(4.1)

where y(x) is an arbitrary function, continuously differentiable on [a, b]. Following Lambert [19] and Fatunla [12], we can write the terms in (4.1) as a Taylor series expansion about the point x to obtain the expression,

$$\begin{aligned} \ell \,[y(x);h]=C_0 y(x)+C_1 h{y}'(x)+C_2 h^2{y}''(x)+\cdots +C_p h^py^p(x)+\cdots , \end{aligned}$$

(4.2)

where the constant coefficients $C_p$, p = 0,1,2,... are given as follows:

$$\begin{aligned}&C_0 =\sum \limits _{j=0}^r {\phi _j }\\&C_1 =\sum \limits _{j=1}^r {j\phi _j -\sum \limits _{j=0}^s {\psi _j } }\\&\begin{array}{l} C_2 =\frac{1}{2!}\left( {\sum \limits _{j=1}^r {j^2\phi _j -2\sum \limits _{j=0}^s {j\psi _j } } }\right) \\ \qquad \qquad \vdots \qquad \qquad \qquad \qquad \qquad \vdots \\ \end{array}\\&C_q =\frac{1}{q!}\left( {\sum \limits _{j=1}^r {j^q\phi _j -\frac{1}{\left( {q-1}\right) !}\sum \limits _{j=1}^s {j^{q-1}\psi _j -\frac{1}{\left( {q-2}\right) !}\sum \limits _{j=1}^t {j^{q-2}} \omega _j } } }\right) , q=3,4,\ldots \end{aligned}$$

According to Lambert [19], the multistep collocation method (2.5) has order p if

$$\begin{aligned} \ell \,[y(x);h]=\mathrm{O}( {h^{p+1}}), C_0 =C_1 =\ldots =C_p =0,\qquad C_{p+1} \ne 0. \end{aligned}$$

(4.3)

Therefore, $C_{p+1}$ is the error constant and $C_{p+1} h^{p+1}y^{(p+1)}(x_n )$ is the principal local truncation error at the point $x_n$ [22]. Hence, from our calculation the order and error constants for the constructed methods are presented in Table 1. It is clear from the Table that the block second-derivative high-order method (3.2) is of uniform accurate order eight. The members of the block second-derivative high-order method (3.4) are of uniformly accurate order eleven. The members of this block method have smaller error constants and hence more accurate than those members of the block method (3.2).

Table 1 Order and error constants of the second-derivative high-order methods

Definition 4.1

(Consistency) The block second-derivative high-order methods (3.2) and (3.4) are said to be consistent if the order of the individual member is greater or equal to one, that is if $p\ge 1.$

• (i) $\rho (1)=0$ and

• (ii) ${\rho }'(1)=\sigma (1)$, where $\rho (z)$ and $\sigma (z)$ are respectively the 1$^\mathrm{st}$ and 2$^\mathrm{nd}$ characteristic polynomials.

From Table 1 we can attest that the members of the block second-derivative high-order accuracy methods are consistent.

In what follows, the block second-derivative high-order methods (3.2) and (3.4) can generally be rearranged and written as a matrix finite difference equation of the form in (1.2) as follows:

$$\begin{aligned} A^{(1)}Y_{m+1} =A^{(0)}Y_m +hB^{(1)}F_{m+1} +hB^{(0)}F_m +h^2CG_{m+1} +h^2DG_m \end{aligned}$$

(4.4)

where

$$\begin{aligned} Y_{m+1}&=\left( {y_{{n+}{\frac{1}{2}}} ,y_{n+1} ,y_{{n+}{\frac{3}{2}}} ,y_{n+2} ,y_{{n+}{\frac{5}{2}}} ,y_{n+3} }\right) ^{T}\\ Y_m&=\left( {y_{{n-}{\frac{5}{2}}} ,y_{n-2} ,y_{{n-}{\frac{3}{2}}} ,y_{n-1} ,y_{{n-}{\frac{1}{2}}} ,y_n }\right) ^{T}\\ F_{m+1}&=\left( {f_{{n+}{\frac{1}{2}}} ,f_{n+1} ,f_{{n+}{\frac{3}{2}}} ,f_{n+2} ,f_{{n+}{\frac{5}{2}}} ,f_{n+3} }\right) ^{T}\\ F_m&=\left( {f_{{n-}{\frac{5}{2}}} ,f_{n-2} ,f_{{n-}{\frac{3}{2}}} ,f_{n-1} ,f_{{n-}{\frac{1}{2}}} ,f_n }\right) ^{T}\\ G_{m+1}&=\left( {g_{{n+}{\frac{1}{2}}} ,g_{n+1} ,g_{{n+}{\frac{3}{2}}} ,g_{n+2} ,g_{{n+}{\frac{5}{2}}} ,g_{n+3} }\right) ^{T}\\ G_m&=\left( {g_{{n-}{\frac{5}{2}}} ,g_{n-2} ,g_{{n-}{\frac{3}{2}}} ,g_{n-1} ,g_{{n-}{\frac{5}{2}}} ,g_n }\right) ^{T} \end{aligned}$$

and the matrices $A^{(1)},A^{(0)},B^{(1)},B^{(0)},C$ and D are matrices whose entries are given by the coefficients of the block second-derivative high-order methods (3.2) and (3.4).

Definition 4.2

(Zero-stability) The block second-derivative high-order methods (3.2) and (3.4) are said to be zero-stable if the roots

$$\begin{aligned} \rho (\lambda )=\det \left[ {\sum \limits _{i=0}^k {A^{(i)}} \lambda ^{k-i}} \right] =0 \end{aligned}$$

satisfies $\left| {\lambda _j } \right| \le 1,\,\,\,j=1,\ldots ,k$ and for those roots with$\left| {\lambda _j } \right| =1$, the multiplicity does not exceed two, Lambert [19, 20]

Definition 4.3

(Convergence) The necessary and sufficient conditions of the block second-derivative high-order methods (3.2) and (3.4) to be convergent are that they must be consistent and zero-stable Dahlquist [11]. Hence from definitions (4.1) and (4.2) the second-derivative high-order methods are convergent.

5 Regions of absolute stability of the second-derivative of high-order methods

To study the stability properties of the block second-derivative high-order methods we reformulate (3.2) and (3.4) as general linear methods see Burrage and Butcher [2]. Hence, we use the notation introduced by Butcher [6] which a general linear method is represented by a partitioned (s+r)$\times$ (s+r) matrix, (containing A, U, B, V),

$$\begin{aligned} \left[ {\begin{array}{l} Y^{\left[ n \right] } \\ y^{\left[ {n-1} \right] } \\ \end{array}} \right] =\left[ {\frac{A\,\,\left| {\,\,U} \right. }{B\,\,\left| {\,\,V} \right. }} \right] \left[ {\begin{array}{l} hf( {Y^{\left[ n \right] }}) \\ y^{\left[ n \right] } \\ \end{array}} \right] , \quad { n = 1, 2, {\ldots },N,} \end{aligned}$$

(5.1a)

where

$$\begin{aligned} Y^{\left[ n \right] }=\left[ {\begin{array}{c} Y_1^{\left[ n \right] } \\ Y_2^{\left[ n \right] } \\ \vdots \\ Y_s^{\left[ n \right] } \\ \end{array}} \right] , \quad y^{\left[ {n-1} \right] }=\left[ {\begin{array}{c} y_1^{\left[ {n-1} \right] } \\ y_2^{\left[ {n-1} \right] } \\ \vdots \\ y_r^{\left[ {n-1} \right] } \\ \end{array}} \right] , \quad f( {Y^{\left[ n \right] }})=\left[ {\begin{array}{c} f(Y_1^{\left[ n \right] } ) \\ f(Y_2^{\left[ n \right] } ) \\ \vdots \\ f(Y_s^{\left[ n \right] } ) \\ \end{array}} \right] , \quad y^{\left[ n \right] }=\left[ {\begin{array}{c} y_1^{\left[ n \right] } \\ y_2^{\left[ n \right] } \\ \vdots \\ y_r^{\left[ n \right] } \\ \end{array}} \right] , \end{aligned}$$

$$\begin{aligned} A=\left[ {\begin{array}{c} 0\qquad 0 \\ A\qquad B \\ \end{array}} \right] , U=\left[ {\begin{array}{c} I\qquad 0\qquad 0 \\ 0\qquad \mu \qquad e-\mu \\ \end{array}} \right] , B=\left[ {\begin{array}{c} A\qquad B \\ 0\qquad 0 \\ \nu ^T\qquad \omega ^T \\ \end{array}} \right] , \quad V=\left[ {\begin{array}{c} I\qquad \mu \qquad e-\mu \\ 0\qquad 0\qquad I \\ 0\qquad 0\qquad I-\theta \\ \end{array}} \right] , \end{aligned}$$

and $e=[1,\cdots ,1]^T\in R^m$ .

Hence (5.1a) takes the form

$$\begin{aligned} \left[ {\begin{array}{c} Y_1^{\left[ n \right] } \\ Y_2^{\left[ n \right] } \\ \vdots \\ Y_s^{\left[ n \right] } \\ - \\ y_1^{[n]} \\ \vdots \\ y_r^{[n]} \\ \end{array}} \right] =\left[ {\frac{A\,\,\left| {\,\,U} \right. }{B\,\,\left| {\,\,V} \right. }} \right] \,\,\left[ {\begin{array}{c} hf(Y_1^{\left[ n \right] } ) \\ hf(Y_2^{\left[ n \right] } ) \\ \vdots \\ hf(Y_s^{\left[ n \right] } ) \\ - \\ y_1^{[n-1]} \\ \vdots \\ y_r^{[n-1]} \\ \end{array}} \right] \end{aligned}$$

(5.1b)

where r denotes quantities as output from each step and input to the next step and s denotes stage values used in the computation of the step $y_1$,$y_2$,...,$y_s$. The coefficients of these matrices indicate the relationship between the various numerical quantities that arise in the computation of stability regions. The elements of the matrices A, U, B and V are substituted into the stability matrix. In the sense of [9] we apply (5.1) to the linear test equation ${y}'=\lambda y,x\ge 0$ and $\lambda \in C$ but for the second-derivative high-order method we use ${y}''=\lambda ^2y,$ which leads to the recurrence relation $y^{\left[ {n+1} \right] }=M(z)y^{\left[ n \right] }$, n = 1,2,...,N-1, $z=\lambda h$, where the stability matrix M(z) is defined by

$$\begin{aligned} M(z)=V+zB(1-zA)^{-1}U. \end{aligned}$$

(5.2)

We also define the stability polynomial $p(\eta ,z)$ by the relation

$$\begin{aligned} \rho (\eta ,\,z)=\det ( {\eta I-M(z)}) \end{aligned}$$

(5.3)

and the absolute stability region $\mathfrak {R}$ of the method is given by

$$\begin{aligned} \mathfrak {R}=x\in C:\rho (\eta ,z)=1\Rightarrow \left| \eta \right| \le 1. \end{aligned}$$

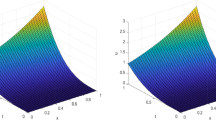
To compute the region of absolute stability we substitute the elements of the matrices A, U, B and V into the stability function (5.2) and finally into the stability polynomial of the methods, which is plotted to produce the required graphs of the absolute stability regions of the methods as shown in Fig. 1.

Fig. 1

Regions of absolute stability of the second-derivative high-order methods

6 Numerical experiments

In this section, the performance of the second-derivative high-order accuracy methods is examined on five tests of initial value problems, particularly stiff systems. The results obtained are compared side by side in Tables. We also show the efficiency curves for some of the problem considered and compared with the ode code of Matlab. In order to provide a direct comparison, the tests were carried out with a fixed step length, using Matlab. In the computation we use nfe to denote the number of function evaluations.

Example 1

The first test problem is a well-known classical system. It is a mildly stiff problem composed of two first order equations,

$$\begin{aligned} \left[ {\begin{array}{l} {y}'_1 (x) \\ {y}'_2 (x) \\ \end{array}} \right] =\left[ {\begin{array}{l} 998 \qquad 1998 \\ -999 \quad -1999 \\ \end{array}} \right] \left[ {\begin{array}{l} y_1 (x) \\ y_2 (x) \\ \end{array}} \right] ,\,\,\,\,\,\,\,\left[ {\begin{array}{l} y_1 (0) \\ y_2 (0) \\ \end{array}} \right] =\left[ {\begin{array}{l} 1 \\ 1 \\ \end{array}} \right] \end{aligned}$$

and the exact solution is given by the sum of two decaying exponential components

$$\begin{aligned} \left\{ {\begin{array}{l} y_1 (x)=4e^{-x}-3e^{-1000x} \\ y_2 (x)=-2e^{-x}+3e^{-1000x} \\ \end{array}} \right. \end{aligned}$$

The stiffness ratio is 1:1000. We solve the problem in the interval [0, 40] and the computed results are shown side by side in Table 2.

Table 2 Absolute errors in the numerical integration of example 1

Example 2

Stiff nonlinear problem (The Kaps problem)

Consider the stiff system of two dimensional Kaps problem with corresponding initial conditions:

$$\begin{aligned} \left[ {\begin{array}{l} {y}'_1 (x) \\ {y}'_2 (x) \\ \end{array}} \right] =\left[ {\begin{array}{l} -1002y_1 (x)+1000y_2 (x)^2 \\ y_1 (x)-y_2 (x)(1+y_2 (x)) \\ \end{array}} \right] ,\,\,\,\,\,\,\,\left[ {\begin{array}{l} y_1 (0) \\ y_2 (0) \\ \end{array}} \right] =\left[ {\begin{array}{l} 1 \\ 1 \\ \end{array}} \right] . \end{aligned}$$

The exact solution is

$$\begin{aligned} \,\left[ {\begin{array}{l} y_1 (x) \\ y_2 (x) \\ \end{array}} \right] =\left[ {\begin{array}{l} \exp (-2x) \\ \exp (-x) \\ \end{array}} \right] . \end{aligned}$$

In Table 3, the computed solutions of the problem using the new methods on the interval of [0, 10] are shown side by side. From this example, it is clearly confirmed that the second-derivative high-order accuracy methods are appropriate for stiff problems.

Table 3 Absolute errors in the numerical integration of example 2

Example 3

The third example is a highly stiff system (see [5])

$$\begin{aligned} \left[ {\begin{array}{l} {y}'_1 (x) \\ {y}'_2 (x) \\ \end{array}} \right] =\left[ {\begin{array}{l} -10^7\quad 0.075 \\ 7500 \quad -0.075 \\ \end{array}} \right] \left[ {\begin{array}{l} y_1 (x) \\ y_2 (x) \\ \end{array}} \right] , \left[ {\begin{array}{l} y_1 (0) \\ y_2 (0) \\ \end{array}} \right] =\left[ {\begin{array}{l} 1 \\ -1 \\ \end{array}} \right] . \end{aligned}$$

The eigenvalues of the Jacobian of the system are approximately $\lambda _{1}$= $-$1.000000000562500$\times$10$^{6}$, and $\lambda _{2}$ = $-$0.07443749995813. We solve the problem in the range [0, 40] and the computed results are shown in Table 4.

Table 4 Absolute errors in the numerical integration of example 3

Example 4

Chemistry Problem suggested by Gear [15],

$$\begin{aligned} \begin{array}{l} {y}'_1 =-0.013y_1 -1000y_1 y_3 ,\qquad \qquad \qquad \quad \quad y_1 (0)=1, \\ {y}'_2 =-2500y_2 y_3 ,\qquad \qquad \qquad \qquad \qquad \qquad \quad \quad y_2 (0)=1, \\ {y}'_3 =-0.013y_1 -1000y_1 y_3 -2500y_2 y_3 ,\qquad y_3 (0)=0. \\ \end{array} \end{aligned}$$

This problem was integrated using the newly constructed methods within the range [0, 10] and the efficiency curves obtained are compared with the ode code of Matlab in Fig. 2.

Fig. 2

Graphical plots of Example 4 using second-derivative high-order methods

Example 5

Another chemistry problem considered by Robertson [25].

Many authors believed that this problem is a fairly hard test problem for stiff ordinary differential equation integrators [1, 5, 17, 29], so it is vital to demonstrate the efficiency of the new algorithms on this problem.

$$\begin{aligned} \begin{array}{l} {y}'_1 =-0.04y_1 +10^4y_2 y_3 ,\qquad \qquad \qquad \qquad \qquad y_1 (0)=1, \\ {y}'_2 =0.04y_1 -10^4y_2 y_3 -3\times 10^7y_2^2 ,\qquad \qquad y_2 (0)=0, \\ {y}'_3 =3\times 10^7y_2^2 ,\qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad y_3 (0)=0. \\ \end{array} \end{aligned}$$

Here we applied the newly constructed methods and the results obtained are shown in Table 5 and for fair comparison see [5] page 426.

Table 5 Absolute errors in the numerical integration of example 5

7 Concluding remarks

What we know is that very little literature exist on the second-derivative type of methods which utilize second derivative. It is for this reason that we subjected the newly derived methods to detailed implementations using different systems of first order initial value problems in ordinary differential equations. The results from the new high-order methods are very promising for stiff systems therefore encouraging further investigation of the new methods is necessary.