1 Introduction and preliminaries

If G is a connected graph, the distance d(x,y) between two vertices \(\textit{x},\textit{y}\in V(G)\) is the length of a shortest distance between them. Let \(W=\{{w_{1},w_{2},w_{3},\ldots ,w_{k}}\}\) be an ordered set of vertices of G and let x be a vertex of \(G\mid W\). The representation \(r(\textit{x}\mid W)\) of x with respect to W is the k-tuple \((d(x,w_{1}),d(x,w_{2}),d(x,w_{3}),\ldots ,d(x,w_{k}))\). If distinct vertices of G have distinct representations with respect to W then W is named as a resolving set for G. A resolving set containing a minimum number of vertices is called a metric basis for G and the number of vertices in a metric basis is called metric dimension of G denoted by dim(G). The metric dimension problem is NP-complete problem, to determine whether metric dimension is less than a given value. It was first introduced by Slater (1975) and Haray and Melter (1976). The concept of resolving set has proved to be useful to a variety of fields such as structure of chemical compounds [3], image processing, robotic navigation, combinatorial research and optimization etc. The join of two graphs \(G_{1}\) and \(G_{2}\) is the graph consisting of the union of the graphs \(G_{1}\) and \(G_{2}\) and all the edges joining \(V(G_{1})\) and \(V(G_{1})\). A fan is defined as \(f_{n}=K_{1}\)+\(P_{n}\) for \(n \ge 1\) and Jahangir graph \(J_{2n}\) obtained from wheel graph \(W_{2n}\). Tomescu and Javaid [8] determined the dimension of \(J_{2n}\), Caceres et al. [10] the dimension of fan \(f_{n}\) and Imran et al. [4] the dimension of harary graphs \(H_{5,n}\).

Theorem 1

([4, 8, 10]) Let \(K_{n}\) be a complete graph, \(K_{s,t}\) an n-vertex complete bipartite graph, \(J_{2n}\) be a jahangir graph and \(f_{n}\) a fan of order \(n \ge 1\), then

  1. 1.

    \(dim(K_{n})=n-1\)

  2. 2.

    \(dim(K_{s,t})=n-2\)

  3. 3.

    For \(n \ge 4\), \(dim(J_{2n})=\left\lfloor \frac{2n}{3} \right\rfloor \)

  4. 4.

    For \(n \ge 7\), \(dim(f_{n})=\left\lfloor \frac{2n+2}{5}\right\rfloor \)

The metric dimension of all these graphs depend upon the number of vertices in the graphs. We say that a family \(\mathcal {G}\) of connected graphs is a family with constant metric dimension if dimension of G is finite and does not depend upon the number of choices of G in \(\mathcal {G}\). It is shown in [3] that the dimension of a path is 1, thus paths with n vertices constitute a family of graphs with constant metric dimension. Similarly cycles with \(\textit{n}({\ge }3)\) vertices is also a family of such graphs because their dimension is 2. Imran et al. [4] proved that metric dimension of flower snarks is 3 and dimension of an antiprism \(A_{n}\) is 3. Prisms are the 3-regular trivalent graphs obtained by the cross product of path \(P_{2}\) and cycle \(C_{n}\) and

$$\begin{aligned} dim(D_{n})= \left\{ \begin{array}{l@{\quad }l} 2, &{} \hbox { if } n \hbox { is odd}\\ 3, &{} \,\,\hbox {if } n \hbox { is even} \end{array} \right. \end{aligned}$$

Ali et al. [1] proved that the dimension of extension of a prism is 3. Hence all these classes constitute a family of graphs with constant metric dimension. Also the 4-regular graphs obtained by the cartesian product of two cycles(also called torus grids) are a family of graphs with constant metric dimension as

$$\begin{aligned} dim(C_{m}\times C_{n})= \left\{ \begin{array}{l@{\quad }l} 3, &{} \hbox {if } m \hbox { or } n \hbox { is odd}\\ 4, &{} \hbox {otherwise} \end{array} \right. \end{aligned}$$

The generalized peterson graph \(P(n,3)\) has constant metric dimension [11]. Thus the problem of determining \(dim(G)\le k\) is an NP-complete problem. In this paper we extend the study of the metric dimension of convex polytopes and present two special types of convex polytopes which have constant metric dimension.

2 The graph of convex polytope \(R_{n}\)

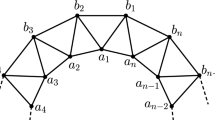
The graph of convex polytope \( R_{n}\) (Fig. 1) consists of 2n number of 3-sided faces, n number of 4-sided faces, n number of 6-sided faces and a pair of n-sided.

Fig. 1
figure 1

The graph of convex polytope \(R_{n}\)

Full size image

For our purpose we call the cycle induced by \(\{{a_{i}:1\le i\le n}\}\), the inner cycle, set of vertices \(\{{b_{i}:1\le i\le n}\}\) the set of interior vertices, set of vertices \(\{{c_{i}:1\le i\le n}\}\) the set of exterior vertices, cycle induced by \(\{{d_{i}:1\le i\le n}\}\) the middle cycle and the cycle induced by \(\{{e_{i}:1\le i\le n}\}\) the outer cycle.

Theorem 2

For \(n\ge 6\), \(dim(R_{n})=3\).

Proof

We will prove the result by double inequalities. Here we consider two cases:

Case (i) When n is even.

In this case, we can write \(\textit{n}=2\textit{k}\), \(\textit{k}\ge 3\), \(\textit{k}\in Z^{+}\). Let \(W=\{{a_{1},a_{2},a_{k+1}}\}\subset V(R_{n})\), it is to be shown that W is a resolving set for \(R_{n}\). For this we give representations of any vertex \(V(S_{n})\mid W\) with respect to W.

Representations of vertices on the inner cycle are:

$$\begin{aligned} r\left( a_{i}\mid W\right) = \left\{ \begin{array}{l@{\quad }l} (i-1,i-2,k-i+1), &{}3\le i\le k\\ (2k-i+1,2k-i+2,i-k-1), &{}k+2\le i\le 2k \end{array} \right. \end{aligned}$$

Representations of the set of interior vertices are:

$$\begin{aligned} r\left( b_{i}\mid W\right) = \left\{ \begin{array}{l@{\quad }l} (1,1,k), &{}i=1\\ (i,i-1,k-i+1), &{}2\le i\le k\\ (2k-i+1,i-1,1), &{}i=k+1\\ (2k-i+1,2k-i+2,i-k), &{}k+2\le i\le 2k \end{array} \right. \end{aligned}$$

Representations of the set of exterior vertices are:

$$\begin{aligned} r\left( c_{i}\mid W\right) = \left\{ \begin{array}{l@{\quad }l} (2,2,k+1), &{}i=1\\ (i+1,i,k-i+2), &{}2\le i\le k\\ (2k-i+2,i,2), &{}i=k+1\\ (2k-i+2,2k-i+3,i-k+1), &{}k+2\le i\le 2k \end{array}\right. \end{aligned}$$

Representations of vertices on the middle cycle are:

$$\begin{aligned} r\left( d_{i}\mid W\right) = \left\{ \begin{array}{l@{\quad }l} (3,3,k+1), &{}i=1\\ (i+2,i+1,k-i+2), &{}2\le i\le k-1\\ (2k-i+2,i+1,3), &{}i=k,k+1\\ (2k-i+2,2k-i+3,i-k+2), &{}k+2\le i\le 2k-1\\ (3,3,k+2), &{}i=2k \end{array}\right. \end{aligned}$$

Representations of vertices on the outer cycle are:

$$\begin{aligned} r\left( e_{i}\mid W\right) = \left\{ \begin{array}{l@{\quad }l} (4,4,k+2), &{}i=1\\ (i+3,i+2,k-i+3), &{}2\le i\le k-1\\ (2k-i+3,i+2,4), &{}i=k,k+1\\ (2k-i+3,2k-i+4,i-k+3), &{}k+2\le i\le 2k-1\\ (4,4,k+3), &{}i=2k \end{array}\right. \end{aligned}$$

It is to be noted that there are no two vertices having same representations. This implies that \(dim(R_{n})\le 3\). We will now prove the opposite inequality by contradiction. Suppose that \(dim(R_{n})=2\). Without loss of generality suppose that first resolving vertex is \(a_{1}\), \(b_{1}\), \(c_{1}\), \(d_{1}\) or \(e_{1}\) and the other lies in inner cycle, set of interior and exterior vertices, middle and outer cycles then we have following diffrent possibilities:

Resolving vertices

Contradictions

\(\left\{ a_{1},a_{t}\right\} \), \(a_{t}\left( 2\le t\le n\right) \)

For \(2\le t\le k\), \(r(a_{n}\mid \{{a_{1},a_{t}}\}) =r(b_{n}\mid \{{a_{1},a_{t}}\})=(1,t)\), for \(t=k+1\), \(r(a_{n}\mid \{{a_{1},a_{k+1}}\}) =r(a_{2}\mid \{{a_{1},a_{k+1}}\})=(1,k-1)\) and for \(k+2\le t\le n\), \(r(a_{2}\mid \{{a_{1},a_{t}}\}) =r(b_{1}\mid \{{a_{1},a_{t}}\})=(1,n-t+2)\), a contradiction

\(\left\{ b_{1},b_{t}\right\} \), \(b_{t}\left( 2\le t\le n\right) \)

For \(2\le t\le k-1\), \(r(a_{n}\mid \{{b_{1},b_{t}}\}) =r(b_{n}\mid \{{b_{1},b_{t}}\})=(2,t+1)\), for \(t=k\), \(r(d_{n}\mid \{{b_{1},b_{k}}\}) =r(b_{n}\mid \{{b_{1},b_{k}}\})=(2,k+1)\), for \(t=k+1\), \(r(a_{1}\mid \{{b_{1},b_{k+1}}\}) =r(a_{2}\mid \{{b_{1},b_{k+1}}\})=(1,k)\) and for \(k+2\le t\le n\), \(r(d_{t-1}\mid \{{b_{1},b_{t}}\}) =r(b_{t-1}\mid \{{b_{1},b_{t}}\})=(n-t+3,2)\), a contradiction

\(\left\{ c_{1},c_{t}\right\} \), \(c_{t}\left( 2\le t\le n\right) \)

For \(2\le t\le k+1\), \(r(a_{t}\mid \{{c_{1},c_{t}}\}) =r(e_{t-1}\mid \{{c_{1},c_{t}}\})=(t,2)\) and for \(k+2\le t\le n\), \(r(a_{t}\mid \{{c_{1},c_{t}}\}) =r(e_{t-1}\mid \{{c_{1},c_{t}}\})=(n-t+3,2)\), a contradiction

\(\left\{ d_{1},d_{t}\right\} \), \(d_{t}\left( 2\le t\le n\right) \)

For \(2\le t\le k\), \(r(c_{1}\mid \{{d_{1},d_{t}}\} =r(e_{1}\mid \{{d_{1},d_{t}}\})=(1,t)\), for \(t=k+1\), \(r(c_{t}\mid \{{d_{1},d_{k+1}}\}) =r(c_{t+1}\mid \{{d_{1},d_{k+1}}\})=(k,1)\) and for \(k+2\le t\le n\), \(r(c_{t}\mid \{{d_{1},d_{t}}\}) =r(e_{t}\mid \{{d_{1},d_{t}}\})=(n-t+2,1)\), a contradiction

\(\left\{ e_{1},e_{t}\right\} \), \(e_{t}\left( 2\le t\le n\right) \)

For \(2\le t\le k\), \(r(e_{n}\mid \{{e_{1},e_{t}}\} =r(d_{1}\mid \{{e_{1},e_{t}}\})=(1,t)\), for \(t=k+1\), \(r(c_{k+1}\mid \{{e_{1},e_{k+1}}\}) =r(c_{k+2}\mid \{{e_{1},e_{k+1}}\})=(k+1,2)\) and for \(k+2\le t\le n\), \(r(c_{k+2}\mid \{{e_{1},e_{t}}\}) =r(d_{k+1}\mid \{{e_{1},e_{t}}\})=(k+1,t-k)\), a contradiction

\(\left\{ a_{1},b_{t}\right\} \), \(b_{t}\left( 2\le t\le n\right) \)

For \(1\le t\le k-1\), \(r(a_{n}\mid \{{a_{1},b_{t}}\} =r(b_{n}\mid \{{a_{1},b_{t}}\})=(1,t+1)\), for \(t=k\), \(r(a_{n}\mid \{{a_{1},b_{k}}\}) =r(b_{1}\mid \{{a_{1},b_{k}}\})=(1,k)\), for \(t=k+1\), \(r(a_{2}\mid \{{a_{1},b_{k+1}}\}) =r(b_{n}\mid \{{a_{1},b_{k+1}}\})=(1,k)\) and for \(k+2\le t\le n\), \(r(a_{2}\mid \{{a_{1},b_{t}}\})=r(b_{1}\mid \{{a_{1},b_{t}}\})=(1,n-t+2)\), a contradiction

\(\left\{ a_{1},c_{t}\right\} \), \(c_{t}\left( 2\le t\le n\right) \)

For \(1\le t\le k-1\), \(r(a_{n}\mid \{{a_{1},c_{t}}\} =r(b_{n}\mid \{{a_{1},c_{t}}\})=(1,t+2)\), for \(t=k\), \(r(b_{1}\mid \{{a_{1},c_{k}}\}) =r(a_{n}\mid \{{a_{1},c_{k}}\})=(1,k+1)\), for \(t=k+1\), \(r(a_{2}\mid \{{a_{1},c_{k+1}}\}) =r(b_{n}\mid \{{a_{1},c_{k+1}}\})=(1,k+1)\) and for \(k+2\le t\le n\), \(r(a_{2}\mid \{{a_{1},b_{t}}\}) =r(b_{1}\mid \{{a_{1},b_{t}}\})=(1,n-t+3)\), a contradiction

\(\left\{ a_{1},d_{t}\right\} \), \(d_{t}\left( 2\le t\le n\right) \)

For \(t=1\), \(r(a_{2}\mid \{{a_{1},d_{1}}\} =r(b_{n}\mid \{{a_{1},d_{1}}\})=(1,3)\), for \(2\le t\le k\), \(r(a_{2}\mid \{{a_{1},d_{t}}\} =r(b_{1}\mid \{{a_{1},d_{t}}\})=(1,t+1)\), for \(k+1\le t\le n-2\), \(r(a_{n}\mid \{{a_{1},d_{t}}\}) =r(b_{n}\mid \{{a_{1},d_{t}}\})=(1,n-t+1)\), for \(t=n-1\), \(r(b_{1}\mid \{{a_{1},d_{n-1}}\}) =r(a_{n}\mid \{{a_{1},d_{n-1}}\})=(1,3)\) and for \(t=n\), \(r(b_{1}\mid \{{a_{1},d_{n}}\}) =r(b_{n}\mid \{{a_{1},d_{n}}\})=(2,1)\), a contradiction

\(\left\{ a_{1},e_{t}\right\} \), \(e_{t}\left( 1\le t\le n\right) \)

For \(t=1\), \(r(a_{2}\mid \{{a_{1},e_{1}}\} =r(b_{n}\mid \{{a_{1},e_{1}}\})=(1,4)\), for \(2\le t\le k\), \(r(a_{2}\mid \{{a_{1},e_{t}}\} =r(b_{1}\mid \{{a_{1},e_{t}}\})=(1,t+2)\), for \(k+1\le t\le n-2\), \(r(a_{n}\mid \{{a_{1},e_{t}}\}) =r(b_{n}\mid \{{a_{1},e_{t}}\})=(1,n-t+4)\), for \(t=n-1\), \(r(b_{1}\mid \{{a_{1},e_{n-1}}\}) =r(a_{n}\mid \{{a_{1},e_{n-1}}\})=(1,4)\) and for \(t=n\), \(r(b_{1}\mid \{{a_{1},e_{n}}\}) =r(b_{n}\mid \{{a_{1},e_{n}}\})=(2,2)\), a contradiction

\(\left\{ b_{1},c_{t}\right\} \), \(c_{t}\left( 1\le t\le n\right) \)

For \(1\le t\le k-1\), \(r(a_{n}\mid \{{b_{1},c_{t}}\} =r(b_{n}\mid \{{b_{1},c_{t}}\})=(2,t+1)\), for \(t=k\), \(r(b_{2}\mid \{{b_{1},c_{k}}\}) =r(d_{n}\mid \{{b_{1},c_{k}}\})=(2,k)\) and for \(k+1\le t\le n\), \(r(a_{1}\mid \{{b_{1},c_{t}}\}) =r(c_{1}\mid \{{b_{1},c_{t}}\})=(1,n-t+2)\), a contradiction

\(\left\{ b_{1},d_{t}\right\} \), \(d_{t}\left( 1\le t\le n\right) \)

For \(1\le t\le k-1\), \(r(c_{n}\mid \{{b_{1},d_{t}}\} =r(e_{n}\mid \{{b_{1},d_{t}}\})=(3,t+1)\), for \(t=k\), \(r(e_{1}\mid \{{b_{1},d_{k}}\}) =r(c_{n}\mid \{{b_{1},d_{k}}\})=(3,k)\), for \(t=k+1\), \(r(c_{k+2}\mid \{{b_{1},d_{k+1}}\}) =r(d_{k}\mid \{{b_{1},d_{k+1}}\})=(k+1,1)\) and for \(k+2\le t\le n\), \(r(e_{t}\mid \{{b_{1},d_{t}}\}) =r(c_{t}\mid \{{b_{1},d_{t}}\})=(n-t+3,1)\), a contradiction

\(\left\{ b_{1},e_{t}\right\} \), \(e_{t}\left( 1\le t\le n\right) \)

For \(t=1\), \(r(a_{1}\mid \{{b_{1},e_{1}}\}) =r(a_{2}\mid \{{b_{1},e_{1}}\})=(1,4)\), for \(2\le t\le k\), \(r(d_{n}\mid \{{b_{1},e_{t}}\} =r(b_{2}\mid \{{b_{1},e_{t}}\})=(2,t+1)\), for \(t=k+1\), \(r(a_{n}\mid \{{b_{1},e_{k+1}}\}) =r(d_{1}\mid \{{b_{1},e_{k+1}}\})=(2,k+1)\), for \(k+2\le t\le n-2\), \(r(a_{n}\mid \{{b_{1},e_{t}}\}) =r(b_{n}\mid \{{b_{1},e_{t}}\})=(2,n-t+2)\), for \(t=n-1\), \(r(c_{n}\mid \{{b_{1},e_{n-1}}\}) =r(e_{1}\mid \{{b_{1},e_{n-1}}\})=(3,2)\) and for \(t=n\), \(r(a_{1}\mid \{{b_{1},e_{n}}\}) =r(a_{2}\mid \{{b_{1},e_{n}}\})=(1,4)\), a contradiction

\(\left\{ c_{1},d_{t}\right\} \), \(d_{t}\left( 1\le t\le n\right) \)

For \(t=1\), \(r(a_{1}\mid \{{c_{1},d_{1}}\}) =r(a_{2}\mid \{{c_{1},d_{1}}\}=(2,3)\), for \(2\le t \le k\), \(r(c_{n}\mid \{{c_{1},d_{t}}\}) =r(e_{n}\mid \{{c_{1},d_{t}}\})=(2,t+1)\), for \(t=k\), \(r(c_{n}\mid \{{c_{1},d_{k}}\}) =r(e_{1}\mid \{{c_{1},d_{k}}\})=(2,k)\), for \(t=k+1\), \(r(c_{2}\mid \{{c_{1},d_{k+1}}\}) =r(e_{n}\mid \{{c_{1},d_{k+1}}\})=(2,k)\)

 

For \(k+2\le t\le n-1\), \(r(a_{1}\mid \{{c_{1},d_{t}}\}) =r(e_{1}\mid \{{c_{1},d_{t}}\})=(2,n-t+2)\) and for \(t=n\), \(r(c_{n}\mid \{{c_{1},d_{n}}\}) =r(e_{n}\mid \{{c_{1},d_{n}}\})=(2,1)\), a contradiction

\(\left\{ c_{1},e_{t}\right\} \), \(e_{t}\left( 1\le t\le n\right) \)

For \(t\in \{1,n\}\), \(r(a_{1}\mid \{{c_{1},e_{t}}\}) =r(a_{2}\mid \{{c_{1},e_{t}}\}=(2,4)\), for \(2\le t \le k\), \(r(c_{2}\mid \{{c_{1},e_{t}}\}) =r(e_{n}\mid \{{c_{1},e_{t}}\})=(2,t)\), for \(k+1\le t\le n-2\), \(r(a_{n}\mid \{{c_{1},e_{t}}\}) =r(b_{n}\mid \{{c_{1},e_{t}}\})=(3,n-t+2)\) and for \(t=n-1\),\(r(c_{n}\mid \{{c_{1},e_{n-1}}\}) =r(e_{1}\mid \{{c_{1},e_{n-1}}\})=(2,2)\), a contradiction

\(\left\{ d_{1},e_{t}\right\} \), \(e_{t}\left( 1\le t\le n\right) \)

For \(t=1\), \(r(c_{1}\mid \{{d_{1},e_{1}}\}) =r(c_{2}\mid \{{d_{1},e_{1}}\}=(1,2)\), for \(2\le t\le k-1\), \(r(a_{1}\mid \{{d_{1},e_{t}}\} =r(b_{n}\mid \{{d_{1},e_{t}}\})=(3,t+3)\), for \(t=k\), \(r(d_{2}\mid \{{d_{1},e_{k}}\}) =r(e_{1}\mid \{{d_{1},e_{k}}\})=(1,k-1)\) and for \(k+1\le t\le n\), \(r(e_{1}\mid \{{d_{1},e_{t}}\}) =r(d_{n}\mid \{{d_{1},e_{t}}\})=(1,n-t+1)\), a contradiction

From all the possibilities it is shown that there is no resolving set with two vertices which proves that \(dim(R_{n})\ge 3\). Thus we have \(dim(R_{n})=3\) when n is even.

Case (ii) When n is odd.

In this case, we can write \(\textit{n}=2\textit{k}+1\), \(k\ge 3\),\(k\in Z^{+}\). Let \(W=\{{a_{1},a_{2},a_{k+1}}\}\subset V(R_{n})\), we show that W is a resolving set for \(R_{n}\). For this we give representations of vertices of \(V(S_{n})\mid W\) with respect to W.

Representations of vertices on the inner cycle are:

$$\begin{aligned} r(a_{i}\mid W)= \left\{ \begin{array}{l@{\quad }l} (i-1,i-2,k-i+1), &{}3\le i\le k\\ (n-i+1,n-i+2,i-k-1), &{}k+2\le i\le 2k+1 \end{array} \right. \end{aligned}$$

Representations of the set of interior vertices are:

$$\begin{aligned} r(b_{i}\mid W)= \left\{ \begin{array}{l@{\quad }l} (1,1,k), &{}i=1\\ (i,i-1,k-i+1), &{}2\le i\le k\\ (2k-i+2,i-1,1), &{}i=k+1\\ (2k-i+2,2k-i+3,i-k), &{}k+2\le i\le 2k+1 \end{array} \right. \end{aligned}$$

Representations of the set of exterior vertices are:

$$\begin{aligned} r(c_{i}\mid W)= \left\{ \begin{array}{l@{\quad }l} (2,2,k+1), &{}i=1\\ (i+1,i,k-i+2), &{}2\le i\le k\\ (2k-i+3,i,2), &{}i=k+1\\ (2k-i+3,2k-i+4,i-k+1), &{}k+2\le i\le 2k+1 \end{array} \right. \end{aligned}$$

Representations of vertices on the middle cycle are:

$$\begin{aligned} r(d_{i}\mid W)= \left\{ \begin{array}{l@{\quad }l} (3,3,k+1), &{}i=1\\ (i+2,i+1,k-i+2), &{}2\le i\le k-1\\ (2k-i+2,i+1,3),&{}i=k\\ (2k-i+3,i+1,3), &{}i=k+1\\ (2k-i+3,2k-i+4,i-k+2), &{}k+2\le i\le 2k\\ (3,3,k+2), &{}i=2k+1 \end{array} \right. \end{aligned}$$

Representations of vertices on the outer cycle are:

$$\begin{aligned} r(e_{i}\mid W)= \left\{ \begin{array}{l@{\quad }l} (4,4,k+2), &{}i=1\\ (i+3,i+2,k-i+3), &{}2\le i\le k-1\\ (2k-i+3,i+2,4),&{}i=k\\ (2k-i+4,i+2,4), &{}i=k+1\\ (2k-i+4,2k-i+5,i-k+3), &{}k+2\le i\le 2k\\ (4,4,k+3), &{}i=2k+1 \end{array} \right. \end{aligned}$$

Again we see that there are no two vertices having same representations implying that \(dim(R_{n})\le 3\).

Now we are to prove the opposite inequality \(dim(R_{n})\ge 3\) by contradiction. Therefore we suppose that \(dim(R_{n})=2\) then there the same possibilities as discussed in case (i) and contradiction can be obtained similarly. It follows that \(dim(R_{n})=3\) which completes the proof. \(\square \)

3 The graph of convex polytope \(T_{n}\)

The graph of convex polytope \(T_{n}\); n is even (Fig. 2) consists of n/2 number of 3-sided faces, n/2 number of 4-sided faces, 2n number of 5-sided faces and a pair of n-sided faces and is obtained by the adding the new edges \(\{a_{2i}b_{2i+1}; 1\le i\le n/2-1, a_{n}b_{1}\}\) in the graph of convex polytope \(U_{n}\) in [2]. Here \(\textit{n}=2\textit{k} ; k \ge 3, k \in Z^{+}\), n an even integer because parallelograms and triangles occur alternatively. For odd n two parallelograms occur consecutively and we cannot have a convex polytope of this type.

Fig. 2
figure 2

The graph of convex polytope \(T_{n}\)

Full size image

For our purpose we call the cycle induced by \(\{{a_{i}:1\le i\le n}\}\), the inner cycle, cycle induced by \(\{{b_{i}:1\le i\le n}\}\) the interior cycle, cycle induced by \(\{{c_{i}:1\le i\le n}\}\) \(\cup \) \(\{{d_{i}:1\le i\le n}\}\) the exterior cycle and the cycle induced by \(\{{e_{i}:1\le i\le n}\}\) the outer cycle.

Theorem 3

For \(n\ge 6\), the metric dimension of convex polytope \(T_{n}\) is exactly 3 i,e. \(dim(T_{n})=3\).

Proof

We will prove the result by double inequalities. Let \(W=\{{a_{1},a_{2},a_{k+1}}\}\subset V(R_{n})\), we show that W is a resolving set for \(T_{n}\). For this we give representations of any vertex \(V(T_{n})\mid W\) with respect to W.

Representations of vertices on the inner cycle are:

$$\begin{aligned} r(a_{i}\mid W)= \left\{ \begin{array}{l@{\quad }l} (i-1,i-2,k-i+1), &{}3\le i\le k\\ (2k-i+1,2k-i+2,i-k-1), &{}k+2\le i\le 2k \end{array} \right. \end{aligned}$$

Representations of vertices on the interior cycle are:

$$\begin{aligned} r(b_{i}\mid W)= \left\{ \begin{array}{l@{\quad }l} (1,2,k+1), &{}i=1\\ (2,1,k), &{}i=2\\ (i-1,i-2,k-i+2), &{}3\le i\le k+1\\ (k,k,2-k(mod2)), &{}i=k+2\\ (2k-i+2,2k-i+3,i-k-1), &{}k+3\le i\le 2k\\ \end{array} \right. \end{aligned}$$

Representations of vertices on exterior cycle are:

$$\begin{aligned}&r(c_{i}\mid W)= \left\{ \begin{array}{l@{\quad }l} (2,3,k+2), &{}i=1\\ (3,2,k+1), &{}i=2\\ (i,i-1,k-i+3), &{}3\le i\le k+1\\ (k+1,k+1,3-k(mod2)), &{}i=k+2\\ (2k-i+3,2k-i+4,i-k), &{}k+3\le i\le 2k\\ \end{array} \right. \\&r(d_{i}\mid W)= \left\{ \begin{array}{l@{\quad }l} (3,3,k+2), &{}i=1\\ (4,3,k+1), &{}i=2\\ (i+1,i,k-i+3), &{}3\le i\le k\\ (k+2,k+1,3), &{}i=k+1\\ (k+1,k+2,4-k(mod2)), &{}i=k+2\\ (2k-i+3,2k-i+4,i-k+1), &{}k+3\le i\le 2k \end{array}\right. \end{aligned}$$

Representations of vertices on the outer cycle are:

$$\begin{aligned} r(e_{i}\mid W)= \left\{ \begin{array}{l@{\quad }l} (4,4,k+3), &{}i=1\\ (5,4,k+2), &{}i=2\\ (i+2,i+1,k-i+4), &{}3\le i\le k\\ (k+3,k+2,4), &{}i=k+1\\ (k+2,k+3,5-k(mod2)), &{}i=k+2\\ (2k-i+4,2k-i+5,i-k+2), &{}k+3\le i\le 2k \end{array} \right. \end{aligned}$$

Note that there are no two vertices having same representations. This implies that \(dim(T_{n})\le 3\). Now on the other hand we show that \(dim(T_{n})\ge 3\). On contrary suppose that \(dim(T_{n})=2\). We consider two cases:

Case (i) When k is even then without loss of generality we assume that one resolving vertex is \(a_{1}\), \(b_{1}\), \(c_{1}\), \(d_{1}\) or \(e_{1}\) and the other lies in inner cycle, interior cycle, exterior and outer cycles then there are following possibilities to be discussed:

Resolving vertices

Contradictions

\(\{a_{1},a_{t}\}\), \(a_{t}(2\le t\le n)\)

For \(2\le t\le k\), \(r(a_{n}\mid \{{a_{1},a_{t}}\}) =r(b_{1}\mid \{{a_{1},a_{t}}\})=(1,t)\) for \(t=k+1\), \(r(a_{n}\mid \{{a_{1},a_{k+1}}\}) =r(b_{n}\mid \{{a_{1},a_{k+1}}\})=(1,k-1)\) and for \(k+2\le t\le n\), \(r(b_{2}\mid \{{a_{1},a_{t}}\})\) \(=r(c_{1}\mid \{{a_{1},a_{t}}\})=(2,n-t+2)\), a contradiction

\(\{b_{1},b_{t}\}\), \(b_{t}(2\le t\le n)\)

for \(t=2\), \(r(a_{1}\mid \{{b_{1},b_{2}}\})=r(c_{1}\mid \{{b_{1},b_{2}}\})=(1,2)\), For \(3\le t\le k\), \(r(a_{n}\mid \{{b_{1},b_{t}}\}) =r(c_{1}\mid \{{b_{1},b_{t}}\})=(1,t)\), for \(t=k+1\), \(r(a_{1}\mid \{{b_{1},b_{t}}\})=r(a_{n}\mid \{{b_{1},b_{t}}\})=(1,k-1)\) and for \(k+2\le t\le n\), \(r(a_{1}\mid \{{b_{1},b_{t}}\}) =r(b_{2}\mid \{{b_{1},b_{t}}\})=(1,n-t+2)\)

\(\{c_{1},c_{t}\}\), \(c_{t}(2\le t\le n)\)

For \(t=2\), \(r(a_{n}\mid \{{c_{1},c_{2}}\})=r(e_{n}\mid \{{c_{1},c_{2}}\})=(2,3)\), for \(3\le t\le k+1\), \(r(e_{1}\mid \{{c_{1},c_{t}}\}) =r(a_{1}\mid \{{c_{1},c_{t}}\})=(2,t)\)

 

and for \(k+2\le t\le n\), \(r(a_{n}\mid \{{c_{1},c_{t}}\}) =r(e_{n}\mid \{{c_{1},c_{t}}\})=(2,n-t+2)\), a contradiction

\(\{d_{1},d_{t}\}\), \(d_{t}(2\le t\le n)\)

For \(2\le t\le k\), \(r(b_{1}\mid \{{d_{1},d_{t}}\} =r(e_{n}\mid \{{d_{1},d_{t}}\})=(2,t+1)\), for \(k+2\le t\le n-2\), \(r(b_{1}\mid \{{d_{1},d_{t}}\}) =r(d_{n}\mid \{{d_{1},d_{t}}\})=(2,n-t+2)\), for \(t=n-1\), \(r(c_{1}\mid \{{d_{1},d_{n-1}}\}) =r(e_{1}\mid \{{d_{1},d_{n-1}}\})=(1,3)\) and for \(t=n\), \(r(b_{2}\mid \{{d_{1},d_{n}}\}) =r(e_{2}\mid \{{d_{1},d_{n}}\})=(2,3)\), a contradiction

\(\{e_{1},e_{t}\}\), \(e_{t}(2\le t\le n)\)

For \(2\le t\le k\) \(r(e_{n}\mid \{{e_{1},e_{t}}\} =r(d_{1}\mid \{{e_{1},e_{t}}\})=(1,t)\), for \(t=k+1\), \(r(e_{2}\mid \{{e_{1},e_{k+1}}\}) =r(e_{n}\mid \{{e_{1},e_{k+1}}\})=(1,k-1)\) and for \(k+2\le t\le n\), \(r(e_{2}\mid \{{e_{1},e_{t}}\}) =r(d_{1}\mid \{{e_{1},e_{t}}\})=(1,n-t+2)\), a contradiction

\(\left\{ a_{1},b_{t}\right\} \), \(b_{t}\left( 1\le t\le n\right) \)

For \(1\le t\le k\), \(r(c_{n}\mid \{{a_{1},b_{t}}\} =r(d_{n}\mid \{{a_{1},b_{t}}\})=(3,t+1)\), for \(t=k+1\), \(r(b_{1}\mid \{{a_{1},b_{k+1}}\}) =r(a_{n}\mid \{{a_{1},b_{k+1}}\})=(1,k)\) and for \(k+2\le t\le n\), \(r(a_{n}\mid \{{a_{1},b_{t}}\}) =r(b_{1}\mid \{{a_{1},b_{t}}\})=(1,n-t+1)\), a contradiction

\(\left\{ a_{1},c_{t}\right\} \), \(c_{t}\left( 1\le t\le n\right) \)

For \(t=1\), \(r(d_{1}\mid \{{a_{1},c_{1}}\}) =r(d_{n}\mid \{{a_{1},c_{1}}\})=(3,1)\), for \(t=2\), \(r(b_{3}\mid \{{a_{1},c_{2}}\}) =r(c_{1}\mid \{{a_{1},c_{2}}\})=(2,2)\), for \(t=3\), \(r(e_{2}\mid \{{a_{1},c_{3}}\}) =r(e_{3}\mid \{{a_{1},c_{3}}\})=(5,2)\), for \(4\le t\le k+1\), \(r(a_{t}\mid \{{a_{1},c_{t}}\} =r(c_{t-1}\mid \{{a_{1},c_{t}}\})=(t-1,2)\) and for \(k+2\le t\le n\), \(r(a_{n}\mid \{{a_{1},c_{t}}\}) =r(b_{1}\mid \{{a_{1},c_{t}}\})=(1,n-t+2)\), a contradiction

\(\left\{ a_{1},d_{t}\right\} \), \(d_{t}\left( 1\le t\le n\right) \)

For \(t=1\), \(r(a_{2}\mid \{{a_{1},d_{1}}\} =r(a_{n}\mid \{{a_{1},d_{1}}\})=(1,3)\), for \(t=2\), \(r(a_{2}\mid \{{a_{1},d_{2}}\} =r(b_{1}\mid \{{a_{1},d_{2}}\})=(1,3)\), for \(3\le t\le k-1\), \(r(b_{n}\mid \{{a_{1},d_{t}}\}) =r(c_{1}\mid \{{a_{1},d_{t}}\})=(2,t+2)\), for \(t=k\), \(r(d_{k-1}\mid \{{a_{1},d_{k}}\}) =r(b_{k+1}\mid \{{a_{1},d_{k}}\})=(k,2)\), for \(t=k+1\), \(r(a_{2}\mid \{{a_{1},d_{k+1}}\}) =r(a_{n}\mid \{{a_{1},d_{k+1}}\})=(1,k+1)\), for \(k+2\le t\le n-1\), \(r(a_{n}\mid \{{a_{1},d_{t}}\}) =r(b_{1}\mid \{{a_{1},d_{t}}\})=(1,n-t+2)\) and for \(t=n\), \(r(d_{n-1}\mid \{{a_{1},d_{n}}\}) =r(e_{1}\mid \{{a_{1},d_{n}}\})=(4,2)\), a contradiction

\(\left\{ a_{1},e_{t}\right\} \), \(e_{t}\left( 1\le t\le n\right) \)

For \(t=1\), \(r(c_{2}\mid \{{a_{1},e_{1}}\} =r(d_{n}\mid \{{a_{1},e_{1}}\})=(3,2)\), for \(t=2\), \(r(a_{2}\mid \{{a_{1},e_{2}}\} =r(b_{1}\mid \{{a_{1},e_{2}}\})=(1,4)\), for \(3\le t\le k\), \(r(b_{2}\mid \{{a_{1},e_{t}}\} =r(c_{1}\mid \{{a_{1},e_{t}}\})=(2,t+1)\), for \(t=k+1\), \(r(a_{2}\mid \{{a_{1},e_{k+1}}\}) =r(a_{n}\mid \{{a_{1},e_{k+1}}\})=(1,k+2)\), for \(k+2\le t\le n-1\), \(r(a_{n}\mid \{{a_{1},e_{t}}\}) =r(b_{1}\mid \{{a_{1},e_{t}}\})=(1,n-t+3)\) and for \(t=n\), \(r(c_{n}\mid \{{a_{1},e_{n}}\} =r(d_{1}\mid \{{a_{1},e_{n}}\})=(3,2)\), a contradiction

\(\left\{ b_{1},c_{t}\right\} \), \(c_{t}\left( 1\le t\le n\right) \)

For \(1\le t\le k\), \(r(a_{n}\mid \{{b_{1},c_{t}}\} =r(b_{n}\mid \{{b_{1},c_{t}}\})=(1,t+1)\), for \(k+1\le t\le n-1\), \(r(a_{1}\mid \{{b_{1},c_{t}}\}) =r(c_{1}\mid \{{b_{1},c_{t}}\})=(1,n-t+3)\) and for \(t=n\), \(r(a_{n}\mid \{{b_{1},c_{n}}\}) =r(c_{1}\mid \{{b_{1},c_{n}}\})=(1,2)\), a contradiction

\(\left\{ b_{1},d_{t}\right\} \), \(d_{t}\left( 1\le t\le n\right) \)

For \(1\le t\le k\), \(r(a_{n}\mid \{{b_{1},d_{t}}\} =r(b_{n}\mid \{{b_{1},d_{t}}\})=(1,t+2)\), for \(t=k+1\), \(r(c_{1}\mid \{{b_{1},d_{k+1}}\}) =r(a_{1}\mid \{{b_{1},d_{k+1}}\})=(1,k+2)\), for \(k+2\le t\le n-2\), \(r(a_{1}\mid \{{b_{1},d_{t}}\}) =r(c_{1}\mid \{{b_{1},d_{t}}\})=(1,n-t+3)\) and for \(t=n-1,n\), \(r(c_{1}\mid \{{b_{1},d_{t}}\}) =r(a_{n}\mid \{{b_{1},d_{t}}\})=(1,n-t+2)\), a contradiction

\(\left\{ b_{1},e_{t}\right\} \), \(e_{t}\left( 1\le t\le n\right) \)

For \(t=1,2\), \(r(a_{1}\mid \{{b_{1},e_{t}}\}) =r(a_{n}\mid \{{b_{1},e_{t}}\})=(1,t+3)\), for \(3\le t\le k\), \(r(b_{2}\mid \{{b_{1},e_{t}}\} =r(c_{1}\mid \{{b_{1},e_{t}}\})=(1,t+1)\), for \(t=k+1\), \(r(a_{n}\mid \{{b_{1},e_{k+1}}\}) =r(b_{2}\mid \{{b_{1},e_{k+1}}\})=(1,k+2)\), for \(k+2\le t\le n-1\), \(r(d_{n}\mid \{{b_{1},e_{t}}\}) =r(c_{n}\mid \{{b_{1},e_{t}}\})=(2,n-t+1)\) and for \(t=n\), \(r(d_{1}\mid \{{b_{1},e_{n}}\}) =r(c_{n}\mid \{{b_{1},e_{n}}\})=(2,2)\), a contradiction

\(\left\{ c_{1},d_{t}\right\} \), \(d_{t}\left( 1\le t\le n\right) \)

For \(t=1\), \(r(b_{1}\mid \{{c_{1},d_{1}}\}) =r(d_{n}\mid \{{c_{1},d_{1}}\}=(1,2)\), for \(2\le t \le k+1\), \(r(b_{2}\mid \{{c_{1},d_{t}}\}) =r(e_{1}\mid \{{c_{1},d_{t}}\})=(2,t)\), for \(k+2\le t\le n-1\), \(r(b_{n}\mid \{{c_{1},d_{t}}\}) =r(e_{n}\mid \{{c_{1},d_{t}}\})=(2,n-t+1)\) and for \(t=n\), \(r(b_{n}\mid \{{c_{1},d_{n}}\}) =r(e_{1}\mid \{{c_{1},d_{n}}\})=(2,2)\), a contradiction

\(\left\{ c_{1},e_{t}\right\} \), \(e_{t}\left( 1\le t\le n\right) \)

Due to the symmetry of the graph this case is analogue to the case when one resolving vertex is in the set \(\{{b_{t}:1\le t\le n}\}\) and the other is in the set \(\{{d_{t}:1\le t\le n}\}\)

\(\{d_{1},e_{t}\}\), \(e_{t}(1\le t\le n)\)

Due to the symmetry of the graph this case is analogue to the case when one resolving vertex is in the set \(\{{b_{t}:1\le t\le n}\}\) and the other is in the set \(\{{c_{t}:1\le t\le n}\}\)

Hence from all above contradictions it follows that there is no resolving set with two vertices. This implies that \(dim(T_{n})\ge 3\). Hence \(dim(T_{n})=3\) when k is even.

Case (ii) When k is odd then there are the same possibilities as discussed in case (i) and contradictions can be obtained analogously. Hence \(dim(T_{n})=3\) in this case and this completes the proof. \(\square \)

4 Concluding remarks

In this paper, we have studied the metric dimension of two special classes of convex polytopes and proved that these classes have constant metric dimension that does not depend upon the number of vertices in these graphs and only three vertices choosen sufficiently resolve all the vertices of these classes of convex polytopes.