Thermomechanical Response of Smart Magneto-Electro-Elastic FGM Nanosensor Beams with Intended Porosity

Abstract

This study investigates the behavior of free vibrations in a variety of porous functionally graded nanobeams composed of ferroelectric barium-titanate (BaTiO₃) and magnetostrictive cobalt-ferrite (CoFe₂O₄). There are four different models of porous nanobeams: the uniform porosity model (UPM), the symmetric porosity model (SPM), the porosity concentrated in the bottom region model (BPM), and the porosity concentrated in the top region model (TPM). The nanobeam constitutive equation calculates strains based on various factors, including classical mechanical stress, thermal expansion, magnetostrictive and electroelastic properties, and nonlocal elasticity. The study investigated the effects of various factors on the free vibration of nanobeams, including thermal stress, thermo-magneto-electroelastic coupling, electric and magnetic field potential, nonlocal features, porosity models, and changes in porosity volume. The temperature-dependent mechanical properties of BaTiO₃ and CoFe₂O₄ have been recently explored in the literature for the first time. The dynamics of nanosensor beams are greatly influenced by temperature-dependent characteristics. As the ratios of CoFe₂O₄ and BaTiO₃ in the nanobeam decrease, the dimensionless frequencies decrease and increase, respectively, based on the material grading index. The dimensionless frequencies were influenced by the nonlocal parameter, external electric potential, and temperature, causing them to rise. On the other hand, the slenderness ratio and external magnetic potential caused the frequencies to drop. The porosity volume ratio has different effects on frequencies depending on the porosity model.

1 Introduction

Thermo-magneto-electro-elastic materials have been popularly used in microelectromechanical systems (MEMs) and nanoelectromechanical systems (NEMs) applications in recent years [1,2,3,4,5]. Since the mechanical properties of these materials may be affected by both magnetic and electric potential [6, 7], they have great usage advantages in many applications such as micro and nano scale soft robotic actuator, wearable technology, nano drug transfer [8,9,10,11,12,13,14,15]. In the current investigation, the free vibration response of a nanobeam, which consists of ferroelectric (electroelastic) barium-titanate (BaTiO₃) and magneto strictive (magneto-elastic) cobalt-ferrite (CoFe₂O₄) materials is modeled and analyzed by using first-order shear theory (FSDT) and nonlocal gradient strain theories. Literature studies have shown that as a result of the powder metallurgy method used in the production of nanobeam components, porosity can be found up to 30–40% in the beam [16]. Therefore, in this study, the effect of porosity on the mechanical behavior was considered and the cases where the porosity was distributed along the beam height in 4 different functions were examined separately. Since the beam dimensions are at the nanoscale, non-classical mechanical behavior must be considered. The small scale nonlocal effect and size effect have been the subject of research for nearly 50 years and have been most widely provided by the nonlocal theory of elasticity (NET) [17,18,19,20,21,22]. In this theory, Experimental and theoretical research have demonstrated that the magnitude of the softening effect in the structure is related to the value of the nonlocal parameter e₀a. Later, strain gradient elasticity theory (SGT) was established to account for the impact of material size for micro beams [23, 24]. Modified coupled stress theory (MCST) was proposed (NSGT), that incorporates both Eringen's nonlocal theory and strain gradient elasticity theory, has been proposed [25,26,27,28,29,30].

There are also different studies in the literature examining mechanical effects such as surface effect for nano-sized systems. The size dependent effect of FG nanobeams vibrations has been explored by [31] using Timoshenko beam theory and investigated the effects of length scale parameter, the material grading index and length-thickness ratio on the FG nanobeams vibrations. The importance of linear and nonlinear temperature change on the vibration of FG nanobeams has been studied by [32] based on NET, the nonlocal governing equations have been derived by Hamilton’s principle and solved by applying a semi-analytical differential transform method (DTM). Influence of various parameters such as material composition, slenderness ratio nonlocality, linear, shear and viscous layers of foundation, magnetic potential, electric voltage, damping coefficient, and several boundary conditions for the nanobeam vibration analysis consisting of a nonlocal magneto-electro-viscoelastic functionally graded nanobeam are provided by [33] through Hamilton's principle and NET to obtain equations of motion. The vibration characteristics of porous FG micro/nanobeams considering various types of thermal loadings have been discussed by [34] based on MCST and also the effects of various parameters, like porosity-volume fraction, thermal loadings, slenderness ratio, material grading index or power-law exponent in some literature [35], scale parameter and various boundary conditions on natural frequencies of the modeled beam has been examined. The effects of porosity, magnetic potential, elastic foundation, magnetic potential, scale coefficient, applied voltage, slenderness ratio and material gradation on the vibrational behavior of the magneto-electro elastic functionally graded (MEE-FG) nanoscale beams and plates have been examined by [36,37,38,39] through third-order shear deformation beam model derived from NET. To derive the nonlocal equations, Hamilton's principle has been used and they have been solved analytically in this work. Using NGST, [40] investigated the buckling response of magneto-electro-elastic (MEE) functionally graded sandwich nanoplate on Pasternak foundation and exposed to hygrothermal loads and FSDT considering the impact of the nanoplate's uniform porosity. The size-dependent vibration response of porous MEE functionally graded nanobeams, which is focused on the visco-Pasternak foundation, has been explored by [41] using the Kelvin-Voight viscoelastic model and the Timoshenko beam theory. Besides in this study, the effects of several factors such as the porosity volume fraction, power-law exponent, nonlocal parameter, boundary condition, porosity distribution, viscoelastic foundation parameters and damping coefficient as well as magnetic potential and electric voltage have been shown in detail. The porosity models of FG deep beams have been obtained and the effects of porosity parameters on forced vibration analysis of FG porous deep beams under load have been examined by [35] using the plane solid continua model and solved by applying finite element method (FEM). The free vibrations and static bending of MEE- FGM considering the MCST Timoshenko microbeams have been investigated by [42, 43], and they showed the differences of vibrational behaviors of thin ad thick MEE microbeams. A finite element (FE) model integrated with MEE fields determined by [44] and the numerical examples presented in this paper provide a reference for static and dynamic analysis of FG-MEE plates and shells, as well as verifying the accuracy and robustness of the proposed numerical model.

1.1 The Novelty of the Presented Study

The studies on the static and dynamic behavior of beams made of thermo-magneto-electro-elastic material are limited in the literature. In the present work, a model that accurately reflects reality was created by considering the porosity that can be found in the nanobeam, and the effect of the porosity distribution functions along the beam height. According to the experimental studies in literature, it has been reported that the porosity ratio can exceed 40% in smart structures made of barium-titanate and cobalt-ferrite ceramics [16, 45, 46]. Four various porosity distribution functions (uniform porosity, symmetrical porosity, porosity concentrated in the bottom area, and porosity concentrated in the top region) were explored throughout the thickness by examining porosity volume ratio values between 0 and 0.6. The non-classical strain effect at small dimensions is considered by the nonlocal strain gradient theory. The effects of the porosity volume ratio and the porosity models on the free vibration behavior of the nanobeam, the effect of nonlocal parameters, size parameter, FG material grading index is examined in detail.

The temperature-dependent material properties of nanobeam materials are neglected in the literature. The present study formulated the temperature-dependent modulus of elasticity, and thermal conductivity and expansion coefficient of barium-titanate and cobalt-ferrite based on experimental data and provided these findings to the researchers. The results of this study will contribute to actuator/sensor applications in nanoelectromechanical systems, gripper designs of soft robotics applications, wearable technologies, nano surgical operations, nano drug delivery, sampling and sample transfer in high temperature environments and gas sensing etc.

2 Theoretical Formulation

2.1 Material Properties of Thermo-Magneto-Electro Elastic Functionally Graded Porous Nanobeams

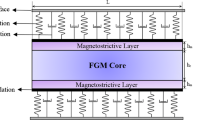
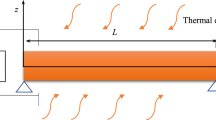
Figure 1 shows a thermo-magneto-electro-elastic functionally graded (TMEE-FG) porous nanobeam with the dimensions of length L, thickness h and width b. The beam is subjected to an externally applied electric potential Φ(x,z,t) and magnetic potential Ψ(x,z,t). The nanobeam is made of BaTiO₃ and CoFe₂O₄ materials with temperature-dependent characteristics (Table 1) and their volume fractions change across the beam thickness in power-law distribution form. The bottom surface at z = -h/2 of the nanobeam and top surface at z =  + h/2 of the nanobeam completely are BaTiO₃ and CoFe₂O₄, respectively.

Fig. 1

TMEE-FG porous nanobeam

Table 1 Temperature-dependent coefficients for the properties of barium-titanate and cobalt-ferrite [56]

The effective material property of functionally graded nanobeam P(z) like density, couple stress stiffness, elastic stiffness, magneto-dielectric constant, piezoelectric and piezomagnetic constants, dielectric and magnetic permeability constants, can be defined as [47],

$$P\left(z\right)={P}_{t}{V}_{t}+{P}_{b}{V}_{b}$$

(1)

here, V_t and V_b are the total volume fractions of CoFe₂O₄ and BaTiO₃, respectively; P_t and P_b are effective material properties of CoFe₂O₄ and BaTiO₃, respectively [48,49,50]. V_t and V_b can be expressed as,

$${V}_{t}\left(z\right)={\left(\frac{z}{h}+0.5\right)}^{m},{V}_{b}=1-{V}_{t}$$

(2)

where m (0 ≤ m < ∞) must be greater than or equal 0 and it is called as the material grading index. It determines the material variations along the direction of the nanobeam thickness as seen in Fig. 2. When m = 0, the nanobeam will be made of material from the top side (100% CoFe₂O₄), and when m → ∞, the whole beam will be made of material from the bottom side (100% BaTiO₃).

Fig. 2

The change of volume fractions of CoFe₂O₄ along the nanobeam thickness

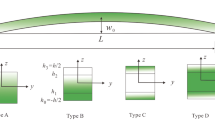
Pore formation is a critical part in producing ceramic-based structures [16, 46, 51]. As a result, Uniform Porosity Model (UPM), Symmetric Porosity Model (SPM), Top Porosity Model (TPM) and Bottom Porosity Model (BPM) were considered as the porosity distribution functions in this study. Figure 3 shows how the studied porosity distribution changes across the nanobeam thickness. Consequently, the following Eq. (3) describes the effective material properties P(z) for the UPM situation [52].

$$P\left(z\right)={P}_{t}{V}_{t}+{P}_{b}{V}_{b}-\frac{\chi }{2}\left[{P}_{t}+{P}_{b}\right]$$

(3)

where $\chi$ (0≤ $\chi$  < 1) represents the total porosity volume ratio in the nanobeam.

Fig. 3

Four different porosity models distributed along the nanobeam thickness

In the SPM, the porosity was thought to gather around the beam's mid-plane and decrease proportionally from the midplane to the top and bottom surfaces. The effective material properties of the SPM are stated in Eq. (4).

$$P(z)=[{P}_{t}-{P}_{b}]{V}_{t}+{P}_{b}\left\{1-\chi cos\left[\pi \frac{z}{h}\right]\right\}$$

(4)

The porosity was theorized to accumulate around the beam's top surface and decrease proportionately from the top toward the bottom surface in the TPM. As a result, the effective material properties of the TPM are given in Eq. (5).

$$P(z)=[{P}_{t}-{P}_{b}]{V}_{t}+{P}_{b}\left\{1-\chi cos\left[\frac{\pi }{2}\left(\frac{z}{h}-\frac{1}{2}\right)\right]\right\}$$

(5)

In the BPM, the porosity was considered to concentrate around the beam's bottom surface and decrease proportionately from the bottom to the top surface. Hereby, the Eq. (6) indicate the effective material properties in the situation of the BPM.

$$P(z)=[{P}_{t}-{P}_{b}]{V}_{t}+{P}_{b}\left\{1-\chi cos\left[\frac{\pi }{2}\left(\frac{z}{h}+\frac{1}{2}\right)\right]\right\}$$

(6)

2.2 Temperature-dependent material properties

The nano sensor beam is composed of ceramic-based materials which are barium-titanate and cobalt-ferrite. The temperature-dependent properties of these materials are described as [47, 53,54,55,56]:

$$P={P}_{0}({P}_{-1}{T}^{-1}+1+{P}_{1}T+{P}_{2}{T}^{2}+{P}_{3}{T}^{3})$$

(7)

where P₀, P_-1, P₁, P₂, and P₃ are specific temperature-dependent coefficients. In the literature there is no study on the temperature dependent material properties on barium-titanate and cobalt-ferrite. In this study the effective thermal conductivity and thermal expansion coefficients of barium-titanate were obtained from the experimental studies [57] and [58]. The thermal conductivity and thermal expansion coefficients of cobalt-ferrite are derived from the experimental study [59].

Assuming the stress-free state at T₀ = 300 K for uniform temperature rise, the temperature of the FGM beam's whole body is risen to the final temperature T with:

$$\Delta T=T-{T}_{0}.$$

(8)

The bottom surface temperature is set at ${T}_{b}$, and it is expected to increase linearly across the thickness, from ${T}_{b}$ to ${T}_{t}$, for the linear temperature change. Therefore, a beam's temperature at z in the thickness [60]:

$$ T\left( z \right) = T_{b} + \left( {T_{t} - T_{b} } \right)\left( {\frac{h + 2z}{{2h}}} \right) $$

(9)

In the event of nonlinear temperature change, following steady-state one-dimensional heat transfer equation with bottom and top surface temperatures as boundary conditions yields the FGM beam's temperature [61, 62]. Thus, for the given boundary conditions and the variable coefficient of thermal conductivity $\kappa \left( z \right)$, the temperature at z:

$$ \begin{gathered} - \frac{d}{dz}\left( {\kappa \left( z \right)\frac{dT}{{dz}}} \right) = 0, T\left( \frac{h}{2} \right) = T_{t} , T\left( { - \frac{h}{2}} \right) = T_{b} , \hfill \\ T\left( z \right) = T_{b} + \left( {T_{t} - T_{b} } \right)\frac{{\mathop \smallint \nolimits_{{ - \frac{h}{2}}}^{z} \frac{1}{\kappa \left( z \right)}dz{ }}}{{\mathop \smallint \nolimits_{{ - \frac{h}{2}}}^{\frac{h}{2}} \frac{1}{\kappa \left( z \right)}dz}} \hfill \\ \end{gathered} $$

(10)

In this study, the nonlinear temperature distribution (Eq. 10) along the thickness is considered.

2.3 Kinematic Relations

The displacement field at nanobeam may be described using shear deformation beam theory:

$$ \begin{gathered} u_{1} \left( {x,z,t} \right) = u\left( {x,t} \right) - z\frac{{\partial w_{b} }}{\partial x} + f\left( z \right)\frac{{\partial w_{s} }}{\partial x}, u_{2} \left( {x,z,t} \right) = 0, \hfill \\ u_{3} \left( {x,z,t} \right) = w_{b} \left( {x,t} \right) + w_{s} \left( {x,t} \right) \hfill \\ \end{gathered} $$

(11)

where ${w}_{s}$, ${w}_{b}$ are the shear and bending components of the transverse displacement of a point on the beam's mid-plane, respectively, and the displacement of the mid-plane along the x-axis is given by u. $f(z)$ is a shape function that estimates shear stress distribution over beam thickness. As a result, no shear correction factor is necessary [33]. The current theory serves the following function:

$$f(z)=z-sin\left(\xi z\right)/\xi $$

(12)

Both the magnetic and electric potential distributions throughout the thickness are usually obtained to approach the quasi-static solution of Maxwell's equation as follow [33, 63]:

$$\Phi \left(x,z,t\right)=-cos\left(\xi \left(z\right)\right)\Phi \left(x,y,t\right)+\frac{2\left(z\right)}{h}V$$

(13)

$$\Psi \left(\text{x},\text{z},\text{t}\right)=-cos\left(\xi \left(z\right)\right)\Psi \left(x,y,t\right)+\frac{2\left(z\right)}{h}\Omega $$

(14)

where $\Omega$ and $V$ denote the external magnetic and electric potential applied to the nanobeam, respectively, and ξ = π/h. Nonzero stresses in the current beam model are represented by:

$${\varepsilon }_{xx}=\frac{\partial u}{\partial x}-\frac{{\partial }^{2}{w}_{b }}{\partial {x}^{2}}-f\left(z\right)\frac{{\partial }^{2}{w}_{s }}{\partial {x}^{2}}, {\gamma }_{xz}=\frac{\partial {w}_{s }}{\partial x}$$

(15)

The relation between electric potential ($\Phi$) and electric field (${E}_{x}$, ${E}_{z}$) can be expressed using Eq. (13) as follows:

$$ \begin{gathered} E_{x} = - \Phi_{x} = - {\text{cos}} \xi \left( z \right)\frac{{\partial {\Phi }}}{\partial x}, \hfill \\ E_{z} = - \Phi_{z} = - \xi {\text{sin }}\xi \left( z \right)\frac{{\partial {\Phi }}}{\partial x} - \frac{2V}{h} \hfill \\ \end{gathered} $$

(16)

Furthermore, Eq. (14) provides for the statement of the connection between magnetic potential ($\Psi$) and magnetic field (H_x, H_z) as:

$$ \begin{gathered} H_{x} = - {\Psi }_{x} = cos \xi \left( z \right)\frac{{\partial {\Psi }}}{\partial x}, \hfill \\ H_{z} = - {\Psi }_{z} = \xi sin \xi \left( z \right){\Psi } - \frac{2\Omega }{h} \hfill \\ \end{gathered} $$

(17)

In response to temperature increase, the force ${N}^{T}$ and moment ${M}^{T}$ can be derived by:

$$ \begin{gathered} N^{T} = b\mathop \smallint \nolimits_{ - h/2}^{h/2} C\left( {z,T} \right)\alpha \left( {z,T} \right)\Delta Tdz, \hfill \\ M^{T} = b\mathop \smallint \nolimits_{ - h/2}^{h/2} C\left( {z,T} \right)z\alpha \left( {z,T} \right)\Delta Tdz \hfill \\ \end{gathered} $$

(18)

The motion equations can be extracted by means of Hamilton's principle as:

$$\int_{0}^{t}\delta \left({\Pi }_{s}-{\Pi }_{k}+{\Pi }_{w}\right)dt=0$$

(19)

in which ${\Pi }_{s}, {\Pi }_{k}$ and ${\Pi }_{w}$ represent strain energy, kinetic energy, and work done by external forces, respectively. The virtual variation of strain energy is obtained as:

$$\delta {\Pi }_{s} = \int_{V}{\sigma }_{{i} j}{\delta }_{{i} j}dV={\int }_{V}{(\sigma }_{x}\delta {\varepsilon }_{xx}+{\sigma }_{xz}\delta {\gamma }_{xz}-{D}_{x}\delta {E}_{x}-{D}_{z}\delta {E}_{z}-{B}_{x}\delta {H}_{x}-{B}_{z}\delta {H}_{z})dV$$

(20)

Equations (15) – (17) are substituted into Eq. (21) to produce:

$$ \begin{aligned} \delta \Pi_{s} &= \mathop \smallint \limits_{0}^{l} \left[ {N_{x} \frac{\partial \delta u}{{\partial x}} - M_{x}^{b} \frac{{\partial^{2} \delta w_{b} }}{{\partial x^{2} }} - M_{x}^{s} \frac{{\partial^{2} \delta w_{s} }}{{\partial x^{2} }} - Q_{xz} \frac{{\partial \delta w_{s} }}{{\partial x^{2} }}} \right]{\text{d}}x \\ &\quad + \mathop \smallint \limits_{0}^{l} \mathop \smallint \limits_{{{\raise0.7ex\hbox{${ - h}$} \!\mathord{\left/ {\vphantom {{ - h} 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}}^{{{\raise0.7ex\hbox{$h$} \!\mathord{\left/ {\vphantom {h 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} \left[ {D_{x} {\text{cos }}\left( {\xi z} \right)\delta \left( {\frac{{\partial {\Phi }}}{\partial x}} \right) + D_{z} {\text{sin}}\xi \left( {\xi z} \right)\delta {\Phi } - B_{x} {\text{cos}} \left( {\xi z} \right)\delta \left( {\frac{{\partial {\Psi }}}{\partial x}} \right) + B_{z} {\text{sin}}\xi \left( {\xi z} \right)\delta {\Psi }} \right]{\text{d}}z{\text{d}}x \\ \end{aligned} $$

(21)

The variables in the final statement are stated as follows:

$$\left({N}_{i},{M}_{i}^{b},{M}_{i}^{s}\right)={\int }_{A}\left(1,z,f\right){\sigma }_{i}dA, i=\left(x,y,xy\right)$$

(22)

$$ {Q}_{i}=\int_\text{A} g{\sigma }_{i }dA, i =\left(xz,yz\right)$$

(23)

The variation of work done by applied forces can be given as:

$$\delta {\Pi }_{w}={\int }_{0}^{l}\left({N}_{x}^{0} \frac{\partial ({w}_{b }+{w}_{s) }}{\partial x} \frac{\partial \delta \left({w}_{b }+{w}_{s}\right)}{\partial x}+q\delta \left({w}_{b }+{w}_{s}\right)\right)dx$$

(24)

In which ${N}_{x}^{0}$ and q denotes applied loads in plane and the external transverse load, respectively.

To define the first variational of the given model's virtual kinetic energy:

$$\begin{aligned} \delta {\Pi }_{k} &= {\int }_{0}^{l}\left[{l}_{0}\left( \frac{\partial u }{\partial t} \frac{\partial \delta u}{\partial t}+\frac{\partial \left({w}_{b }+{w}_{s}\right)}{\partial t} \frac{\partial \delta u\left({w}_{b }+{w}_{s}\right)}{\partial t}\right) \right. \\ & \quad \left. -{I}_{1}\left(\frac{\partial u }{\partial t} \frac{\partial \delta {w}_{b}}{\partial x\partial t}+\frac{\partial {w}_{b}}{\partial x\partial t} \frac{\partial \delta u}{\partial t}\right)\right. \\ & \quad \left. -{J}_{1}\left(\frac{\partial u }{\partial t} \frac{\partial \delta {w}_{s}}{\partial x\partial t}+\frac{\partial {w}_{s} }{\partial x\partial t} \frac{\partial \delta u}{\partial t}\right)+{J}_{2}\left(\frac{\partial {w}_{b} }{\partial x\partial t} \frac{\partial \delta {w}_{b}}{\partial x\partial t}\right)\right. \\ & \quad \left. +{K}_{2}\left(\frac{\partial {w}_{s} }{\partial x\partial t} \frac{\partial \delta {w}_{s}}{\partial x\partial t}\right)\right. \\ & \quad \left. +{J}_{2}\left(\frac{\partial {w}_{b} }{\partial x\partial t} \frac{\partial \delta {w}_{s}}{\partial x\partial t}+\frac{\partial {w}_{s} }{\partial x\partial t} \frac{\partial \delta {w}_{b}}{\partial x\partial t}\right)\right]dAdx \end{aligned}$$

(25)

where I₀, I₁, J₁, I₂, J₂ and K₂ are known as mass inertia and are identified as:

$$\left({I}_{0},{I}_{1}, {J}_{1},{I}_{2},{J}_{2},{K}_{2}\right)={\int }_{-h/2}^{h/2}\left(1,z,f, {z}^{2},zf,{f}^{2}\right)\rho (z)dz$$

(26)

When the coefficients of $\delta u$, $\delta {w}_{b}$, $\delta {w}_{s}$, $\delta\Phi$ and $\delta\Psi$ are all equal to zero, and Eqs. (21), (24), and (25) are inserted into Eq. (19), the following equations are derived:

$$\frac{\partial {N}_{x}}{\partial x}={I}_{0}\frac{{\partial }^{2}u}{\partial {t}^{2}}-{I}_{1}\frac{{\partial }^{3}{w}_{b}}{\partial x\partial {t}^{2}}-{J}_{1}\frac{{\partial }^{3}{w}_{s}}{\partial x\partial {t}^{2}}$$

(27)

$$\frac{{\partial }^{2}{M}_{x}^{b}}{\partial {x}^{2}}-\left({N}^{E}+{N}^{H}\right){\nabla }^{2}\left({w}_{b}+{w}_{s}\right)={I}_{0}\frac{{\partial }^{2}\left({w}_{b}+{w}_{s}\right)}{\partial {t}^{2}}+{I}_{1}\left(\frac{{\partial }^{3}u}{\partial x\partial {t}^{2}}\right)-{I}_{2}{\nabla }^{2}\left(\frac{{\partial }^{2}{w}_{b}}{\partial {t}^{2}}\right)-{J}_{2}{\nabla }^{2}\left(\frac{{\partial }^{2}{w}_{s}}{\partial {t}^{2}}\right)+q$$

(28)

$$\frac{{\partial }^{2}{M}_{x}^{s}}{\partial {x}^{2}}+\frac{\partial {Q}_{xz}}{\partial x}-\left({N}^{E}+ {N}^{H}+{N}^{T}\right){\nabla }^{2}\left({w}_{b}+{w}_{s}\right)={J}_{0}\frac{{\partial }^{2}\left({w}_{b}+{w}_{s}\right)}{\partial {t}^{2}}+{J}_{1}\left(\frac{{\partial }^{3}u}{\partial x\partial {t}^{2}}\right)-{J}_{2}{\nabla }^{2}\left(\frac{{\partial }^{2}{w}_{b}}{\partial {t}^{2}}\right)-{K}_{2}{\nabla }^{2}\left(\frac{{\partial }^{2}{w}_{s}}{\partial {t}^{2}}\right)+q$$

(29)

$${\int }_{-h/2}^{h/2}\left(\text{cos}\left(\xi z\right)\frac{\partial {D}_{x}}{\partial x}+\xi \text{sin} \left(\xi z\right){D}_{z}\right)dz=0$$

(30)

$${\int }_{-h/2}^{h/2}\left(\text{cos }\left(\xi z\right)\frac{\partial {B}_{x}}{\partial x}+\xi \text{sin }\left(\xi z\right){B}_{z}\right)dz=0$$

(31)

According to Eringen’s nonlocal theory, stress at a place is a function of all elastic body stresses. [18, 22]. Based on the magnitude of nonlocal impacts, this hypothesis makes the structure behave differently from classical structures. Conversely, strain gradient theory examines the material size influence improving structural stiffness. Finally, nonlocal strain gradient elasticity has been developed, integrating these two theories in a single model [26, 64,65,66]. As a result, the following statement establishes the basic relationships for a nonlocal magneto-electro-elastic structural element with zero body force:

$$ \sigma_{i,j} = \mathop \smallint \limits_{v} \alpha \left( {\left| {\acute{x} - x} \right|,\tau } \right)\left[ {C_{ijkl} \varepsilon_{k} \left( {\acute{x} } \right) - e_{mij} E_{m} \left( {\acute{x} } \right) - q_{mij} H_{n} \left( {\acute{x} } \right)} \right]{\text{d}}v\left( {\acute{x} } \right) $$

(32)

$$ D_{i} = \mathop \smallint \limits_{v} \alpha \left( {\left| {\acute{x} - x} \right|,\tau } \right)\left[ {e_{ikl} \varepsilon_{kl} + s_{im} E_{m} \left( {\acute{x} } \right) - d_{in} H_{n} \left( {\acute{x} } \right)} \right]dv\left( {\acute{x} } \right) $$

(33)

$$ B_{i} = \mathop \smallint \limits_{v} \alpha \left( {\left| {\acute{x} - x} \right|,\tau } \right)\left[ {q_{ikl} \varepsilon_{kl} \left( {\acute{x} } \right) + d_{im} E_{m} \left( {\acute{x} } \right) + \chi_{in} H_{n} \left( {\acute{x} } \right)} \right]dv\left( {\acute{x} } \right) $$

(34)

The terms stress, strain, magnetic field, magnetic induction components, electric displacement, and electric field components are denoted by the letters ${\sigma }_{i,j}$, ${\varepsilon }_{i,j}$, ${B}_{i}$, ${H}_{i}$, ${D}_{i}$ and ${E}_{i}$ respectively. Piezoelectric, elastic, dielectric, piezomagnetic, magnetic, and magnetoelectric constants are denoted by the letters ${e}_{mij}$, ${C}_{ijkl}$, ${q}_{mij}$, ${s}_{im}$, ${d}_{im}$, and ${\chi }_{in}$. The nonlocal kernel function and the Euclidean distance are α(|$\left| {\acute{x} - x} \right|,\tau$) and $\left| {\acute{x} - x} \right|$, respectively. Finally, an alternative differential form for a MEE solid's constitutive relations including the strain gradient elasticity can be defined as [33]:

$${\sigma }_{i,j }-{\left({e}_{0}a\right)}^{2}{\nabla }^{2}{\sigma }_{i,j }=\left[{C}_{ijkl}{\varepsilon }_{k}-{e}_{mij}{E}_{m}-{q}_{mij}{H}_{n}\right]$$

(35)

$${D}_{i }-{\left({e}_{0}a\right)}^{2}{\nabla }^{2}{d}_{i }=\left[{e}_{ikl}{\varepsilon }_{ikl}+{s}_{im}{E}_{m}+{d}_{in}{H}_{n}\right]$$

(36)

$${B}_{i }-{\left({e}_{0}a\right)}^{2}{\nabla }^{2}{B}_{i }=\left[{q}_{ikl}{\varepsilon }_{k}+{d}_{im}{E}_{m}+{\chi }_{in}{H}_{n}\right]$$

(37)

where ${e}_{0}a$ and $\nabla^{2}$ denotes a nonlocal variable and Laplacian operator that introduce the small size effects, respectively [67,68,69]. The following are the stress–strain relationships,

$$\left(1-{\left({e}_{0}a\right)}^{2}{\nabla }^{2}\right){\sigma }_{xx}=\left[{C}_{11}{\varepsilon }_{xx}-{e}_{31}{E}_{z}-{q}_{31}{H}_{z}\right]$$

(38)

$$\left(1-{\left({e}_{0}a\right)}^{2}{\nabla }^{2}\right){\sigma }_{xz}=\left[{C}_{55}{\gamma }_{xz}-{e}_{15}{E}_{x}-{q}_{15}{H}_{x}\right]$$

(39)

$$\left(1-{\left({e}_{0}a\right)}^{2}{\nabla }^{2}\right){D}_{x}=\left[{e}_{15}{\gamma }_{xz}+{s}_{11}{E}_{x}+{d}_{11}{H}_{x}\right]$$

(40)

$$\left(1-{\left({e}_{0}a\right)}^{2}{\nabla }^{2}\right){D}_{z}=\left[{e}_{31}{\varepsilon }_{xx}+{s}_{33}{E}_{z}+{d}_{33}{H}_{z}\right]$$

(41)

$$\left(1-{\left({e}_{0}a\right)}^{2}{\nabla }^{2}\right){B}_{x}=\left[{q}_{15}{\gamma }_{xz}+{d}_{11}{E}_{x}+{x}_{11}{H}_{x}\right]$$

(42)

$$\left(1-{\left({e}_{0}a\right)}^{2}{\nabla }^{2}\right){B}_{z}=\left[{q}_{31}{\varepsilon }_{xx}+{d}_{33}{E}_{z}+{x}_{33}{H}_{x}\right]$$

(43)

Including Eqs. (38)–(43), the Eqs. (27)–(31) can be obtained as:

$$\left(1-{\left({e}_{0}a\right)}^{2}\frac{{\partial }^{2}}{\partial {x}^{2}}\right){N}_{x}=\left[{A}_{11}\frac{\partial u}{\partial x}-{B}_{11}\frac{{\partial }^{2}{w}_{b}}{\partial {x}^{2}}-{B}_{11}^{s}\frac{{\partial }^{2}{w}_{s}}{\partial {x}^{2}}+{A}_{31}^{e}\Phi +{A}_{31}^{m}\Psi -{N}_{x}^{E}-{N}_{x}^{H}\right]$$

(44)

$$\left(1-{\left({e}_{0}a\right)}^{2}\frac{{\partial }^{2}}{\partial {x}^{2}}\right){M}_{x}^{b}=\left[{B}_{11}\frac{\partial u}{\partial x}-{D}_{11}\frac{{\partial }^{2}{w}_{b}}{\partial {x}^{2}}-{D}_{11}^{s}\frac{{\partial }^{2}{w}_{s}}{\partial {x}^{2}}+{E}_{31}^{e}\Phi +{E}_{31}^{m}\Psi -{M}_{bx}^{E}-{M}_{bx}^{H}\right]$$

(45)

$$\left(1-{\left({e}_{0}a\right)}^{2}\frac{{\partial }^{2}}{\partial {x}^{2}}\right){M}_{x}^{s}=\left[{B}_{11}^{s}\frac{\partial u}{\partial x}-{D}_{11}^{s}\frac{{\partial }^{2}{w}_{b}}{\partial {x}^{2}}-{H}_{11}^{s}\frac{{\partial }^{2}{w}_{s}}{\partial {x}^{2}}+{F}_{31}^{e}\Phi +{F}_{31}^{m}\Psi -{M}_{sx}^{E}-{M}_{sx}^{H}\right]$$

(46)

$$\left(1-{\left({e}_{0}a\right)}^{2}\frac{{\partial }^{2}}{\partial {x}^{2}}\right){Q}_{xz}=\left[{A}_{55}^{s}\frac{\partial {w}_{s}}{\partial x}-{A}_{15}^{e}\frac{\partial\Phi }{\partial x}-{A}_{15}^{m}\frac{\partial\Psi }{\partial x}\right]$$

(47)

$${\int }_{-h/2}^{h/2}\left(1-{\left({e}_{0}a\right)}^{2}\frac{{\partial }^{2}}{\partial {x}^{2}}\right){D}_{x}\text{cos }\left(\xi z\right)dz=\left[{E}_{15}^{e}\frac{\partial {w}_{s}}{\partial x}+{F}_{11}^{e}\frac{\partial\Phi }{\partial x}+{F}_{11}^{m}\frac{\partial\Psi }{\partial x}\right]$$

(48)

$${\int }_{-h/2}^{h/2}\left(1-{\left({e}_{0}a\right)}^{2}\frac{{\partial }^{2}}{\partial {x}^{2}}\right){D}_{z}\xi \text{sin }\left(\xi z\right)dz=\left[{A}_{31}^{e}\left(\frac{\partial u}{\partial x}\right)-{E}_{31}^{e}{\nabla }^{2}{w}_{b}-{F}_{31}^{e}{\nabla }^{2}{w}_{s}-{{F}_{33}^{e}\Phi -F}_{33}^{m}\Psi \right]$$

(49)

$${\int }_{-h/2}^{h/2}\left(1-{\left({e}_{0}a\right)}^{2}\frac{{\partial }^{2}}{\partial {x}^{2}}\right){B}_{x}\text{cos}\xi \left(\xi z\right)dz=\left[{E}_{15}^{m}\frac{\partial {w}_{s}}{\partial x}+{F}_{11}^{m}\frac{\partial\Psi }{\partial x}+{X}_{11}^{m}\frac{\partial\Psi }{\partial x}\right]$$

(50)

$${\int }_{-h/2}^{h/2}\left(1-{\left({e}_{0}a\right)}^{2}\frac{{\partial }^{2}}{\partial {x}^{2}}\right){B}_{z}\text{sin}\xi \left(\xi z\right)dz=\left[{A}_{15}^{m}\left(\frac{\partial u}{\partial x}\right)-{E}_{31}^{m}{\nabla }^{2}{w}_{b}-{F}_{33}^{m}\Psi -{x}_{33}^{m}\Psi \right]$$

(51)

where the cross-sectional rigidities are defined as follows:

$$\left\{{A}_{11},{B}_{11},{B}_{11}^{s},{D}_{11,},{H}_{11}^{s}\right\}={\int }_{-h/2}^{h/2}\left\{{c}_{11}\right\}\left(1,z,f,{z}^{2},zf,{f}^{2}\right)\text{d}z$$

(52)

$$\left\{{A}_{31}^{e},{E}_{31}^{e},{F}_{31}^{e}\right\}={\int }_{-h/2}^{h/2}{e}_{31}\xi \text{sin }\left(\xi z\right)\left(1,z,f\right)\text{d}z$$

(53)

$$\left\{{A}_{31}^{m},{E}_{31}^{m},{F}_{31}^{m}\right\}={\int }_{-h/2}^{h/2}{q}_{31}\xi \text{sin }\left(\xi z\right)\left(1,z,f\right)\text{d}z$$

(54)

$$\left\{{A}_{15}^{e} ,{E}_{15}^{e}\right\}={\int }_{-h/2}^{h/2}{e}_{15}\text{cos }\left(\xi z\right)\left(1,g\right)\text{d}z$$

(55)

$$\left\{{A}_{15}^{m} ,{E}_{15}^{m}\right\}={\int }_{-h/2}^{h/2}{q}_{15}\text{cos }\left(\xi z\right)\left(1,g\right)\text{d}z$$

(56)

$$\left\{{F}_{15}^{e} ,{F}_{33}^{e}\right\}={\int }_{-h/2}^{h/2}\left\{{s}_{11}{\text{cos}}^{2}\left(\xi z\right), {s}_{33}{\xi }^{2} {\text{sin}}^{2}\left(\xi z\right) \right\}\text{d}z$$

(57)

$$\left\{{F}_{11}^{m} ,{F}_{33}^{m}\right\}={\int }_{-h/2}^{h/2}\left\{{d}_{11}{\text{cos}}^{2}\left(\xi z\right), {d}_{33}{\xi }^{2} {\text{sin}}^{2}\left(\xi z\right) \right\}\text{d}z$$

(58)

$$\left\{{x}_{11}^{m} ,{x}_{33}^{m}\right\}={\int }_{-h/2}^{h/2}\left\{{x}_{11}{\text{cos}}^{2}\left(\xi z\right), {x}_{33}{\xi }^{2} {\text{sin}}^{2}\left(\xi z\right) \right\}\text{d}z$$

(59)

$${A}_{55}^{s}={\int }_{-h/2}^{h/2}{c}_{55}{g}^{2}dz$$

(60)

The normal forces and moments originating from the magnetoelectric field are defined in Eqs. (61)–(63).

$${N}_{x}^{E}=-{\int }_{-h/2}^{h/2}{e}_{31}\frac{2V}{h}\text{d}z, { N}_{x}^{H}=-{\int }_{-h/2}^{h/2}{q}_{31}\frac{2\Omega }{h}\text{d}z$$

(61)

$${M}_{bx}^{E}=-{\int }_{-h/2}^{h/2}{e}_{31}\frac{2V}{h}\text{d}z, {M}_{bx}^{H}=-{\int }_{-h/2}^{h/2}{q}_{31}\frac{2\Omega }{h}\text{d}z$$

(62)

$${M}_{sx}^{E}=-{\int }_{-h/2}^{h/2}{e}_{31}\frac{2V}{h}f\left(z\right)\text{d}z, {M}_{sx}^{H}=-{\int }_{-h/2}^{h/2}{q}_{31}\frac{2\Omega }{h}f\left(z\right)\text{d}z$$

(63)

To obtain the revised nanobeam's governing equations in terms of displacement, Eqs. (44) – (51) may be substituted into Eqs. (27) – (31):

$$\left[{A}_{11}\frac{{\partial }^{2}u}{\partial {x}^{2}}-{B}_{11}\frac{{\partial }^{3}{w}_{b}}{\partial {x}^{3}}-{B}_{11}^{s}\frac{{\partial }^{3}{w}_{s}}{\partial {x}^{3}}+{A}_{31}^{e}\frac{\partial\Phi }{\partial x}+{A}_{31}^{m}\frac{\partial\Psi }{\partial x}\right]+\left(1+{\left({e}_{0}a\right)}^{2}\frac{{\partial }^{2}}{\partial {x}^{2}}\right)\left(-{I}_{0}\frac{{\partial }^{2}u}{\partial {x}^{2}}+{I}_{1}\frac{{\partial }^{3}{w}_{b}}{\partial x\partial {t}^{2}}+{J}_{1}\frac{{\partial }^{3}{w}_{s}}{\partial x\partial {t}^{2}}+\right)=0$$

(64)

$$\begin{aligned}& \left[{B}_{11}\frac{{\partial }^{3}u}{\partial {x}^{3}}-{D}_{11}\frac{{\partial }^{4}{w}_{b}}{\partial {x}^{4}}-{D}_{11}^{s}\frac{{\partial }^{4}{w}_{s}}{\partial {x}^{4}}\right. \\ & \quad \left. +{E}_{31}^{e}\left(\frac{{\partial }^{2}\Phi }{\partial {x}^{2}}\right)-{A}_{15}^{e}\left(\frac{{\partial }^{2}\Phi }{\partial {x}^{2}}\right)\right. \\ & \quad \left.+{E}_{31}^{m}\left(\frac{{\partial }^{2}\Psi }{\partial {x}^{2}}\right)-{A}_{15}^{m}\left(\frac{{\partial }^{2}\Psi }{\partial {x}^{2}}\right)\right] \\ & \quad +\left(1+{\left({e}_{0}a\right)}^{2}\frac{{\partial }^{2}}{\partial {x}^{2}}\right)\left[-{I}_{1}\frac{{\partial }^{3}u}{\partial x\partial {t}^{2}}\right. \\ & \quad \left.-{I}_{0}\frac{{\partial }^{2}\left({w}_{b}+{w}_{s}\right)}{\partial {t}^{2}}+{I}_{2}\frac{{\partial }^{4}{w}_{b}}{\partial {x}^{2}\partial {t}^{2}}+{J}_{2}\frac{{\partial }^{4}{w}_{s}}{\partial {x}^{2}\partial {t}^{2}}\right. \\ & \quad \left.-\left({N}^{E}+ {N}^{H}+{N}^{T}\right)\left(\frac{{\partial }^{2}\left({w}_{b}+{w}_{s}\right)}{\partial {x}^{2}}\right)\right]=0 \end{aligned}$$

(65)

$$\begin{aligned} & \left[{B}_{11}^{s}\frac{{\partial }^{3}u}{\partial {x}^{3}}-{D}_{11}^{s}\frac{{\partial }^{4}{w}_{b}}{\partial {x}^{4}}-{H}_{11}^{s}\frac{{\partial }^{4}{w}_{s}}{\partial {x}^{4}}+{A}_{55}^{s}\frac{{\partial }^{2}{w}_{s}}{\partial {x}^{2}}\right. \\ & \left. \quad -{A}_{15}^{e}\left(\frac{{\partial }^{2}\Phi }{\partial {x}^{2}}\right)+{F}_{31}^{e}\left(\frac{{\partial }^{2}\Phi }{\partial {x}^{2}}\right)+{F}_{31}^{m}\left(\frac{{\partial }^{2}\Psi }{\partial {x}^{2}}\right)-{A}_{15}^{m}\left(\frac{{\partial }^{2}\Psi }{\partial {x}^{2}}\right)\right] \\ & \quad +\left(1+{\left({e}_{0}a\right)}^{2}\frac{{\partial }^{2}}{\partial {x}^{2}}\right)\left[-{I}_{0}\frac{{\partial }^{2}\left({w}_{b}+{w}_{s}\right)}{\partial {t}^{2}}-{J}_{1}\frac{{\partial }^{3}u}{\partial x\partial {t}^{2}}\right. \\ & \left. \quad +{J}_{2}\left(\frac{{\partial }^{4}{w}_{b}}{\partial {x}^{2}\partial {t}^{2}}\right){+K}_{2}\left(\frac{{\partial }^{4}{w}_{b}}{\partial {x}^{2}\partial {t}^{2}}\right)\right. \\ & \left. \quad -\left({N}^{E}+ {N}^{H}+{N}^{T}\right)\left(\frac{{\partial }^{2}\left({w}_{b}+{w}_{s}\right)}{\partial {x}^{2}}\right)\right]=0 \end{aligned}$$

(66)

$$\left[{A}_{31}^{e}\left(\frac{\partial u}{\partial x}\right)-{E}_{31}^{e}\left(\frac{{\partial }^{2}{w}_{b}}{\partial {x}^{2}}\right)-\left({F}_{31}^{e}-{E}_{15}^{e}\right)\left(\frac{{\partial }^{2}{w}_{s}}{\partial {x}^{2}}\right)+{F}_{11}^{e}\left(\frac{{\partial }^{2}\Phi }{\partial {x}^{2}}\right){+ F}_{11}^{m}\left(\frac{{\partial }^{2}\Psi }{\partial {x}^{2}}\right)- {F}_{33}^{e}\Phi - {F}_{33}^{m}\Psi \right]=0$$

(67)

$$\left[{A}_{31}^{m}\left(\frac{\partial u}{\partial x}\right)-{E}_{31}^{m}\left(\frac{{\partial }^{2}{w}_{b}}{\partial {x}^{2}}\right)-\left({F}_{31}^{m}-{E}_{15}^{m}\right)\left(\frac{{\partial }^{2}{w}_{s}}{\partial {x}^{2}}\right)+{F}_{11}^{m}\left(\frac{{\partial }^{2}\Phi }{\partial {x}^{2}}\right){+ X}_{11}^{m}\left(\frac{{\partial }^{2}\Psi }{\partial {x}^{2}}\right)- {F}_{33}^{m}\Phi - {X}_{33}^{m}\Psi \right]=0$$

(68)

$${N}_{x}^{0}= {N}^{E}+ {N}^{H}$$

(69)

For simply supported (S):

$${w}_{b}= {w}_{s}= {N}_{x}= {M}_{x}=0 at=0,L$$

(70)

For clamped (C):

$${u=w}_{b}= {w}_{s}=0 at x=0,L$$

(71)

Table 2 shows the additional boundary conditions and the associated displacement functions.

Table 2 The admissible shape function X_m and boundary conditions of the study

To correspond with mentioned above boundary requirements, the displacement amounts are stated as:

$$u=\sum_{n=1}^{\infty }{U}_{n}\frac{\partial {X}_{n}(x)}{{\partial }_{x}}{e}^{i{\omega }_{n}t}$$

(72)

$${w}_{b}=\sum_{n=1}^{\infty }{W}_{bn}{X}_{n}(x){e}^{i{\omega }_{n}t}$$

(73)

$${w}_{s}=\sum_{n=1}^{\infty }{W}_{sn}{X}_{n}(x){e}^{i{\omega }_{n}t}$$

(74)

$$ {\Phi } = \mathop \sum \limits_{n = 1}^{\infty } \phi_{n} X_{n} \left( x \right)e^{{i\omega_{n} t}} $$

(75)

$$\Psi =\sum_{n=1}^{\infty }{\text{Y}}_{n}{X}_{n}(x){e}^{i{\omega }_{n}t}$$

(76)

The assumed displacement Eqs. (72)–(76) are utilized for the trigonometric solution of Eqs. (64)–(68) for the required boundary conditions stated in Table 2. Finally, the eigenvalue equations in Appendix (82)–(86) for the displacement quantities are derived, and the following matrix equation helps shorten the equations:

$$ \left\{ {\left[ K \right] - { }\left[ M \right]{ }\omega^{2} } \right\}{ }\left\{ {\begin{array}{*{20}c} {U_{n} } \\ {W_{bn} } \\ {W_{sn} } \\ {\phi_{n} } \\ {{\text{Y}}_{n} } \\ \end{array} } \right\} = 0 $$

(77)

3 Temperature-Dependent Effective Material Properties

Some numerical examples of the temperature dependent effective material properties of barium-titanate and cobalt-ferrite porous FG nanobeams are investigated under this chapter. In all analyzes, porosity volume fraction χ values ranging from 0 to 0.6 and temperature rise values ΔT ranging from 0 to 600 K were used, respectively. Table 3 lists the mechanical and thermodynamic properties of the material. The numerical studies considered a simply supported beam with the length L = 10 nm, the cross-section area A = h x b, the thickness h = 1 nm (L/h = 10) and the width b = h. The effective elasticity module (E_eff), effective thermal expansion coefficient (α_eff), and effective thermal conductivity coefficients (κ_eff) are the main parameters examined in this chapter, which are dependent on temperature by using Eq. (7).

Table 3 Piezoelectric, electro, magnetic, and thermal characteristics of BaTiO₃ and CoFe₂O₄ [46, 70,71,72,73,74,75,76,77,78]

The temperature-dependent variation of the effective (Eq. 78) elastic modulus, coefficient of thermal conductivity and coefficient of thermal expansion of non-porous nanobeam of selected sizes for material grading index values of m = 0, 0.6, 1 and 100 are given in Fig. 4. Here, the value where m = 0 indicates that the nanobeam is composed entirely of cobalt-ferrite and when m = 100, 90.91% of the nanobeam is composed of barium-titanate. These values were chosen to see the temperature-dependent behavior of approximately pure cobalt-ferrite and 90.91% barium-titanate. In Fig. 4a, when we look at the variation in the modulus of elasticity, in general, the trends of the change graph are similar because cobalt-ferrite and barium-titanate are ceramic based. However, since the c_ij the elastic terms of barium-titanate are less when compared to those of cobalt-ferrite as seen in Table 3, the variation of the composition consisting of barium-titanate is formed at the bottom. Similarly, Fig. 4b shows the temperature-dependent change in the nanobeam effective thermal expansion coefficient. Accordingly, the thermal expansion coefficient of barium-titanate is more affected by temperature than cobalt-ferrite. In Fig. 4c, the nanobeam effective thermal conductivity coefficient is given and the figure presents that the thermal conductivity generally decreases nonlinearly with temperature. Although temperature-dependent variation of the effective characteristics of non-porous nanobeam are considered for in Fig. 4, porosity was also found to contribute to temperature-dependent variation of the effective characteristics in a similar trend for all porosity models. The material properties P(z) in Eq. (78) are calculated according to the temperature-dependent material characteristics equation given in Eq. (7), Table 1 lists cobalt-ferrite and barium-titanate characteristics, and the porosity distribution functions shown in Eq. (3)–(6).

Fig. 4

Variation of the effective material characteristics of the non-porous (χ = 0) FG nanobeam for different material grading indices (m = 0, 0.6, 1 and 100), considering the nonlinear changes in temperature within 0 K and 600 K

$${P}_{\text{eff}}=\frac{1}{h}{\int }_{-h/2}^{h/2}P\left(z\right)\text{d}z$$

(78)

Figure 5 shows the comparative effect of all porosity models on material properties for m = 1 and χ = 0.3. As shown in Fig. 5a, the effective modulus of elasticity is uniform (blue), top (purple), symmetric (red) and bottom (yellow) porosity models in order from lowest to highest. In Fig. 5b, when the thermal expansion coefficients are ordered from lowest to highest, they appear as uniform (blue), bottom (yellow), symmetric (red) and top (purple) porosity models. Finally, when the thermal conductivity coefficients are arranged from lowest to highest in Fig. 5c, uniform (blue), top (purple), symmetric (red), and bottom (yellow) porosity patterns are formed, as shown in Fig. 5a.

Fig. 5

Comparison of effective material characteristics of porosity models UPM, SPM, BPM and TPM; considering the nonlinear changes in temperature within 0 K and 600 K, porosity volume fraction (χ = 0.3) and material grading index (m = 1)

The change of UPM’s effective material properties for 4 different porosity volume ratios χ = 0, 0.2, 0.4 and 0.6 based on variation in the nonlinear temperature within 0 K and 600 K. and the material grading index (m = 1) is given in Fig. 6. When the porosity volume ratios χ = 0 and 0.6 are taken for the nanobeam in Fig. 6a, the effective modulus of elasticity (E_eff) at ΔT = 0 K is 2.1886e + 11 Pa and 8.7544e + 10 Pa, respectively, while at ΔT = 600 K it is 1.8392e + 11 Pa and 7.3570e + 10 Pa, respectively. When the porosity volume ratios χ = 0 and 0.6 are used for the nanobeam in Fig. 6b, the effective thermal expansion coefficient (α_eff) at ΔT = 0 K is 1.0876e-05 K⁻¹ and 4.3505e-06 K⁻¹, respectively, while at ΔT = 600 K it is 2.8359e-05 K⁻¹ and 1.1344e-05 K⁻¹. Finally, taking the porosity volume ratios χ = 0 and 0.6 for the nanobeam in Fig. 6c, the effective thermal conductivity coefficient (κ_eff) at ΔT = 0 K values 3.4495 Wm⁻¹ K⁻¹ and 1.3798 Wm⁻¹ K⁻¹, respectively. while it took the values of 2.8517430 Wm⁻¹ K⁻¹ and 1.1407 Wm⁻¹ K⁻¹ at ΔT = 600 K, respectively. All material properties of the nanobeam in Fig. 6 appear to decrease with increasing porosity volume fraction. At ΔT = 0 K, the reduction in effective material properties between χ = 0 (non-porous) and χ = 0.6 (uniform porosity model) is 60%.

Fig. 6

Variation of the uniform porosity model’s effective material properties for different porosity volume fraction χ = 0, 0.2, 0.4 and 0.6; based on material grading index (m = 1) and the nonlinear changes in temperature within 0 K and 600 K

4 Model Verification

Using a simply supported FGM beam constructed of Steel and Alumina, the obtained dimensionless frequencies ${\lambda }_{i}={\omega }_{i}{L}^{2}\sqrt{{\rho }_{c}A/{E}_{c}I}$ of a FGM nanobeam with material grading index m = 0 and 1 was supported by the results of nonlocal FG Timoshenko beams reported by Rahmani and Pedram [31], which are shown in Table 4–5. The material characteristics used in this work are as follows: E_t = 390 GPa, v_t = 0.24, ρ_t = 3960 kg/m³ for Alumina and E_t = 210 GPa, v_t = 0.3, ρ_t = 7800 kg/m³ for Steel. The nanobeam dimensions are: L (length) = 10 nm, h (thickness) = variable, and I = h³/12 is the moment of inertia of the beam's cross-section.

Table 4 Comparisons of the dimensionless frequency ${\lambda }_{1}$ for different nonlocal parameters (m = 0)

Table 5 Comparisons of the dimensionless frequency ${\lambda }_{1}$ for different nonlocal parameters (m = 1)

5 Results

The dimensionless frequencies in this case are defined by the following equation:

$${\lambda }_{i}={\omega }_{i}{L}^{2}\sqrt{{\rho }_{t}A/{C}_{t11}I},$$

(79)

where ${C}_{t11}$ and ${\rho }_{t}$ are elastic modulus and specific gravity of pure cobalt-ferrite, respectively.

In Fig. 7a where the thermal properties of nanobeam components are not considered, and in Fig. 7b where they are considered are presented. When Fig. 7a and b are examined for the material grading index m = 0, 1, 2 and 10, the buckling temperatures in Fig. 7a are ΔT = 202, 613, 603 and 641 K, respectively and considering the effect of temperature on the properties of the material in Fig. 7b, the results obtained were ΔT = 166, 377, 376 and 393 K for m = 0, 1, 2 and 10, respectively. In the calculations made for the cases where the temperature-dependent mechanical properties of barium-titanate and cobalt-ferrite are considered, the buckling temperatures are 21.69% for m = 0, 63.60% for m = 1, 60.37% for m = 2 and finally 63.10% for m = 10 lower.

Fig. 7

The difference of considering the temperature dependent mechanical properties of constituent materials cobalt-ferrite and barium-titanate; a non-accounting the temperature dependent properties b accounting the temperature dependent properties

The curve drawn with the blue line in Fig. 8 is presented to give the variation of the dimensionless frequency of the nano TMEE beam at ΔT = 0. Here, first of all, it is emphasized that the composition of the beam material is important in the frequency behavior of the nanobeam. At material grading index m = 0, the entire nanobeam material is composed of cobalt-ferrite. Starting from the bottom, the composition of barium-titanate decreases with height, while the amount of cobalt-ferrite increases. At m = 1, 50% of the nanobeam is barium-titanate and 50% cobalt-ferrite. At material grading index m = 5, 83.3% of the nanobeam is barium-titanate and 16.7% cobalt-ferrite. If the material grading index m = ∞, the nanobeam is expected to be completely barium-titanate. Figure 2 show fractional volume charts of the nanobeam components. The modulus of elasticity at room temperature in the 1,1 direction of cobalt-ferrite is C_t11 = 286 GPa, and that of barium-titanate is C_b11 = 162 GPa. Because the cobalt-ferrite ratio in the nanobeam is high at values of m close to 0 and cobalt-ferrite's modulus of elasticity is greater than barium-titanate's, dimensionless frequencies are higher at small values of m than at large values of m. Natural frequencies decrease rapidly in the range of m = 0–3 and as m gets larger, the frequency change rate decreases after m = 3 and goes toward the limit. This is because at large values of m, the nanobeam approaches toward the isotropic material composition. When ΔT = 0 K is at m = 0, the dimensionless natural frequency is λ₁ = 18.1286, at m = 1 λ₁ = 16.6148, at m = 5 λ₁ = 15.9377. The variation between m = 0 and m = 1 is -8.35%, while the variation between m = 1 and m = 5 is -4.08% on average. As seen in the Fig. 8, the frequency change between m = 0 and m = 5 at other temperatures shows a similar trend as above. It is also seen in the Fig. 8 that the temperature decreases the frequencies. As can be seen, an important point in the temperature-dependent variation is that the decrease in frequency with increasing barium-titanate is higher than ΔT = 0 K. This is because barium titanate has a higher thermal expansion coefficient than cobalt-ferrite as shown in Fig. 4.

Fig. 8

Variation of the dimensionless frequency λ₁ versus material grading index m for various temperature rise ΔT = 0, 50, 100 and 150 K; nonlocal parameter e₀a = 0; dimensionless magnetic potential H_m = 0; dimensionless electric potential V_m = 0; porosity volume fraction χ = 0; slenderness ratio L/h = 20

Figure 9 depicts the variation of dimensionless frequency versus temperature rise of four different porous TMEE nanobeams. The importance of the temperature-dependent nanobeam frequency response and the porosity position in the beam is emphasized here. The material grading index was held constant as m = 1 while obtaining the graph, and assuming the nanobeam as non-porous, the nanobeam is reported to be composed of barium-titanate (50%) and cobalt-ferrite (50%). The increase in temperature resulted in a decrease in dimensionless frequencies, with the percentage change varied among almost all porous models. In UPM, the dimensionless natural frequency is λ₁ = 16.6148 when ΔT = 0 K, and λ₁ = 14.9541 when ΔT = 150 K. The percentage change in dimensionless natural frequency between ΔT = 0 K and ΔT = 150 K is -9.9%. In SPM, the dimensionless natural frequency becomes λ₁ = 15.9830 when ΔT = 0 K, and λ₁ = 13.9143 when ΔT = 150 K. For SPM, the percentage of the variation in dimensionless natural frequency between ΔT = 0 K and ΔT = 150 K was -12.94%. When it takes ΔT = 0 K and ΔT = 150 K values in BPM, the dimensionless natural frequencies are calculated as λ₁ = 16.5755 and λ₁ = 14.5547, respectively. The amount of the change in dimensionless natural frequency between ΔT = 0 K and ΔT = 150 K was calculated as -12.19% for BPM. Finally, looking at the TPM, it is seen that the dimensionless natural frequency is read as λ₁ = 16.4141 at ΔT = 0 K, and λ₁ = 14.4360 at ΔT = 150 K. According to these values, the percentage shift in the dimensionless natural frequency between ΔT = 0 K and ΔT = 150 K was calculated as -12.05%. As can be seen, in the change depending on the porosity model, the decrease in the frequency as a percentage with the increase in temperature was the highest in the SPM and the least in the UPM. The change in the effective material characteristics presented in Figs. 4, 5, 6, which depends on temperature, porosity ratio and porosity distribution function is the key to understanding the physical explanation for this phenomenon. In summary, the coefficient of thermal expansion is primarily affected by temperature and increases parabolically depending on the temperature. At the same time, porosity and the distribution ratio of porosity also affect the thermal expansion coefficient.

Fig. 9

Variation of the dimensionless frequency λ₁ versus temperature rise ΔT for various porosity models UPM, SPM, TPM and BPM; material grading index m = 1; porosity volume fraction χ = 0.3; nonlocal parameter e₀a = 0; dimensionless magnetic potential H_m = 0; dimensionless electric potential V_m = 0; slenderness ratio L/h = 20

The variation of dimensionless frequency versus material grading index of the non-porous nano TMEE beam is shown in Fig. 10. First, it is demonstrated that nonlocal parameter variation is significant for the frequency behavior of the nanobeam due to the power-law exponent. Because of the change in the power-law exponent, a similar decrease in the dimensionless frequencies is observed for all nonlocal parameters considered. As m increases between 0 and 3, the natural frequencies decrease rapidly in all nonlocal parameters, and as material grading index takes the values greater than m = 3, the rate of frequency change decreases and goes toward the limit. For e₀a = 0, the dimensionless natural frequency λ₁ = 18.1286 at m = 0 and λ₁ = 15.9377 at m = 5. When e₀a = 1, the dimensionless natural frequency λ₁ = 17.2951 at m = 0. When e₀a = 1.41, the dimensionless natural frequencies at m = 0 and m = 5 are λ₁ = 16.5751 and λ₁ = 14.5751, respectively. Finally, at e₀a = 2, the dimensionless natural frequency λ₁ = 15.3498 at m = 0 and λ₁ = 13.4947 at m = 5. It is observed that the average percentage shift between m = 0 and m = 5 is -12.09% for all nonlocal parameter values considered. As can be observed, increasing the nonlocal parameter values decreased the frequencies, but the percentage change in the frequencies while increasing the material grading index was the same for all nonlocal parameters considered.

Fig. 10

Variation of the dimensionless frequency λ₁ versus material grading index m for various nonlocal parameters e₀a = 0, e₀a = 1, e₀a = 1.41 and e₀a = 2; porosity volume fraction χ = 0; temperature rise ΔT = 0; dimensionless magnetic potential H_m = 0; dimensionless electric potential V_m = 0; slenderness ratio L/h = 20

The variation of dimensionless frequency versus nonlocal parameter rise of 4 different porous models of TMEE nanobeam is depicted in Fig. 11. Here, it is aimed to demonstrate that the frequency behavior of the nanobeam depends on the nonlocal parameter, and the location of the porosity in the beam is important. In the graph, the material rating index was taken as m = 1, and therefore, if the nanobeam is considered as non-porous, half of the nanobeam material is made of barium titanate, while the other half is made of cobalt ferrite. Due to the nonlocal parameter rise, a decrease was observed in dimensionless frequencies, and this decrease occurred differently in almost all porosity models. In UPM, the dimensionless natural frequency is λ₁ = 16.6148 at e₀a = 0, and λ₁ = 14.0683 at e₀a = 2. The percentage variation in the dimensionless natural frequency between e0a = 0 and e0a = 2 was calculated as -15.33%. Considering the SPM, it was found that λ₁ = 15.9830 at e₀a = 0, while λ₁ = 13.5333 at e₀a = 2. When the percentage of the change in the dimensionless natural frequency between e0a = 0 and e0a = 2 is calculated, it was observed to be -15.33%. When we look at the BPM, while the dimensionless natural frequency is λ₁ = 16.5755 at e₀a = 0, it takes the value λ₁ = 14.0247 at e₀a = 2. When we look at these two nonlocal parameter values, the amount of the shift in dimensionless natural frequencies is -15.39%. Finally, at e₀a = 0 and e₀a = 2 in TPM, λ₁ took the values of 16.4141 and 13.9226, respectively. According to these values, the percentage change in the dimensionless natural frequency between e₀a = 0 and e₀a = 2 was calculated as -15.18%. As can be stated, the decrease in frequency with the increase in the value of the nonlocal parameter in the change based on the porosity model was the highest in BPM.

Fig. 11

Variation of the dimensionless frequency λ₁ versus nonlocal parameter e₀a for various porosity models UPM, SPM, TPM and BPM; material grading index m = 1; porosity volume fraction χ = 0.3; temperature rise ΔT = 0; dimensionless magnetic potential H_m = 0; dimensionless electric potential V_m = 0; slenderness ratio L/h = 20

For a parametric investigation of the effect of the magnetic potential on the dynamics of the TMEE nanobeam, the following nondimensional relation is defined as

$${H}_{0}=\frac{{H}_{m}}{{C}_{t11}I}$$

(80)

Figure 12 illustrates the change in dimensionless frequency versus material grading index for the non-porous form of the TMEE nanobeam. Primarily, it is explained that dimensionless magnetic potential values are also effective on the material grading index dependent frequency behavior of the nanobeam. For all dimensionless magnetic potential values considered, a decrease in the dimensionless frequencies was observed as material grading index values increased and the amount of this decrease was found in different ways. For dimensionless magnetic potentials H_m = 0, H_m = 0.01, H_m = 0.02 and H_m = 0.03, dimensionless natural frequencies at m = 0 are 18.1286, 75.0028, 107.6081 and 132.4144, respectively, while at m = 5 they are 15.9377, 26.0015, 40.0770 and 50.3613, respectively. For all dimensionless magnetic potential values, the percentage of the variation between m = 0 and m = 5 was calculated as − 12.09%, − 65.33%, − 62.76% and − 61.97%, respectively. As can be indicated, the increase in dimensionless magnetic potential values also increased the frequencies. The reason for this is that one of the two components of the FGM is cobalt-ferrite and it has piezomagnetic properties. Another important point when looking at the graph is that in all dimensionless magnetic potential values, the material grading index raised as frequencies dropped. The reason for this is that while the material grading index rises, the percentage of barium-titanate, the other component of the FGM, increases in the material, barium-titanate is electroelastic, is not affected by the magnetic field and its modulus of elasticity is less than the modulus of elasticity of cobalt-ferrite.

Fig. 12

Variation in the dimensionless frequency λ₁ versus material grading index m for various dimensionless magnetic potentials H_m = 0, H_m = 0.01, H_m = 0.02 and H_m = 0.03; porosity volume fraction χ = 0; temperature rise ΔT = 0; nonlocal parameter e₀a = 0; dimensionless electric potential V_m = 0; slenderness ratio L/h = 20

The change in dimensionless frequency versus rise in dimensionless magnetic potential of 4 different porous TMEE nanobeams is shown in Fig. 13. First of all, it is aimed to show how important the frequency behavior of the location of the porosity in the nanobeam depends on the dimensionless magnetic potential value. Here, the material grading index is taken as m = 1, so if we consider the nanobeam as non-porous, half of the nanobeam material is made of barium titanate, while the other half is made of cobalt-ferrite. Due to the rise in the dimensionless magnetic potential value, an increase in dimensionless frequencies was observed and this increase occurred differently in all porosity models. When the porous nanobeam models are taken as UPM, SPM, BPM and TPM, the dimensionless natural frequencies at H_m = 0 are 18.6737, 19.2172, 19.8052 and 17.7014, respectively, while at H_m = 0.05 they have the values of 118.7153, 118.8020, 122.7440 and 114.6042, respectively. The difference between H_m = 0 and H_m = 0.05 for all porous nanobeam models considered was calculated as 100.0416, 99.5848, 102.9388 and 96.9027, respectively. As can be revealed, regardless of the porosity model, increasing the dimensionless magnetic potential value raised the frequencies. Because in all porosity models discussed, one of the two components forming the beam is cobalt-ferrite and it has piezomagnetic property. Looking at the graph again, the increase in the frequency was highest in BPM with the increase in the dimensionless magnetic potential value. This is due to the fact that the cobalt-ferrite to barium-titanate ratios are 1:1 at m = 1, and barium-titanate is mostly in the lower part and when compared to cobalt-ferrite, its modulus of elasticity is less. As a result of the decreased barium-titanate in the BPM and the increasing amount of cobalt-ferrite, the dimensionless frequency rises.

Fig. 13

Variation of the dimensionless frequency λ₁ versus dimensionless magnetic potential H_m for various porosity models UPM, SPM, TPM and BPM; material grading index m = 1; porosity volume fraction χ = 0.3; temperature rise ΔT = 0; nonlocal parameter e₀a = 0; dimensionless electric potential V_m = 0; slenderness ratio L/h = 20

The following nondimensional relation is constructed for a parametric analysis of the influence of the electric potential on the dynamics of the TMEE nanobeam,

$${V}_{0}=\frac{{V}_{m}}{{C}_{t11}I}$$

(81)

Figure 14 shows the change of dimensionless frequency versus material grading index change in a non-porous TMEE nanobeam. The purpose here is to demonstrate that the change in frequency behavior of the nanobeam depending on the material grading index is also important in the dimensionless electric potential. A parabolic decrease was observed for all dimensionless electric potential values considered at dimensionless frequencies due to the material grading index change While m increases from 0 to 3, the natural frequencies decrease rapidly in all nonlocal parameters, and as material grading index gets the values above m = 3, the rate of frequency change decreases and reaches the limit. For V_m = 0, the dimensionless natural frequency is λ₁ = 18.1286 at m = 0 and λ₁ = 15.9377 at m = 5. When V_m = 0.01, the dimensionless natural frequency at m = 0 takes the value λ₁ = 18.1162. At m = 5, λ₁ = 14.7902 was found. When V_m = 0.02, it can be noted that the dimensionless frequencies at m = 0 and m = 5 take the values of λ₁ = 18.1037 and λ₁ = 13.5458, respectively. Finally, at V_m = 0.03, the dimensionless natural frequency was calculated as λ₁ = 18.0912 at m = 0, while it was calculated as λ₁ = 12.1749 at m = 5. For all dimensionless electric potential values considered, V_m = 0, V_m = 0.01, V_m = 0.02, and V_m = 0.03, the percentage change between m = 0 and m = 5 is calculated -12.09%, -18.36%, -15.18% and -32.70%, respectively. As can be seen, the rise in dimensionless electric potential values decreased the frequencies. The reason for this is that one of the two components of FGM is barium-titanate and it has electroelastic property. Looking at the graph, another important point is that in all levels of the dimensionless electric potential, the frequencies decreased as the material grading index rose. The reason for this is that while the material grading index goes up, cobalt-ferrite content decreases, on the contrary, barium-titanate increases, and cobalt-ferrite's elasticity module is greater than barium-titanate's.

Fig. 14

Change in the dimensionless frequency λ₁ versus material grading index m for various dimensionless electric potentials V_m = 0, V_m = 0.01, V_m = 0.02 and V_m = 0.03; porosity volume fraction χ = 0; temperature rise ΔT = 0; nonlocal parameter e₀a = 0; dimensionless magnetic potential H_m = 0; slenderness ratio L/h = 20

The variation of dimensionless electric potential versus dimensionless frequency of 4 different porous TMEE nanobeams is presented in Fig. 15. The aim here is to emphasize that the frequency behavior of the porous TMEE nanobeam depends on the dimensionless electric potential value and the location of the porosity in the beam is also effective. While the graph was being obtained, the material rating index was taken as m = 1 to beam is also effective. While the graph was being obtained, the material rating index was taken as m = 1 to make the non-porous nanobeam material half and half from barium-titanate and cobalt-ferrite. While the dimensionless electric potential value raised, a decrease was observed in dimensionless frequencies and the percentage change was almost different in all porous models. When it takes the values of V_m = 0 and V_m = 0.05 in the UPM, the dimensionless natural frequencies are calculated as λ₁ = 16.6148 and λ₁ = 12.9266, respectively. The amount of the change in dimensionless natural frequency between V_m = 0 and V_m = 0.05 was calculated as -22.20% for UPM. Looking at the SPM, it is seen that while the dimensionless natural frequency is read as λ₁ = 15.9830 at V_m = 0, it takes the values of λ₁ = 12.1038 at V_m = 0.05. According to these values, the percentage shift in the dimensionless natural frequency between V_m = 0 and V_m = 0.05 was calculated and found as -24.27% for SPM. In BPM, the dimensionless natural frequency is λ₁ = 16.5755 when V_m = 0, and λ₁ = 13.1349 when V_m = 0.05. In the case of BPM, the percentage variation in dimensionless natural frequency between V_m = 0 and V_m = 0.05 is -20.76%. Finally, when V_m = 0 in TPM, the dimensionless natural frequency becomes λ₁ = 16.4141 and when V_m = 0.05, it becomes λ₁ = 12.4007. For TPM, the change in the percentage of dimensionless natural frequency between V_m = 0 and V_m = 0.05 occurred as -24.45%. As can be observed, the increase in the dimensionless electric potential value, regardless of the porosity model, also decreased the frequencies. Because in all porosity models discussed, one of the two components forming the beam is barium-titanate and it has electro elastic property. Again, when we look at the graph, the decrease in the frequency as a percentage with rising dimensionless electric potential value was highest in TPM. The reason for this is that the ratios of cobalt-ferrite and barium-titanate are half and half at m = 1, cobalt-ferrite is mostly in the upper part and the modulus of elasticity is higher than barium-titanate. Because of the decreased ratio of cobalt-ferrite in the TPM and the increasing amount of barium-titanate, the dimensionless frequency decreases.

Fig. 15

Variation of the dimensionless frequency λ₁ versus dimensionless electric potential V_m for various porosity models UPM, SPM, TPM and BPM; material grading index m = 1; porosity volume fraction χ = 0.3; temperature rise ΔT = 0; nonlocal parameter e₀a = 0; dimensionless magnetic potential H_m = 0; slenderness ratio L/h = 20

The variation of the dimensionless frequency versus the variation of the material grading index of the non-porous TMEE nanobeam is shown in Fig. 16. Here, first of all, it is aimed to show that the variation of the slenderness ratio is important for the frequency behavior of the nanobeam depending on the material grading index. Considering all slenderness ratios, similar decrease of the dimensionless frequencies due to change in the material grading index is observed. As m increases from 0 to 1, the natural frequencies decrease rapidly in all nonlocal parameters, and as material grading index gets the values above m = 1, the rate of frequency change decreases and moves toward the limit. For L/h = 10, the dimensionless natural frequency λ₁ = 8.9394 at m = 0 and λ₁ = 6.0012 at m = 5. When L/h = 20, the dimensionless natural frequency λ₁ = 18.1286 at m = 0 and λ₁ = 15.9377 at m = 5. When L/h = 30, the dimensionless natural frequencies at m = 0 and m = 5 were λ₁ = 27.2622 and λ₁ = 24.9163 respectively. Finally, at L/h = 40, the dimensionless natural frequency λ₁ = 36.3820 at m = 0 and λ₁ = 33.6876 at m = 5. For all the slenderness ratios considered, the variation in the percentage between m = 0 and m = 5 was calculated as -32.87%, -12.09%, -8.61% and -7.41%, respectively. As can be demonstrated, rising the slenderness ratios increased the frequencies but decreased the percentage changes. In addition, for all the slenderness ratios considered, the material grading index rose while the frequencies declined.

Fig. 16

Change in the dimensionless frequency λ₁ versus material grading index m for slenderness ratios L/h = 10, 20, 30 and 40; porosity volume fraction χ = 0; temperature rise ΔT = 0; nonlocal parameter e₀a = 0; dimensionless magnetic potential H_m = 0; dimensionless electric potential V_m = 0

Figure 17 depicts the fluctuation of the dimensionless frequency with the increase in the slenderness ratio of four special porous models of the TMEE nanobeam. The goal here is to illustrate how the frequency behavior of the nanobeam is affected by the slenderness ratio, as well as the position of the porosity in the beam. If we assume the nanobeam to be non-porous, the material grading index is set to m = 1 when developing the graph, resulting in 50% cobalt-ferrite and 50% barium-titanate materials. An increase in dimensionless frequencies was noticed when the slenderness ratio increased, and this rise happened about identically in almost all porosity models. In UPM, the dimensionless natural frequency is λ₁ = 7.2524 when L/h = 0, and λ₁ = 34.2840 when L/h = 40. The difference in dimensionless natural frequency between L/h = 0 and L/h = 40 was determined to be 372.73%. Considering the SPM, it was found that λ₁ = 6.8933 at L/h = 0, and λ₁ = 33.0562 at L/h = 40. The dimensionless natural frequency changed 379.54% between L/h = 0 and L/h = 40. When we look at the BPM, while the dimensionless natural frequency took the value λ₁ = 7.3073 at L/h = 0, it took the value λ₁ = 34.1368 at L/h = 40. When we look at these two slenderness ratio values, the percentage variation in dimensionless natural frequencies is 367.16%. Finally, at L/h = 0 and L/h = 40 in TPM, λ₁ took the values of 7.0606 and 33.9642, respectively. According to these values, the amount of the shift in the dimensionless natural frequency between L/h = 0 and L/h = 40 was calculated as 381.04%. As can be seen, the porosity model-based analysis revealed that the highest increase in frequency was observed in TPM, as the slenderness ratio increased.

Fig. 17

Variation of the dimensionless frequency λ₁ versus slenderness ratios L/h for various porosity models UPM, SPM, TPM and BPM; material grading index m = 1; porosity volume fraction χ = 0.3; temperature rise ΔT = 0; nonlocal parameter e₀a = 0; dimensionless magnetic potential H_m = 0; dimensionless electric potential V_m = 0

Figure 18 displays the changes of dimensionless frequency versus material grading index variation for the non-porous model of the TMEE nanobeam. The material grading index is effective in the frequency behavior for considered all porosity volume fractions, as seen here. While the power-law exponent values increased for all porosity volume ratio values studied, a drop in dimensionless frequencies was noted, and this decline was seen to be distinct. When the porosity volume fraction is set to χ = 0, χ = 0.1, χ = 0.2, or χ = 0.3, the dimensionless natural frequencies at m = 0 are 18.1286, 18.2809, 18.4623, and 18.6977, respectively, but at m = 5, they are 15.9377, 15.8374, 15,7121, and 15,5510. The percentage change between m = 0 and m = 5 for all porosity volume fraction values examined was determined as -12.093, -13.37%, -14.90%, and -16.83%, respectively. As can be observed, The material grading index approached m = 1 as porosity volume fraction values increased and then decreased. The reason for this is that the cobalt-ferrite ratio is greater in the nanobeam until m = 1, and it has a larger elasticity modulus than barium-titanate. As the barium-titanate ratio grows after m = 1, the frequencies drop. Another key item to note from the graph is that, while the material grading index raised across the whole porosity volume fraction values addressed, the frequencies decreased.

Fig. 18

Variation of the dimensionless frequency λ₁ versus material grading index m for porosity volume fraction χ = 0, χ = 0.1, χ = 0.2 and χ = 0.3; temperature rise ΔT = 0; nonlocal parameter e₀a = 0; dimensionless magnetic potential H_m = 0; dimensionless electric potential V_m = 0; slenderness ratio L/h = 20

The variation of the dimensionless frequency of four different porosity TMEE nanobeams against the increase in porosity volume fraction is shown in Fig. 19. To begin with, it is designed to demonstrate how crucial the position of the porosity in the nanobeam is for the frequency behavior dependent on the porosity volume fraction value. When the nanobeam is assumed to be non-porous, it was divided into two halves, one made of barium-titanate and the other of cobalt-ferrite, using the power-law exponent m = 1. Numerous variations occurred in the dimensionless frequencies for all porosity models when the porosity volume fraction value increased. Taking the porous nanobeam models as UPM, SPM, BPM and TPM, at χ = 0, the dimensionless natural frequencies all take the value of 16.6148 because at χ = 0 all porosity models behave as non-porosity. At χ = 0.4, the dimensionless natural frequencies are 16.6148, 15.6823, 16.5580 and 16.3242, respectively. The percentage change between χ = 0 and χ = 0.4 for all porosity nanobeam models were calculated as 0%, -5.62%, -0.34% and -1.75%, respectively. As is plainly seen here, increasing the porosity volume ratio value lowered the frequencies in all porosity models except the UPM. It can be also seen that the highest decrease among all porosity models was in SPM.

Fig. 19

Variation of the dimensionless frequency λ₁ versus porosity volume fraction χ for various porosity models UPM, SPM, TPM and BPM; power-law exponent m = 1; temperature rise ΔT = 0; nonlocal parameter e₀a = 0; dimensionless magnetic potential H_m = 0; dimensionless electric potential V_m = 0; slenderness ratio L/h = 20

6 Conclusion

This study focused on the free vibration of a FG porous beam subjected to heat, magnetic and electric fields. The examined FG nanobeam's material composition is cobalt-ferrite at the top and barium-titanate at the bottom. In addition to the temperature impact, magnetic end electric field, the effects of factors such as material grading index, nonlocal parameter, slenderness ratio, and the nanobeam porosity ratio were deeply studied. In addition to this, the impact of the composition of the material, the porosity of the material, and the nonlinear temperature rise had on the FG nanobeam’s effective material characteristics was also investigated.

The equations of motion for the nanobeam's free vibration response are derived considering the nonlocal micromechanical effect and employing the theory of trigonometric higher-order shear deformation. The impacts of porosity volume fraction, porosity distribution, magnetic and electric fields, nonlocal factors, slenderness ratio and nonlinear temperature on the nanobeam’s free vibration behavior have been simulated and examined in detail. UPM, SPM, BPM and TPM are examined as function of porosity distribution. Lastly, a summary of the findings of the analysis is presented below.

• 1. While the effective thermal conductivity coefficient and modulus of elasticity decrease nonlinearly with temperature, the thermal expansion coefficient rises nonlinearly for non-porous FG nanobeam. All models of porosity for FG nanobeam show a general trend of variation in effective elasticity, thermal expansion, and thermal conductivity similar to the non-porous model, but porosity ratio affects all effective material properties more than temperature. In addition, there seem to be specific differences between the porosity models.

• 2. The ratio of barium-titanate in the nanobeam content rises with the increase of the material grading index, and thus the dimensionless frequency of the material reduces. It is also observed that the dimensionless frequency of the material reduces also with the rise of the temperature, because the thermal expansion coefficient of barium-titanate is larger than that of cobalt-ferrite. At the same time, porosity and the distribution ratio of porosity also affect the thermal expansion coefficient. In the dimensionless natural frequency change dependent on porosity model, it is discovered that when temperature increases, the percentage decrease in frequency is largest in SPM and lowest in UPM.

• 3. Increasing the nonlocal parameter values decreases the dimensionless natural frequencies. It is also observed that the decrease in frequency with the increase in the value of the nonlocal parameter in the change due to the porosity model is the highest in BPM.

• 4. The increase in dimensionless magnetic potential values also rises the frequencies. The increase in the frequency is highest in BPM with the increase in the dimensionless magnetic potential value. As a result of the decreased barium-titanate in the BPM and the increasing amount of cobalt-ferrite, the natural frequency rises.

• 5. The rise in dimensionless electric potential values decreases the frequencies. The decrease in the frequency as a percentage with rising dimensionless electric potential value is highest in TPM. Because of the decreased ratio of cobalt-ferrite in the TPM and the increasing amount of barium-titanate, the natural frequency decreases.

• 6. Rising the slenderness ratios increases the frequencies but decreases the percentage changes. Furthermore, for all the slenderness ratios considered, the power-law exponent increases while the frequencies decrease. In addition, the increase in frequency with the increase in the slenderness ratio in the change based on the porosity model is the highest in TPM.

• 7. Increasing the porosity volume fraction values raises the change in frequencies until the material grading index reached m = 1 and then decreases. In addition, increasing the porosity volume fraction value decreases the frequencies in all porosity models except the UPM. The highest decrease among all porosity models is in SPM.

Appendix A

The eigenvalue equations for trigonometric solution considering general boundary conditions presented in Table 2.

$$ \begin{gathered} \left[ {A_{11} r_{3} + I_{0} \omega_{n}^{2} \left( {r_{1} + \left( {e_{0} a} \right)^{2} r_{3} } \right)} \right]U_{n} - \left[ {B_{11} r_{3} + I_{1} \omega_{n}^{2} r_{1} + \left( {e_{0} a} \right)^{2} I_{1} \omega_{n}^{2} r_{3} } \right]W_{bn} \hfill \\ + \left[ { - B_{11}^{s} r_{3} + J_{1} \omega_{n}^{2} \left( {r_{1} + \left( {e_{0} a} \right)^{2} r_{3} } \right)W_{sn} } \right] + A_{31}^{e} \left( {r_{1} } \right) \phi_{n} + A_{31}^{m} \left( {r_{1} } \right) Y_{n} = 0 \hfill \\ \end{gathered} $$

(82)

$$ \begin{aligned} & \left[ {B_{11} r_{9} + I_{1} \omega_{n}^{2} \left( {r_{7} + \left( {e_{0} a} \right)^{2} r_{9} } \right)} \right]U_{n}\\ &\quad + \left[ { - D_{11} r_{9} - I_{2} \omega_{n}^{2} \left( {r_{7} + \left( {e_{0} a} \right)^{2} r_{9} } \right) + I_{0} \omega_{n}^{2} \left( {r_{5} + \left( {e_{0} a} \right)^{2} r_{7} } \right) + (N^{E} + N^{H} + N^{T} } \right) \hfill \\ &\quad \left( {r_{7} + \left( {e_{0} a} \right)^{2} r_{9} } \right)\left] {W_{bn} + } \right[ - D_{11}^{s} r_{9} - I_{0} \omega_{n}^{2} \left( {r_{5} + \left( {e_{0} a} \right)^{2} r_{7} } \right) \hfill \\ &\quad + J_{2} \omega_{n}^{2} \left( {r_{7} + \left( {e_{0} a} \right)^{2} r_{9} } \right)\\ &\quad + (N^{E} + N^{H} + N^{T} )\left( {r_{7} + \left( {e_{0} a} \right)^{2} r_{9} } \right)\left] { W_{sn}}+ \right[(E_{31}^{e} - A_{15}^{e} ) r_{7} \left] {\phi_{n} + } \right[(E_{31}^{m} - A_{15}^{m} ) r_{7} ]Y_{n}\\ &\quad = 0 \hfill \\ \end{aligned} $$

(83)

$$ \begin{aligned} & \left[ {B_{11}^{s} r_{9} + J_{1} \omega_{n}^{2} \left( {r_{7} + \left( {e_{0} a} \right)^{2} r_{9} } \right)} \right]U_{n}\\ & \quad + \left[ { - D_{11}^{s} r_{9} - J_{2} \omega_{n}^{2} \left( {r_{7} + \left( {e_{0} a} \right)^{2} r_{9} } \right) - I_{0} \omega_{n}^{2} \left( {r_{5} + \left( {e_{0} a} \right)^{2} r_{7} } \right) } \right) \\ &\quad - D_{11}^{s} r_{9} - I_{0} \omega_{n}^{2} \left( {r_{5} + \left( {e_{0} a} \right)^{2} r_{7} } \right) \hfill \\ &\quad + (N^{E} + N^{H} + N^{T} )\left( {r_{7} + \left( {e_{0} a} \right)^{2} r_{9} } \right)]W_{bn} \hfill \\ &\quad + \left[ {A_{44}^{s} \left( {r_{7} } \right) - H_{11}^{s} r_{9} + (N^{E} + N^{H} + N^{T} } \right)\left( {r_{7} + \left( {e_{0} a} \right)^{2} r_{9} } \right)\\ &\quad - I_{0} \omega_{n}^{2} \left( {r_{5} + \left( {e_{0} a} \right)^{2} r_{7} } \right) - K_{2} \omega_{n}^{2} \left( {r_{7} + \left( {e_{0} a} \right)^{2} r_{9} } \right)\left] {W_{sn} + } \right[(F_{31}^{e} - A_{15}^{e} )r_{7} ]\phi_{n} \\ &\quad + \left[ {\left( {F_{31}^{m} - A_{15}^{m} } \right)r_{7} } \right]Y_{n} = 0 \hfill \\ \end{aligned} $$

(84)

$$ \left[ {A_{31}^{e} r_{1} } \right]{\text{U}}_{n} + \left[ { - E_{31}^{e} r_{1} \left] {{\text{W}}_{bn} + } \right[\left( {F_{31}^{e} - A_{15}^{e} } \right)r_{7} \left] {{\text{W}}_{sn} + } \right[F_{11}^{e} r_{7} - F_{33}^{e} r_{5} \left] {\phi_{n} + } \right[F_{11}^{m} r_{7} - F_{33}^{m} r_{5} } \right]{\text{Y}}_{n} = 0{ } $$

(85)

$$ \left[ {A_{31}^{m} r_{1} } \right]{\text{U}}_{n} - \left[ {E_{31}^{m} r_{1} } \right]{\text{W}}_{bn} + \left[ {\left( {E_{15}^{m} - F_{31}^{m} } \right)r_{7} } \right]{\text{W}}_{sn} + \left[ {F_{11}^{m} r_{7} - F_{33}^{m} r_{5} \left] {\psi_{n} + } \right[X_{11}^{m} r_{7} - X_{33}^{m} r_{5} } \right]{\text{Y}}_{n} = 0 $$

(86)

Where

$${r}_{1}={\int }_{0}^{L}{X}_{n}^{\prime}{X}_{n}^{\prime}dx, {r}_{3}={\int }_{0}^{L}{X}_{n}^{{\prime \prime \prime}}{X}_{n}^{\prime}dx, {r}_{5}={\int }_{0}^{L}{X}_{n}{X}_{n}dx, {r}_{7}={\int }_{0}^{L}{X}_{n}^{{\prime \prime}}{X}_{n}dx, {r}_{9}={\int }_{0}^{L}{X}_{n}^{{\prime}{\prime}{\prime}{\prime}}{X}_{n}dx, {r}_{10}={\int }_{0}^{L}{X}_{n}^{{\prime}{\prime}{\prime}{\prime}{\prime}}{X}_{n}^{\prime}dx, {r}_{11}={\int }_{0}^{L}{X}_{n}^{{\prime}{\prime}{\prime}{\prime}{\prime}{\prime}}{X}_{n}dx$$

(87)