1 Introduction

Fluids are studied depending on their physical behavior. Here we inspect a class of fluids known as non-Newtonian fluids, where stress and viscosity changes are in independent relation and have numerous useful applications in practical existence. A non-Newtonian fluid is called Casson fluid where shear thinning is thought in the order of negligible viscosity at an unlimited shear rate, an infinite yield stress, and no flow below the yield stress. Extensive practical applications of Casson flow may be found in the fields of mining, material science, metallurgy, food manufacturing, and nanotechnology. Because of the computational and experimental studies of the fluid, experts have lately become interested in the relevance of Casson fluid in microchannels. Ndolane [1] has created a novel technique for addressing the fractional generalized Casson flows model of the Caputo fractional operator. Motor oil uses were carefully considered by Arif et al. [2] applying a fractional mathematical model of Casson flows with ramping wall temperature. Wright’s function solutions for time-fractional Casson flow in natural convection were reported by Ali et al. [3]. Due to an infinite perpendicular plate, Raza et al. [4] investigated the thermal motion of conservative Casson nanoparticles via ramping temperature using a fractional derivative. Because of the infinite plate, Khan et al. [5] looked into the Casson flow fractional operator generalized unsteady flow.

Fractional calculus is a mathematical extension spanning more than 300 years. A communication that lasted for many months in 1695 between Leibniz and L’Hospital prompted the creation of fractional calculus (FC). Although this subject was primarily established somewhere in a mathematical framework, over the past several decades, it is now seen as a useful tool for understanding and modeling a diverse range of natural and artificial processes. Fractional calculus made integration and differentiation more generic to the non-integer order [6]. Due to the non-locality and historical authenticity of fractional order operators, fractional calculus has become a critical element for the analysis of stochastic processes. Scholars working on systems modeling and control with a wide range of implications to practical concerns have already been drawn to linear, nonlinear, and complex dynamical systems [7]-[8]. A new and fresh approach called Caputo–Fabrizio (CF) derivative using exponential Kernal was imposed by Caputo and Fabrizio [9] in 2015. Sheikh et al. [10] discussed the AB derivative to discuss the Casson fluids in the flow of generalized free convection including coupled temperature and concentration gradients, thermodynamic efficiency, and first-order chemical reactions. For solving the problem, he used Caputo–Fabrizio derivative in order to make comparisons. Ali et al. [11] in their research work examined the thermal and magnetic influences on Casson fluid in cylindrical dimensions with oscillatory boundary conditions using Caputo–Fabrizio time-fractional derivatives, both Laplace and Hankel transforms were used in closed forms. The effect of the fractional Caputo–Fabrizio (CF) derivative on MHD Casson fluid under the influence of heat radiation and chemical processes was proven analytically by Reyaz et al. [12]. Analysis of heat transfer for MHD Jeffrey fluid in a channel according to generalized boundary constraints is done by Aleem et al. [13]. The references in [14]-[16] and several other intriguing research may be found there.

Abro et al. [17] analyzed the fractional operator without singular Kernal on the double convective Casson flow over a vertically oscillating plate both with and without a magnetic field and porous media. Casson flow was used to simulate how blood might move when subjected to fluctuating pressure gradients and an evenly distributed magnetic flux and model was expressed using CF derivatives in [18]. On an infinite vertically oscillating plate, MHD Casson fluid has been applied with ramping temperature using time-fractional Caputo derivative in [19]-[20]. Time-fractional derivatives are used to examine free convection of Casson flow through vertical microchannels with uniform wall temperature with non-singular Kernel utilized in [21]. Quantitative analysis is done to determine the influence of the Casson fractional derivative caused by an accelerating plate using Caputo derivatives [22]. Murtaza et al. [23] worked on a finite difference simulation method for fractal fractional Casson fluid’s elector-osmotic flow model in a microchannel. In a rotational system, time-fractional comparative evaluation is performed for a generalized Jeffrey nanofluid that has been investigated while taking a porous medium and a strong transversal magnetic field into account using CF and AB derivatives in [24].

Sehra et al. [25] explained how mass and heat transfer occurs when a non-Newtonian Casson flows through a permeable medium under the effect of exponential and MHD heating. Dusty Casson fluid flows freely across parallel plates in an extended magnetohydrodynamic two-phase model by Ali et al. [26]. Osman et al. [27] considered time-varying temperature Casson fluid flows axially symmetric and unsteady through a vertical cylinder under the effect of an external transverse magnetic field and also highlighted the impact of temperature gradient on energy transfer and fluid flow motion. Sheikh [28]-[30] worked on the comparison analysis of Caputo–Fabrizio and AB operators for generalized Casson flow and nanofluid flow models. Ramzan et al. [31] discussed the analytical outputs of thermo diffusion impacts on a fractionalized MHD Casson flow in a permeable media across a vertical plate using different fractional derivatives methods. Reyaz et al. [32] explored an analytical solution for the impacts of an infinite Riga plate that is accelerating over a convective MHD Casson flow that incorporates the fractional Caputo derivative. The coupled stress Casson flow via an unstable area with a convective situation and chemical reaction will be examined in three dimensions using MHD analysis [33].

As technology and industry advance, more and more applications of mass and heat transfer are being used [34]-[36]. During a flow, how are mass and heat transferred, according to Chen [37]? In the presence of producing heat energy, a magnetic influence, and a stretchy sheet, Samad and Mohebujjaman [38] looked into the natural convection flow. The concept of the flow of viscoelastic fluid along a vertical conduit transferring mass and heat was investigated by Farooq et al. [39]. In addition to the effects of limited liquid film evaporation, Wei-Mon [40] proposed the concept of mixed convective transfer of heat and mass throughout the flow of liquid from a vertical channel.

Nonlinear convection has been studied by Waqas et al. [41] and many others, but the literature on it utilizing microchannels is few. The non-Newtonian theory made it feasible to characterize the characteristics of many different materials, including paint and printing inks. Casson created the Casson flow model, which included characteristics like high shear viscosity and was used to characterize viscoelastic fluids. Casson fluid is used extensively in the petrochemical and metallurgical industries. In the current study, a non-Newtonian fluid model developed by Casson [42] in a microchannel is taken into consideration as a result of the discussion above and to close a gap in the literature. Human blood, soup, tomato sauce, jam, concentrated fruit juices, honey, and jellies are some examples of Casson fluids that are used in everyday life [43].

In their previous work, Khalid et al. [46] presented a model that examined the behavior of unsteady Casson fluid flow across an oscillating vertical plate with a constant temperature. Their investigation primarily focused on small-time values. However, despite the relevance of fractional derivatives, there exists a notable scarcity of studies on non-Newtonian fluids moving in microchannels that utilize the Caputo–Fabrizio fractional derivative method. Therefore, the main objective of the current study is to address this research gap by solving fractional time equations of motion in a microchannel. Additionally, the study takes into consideration the effect of heat radiation on Casson convective flow. To achieve these objectives, apply the Laplace transform method to obtain an analytical solution. They then employ the inversion of the Laplace transform to calculate essential quantities such as concentration, temperature, and velocity profiles of the fluid in the microchannel. The Caputo–Fabrizio time-fractional operator is chosen for its convenience in the application of the Laplace transform. This choice enhances the efficiency of the analytical approach. Mathcad software is utilized to produce graphical representations of different quantities of the fractional parameter, as well as several significant physical parameters, including the Casson fluid parameter.

2 Description of the Problem

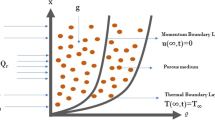
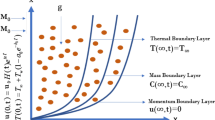
This research assumes that Casson fluid is moving through a microchannel formed of 2 vertical parallel plates separated by a certain distance d from one another. Motion is along the x-axis direction, and perpendicular to the y-axis direction. Figure 1 depicts the geometry of the problem. The fluid is initially at rest at time t = 0, and at y = 0, the plate temperature is \(T_0\). As plate temperature (t) increases at y = d, At u(y, t) = \(U\cos \omega t\) the plate starts to oscillate. In this case, the oscillation’s frequency is \(\omega \), and the amplitude is U.

The Casson fluid model’s representation of the rheological equation of the state of an incompressible flow is given below [44]:

$$\begin{aligned} \tau ^*_{ij}= {\left\{ \begin{array}{ll} 2\times (\mu ^*_b+\frac{p^*_y}{\sqrt{2\pi ^*}})e^*_{ij} &{} \text {if} \,\,\,\, \pi ^*>\pi ^*_c\\ 2\times (\mu ^*_b+\frac{p^*_y}{\sqrt{2\pi ^*_c}})e^*_{ij} &{} \text {if} \,\,\,\, \pi ^*\le \pi ^*_c \end{array}\right. } \end{aligned}$$
(1)

In the given expression, \(\pi ^* = e^*_{ij}\cdot e^*_{ij}\) denotes the product of the deformation rate with itself, \(\pi ^*_c\) is a critical value derived from the non-Newtonian model, \(\mu ^*_b\) represents the plastic dynamic viscosity of the non-Newtonian fluid, and \(p^*_y\) signifies the yield stress of the fluid.

If \(\pi ^* \le \pi ^*_c\), Eq. (1) can be represented as:

$$\begin{aligned} \tau ^*_{ij}=2\mu ^*_b\left( 1+\frac{1}{\beta }\right) e^*_{ij}, \end{aligned}$$
(2)

here \(\beta = \frac{\mu ^*_b\sqrt{2\pi ^*_c}}{p^*_y}\) is the Casson fluid parameter.

Fig. 1
figure 1

Coordinate system and flow geometry

Full size image

The governing equation is made up of momentum, energy, and mass equations based on the above assumptions [45, 46]

$$\begin{aligned}{} & {} \frac{\partial u}{\partial t} = \nu \bigg (1+ \frac{1}{\beta _o} \bigg ) \frac{\partial ^2 u}{\partial y^2} + g\beta _{T}(T-T_{0}) + g\beta _{C}(C-C_{0})\;,\nonumber \\ \end{aligned}$$
(3)
$$\begin{aligned}{} & {} \rho C_{p} \frac{\partial T}{\partial t} + \frac{\partial q_{r}}{\partial y} = k \frac{\partial ^2 T}{\partial y^2}, \end{aligned}$$
(4)
$$\begin{aligned}{} & {} \frac{\partial C}{\partial t} = D \frac{\partial ^2 C}{\partial y^2}, \end{aligned}$$
(5)

Complying with the IBCs

$$\begin{aligned}{} & {} u(d,t)= U \cos \omega t,\nonumber \\ {}{} & {} u(y,0)= 0,\nonumber \\ {}{} & {} u(0,t)= 0,\nonumber \\ {}{} & {} T(d,t)= T_{w},\nonumber \\ {}{} & {} T(y,0)= T_{0},\nonumber \\ {}{} & {} T(0,t)= T_{0},\nonumber \\ {}{} & {} C(d,t)= C_{w},\nonumber \\ {}{} & {} C(y,0)= C_{0},\nonumber \\ {}{} & {} C(0,t)= C_{0}. \end{aligned}$$
(6)

In the given context, the variables are defined as follows: \(\nu \) represents the kinematic viscosity, \(\beta _o\) is the Casson flow parameter, g denotes the gravitational acceleration, \(\beta _T\) stands for the thermal expansion coefficient, \(\beta _C\) represents the concentration expansion coefficient, \(\rho \) is the fluid density, \(C_p\) denotes the specific heat capacity, k represents the thermal conductivity parameter, \(q_r\) signifies the thermal radiation parameter, u stands for the fluid velocity, and d represents the distance between two plates.

In one space coordinate y, the radiative heat flow for an optically thick fluid is represented as [45]

$$\begin{aligned} q_{r} = -\frac{4\sigma }{3 k_{1}} \frac{\partial T^4}{\partial y}, \end{aligned}$$
(7)

where mean absorption coefficient = \(k_1\), and Stefan-Boltzmann constant = \(\sigma \). After linearizing \(T^4\) using a Taylor series centered on \(T_0\) and ignoring higher power components, owing to the negligible variation among T and \(T_0\)

$$\begin{aligned} T^4= 4 {T_{0}}^3 T - 3{T_{0}}^4. \end{aligned}$$
(8)

The energy equation is transformed into the following by applying Eqs. (7-8) to Eq. (4)

$$\begin{aligned} \rho C_{p} \frac{\partial T}{\partial t} = K \bigg (1+ \frac{16 \sigma {T_{0}}^3}{3 k k_{1}}\bigg ) \frac{\partial ^2 T}{\partial y^2}. \end{aligned}$$
(9)

Following are some dimensionless variables that we shall use now

$$\begin{aligned} u=\frac{u}{U},\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \tau = \frac{t \nu }{d^2},\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\xi = \frac{y}{d}, \\ \theta = \frac{T-T_{0}}{T_{w}-T_{0}},\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \phi = \frac{C-C_{0}}{C_{w}-C_{0}}, \end{aligned}$$

Upon substituting the non-dimensional variables in Eqs. (3)–(6) and Eq. (9), we arrive at the following system in its dimensionless form

$$\begin{aligned}{} & {} \frac{\partial u}{\partial \tau } = \frac{1}{\beta } \frac{\partial ^2 u}{\partial \xi ^2} + \text {Gr} \theta + \text {Gm}\phi . \end{aligned}$$
(10)
$$\begin{aligned}{} & {} \frac{\partial \theta }{\partial \tau }= \frac{1}{\text {Pr}_{\text {eff}}} \frac{\partial ^2 \theta }{\partial \xi ^2}, \end{aligned}$$
(11)
$$\begin{aligned}{} & {} \frac{\partial \phi }{\partial \tau }= \frac{1}{\text {Sc}} \frac{\partial ^2 \phi }{\partial \xi ^2}, \end{aligned}$$
(12)

with no dimensions conditions

$$\begin{aligned}{} & {} u(\xi ,0)= 0,\nonumber \\ {}{} & {} u(0,\tau )= 0,\nonumber \\ {}{} & {} u(1,\tau )= \cos \omega \tau \nonumber \\ {}{} & {} \theta (\xi ,0)= 0,\nonumber \\ {}{} & {} \theta (0,\tau )=0,\nonumber \\ {}{} & {} \theta (d,\tau )=1,\nonumber \\ {}{} & {} \phi (\xi ,0)=0,\nonumber \\ {}{} & {} \phi (0,\tau )= 0,\nonumber \\ {}{} & {} \phi (d,\tau )= 1. \end{aligned}$$
(13)

where

$$\begin{aligned}{} & {} \frac{1}{\beta }= \bigg (\frac{\beta _o}{\beta _o + 1} \bigg ),\,\,\,\,\,\\{} & {} \quad \text {Gr} = \frac{d^2 g \beta _{T}(T_{w}-T_{0})}{\nu U},\\{} & {} \quad \text {Gm} = \frac{d^2 g \beta _{C}(C_{w}-C_{0})}{\nu U},\\{} & {} \quad \text {Pr}= \frac{\mu _{B} C_{p}}{K},\,\,\,\,\, \text {Sc} = \frac{\nu }{D},\,\,\,\,\,\\{} & {} \quad \text {R}= \frac{16 \sigma {T_{0}}^3}{3 kk_{1}},\,\,\,\,\, \text {Pr}_{\text {eff}}=\frac{\text {Pr}}{(1+R)}. \end{aligned}$$

Here, the variables Gm, Gr, \(\beta \), Sc, Pr, R, and \(\hbox {Pr}_{\text {eff}}\) represent the mass Grashof number, Grashof number, Casson parameter, Schmidt number, Prandtl number, radiation parameter, and effective Prandtl number, respectively.

3 Fractional Model with Caputo–Fabrizio Derivative

$$\begin{aligned}{} & {} ^{CF}D^\alpha _t u(\xi ,\tau )= \frac{1}{\beta } \frac{\partial ^2 u(\xi ,\tau )}{\partial \xi ^2}+ \text {Gr}\theta (\xi ,\tau ) + \text {Gm} \phi (\xi ,\tau ),\nonumber \\ \end{aligned}$$
(14)
$$\begin{aligned}{} & {} \text {Pr}_{\text {eff}}\,\,\, ^{CF}D^\alpha _t \theta (\xi ,\tau )= \frac{\partial ^2 \theta (\xi ,\tau )}{\partial \xi ^2}, \end{aligned}$$
(15)
$$\begin{aligned}{} & {} \text {Sc} \,\,\,^{CF}D^\alpha _t \phi (\xi ,\tau )= \frac{\partial ^2 \phi (\xi ,\tau )}{\partial \xi ^2}, \end{aligned}$$
(16)

where the \(^{CF}D^{\gamma }_{t}(\cdot )\) is known as the fractional Caputo–Fabrizio (CF) derivatives, which is expressed in [9] and as

$$\begin{aligned} \,\,^{CF}D^{\gamma }_{t} h(t) = \frac{1}{1-\gamma }\int _{0}^{t}\exp (\frac{\gamma (t-\tau )}{1-\gamma })h'(\tau )d\tau . \end{aligned}$$

and its Laplace transform of Caputo–Fabrizio derivatives is

$$\begin{aligned} \,\,^{CF}D^{\gamma }_{t} h(t) = \frac{s\mathcal {L}{\{h(t)\}}-h(0)}{(1-\gamma )s+\gamma }. \end{aligned}$$

3.1 Solution of Temperature

To Eq. (15), the Laplace transform is apply, and we arrive at the following expression

$$\begin{aligned} \frac{ s }{s + \alpha (1-s)}\tilde{\theta }(\xi ,s) = \frac{1}{\text {Pr}_{\text {eff}}} \frac{d^2\tilde{\theta }(\xi ,s)}{d \xi ^2}, \end{aligned}$$
(17)
$$\begin{aligned} \frac{1}{\text {Pr}_{\text {eff}}} \frac{d^2\tilde{\theta }}{d \xi ^2} - \frac{s}{s + \alpha (1-s)}\tilde{\theta } = 0, \end{aligned}$$
(18)

satisfy

$$\begin{aligned} \tilde{\theta }(0,s)=0,\,\,\,\,\,\,\, \tilde{\theta }(1,s)=\frac{1}{s}. \end{aligned}$$
(19)

We obtain result of Eq. (18) using to condition Eq. (19)

$$\begin{aligned} \tilde{\theta }(\xi ,s)= & {} \frac{1}{s\left[ e^{\sqrt{\frac{s\text {Pr}_{\text {eff}}}{s + \alpha (1-s)}}}-e^{ - \sqrt{\frac{s\text {Pr}_{\text {eff}}}{s + \alpha (1-s)}}}\right] }\nonumber \\{} & {} \left[ e^{\xi \sqrt{\frac{s\text {Pr}_{\text {eff}}}{s + \alpha (1-s)}}}-e^{ -\xi \sqrt{\frac{s\text {Pr}_{\text {eff}}}{s + \alpha (1-s)}}}\right] . \end{aligned}$$
(20)

3.2 Solution of Concentration

We can apply Laplace transform for concentration Eq. (16) on both sides and obtain

$$\begin{aligned}{} & {} \frac{s}{s + \alpha (1-s)}\tilde{\phi }(\xi ,s) = \frac{1}{\text {Sc}} \frac{d^2\tilde{\phi }(\xi ,s)}{d \xi ^2}, \end{aligned}$$
(21)
$$\begin{aligned}{} & {} \frac{1}{\text {Sc}}\frac{d^2\tilde{\phi }}{d \xi ^2} - \frac{s}{s + \alpha (1-s)}\tilde{\phi } = 0, \end{aligned}$$
(22)

satisfy

$$\begin{aligned} \tilde{\phi }(0,s)=0,\,\,\,\,\,\,\, \tilde{\phi }(1,s)=\frac{1}{s}. \end{aligned}$$
(23)

Given condition (23), we have the answer to Eq. (22)

$$\begin{aligned}{} & {} \tilde{\phi }(\xi ,s) = \frac{1}{\left[ e^{\sqrt{\frac{s\text {Sc}}{s + \alpha (1-s)}}}-e^{ - \sqrt{\frac{s\text {Sc}}{s + \alpha (1-s)}}}\right] s}\nonumber \\{} & {} \quad \left[ e^{\xi \sqrt{\frac{s\text {Sc}}{s + \alpha (1-s)}}}-e^{ -\xi \sqrt{\frac{s\text {Sc}}{s + \alpha (1-s)}}}\right] . \end{aligned}$$
(24)

3.3 Solution of Velocity

Equation (14) is transformed using the Laplace transform, and we obtain the following result

$$\begin{aligned} \frac{ s \tilde{u}(\xi ,s)}{s + \alpha (1-s)} = \frac{1}{\beta } \frac{d^2 u(\xi ,s)}{d\xi ^2} +\text { Gr} \tilde{\theta }(\xi ,s) + \text {Gm} \tilde{\phi }(\xi ,s),\nonumber \\ \end{aligned}$$
(25)

When the values of \(\tilde{\theta }(\xi ,s)\) and \(\tilde{\phi }(\xi ,s)\) are substituted in the equation above, we get

$$\begin{aligned} \frac{d^2 u}{d\xi ^2} - \frac{\beta s}{s + \alpha (1-s)} u= & {} -\frac{\beta \text {Gr}}{s\left[ e^{\sqrt{\frac{s\text {Pr}_{\text {eff}}}{s + \alpha (1-s)}}}-e^{ - \sqrt{\frac{s\text {Pr}_{\text {eff}}}{s + \alpha (1-s)}}}\right] }\nonumber \\{} & {} \times \left[ e^{\xi \sqrt{\frac{s\text {Pr}_{\text {eff}}}{s + \alpha (1-s)}}}-e^{ -\xi \sqrt{\frac{s\text {Pr}_{\text {eff}}}{s + \alpha (1-s)}}}\right] \nonumber \\{} & {} -\frac{\beta \text {Gm}}{s\left[ e^{\sqrt{\frac{s\text {Sc}}{s + \alpha (1-s)}}}-e^{ - \sqrt{\frac{s\text {Sc}}{s + \alpha (1-s)}}}\right] }\nonumber \\{} & {} \times \left[ e^{\xi \sqrt{\frac{s\text {Sc}}{s + \alpha (1-s)}}}-e^{ -\xi \sqrt{\frac{s\text {Sc}}{s + \alpha (1-s)}}}\right] ,\nonumber \\ \end{aligned}$$
(26)

satisfy

$$\begin{aligned} \tilde{u}(0,s)= 0, \,\,\,\,\,\,\, \text {and} \,\,\,\,\,\,\, \tilde{u}(1,s)= \frac{s}{s^2+\omega ^2}. \end{aligned}$$
(27)

General solution is

$$\begin{aligned}{} & {} \tilde{u}(\xi ,s)\!\!\!\,=\,\!\!\!\frac{F}{\left[ e^{\sqrt{\frac{\beta s}{ s+\alpha (1-s)}}}-e^{-\sqrt{\frac{\beta s}{ s+\alpha (1-s)}}}\right] } \nonumber \\{} & {} \bigg [ e^{\xi \sqrt{\frac{\beta s}{s+\alpha (1-s)}}} - e^{-\xi \sqrt{\frac{\beta s}{s+\alpha (1-s)}}} \bigg ] \nonumber \\ {}{} & {} -\, \frac{\beta \text {Gr}}{s\left[ e^{\sqrt{\frac{s\text {Pr}_{\text {eff}}}{s+\alpha (1-s)}}} - e^{-\sqrt{\frac{s\text {Pr}_{\text {eff}}}{s+\alpha (1-s)}}}\right] }\nonumber \\{} & {} \times \frac{1}{\left[ \frac{s\text {Pr}_{\text {eff}}}{s+\alpha (1-s)}-\frac{\beta s}{s+\alpha (1-s)}\right] }\times \bigg [e^{\xi \sqrt{\frac{s\text {Pr}_{\text {eff}}}{s+\alpha (1-s)}}} - e^{-\xi \sqrt{\frac{s\text {Pr}_{\text {eff}}}{s+\alpha (1-s)}}} \bigg ] \nonumber \\ {}{} & {} - \frac{\beta \text {Gm}}{s\left[ e^{\sqrt{\frac{\text {Sc}s}{s+\alpha (1-s)}}} - e^{-\sqrt{\frac{\text {Sc}s}{s+\alpha (1-s)}}}\right] } \times \frac{1}{\left[ \frac{\text {Sc}s}{s+\alpha (1-s)}-\frac{\beta s}{s+\alpha (1-s)}\right] }\nonumber \\{} & {} \times \bigg [e^{\xi \sqrt{\frac{\text {Sc}s}{s+\alpha (1-s)}}} - e^{-\xi \sqrt{\frac{\text {Sc}s}{s+\alpha (1-s)}}} \bigg ], \end{aligned}$$
(28)

where

$$\begin{aligned}{} & {} F = \frac{s}{s^2+\omega ^2} + \frac{\beta \text {Gr}}{s\left[ e^{\sqrt{\frac{s\text {Pr}_{\text {eff}}}{s+\alpha (1-s)}}} - e^{-\sqrt{\frac{s\text {Pr}_{\text {eff}}}{s+\alpha (1-s)}}}\right] }\\{} & {} \times \frac{1}{\left[ \frac{s\text {Pr}_{\text {eff}}}{s+\alpha (1-s)}-\frac{\beta s}{s+\alpha (1-s)}\right] }\\{} & {} \times \bigg [e^{\xi \sqrt{\frac{s\text {Pr}_{\text {eff}}}{s+\alpha (1-s)}}} - e^{-\xi \sqrt{\frac{s\text {Pr}_{\text {eff}}}{s+\alpha (1-s)}}} \bigg ] \\ {}{} & {} + \frac{\beta \text {Gm}}{s\left[ e^{\sqrt{\frac{\text {Sc}s}{s+\alpha (1-s)}}} - e^{-\sqrt{\frac{\text {Sc}s}{s+\alpha (1-s)}}}\right] } \times \frac{1}{\left[ \frac{\text {Sc}s}{s+\alpha (1-s)}-\frac{\beta s}{s+\alpha (1-s)}\right] }\\{} & {} \times \bigg [e^{\xi \sqrt{\frac{\text {Sc}s}{s+\alpha (1-s)}}} - e^{-\xi \sqrt{\frac{\text {Sc}s}{s+\alpha (1-s)}}} \bigg ]. \end{aligned}$$

4 Result and Discussion

In a microchannel, the unsteady Casson free convection flow has been studied. Analysis has been done on the influence of several embedded variables, including Pr, Sc, Gr, Gm, R, \(\alpha \), and \(\beta \), on velocity, concentration, and temperature.

The velocity profiles rise as Gr rises, this is seen in Fig. 2. The buoyancy force is affected favorably by Gr’s value. The fluid velocity is therefore significantly impacted by it. The reason behind this behavior of velocity profiles can be explained physically by considering the Grashof number (Gr), which represents the ratio of buoyancy forces (resulting from temperature gradient) to inertial forces. When the Grashof number is higher, it indicates a stronger influence of buoyancy forces, leading to more pronounced convectional effects. In other words, an increase in buoyancy forces contributes to a more significant impact on the overall velocity profiles of the fluid. Figure 3 illustrates the effect of the mass Grashof number on the velocity of the Casson flow. The depicted figures demonstrate that the rising function of this integer is velocity. Physically, it is accurate because when Gm rises, buoyant forces also rise, causing the viscosity fluid’s to slow and, due to this, velocity to rise. Figure 4 showcases the impact of the Prandtl number (Pr) on the profile of velocity. The velocity fluid is reduced when increasing the Pr values. Pr determines the ratio of viscous to thermal forces, this significantly affects the velocity of the fluid. Consequently, with a rise in the Prandtl number, the fluid’s velocity drops. Figure 5 depicts the fluid behavior as the Schmidt number, Sc, varies. This figure shows that a rise in Schmidt’s number is accompanied by a decay in fluid velocity. Kinematic viscosity in relation to molecular diffusion is referred to as the Schmidt number. Fluid flow is slowed down by the fact that molecule diffusion tends to decline as the Schmidt number rises.

Fig. 2
figure 2

Impacts of Gr on velocity profile

Full size image
Fig. 3
figure 3

Impacts of Gm on velocity profile

Full size image
Fig. 4
figure 4

Impacts of Pr on velocity profile

Full size image
Fig. 5
figure 5

Impacts of Sc on velocity profile

Full size image

Figure 6 displays the impact of the parameter R on the velocity of the fluid. The velocity fluid rises as R rise. The convection effect is larger and produces the velocity profile rising as the value of R becomes larger. Figure 7 presents the plot showing how the parameter \(\alpha \) influences the velocity of the fluid. The velocity distribution expands as \(\alpha \) rises. At \(\alpha \) = 1, the thickness of the momentum boundary layer is smaller compared to that of the thermal boundary layer, the ordinary velocity profile is said to be at its maximum. Figure 8 depicts the effect of \(\beta \) when the other parameters remain constant. This figure indicates a bigger level of \(\beta \) tends to reduce velocity fluid. This phenomenon can be attributed to the physical influence of \(\beta \), which favors viscous forces over thermal forces when it has a higher value. As a result, there will be a tendency for the fluid velocity to decrease. Figure 9 depicts the inverted Laplace transform of a velocity field using the algorithms Stehfest and Tzou because the Laplace inverse of the velocity profile cannot be computed analytically easily.

Fig. 6
figure 6

Impacts of R on velocity profile

Full size image
Fig. 7
figure 7

Impacts of \(\alpha \) on velocity profile

Full size image
Fig. 8
figure 8

Impacts of \(\beta \) on velocity profile

Full size image
Fig. 9
figure 9

Inverse of velocity profile

Full size image

Figure 10 shows how the Prandtl number Pr affects the temperature profile. It demonstrates that temperature is the decline function of Pr. Physically, this observation is accurate, as the Pr represents the ratio of fluid viscosity to thermal diffusivity, and it decreases with the rising values of Pr. Consequently, with a rise in Prandtl number, the temperature also decays. The temperature profiles are shown in Fig. 11 along with different R values. This figure depicts the profiles of rising R, which has a conflicting influence on the temperature profiles where it exhibits an increasing tendency. Figure 12 shows how the fractional parameter \(\alpha \) influences the temperature distribution. It is evident that the temperature becomes the rising function of \(\alpha \) as \(\alpha \) goes from small to big values. An increase in boundary layer thickness as \(\alpha \) rises leads to a temperature rise. The results for \(\alpha \rightarrow \) 1, which are already documented in the literature [28], are simple to confirm. Inverting the Laplace transform of the temperature field is shown in Fig. 13. To compute analytically the inverse Laplace transform of the temperature distribution is more complex. Hence, well-known algorithms such as Stehfest’s and Tzou’s are employed to determine the inverse Laplace transform of the temperature field. These algorithms offer efficient and accurate solutions to handle the complexity involved in the calculation process.

Fig. 10
figure 10

Impacts of Pr on temperature profile

Full size image
Fig. 11
figure 11

Impacts of R on temperature profile

Full size image
Fig. 12
figure 12

Impacts of \(\alpha \) on temperature profile

Full size image
Fig. 13
figure 13

Inverse of temperature profile

Full size image

The concentration distribution with various Sc values is shown in Fig. 14 as a final illustration. It has been shown that the concentration profile declines as Sc values rise. The rise in Sc values leads to a rise in the viscous force acting on fluid flow, resulting in a decrease in the concentration of fluid flow. In Fig. 15, the fractional parameter \(\alpha \) control over the concentration profile is shown. We see that when \(\alpha \) ranges from small to high, the concentration turns into an increasing function of \(\alpha \). Boundary layer thickness increases leading to an increase in concentration as \(\alpha \) rises. Figure 16 depicts the concentration field’s inverse Laplace transform. Stehfest and Tzou algorithms are employed to compute the invert Laplace transform of the concentration field, as exact solutions tend to be more intricate and challenging to obtain. These algorithms provide effective techniques to handle the complexity and accurately determine the concentration profile in such cases.

Fig. 14
figure 14

Impacts of Sc on concentration profile

Full size image
Fig. 15
figure 15

Impacts of \(\alpha \) on concentration profile

Full size image
Fig. 16
figure 16

Inverse of concentration profile

Full size image

Figures 17 and 18 investigate the impact of the fractional parameter on velocity by comparing Classical, Caputo, and Caputo–Fabrizio fractional derivatives. These figures clearly demonstrate that the Caputo–Fabrizio derivative exhibits a superior memory effect when compared to Caputo and Classical derivatives, as observed in [46, 47]. As \(\alpha \) increases, the viscosity of thermal and momentum boundary layers expands. In Fig. 19, a comparison between Casson-type fractional fluid and Khalid’s work [46] is presented. The figure indicates that the fractional derivative is the optimal choice for enhancing fluid motion. Notably, if we set the fractional parameters as \(\alpha \rightarrow 1\), Gm = 0, and \(q_r\) = 0, the fluid profiles become identical, highlighting the authenticity and validity of the present study.

Fig. 17
figure 17

Comparison between the velocities with Classical, Caputo, and Caputo–Fabrizio derivatives

Full size image
Fig. 18
figure 18

Comparison between the velocities with Classical, Caputo, and Caputo–Fabrizio derivatives

Full size image
Fig. 19
figure 19

Velocity distribution for comparison of our work with Khalid [46]

Full size image

5 Conclusion

The convection flow of Casson flow in a microchannel, considering the influence of heat radiation, is modeled utilizing the Caputo–Fabrizio derivative. Laplace transform method is apply to provide semi-analytical solutions. Graphical studies have been done on significant physical factors as the fractional, Casson, and thermal radiation parameters. It is possible to draw the following conclusions from the data:

  • A higher value of Gr and Gm results in a higher velocity profile.

  • Increasing value of Pr and Sc, velocity fluid is shown to decay or slow down.

  • As the value of the Casson flow parameter \(\beta \) increases, the velocity profile shows a decreasing trend.

  • With a higher value of \(\alpha \), the temperature, concentration, and velocity distributions exhibit an increase.

  • When a radiation parameter is present, fluid velocity rises.

  • In the presence of radiation parameters, the fluid temperature rises.

  • When it comes to improving fluid motion, the Caputo–Fabrizio fractional derivative stands out as the superior choice when compared to ordinary fluid behavior.

  • Microchannels are extensively used in microfluidic devices for various applications, including lab-on-a-chip systems, biomedical devices, and chemical analysis. Exploring the mass and heat transfer characteristics of Casson fluids in microchannels is crucial for designing efficient microfluidic systems.

  • In microscale heat exchangers and cooling systems, the behavior of non-Newtonian fluids like Casson fluids can affect thermal management and overall energy efficiency.

  • This research can have implications in biomedical engineering, where microchannels are used for drug delivery, cell manipulation, and tissue engineering. Understanding the behavior of Casson fluids in such applications can help improve efficiency and efficacy.