Skip to main content
SpringerLink
Log in

Numerical Investigation of Memory-Based Diffusivity Equation: The Integro-Differential Equation

  • Research Article - Petroleum Engineering
  • Published:
Arabian Journal for Science and Engineering Aims and scope Submit manuscript

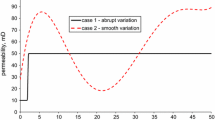
Abstract

The classical momentum balance equation discovered by Darcy in 1856 is expressed as the flux is proportional to the pressure gradient. However, the passage of the fluid through the porous matrix is very complex in general and hence may cause a local variation of the permeability. Thus, a one-dimensional model for an oil reservoir is introduced by considering the modification of conventional momentum balance equation. The modification is performed by introducing a derivative of fractional distributed orders as memory formalism. The fractional order is equivalent to a time-dependent diffusivity, and the distributed orders represent a variety of memory mechanisms to model the pressure response with a varied distribution of porosity and permeability. The time-domain and space-domain solutions are obtained by means of a numerical solution of the model equation. Results show that memory-based diffusivity equation has less pressure drops compared to Darcy model for a given distance and time. The differences in pressure drop between the two models become more significant when reservoir life becomes longer. The memory has an effect on the reservoir porosity and permeability which increases with time. If reservoir production continues, memory effect becomes more visible and contributes more in pressure response, which may be considered as a memory-driven mechanism. The proposed model is validated using Middle East filed data. The findings of this research establish the contribution of memory in reservoir fluid flow through porous media.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Abbreviations

a :

Lithology factor, dimensionless

A yz :

Cross- sectional area of rock perpendicular to the flow of flowing fluid, \({{m}^{2}}\)

c f :

\({c_o + c_{w } =}\) total fluid compressibility of the system, 1/pa

c s :

Formation rock compressibility of the system, 1/pa

c t :

\({c_f + c_{s } =}\) total compressibility of the system, 1/pa

c w :

Formation water compressibility of the system, 1/pa

k :

Variable reservoir permeability, \({{m}^{2}}\)

k o :

Initial reservoir permeability, \({{m}^{2}}\)

L :

Distance between production well and outer boundary along x- direction, m

p :

Pressure of the system, \({{N/m}^{2}}\)

p o :

Initial or reference pressure of the system, N/m2

q   :

Volume production rate at time t, \({{m}^{3}/{s}}\)

q i :

Au = initial volume production rate, \({{m}^{3}/{s}}\)

t :

Time, s

x :

Flow direction for 1D for a particular point, x from wellbore, m

\({\alpha }\) :

Fractional order of differentiation, dimensionless

\({\rho }\) :

Density at pressure p, \({{kg/m}^{3}}\)

\({\rho _o }\) :

Density at a reference pressure p o , \({{kg/m}^{3}}\)

\({\phi }\) :

Porosity of fluid media at pressure p, \({{m}^{3}/{m}^{3}}\)

ϕ o :

Initial porosity of fluid media at reference pressure \({p_o, {m}^{3}/{m}^{3}}\)

\({\mu }\) :

Fluid dynamic viscosity, \({{pas}}\)

\({\mu _0 }\) :

Initial fluid viscosity, \({{pas}}\)

\({\eta }\) :

\({\frac{k}{\mu } \left( t \right)^{\alpha } =}\) ratio of the pseudopermeability of the medium with memory to fluid viscosity, \({{m}^{3} {s}^{1+\alpha }/{kg}}\)

\({\xi }\) :

A dummy variable for time, i.e., real part in the plane of the integral, s

\({{\Gamma }}\) :

Euler gamma function

\({\Delta {t}}\) :

Time step, s

\({{\Delta }x}\) :

Grid block size, m

\({{\Delta \xi }}\) :

Dummy time step, s

References

  1. Taleghani A.D.: An improved closed-loop heat extraction method from geothermal resources. J. Energy Resour. Technol. 135, 0429041–0429047 (2013)

    Google Scholar 

  2. Majer E.L., Baria R., Stark M., Oates S., Bommer J., Smith B., Asanuma H.: Induced seismicity associated with enhanced geothermal systems. Geothermics 36(3), 185–222 (2007)

    Article  Google Scholar 

  3. Khatami F.S.R., Safavisohi B., Sharbati E.: Porosity and permeability effects on centerline temperature distributions, peak flame temperature, flame structure, and preheating mechanism for combustion in porous media. J. Energy Resour. Technol. 129, 59–65 (2007)

    Google Scholar 

  4. Bell M.L., Nur A.: Strength changes due to reservoir-induced pore pressure and stresses and application to lake oroville. J. Geophys. Res. 83, 4469–4483 (1978)

    Article  Google Scholar 

  5. Roeloffs E.A.: Fault stability changes induced beneath a reservoir with cyclic variations in water level. J. Geophys. Res. 93, 2107–2124 (1988)

    Article  Google Scholar 

  6. Caputo M.: Diffusion of fluids in porous media with memory. Geothermics 23, 113–130 (1999)

    Article  Google Scholar 

  7. Caputo M.: Models of flux in porous media with memory. Water Resour. Res. 36(3), 693–705 (2000)

    Article  Google Scholar 

  8. Barry D.A., Sposito G.: Analytical solution of a convection-dispersion model with time-dependent transport coefficients. Water Resour. Res. 25(12), 2407–2416 (1989)

    Article  Google Scholar 

  9. Kabala Z.J., Sposito G.: A stochastic model of reactive solute transport with time-varying velocity in a heterogeneous aquifer. Water Resour. Res. 27(3), 341–350 (1991)

    Article  Google Scholar 

  10. Steefel C.I., Lasaga A.C.: A coupled model for transport of multiple chemical species and kinetic precipitation/dissolution reactions with application to reactive flow in single phase hydrothermal system. Am. J. Sci. 294, 529–592 (1994)

    Article  Google Scholar 

  11. Dewers T., Ortoleva P.: Nonlinear dynamical aspects of deep basin hydrology: fluid compartment formation and episodic fluid release. Am. J. Sci. 294, 723–755 (1994)

    Article  Google Scholar 

  12. Kaviany, M.: Principles of Heat Transfer in Porous Media. Springer, New York (1995)

  13. Cushman J.H.: The Physics of Fluids in Hierarchical Porous Media: Angstroms to Miles. Kluwer, Dordrecht (1997)

    Book  Google Scholar 

  14. Wang L.: Flows through porous media: a theoretical development at macroscale. Transp. Porous Media 39, 1–24 (2000)

    Article  MathSciNet  Google Scholar 

  15. Di Giuseppe E., Moroni M., Caputo M.: Flux in porous media with memory: models and experiments. Transp. Porous Media 83(3), 479–500 (2010) doi: 10.1007/s11242-009-9456-4

    Article  Google Scholar 

  16. Hu X., Cushman J.: Non equilibrium statistical mechanical derivation of a non-local Darcy’s law for unsaturated/saturated flow. Stoch. Hydrol. Hydraul. 8, 109–116 (1991)

    Article  MATH  Google Scholar 

  17. Iaffaldano G., Caputo M., Martino S.: Experimental and theoretical memory diffusion of water in sand. Hydrol. Earth Syst. Sci. 10, 93–100 (2006)

    Article  Google Scholar 

  18. Shin M., Kim D.S., Lee J.W.: Deposition of inertia-dominated particles inside a turbulent boundary layer. Int. J. Multiph. Flow 29, 893–926 (2003)

    Article  MATH  Google Scholar 

  19. Chen M., Rossen W., Yortsos Y.C.: The flow and displacement in porous media of fluids with yield stress. Chem. Eng. Sci. 60, 4183–4202 (2005)

    Article  Google Scholar 

  20. Wyss W.: The fractional diffusion equation. J. Math. Phys. 27, 2782–2785 (1986)

    Article  MathSciNet  MATH  Google Scholar 

  21. Mainardi F., Mura A., Pagnini G., Gorenflo R.: Time-fractional diffusion of distributed order. J. Vib. Control 14, 1267–1290 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  22. Caputo M., Carcione J.M.: A memory model of sedimentation in water reservoirs. J. Hydrol. 476, 426–432 (2013) doi: 10.1016/j.jhydrol.2012.11.016

    Article  Google Scholar 

  23. Neuman S.: Eulerian-Lagrangian theory of transport in space-time nonstationary velocity-fields: exact nonlocal formalism by conditional moments and weak approximation. Water Resour. Res. 29(3), 633–645 (1993)

    Article  MathSciNet  Google Scholar 

  24. Gafiychuk V., Datsko B.: Different types of instabilities and complex dynamics in reaction-diffusion systems with fractional derivatives. J. Comput. Nonlinear Dyn. 7, 031001–031010 (2012)

    Article  Google Scholar 

  25. Blanc E., Chiavassa G., Lombard B.: A time-domain numerical modeling of two-dimensional wave propagation in porous media with frequency-dependent dynamic permeability. J. Acoust. Soc. Am. 134, 4610–4623 (2013)

    Article  Google Scholar 

  26. Hossain, M.E.; Mousavizadegan, S.H.; Islam, M.R.: A new porous media diffusivity equation with the inclusion of rock and fluid memories. In: SPE-114287-MS (2008)

  27. Oldham K.B., Spanier J.: The Fractional Calculus. Academic Press, New York (1974)

    MATH  Google Scholar 

  28. Podlubny I.: Fractional Differential Equations. Academic Press, San Diego (1999)

    MATH  Google Scholar 

  29. Samko S.G., Kilbas A.A., Marichev O.I.: Fractional Integrals and Derivatives: Theory and Applications. Gordon and Breach Science Publishers, Amsterdam (1993)

    MATH  Google Scholar 

  30. Kilbas A.A., Srivastava H.M., Trujillo J.J.: Theory and Applications of Fractional Differential Equations. Elsevier, Amsterdam (2006)

    MATH  Google Scholar 

  31. Caputo M., Cametti C.: The memory formalism in the diffusion of drugs through skin membrane. J. Phys. D Appl. Phys. 42, 125505–125512 (2009) doi:10.1088/0022-3727/42/12/125505

    Article  Google Scholar 

  32. Diethelm, K.: The Analysis of Fractional Differential Equations. Lecture Notes in Mathematics, 2004. Springer, Heidelberg (2010).

  33. Ortigueira, M.D.: Fractional Calculus for Scientists and Engineers. Lecture Notes in Electrical Engineering, vol. 84, Springer, Heidelberg (2011)

  34. Arenzon J.J., Levin Y., Sellitto M.: Slow dynamics under gravity: a nonlinear diffusion model. Phys. A 325, 371–395 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  35. Zhang H.M.: Driver memory traffic viscosity and a viscous vehicular traffic flow model. Transp. Res. Part B 37, 27–41 (2003)

    Article  Google Scholar 

  36. Caputo M.: Elasticitá e dissipazione. Zanichelli, Bologna (1969)

    Google Scholar 

  37. Hossain M.E., Mousavizadegan S.H., Ketata C., Islam M.R.: A novel memory based stress–strain model for reservoir characterization. J. Nat. Sci. Sustain. Technol. 1(4), 653–678 (2007)

    Google Scholar 

  38. Rammay, M.H.; Hassan, A.M.; Hossain, M.E.: A comparative study of PVT properties variations using Darcy and memory-based diffusivity equation. J. Nat. Sci. Sustain. Technol. 10(1), (2016). Accepted on Sep 02, 2015, in press

  39. Rammay, M.H.; Hassan, A.M.; Hossain, M.E.: A comparative study of porosity and permeability variations using Darcy and memory-based diffusivity equations. J. Nat. Sci. Sustain. Technol. 10 (1), (2016). Accepted on Sep 02, 2015, in press

  40. Timur, A.: An investigation of permeability, porosity, and residual water saturation relationships. In: SPWLA 9th Annual Logging Symposium, June, 23–26 (1968)

Download references

Author information

Authors and Affiliations

  1. Oil and Gas Program, Department of Process Engineering, Faculty of Engineering and Applied Science, Memorial University of Newfoundland, 240 Prince Philip Drive, St. John’s, NL, A1B 3X5, Canada

    M. Enamul Hossain

Authors
  1. M. Enamul Hossain
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to M. Enamul Hossain.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Hossain, M.E. Numerical Investigation of Memory-Based Diffusivity Equation: The Integro-Differential Equation. Arab J Sci Eng 41, 2715–2729 (2016). https://doi.org/10.1007/s13369-016-2170-y

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s13369-016-2170-y

Keywords

Search

Navigation