Skip to main content
SpringerLink
Log in

Non-existence of polyhedral immersions of triangulated surfaces in \(\mathbb R^3\)

  • Original Paper
  • Published:
Beiträge zur Algebra und Geometrie / Contributions to Algebra and Geometry Aims and scope Submit manuscript

Abstract

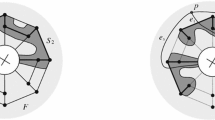
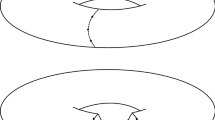
We present and apply a method for disproving the existence of polyhedral immersions in \(\mathbb R^3\) of certain triangulations on non-orientable surfaces. In particular, it is proved that neither of the two vertex-minimal, neighborly 9-vertex triangulations of the non-orientable surface of genus 5 are realizable as immersed polyhedral surfaces in \(\mathbb R^3\).

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

References

  • Archdeacon, D., Bonnington, C.P., Ellis-Monaghan, J.A.: How to exhibit toroidal maps in space. Discrete Comput. Geom. 38(3), 573–594 (2007). doi:10.1007/s00454-007-1354-3

  • Banchoff, T.F.: Triple points and surgery of immersed surfaces. Proc. Am. Math. Soc. 46, 407–413 (1974)

    Article  MathSciNet  MATH  Google Scholar 

  • Bokowski, J., Brehm, U.: A new polyhedron of genus \(3\) vertices. In: Intuitive geometry (Siófok, 1985), Colloq. Math. Soc. János Bolyai, vol. 48, pp. 105–116. North-Holland, Amsterdam (1987)

  • Bokowski, J., Brehm, U.: A polyhedron of genus \(4\) with minimal number of vertices and maximal symmetry. Geom. Dedicata 29(1), 53–64 (1989). doi:10.1007/BF00147470

  • Bokowski, J., Guedes de Oliveira, A.: On the generation of oriented matroids. Discrete Comput. Geom. 24(2–3), 197–208 (2000). doi:10.1007/s004540010027. The Branko Grünbaum birthday issue

  • Bokowski, J., Sturmfels, B.: Computational Synthetic Geometry. Lecture Notes in Mathematics, vol. 1355. Springer, Berlin (1989)

  • Bokowski, J.: A geometric realization without self-intersections does exist for Dyck’s regular map. Discrete Comput. Geom. 4(6), 583–589 (1989). doi:10.1007/BF02187748

  • Bokowski, J.: On heuristic methods for finding realizations of surfaces. In: Discrete differential geometry, Oberwolfach Semin., vol. 38, pp. 255–260. Birkhäuser, Basel (2008). doi:10.1007/978-3-7643-8621-4_13

  • Brehm, U., Leopold, U.: Polyhedral embeddings and immersions of many triangulated \(2\)-manifolds with few vertices. arXiv:1603.04877 (2016)

  • Brehm, U., Schulte, E.: Polyhedral maps. In: Handbook of discrete and computational geometry, CRC Press Ser. Discrete Math. Appl., pp. 345–358. CRC, Boca Raton (1997)

  • Brehm, U.: A maximally symmetric polyhedron of genus \(3\) vertices. Mathematika 34(2), 237–242 (1987). doi:10.1112/S0025579300013486

  • Brehm, U.: A nonpolyhedral triangulated Möbius strip. Proc. Am. Math. Soc. 89(3), 519–522 (1983). doi:10.2307/2045508

  • Brehm, U.: How to build minimal polyhedral models of the Boy surface. Math. Intelligencer 12(4), 51–56 (1990). doi:10.1007/BF03024033

  • Brehm, U.: Maximally symmetric polyhedral realizations of Dyck’s regular map. Mathematika 34(2), 229–236 (1987). doi:10.1112/S0025579300013474

  • Brehm, U.: Polyeder mit zehn Ecken vom Geschlecht drei. Geom. Dedicata 11(1), 119–124 (1981). doi:10.1007/BF00183194

  • Cervone, D.P.: Vertex-minimal simplicial immersions of the Klein bottle in three space. Geom. Dedicata 50(2), 117–141 (1994). doi:10.1007/BF01265307

  • Császár, Á.: A polyhedron without diagonals. Acta Univ. Szeged. Sect. Sci. Math. 13, 140–142 (1949)

    MathSciNet  MATH  Google Scholar 

  • Heawood, P.: Map colour theorem. Q. J. Math. 24, 332–338 (1890)

    MATH  Google Scholar 

  • Hougardy, S., Lutz, F.H., Zelke, M.: Surface realization with the intersection segment functional. Exp. Math. 19(1), 79–92 (2010). http://projecteuclid.org/euclid.em/1268404804

  • Jungerman, M., Ringel, G.: Minimal triangulations on orientable surfaces. Acta Math. 145(1–2), 121–154 (1980). doi:10.1007/BF02414187

  • Leopold, U.: Polyhedral embeddings and immersions of triangulated 2-manifolds. Diploma Thesis, TU Dresden (2009)

  • Lutz, F.H.: Enumeration and random realization of triangulated surfaces. In: Discrete Differential Geometry, Oberwolfach Semin., vol. 38, pp. 235–253. Birkhäuser, Basel (2008). doi:10.1007/978-3-7643-8621-4_12

  • Lutz, F.H.: The manifold page. TU Berlin. http://www.math.tu-berlin.de/diskregeom/stellar/ (2016)

  • McMullen, P., Schulz, C., Wills, J.M.: Polyhedral \(2\) with unusually large genus. Israel J. Math. 46(1–2), 127–144 (1983). doi:10.1007/BF02760627

  • Ringel, G.: Wie man die geschlossenen nichtorientierbaren Flächen in möglichst wenig Dreiecke zerlegen kann. Math. Ann. 130, 317–326 (1955)

    Article  MathSciNet  MATH  Google Scholar 

  • Schewe, L.: Nonrealizable minimal vertex triangulations of surfaces: showing nonrealizability using oriented matroids and satisfiability solvers. Discrete Comput. Geom. 43(2), 289–302 (2010). doi:10.1007/s00454-009-9222-y

  • Steinitz, E.: Polyeder und Raumeinteilungen. Encyclopädie der mathematischen Wissenschaften 3 (Geometrie), 1–139 (1922)

  • Ziegler, G.M.: Lectures on Polytopes, Graduate Texts in Mathematics, vol. 152. Springer, New York (1995). doi:10.1007/978-1-4613-8431-1

Download references

Acknowledgments

The author would like to thank Ulrich Brehm for the support and guidance received while working on her Diploma Thesis at TU Dresden under his supervision, as well as for the continuing stimulating discussions on the subject.

Author information

Authors and Affiliations

  1. Technische Universität Chemnitz, Fakultät für Mathematik, 09107, Chemnitz, Germany

    Undine Leopold

Authors
  1. Undine Leopold
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Undine Leopold.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Leopold, U. Non-existence of polyhedral immersions of triangulated surfaces in \(\mathbb R^3\) . Beitr Algebra Geom 58, 247–265 (2017). https://doi.org/10.1007/s13366-016-0319-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s13366-016-0319-1

Keywords

Mathematics Subject Classification

Search

Navigation