1 Introduction

Building resilient infrastructure, promoting inclusive and sustainable industrialization and fostering innovation are among the Sustainable Development Goals set by the United Nations for 2030 [1]. Aligned with these goals, technological evolution, the Internet of Things and big data have significantly advanced structural health monitoring in infrastructure in recent years.

In addition, as the major communication axes are completed, conservation becomes increasingly important compared to the construction of new infrastructure because, immediately after its traffic opening, the administration in charge of its management has the responsibility of its maintenance.

Within large linear works, bridges can be considered one of the most critical elements, both due to their strategic nature in the communications system and because of their technical complexity. For this reason, on-site preventive inspections are generally carried out on structures in service.

The monitoring of structures opened to traffic makes it possible to carry out quasi-continuous preventive maintenance, which allows detecting incidents at an early stage and saving on eventual repair costs. In fact, each moving load can be considered a test. These actions contribute to a more efficient management of the infrastructure network.

Several studies may be mentioned. Among others, in terms of eigenfrequencies, there are studies about the Europa Bridge (Austria), where a structural health monitoring system was installed on the basis of the first eigenfrequency [2], about the Infante Don Enrique Bridge (Porto, Portugal), where a model was established to base the structural health monitoring system based on the correction of the eigenfrequencies registers by taking into account several environmental variables such as temperature and the maximum accelerations [3,4,5], about the Paderno Bridge (Italy) about the variation of the eigenfrequencies as a function of the excitation changes [6], and about the Valladolid Footbridge (Spain), where it was confirmed that the modal parameters depend on temperature [7, 8].

More specifically, in relation with the possibility of damage detection on the basis of changes in the damping factor references which may be mentioned are: a study on the Regau Bridge (Austria) [2] and the reduced scale test made by Kölling, Resnik and Sargsyan [9]; on the actual damaged structure, damping increased by 85% while for the reduced scale model the damping increase ranged between 50 and 100% in the forced vibrations tests and a reduction in the ambient vibrations ranging between 10 and 20%.

In other branches of engineering, such as the aeronautics industry, a very important line of work is the detection of incidents based on changes in the dynamic behaviour of structures. However, given that the construction of bridges is not an industrialized process and each structure is adapted to the specific needs of its location, the extrapolation of conclusions to the world of civil engineering is not immediate.

Furthermore, not all structures always have instrumentation that allows continuous detailed studies, but usually have certain instrumentation for a limited period of time. Consequently, methods of easy application in the field are needed.

Similarly, the results must be sensitive enough to detect changes in dynamic behaviour as early as possible but, at the same time, reliable to avoid false positives.

Dynamic studies of civil engineering structures normally include, among other parameters, calculation of the natural frequencies of vibration and modal damping ratios associated with these frequencies because the variations can be used as an element of structural diagnosis.

However, it has been observed that in the study of specific dynamic events of structures opened to traffic, there are important variations in the values of the modal damping ratio according to the calculation methods applied for its determination [10,11,12]. In this same sense, as studies start from a continuous monitoring, calculation methods must be automated and give as a result trustworthy values.

For this reason, the objective of this paper is first to review the methods for calculating the modal damping ratio commonly applied. For these purposes, the methods are classified according to whether they require excitation control and, if not, if they are applicable to specific dynamic event records or continuous records.

Second, a possible alternative method is proposed that helps to improve the calculation of the modal damping ratio. This method is a consequence of the practical expertise of the authors in the analysis of bridges opened to traffic and the detected needs along these studies, among them the convenience of having a sufficiently trustworthy tool that can be directly applied to systems with various degrees of freedom (DOFs) under the conditions that are examined in the following sections.

Third and last, a comparative analysis of the several calculation methods of the modal damping ratio is carried out, studying its behaviour both over a group of signals generated through simulation and in the case of a real structure opened to traffic.

2 Existing experimental calculation methods

Various methods for evaluating the modal damping factor are traditionally studied in the literature on structural dynamics [2, 13,14,15,16,17,18]. The content of the present paper is restricted to the case of viscous damping, which is usually considered in bridges in service condition.

Next, a brief review of the methods that are more frequently used is presented, and the particularities they present for their application in experimentally registered accelerograms in bridges are indicated.

2.1 Experimental calculation methods with excitation control

First, there is a set of experimental calculation methods to obtain the modal damping ratio that require controlling the excitation to which the structure is subjected [13, 14]:

  • In the resonant amplification method, the structure is subjected to harmonic loads of equal amplitude and different frequencies over a range wide enough to include the natural frequency of the system. The modal damping ratio is obtained from the relationship between the static displacement and the maximum recorded displacement.

  • The bandwidth method over the frequency-response curve, also known as the half-power method, is based on the fact that the shape of the curve of response versus frequency depends on the damping of the system. In this case, the modal damping ratio is obtained from the relationship between the frequencies in which the response amplitude is reduced to \(1/\sqrt{2}\) of its maximum value.

  • The resonance energy loss per cycle method, whose basis is the theoretical relationship between the maximum damping force and the maximum speed of the system, is associated with resonance of the system.

In these three cases, those methods require:

  • Carrying out a test whose implementation is relatively complex in structures opened to traffic because it usually requires traffic interruption.

  • Having great control over the excitation source in such a way as to allow a sufficiently precise frequency sweep.

  • Finally, bringing the structure to frequencies close to the resonance, which implies, on the one hand, that the response to the excitation must be relevant and, on the other hand, that it can cause structural damage.

Therefore, this set of calculation methods is not directly applicable to the analysis of environmental vibrations, so they are not the object of the comparative study carried out throughout the paper.

2.2 Experimental calculation methods without excitation control (ambient vibrations)

2.2.1 Methods applicable to specific dynamic event records

This set of calculation methods is applied to specific dynamic events that are the result of ambient vibrations; therefore, the excitation is not controlled. In each event, after the initial phase of forced vibrations, the selection of the period of free vibrations and its subsequent analysis follow. The main calculation methods within this set are as follows:

  • First, the classic procedure par excellence is the logarithmic decrement method, which is directly applicable to single-DOF systems undergoing free vibrations [13]. In this case, as is well known, the modal damping ratio \(\xi\) can be approximately determined as the ratio between two maximum displacements (\(x_{q}\) and \(x_{q+n}\)) measured over n consecutive cycles:

    $$\begin{aligned} \xi =\frac{\delta _{n}}{2\,\pi \,n\left( \omega / \omega _{D}\right) }\approx \frac{\delta _{n}}{2\,\pi \,n}=\frac{\ln \left( x_{q}/x_{q+n}\right) }{2\,\pi \,n}\, \end{aligned}$$
    (1)

    where \(\delta _{n}\) is the logarithmic decrement in n cycles and \(\omega\) and \(\omega _{D}\) are the circular frequencies of the undamped and damped systems, respectively. Alternatively, this same expression can be applied to the records of the accelerograms of the structure opened to traffic, which is the usual practice. The approximation of Expression (1) can be used with only a 2% error even when \(\xi =0.20\). Nevertheless, the normal situation in bridges is that the modal damping ratio has reduced values; therefore, this expression is very precise. The only exception is the case of very extreme circumstances, such as the case in which the behaviour approaches the elastic limit under seismic actions. However, in practice, in accelerograms experimentally recorded in bridges, several vibration modes are superimposed, requiring the use of filters on the recorded signals [19, 20], which is valid only when the natural frequencies are sufficiently separated in the spectrum. Additionally, once the signal is isolated for a given frequency, a criterion must be established to determine between which extreme values to carry out the calculation. It is possible to take different values separated by several cycles and take their average, calculate a regression line on the extreme values of the accelerogram or even make a least squares adjustment to approximate the filtered signal to the theoretical curve of the damped free vibrations.

  • The second of the most common methods is the bandwidth method applied over the signal spectrum instead of over the response-frequency curve [2]. After determining the frequencies \(f_{1}\) and \(f_{2}\) at which the peak of the curve is reduced to \(1/\sqrt{2}\) its maximum value, the formulation corresponding to the half-power method is applied:

    $$\begin{aligned} \xi \approx \frac{f_{2}-f_{1}}{f_{2}+f_{1}}. \end{aligned}$$
    (2)

    In opposition to the practical difficulties in obtaining the response-frequency curve in an opened-to-traffic bridge, the application of this method to the signal spectrum is quick and easy and is also easily extrapolated to the case of systems with several natural frequencies. However, technical references [2] suggest that the results are a poor indication of the modal damping ratio. Therefore, the application of this method on the signal spectrum is ideal when a precise value of the damping is not needed or when the objective is simply to compare different structures with each other.

  • Alternatively, another formulation can be used for the bandwidth method applied to the signal spectrum based on the half-quadratic gain method [21]:

    $$\begin{aligned} \xi =\sqrt{\frac{1}{2}-\sqrt{\left( 4+4\left( \frac{f_{2}-f_{1}}{f_{p}}\right) ^{2}-\left( \frac{f_{2}-f_{1}}{f_{p}}\right) ^{4}\right) ^{-1}}}\, \end{aligned}$$
    (3)

    where \(f_{p}\) is the registered peak frequency.

  • The fourth and last of the methods in this set is the adjustment of the accelerogram \( a(t)\) to the theoretical curve of the damped free vibrations (using a curve fitting or adjustment method) [2]:

    $$\begin{aligned} a(t)=A_{0}\,e^{-\xi \,\omega \,t}\,\cos (\omega \,t-\alpha _{0})\, \end{aligned}$$
    (4)

    where \(A_{0}\) is the initial amplitude and \(\alpha _{0}\) is the initial phase difference of the wave. In this case, in addition to the need to arrange the filtered wave, there are three unknown variables in total, since together with the modal damping ratio, neither the amplitude nor the initial phase of the wave are known, which complicates the calculation. Sometimes, in addition, in practice, several iterations are necessary to obtain a reasonably precise modal damping ratio value, and when the accelerograms have some anomaly, achieving convergence is not always easy.

Currently, having a set of punctually recorded events, which either come from different test campaigns or are the result of having set certain thresholds on a continuous auscultation system, is the most common case in the dynamic study of bridges opened to traffic. Therefore, the comparative analysis of these calculation methods and their improvement proposal is the main object of this paper.

2.2.2 Methods applicable to continuous dynamic records

Within the third set of modal damping ratio calculation methods, there are those that do not require excitation control and are applicable to continuous dynamic records, such as those obtained from environmental vibrations. The most widespread are the following:

  • First, the random decrement technique (RDT) arose as a consequence of the desire to monitor the behaviour of aeronautical structures in real time and to be able to prematurely detect anomalies [9, 22,23,24,25,26]. The random decrement \(\delta _{a}(\tau )\) is mathematically defined as:

    $$\begin{aligned} \left\{ \begin{array}{l} x_{0}(t)=x(t)-x_{s} \\ \delta _{a}(\tau )=\dfrac{1}{n}\sum \limits _{i=1}^{n}x_{0}\ (t_{i}+\tau ) \end{array} \right. \, \end{aligned}$$
    (5)

    with the condition that \(t_{i}=t\) when \(x_{0}=0\). Upon applying Expression (5), as the time segments are averaged, the random part tends to become zero in the curve of the random decrement \(\delta _{a}\left( \tau \right)\). Therefore, this new curve can be interpreted as a free oscillation, and from it, the modal damping ratio can be determined. The two essential parameters are the selection threshold and the temporal length of the segments. Therefore, some previous knowledge of the signal is necessary. Some authors [9] propose taking fixed values for the selection threshold above the standard deviation of the signal and a number of segments sufficient to guarantee a meaningful average. For this last parameter, these same authors suggest, in order to obtain a robust estimation of the damping, that this must contain at least a part of the accelerogram that includes the complete free vibration. Among the advantages of this method is the fact that in the tests carried out, the random decrement remains practically invariant until the structure presents some type of damage, so the method can be used in structural health monitoring systems. As the main drawbacks of the method, it should be noted that other authors [2] have detected problems when the method is applied to systems where two or more differentiated frequencies coexist, recommending the use of a band-pass filter before processing the time series. Likewise, it is noted that the choice of filter also affects the results. Another drawback is the fact that although the initial time series required does not have to be very long, a high rate of digitalization is required to obtain a valid result.

  • The second of the methods included in this section is known as stochastic subspace identification (SSI), which was developed by Van Overschee and De Moor [27]. The general stochastic identification problem can be described as follows. Given s measures of \({\textbf {y}}_{k} \in \Re ^{l}\), generated by the unknown stochastic system of order n:

    $$\begin{aligned} \left\{ \begin{array}{l} {\textbf {x}}_{k+1}^{s}={\textbf {A}}\ {\textbf {x}}_{k}^{s}+{\textbf {w}}_{k} \\ {\textbf {y}}_{k}={\textbf {C}}\ {\textbf {x}}_{k}^{s}+{\textbf {v}}_{k} \end{array} \right. \, \end{aligned}$$
    (6)

    with the vectors \({\textbf {w}}_{k}\) and \({\textbf {v}}_{k}\) of the null mean and covariance matrix satisfying

    $$\begin{aligned} \textrm{E}\ \left[ \left( \begin{array}{c} {\textbf {w}}_{p} {\textbf {v}}_{p} \end{array} \right) \ \left( \begin{array}{cc} {\textbf {w}}_{q}^{\textrm{T}}&{\textbf {v}}_{q}^{\textrm{T}} \end{array} \right) \right] = \left( \begin{array}{ll} {\textbf {Q}} &{}\quad {\textbf {S}} \\ {\textbf {S}}^{\textrm{T}} &{}\quad {\textbf {R}} \\ \end{array} \right) \ \delta _{pq} \, \end{aligned}$$
    (7)

    determine the order n of the unknown system, as well as the matrices of the system \({\textbf {A}}\in \Re ^{n\times n}\) and \({\textbf {C}}\in \Re ^{l\times n}\). Upon making use of the developed technique, all matrices can be determined. Finally, the modal damping ratio is determined from the relationship between it and the eigenvalues of matrix \({\textbf {A}}\).

As in the previous section, these methods are applicable to structures opened to traffic and do not require knowing the original excitation. However, they require continuous instrumentation in and on the bridge, which is becoming increasingly infrequent due to its cost, but it is not the usual practice except in structures that must be subjected to a specific study.

By its conception, this set of methods is not part of the main object of the paper. However, to provide the broadest possible view from the academic point of view, an adaptation of the random decrement technique, whose formulation is simpler and, therefore, more readily applied in real structures, is included in the comparative study when possible.

3 Alternative calculation method proposal based on signal spectrum reduction

As a consequence of the practical experience of the authors in the study of accelerograms of bridges opened to traffic, an alternative calculation method for the modal damping ratio is formulated below, based on the signal spectrum reduction (spectrum reduction method, SRM), conceived for the study of specific dynamic events caused by ambient vibrations in multiple-DOF systems whose vibration modes are reasonably separated and where the damped free vibration predominates in the registered accelerogram.

This proposal starts from the fact that the theoretical accelerogram a(t) of a damped single-DOF system can be modelled as:

$$\begin{aligned} a(t)=A_{1}e^{-\xi _{1}\,\omega _{1}\,t}\cos (\omega _{1}\,t-\alpha _{1})\, \end{aligned}$$
(8)

where \(A_{1}\) is the initial amplitude, \(\xi _{1}\) is the modal damping ratio, \(\omega _{1}\) is the natural circular frequency and \(\alpha _{1}\) is the initial phase difference of the system. The Fourier transform of the wave is a function of the frequency \(\omega\) and directly proportional to the amplitude due to the property of linearity:

$$\begin{aligned} \mathcal {F}\left[ a(t)\right]= & {} \int _{-\infty }^{+\infty }a(t)\,e^{-j\,\omega \,t}\textrm{d}t \nonumber \\ {}= & {} A_{1}\int _{-\infty }^{+\infty }e^{-\xi _{1}\,\omega _{1}\,t}\cos (\omega _{1}\,t-\alpha _{1})\,e^{-j\,\omega \,t}\textrm{d}t\, \end{aligned}$$
(9)

where j is the imaginary unit.

That is, to study the modal damping ratio, instead of analysing how the amplitude of the original wave decreases in the time domain, one can alternatively see how its Fourier transform, or its spectrum of magnitudes, decreases in the frequency domain.

Starting from (8), the expression of the same damped wave shifted by a time increment \(\Delta t\) equivalent to n cycles is:

$$\begin{aligned} a(t+\Delta t)=A_{1}e^{-\xi _{1}\,\omega _{1}\,(t+\Delta t)}\cos (\omega _{1}\,(t+\Delta t)-\alpha _{1}). \end{aligned}$$
(10)

Applying that:

$$\begin{aligned} \Delta t=\frac{2\, \pi }{\omega _{1}}n\, \end{aligned}$$
(11)

the relation between \(a(t+\Delta t)\) and a(t) is as follows:

$$\begin{aligned} \begin{aligned} a(t+\Delta t)&=A_{1}e^{-\xi _{1}\,\omega _{1}\,\left( t+\frac{2\, \pi }{\omega _{1}}n\right) }\cos \left( \omega _{1}\,\left( t+\frac{2\, \pi }{\omega _{1}}n\right) -\alpha _{1}\right) \\&=A_{1}e^{-\xi _{1}\,\omega _{1}\,t}e^{-2\pi \,\xi _{1}\,n}\cos (\omega _{1}\,t-\alpha _{1}+2\,\pi \,n) \\&=e^{-2\pi \,\xi _{1}\,n}A_{1}e^{-\xi _{1}\,\omega _{1}\,t}\cos (\omega _{1}\,t-\alpha _{1}) \\&=e^{-2\pi \,\xi _{1}\,n}a(t). \end{aligned} \end{aligned}$$
(12)

Thus, the relationship between the Fourier transforms of the same damped wave shifted n cycles is:

$$\begin{aligned} \begin{aligned} \mathcal {F}\left[ a(t+\Delta t)\right]&=\int _{-\infty }^{+\infty }a(t+\Delta t)\,e^{-j\,\omega \,t}\textrm{d}t \\&= \int _{-\infty }^{+\infty }e^{-2\pi \,\xi _{1}\,n}a(t)\,e^{-j\,\omega \,t}\textrm{d}t \\&= e^{-2\pi \,\xi _{1}\,n} \int _{-\infty }^{+\infty }a(t)\,e^{-j\,\omega \,t}\textrm{d}t \\&= e^{-2\pi \,\xi _{1}\,n} \mathcal {F}\left[ a(t)\right] \\&= e^{-2\pi \,\xi _{1}\,f_{1}\,\Delta t} \mathcal {F}\left[ a(t)\right] . \end{aligned} \end{aligned}$$
(13)

As a consequence of Expression (13), the theoretical relationship between the Fourier transforms is constant and depends only on the modal damping ratio and the number of cycles of the displacement or, equivalently, on the modal damping ratio, the natural frequency and the time increment.

The previous reasoning allows, from the procedure represented schematically in Fig. 1, to obtain the modal damping ratio of a simple DOF system. Indeed, if the magnitude spectra of the initial and final parts of the accelerogram are calculated, separated \(\Delta t\) or n cycles, represented in red and green, respectively, the relationship between both is as indicated in Expression (13). Taking, for example, the peak values of the magnitude spectra, \(A_{1,q}\) and \(A_{1,q+n}\), which in practice is interesting to reduce the numerical calculation errors produced by taking smaller values, the following expression is reached:

$$\begin{aligned} \xi _{1}=\frac{\ln {(A_{1,q}/A_{1,q+n})}}{2\,\pi \,n}=\frac{\ln {(A_{1,q}/A_{1,q+n})}}{2\,\pi \,f_{1}\,\Delta t}\, \end{aligned}$$
(14)

similar to Expression (1) but in terms of the magnitude spectrum.

Fig. 1
figure 1

Application of the SRM in single-DOF systems

Full size image

Up to this point, the SRM proposed does not present any practical operational advantage since instead of applying Expression (1) directly to the accelerogram, it requires calculating two magnitude spectra on which a similar expression is finally applied.

However, the main advantage of the proposed alternative calculation method is that it is also directly applicable to multiple DOFs, as long as they are reasonably separated, as is seen below.

Indeed, in a multiple-DOF system, because of the principle of modal superposition, the damped wave can be modelled as a sum of waves by means of the following expression, where each i-th wave has an amplitude \(A_{i}\), a circular frequency \(\omega _{i}\), a phase difference \(\alpha _{i}\) and an associated modal damping ratio \(\xi _{i}\):

$$\begin{aligned} a(t)=\sum _{i}A_{i}e^{-\xi _{i}\,\omega _{i}\,t}\cos (\omega _{i}\,t-\alpha _{i}). \end{aligned}$$
(15)

Upon applying the property of linearity, the Fourier transforms of the original wave and the same wave shifted in time are equal to the sum of the Fourier transforms of the waves associated with each mode:

$$\begin{aligned} \mathcal {F}\left[ a(t)\right]= & {} \sum _{i}\mathcal {F}\left[ a_{i}(t)\right] \ \ \ \text {and} \end{aligned}$$
(16)
$$\begin{aligned} \mathcal {F}\left[ a(t+\Delta t)\right]= & {} \sum _{i}\mathcal {F}\left[ a_{i}(t+\Delta t)\right] . \end{aligned}$$
(17)

If the modes of vibration are reasonably separated, in the neighbourhood of each k-th natural frequency, the contributions to the magnitude spectrum of the remaining modes of vibration are negligible with respect to the contribution of vibration mode k. Therefore, around the k-th natural frequency, the Fourier transform of the wave is approximately equal to the Fourier transform of the k-th vibration mode:

$$\begin{aligned} \mathcal {F}\left[ a(t)\right] \arrowvert _{(f_{k})}=\sum _{i}\mathcal {F}\left[ a_{i}(t)\right] \arrowvert _{(f_{k})}\approx \mathcal {F}\left[ a_{k}(t)\right] . \end{aligned}$$
(18)

Analogously, in the case of the displaced wave:

$$\begin{aligned} \begin{aligned} \mathcal {F}\left[ a(t+\Delta t)\right] \arrowvert _{(f_{k})}&=\sum _{i}\mathcal {F}\left[ a_{i}(t+\Delta t)\right] \arrowvert _{(f_{k})} \\&\approx \mathcal {F}\left[ a_{k}(t+\Delta t)\right] \\&\approx e^{-2\pi \,\xi _{k}\,f_{k}\,\Delta t} \mathcal {F}\left[ a_{k}(t)\right] . \end{aligned} \end{aligned}$$
(19)

Therefore, from Expression (19) it follows that the k-th modal damping factor can be approximated by the following expression:

$$\begin{aligned} \xi _{k}\approx \frac{\ln {(A_{k,q}/A_{k,q+n})}}{2\,\pi \,f_{k}\,\Delta t}\, \end{aligned}$$
(20)

again similar to Expression (1) but in terms of the magnitude spectrum.

Figure 2 schematically represents the practical application of the SRM proposed for multiple-DOF systems. As can be seen from the accelerogram a(t), the magnitude spectra of its initial and final parts are obtained, represented in red and green, respectively. Upon applying Expression (20) to the peaks of the magnitude spectrum corresponding to each natural frequency, the modal damping ratios associated with each frequency can be obtained in an approximate way. The main advantage of this method is that it is possible to approach the study of multiple-DOF systems whose modes are reasonably separated, which usually happens in bridges, without the need to apply filters on the original signal to isolate each mode of vibration.

The theoretical formulation does not impose any limit to the length of the segments nor to the separation cycles between them. Nevertheless, the practical application of the method suggests:

  • First, the length of the segments must be such that it may allow an adequate characterization of the wave or, in another way, the nature of the different eigenfrequencies being excited has to become clear. In this sense, it is interesting to study the sensitivity of the theoretical waves which is explained later on, at Sect. 4.3, and graphically represented in Fig. 9. It may be observed that even with 1 s long segments, the results were exact in all cases, in spite of having a very reduced length.

  • Second, the separation between the cycles must make it possible to appreciate damping of the structure at free vibration.

It is noted that, in the case that the free damped vibration does not predominate in the recorded accelerogram, this method would not be applicable since the system would be excited by external forces and the exposed formulation would not be valid.

Furthermore, to be sure that the vibration modes are reasonably spaced, a certain previous knowledge of the structure is required. This happens in the case of the example which is presented in the paper. But it may not be true in other cases and, consequently, the application of SRM should be done with caution or it may even not be possible. It has to be reminded that one of the hypotheses which has been used in the demonstration is that the contribution of other modes in the neighbourhood of an eigenfrequency must be negligible.

In addition to its theoretical formulation, in the following sections, it is shown that the practical results obtained, both in simulations and in real cases, support the use of SRM.

Fig. 2
figure 2

Application of the SRM in multiple-DOF systems

Full size image

4 Comparative analysis of theoretical simulations

4.1 Description of the theoretical simulations

In this section, a comparative analysis of the different calculation methods of the modal damping ratio is carried out on the following theoretically simulated waves, whose parameters are of an order of magnitude similar to those of real structures:

  • A first simple wave, \(w_{1}\), of amplitude 0.005 g, frequency 1 Hz, modal damping ratio 2% and zero phase difference.

  • A second simple wave, \(w_{2}\), of amplitude 0.001 g, frequency 2 Hz, modal damping ratio 1% and phase difference equal to \(\pi /4\) rad.

  • A third simple wave, \(w_{3}\), of amplitude 0.0005 g, frequency 4 Hz, modal damping ratio 0.5% and phase difference equal to \(\pi /3\) rad.

  • A fourth composed wave, \(w_{4}\), equal to the sum of the first three.

  • A fifth and last wave, also composed, \(w_{5}\), equal to the sum of the first three to which a random noise of maximum amplitude 0.0001 g has been added. As a reference, the accelerometers that were used in the instrumentation of the real structure that is analysed in Sect. 5, have a resolution of \(1.3\times 10^{-6}\ \text {g}\) for frequencies lower than 10 Hz [28]. To simulate the effect of the real instrumentation, initially, random noise with a maximum amplitude of \(10^{-5}\ \text {g}\) was considered. However, that value did not lead to any appreciable difference between the results of waves \(w_{4}\) and \(w_{5}\). Therefore, the amplitude value was increased to 0.0001 g in these simulations. Despite this, as seen later, the differences in the results remained very small.

In all cases, the waves were simulated with a total duration of 50 s, and discrete data were generated every 0.02 s, which is a common sampling frequency in structure monitoring.

4.2 Methodology for obtaining the values of the modal damping ratio

For the construction of the magnitude spectra, the discrete Fourier transform (DFT) was used. For a known vector in the time domain \({\textbf{u}}=\left\{ u_{r}\right\}\), the DFT is defined as the following vector in the frequency domain [29]:

$$\begin{aligned} {\textbf{v}}=\left\{ v_{s}\right\} =\frac{1}{n^{(1-a)/2}} \sum _{r=1}^{n} u_{r}\,e^{2\,\pi \,j\,b\,(r-1)\,(s-1)/n}\, \end{aligned}$$
(21)

where:

  • a and b are the DFT parameters, which by default are taken as 0 and 1, respectively, and

  • j is the imaginary unit (\(j^{2}=-1\)).

The DFT converts a time domain vector between 0 and \(t_{\max }\), with a time increment (step) between the initial data p, into a symmetric vector in the frequency domain between 0 and 1/p, which for these effects takes only the first half, between 0 and \(1/2\,p\). This is consistent with the Nyquist–Shannon sampling theorem, which indicates that to accurately analyse a wave, a sampling frequency greater than twice the maximum frequency must be used. However, the maximum discretization that can be obtained in the frequency domain is a function of the length of the initial vector. Thus, the natural frequency increments that are obtained, p, are equal to \(1/t_{\max }\).

Therefore, in the theoretical cases studied, the maximum sampling frequency was equal to 25 Hz with a maximum discretization in the frequency domain of 0.02 Hz.

As an example, Fig. 3 shows the graphical representation of the theoretically simulated wave \(w_{5}\) and its corresponding magnitude spectrum.

Fig. 3
figure 3

Theoretically simulated wave \(w_{5}\) (accelerogram and magnitude spectrum)

Full size image

For the application of the set of methods for calculating the modal damping factor to theoretically simulated waves, the following issues were taken into account:

  • In all cases, we had the help of a symbolic calculation computer program (Wolfram Mathematica), where the necessary algorithms were implemented.

  • In the calculation methods that required a previous filtering of the signal (logarithmic decrement and curve adjustment, applied both to the original signal and to the RDT curve), with the aim to avoid introducing additional perturbations, an ideal pass-band of \(\pm 0.2\) Hz was applied to the simulated signal in the vicinity of each frequency. Similarly, the central part of the waves were selected in the filtered accelerograms since, as a consequence of the application of the filters, disturbances appeared at the ends, which were eliminated.

  • In the case of the logarithmic decrement method, after having filtered the signal, selected its central part and located the extremes, Formulation (1) was applied to all possible pairs of extremes as long as they were separated by at least 5 consecutive cycles. The modal damping ratio was obtained by averaging all possible combinations.

  • For the two methods based on bandwidth, the values to apply expressions (2) or (3) on the magnitude spectra were obtained by performing linear interpolation.

  • For the application of the curve adjustment method, each iteration started from a range of values of amplitude, modal damping ratio and phase difference. Initially, a subdivision of 10 intervals was made in each case, but it was seen that this would not be enough to assure convergence. Therefore, the subdivision was increased to 20 intervals, corresponding to a total of \(21^{3}\) estimates for each iteration. Under this framework, the residuals for each estimate were calculated, the lowest value was sought and the three variables that correspond to said residual were identified. In all cases, two iterations were carried out, the first one starting with a range of amplitudes between 0 and twice the maximum value of the accelerogram, a range of modal damping factors between 0 and 5% and a range of phase difference between \(-\pi\) and \(\pi\), which gave a first triple of variables of amplitude, modal damping ratio and phase difference. The second iteration was calculated centred on the triple resulting from the previous iteration, with a range of \(\pm 25\%\), avoiding values outside the possible ranges.

  • In the case of the SRM, the initial and final spectra were calculated from the isolated signals between 0 and 10 s and between 40 and 50 s, respectively.

  • Last, although the RDT method is designed for continuous records and not specifically for the study of particular events, to analyse its behaviour in these cases, RDT curves were obtained by setting the threshold at 95% of the maximum recorded value of the accelerogram and taking intervals of 20 s duration. Subsequently, the logarithmic decrement and curve adjustment methods were applied to these RDT curves under the same conditions as described above.

4.3 Obtained results and discussion

The obtained results are summarized in Table 1 and Fig. 4. As main conclusions, the following can be highlighted:

Table 1 Comparison of modal damping ratios obtained from the theoretically simulated waves
Full size table
Fig. 4
figure 4

Comparison of modal damping ratios obtained from the theoretically simulated waves

Full size image

  • First, it should be noted that, in general and with the particularities described below, the values of the modal damping ratio obtained by applying the different calculation methods were reasonably close to the theoretical values.

  • In the case of the logarithmic decrement method, the error was introduced in the signal filtering process, which is a strictly necessary step when there are several simultaneous vibration modes, which is the situation that usually occurs in real cases. However, the average relative error reached was less than 1%, and the maximum never reached the value of 2%.Footnote 1 A study is made of how the results of wave \(w_{5}\) vary according to the number of consecutive cycles that are adopted to calculate the values to be averaged, taking as a reference 2, 5, 10, 15 and up to 20 consecutive cycles when possible. As shown in Fig. 5, no significant changes were observed since the variations detected were on the order of \(10^{-4}\) or even less.

  • When the two formulations based on the bandwidth method were applied to the signal spectrum, the average relative error was on the order of 1%, even having reached the order of hundreds in the case of the three simple waves \(w_{1}\), \(w_{2}\) and \(w_{3}\).

  • In the case of the curve adjustment method, the obtained values of the modal damping ratio were exact in the case of waves \(w_{1}\), \(w_{2}\) and \(w_{3}\) but not in the case of the two composed waves \(w_{4}\) and \(w_{5}\) as a consequence of the mismatches introduced in the signal filtering process. In these last two waves, the highest relative errors were reached, which were on the order of 15% in the case of the second natural frequency and 42% in the case of the third natural frequency. On wave \(w_{5}\), the effect of the number of iterations on the results of the three parameters obtained was studied: modal damping ratio, amplitude and phase difference (Figs. 6, 7 and 8). Although in the vast majority of the cases with two iterations it was enough to stabilize the results, for higher frequencies it can be necessary more iterations. Once a certain value is reached, with the implemented routines, no improvements in the results were achieved even with further iteration. It must be noted that results are also a function of the maximum number of iterations. For a reasonable computation effort, the maximum number of iterations were fixed to 2 in this study. But, as it may be seen on Fig. 6, a relevant increase in the number of iterations could also drive to almost exact results for this method. As an example, for 10 iterations and after the stabilization of the results, the damping values would be 2.05, 1.07 and 0.52% respectively for the first three eigenfrequencies of the simulated wave number 5. This means that the relative errors, although being still high, would be significantly reduced up to 2.4, 6.7 and 4.5% respectively.

  • The SRM provided exact values of the modal damping ratio in all cases, which gives an idea of the potential of the proposed method since the same did not happened with the other methods. To assess the sensitivity of the method, new analyses were performed to discover what happened in wave \(w_{5}\) adopting different durations of the initial and final intervals, equal to 1, 5, 10, 15 and 20 s. As shown in Fig. 9, in all cases, exact values were achieved for the simulated waves, even taking a duration of 1 s, which can be considered a very low value for the interval.

  • When it was applied the RDT method combined with the logarithmic decrement method, some reasonably accurate values were obtained, but on other occasions the relative errors were as high as 5%. The RDT curves were calculated in accordance with the indications given in the preceding section. However, the values of the modal damping factor depend on both the duration of the interval that is taken and the threshold that was adopted. Figure 10 includes the study of the sensitivity of the results combining, for each frequency, four durations for the interval (10, 15, 20 and 25 s) with four thresholds (90.0, 92.5, 95.0 and 97.5%). In these cases, it can be seen that the longer the interval, the closer the results obtained are to the theoretical value, with practically no influence on the threshold adopted.

  • Finally, by combining the RDT and curve adjustment methods, exact values for waves \(w_{1}\), \(w_{2}\), \(w_{3}\) and the first frequency of waves \(w_{4}\) and \(w_{5}\) were obtained. In the case of the second and third frequencies of waves \(w_{4}\) and \(w_{5}\) the relative errors were 6.25% and 7.50%, respectively. The resulting values for the amplitude had a maximum relative error on the order of 4%. Last, because of the adjustments made to obtain the RDT curve, the values obtained for the phase difference cannot be considered. For this combination of methods, a sensitivity analysis similar to that indicated in the previous point was carried out, as shown in Fig. 11. The results obtained were similar; that is, the greater the duration of the interval, the closer the results are to the theoretical value, and the adopted threshold has little influence.

Fig. 5
figure 5

Sensitivity analysis of the different methods for the calculation of the modal damping ratio (logarithmic decrement method)

Full size image
Fig. 6
figure 6

Sensitivity analysis of the different methods for the calculation of the modal damping ratio (curve adjustment method—modal damping ratio)

Full size image
Fig. 7
figure 7

Sensitivity analysis of the different methods for the calculation of the modal damping ratio (curve adjustment method—amplitude)

Full size image
Fig. 8
figure 8

Sensitivity analysis of the different methods for the calculation of the modal damping ratio (curve adjustment method—phase difference)

Full size image
Fig. 9
figure 9

Sensitivity analysis of the different methods for the calculation of the modal damping ratio (spectrum reduction method)

Full size image
Fig. 10
figure 10

Sensitivity analysis of the different methods for the calculation of the modal damping ratio (RDT + logarithmic decrement method)

Full size image
Fig. 11
figure 11

Sensitivity analysis of the different methods for the calculation of the modal damping ratio (RDT + curve adjustment method)

Full size image

If we use the average of the relative errors obtained for the different simulations carried out as a reference indicator for each calculation method, the method that gives the best results is the SRM because in all cases, the obtained results are exact. After this, it is the logarithmic decrement method, with an average relative error of 0.86%. This method is followed by the two formulations of the bandwidth method, with average relative errors of 1.14 and 1.16%. Fourth, there are the results based on the RDT method, with an average error of 2.15% when it is combined with the logarithmic decrement method, and 3.06% when it is combined with the curve adjustment method. Finally, there is the curve adjustment method, with an average relative error of 14.37%.

Therefore, in the study of these simulations in the theoretical field, the advantages of using the SRM are clear, since it presents the lowest average relative error—in fact, it gives exact values—can be applied to ambient vibrations analysis, does not require the use of filters, and the results are not affected by the only parameter that needs to be fixed, namely, the duration of the intervals of the spectrum of the initial and final parts of the accelerogram.

5 Application to a real case

5.1 Description of the study case

The viaduct over the Tagus River called “The Arches of Alconétar”, on highway A-66 of the State Highway Network in Spain (Fig. 12), is chosen as a real application case due to the large number of technical studies to which it has been the subject and, consequently, the extensive knowledge of its dynamic behaviour [30,31,32,33,34,35,36]. The viaduct has two twin structures of 400 m in length, whose 220 m main span is a metal arch of 42.5 m rise with an upper deck. Each arch is formed by two longitudinal box sectioned parts braced to each other.

Fig. 12
figure 12

Viaduct “The Arches of Alconétar”; general aerial view

Full size image

For the purpose of this paper, it is relevant to know that each structure featured instrumentation equipped with five accelerometers: three vertical accelerometers in the haunches of the arch (two in the south haunch and one in the north haunch) and two accelerometers in the keystone of the arch, one of them vertical and the other one transverse.

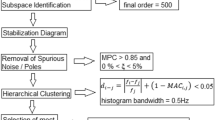
The experimental accelerograms that are analysed were recorded during 2010, period when dynamic monitoring was operative between the months of March and September, and correspond to 32 events of the left roadway on which it was feasible to perform the dynamic analysis at the time in terms of both eigenfrequencies and the modal damping ratio.Footnote 2 As a result of this analysis, a total of 228 valid measurements of the modal damping ratio were obtained, which are now used as a starting point for the comparative study object of this paper.

As an example, Fig. 13 shows one of the accelerograms studied, in which the records corresponding to the five installed accelerometers are represented.Footnote 3 In this case, the analysis in the frequency domain of the same records is represented in Fig. 14. The interval corresponding to the damped free vibrations is considered between 45 and 175 s. Although the duration of the isolated accelerogram of 130 s, together with a sampling frequency of 0.02 s, allows the study of the spectrum in the interval between 0 and 25 Hz, with a maximum discretization of 0.008 Hz, only the interval between 0 and 5 Hz is represented because it is where the frequencies with the highest associated energy content are concentrated. In this specific example, the frequency in which the greatest dynamic effect is manifested in the five accelerometers at the same time is that corresponding to 1.667 Hz, which is associated with the vibration mode of the computational model of the structure corresponding to the frequency of 1.681 Hz, in which the arch and deck bend in the plane of the structure while the haunches vibrate in opposition to the keystone (mode of vibration number 13). However, it should be noted that, although with much less energy, other natural frequencies are also reflected in the spectrum, which are referred to later. Given that in this event, only this eigenfrequency is adopted for the calculation of the modal damping ratio, the ideal band-pass filters are set between 1.5 and 1.8 Hz.

Fig. 13
figure 13

Viaduct “The Arches of Alconétar”. Example of dynamic events studied (accelerogram)

Full size image
Fig. 14
figure 14

Viaduct “The Arches of Alconétar”. Example of a studied dynamic event (spectrum)

Full size image

5.2 Methodology for obtaining the values of the modal damping ratio

The original values of the modal damping ratio were calculated using the logarithmic decrement method. To do this, from the recorded accelerograms, the largest possible part corresponding to the damped free vibrations was isolated, an analysis was performed in the frequency domain to identify the vibration modes, and ideal pass-band filters centred around the detected natural frequencies were applied to the accelerogram to avoid introducing additional disturbances. Finally, on the filtered accelerograms, the greatest possible central part of the curves were analysed, discarding edge disturbances, and the formulation of the logarithmic decrement method was applied, obtaining an average value.

Since these values, obtained with the logarithmic decrement method, were used in the preceding specific dynamic studies [30, 31], they were adopted as reference values to analyse the behaviour of the rest of the calculation methods.

For the application of the rest of the calculation methods for the modal damping ratio, the procedure indicated in Sects. 2, 3 and 4.2 was followed, with these particular details:

  • In the case of the bandwidth method over the spectrum of the signal, once the peaks corresponding to the natural frequencies were located, and given that they were relatively spaced, the frequencies at which said extreme was reduced to \(1/\sqrt{2}\) times its maximum value were obtained by linear interpolation, on which Formulations (2) and (3) were applied.

  • When the curve adjustment method was applied, to ensure correct behaviour of the method, it was found convenient to start the iterations with a wider range in the case of the amplitudes, so the initial range was set between 0 and 10 times the maximum value of the accelerogram. In a very specific way, on four occasions only, the adjustment of the real curve to the theoretical one was not achieved, so these values were discarded.

  • In the case of SRM, initial and final intervals of the accelerogram with a duration of 10 s were ideally taken. However, in some dynamic events shorter intervals (5 s) and longer intervals (20 s) were taken to investigate the behaviour of the method. An example of this can be seen in Fig. 15.

  • Finally, for the application of the RDT method, the following issues were observed:

    • Although the criterion of setting intervals of 20 s duration was maintained, it was found that it was not always feasible to leave the threshold at 95% of the maximum value recorded in the accelerogram, since in some cases this threshold did not allow construction of the RDT curve. In these cases, the threshold was progressively lowered in steps of 5% until the construction of the RDT curve was possible, reaching 75% in some events.

    • The cases in which the filtered RDT curves did not take the form of damped free vibrations were ruled out to avoid addressing anomalous values of the modal damping ratio, which occurred in approximately 20% of the cases.

Fig. 15
figure 15

Viaduct “The Arches of Alconétar”. Example of a studied dynamic event (application of SRM)

Full size image

5.3 Obtained results and discussion

The results obtained are shown in Figs. 16 and 17, as well as in Table 2. Analogous to the theoretical case, the average of the relative errors for the different natural frequencies is used as an indicator for each calculation method, assuming the hypothesis that the reference values are those obtained in previous studies using the logarithmic decrement method. The most relevant conclusions are as follows:

Table 2 Modal damping ratios obtained in the analysed real case
Full size table
Fig. 16
figure 16

Comparison among the calculation methods for the modal damping ratio in a real case. Average

Full size image
Fig. 17
figure 17

Comparison among the calculation methods for the modal damping ratio in a real case. Standard Deviation

Full size image

  • First, it is clear that, in a real case, the results obtained may vary significantly depending on the calculation method of the modal damping ratio that is applied, unlike what happens in theoretical cases. For this reason, in general, it is important to know what method has been used to calculate the modal damping ratio and to be very careful when setting thresholds, especially if these values are to be used in structural health monitoring systems.

  • The application of the calculation methods based on the bandwidth applied on the signal spectrum shows the greatest differences with respect to the reference values. Except in the case of natural frequencies 7 and 8, where the relative errors are close to 30%, in general, the values obtained are several orders of magnitude higher, so they must be discarded. Additionally, in this case, the largest standard deviations of the results are given (5.41% and 3.16% for each formulation). In our opinion, we do not think that this may be due to a low resolution in the frequencies of the experimental waves because for the simulated waves, which have the same characteristics as the real ones in terms of amplitude, natural frequency and damping, results were very precise. The possibility of obtaining this type of result is an issue that has been noted by other authors [2], especially when the spectra have a very pointed shape. However, it would undoubtedly be an issue which should be studied and, therefore, the application of the formulation corresponding to this calculation method must be done with extreme caution in this type of case. On the other hand, the use of the two formulations (half-power and half-quadratic gain) gives very similar values. Significant differences are seen only when the values are very high, which happens unusually and exclusively with the second natural frequency.

  • In the case of the curve adjustment method, the values obtained have a fairly acceptable average relative error of approximately 23.9% and an average standard deviation of 0.17%.

  • The lowest average relative error occurs with the SRM, being 11.8%. Upon taking as reference the values obtained by the logarithmic decrement method, in the case of two of the natural frequencies (\(f_{3}\) and \(f_{5}\)), the differences are on the order of 1% or even less; at another of the natural frequencies (\(f_{2}\)), the difference is found to be 4%; and in the rest, the differences range between approximately 11% and 20%. These results, together with an average standard deviation of 0.17%, validate the goodness-of-fit of this method for its application in this type of real case.

  • Finally, the application of the RDT method gives average relative errors of 34.1% and 81.5%, together with an average standard deviation of 0.19% and 0.45%, when it is applied in combination with the logarithmic decrement and the curve adjustment methods, respectively. Therefore, in the case of this particular structure and for this type of dynamic event, the application of this type of method does not compensate since the extraordinary calculation effort to obtain the RDT curve, which is also not always possible, is not always accompanied by more accurate values in the resulting modal damping ratio.

As a final comment, it should be noted that we decided to adopt the hypothesis that the logarithmic decrement values would be the reference values because these were the data which were available about the dynamic behaviour of the structure. But, certainly, by looking at results which are so different between the different calculation methods, any other hypothesis could be justified.

If, as an alternative hypothesis, the reference value were defined as the mean of all the values which were obtained by using all the methods, but excluding the two bandwidth methods which yield anomalous results, there would be three sets of methods: logarithmic decrement, curve adjustment, SRM and RDT combined with logarithmic decrement methods would yield minimum relative errors, ranging between 13 and 23%; RDT method combined with curve adjustment would yield a mean error of 58%; finally, both bandwidth formulations would yield much larger errors, in the order of 300%.

5.3.1 Possible correlation between calculation methods

On the other hand, the possibility of correlating the values of the reference modal damping ratio obtained using the logarithmic decrement method and those obtained using the different calculation methods is studied.

As it may be seen along the paper, damping factor values are very much dependent on the calculation method to be used. Then, it must be known if, generally speaking, a value which has been obtained by using a particular method may be comparable a value obtained by using another method. This is important when studying the structural health of a bridge or any other structure.

In our application example, since the values which were adopted as reference were those coming from the logarithmic decrement, the relation between this method and the others has been studied. If there was a perfect correlation, there would be a total correspondence between the values from any method and those from the logarithmic decrement method.

The results of the regression analysis are shown in Table 3. It is observed that there is a certain correlation in the case of the curve adjustment method and the SRM, being very high, with a coefficient of determination (\(R^{2}\))Footnote 4 close to 90%, in the latter case. This is graphically represented in Figs. 18 and 19, where each point is a measurement of the modal damping ratio for an event, a channel and a given natural frequency using different calculation methods.

Table 3 Regression analysis of predictive models for the modal damping ratio
Full size table
Fig. 18
figure 18

Regression analysis between the different calculation methods and the logarithmic decrement method in the real case (curve adjustment method)

Full size image
Fig. 19
figure 19

Regression analysis between the different calculation methods and the logarithmic decrement method in the real case (SRM)

Full size image

5.3.2 Influence of the calculation methods over previous predictive models

Finally, when the original dynamic study of this structure was carried out, the possibility of implementing linear predictive models of the dynamic parameters based on different variables, such as temperature, wind speed or the maximum accelerations recorded, was analysed.

The study reflected that, in this particular case, there was no relation between damping factor and temperature. Nevertheless, it was possible to establish a model which could predict for certain eigenfrequencies the damping factor as a function of mean wind velocity and maximum accelerations although the correlation factors were very modest, among other issues because there were some dispersions in the data.

Although good results were obtained for natural frequencies, the same was not true for modal damping ratios. It is worth evaluating if there is any improvement in these predictive models when using other calculation methods.

In this sense, the same linear models are reconsidered, which in the case of the modal damping ratio are dependent on the mean wind speed, the maximum vertical acceleration and the maximum transverse acceleration, but considering the values of the modal damping ratio obtained according to the different calculation methods. The study of the values obtained with the RDT method has not been carried out because, since no results were obtained in 20% of the events, a very high number of data had to be omitted or replaced. In the case of the curve adjustment method, the four unavailable point values (3 of the first natural frequency and one of the fourth natural frequency) were replaced by the values obtained with the logarithmic decrement method.

After performing the regression analysis, the values of the coefficient of determination are as shown in Table 4. Although there are changes in the values obtained, some upwards and others downwards, overall, no significant improvement is seen through the use of any of the proposed alternative calculation methods.

Table 4 Regression analysis of predictive models for the modal damping factor
Full size table

6 Conclusions

Throughout this paper, various calculation methods available to evaluate the modal damping ratio on bridges in service have been reviewed. In the case of experimentally recorded accelerograms, the most common calculation methods are the logarithmic decrement method, the bandwidth method applied over the spectrum (with two possible formulations) and the curve adjustment method. Likewise, when feasible, the random decrement technique combined with the logarithmic decrement and curve adjustment methods has been included in the analysis.

Additionally, an alternative calculation method for the modal damping ratio has been formulated based on the reduction of the signal spectrum (spectrum reduction method, SRM), whose main advantage lies in the fact that it allows the study of systems with several degrees of freedom, as usually happens in structures, to be carried out directly, without the need to apply filters.

A comparative study of the different calculation methods has been carried out, first on a set of theoretically simulated waves. In these cases, the obtained results are reasonably close to the theoretical values. However, analyzing the values obtained in detail, the best results are obtained for the SRM, followed by the logarithmic decrement method, the two formulations for the bandwidth method, the random decrement technique and the curve adjustment method. The inevitable use of filters in the signals to be able to apply some of the methods in systems with various degrees of freedom is a source of errors in the results. Similarly, a sensitivity study of the different parameters used in the different calculation methods has been carried out.

Second, a comparative study has been carried out on the accelerograms recorded during a test campaign of a real structure, the viaduct “The Arches of Alconétar”. In this case, it has been observed that, unlike what happens with theoretical simulations, the results obtained can vary significantly depending on the calculation method applied. For this reason, in real cases, it is important to know what method has been used to calculate the modal damping ratio and to be careful when setting thresholds, especially if these values are going to be used in structural health monitoring systems.

In the case of the real structure, the greatest differences with respect to the reference values, which were calculated by means of the logarithmic decrement method, have been found in the two formulations of the calculation method based on the bandwidth method applied over the spectrum of the signal, which is attributed to the very pointed shape of the spectra. The lowest average relative error occurs with the SRM, followed by the curve adjustment method and, last, the random decrement technique.

Finally, the possibility of correlating the values of the reference modal damping ratio and those obtained through the different calculation methods has also been studied. It has been observed that there is a certain correlation in the case of the curve fitting method and the SRM, being very high, with a determination coefficient close to 90%, in the latter case.

As a consequence, it is considered that the proposed alternative calculation method, the SRM, allows simplification of the calculation procedures and avoids the effect of the application of filters on the signals without affecting the precision of the results. These benefits have been corroborated both in the theoretical simulations carried out and in the real structure studied.