Skip to main content
SpringerLink
Log in

Automation in Bayesian operational modal analysis using clustering-based interpretation of stabilization diagram

  • Original Paper
  • Published:
Journal of Civil Structural Health Monitoring Aims and scope Submit manuscript

A Correction to this article was published on 07 January 2023

This article has been updated

Abstract

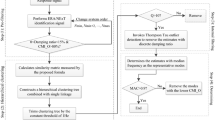
Long-term structural health monitoring (SHM) requires processing a large amount of data with human intervention often involved. Operational modal analysis (OMA) is generally treated as prerequisite for vibration-based SHM to obtain modal parameters, including natural frequency, damping ratio and mode shape. Bayesian modal analysis has received considerable attention in recent years, as it identifies modal parameters but also provides their uncertainties. In conventional Bayesian OMA, manual operation includes initial frequency and bandwidth selection. The former is often visually picked from a singular value spectrum, while the latter is chosen with the consideration of a trade-off between the data used for making inference and modeling error involved. The above procedures have limited the application of Bayesian approach in processing long-term data. This work aims at developing an automation technique for Bayesian fast Fourier transform modal identification. A stabilization diagram is first built and automatically interpreted by modal validation criteria and clustering strategy to obtain the initial frequency. Spurious modes are also cleared in this step. A series of effective bandwidth factors within a predefined factor range are then determined for the selection of frequency band. The proposed automation method is verified by a numerical example and then applied on the Z24 benchmark bridge for long-term data analysis. Results show that the automation method is able to accurately identify modal parameters with minimum human intervention, even for closely spaced and weakly excited modes. It is also shown that the method is adequate to automatically analyze long-term monitoring data.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22
Fig. 23
Fig. 24
Fig. 25
Fig. 26

Similar content being viewed by others

Data available statement

Data, models, and codes generated and used during the study are available from the corresponding author upon reasonable request.

Change history

References

  1. Lee H, Kim J, Sho K et al (2010) A wireless vibrating wire sensor node for continuous structural health monitoring. Smart Mater Struct 19(5):055004

    Article  Google Scholar 

  2. Gentile C, Ruccolo A, Canali F (2019) Continuous monitoring of the Milan Cathedral: dynamic characteristics and vibration-based SHM. J Civ Struct Heal Monit 9(5):671–688

    Article  Google Scholar 

  3. Farrar CR, Worden K (2010) An introduction to structural health monitoring. In: New trends in vibration based structural health monitoring, pp 1–17

  4. Pereira S, Magalhães F, Gomes JP et al (2021) Modal tracking under large environmental influence. J Civil Struct Health Monitor

  5. Brownjohn J, Magalhaes F, Caetano E et al (2010) Ambient vibration re-testing and operational modal analysis of the Humber Bridge. Eng Struct 32(8):2003–2018

    Article  Google Scholar 

  6. Yang X-M, Yi T-H, Qu C-X et al (2019) Automated eigensystem realization algorithm for operational modal identification of bridge structures. J Aerosp Eng 32(2):04018148

    Article  Google Scholar 

  7. Zhang G, Ma J, Chen Z et al (2014) Automated eigensystem realisation algorithm for operational modal analysis. J Sound Vib 333(15):3550–3563

    Article  Google Scholar 

  8. Ye X, Huang P, Pan C et al (2021) Innovative stabilization diagram for automated structural modal identification based on ERA and hierarchical cluster analysis. J Civ Struct Heal Monit 11(5):1355–1373

    Article  Google Scholar 

  9. Cabboi A, Magalhães F, Gentile C et al (2017) Automated modal identification and tracking: application to an iron arch bridge. Struct Control Health Monit 24(1):e1854

    Article  Google Scholar 

  10. He M, Liang P, Li J et al (2021) Fully automated precise operational modal identification. Eng Struct 234:111988

    Article  Google Scholar 

  11. Sarlo R, Tarazaga PA, Kasarda ME (2018) High resolution operational modal analysis on a five-story smart building under wind and human induced excitation. Eng Struct 2018(176):279–292

    Article  Google Scholar 

  12. Charbonnel PÉ (2021) Fuzzy-driven strategy for fully automated modal analysis: application to the SMART2013 shaking-table test campaign. Mech Syst Signal Process 152:107388

    Article  Google Scholar 

  13. Vanlanduit S, Verboven P, Guillaume P et al (2003) An automatic frequency domain modal parameter estimation algorithm. J Sound Vib 265(3):647–661

    Article  Google Scholar 

  14. Peeters B, Van der Auweraer H (2005) PolyMAX: a revolution in operational modal analysis. In: 1st International Operational Modal Analysis Conference. IOMAC Copenhagen, Denmark

  15. Reynders E, Houbrechts J, De Roeck G (2012) Fully automated (operational) modal analysis. Mech Syst Signal Process 2012(29):228–250

    Article  Google Scholar 

  16. Zonno G, Aguilar R, Boroschek R et al (2018) Automated long-term dynamic monitoring using hierarchical clustering and adaptive modal tracking: validation and applications. J Civ Struct Heal Monit 8(5):791–808

    Article  Google Scholar 

  17. Beck JL, Katafygiotis LS (1998) Updating models and their uncertainties. I: Bayesian statistical framework. J Eng Mech 124(4):455–461

    Google Scholar 

  18. Yuen K-V, Katafygiotis LS (2003) Bayesian fast Fourier transform approach for modal updating using ambient data. Adv Struct Eng 6(2):81–95

    Article  Google Scholar 

  19. Katafygiotis LS, Yuen KV (2001) Bayesian spectral density approach for modal updating using ambient data. Earthquake Eng Struct Dynam 30(8):1103–1123

    Article  Google Scholar 

  20. Yuen KV, Beck JL, Katafygiotis LS (2002) Probabilistic approach for modal identification using non-stationary noisy response measurements only. Earthquake Eng Struct Dynam 31(4):1007–1023

    Article  Google Scholar 

  21. Au S-K (2011) Fast Bayesian FFT method for ambient modal identification with separated modes. J Eng Mech 137(3):214–226

    Google Scholar 

  22. Au S-K (2012) Fast Bayesian ambient modal identification in the frequency domain, Part II: posterior uncertainty. Mech Syst Signal Process 26:76–90

    Article  Google Scholar 

  23. Zhu Z, Au S-K, Li B et al (2021) Bayesian operational modal analysis with multiple setups and multiple (possibly close) modes. Mech Syst Signal Process 150:107261

    Article  Google Scholar 

  24. Zhu Y-C, Xie Y-L, Au S-K (2018) Operational modal analysis of an eight-storey building with asynchronous data incorporating multiple setups. Eng Struct 165:50–62

    Article  Google Scholar 

  25. Zhang FL, Xiong HB, Shi WX et al (2016) Structural health monitoring of Shanghai Tower during different stages using a Bayesian approach. Struct Control Health Monit 23(11):1366–1384

    Article  Google Scholar 

  26. Au S-K, Zhang F-L (2011) On assessing the posterior mode shape uncertainty in ambient modal identification. Probab Eng Mech 26(3):427–434

    Article  Google Scholar 

  27. Ni Y-Q, Zhang F-L, Xia Y-X et al (2015) Operational modal analysis of a long-span suspension bridge under different earthquake events. Earthquakes and structures 8(4):859–887

    Article  Google Scholar 

  28. Zhang F-L, Ni Y-Q, Ni Y-C (2016) Mode identifiability of a cable-stayed bridge based on a Bayesian method. Smart Struct Syst 17(3):471–489

    Article  Google Scholar 

  29. Au S-K (2016) Model validity and frequency band selection in operational modal analysis. Mech Syst Signal Process 81:339–359

    Article  Google Scholar 

  30. Au S-K (2012) Fast Bayesian ambient modal identification in the frequency domain, Part I: posterior most probable value. Mech Syst Signal Process 26:60–75

    Article  Google Scholar 

  31. Reynders E, Pintelon R, De Roeck G (2008) Uncertainty bounds on modal parameters obtained from stochastic subspace identification. Mech Syst Signal Process 22(4):948–969

    Article  Google Scholar 

  32. Zeng J, Hoon Kim Y (2021) A two-stage framework for automated operational modal identification. Struct Infrastruct Eng. https://doi.org/10.1080/15732479.2021.1919151

    Article  Google Scholar 

  33. Peeters B, De Roeck G (1999) Reference-based stochastic subspace identification for output-only modal analysis. Mech Syst Signal Process 13(6):855–878

    Article  Google Scholar 

  34. Fan G, Li J, Hao H (2019) Improved automated operational modal identification of structures based on clustering. Struct Control Health Monit 26(12):e2450

    Article  Google Scholar 

  35. de Almeida Cardoso R, Cury A, Barbosa F (2017) A clustering-based strategy for automated structural modal identification. Struct Health Monit 17(2):201–217

    Article  Google Scholar 

  36. Sun M, Alamdari MM, Kalhori H (2017) Automated operational modal analysis of a cable-stayed bridge. J Bridg Eng 22(12):05017012

    Article  Google Scholar 

  37. Li B, Au S-K (2019) An expectation-maximization algorithm for Bayesian operational modal analysis with multiple (possibly close) modes. Mech Syst Signal Process 132:490–511

    Article  Google Scholar 

  38. Pereira S, Reynders E, Magalhães F et al (2020) The role of modal parameters uncertainty estimation in automated modal identification, modal tracking and data normalization. Eng Struct 224:111208

    Article  Google Scholar 

  39. Li J, Bao T, Ventura CE (2022) An automated operational modal analysis algorithm and its application to concrete dams. Mech Syst Signal Process 168:108707

    Article  Google Scholar 

  40. Lorenzoni F, Casarin F, Caldon M et al (2016) Uncertainty quantification in structural health monitoring: applications on cultural heritage buildings. Mech Syst Signal Process 66:268–281

    Article  Google Scholar 

  41. Cruz C, Miranda E (2017) Evaluation of the Rayleigh damping model for buildings. Eng Struct 138:324–336

    Article  Google Scholar 

  42. Elmenshawi A, Sorour M, Mufti A et al (2010) Damping mechanisms and damping ratios in vibrating unreinforced stone masonry. Eng Struct 32(10):3269–3278

    Article  Google Scholar 

  43. Au S (2017) Operational modal analysis: modeling, Bayesian inference, uncertainty laws. Springer, Singapore

    Book  MATH  Google Scholar 

  44. Mao JX, Wang H, Fu YG et al (2019) Automated modal identification using principal component and cluster analysis: Application to a long‐span cable‐stayed bridge. Struct Control Health Monitor 26(10)

  45. Tran TTX, Ozer E (2020) Automated and model-free bridge damage indicators with simultaneous multiparameter modal anomaly detection. Sensors (Basel) 20(17)

  46. Wu W-H, Wang S-W, Chen C-C et al (2018) Modal parameter identification for closely spaced modes of civil structures based on an upgraded stochastic subspace methodology. Struct Infrastruct Eng 15(3):296–313

    Article  Google Scholar 

  47. Priori C, De Angelis M, Betti R (2018) On the selection of user-defined parameters in data-driven stochastic subspace identification. Mech Syst Signal Process 100:501–523

    Article  Google Scholar 

  48. Charbonnel P-É (2021) Fuzzy-driven strategy for fully automated modal analysis: application to the SMART2013 shaking-table test campaign. Mech Syst Signal Process 152:107388

    Article  Google Scholar 

  49. He Y, Yang JP, Li X-F (2022) A three-stage automated modal identification framework for bridge parameters based on frequency uncertainty and density clustering. Eng Struct 255:113891

    Article  Google Scholar 

  50. Afshar M, Khodaygan S (2019) Enhanced stabilization diagram for automated modal parameter identification based on power spectral density transmissibility functions. Struct Control Health Monit 26(7):e2369

    Article  Google Scholar 

  51. Pan C, Ye X, Mei L (2021) Improved automatic operational modal analysis method and application to large-scale bridges. J Bridg Eng 26(8):04021051

    Article  Google Scholar 

  52. Ubertini F, Gentile C, Materazzi AL (2013) Automated modal identification in operational conditions and its application to bridges. Eng Struct 2013(46):264–278

    Article  Google Scholar 

  53. Au S-K, Brownjohn JM, Mottershead JE (2018) Quantifying and managing uncertainty in operational modal analysis. Mech Syst Signal Process 102:139–157

    Article  Google Scholar 

  54. Maeck J, De Roeck G (2003) Description of Z24 benchmark. Mech Syst Signal Process 17(1):127–131

    Article  Google Scholar 

  55. Peeters B, De Roeck G (2001) One-year monitoring of the Z24-Bridge: environmental effects versus damage events. Earthquake Eng Struct Dynam 30(2):149–171

    Article  Google Scholar 

  56. Worden K, Cross EJ (2018) On switching response surface models, with applications to the structural health monitoring of bridges. Mech Syst Signal Process 98:139–156

    Article  Google Scholar 

  57. Cigada A, Caprioli A, Redaelli M et al (2008) Vibration testing at Meazza stadium: reliability of operational modal analysis to health monitoring purposes. J Perform Constr Facil 22(4):228–237

    Article  Google Scholar 

Download references

Acknowledgements

The first author would like to express gratitude and sincere appreciation for the partial financial support by the University of Louisville. The second author is funded by the National Key R&D Program of China (2019YFB2102702) and Shenzhen Science and Technology Program (JSGG20210802093207022). Authors would also like to acknowledge KU. Leuven for the open access data used in this paper.

Author information

Authors and Affiliations

  1. Department of Civil and Environment Engineering, University of Louisville, Louisville, 40292, KY, USA

    Jice Zeng & Young Hoon Kim

  2. College of Civil and Transportation Engineering, Shenzhen University, Shenzhen, Guangdong, 518060, China

    Yan-Long Xie

  3. Design and Information Department, China Railway South Investment Group Co.Ltd, Shenzhen, 518000, China

    Junfang Wang

Authors
  1. Jice Zeng
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yan-Long Xie
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Young Hoon Kim
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Junfang Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yan-Long Xie.

Ethics declarations

Conflict of interest

The authors declare no potential conflict of interests.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

The original online version of this article was revised: " In this article the authors Jice Zeng, Young Hoon Kim and Yan-Long Xie afliation details was corrected.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zeng, J., Xie, YL., Kim, Y.H. et al. Automation in Bayesian operational modal analysis using clustering-based interpretation of stabilization diagram. J Civil Struct Health Monit 13, 443–467 (2023). https://doi.org/10.1007/s13349-022-00644-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s13349-022-00644-7

Keywords

Search

Navigation