Skip to main content
SpringerLink
Log in

Seismic performance assessment of isolated bridges for different limit states

  • Original Paper
  • Published:
Journal of Civil Structural Health Monitoring Aims and scope Submit manuscript

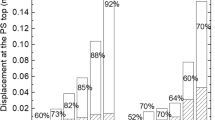
Abstract

This study aims to evaluate the seismic performances of bridges isolated by the friction pendulum system (FPS) bearings considering the seismic hazard of Sant’Angelo dei Lombardi site (Italy), to provide useful and preliminary recommendations in terms of health assessment for design or retrofit of new or existing bridges, respectively. Single- and two-degree-of-freedom models are considered to describe the isolated bridge behavior taking into account an infinitely rigid deck and the isolated bridge behavior having an infinitely rigid deck with the elastic pier, respectively. In both models, a velocity-dependent rule for the FPS isolators is assumed. Seismic excitations are properly modeled as non-stationary stochastic processes having different intensities corresponding to different limit states and with frequency contents related to the medium soil condition, representative of the soil type in Sant’Angelo dei Lombardi site (Italy). The statistics of deck and pier responses of the isolated bridge are evaluated for different system parameters such as mass ratio, isolation period, pier period and friction coefficient of the FPS considering both Life Safety and Collapse Prevention limit states according to Italian seismic codes. The results, deriving mainly from the two-degree-of-freedom (2dof) model analyses, show that particular values of the friction coefficient allow to minimize the response of the pier depending on the different system properties and the different limit states. In particular, the optimum friction coefficient of the FPS ranges from 0.01 to 0.04 and from 0.01 to 0.05 for Life Safety and for Collapse Prevention limit state, respectively, depending on the structural properties.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14

Similar content being viewed by others

References

  1. Clemente P (2017) Seismic isolation: past, present and the importance of SHM for the future. J Civil Struct Health Monit 7(2):217–231

    Article  Google Scholar 

  2. Halabian AM, Zafarani MM, Soheilipour MS, Behbahani S (2016) Optimal semi-active control of seismically excited MR-equipped nonlinear buildings using FLC and multi-objective NSGAII algorithms considering ground excitations. J Civil Struct Health Monit 6(3):561–586

    Article  Google Scholar 

  3. Jangid RS (2004) Seismic response of isolated bridges. J Bridge Eng 9(2):156–166

    Article  Google Scholar 

  4. Tsopelas P, Constantinou MC, Okamoto S, Fujii S, Ozaki D (1996) Experimental study of bridge seismic sliding isolation systems. Eng Struct 18(4):301–310

    Article  Google Scholar 

  5. Ghobarah A, Ali HM (1988) Seismic performance of highway bridges. Eng Struct 10:157–166

    Article  Google Scholar 

  6. Tongaonkar NP, Jangid RS (2003) Seismic response of isolated bridges with soil–structure interaction. Soil Dyn Earthq Eng 23:287–302

    Article  Google Scholar 

  7. Su L, Ahmadi G, Tadjbakhsh IG (1989) Comparative study of base isolation systems. J Eng Mech 115(9):1976–1992

    Article  Google Scholar 

  8. Zayas VA, Low SS, Mahin SA (1990) A simple pendulum technique for achieving seismic isolation. Earthq Spectra 6(2):317–333

    Article  Google Scholar 

  9. Mosqueda G, Whittaker AS, Fenves GL (2004) Characterization and modeling of Friction Pendulum bearings subjected to multiple components of excitation. J Struct Eng 130(3):433–442

    Article  Google Scholar 

  10. Mokha A, Constantinou MC, Reinhorn AM (1990) Teflon bearings in base isolation. I: testing. J Struct Eng 116(2):438–454

    Article  Google Scholar 

  11. Constantinou MC, Mokha A, Reinhorn AM (1990) Teflon bearings in base isolation. II: modeling. J Struct Eng 116(2):455–474

    Article  Google Scholar 

  12. Constantinou MC, Whittaker AS, Kalpakidis Y, Fenz DM, Warn GP (2007) Performance of seismic isolation hardware under service and seismic loading. Technical Report MCEER-07-0012

  13. Almazàn JL, De la Llera JC (2003) Physical model for dynamic analysis of structures with FPS isolators. Earthq Eng Struct Dyn 32(8):1157–1184

    Article  Google Scholar 

  14. Landi L, Grazi G, Diotallevi PP (2016) Comparison of different models for friction pendulum isolators in structures subjected to horizontal and vertical ground motions. Soil Dyn Earthq Eng 81:75–83

    Article  Google Scholar 

  15. Castaldo P, Palazzo B, Della Vecchia P (2015) Seismic reliability of base-isolated structures with friction pendulum bearings. Eng Struct 95:80–93

    Article  Google Scholar 

  16. Castaldo P, Palazzo B, Della Vecchia P (2016) Life-cycle cost and seismic reliability analysis of 3D systems equipped with FPS for different isolation degrees. Eng Struct 125:349–363. doi:10.1016/j.engstruct.2016.06.056

    Article  Google Scholar 

  17. Castaldo P, Amendola G, Palazzo B (2017) Seismic fragility and reliability of structures isolated by friction pendulum devices: seismic reliability-based design (SRBD). Earthq Eng Struct Dyn 46(3):425–446. doi:10.1002/eqe.2798

    Article  Google Scholar 

  18. Palazzo B, Castaldo P, Della Vecchia P (2014) Seismic reliability analysis of base-isolated structures with friction pendulum system. EESMS 2014–2014 IEEE Workshop on Environmental, Energy and Structural Monitoring Systems, pp 114–119

  19. Castaldo P, Palazzo B, Ferrentino T (2017) Seismic reliability-based ductility demand evaluation for inelastic base-isolated structures with friction pendulum devices. Earthq Eng Struct Dyn 46(8):1245–1266. doi:10.1002/eqe.2854

    Article  Google Scholar 

  20. Castaldo P, Tubaldi E (2015) Influence of FPS bearing properties on the seismic performance of base-isolated structures. Earthq Eng Struct Dyn 44(15):2817–2836

    Article  Google Scholar 

  21. Kim YS, Yun CB (2007) Seismic response characteristics of bridges using double concave friction pendulum bearings with tri-linear behaviour. Eng Struct 29:3082–3093

    Article  Google Scholar 

  22. Eröz M, DesRoches R (2008) Bridge seismic response as a function of the friction pendulum system (FPS) modeling assumptions. Eng Struct 30:3204–3212

    Article  Google Scholar 

  23. Castaldo P, Ripani M (2016) Optimal design of friction pendulum system properties for isolated structures considering different soil conditions. Soil Dyn Earthq Eng 90:74–87. doi:10.1016/j.soildyn.2016.08.025

    Article  Google Scholar 

  24. Jangid RS (2005) Optimum friction pendulum system for near-fault motions. Eng Struct 27(3):349–359

    Article  Google Scholar 

  25. Malekzadeh M, Taghikhany T (2012) Multi-stage performance of seismically isolated bridge using triple pendulum bearings. Adv Struct Eng 15(7):1181–1196

    Article  Google Scholar 

  26. NTC08. Norme tecniche per le costruzioni. Gazzetta Ufficiale del 04.02.08, DM 14.01.08, Ministero delle Infrastrutture

  27. Shinozuka M, Deodatis G (1991) Simulation of stochastic processes by spectral representation. Appl Mech Rev 44(4):191–203

    Article  MathSciNet  Google Scholar 

  28. Pinto P, Giannini R, Franchin P (2004) Seismic reliability analysis of structures. Iuss Press, Pavia

    Google Scholar 

  29. Kelly JM (1997) Earthquake-resistant design with rubber, 2nd edn. Springer, Berlin

    Book  Google Scholar 

  30. Building Seismic Safety Council (2006) NEHRP recommended provisions: design examples FEMA 451—Washington, DC, August 2006

  31. Priestley MJN, Seible F, Calvi GM (1996) Seismic design and retrofit of bridges. Wiley, New York

    Book  Google Scholar 

  32. Kulkarni JA, Jangid RS (2003) Effects of superstructure flexibility on the response of base-isolated structures. Shock Vib 26:1–13

    Google Scholar 

  33. Pradlwarter HJ, SchuiRler GI, Dorka U (1998) Reliability of MDOF-systems with hysteretic devices. Eng Struct 20(8):685–691

    Article  Google Scholar 

  34. Tung ATY, Wang JN, Kiremidjian A, Kavazanjian E (1992) Statistical parameters of AM and PSD functions for the generation of site-specific strong ground motions. In: Proceedings of the 10th World Conference on Earthquake Engineering, Madrid, Spain, 2:867–872

  35. Kanai K (1957) Semiempirical formula for the seismic characteristics of the ground. Bull Earthq Res Inst 35:309–325

    Google Scholar 

  36. Tajimi H (1960) A statistical method of determining the maximum response of a building structure during an earthquake. In: Proceeding, 2nd World Conference on earthquake Engineering, II:781–798

  37. Clough RW, Penzien J (1993) Dynamics of structures, 2nd edn. McGraw-Hill, New York

    MATH  Google Scholar 

  38. Zentner I, Allain F, Humbert N, Caudron M (2014) Generation of spectrum compatible ground motion and its use in regulatory and performance-based seismic analysis. In: Proceedings of the 9th International Conference on Structural Dynamics, EURODYN 2014

  39. Peng Y, Chen J, Li J (2014) Nonlinear response of structures subjected to stochastic excitations via probability density evolution method. Adv Struct Eng 17(6):801–816

    Article  Google Scholar 

  40. Li C, Liu Y (2004) Ground motion dominant frequency effect on the design of multiple tuned mass dampers. J Earthq Eng 8(1):89–105

    Google Scholar 

  41. Lopez-Garcia D, Soong TT (2009) Assessment of the separation necessary to prevent seismic pounding between linear structural systems. Prob Eng Mech 24:210–223

    Article  Google Scholar 

  42. Tubaldi E, Barbato M, Ghazizadeh S (2012) A probabilistic performance-based risk assessment approach for seismic pounding with efficient application to linear systems. Struct Saf 36–37:14–22

    Article  Google Scholar 

  43. Saritaş F, Hasgür Z (2014) Dynamic behavior of an isolated bridge pier under earthquake effects for different soil layers and support conditions. Digest 1733–1756

  44. Talaslidis DG, Manolis GD, Paraskevopoulos EA, Panagiotopoulos CG (2004) Risk analysis of industrial structures with hazardous materials under seismic input. In: 13th World Conference on Earthquake Engineering, August 1–6

  45. http://www.comune.santangelodeilombardi.av.it/c064092/zf/index.php/servizi-aggiuntivi/index/index/idtesto/20079. Aug 2017

  46. Shinozuka M, Sato Y (1967) Simulation of nonstationary random process. J Eng Mech Div 93(1):11–40

    Google Scholar 

  47. Hancock J, Bommer JJ (2006) A state-of-knowledge review of the influence of strong- motion duration on structural damage. Earthq Spectra 22(3):827–845

    Article  Google Scholar 

  48. Hancock J, Bommer JJ (2007) Using spectral matched records to explore the influence of strong-motion duration on inelastic structural response. Soil Dyn Earthq Eng 27:291–299

    Article  Google Scholar 

  49. Barroso LR, Winterstein S (2002) Probabilistic seismic demand analysis of controlled steel moment-resisting frame structures. Earthq Eng Struct Dyn 31(12):2049–2066

    Article  Google Scholar 

  50. Armouti NS (2003) Response of structures to synthetic earthquakes. Emerging technologies in structural engineering. In: Proceedings of the 9th Arab Structural Engineering Conference, Nov 29–Dec 1, Abu Dhabi, UAE, 331–340

  51. Aslani H, Miranda E (2005) Probability-based seismic response analysis. Eng Struct 27(8):1151–1163

    Article  Google Scholar 

  52. Porter KA (2003) An overview of PEER’s performance-based earthquake engineering methodology. In: Proceedings of the 9th International Conference on Application of Statistics and Probability in Civil Engineering (ICASP9), San Francisco, California, 2003

  53. Ryan K, Chopra A (2004) Estimation of seismic demands on isolators based on nonlinear analysis. J Struct Eng 130(3):392–402

    Article  Google Scholar 

  54. Karavasilis T, Seo C (2011) Seismic structural and non-structural performance evaluation of highly damped self-centering and conventional systems. Eng Struct 33(8):2248–2258

    Article  Google Scholar 

  55. Math Works Inc (1997) MATLAB-high performance numeric computation and visualization software. User’s guide. Natick: MA, USA

  56. Jangid RS (2000) Optimum frictional elements in sliding isolation systems. Comput Struct 76(5):651–661

    Article  Google Scholar 

  57. Chung LL, Kao PS, Yang CY, Wu LY, Chen HM (2013) Optimal frictional coefficient of structural isolation system. J Vib Control. doi:10.1177/1077546313487938 (Early view)

    Google Scholar 

  58. Iemura H, Taghikhany T, Jain S (2007) Optimum design of resilient sliding isolation system for seismic protection of equipments. Bull Earthq Eng 5(1):85–103

    Article  Google Scholar 

  59. Fallah N, Zamiri G (2013) Multi-objective optimal design of sliding base isolation using genetic algorithm. Sci Iran A 20(1):87–96

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Structural, Geotechnical and Building Engineering (DISEG), Politecnico di Torino, Turin, Italy

    P. Castaldo

  2. Department of Civil Engineering, University of Salerno, Fisciano, Italy

    R. Lo Priore

Authors
  1. P. Castaldo
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. R. Lo Priore
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to P. Castaldo.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Castaldo, P., Lo Priore, R. Seismic performance assessment of isolated bridges for different limit states. J Civil Struct Health Monit 8, 17–32 (2018). https://doi.org/10.1007/s13349-017-0255-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s13349-017-0255-2

Keywords

Search

Navigation