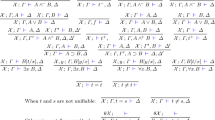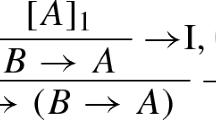Skip to main content
SpringerLink
Log in

Reciprocal Influences Between Proof Theory and Logic Programming

  • Research Article
  • Published:
Philosophy & Technology Aims and scope Submit manuscript

Abstract

The topics of structural proof theory and logic programming have influenced each other for more than three decades. Proof theory has contributed the notion of sequent calculus, linear logic, and higher-order quantification. Logic programming has introduced new normal forms of proofs and forced the examination of logic-based approaches to the treatment of bindings. As a result, proof theory has responded by developing an approach to proof search based on focused proof systems in which introduction rules are organized into two alternating phases of rule application. Since the logic programming community can generate many examples and many design goals (e.g., modularity of specifications and higher-order programming), the close connections with proof theory have helped to keep proof theory relevant to the general topic of computational logic.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

Notes

  1. We use the syntax of λ Prolog instead of Prolog: for simple programs, the difference between these languages is small.

References

  • Aït-Kaci, H. (1991). Warren’s abstract machine: a tutorial reconstruction. Logic Programming Research Reports and Notes. Cambridge: MIT Press. http://wambook.sourceforge.net/.

    Google Scholar 

  • Andreoli, J.M. (1990). Proposal for a synthesis of logic and object-oriented programming paradigms. Ph.D. Thesis University of Paris VI.

  • Andreoli, J.M. (1992). Logic programming with focusing proofs in linear logic. Journal of Logic and Computation, 2(3), 297–347. https://doi.org/10.1093/logcom/2.3.297.

    Article  Google Scholar 

  • Andreoli, J.M., & Pareschi, R. (1991). Communication as fair distribution of knowledge. In: Proceedings of OOPSLA 91 (pp. 212–229).

  • Andreoli, J.M., & Pareschi, R. (1991). Linear objects: logical processes with built-in inheritance. New Generation Computing, 9(3-4), 445–473.

    Google Scholar 

  • Andrews, P.B. (1971). Resolution in type theory. Journal of Symbolic Logic, 36, 414–432.

    Google Scholar 

  • Apt, K.R., & van Emden, M.H. (1982). Contributions to the theory of logic programming. Journal of the ACM, 29(3), 841–862.

    Google Scholar 

  • Barendregt, H. (1997). The impact of the lambda calculus in logic and computer science. Bulletin of Symbolic Logic, 3(2), 181–215.

    Google Scholar 

  • de Bruijn, N.G. (1972). Lambda calculus notation with nameless dummies, a tool for automatic formula manipulation, with an application to the Church-Rosser theorem. Indagationes Mathematicae, 34(5), 381–392.

    Google Scholar 

  • Bruscoli, P., & Guglielmi, A. (2006). On structuring proof search for first order linear logic. Theoretical Computer Science, 360(1-3), 42–76.

    Google Scholar 

  • Bugliesi, M., Lamma, E., Mello, P. (1994). Modularity in logic programming. Journal of Logic Programming, 19(/20), 443–502.

    Google Scholar 

  • Burns, A.R. (1988). Programming in OCCAM 2. Addison-Wesley.

  • Cervesato, I., & Pfenning, F. (2002). A linear logical framework. Information & Computation, 179(1), 19–75.

    Google Scholar 

  • Chen, W., Kifer, M., Warren, D.S. (1993). HILOG: A foundation for higher-order logic programming. Journal of Logic Programming, 15(3), 187–230.

    Google Scholar 

  • Church, A. (1940). A formulation of the simple theory of types. Journal of Symbolic Logic, 5, 56–68. https://doi.org/10.2307/2266170.

    Article  Google Scholar 

  • Church, A. (1985). The calculi of lambda conversion. (AM-6) (Annals of Mathematics Studies). Princeton: Princeton University Press.

    Google Scholar 

  • Colmerauer, A., & Roussel, P. (1993). The birth of Prolog. SIGPLAN Notices, 28(3), 37–52.

    Google Scholar 

  • Coquand, T., & Huet, G. (1988). The calculus of constructions. Information and Computation, 76(2/3), 95–120.

    Google Scholar 

  • Dunchev, C., Guidi, F., Coen, C.S., Tassi, E. (2015). ELPI: fast, embeddable, λ Prolog interpreter. In Davis, M., Fehnker, A., McIver, A., Voronkov, A. (Eds.) Logic for programming, artificial intelligence, and reasoning - 20th International Conference, LPAR-20 2015, Suva, Fiji, November 24-28, 2015, Proceedings, LNCS, (Vol. 9450 pp. 460–468). Berlin: Springer.. https://doi.org/10.1007/978-3-662-48899-7_32

  • Emerson, E.A. (2008). The beginning of model checking: a personal perspective. In Grumberg, O., & Veith, H. (Eds.) 25 years of model checking - history, achievements, perspectives, lecture notes in computer science, (Vol. 5000 pp. 27–45). https://doi.org/10.1007/978-3-540-69850-0_2. Berlin: Springer.

  • Engberg, U., & Winskel, G. (1990). Petri nets and models of linear logic. In Arnold, A. (Ed.) CAAP’90, LNCS 431 (pp. 147–161). Springer.

  • Fages, F., Ruet, P., Soliman, S. (1998). Phase semantics and verification of concurrent constraint programs. In Pratt, V. (Ed.) 13th symp.on logic in computer science. IEEE.

  • Felty, A. (1991). Transforming specifications in a dependent-type lambda calculus to specifications in an intuitionistic logic. In Huet, G., & Plotkin, G.D. (Eds.) Logical Frameworks. Cambridge University Press.

  • Fitting, M. (1987). Resolution for intuitionistic logic. In: Proc. International Symposium of Methodologies for Intelligent Systems ISMIS’87 (pp. 400–407).

  • Gabbay, D.M. (1985). N-prolog: An extension of Prolog with hypothetical implication II—logical foundations, and negation as failure. Journal of Logic Programming, 2(4), 251–283.

    Google Scholar 

  • Gabbay, D.M., & Reyle, U. (1984). N-Prolog: an extension of Prolog with hypothetical implications. I. Journal of Logic Programming, 1, 319–355.

    Google Scholar 

  • Gazdar, G., Klein, E., Pullum, G., Sag, I. (1985). Generalized Phrase Structure Grammar. Cambridge: Harvard University Press.

    Google Scholar 

  • Gentzen, G. (1935). Investigations into logical deduction. In Szabo, M. E. (Ed.), The Collected Papers of Gerhard Gentzen (pp. 68–131), North-Holland, Amsterdam. https://doi.org/10.1007/BF01201353.

  • Gentzen, G. (1938). New version of the consistency proof for elementary number theory. In Szabo, M. E. (Ed.) Collected papers of Gerhard Gentzen (pp. 252–286). North-Holland, Amsterdam, Originally published 1938.

  • Girard, J.Y. (1987). Linear logic. Theoretical Computer Science, 50 (1), 1–102. https://doi.org/10.1016/0304-3975(87)90045-4.

    Google Scholar 

  • Gödel, K. (1965). On formally undecidable propositions of the principia mathematica and related systems. I. In Davis, M. (Ed.) The undecidable. Raven press.

  • Green, C. (1969). Theorem proving by resolution as a basis for question-answering systems. Machine Intelligence 4.

  • Hallnȧs, L., & Schroeder-Heister, P. (1991). A proof-theoretic approach to logic programming. II. Programs as definitions. Journal of Logic and Computation, 1(5), 635–660.

    Google Scholar 

  • Halpern, J.Y., Harper, R., Immerman, N., Kolaitis, P.G., Vardi, M.Y., Vianu, V. (2001). On the unusual effectiveness of logic in computer science. Bulletin of Symbolic Logic, 7(1), 213–236.

    Google Scholar 

  • Hardy, G.H. (1940). A mathematician’s apology. Cambridge University Press.

  • Harland, J., Pym, D., Winikoff, M. (1996). Programming in lygon: an overview. In Proceedings of the Fifth International Conference on Algebraic Methodology and Software Technology (pp. 391–405).

  • Harper, R., Honsell, F., Plotkin, G. (1993). A framework for defining logics. Journal of the ACM, 40(1), 143–184.

    Google Scholar 

  • Hoare, C.A.R. (1985). Communicating sequential processes. Prentice-Hall.

  • Hodas, J., & Miller, D. (1990). Representing objects in a logic programming language with scoping constructs. In Warren, D.H.D., & Szeredi, P. (Eds.) 1990 International Conference in Logic Programming (pp. 511–526). MIT Press.

  • Hodas, J., & Miller, D. (1994). Logic programming in a fragment of intuitionistic linear logic. Information and Computation, 110(2), 327–365.

    Google Scholar 

  • Hodas, J.S. (1994). Logic programming in intuitionistic linear logic: theory, design, and implementation. Ph.D. thesis, University of Pennsylvania Department of Computer and Information Science.

  • Huet, G.P. (1973). A mechanization of type theory. In Proceedings of the 3rd International Joint Conference on Artificial Intelligence (pp. 139–146).

  • Jaffar, J., & Lassez, J.L. (1987). Constraint logic programming. In Proceedings of the 14th ACM Symposium on the Principles of Programming Languages.

  • Kanovich, M. (1994). The complexity of Horn fragments of linear logic. Annals of Pure and Applied Logic, 69, 195–241.

    Google Scholar 

  • Kanovich, M.I. (1995). Petri nets, Horn programs, linear logic and vector games. Annals of Pure and Applied Logic, 75(1–2), 107–135. https://doi.org/10.1017/S0960129500001328.

    Article  Google Scholar 

  • Kleene, S.C. (1935). A theory of positive integers in formal logic, part I. American Journal of Mathematics, 57, 153–173.

    Google Scholar 

  • Kleene, S.C. (1952). Permutabilities of inferences in Gentzen’s calculi LK and LJ. Memoirs of the American Mathematical Society, 10, 1–26.

    Google Scholar 

  • Kobayashi, N., & Yonezawa, A. (1993). ACL - A concurrent linear logic programming paradigm. In Miller, D. (Ed.) Logic programming - Proceedings of the 1993 International Symposium (pp. 279–294). MIT Press.

  • Kobayashi, N., & Yonezawa, A. (1994). Asynchronous communication model based on linear logic. Formal Aspects of Computing, 3, 279–294.

    Google Scholar 

  • Kowalski, R.A. (1974). Predicate logic as a programming language. Information Processing, 74, 569–574.

    Google Scholar 

  • Kowalski, R.A., & Kuehner, D. (1971). Linear resolution with selection function. Artificial Intelligence, 2, 227–260.

    Google Scholar 

  • Lambek, J., & Scott, P.J. (1986). Introduction to higher order categorical logic. Cambridge University Press.

  • Lawvere, F.W. (1963). Functorial semantics of algebraic theories. Proceedings National Academy of Sciences USA, 50, 869–872.

    Google Scholar 

  • Liang, C., & Miller, D. (2009). Focusing and polarization in linear, intuitionistic, and classical logics. Theoretical Computer Science, 410(46), 4747–4768. https://doi.org/10.1016/j.tcs.2009.07.041.

    Article  Google Scholar 

  • Lincoln, P., & Saraswat, V. (1993). Higher-order, linear, concurrent constraint programming. ftp://parcftp.xerox.com/pub/ccp/lcc/hlcc.dvi.

  • Lobo, J., Minker, J., Rajasekar, A. (1992). Foundations of disjunctive logic programming. MIT Press.

  • Martin-Löf, P. (1985). Constructive mathematics and computer programming. In Hoare, C.A.R., & Shepherdson, J.C. (Eds.) Mathematical logic and programming languages (pp. 167–184). Prentice-Hall.

  • McCarty, L.T. (1988). Clausal intuitionistic logic I. Fixed point semantics. Journal of Logic Programming, 5, 1–31.

    Google Scholar 

  • McCarty, L.T. (1988). Clausal intuitionistic logic II. Tableau proof procedure. Journal of Logic Programming, 5, 93–132.

    Google Scholar 

  • Miller, D. (1986). A theory of modules for logic programming. In Keller, R.M. (Ed.) Third Annual IEEE Symposium on Logic Programming (pp. 106–114). Salt Lake City.

  • Miller, D. (1987). A compact representation of proofs. Studia Logica, 46(4), 347–370.

    Google Scholar 

  • Miller, D. (1989). A logical analysis of modules in logic programming. Journal of Logic Programming, 6(1-2), 79–108.

    Google Scholar 

  • Miller, D. (1990). Abstractions in logic programming. In Odifreddi, P. (Ed.) Logic and Computer Science (pp. 329–359): Academic Press. http://www.lix.polytechnique.fr/Labo/Dale.Miller/papers/AbsInLP.pdf.pdf.

  • Miller, D. (1991). A logic programming language with lambda-abstraction, function variables, and simple unification. Journal of Logic and Computation, 1(4), 497–536.

    Google Scholar 

  • Miller, D. (1992). Unification under a mixed prefix. Journal of Symbolic Computation, 14(4), 321–358.

    Google Scholar 

  • Miller, D. (1993). The π-calculus as a theory in linear logic: preliminary results. In Lamma, E., & Mello, P. (Eds.) 3rd Workshop on Extensions to Logic Programming, no. 660 in LNCS. http://www.lix.polytechnique.fr/Labo/Dale.Miller/papers/pic.pdf (pp. 242–265). Bologna: Springer.

  • Miller, D. (1994). A multiple-conclusion meta-logic. In Abramsky, S. (Ed.) 9Th symp.on Logic in Computer Science (pp. 272–281). Paris: IEEE Computer Society Press.

  • Miller, D. (1996). Forum: a multiple-conclusion specification logic. Theoretical Computer Science, 165(1), 201–232.

    Google Scholar 

  • Miller, D. (2003). Encryption as an abstract data-type: an extended abstract. In Cervesato, I. (Ed.) Proceedings of FCS’03: Foundations of Computer Security (pp. 3–14).

  • Miller, D. (2004). Bindings, mobility of bindings, and the ∇-quantifier. In Marcinkowski, J., & Tarlecki, A. (Eds.) 18th International Conference on Computer Science Logic (CSL) 2004, LNCS, (Vol. 3210 p. 24). https://doi.org/10.1007/978-3-540-30124-0_4.

  • Miller, D. (2004). Overview of linear logic programming. In Ehrhard, T., Girard, J.Y., Ruet, P., Scott, P. (Eds.) Linear Logic in Computer Science, London Mathematical Society Lecture Note, (Vol. 316 pp. 119–150). Cambridge: Cambridge University Press.

  • Miller, D. (2018). Mechanized metatheory revisited. Journal of Automated Reasoning. https://doi.org/10.1007/s10817-018-9483-3.

  • Miller, D., & Nadathur, G. (2012). Programming with higher-order logic. Cambridge University Press. https://doi.org/10.1017/CBO9781139021326.

  • Miller, D., Nadathur, G., Pfenning, F., Scedrov, A. (1991). Uniform proofs as a foundation for logic programming. Annals of Pure and Applied Logic, 51 (1–2), 125–157.

    Google Scholar 

  • Miller, D., Nadathur, G., Scedrov, A. (1987). Hereditary Harrop formulas and uniform proof systems. In Gries, D. (Ed.) 2nd symp.on Logic in Computer Science (pp. 98–105). Ithaca.

  • Milner, R. (1980). A calculus of communicating systems LNCS Vol. 92. New York: Springer.

    Google Scholar 

  • Milner, R. (1999). Communicating and systems: the π-calculus. New York: Cambridge University Press.

    Google Scholar 

  • Milner, R., Parrow, J., Walker, D. (1992). A calculus of mobile processes, Part I. Information and Computation, 100(1), 1–40.

    Google Scholar 

  • Milner, R., Tofte, M., Harper, R. (1990). The definition of standard ML. MIT press.

  • Minker, J., & Seipel, D. (2002). Disjunctive logic programming: a survey and assessment. In Computational logic: logic programming and beyond, (Vol. 2407 pp. 472–511). Berlin: Springer.

  • Nadathur, G. (1987). A higher-order logic as the basis for logic programming. Ph.D. thesis, University of Pennsylvania.

  • Nadathur, G., Jayaraman, B., Kwon, K. (1995). Scoping constructs in logic programming: implementation problems and their solution. Journal of Logic Programming, 25(2), 119–161. https://doi.org/10.1016/0743-1066(95)00037-K.

    Article  Google Scholar 

  • Nadathur, G., & Miller, D. (1988). An overview of λ Prolog. In Fifth International Logic Programming Conference (pp. 810–827). Seattle: MIT Press. http://www.lix.polytechnique.fr/Labo/Dale.Miller/papers/iclp88.pdf.

  • Nadathur, G., & Miller, D. (1990). Higher-order Horn clauses. Journal of the ACM, 37(4), 777–814.

    Google Scholar 

  • Nadathur, G., & Mitchell, D.J. (1999). System description: Teyjus— a compiler and abstract machine based implementation of λ prolog. In Ganzinger, H. (Ed.) 16Th Conf.on Automated Deduction (CADE), no. 1632 in LNAI (pp. 287–291). Trento: Springer.

  • Ong, C.L., & Stewart, C.A. (1997). A Curry-Howard foundation for functional computation with control. In Conference record of POPL’97: the 24th ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, Paris, France, 15-17 January 1997 (pp. 215–227). https://doi.org/10.1145/263699.263722.

  • Pareschi, R. (1989). Type-driven natural language analysis. Ph.D. thesis, University of Edinburgh.

  • Pareschi, R., & Miller, D. (1990). Extending definite clause grammars with scoping constructs. In Warren, D.H.D., & Szeredi, P. (Eds.) 1990 International Conference in Logic Programming (pp. 373–389): MIT Press.

  • Paulson, L.C. (1989). The foundation of a generic theorem prover. Journal of Automated Reasoning, 5, 363–397.

    Google Scholar 

  • Pfenning, F., & Schürmann, C. (1999). System description: Twelf — a meta-logical framework for deductive systems. In Ganzinger, H. (Ed.) 16th Conf.on Automated Deduction (CADE), no. 1632 in LNAI (pp. 202–206). Trento: Springer. https://doi.org/10.1007/3-540-48660-7_14.

  • Plotkin, G.D. (2004). A structural approach to operational semantics. Journal of Logic and Algebraic Programming, 60-61, 17–139.

    Google Scholar 

  • Prawitz, D. (1965). Natural deduction. Uppsala: Almqvist & Wiksell.

    Google Scholar 

  • Pym, D.J., & Harland, J.A. (1994). The uniform proof-theoretic foundation of linear logic programming. Journal of Logic and Computation, 4(2), 175–207.

    Google Scholar 

  • Qi, X., Gacek, A., Holte, S., Nadathur, G., Snow, Z. (2015). The Teyjus system – version 2. http://teyjus.cs.umn.edu/.

  • Robinson, J.A. (1965). A machine-oriented logic based on the resolution principle. JACM, 12, 23–41.

    Google Scholar 

  • Ruet, P., & Fages, F. (1997). Concurrent constraint programming and non-commutative logic. In Proceedings of the 11t h Conference on Computer Science Logic, LNCS. Springer.

  • Sangiorgi, D., & Walker, D. (2001). π-calculus: a theory of mobile processes Cambridge University Press.

  • Saraswat, V. (1993). A brief introduction to linear concurrent constraint programming. Tech. rep., Xerox Palo Alto Research Center. ftp://parcftp.xerox.com/pub/ccp/lcc/lcc-intro.dvi.Z.

  • Sørensen, M.H., & Urzyczyn, P. (2006). Lectures on the Curry-Howard Isomorphism, Studies in Logic, vol. 149 Elsevier.

  • Stoy, J.E. (1977). Denotational semantics: the Scott-Strachey approach to programming language theory. Cambridge: MIT Press.

    Google Scholar 

  • Tammet, T. (1996). A resolution theorem prover for intuitionistic logic. In Automated deduction — CADE-13, LNCS, (Vol. 1104 pp. 2–16).

  • Tarski, A. (1954). Contributions to the theory of models. I. Indagationes Mathematicae, 16, 572–581.

    Google Scholar 

  • Wadler, P. (1990). Linear types can change the world!. In Programming Concepts and Methods (pp. 561–581). North holland.

  • Warren, D.H.D. (1983). An abstract Prolog instruction set. Tech. Rep. 309 SRI International.

Download references

Acknowledgments

I thank the participants of the “Fourth Symposium on the History and Philosophy of Programming” (HaPoP 2018) meeting and the members of the ANR project PROGRAMme (ANR-17-CE38-0003-01) for their comments on a talk based on an earlier version of this paper.

Author information

Authors and Affiliations

  1. Inria Saclay and LIX/École Polytechnique, Palaiseau, France

    Dale Miller

Authors
  1. Dale Miller
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Dale Miller.

Additional information

Publisher’s Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Miller, D. Reciprocal Influences Between Proof Theory and Logic Programming. Philos. Technol. 34, 75–104 (2021). https://doi.org/10.1007/s13347-019-00370-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s13347-019-00370-x

Keywords

Search

Navigation