On the regularity of null cones and geodesic spheres

Abstract

We show a property on the null cones in a Lorentzian manifold near a conjugate point, which contributes to the understanding of the behaviour of the exponential map. We also give an analogous property in the Riemannian case.

1 Introduction

An important fact about the behaviour of the exponential map in a Riemannian manifold is that it is never injective near a conjugate point. In fact, if $\exp _{p_0}$ is singular at $v\in T_{p_0}M$, then it is not injective on any neighbourhood of v, [23]. This result goes back ninety years ago to the works of Morse and Littauer [18] and Savage [21]. It was generalized to the Lorentzian setting in [22] in the case v is timelike or lightlike.

Recall that this is not a general behaviour of a map at a singular point. An easy example, given also in [23], is the map $\varphi :\mathbb {R}^2\rightarrow \mathbb {R}^2$ defined by $\varphi (x,y)=(x^3,y)$, which has a singular point at (0, 0) but it is injective.

In order to get similar properties on the behaviour of the exponential map in a Lorentzian or Riemannian manifold, we deal with null hypersurfaces. Recall that a null hypersurface of a Lorentzian manifold is a hypersurface such that the inherited metric is degenerated. They constitute a distinguished family of hypersurfaces and they are a key geometric structure in Physics. Null hypersurfaces have been extensively used in the study of black hole and other topics in General Relativity.

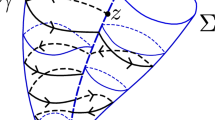
On the other hand, a null cone with vertex at a point $p_0$ in a Lorentzian manifold is the set formed by null geodesics emanating from $p_0$ such that their initial velocities are in the same timecone than a fixed timelike vector $e_0$. It can be seen as the image by the exponential map at $p_0$ of a embedded hypersurface in $T_{p_0}M$, namely, the lightlike cone of $e_0$. A null cone is a null hypersurface near the vertex, but we cannot ensure the same in a neighbourhood of a null conjugate point since it is the image of a singular point. However, a priori, we can not ensure the contrary either and there are not reasons to think that the null cone is not an embedded null hypersurface, even if it contains a null conjugate point. The following easy example can be useful to clarify the above issue. Take $\varphi :\mathbb {R}^2\rightarrow \mathbb {R}^3$ given by $\varphi (x,y)=\left( x,y^3,x^3\right)$. The point (0, 0) is a singular point, but the image of $\varphi$ is an embedded surface in $\mathbb {R}^3$. Hence, we may wonder the following.

Question 1

Can be a null cone, regarded as a subset of M, be considered as a smooth (null) hypersurface despite the presence of null conjugate points?

The lack of the injectivity near a conjugate point proven in [22] seems to suggest that the question posed above has a negative answer. However there are examples of maps which are not injective around a singular point but their images are embedded hypersurfaces. Indeed, take $\varphi :\mathbb {R}^2\rightarrow \mathbb {R}^3$ given by $\varphi (x,y)=(x^2-y^2,xy,0)$. It has an isolated singular point at (0, 0), it is not injective in any neighborhood of (0, 0) and $\varphi (\mathbb {R}^2)=\{(x,y,0)\in \mathbb {R}^3:x,y\in \mathbb {R}\}$ is an embedded surface in $\mathbb {R}^3$. Moreover, we can check that

$$\begin{aligned} \varphi \left( \{(x,y)\in \mathbb {R}^2:x^4+y^4<R^2\}\right) = \{(x,y,0)\in \mathbb {R}^3:x^2+2y^2<R^2\} \end{aligned}$$

for all $R>0$. Therefore, there are arbitrary small neighbourhoods of the singular point (0, 0) such that its image is an embedded hypersurface in $\mathbb {R}^3$.

Summarizing, Question (1) deserves a detailed study because it is more subtle that it seems and its answer unveils a nice property of null cones.

In Corollary 1 we prove that the answer to Question (1) is actually negative. In other words, the presence of a null conjugate point to the vertex destroys the hypersurface structure of the null cone. Indeed, we prove in Theorem 1 a little more general fact. We show that there is no neighbourhood of a singular point in the null cone of the exponential map which image is contained in a null hypersurface. To prove this, we use as a key tool the rigging technique introduced by the authors for null hypersurfaces in [10] and for null submanifolds in [17] (see [14] for a review). It consists in defining a Riemannian metric on the null hypersurface from an arbitrary chosen transverse vector field called rigging. This allows us to use Riemannian techniques to study null hypersurfaces, which opens up a wide range of possibilities. In the proof of Theorem 1, assuming the contrary of its statement, we construct a Riemann metric such that its curvature diverges as we approach the conjugate point, which gives us a contradiction.

In the last section we prove an analogous result for a Riemannian manifold. In this case, geodesic spheres (the image by the exponential map of a sphere in the tangent space) are considered. We show in Theorem 2 that there is no neighbourhood of a singular point of the exponential map such that it is injective and its image is a hypersurface, always restricted to a sphere in the tangent space. In the proof, we suppose the existence of such neighbourhood and we construct a null hypersurface which contains a piece of the null cone in the Lorentzian direct product formed by a $\mathbb {R}$ factor and the Riemannian manifold. This allows us to apply Theorem 1 to get a contradiction.

2 Null hypersurfaces

All hypersurface considered in this paper are embedded. A null hypersurface is a hypersurface such that the induced metric tensor from the ambient space (M, g) is degenerated at each point. Due to this degeneracy, the orthogonal complement of the tangent space is contained in its tangent space itself, so this type of hypersurfaces can not be handled as timelike or spacelike submanifols. The study of null hypersurfaces needs the choice of some arbitrary geometric objects. The rigging technique introduced in [10] tries to minimize this arbitrariness inducing all the needed geometric objects from only one choice. It consists on fixing a vector field $\zeta$ defined on an open set containing the null hypersurface L (alternatively, it can be defined only on L if necessary) such that $\zeta _p\notin T_p L$ for all $p\in L$, which is called a rigging for L. If we call $\alpha$ the metrically equivalent one-form to $\zeta$ and $\omega =i^*\alpha$, where $i:L\rightarrow M$ is the canonical inclusion, then

$$\begin{aligned} {\widetilde{g}}=i^*g+\omega \otimes \omega \end{aligned}$$

is a Riemannian metric on L. It can be used as an auxiliary tool to study null hypersurfaces and their interactions with the ambient space, see for example [1,2,3,4,5, 7, 12, 13, 15, 19]. It have also been used to construct some geometrical structures such as contact and Sasaki structures on a null hypersurface, [6].

The ${\widetilde{g}}$-metrically equivalent vector field to $\omega$, which we denote by $\xi$, is unitary and it is called the rigged vector field induced by $\zeta$. It is also characterized as the unique null vector field $\xi \in {\mathfrak {X}}(L)$ normalized by

$$\begin{aligned} g(\xi ,\zeta )&=1. \end{aligned}$$

(1)

We define a screen distribution given by ${\mathcal {S}}_p=T_p L\cap \zeta ^\perp _p$ for all $p\in L$, which is a spacelike distribution such that $T_p L={\mathcal {S}}_p\oplus span\{\xi _p\}$.

Both the screen distribution as the null section $\xi$ can be constructed in a local and independent way without using a rigging, [9]. However, we can achieve a good coupling if both come from a rigging. On the other hand, given a null hypersurface maybe it does not exist a globally defined rigging for it, but it always exists at least locally. In a spacetime, any timelike vector field is an example of a rigging for any null hypersurface, showing that riggings are abundant.

The rigged vector field holds $\nabla _\xi \xi =-\tau (\xi )\xi$, where $\tau$ is the one-form given by $\tau (U)=-g(\nabla _U\xi ,\zeta )$ for all $U\in {\mathfrak {X}}(L)$, [9, 10]. Thus, $\xi$ is a pre-geodesic vector field and the null hypersurface is foliated by null geodesics. The rigged vector field is used to define the null second fundamental form of L as $B(u,v)=-g(\nabla _u \xi ,v)$ for all $u,v\in T_{p}L$ and $p\in L$.

If $\zeta '$ is another rigging for L, then a simple calculation shows that its induced rigged vector field and its null second fundamental form are related to those of $\zeta$ by

$$\begin{aligned} \xi '&=\frac{1}{g(\xi ,\zeta ')}\xi , \end{aligned}$$

(2)

$$\begin{aligned} B'&=\frac{1}{g(\xi ,\zeta ')}B. \end{aligned}$$

(3)

In particular, if we change the sign of the rigging, then the rigged vector field and the null second fundamental form change their sign. We can also express the one-form $\tau '$ in terms of $\tau$ under a simple rigging change. If $f\in C^\infty (L)$ is a never vanishing function and we consider $\zeta '=\frac{1}{f} \zeta$, then

$$\begin{aligned} \tau '&=\tau -\frac{df}{f}, \end{aligned}$$

thus

$$\begin{aligned} \tau '(\xi ')=f\tau (\xi )-df(\xi ). \end{aligned}$$

(4)

In [17] it is shown how all geometric objects of a null hypersurface are affected under a general change of the rigging.

A careful choice of the rigging provides us with simple relationships between the null hypersurface and the Riemannian manifold $(L,{\widetilde{g}})$. We say that the rigging $\zeta$ is closed if its g-metrically equivalent one-form $\alpha$ is closed, $d\alpha =0$. In this case, the screen distribution is integrable and the rigged vector field is ${\widetilde{g}}$-geodesic. Moreover, we have the following key result.

Lemma 1

([10]) Let $\zeta$ be a closed rigging for a null hypersurface L.

• 1. The second fundamental form of the leaves of the screen distribution, as hypersurfaces of $(L,{\widetilde{g}})$, is $\widetilde{\mathbb {I}}(X,Y)=B(X,Y)\xi$ for all $X,Y\in {\mathcal {S}}$.

• 2. The sectional curvature of a plane $\Pi =span\{v,\xi \}$ in $(L,{\widetilde{g}})$ is given by

  $$\begin{aligned} {\widetilde{K}}(\Pi )={\mathcal {K}}_\xi (\Pi )-\tau (\xi )\frac{B(v,v)}{g(v,v)}, \end{aligned}$$

  where ${\mathcal {K}}_\xi$ denotes the null sectional curvature respect to $\xi$.

Recall that ${\mathcal {K}}_\xi (\Pi )=\frac{g(R_{v\xi }\xi ,v)}{g(v,v)}$, which does not depend on the chosen spacelike vector $v\in \Pi$.

We can always ensure locally the existence of a closed rigging for a null hypersurface but, for example, its global existence is not possible for compact hypersurfaces in simply connected Lorentzian manifolds, [10, 17].

3 Non-regularity of a null cone at null conjugate points

Let $p_0\in M$ be a point and $e_0\in T_{p_0}M$ a fixed timelike vector. We call

$$\begin{aligned} {\widehat{C}}_{e_{0}}=\{u\in T_{p_{0}}M:g(u,u)=0,\ g(u,e_{0})<0\} \end{aligned}$$

the tangent null cone of $e_0$. The null cone of $e_0$ with vertex at $p_0$ is

$$\begin{aligned} C_{e_0}=\exp _{p_0}\left( {\widehat{\Theta }}\cap {\widehat{C}}_{e_0} \right) , \end{aligned}$$

where ${\widehat{\Theta }}$ is the maximal definition domain of $\exp _{p_0}$. In other words, it is the set of points that can be reached by a null geodesic from $p_0$ such that its initial velocity is a null vector with the same time orientation as $e_0$. Another non-equivalent definition frequently used in the literature for a (future) null cone in a time-orientable Lorentzian manifold is $\partial I^+(p_0)$, i.e. the border of the chronological future of $p_0$. If M is globally hyperbolic and $e_0$ is future pointing, then $\partial I^+(p)\subset C_{e_0}$, [11].

On the other hand, if $\theta =\exp _{p_0}({\widehat{\theta }})$ is a normal neighborhood of $p_{0}$, where $0\in {\widehat{\theta }}\subset T_{p_0}M$, then a local null cone of $e_{0}$ with vertex at $p_0$ is

$$\begin{aligned} C_{e_{0}}^{l}=\exp _{p_{0}}\left( {\widehat{\theta }} \cap {\widehat{C}}_{e_{0}}\right) . \end{aligned}$$

It is well-known that the existence of a conjugate point is equivalent to the existence of a singular point of the exponential map $\exp _{p_0}:{\widehat{\Theta }}\rightarrow M$. The same is true if we restrict to the null cone.

Proposition 1

Take $u\in {\widehat{\Theta }}\cap {\widehat{C}}_{e_0}$ and the null geodesic $\gamma (t)=\exp _{p_0}(tu)$. The following are equivalent.

• 1. $\gamma (1)$ is a conjugate point to $p_0$ along $\gamma (t)$.

• 2. The point u is a singular point of $\exp _{p_0}:{\widehat{\Theta }}\cap {\widehat{C}}_{e_0}\rightarrow M$.

• 3. The point u is a singular point of $\exp _{p_0}:{\widehat{\Theta }}\rightarrow M$.

Proof

We only sketch $1\Rightarrow 2$. The rest is well-known.

Take J(t) a Jacobi vector field along $\gamma$ with $J(0)=J(1)=0$ and express it as $J(t)=\frac{d}{ds} \exp _{p_{0}}(t(u+sv))\vert _{s=0}$ for a certain $v\in T_{p_{0}}M$. We have that $\left( \exp _{p_0}\right) _{*_u}(v)=J(1)=0$, where here v is considered in $T_u T_{p_0}M$. Since $\gamma '(1)=\left( \exp _{p_0}\right) _{*_u}(u)$, using the Gauss Lemma we get

$$\begin{aligned} 0=g(J(1),\gamma '(1))=g( \left( \exp _{p_0}\right) _{*_u}(v) , \left( \exp _{p_0}\right) _{*_u}(u))=g_p(v,u), \end{aligned}$$

which means that v is tangent to ${\widehat{C}} _{e_0}$ at u. Therefore, u is a singular point of $\exp _{p_0}:{\widehat{\Theta }}\cap {\widehat{C}}_{e_0}\rightarrow M$. $\square$

If $p=\exp _{p_0}(u)\in C_{e_0}$ is not a conjugate point along the null geodesic $\exp _{p_0}(tu)$, then there are open sets ${\widehat{U}}, U$ with $u\in {\widehat{U}}\subset {\widehat{\Theta }}$ and $p\in U\subset M$ such that $\exp _{p_0}:{\widehat{U}}\rightarrow U$ is a diffeomorphism. In this situation, we call

$$\begin{aligned} C_{e_0}^R(p)=\exp _{p_0}\left( {\widehat{U}}\cap {\widehat{C}}_{e_0} \right) \subset C_{e_0} \end{aligned}$$

a regular part of the null cone through p. Observe that it can exist different regular parts through a point due to the existence of null crossing points, [11]. Locally it looks like two or more leaves crossing transversely through a point. It is clear that local null cones and regular parts of null cones are null hypersurfaces.

Suppose that $\exp _{p_0}:{\widehat{U}}\rightarrow U$ is a diffeomorphism, where ${\widehat{U}}\subset T_{p_0}M$ and $U\subset M$ are open sets. We can consider the function $h:U\rightarrow \mathbb {R}$ and a vector field $P\in {\mathfrak {X}}(U)$ given by

$$\begin{aligned} h(\exp _{p_0}(v))&=-g(e_0,v),\\ P_{\exp _{p_0}(v)}&=\left( \exp _{p_0}\right) _{*_v}(v), \end{aligned}$$

for all $v\in {\widehat{U}}$. They are called height function and position vector field respectively. If we restrict them to a regular part of the null cone $C^R_{e_0}(p)$, with $p\in C_{e_0}$, then P is a null vector field tangent to $C^R_{e_0}(p)$ and h is positive.

Lemma 2

Let $\gamma :[0,a]\rightarrow M$ be the null geodesic given by $\gamma (t)=\exp _{p_0}(tu)$, where $u\in {\widehat{C}}_{e_{0}}$ with $g(e_0,u)=-1$. If $p=\gamma (t_0)\in C_{e_0}$, with $0<t_0<a$, is not a null conjugate point to $p_0$ along $\gamma$, then $\zeta ^0=\nabla h$ is a rigging for the regular part of the null cone $C_{e_0}^R(p)$ and its rigged vector field is $\xi ^0=\frac{1}{h}P$, which is g-geodesic and it holds $\xi ^0_{\gamma (t)}=\gamma '(t)$.

Moreover, if $J:[0,a]\rightarrow TM$ is a Jacobi vector field along $\gamma$ with $J(0)=0$ and $J(t_0)\perp \gamma '(t_0)$, then the null second fundamental form $B^0$ associated to $\xi ^0$ holds

$$\begin{aligned} B^0(J(t_0),J(t_0))=-g(J'(t_0),J(t_0)). \end{aligned}$$

Proof

Let ${\widehat{U}}\subset T_{p_0}M$ be an open set such that $\exp _{p_0}:{\widehat{U}}\rightarrow U$ is a diffeomorphism with $t_0 u\in {\widehat{U}}$. If we take an arbitrary $v\in {\widehat{U}}\cap {\widehat{C}}_{e_0}$ with $g(e_0,v)=-1$ and the null geodesic $\alpha (t)=\exp _{p_0}(tv)$, then $h(\alpha (t))=t$. Since $\alpha '(t)=\frac{1}{t}P_{\alpha (t)}$, then the above means that $g(\zeta ^0,P_{\alpha (t)})=t$ and so $\zeta ^0$ is a rigging in $C^R_{e_o}(p)$ with rigged vector field $\xi ^0=\frac{1}{h}P$. Finally, $\alpha '(t)=\xi ^0$, showing that $\xi ^0$ is g-geodesic.

For the second part, call $w=J(t_0)$. If $w=0$, then the formula holds trivially, so we suppose $w\ne 0$. Consider the geodesic variation

$$\begin{aligned} X:[0,a]\times (-\varepsilon ,\varepsilon )\rightarrow M \end{aligned}$$

given by $X(t,s)=\exp _{p_0}(t(u+s{\hat{w}}))$, where ${\hat{w}}\in T_{p_0}M$ is such that $X_s(t_0,0)=\left( \exp _{p_0}\right) _{*_{t_0 u}}(t_0{\hat{w}})=w$. Since $X_{s}(t,0)$ is a Jacobi vector field along $\gamma (t)$ with $X_s(0,0)=0$, a uniqueness argument implies $J(t)=X_{s}(t,0)$ for all $t\in [0,a]$, [20]. Now, we have that

$$\begin{aligned} X_{t}(t,s)=\left( \exp _{p_0}\right) _{*_{t(u+s{\hat{w}})}}(u+s{\hat{w}} )=\frac{1}{t}P_{X(t,s)}. \end{aligned}$$

Therefore, evaluating at $(t_0,0)$, (for the two parameter map formalism see [20, Chapter 4]), we have

$$\begin{aligned} g(\nabla _{w}P,w)&=t_0 g(X_{ts}(t_0,0),X_{s}(t_0,0))=t_0 g(X_{st}(t_0,0),X_{s} (t_0,0))\\&=t_0 g(J^{\prime }(t_0),J(t_0)), \end{aligned}$$

thus $B^0(J(t_0),J(t_0))=-g(J'(t_0),J(t_0)).$ $\square$

Lemma 3

Let $\gamma :[0,a]\rightarrow M$ be the null geodesic given by $\gamma (t)=\exp _{p_0}(tu)$, where $u\in {\widehat{C}}_{e_{0}}$, and suppose that $\gamma (a)$ is a null conjugate point to $p_0$ along it. If $J:[0,a]\rightarrow TM$ is a nonzero Jacobi vector field along $\gamma$ with $J(0)=J(a)=0$ then $J'(a)$ is spacelike and there is $\varepsilon >0$ such that $g(J(t),J'(t))<0$ for all $t\in (a-\varepsilon ,a)$.

Proof

Since $J(0)=J(a)=0$, a well-known property on Jacoby fields implies that both $J(t),J'(t)\perp \gamma '(t)$, so $J'(t)$ is zero, spacelike or null for each $t\in [0,a]$. Since J is not identically zero, $J'(a)\ne 0$. If it were null, then $J'(a)=\lambda \gamma '(a)$ for some constant $\lambda \ne 0$, but this jointly with the condition $J(a)=0$ implies $J(t)=\lambda (t-a)\gamma '(t)$ in contradiction with $J(0)=0$. Thus, the only possibility is $g(J'(a),J'(a))>0$.

On the other hand, if we call $r(t)=g(J(t),J'(t))$ then $r(a)=0$ and $r'(a)>0$, so there is $\varepsilon >0$ such that $g(J(t),J'(t))<0$ for all $t\in (a-\varepsilon ,a)$. $\square$

Lemma 4

Let L be a null hypersurface and fix a rigging for it. Suppose that $\gamma :[0,a]\rightarrow L$ is a null geodesic and $J:[0,a]\rightarrow TL$ is a vector field along $\gamma$ such that $J(a)=0$, $J'(a)\ne 0$ and $J'(a)\nparallel \gamma '(a)$. Then there exists $\varepsilon >0$ such that $J(t)\nparallel \gamma '(t)$ for all $t\in (a-\varepsilon ,a)$ and

$$\begin{aligned} \lim _{t\rightarrow a^-} {\widetilde{K}}(span\{\gamma '(t),J(t)\})&={\widetilde{K}}(span\{\gamma '(a),J'(a)\}), \\ \lim _{t\rightarrow a^-} {\mathcal {K}}_{\gamma '(t)}(span\{\gamma '(t),J(t)\})&= {\mathcal {K}}_{\gamma '(a)}(span\{\gamma '(a),J'(a)\}), \end{aligned}$$

where ${\widetilde{K}}$ is the sectional curvature of the rigged metric ${\widetilde{g}}$ and ${\mathcal {K}}_{\gamma '(t)}$ is the null sectional curvature associated to $\gamma '(t)$.

Proof

Take a g-parallel translated orthonormal basis $E_1,\ldots ,E_n:[0,a]\rightarrow TM$ along $\gamma$ and write $J(t)=\sum _{i=1}^n \lambda _i(t)E_i(t)$ for all $t\in [0,a]$ and some functions $\lambda _i:[0,a]\rightarrow \mathbb {R}$. The lemma easily follows because the vector field $V(t)=\sum _{i=1}^n h_i(t)E_i(t)$, where $h_i(t)=\int _0^1 \lambda '_i(a+s(t-a))ds$, yields $J(t)=(t-a)V(t)$ and $V(a)=J'(a)$. $\square$

Lemma 5

Given a null hypersurface L and a point $q\in L$, there exists a neighbourhood U of q in M and a closed timelike rigging $\zeta \in {\mathfrak {X}}(U)$ such that $\tau (\xi _q)\ne 0$.

Proof

We can take a function $f\in C^\infty (U)$ defined in some open neighbourhood U of q with $\nabla f$ timelike, so $\zeta =\nabla f$ is a closed rigging for L. Moreover, we can suppose that f is positive in U. If $\tau (\xi _q)\ne 0$ we are done. If $\tau (\xi _q)= 0$, using Equations (1) and (4), the rigging $\zeta '=\nabla \ln f=\frac{1}{f}\zeta$ has the required properties. $\square$

Now we are ready to prove the main result of this paper.

Theorem 1

Let $p_0\in M$ and $q=\exp _{p_0}(au)\in C_{e_0}$ a conjugate point to $p_0$ along the null geodesic $\gamma (t)=\exp _{p_0}(tu)$, where $u\in {\widehat{C}}_{e_0}$ with $g(e_0,u)=-1$. It does not exist any open set ${\widehat{U}}\subset T_{p_0}M$ with $au\in {\widehat{U}}$ and a null hypersurface L such that $\exp _{p_0}({\widehat{U}}\cap {\widehat{C}}_{e_0})\subset L$.

Proof

Suppose on the contrary that there is an open set ${\widehat{U}}\subset T_{p_0}M$ and a null hypersurface L such that $\exp _{p_0}({\widehat{U}}\cap {\widehat{C}}_{e_0})\subset L$. Using Lemma 5 and shrinking it if necessary, we can take a closed rigging $\zeta$ for L with associated rigged vector field $\xi$ such that $\tau (\xi _q)\ne 0$.

We consider a nonzero Jacobi vector field $J:[0,a]\rightarrow TM$ along $\gamma$ with $J(0)=J(a)=0$. We have that $J(t)\perp \gamma '(t)$ and $J(t)\nparallel \gamma '(t)$ for all $t\in (0,a)$. Moreover, since conjugate points are isolated along $\gamma$ [8, Theorem 10.77], there is $\varepsilon >0$ such that $J(t)\ne 0$ for all $t\in (a-\varepsilon ,a)$. By hypothesis $\gamma (t)\in L$ for t with $tu\in {{\widehat{U}}}$, so we can suppose that $\gamma (t)\in L$ for all $t\in (a-\varepsilon ,a)$.

Take a regular part of the null cone $C^R_{e_0}(\gamma (t_0))\subset L$ for a fixed $t_0\in (a-\varepsilon ,a)$. Since $C^R_{e_0}(\gamma (t_0))$ is a null hypersurface, it is an open subset of L and so it contains a geodesic segment $\gamma _{\vert _{(t_0-\delta ,t_0+\delta )}}$. Consider the rigging $\zeta ^0$ for $C^R_{e_0}(\gamma (t_0))$ given by Lemma 2 with its associated rigged vector field $\xi ^0$. In $C^R_{e_0}(\gamma (t_0))$ we have two rigged vector fields, $\xi ^0$ and $\xi$. Thus, for $t\in (t_0-\delta ,t_0+\delta )$ we have from Eqs. (2) and (3) that $\xi _{\gamma (t)}=f(t)\xi ^0_{\gamma (t)}$ and $B_{\gamma (t)}=f(t)B^0_{\gamma (t)}$, where

$$\begin{aligned} f(t)=\frac{1}{g(\xi ^0_{\gamma (t)},\zeta _{\gamma (t)})}=\frac{1}{g(\gamma '(t), \zeta _{\gamma (t)})}. \end{aligned}$$

(5)

Observe that f is defined for all $t\in (t_0,a)$ and

$$\begin{aligned} \lim _{t\rightarrow a^-}f(t)=\frac{1}{g(\gamma '(a),\zeta _q)}\ne 0. \end{aligned}$$

Now, from Lemma 2 we have

$$\begin{aligned} B_{\gamma (t_0)}(J(t_0),J(t_0))=-f(t_0) g(J'(t_0),J(t_0)). \end{aligned}$$

If we consider the rigged metric induced from $\zeta$ in L, then applying Lemma 1 we have that the sectional curvature of the plane $\Pi _{t_0}=span\{\gamma '(t_0),J(t_0)\}$ is

$$\begin{aligned} {\widetilde{K}}(\Pi _{t_0})=f(t_0)^2{\mathcal {K}}_{\gamma '(t_0)} (\Pi _{t_0})+f(t_0)\tau (\xi _{\gamma (t_0)})\frac{g(J'(t_0),J(t_0))}{g(J(t_0),J(t_0))}. \end{aligned}$$

(6)

Using L’Hôpital’s rule and Lemma 3, we get

$$\begin{aligned} \lim _{t\rightarrow a^-}\frac{g(J'(t),J(t))}{g(J(t),J(t))} =\lim _{t\rightarrow a^-}\frac{g(J'(t),J'(t))}{2g(J'(t),J(t))}=- \infty , \end{aligned}$$

so if we let $t_0$ tend to a in Eq. (6) and we take into account Lemma 4, we get a contradiction. $\square$

As a collorary, we get that if there are conjugate points, then the null cone, regarded as a subset of M, can not be considered a null hypersurface.

Corollary 1

Let $p_0\in M$ and $q=\exp _{p_0}(au)\in C_{e_0}$ a conjugate point to $p_0$ along the null geodesic $\gamma (t)=\exp _{p_0}(tu)$, where $u\in {\widehat{C}}_{e_0}$ with $g(e_0,u)=-1$. It does not exist any open set ${\widehat{U}}\subset T_{p_0}M$ with $au\in {\widehat{U}}$ such that $\exp _{p_0}({\widehat{U}}\cap {\widehat{C}}_{e_0})$, regarded as a subset of M, is a null hypersurface.

Observe that this corollary is not equivalent to the preceding theorem because the exponential map contains a singular point, so it is not necessarily open.

4 Riemannian geodesic spheres

We can adapt Theorem 1 to the Riemann case using a standard trick. First we need some preliminaries.

Consider a Riemannian manifold $(N,g_0)$ and a point $x_0\in N$. We call ${\widehat{\Theta }}$ the maximal definition domain of $\exp _{x_0}$ and ${\widehat{S}}_a=\{u\in T_{x_0} N:g_0(u,u)=a^2\}$. The geodesic sphere of radius a is

$$\begin{aligned} S_a=\exp _{x_0}\left( {\widehat{S}}_a\cap {\widehat{\Theta }}\right) , \end{aligned}$$

provided it is not empty. We use the classical notation $\gamma _v$ for the unique geodesic with initial condition $\gamma '_v(0)=v$.

Lemma 6

Suppose there is an open subset ${\widehat{U}}\subset T_{x_0}N$ such that $\exp _{x_0}$ restricted to $\overline{ {\widehat{U}}\cap {\widehat{S}}_a}$ is injective and $K=\exp _{x_0}({\widehat{U}}\cap {\widehat{S}}_a)$, regarded as a subset of N, is a hypersurface. Let E be a unitary vector field normal to K. Given $z=\exp _{x_0}(v)\in K$, where $v\in {\widehat{U}}\cap {\widehat{S}}_a$, we have, up to sign,

$$\begin{aligned} E_{z}=\gamma '_{\frac{v}{a}}(a). \end{aligned}$$

In particular,

$$\begin{aligned} \gamma _{\frac{v}{a}}(t)=\exp _{z}((t-a)E_z) \end{aligned}$$

(7)

for all t with $\frac{tv}{a}\in {{\widehat{\Theta }}}$.

Proof

If $z=\exp _{x_0}(v)$ is not conjugate to $x_0$ along the geodesic $\exp _{x_0}(tv)$, then the claim is clear because $\exp _{x_0}$ is a diffeomorphism in a neighbourhood of v and we can use Gauss’ Lemma.

Suppose that z is a conjugate point to $x_0$ along the geodesic $\exp _{x_0}(tv)$. Using Sard’s Theorem, the set of critical values of the map $\exp _{x_0}:{\widehat{U}}\cap {\widehat{S}}_a\rightarrow K$ has zero measure. Therefore, there is a sequence $z_n\in K$ such that $z_n$ converges to z, $z_n=\exp _{x_0}(v_n)$ for some vector $v_n\in {\widehat{U}}\cap {\widehat{S}}_a$ and $z_n$ is not a conjugate point to $x_0$ along the geodesic $\exp _{x_0}(tv_n)$.

Moreover, we can assume that the sequence $v_n$ converges to some vector $w\in \overline{{\widehat{U}}\cap {\widehat{S}}_a}$ with $\exp _{x_0}(w)=z$, but being $\exp _{x_0}\vert _{\overline{{\widehat{U}}\cap {\widehat{S}}_a}}$ injective, we have $w=v$. Taking limit in $E_{z_n}=\gamma _{\frac{v_n}{a}}(a)$ we get the result. $\square$

Lemma 7

Let K be a hypersurface in N with normal unitary vector field E. Given $a\in \mathbb {R}$ and $x\in K$ there is a neighbourhood $\theta \subset K$ of x and $\varepsilon >0$ such that the image of

$$\begin{aligned} \Gamma :(a-\varepsilon ,a+\varepsilon )\times \theta \rightarrow \mathbb {R}\times N \end{aligned}$$

given by $\Gamma (t,z)=(t,\exp _{z}((t-a)E_z)$ is a null hypersurface in the Lorentzian direct product $\left( \mathbb {R}\times N,-dt^2+g_0\right)$ which passes through (a, x).

Proof

Given $a\in \mathbb {R}$ and a point $x\in K$ there are $\varepsilon >0$ and neighbourhoods $\theta \subset K$ and $W\subset N$ of x such that $\Psi :(a-\varepsilon ,a+\varepsilon )\times \theta \rightarrow W$ given by $\Psi (t,z)=\exp _{z}((t-a) E_z)$ is a diffeomorphism. Therefore, the image of $\Gamma (t,z)=(t,\Psi (t,z))$ is a hypersurface of $\mathbb {R}\times W$. By construction, $Im(\Gamma )$ is foliated by null geodesics. We have to prove that it is achronal in $\mathbb {R}\times W$ in order to apply [16, Theorem 1] to ensure that it is in fact a null hypersurface.

First we need to show that $\Psi ^*(g_0)=dt^2+h_t$, where $h_t$ is a metric tensor in $\theta$ which depends on t. Fix $z\in \theta$ and $v\in T_zK$. Take a curve $\alpha :I\rightarrow \theta$ with $\alpha '(0)=v$ and consider the geodesic variation $X(t,s)=\Psi (t,\alpha (s))$. Take the Jacobi vector field $J(t)=X_s(t,0)$ along the geodesic $\gamma (t)=X(t,0)$ with $a-\varepsilon<t<a+\varepsilon$. It holds $J(a)=v$ and $J'(a)=X_{st}(a,0)=X_{ts}(a,0)=\nabla _v E$, whereas $\gamma '(a)=E_z$. Thus,

$g_0(J(a),\gamma '(a))=0$ and $g_0(J'(a),\gamma '(a))=g_0(\nabla _vE,E)=0$ since E is unitary. So $g(J(t),\gamma '(t))=0$ for all $t\in (a-\varepsilon ,a+\varepsilon )$.

In other words, $\gamma '(t)=\Psi _{*_{(t,z)}}(\partial t)$ is orthogonal to $J(t)=\Psi _{*_{(t,z)}}(v)$ and this means that $\Psi ^*(g_0)=dt^2+h_t$, where $h_t$ is a metric tensor in $\theta$ for each $t\in (a-\varepsilon ,a+\varepsilon )$.

Now, we show the achronality of $Im(\Gamma )$. Take $\alpha :[0,1]\rightarrow \mathbb {R}\times W$ a timelike curve in $\mathbb {R}\times W$ with $\alpha (0),\alpha (1)\in Im(\Gamma )$. If we write $\alpha (s)=(m(s),x(s))$, then $-m'(s)^2+g_0(x'(s),x'(s))<0$ and we can suppose that $m'(s)>0$ for all $s\in [0,1]$. Write $x(s)=\Psi (t(s),z(s))$ for some $t:[0,1]\rightarrow \mathbb {R}$ and $z:[0,1]\rightarrow \theta$. Since $\alpha (0),\alpha (1)\in Im(\Gamma )$ we have that $t(0)=m(0)$ and $t(1)=m(1)$, but

$$\begin{aligned} t'(s)^2\le t'(s)^2+h_{t(s)}(z'(s),z'(s))=g_0(x'(s),x'(s))<m'(s)^2 \end{aligned}$$

and integrating the inequality $\vert t'(s)\vert <m'(s)$ we get a contradiction. $\square$

Observe that although a hypersurface was foliated by null geodesics, it is not necessarily a null hypersurface. A simple counterexample is a timelike plane in Minkowski space.

Theorem 2

Fix a point $x_0$ in a Riemannian manifold $(N,g_0)$. If $x=\exp _{x_0}(u)$, where $u\in {\widehat{S}}_a$, is a conjugate point to $x_0$ along the geodesic $\exp _{x_0}(tu)$, then it does not exist any neighbourhood ${{\widehat{U}}}$ of u in $T_{x_0}N$ such that $\exp _{x_0}$ restricted to $\overline{{\widehat{U}}\cap {\widehat{S}}_a}$ is injective and $\exp _{x_0}({\widehat{U}}\cap {\widehat{S}}_a)$, regarded as a subset of N, is a hypersurface.

Proof

Suppose on the contrary that there does exist a neighbourhood ${{\widehat{U}}}$ with $u\in {\widehat{U}}\subset T_{x_0}N$ such that $\exp _{x_0}$ restricted to $\overline{{\widehat{U}}\cap {\widehat{S}}_a}$ is injective and $K=\exp _{x_0}({\widehat{U}}\cap {\widehat{S}}_a)$ is a hypersurface.

Let E be a normal and unitary vector field to K with the appropriate sign such that Lemma 6 holds. We construct the null hypersurface L in the Lorentzian direct product

$$\begin{aligned} \left( \mathbb {R}\times N,-dt^2+g_0\right) \end{aligned}$$

which passes through (a, x) as in Lemma 7. We want to see L as the image by the exponential map $\exp ^{\mathbb {R}\times N}_{(0,x_0)}$ of a piece of the lightlike cone of $e_0=\partial _{ t\vert _{(0,x_0)}}$ in $T_{(0,x_0)}(\mathbb {R}\times N)$. Observe that

$$\begin{aligned} {\widehat{C}}_{e_0}=\{(\lambda ,v):g_0(v,v)=\lambda ^2, \lambda >0\}. \end{aligned}$$

If we take an open neighbourhood ${\widehat{\theta }}\subset {\widehat{U}}\cap {\widehat{S}}_a$ with $\exp _{x_0}({\widehat{\theta }})\subset \theta$, where $\theta$ is the open neighbourhood of x in K provided in Lemma 7, then

$$\begin{aligned} {\widehat{W}}=\left\{ \left( \lambda ,\lambda \frac{v}{a}\right) :\lambda \in (a-\varepsilon ,a+\varepsilon ),v\in {\widehat{\theta }}\right\} \end{aligned}$$

is an open subset of $T_{(0,x_0)}(\mathbb {R}\times N)$. Moreover,

$$\begin{aligned} {\widehat{W}}\cap {\widehat{C}}_{e_0}=\left\{ \left( \lambda ,\lambda \frac{v}{a}\right) : \lambda \in (a-\varepsilon ,a+\varepsilon ),v\in {\widehat{\theta }}\cap {\widehat{S}}_a\right\} . \end{aligned}$$

Therefore, a point of $\exp ^{\mathbb {R}\times N}_{(0,x_0)}\left( {\widehat{W}}\cap {\widehat{C}}_{e_0}\right)$ is of the form $\left( \lambda ,\exp _{x_0} \left( \lambda \frac{v}{a}\right) \right) =\left( \lambda ,\gamma _{\frac{v}{a}}(\lambda ) \right)$. Using equation (7), the above belongs to L. Summarizing, we have that

$$\begin{aligned} \exp ^{\mathbb {R}\times N}_{(0,x_0)}\left( {\widehat{W}}\cap {\widehat{C}}_{e_0}\right) \subset L. \end{aligned}$$

Since (a, x) is a conjugate point to $(0,x_0)$ along the null geodesic $\left( t,\exp _{x_0}\left( t\frac{u}{a}\right) \right)$, Theorem 1 gives us a contradiction. $\square$

Observe that $\exp _{x_0}$ restricted to ${\widehat{U}}$ can not be injective, [23]. Nevertheless, $\exp _{x_0}$ restricted to $\overline{{\widehat{U}}\cap {\widehat{S}}_a}$ could be injective.