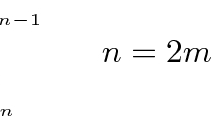Differential geometry of ${\mathsf {SO}}^*(2n)$-type structures-integrability

Abstract

We study almost hypercomplex skew-Hermitian structures and almost quaternionic skew-Hermitian structures, as the geometric structures underlying ${\mathsf {SO}}^*(2n)$- and ${\mathsf {SO}}^*(2n)\mathsf {Sp} (1)$-structures, respectively. The corresponding intrinsic torsions were computed in the previous article in this series, and the algebraic types of the geometries were derived, together with the minimal adapted connections (with respect to certain normalizations conditions). Here we use these results to present the related first-order integrability conditions in terms of the algebraic types and other constructions. In particular, we use distinguished connections to provide a more geometric interpretation of the presented integrability conditions and highlight some features of certain classes. The second main contribution of this note is the illustration of several specific types of such geometries via a variety of examples. We use the bundle of Weyl structures and describe examples of ${\mathsf {SO}}^*(2n)\mathsf {Sp} (1)$-structures in terms of functorial constructions in the context of parabolic geometries.

Appendix A. Topology of \({\mathsf {SO}}^*(2n)\)- and \({\mathsf {SO}}^*(2n)\mathsf {Sp} (1)\)-structures

In this appendix we study some basic topological features of ${\mathsf {SO}}^*(2n)$- and ${\mathsf {SO}}^*(2n)\mathsf {Sp} (1)$-structures. To do so, we should recall first some covering theory related to ${\mathsf {SO}}^*(2n)$. There are several distinguished Lie groups with Lie algebra $\mathfrak {so}^*(2n)$, apart from ${\mathsf {SO}}^{*}(2n)$. Firstly, there is the universal covering $\widetilde{{\mathsf {SO}}}^{*}(2n)$ of ${\mathsf {SO}}^{*}(2n)$. This gives rise to the following short exact sequence

$$\begin{aligned} 0\longrightarrow \mathbb {Z}\longrightarrow \widetilde{{\mathsf {SO}}}^*(2n)\longrightarrow {\mathsf {SO}}^*(2n)\longrightarrow 0\,. \end{aligned}$$

Note that any representation of $\mathfrak {so}^*(2n)$ integrates to representation of $\widetilde{{\mathsf {SO}}}^{*}(2n)$, which however for the finite dimensional case is not faithful. In other words, $\widetilde{{\mathsf {SO}}}^{*}(2n)$ has no finite-dimensional faithful representations. At this point we should however recall that there is a maximal linear group attached to the Lie algebra $\mathfrak {so}^{*}(2n)$, also called the linearizer of $\widetilde{{\mathsf {SO}}}^{*}(2n)$ and denoted by $\mathsf {Spin} ^{*}(2n)$ (see e.g. [25, pp. 264, 320] for this notion).¹ This is characterized by the following universal property:

Any finite dimensional linear representation $\rho : \widetilde{{\mathsf {SO}}}^*(2n)\rightarrow \mathsf {Aut} (W)$ of $\widetilde{{\mathsf {SO}}}^*(2n)$ factors as $\rho = \rho _0 \circ \psi$, where $\psi :\widetilde{{\mathsf {SO}}}^*(2n)\rightarrow \mathsf {Spin} ^{*}(2n)$ is a (covering) homomorphism and $\rho _0 : \mathsf {Spin} ^{*}(2n)\rightarrow \mathsf {Aut} (W)$ is a linear representation of $\mathsf {Spin} ^{*}(2n)$. That is, the following diagram commutes:

Based on the embedding ${\mathsf {SO}}^*(2n)\subset {\mathsf {SO}}(2n, 2n)$ one should view $\mathsf {Spin} ^*(2n)$ as a subgroup of $\mathsf {Spin} (2n, 2n)$. In particular, the faithful representation of $\mathsf {Spin} ^{*}(2n)$ is given by the direct sum

$$\begin{aligned} R(\pi _{n-1})\oplus R(\pi _{n}) \end{aligned}$$

of the (finite-dimensional) half-spin representations of $\mathfrak {so}^*(2n)$, which is the reason behind our notational convention for $\mathsf {Spin} ^*(2n)$. In particular, the group $\mathsf {Spin} ^*(2n)$ is a (double) covering of ${\mathsf {SO}}^{*}(2n)$, which induces the following short exact sequence

$$\begin{aligned} 0\longrightarrow \mathbb {Z}_2\longrightarrow \mathsf {Spin} ^*(2n)\overset{\lambda }{\longrightarrow }{\mathsf {SO}}^*(2n)\longrightarrow 0\,, \end{aligned}$$

such that $\lambda _{*}^{-1}(\mathfrak {spin}^{*}(2n))=\mathfrak {so}^*(2n)$.

In small dimensions $n\le 4$ one may describe further Lie algebras isomorphisms, which we list below and which can be easily interpreted in terms of Satake diagrams (see [16, 17, 25] for more details). For $n=1$, ${\mathsf {SO}}^{*}(2)$ is isomorphic to ${\mathsf {SO}}(2)={{\,\mathrm{{\mathsf {U}}}\,}}(1)$, hence it is compact and non-simple. For $n=2, 3, 4$, the corresponding Satake diagrams admit the following illustration (see [12, 24])

Hence:

• For $n=2$ there is a Lie algebra isomorphism $\mathfrak {so}^{*}(4)\cong \mathfrak {su}(2)\oplus \mathfrak {sl}(2, \mathbb {R})$. Moreover, $\mathsf {Spin} ^*(4)$ coincides with the Lie group $\mathsf {SU} (2) \times \mathsf {SL} (2, \mathbb {R})$ and we have a double covering $\mathsf {SU} (2) \times \mathsf {SL} (2, \mathbb {R}) \rightarrow {\mathsf {SO}}^{*}(4).$ Hence ${\mathsf {SO}}^*(4)$ is semisimple and non-simple.

• For $n=3$, there is a Lie algebra isomorphism $\mathfrak {so}^{*}(6)\cong \mathfrak {su}(1,3)$. Since $Z({\mathsf {SO}}^{*}(6))=\mathbb {Z}_{2}$ and $Z(\mathsf {SU} (1, 3))=\mathbb {Z}_{4}$, we get that $\mathsf {Spin} ^*(6)$ coincides with the Lie group $\mathsf {SU} (1,3)$ and the map $\mathsf {SU} (1,3) \rightarrow {\mathsf {SO}}^{*}(6)$ defines a double covering.

• For $n=4$, there is a Lie algebra isomorphism $\mathfrak {so}^{*}(8)\cong \mathfrak {so}(2,6)$. The half-spin groups associated to ${\mathsf {SO}}(2,6)$ are isomorphic to ${\mathsf {SO}}^*(8)$. On the other side, $\mathsf {Spin} ^*(8)$ and $\mathsf {Spin} (2, 6)$ are both maximal linear groups of $\mathfrak {so}^*(8)$ and hence are identical. This means that there are covering homomorphisms $\mathsf {Spin} (2,6) \rightarrow {\mathsf {SO}}^*(8) \rightarrow P{\mathsf {SO}}(2,6)$, where the latter group is the one which acts faithfully on the projectivization of $\mathbb {R}^8$. In particular, $Z(\mathsf {Spin} ^*(8))=\mathbb {Z}_2\times \mathbb {Z}_2$ (see [25, p. 320]). However, ${\mathsf {SO}}(2,6)$ is not isomorphic to ${\mathsf {SO}}^*(8)$ as Lie groups, since for example the have different maximal compact subgroups, i.e. ${\mathsf {SO}}(2){\mathsf {SO}}(6)\ncong {{\,\mathrm{{\mathsf {U}}}\,}}(4)$. Another argument is coming from topology: ${\mathsf {SO}}^*(8)$ is connected but ${\mathsf {SO}}(2,6)$ has two connected components.

Next we discuss topological obstructions related to ${\mathsf {SO}}^*(2n)$-structures and ${\mathsf {SO}}^*(2n)\mathsf {Sp} (1)$-structures. We begin with the maximal compact subgroup ${{\,\mathrm{{\mathsf {U}}}\,}}(n)$ of ${\mathsf {SO}}^*(2n)$, which can be viewed as the following block diagonal matrix

$$\begin{aligned} \left\{ \begin{pmatrix} A &{} 0 \\ 0 &{} A \end{pmatrix} : A\in {{\,\mathrm{{\mathsf {U}}}\,}}(n)\right\} \subset {{\,\mathrm{{\mathsf {U}}}\,}}(2n)\,, \end{aligned}$$

where ${{\,\mathrm{{\mathsf {U}}}\,}}(2n)$ is the maximal compact subgroup of $\mathsf {Sp} (4n,\mathbb {R})$. This shows that ${{\,\mathrm{{\mathsf {U}}}\,}}(n)$ does not act irreducibly on $\mathsf {E} =\mathbb {C}^{2n}$. However, $\mathsf {Sp} (1)$ coincides with the centralizer $C_{{{\,\mathrm{{\mathsf {U}}}\,}}(2n)}({{\,\mathrm{{\mathsf {U}}}\,}}(n))$ and hence also lies inside ${{\,\mathrm{{\mathsf {U}}}\,}}(2n)\subset \mathsf {Sp} (4n,\mathbb {R})$. Thus, we we finally obtain the following necessary topological conditions, naturally arising within the theory of ${{\,\mathrm{{\mathsf {U}}}\,}}(k)$-structures (see [20, p. 200] or [13, p. 359] and recall also that according to [22, Problem 14-B], the odd-degree Stiefel-Whitney classes of a complex vector bundle must vanish).

Lemma A.1

Let M be a smooth 4n-dimensional manifold admitting a ${\mathsf {SO}}^{*}(2n)\mathsf {Sp} (1)$-structure or a ${\mathsf {SO}}^{*}(2n)$-structure. Then all odd Stiefel-Whitney class $w_{2k+1}(M)\in H^{2k+1}(M; \mathbb {Z}_{2})$ must vanish, $w_{2k+1}(M)=0$, for any $k\in \mathbb {N}$, and the even one must have integral lifts.

Thus, for instance, such manifolds should be oriented, that is $w_{1}(M)=0$, a fact which agrees with our observation in [12] and the orientation constructed via the volume form $\mathsf {vol} =\omega ^{2n}$. Note however that the above condition is only necessary and not sufficient: For instance the tangent bundle $T{{\,\mathrm{S}\,}}^n$ of ${{\,\mathrm{S}\,}}^n$ always satisfies these conditions, but only ${{\,\mathrm{S}\,}}^2$ and ${{\,\mathrm{S}\,}}^6$ admit an almost complex structure, and in particular a ${{\,\mathrm{{\mathsf {U}}}\,}}(n)$-structure. For the compact case one can pose further topological constraints related to the existence of an almost complex structure, which can be read for example in terms of the Euler characteristic of M (see Theorem 3.4 in the appendix of [14]).

Let us now fix an almost qs-H manifold $(M, Q, \omega )$ $(n>1)$, and denote by $\pi : \mathcal {Q}\rightarrow M$ the corresponding principal ${\mathsf {SO}}^*(2n)\mathsf {Sp} (1)$-bundle over M. Then, any point in $\mathcal {Q}$ provides an identification between $T_{x}M$ and $[\mathsf {E} \mathsf {H} ]$, for any $x\in M$. Next we study the lifting problem of the $G={\mathsf {SO}}^*(2n)\mathsf {Sp} (1)$-structure to an $\tilde{G}={\mathsf {SO}}^*(2n)\times \mathsf {Sp} (1)$-structure that allows to associate global bundle analogies of the modules $\mathsf {E}$ and $\mathsf {H}$ over M.

To do so, we view $\mathcal {Q}$ as an element of the first Čech cohomology group $H^{1}(M; G)$ with coefficients in the sheaf of smooth G-valued functions on M. Moreover, $\tilde{G}$ is the double cover of G and so the short exact sequence

$$\begin{aligned} 0\longrightarrow \mathbb {Z}_2 \longrightarrow \tilde{G}\longrightarrow G\rightarrow 0 \end{aligned}$$

induces the coboundary homomorphism

$$\begin{aligned} \updelta : H^{1}(M; G)\rightarrow H^{2}(M; \mathbb {Z}_2)\,. \end{aligned}$$

By setting $\upepsilon :=\updelta (\mathcal {Q})\in H^{2}(M; \mathbb {Z}_2)$ we obtain a canonical cohomology class on M, which we will call the Marchiafava-Romani class. Then, as an analogue of the almost quaternionic-Hermitian case (see [21, 26, 27]), we deduce the following.

Lemma A.2

The Marchiafava-Romani class $\upepsilon \in H^{2}(M; \mathbb {Z}_2)$ is precisely the obstruction to lifting $\mathcal {Q}$ to a principal $\tilde{G}$-bundle $\tilde{\mathcal {Q}}$ over M, or equivalently to the global existence of the vector bundles $E=\mathcal {Q}\times _{G}\mathsf {E}$ and $H=\mathcal {Q}\times _{G}\mathsf {H}$ over M.

Thus, when $\upepsilon =0$, the bundles E and H are globally defined and thus

$$\begin{aligned} T^{\mathbb {C}}M\cong E\otimes H\,. \end{aligned}$$

Recall now that given a pair $(Q, \omega )$ as above, we may visualise the almost quaternionic structure $Q\subset \mathsf {End} (TM)$ via the coefficient bundle associated with the ${\mathsf {SO}}^*(2n)\mathsf {Sp} (1)$-representation $[S^2\mathsf {H} ]^*$ (see for example [26] or [12, Lemma 1.2]). Thus, one can identify $\upepsilon$ with the second Stiefel-Whitney class of Q, i.e. $\upepsilon =w_{2}(Q)$, see [21, 27]. Moreover, in terms of the twistor bundle $Z=\mathbb {P}(\mathsf {H} )\rightarrow M$ which is naturally associated to the almost quaternionic structure Q, one obtains the following

Proposition A.3

Let $(M, Q, \omega )$ be an almost qs-H manifold. Then, the second Stiefel-Whitney class $w_{2}(M)\in H^{2}(M; \mathbb {Z}_2)$ satisfies

Proof

The proof is the same with the one given in [27], for quaternionic Kähler manifolds, although the same result and proof applies for general almost quaternion Hermitian manifolds. $\square$

As is well-known, on a 4n-dimensional oriented manifold M the vanishing of the second Stiefel-Whitney class $w_2$ guarantees the existence of spin structures (see for example [19]) and also of metaplectic structures (see for example [15]). Thus, for 8n-dimensional almost qs-H manifolds, Proposition A.3 certifies that such a manifold should admit these types of structures. In particular, by the inclusion ${\mathsf {SO}}^*(2n)\mathsf {Sp} (1)\subset \mathsf {Sp} (4n, \mathbb {R})$ we conclude that the vanishing of $w_2(M)$ for $n=2m$, guarantees the reduction of the metaplectic structure to a certain 2-fold covering of ${\mathsf {SO}}^*(2n)\mathsf {Sp} (1)$. Such a (unique) 2-fold covering is given by $\mathsf {Spin} ^*(2n)\mathsf {Sp} (1)$, and the corresponding lifts of the G-structure can been seen as a generalization of the so-called $\mathsf {Spin} ^{q}$-structures, discussed in [1, 4, 23]. We plan to examine $\mathsf {Spin} ^*(2n)\mathsf {Sp} (1)$-structures on 8n-dimensional almost qs-H manifolds $(M, Q, \omega )$ in a forthcoming paper in this series.