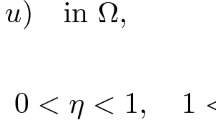Nonlinear singular problems with indefinite potential term

Abstract

We consider a nonlinear Dirichlet problem driven by a nonhomogeneous differential operator plus an indefinite potential. In the reaction we have the competing effects of a singular term and of concave and convex nonlinearities. In this paper the concave term will be parametric. We prove a bifurcation-type theorem describing the changes in the set of positive solutions as the positive parameter $\lambda$ varies.

1 Introduction

Let $\Omega \subseteq \mathbb R^{N}$ be a bounded domain with a $C^2$-boundary $\partial \Omega$. In this paper we study the following nonlinear nonhomogeneous parametric singular problem:

The map $a:\mathbb R^{N} \rightarrow \mathbb R^{N}$ involved in the differential operator of ($P_{\lambda }$) is strictly monotone, continuous (hence maximal monotone, too) and satisfies certain other regularity and growth conditions which are listed in hypotheses H(a) below (see Sect. 2). These conditions are general enough to incorporate in our framework many differential operators of interest such as the p-Laplacian and the (p, q)-Laplacian (that is, the sum of a p-Laplacian and a q-Laplacian). The operator $u\mapsto \mathrm{div}\,a(Du)$ is not homogeneous and this is a source of difficulties in the analysis of problem ($P_{\lambda }$). The potential function $\xi \in L^{\infty }(\Omega )$ is indefinite (that is, sign changing). So the operator $u \mapsto -\mathrm{div}\, a(Du) + \xi (z) |u|^{p-2} u$ is not coercive and this is one more difficulty in the analysis of problem ($P_{\lambda }$). In the reaction (the right-hand side of ($P_{\lambda }$)), the term $\vartheta (\cdot )$ is singular at $x=0$, while the perturbation contains the combined effects of a parametric concave term $x\mapsto \lambda x^{q-1}$ ($x\geqslant 0$) (recall that $q<p$), with $\lambda >0$ being the parameter and of a Carathéodory function f(z, x) (that is, for all $x\in \mathbb R$ the mapping $z\mapsto f(z,x)$ is measurable and for almost all $z\in \Omega$ the mapping $x\mapsto f(z,x)$ is continuous), which is assumed to exhibit $(p-1)$-superlinear growth near $+\infty$, but without satisfying the usual for superlinear problems Ambrosetti-Rabinowitz condition (the AR-condition for short). So in problem ($P_{\lambda }$) we have the competing effects of singular, concave and convex terms.

Using variational methods related to the critical point theory, combined with suitable truncation, perturbation and comparison techniques, we produce a critical parameter value $\lambda ^* >0$ such that

• (i) for all $\lambda \in (0,\lambda ^*)$ problem ($P_{\lambda }$) has at least two positive solutions;

• (ii) for $\lambda = \lambda ^*$ problem ($P_{\lambda }$) has at least one positive solution;

• (iii) for all $\lambda > \lambda ^*$ problem ($P_{\lambda }$) has no positive solutions.

This work continues the recent paper by Papageorgiou et al. [16], where $\xi \equiv 0$ and in the reaction the parametric term is the singular one. It is also related to the works of Papageorgiou and Smyrlis [17] and Papageorgiou and Winkert [19], where the differential operator is the p-Laplacian, $\xi \equiv 0$ and no concave terms are allowed. Singular p-Laplacian equations with no potential term and reactions of special form were considered by Chu et al. [2], Giacomoni et al. [5], Li and Gao [10], Mohammed [12], Perera and Zhang [20], and Papageorgiou et al. [14].

2 Mathematical background and hypotheses

In this section we present the main mathematical tools which we will use in the analysis of problem ($P_{\lambda }$). We also fix our notation and state the hypotheses on the data of the problem.

So, let X be a Banach space, $X^*$ its topological dual, and let $\varphi \in C^1(X).$ We say that $\varphi (\cdot )$ satisfies the “C-condition”, if the following property holds:

$$\begin{aligned} \begin{array}{ll} ``\text{ Every } \text{ sequence }\ \{u_n\}_{n\geqslant 1}\subseteq X\ \text{ such } \text{ that }\\ \{\varphi (u_n)\}_{n\geqslant 1}\subseteq \mathbb R\ \text{ is } \text{ bounded } \text{ and } \ (1+||u_n||_X)\varphi '(u_n)\rightarrow 0\ \text{ in }\ X^*\ \text{ as }\ n\rightarrow \infty ,\\ \text{ admits } \text{ a } \text{ strongly } \text{ convergent } \text{ subsequence }''. \end{array} \end{aligned}$$

This is a compactness-type condition on the functional $\varphi (\cdot )$, which leads to the minimax theory of the critical values of $\varphi (\cdot )$ (see, for example, Papageorgiou et al. [15]). We denote by $K_\varphi$ the critical set of $\varphi$, that is,

$$\begin{aligned} K_{\varphi } = \{ u\in X: \varphi '(u)=0\}. \end{aligned}$$

The main spaces in the analysis of problem ($P_{\lambda }$) are the Sobolev space $W^{1,p}_0(\Omega )$$(1<p<\infty )$ and the Banach space $C_0^1(\overline{\Omega })=\{u\in C^1(\overline{\Omega }): u|_{\partial \Omega } = 0\}$. We denote by $||\cdot ||$ the norm of $W^{1,p}_0$. By the Poincaré inequality we have

$$\begin{aligned} ||u|| = ||Du||_p\ \text{ for } \text{ all }\ u \in W^{1,p}_0(\Omega ). \end{aligned}$$

The Banach space $C_0^1(\Omega )$ is ordered with positive (order) cone

$$\begin{aligned} C_+ = \{u\in C_0^1(\overline{\Omega }): u(z)\geqslant 0\ \text{ for } \text{ all }\ z\in \overline{\Omega } \}. \end{aligned}$$

This cone has a nonempty interior given by

$$\begin{aligned} \begin{array}{ll} \mathrm{int}\, C_+ = \left\{ u\in C_+ : u(z) >0\ \text{ for } \text{ all }\ z\in \Omega ,\ \frac{\partial u}{\partial n} |_{\partial \Omega } <0 \right\} , \\ \text{ with }\ n(\cdot )\ \text{ being } \text{ the } \text{ outward } \text{ unit } \text{ normal } \text{ on }\ \partial \Omega . \end{array} \end{aligned}$$

We will also use two additional ordered Banach spaces. The first one is

$$\begin{aligned} C_0(\overline{\Omega }) = \{ u\in C(\overline{\Omega }):u|_{\partial \Omega } = 0 \}. \end{aligned}$$

This cone is ordered with positive (order) cone

$$\begin{aligned} K_+ = \{ u \in C_0 (\overline{\Omega }): u(z) \geqslant 0\ \text{ for } \text{ all }~ z\in \overline{\Omega }\}. \end{aligned}$$

This cone has a nonempty interior given by

$$\begin{aligned} \mathrm{int}\,K_+ = \{ u \in K_+: c_u \hat{d} \leqslant u \ \text{ for } \text{ some }\ c_u>0 \}, \end{aligned}$$

where $\hat{d}(z) = d(z,\partial \Omega )\ \text{ for } \text{ all }\ z\in \overline{\Omega }$. On account of Lemma 14.16 of Gilbarg and Trudinger [6, p. 355], we have

$$\begin{aligned} ``c_u \hat{d} \leqslant u \ \text{ for } \text{ some }\ c_u> 0\ \text{ if } \text{ and } \text{ only } \text{ if }\ \hat{c}_u \hat{u}_1 \leqslant u\ \text{ for } \text{ some } \ \hat{c}_u > 0 '', \end{aligned}$$

(1)

with $\hat{u}_1$ being the positive, $L^p$-normalized (that is, $||\hat{u}_1||_p=1$) eigenfunction corresponding to the principal eigenvalue $\hat{\lambda }_1>0$ of the Dirichlet p-Laplacian. The nonlinear regularity theory and the nonlinear maximum principle (see, for example, Gasinski and Papageorgiou [4, pp. 737–738]), imply that $\hat{u}_1\in \mathrm{int}\,C_+$.

The second ordered space is $C^1(\overline{\Omega })$ with positive (order) cone

$$\begin{aligned} \hat{C}_+ = \left\{ u \in C^1(\overline{\Omega }): u(z) \geqslant 0 \ \text{ for } \text{ all }\ z\in \overline{\Omega }, \ \frac{\partial u}{\partial n}|_{\partial \Omega \cap u^{-1}(0)} <0 \right\} . \end{aligned}$$

Clearly, this cone has a nonempty interior.

Concerning ordered Banach spaces with an order cone which has a nonempty interior (solid order cone), we have the following result which will be useful in our analysis (see Papageorgiou et al. [15, Proposition 4.1.22]).

Proposition 1

If X is an ordered Banach space with positive (order) cone K, int K $\ne \emptyset$, and $e \in int\,K$, then for every $u\in X$ we can find $\lambda _u >0$ such that $\lambda _u e - u\in K.$

Let $l\in C^1(0,\infty )$ with $l(t)>0$ for all $t>0$. We assume that

$$\begin{aligned} \begin{array}{ll} 0<\hat{c}\leqslant \frac{l'(t)t}{l(t)}\leqslant c_0, c_1 t^{p-1}\leqslant l(t) \leqslant c_2[t^{s-1}+ t^{p-1}] \\ \text{ for } \text{ all }\ t>0,\ \text{ and } \text{ some }\ c_{1},c_{2}>0, 1\leqslant s< p. \end{array} \end{aligned}$$

(2)

Then the conditions on the map $a(\cdot )$ are the following:

$H(a): a(y) = a_0(|y|)y$ for all $y\in \mathbb R^{N}$, with $a_0(t)>0$ for all $t>0$ and

• (i) $a_0\in C^1(0,+\infty ),\ t\mapsto a_0 (t)$ is strictly increasing on $(0,+\infty )$, $a_0(t) t\rightarrow 0^+$ as $t\rightarrow 0^+$ and

  $$\begin{aligned} \lim _{t\rightarrow 0^+}\frac{a'_0(t)t}{a_0(t)} > -1; \end{aligned}$$

• (ii) there exists $c_3>0$ such that

  $$\begin{aligned} |\nabla a(y)| \leqslant c_3 \frac{l(|y|)}{|y|}\ \text{ for } \text{ all }\ y\in \mathbb R^{N} \backslash \{0\}; \end{aligned}$$

• (iii) $(\nabla a(y)\xi ,\xi )_{\mathbb R^{N}} \geqslant \frac{l(|y|)}{|y|}|\xi |^2$ for all $y\in \mathbb R^{n} \backslash \{0\}$, $\xi \in \mathbb R^{N}$;

• (iv) if $G_0(t) = \int _{0}^{t} a_0(s)s ds$, then there exists $\tau \in (q,p]$ such that

  $$\begin{aligned} \limsup _{t\rightarrow 0^+} \frac{\tau G_0(t)}{t^{\tau }} \leqslant c^* \end{aligned}$$

and $0\leqslant p G_0(t) - a_0(t) t^2$ for all $t>0$.

Remark 1

Hypotheses H(a)(i), (ii), (iii) are dictated by the nonlinear regularity theory of Lieberman [10] and the nonlinear maximum principle of Pucci and Serrin [21]. Hypothesis H(a)(iv) serves the needs of our problem, but in fact, it is a mild condition and it is satisfied in all cases of interest (see the examples below). These conditions were used by Papageorgiou and Rădulescu [13] and by Papageorgiou et al. [16].

Hypotheses H(a) imply that the primitive $G_0(\cdot )$ is strictly increasing and strictly convex. We set $G(y) = G_0(|y|)$ for all $y\in \mathbb R^{N}.$ Evidently, $G(\cdot )$ is convex, $G(0) = 0$ and

$$\begin{aligned} \begin{array}{ll} \nabla G(y) = G_0'(|y|)\frac{y}{|y|} = a_0 (|y|)y = a(y)\ \text{ for } \text{ all }\ y\in \mathbb R^{N}\backslash \{0\},\ \nabla G(0)=0,\\ \text{ that } \text{ is },\ G(\cdot ) \ \text{ is } \text{ the } \text{ primitive } \text{ of }\ a(\cdot ).\ \text{ From } \text{ the } \text{ convexity } \text{ of }\ G(\cdot )\ \text{ we } \text{ have } \end{array} \end{aligned}$$

$$\begin{aligned} G(y)\leqslant (a(y),y)_{\mathbb R^{N}}\ \text{ for } \text{ all }\ y\in \mathbb R^{N}. \end{aligned}$$

(3)

Using hypotheses H(a)(i), (ii), (iii) and (2), we can easily obtain the following lemma, which summarizes the main properties of the map $a(\cdot )$.

Lemma 2

If hypotheses H(a)(i), (ii), (iii) hold, then

• (a) the map $y\mapsto a(y)$ is continuous, strictly monotone (hence maximal monotone, too);

• (b) $|a(y)| \leqslant c_4 (|y|^{s-1} +|y|^{p-1})$ for some $c_4>0$, and all $y\in \mathbb R^{N}$;

• (c) $(a(y),y)_{\mathbb R^{N}} \geqslant \frac{c_1}{p-1} |y|^p$ for all $y\in \mathbb R^{N}$.

Using this lemma and (3), we obtain the following growth estimates for the primitive $G(\cdot )$.

Corollary 3

If hypotheses H(a)(i), (ii), (iii) hold, then $\frac{c_1}{p(p-1)} |y|^{p} \leqslant G(y) \leqslant c_5 (1+|y|^p)$ for some $c_5>0$, and all $y\in \mathbb R^{N}$.

The examples that follow confirm that the framework provided by hypotheses H(a) is broad and includes many differential operators of interest (see [13]).

Example 1

• (a) $a(y) = |y|^{p-2}y$ with $1<p<\infty$.

  This map corresponds to the p-Laplace differential operator defined by

  $$\begin{aligned} \Delta _p u= \mathrm{div}\, (|Du|^{p-2} Du)\ \text{ for } \text{ all }\ u\in W^{1,p}_0 (\Omega ). \end{aligned}$$

• (b) $a(y)=|y|^{p-2} y + \mu |y|^{q-2} y$ with $1<q<p<\infty ,\ \mu \geqslant 0$.

  This map corresponds to the (p, q)-Laplace differential operator defined by

  $$\begin{aligned} \Delta _p u+\Delta _q u~\text{ for } \text{ all }\ u\in W^{1,p}_0(\Omega ). \end{aligned}$$

  Such operators arise in models of physical processes. We mention the works of Cherfils and Ilyasov [1] (reaction-diffusion systems) and Zhikov [22] (homogenization of composites consisting of two materials with distinct hardening exponent in elasticity theory).

• (c) $a(y) =(1+|y|^2)^{\frac{p-2}{2}}y$ with $1<p<\infty$.

  This map corresponds to the modified capillary operator.

• (d) $a(y) = |y|^{p-2}y\left( 1+ \frac{1}{1+ |y|^p}\right)$ with $1<p<\infty .$

The hypotheses on the potential term $\xi (\cdot )$ and on the singular part $\vartheta (\cdot )$ of the reaction are the following:

• $H(\xi ): \xi \in L^\infty (\Omega ).$

• $H(\vartheta ): \vartheta :(0,+\infty )\rightarrow (0,+\infty )$ is a locally Lipschitz function such that

  • (i) for some $\gamma \in (0,1)$ we have

    $$\begin{aligned} 0 < c_6\leqslant \liminf _{x\rightarrow 0^+}\vartheta (x)x^{\gamma } \leqslant \limsup _{x\rightarrow 0^+}\vartheta (x) x^\gamma \leqslant c_7; \end{aligned}$$

  • (ii) $\vartheta (\cdot )$ is nonincreasing.

Remark 2

In the literature we almost always encounter the following particular singular term

$$\begin{aligned} \vartheta (x) = x^{-\gamma }\ \text{ for } \text{ all }\ x>0, \ \text{ with }\ 0<\gamma <1. \end{aligned}$$

Of course, hypotheses $H(\vartheta )$ provide a much more general framework and can accomodate also singularities like the ones that follow:

$$\begin{aligned}&\vartheta _1(x)=x^{-\gamma }\left[ 1+\ln (1+x)\right] ,\quad x>0, \\&\vartheta _2(x)=x^{-\gamma }e^{-x},\quad x>0 \\&\vartheta _3(x)= \left\{ \begin{array}{ll} x^{-\gamma }(1-\eta \sin x )&{}\quad 0<x\leqslant \frac{\pi }{2}\\ x^{-\gamma }(1-\eta )&{}\quad \text{ if }\ \frac{\pi }{2}<x \end{array} \ \text{ with }\ 0<\gamma <1. \right. \end{aligned}$$

The following strong comparison principle can be found in Papageorgiou et al. [16, Proposition 6] (see also Papageorgiou and Smyrlis [17, Proposition 4]).

Proposition 4

If hypotheses $H(a),H(\vartheta )$ hold, $\hat{\xi }\in L^{\infty }(\Omega )$, $\hat{\xi }(z) \geqslant 0$ for almost all $z\in \Omega$, $h_1,h_2 \in L^{\infty }(\Omega )$ satisfy

$$\begin{aligned} 0<c_8\leqslant h_2(z) - h_1(z) \ \text{ for } \text{ almost } \text{ all }\ z\in \Omega \end{aligned}$$

and $u,v\in C^{1,\alpha }(\overline{\Omega })$ satisfy $0<u(z)\leqslant v(z)$ for all $z\in \Omega$ and for almost all $z\in \Omega$ we have

• $-\mathrm{div}\, a(Du(z)) - \vartheta (u(z)) + \xi (z) u (z)^{p-1} = h_1(z)$

• $- \mathrm{div}\, a(Dv(z) - \vartheta (v(z)) + \xi (z) v(z)^{p-1} = h_2(z)$,

then $v-u\in \mathrm{int}\,\hat{C}_+.$

In what follows, $p^*$ is the critical Sobolev exponent corresponding to p, that is,

$$\begin{aligned} p^* =\left\{ \begin{array}{ll} \frac{Np}{N-p}&{}\quad \text{ if }\ p<N.\\ +\infty &{}\quad \text{ if }\ N\leqslant p. \end{array} \right. \end{aligned}$$

Now we introduce our hypotheses on the nonlinearity f(z, x).

$H(f): f:\Omega \times \mathbb R\rightarrow \mathbb R_+$ is a Carathéodory function such that $f(z,0)=0$ for almost all $z\in \Omega$ and

• (i) $f(z,x) \leqslant a(z) (1+x^{r-1})$ for almost all $z\in \Omega$, and all $x\geqslant 0$, with $a\in L^{\infty }(\Omega )$, $p<r<p^*;$

• (ii) if $F(z,x)=\int _0^x f(z,s) ds,$

  then $\lim _{x\rightarrow +\infty }\frac{F(z,x)}{x^{p}} = +\infty$ uniformly for almost all $z\in \Omega$;

• (iii) there exists $\sigma \in ((r-p) \max \{ \frac{N}{p}, 1 \},p^*),\ \sigma >q$ such that

  $$\begin{aligned} 0<\hat{\beta }_0\leqslant \liminf _{x\rightarrow +\infty } \frac{f(z,x)x-pF(z,x)}{x^{\sigma }}\ \text{ uniformly } \text{ for } \text{ almost } \text{ all }\ z\in \Omega ; \end{aligned}$$

• (iv) $\limsup _{x\rightarrow 0^+} \frac{f(z,x)}{x^{r-1}} \leqslant \eta _0$ uniformly for almost all $z\in \Omega$;

• (v) for every $\rho >0$, there exists $\hat{\xi }_\rho >0$ such that for almost all $z\in \Omega$ the function

  $$\begin{aligned} x\mapsto f(z,x) + \hat{\xi }_\rho x^{\rho -1} \end{aligned}$$

  is nondecreasing on $[0,\rho ]$.

Remark 3

Since our aim is to find positive solutions and the above hypotheses concern the positive semiaxis $\mathbb R_+ = [0,+\infty )$, we may assume that

$$\begin{aligned} f(z,x) = 0,\ \text{ for } \text{ almost } \text{ all }\ z\in \Omega , \ \text{ and } \text{ all }\ x\leqslant 0. \end{aligned}$$

(4)

Hypotheses H(f)(ii), (iii) imply that

$$\begin{aligned} \lim _{x\rightarrow +\infty } \frac{f(z,x)}{x^{p-1}} = +\infty \ \text{ uniformly } \text{ for } \text{ almost } \text{ all }\ z\in \Omega . \end{aligned}$$

(5)

So, the nonlinearity $f(z,\cdot )$ is $(p-1)$-superlinear near $+\infty$. However, this superlinearity of $f(z,\cdot )$ is not formulated using the AR-condition. We recall that the AR-condition (unilateral version due to (4)), says that there exist $\gamma >p$ and $M>0$ such that

$$\begin{aligned}&0<\gamma F(z,x) \leqslant f(z,x) x \ \text{ for } \text{ almost } \text{ all }\ z\in \Omega ,\ \text{ and } \text{ all }\ x\geqslant M, \end{aligned}$$

(6a)

$$\begin{aligned}&0<\mathrm{ess\,inf}_{\Omega } F(\cdot ,M). \end{aligned}$$

(6b)

If we integrate (6a) and use (6b), we obtain the weaker condition

$$\begin{aligned} \begin{array}{ll} &{}c_9 x^{\gamma } \leqslant F(z,x)\ \text{ for } \text{ almost } \text{ all }\ z\in \Omega ,\ \text{ all }\ x\geqslant M,\ \text{ and } \text{ some }\ c_9>0, \\ &{}\quad \Rightarrow c_9 x^{\gamma -1}\leqslant f(z,x)\ \text{ for } \text{ almost } \text{ all }\ z\in \Omega ,\ \text{ and } \text{ all }\ x\geqslant M. \end{array} \end{aligned}$$

(7)

Therefore the AR-condition implies that $f(z,\cdot )$ exhibits at least $(\gamma -1)$-polynomial growth. Evidently, (7) implies the much weaker condition (5). In this work instead of the standard AR-condition, we employ the less restrictive hypothesis H(f)(iii). In this way we incorporate in our framework also $(p-1)$-superlinear terms with “slower” growth near $+\infty$, which fail to satisfy the AR-condition. The following function satisfies hypotheses H(f) but fails to satisfy the AR-condition (for the sake of simplicity we drop the z-dependence)

$$\begin{aligned} f(x) = x^{p-1}\ln (1+x) \ \text{ for } \text{ all }\ x\geqslant 0. \end{aligned}$$

Finally, let us fix the notation which we will use throughout this work. For $x\in \mathbb R$ we set $x^{\pm } = \max \{ \pm x,0\}.$ Then for $u\in W^{1,p}_0(\Omega )$ we define $u^{\pm }(z) = u(z)^{\pm }$ for almost all $z\in \Omega$. It follows that

$$\begin{aligned} u^{\pm }\in W^{1,p}_0(\Omega ),\ u=u^{+}-u^{-},\ |u|=u^{+} + u^{-}. \end{aligned}$$

If $u,v\in W^{1,p}_0(\Omega )$ and $u\leqslant v$, then we define.

$$\begin{aligned} \begin{array}{ll} &{}[u,v] = \{ y\in W^{1,p}_0(\Omega ): u(z) \leqslant y(z) \leqslant v(z) \ \text{ for } \text{ almost } \text{ all }\ z\in \Omega \}, \\ &{}[u) = \{ y\in W^{1,p}_0(\Omega ): u(z)\leqslant y(z)\ \text{ for } \text{ almost } \text{ all }\ z\in \Omega \}. \end{array} \end{aligned}$$

Also, by $\mathrm{int}_{c_0^1(\overline{\Omega })}[u,v]$ we denote the interior in the $C_0^1(\overline{\Omega })$-norm topology of the set $[u,v]\cap C_0^1(\overline{\Omega })$.

By $A:W^{1,p}_0(\Omega )\rightarrow W^{-1,p'}(\Omega )=W^{1,p}_0(\Omega )^*\ (\frac{1}{p} + \frac{1}{p'} = 1)$ we denote the nonlinear operator defined by

$$\begin{aligned} \langle A(u),h\rangle =\int _{\Omega } (a(Du),Dh)_{\mathbb R^{N}} dz \ \text{ for } \text{ all }\ u,h\in W^{1,p}_0(\Omega ). \end{aligned}$$

We know (see Gasinski and Papageorgiou [4]), that $A(\cdot )$ is continuous, strictly monotone (hence maximal monotone, too) and of type $(S)_+$, that is,

$$\begin{aligned} \begin{array}{ll} ``\text{ if }\ u_n{\mathop {\rightarrow }\limits ^{w}} u \ \text{ in }\ W^{1,p}_0(\Omega ) \ \text{ and }\ \limsup _{n\rightarrow \infty }\langle A(u_n),u_n -u\rangle \leqslant 0, \\ \text{ then }\ u_n\rightarrow u \ \text{ in }\ W^{1,p}_0(\Omega ).'' \end{array} \end{aligned}$$

We introduce the following two sets related to problem ($P_{\lambda }$):

$$\begin{aligned} \begin{array}{ll} \mathcal {L} = \{ \lambda >0 :\ \text{ problem }~(P_{\lambda })~\text{ admits } \text{ a } \text{ positive } \text{ solution } \},\\ S_{\lambda } =\ \text{ the } \text{ set } \text{ of } \text{ positive } \text{ solutions } \text{ for } \text{ problem }~ (P_{\lambda }). \end{array} \end{aligned}$$

We let $\lambda ^* = \sup \mathcal {L}.$

3 Positive solutions

We start by considering the following purely singular problem:

$$\begin{aligned} -\mathrm{div}\, a(Du(z))) + \xi ^+(z)u(z)^{p-1} = \vartheta (u(z))\ \text{ in }\ \Omega ,\ u|_{\partial \Omega } = 0, \ u>0. \end{aligned}$$

(8)

From Papageorgiou et al. [16, Proposition 10], we have the following property.

Proposition 5

If hypotheses $H(a),H(\xi ),H(\vartheta )$ hold, then problem (8) admits a unique positive solution $v\in \mathrm{int}\,C_+$.

Let $\beta > ||\xi ||_\infty$. Then hypotheses H(f)(i), (iv) and since $1<q<p<r$, imply that we can find $c_{10},c_{11}>0$ such that

$$\begin{aligned} \lambda x^{q-1} + f(z,x) \leqslant \lambda c_{10} x^{q-1} + c_{11}x^{r-1} -\beta x^{p-1}\ \text{ for } \text{ almost } \text{ all }\ z\in \Omega ,\ \text{ and } \text{ all }\ x\geqslant 0. \end{aligned}$$

(9)

Let $k_\lambda (x) = \lambda c_{10} x^{q-1} + c_{11}x^{r-1} -\beta x^{p-1}$ for all $x\geqslant 0$. With $v\in \mathrm{int}\,C_+$ from Proposition 5, we consider the following auxiliary Dirichlet problem:

For this problem we prove the following result.

Proposition 6

If hypotheses $H(a),H(\xi ),H(\vartheta )$ hold, then for all small enough $\lambda >0$ problem $(10)_\lambda$ has a smallest positive solution

$$\begin{aligned} \overline{u}_\lambda \in \mathrm{int}\,C_+. \end{aligned}$$

Proof

Recall that $v\in \mathrm{int}\,C_+$ (see Proposition 5). Hence $v\in \mathrm{int}\,K_+$ (see (1)). For $s>N$ we consider the function $\hat{u}^{1/s}_1\in K_+$. According to Proposition 1, we can find $\mu >0$ such that

$$\begin{aligned} \begin{array}{ll} &{}\hat{u}^{1/s}_1\leqslant \mu v,\\ &{}\quad \Rightarrow v^{-\gamma }\leqslant \mu ^{\gamma } \hat{u}_1^{-\gamma /s} . \end{array} \end{aligned}$$

(11)

From the Lemma in Lazer and McKenna [9, p. 726], we have

$$\begin{aligned} \begin{array}{ll} &{}\hat{u}_1^{-\gamma /s} \in L^s (\Omega ),\\ &{}\quad \Rightarrow v^{-\gamma }\in L^s(\Omega )\ (\text{ see }\ (11)). \end{array} \end{aligned}$$

(12)

Hypotheses $H(\vartheta )$ imply that we can find $c_{12}>0$ and $\delta >0$ such that

$$\begin{aligned} 0\leqslant \vartheta (x)\leqslant c_{12}x^{-\gamma } \ \text{ for } \text{ all }\ 0\leqslant x\leqslant \delta \ \text{ and }\ 0\leqslant \vartheta (x) \leqslant \vartheta (\delta )\ \text{ for } \text{ all }\ x>\delta . \end{aligned}$$

(13)

It follows from (12), (13) that

$$\begin{aligned} \vartheta (v(\cdot ))\in L^s(\Omega )\ (s>N). \end{aligned}$$

Let $\hat{k}_\lambda (x) = \lambda c_{10} x^{q-1} + c_{11}x^{r-1}$ for all $x\geqslant 0$ and set $\hat{K}_\lambda (x) = \int _{0}^{x} \hat{k}_\lambda (s)ds$. We consider the $C^1$-functional $\psi _\lambda : W^{1,p}_0(\Omega )\rightarrow \mathbb R$ defined by

$$\begin{aligned}&\psi _\lambda (u) = \int _{\Omega } G(Du)dz+\frac{1}{p}\int _{\Omega }[\xi (z)+\beta ]|u|^p dz-\int _{\Omega }\hat{K}_\lambda (u^+)dz - \int _{\Omega }\vartheta (v) u^+ dz \nonumber \\&\quad \text{ for } \text{ all }\ u\in W^{1,p}_0(\Omega )\nonumber \\&\quad \geqslant \frac{c_1}{p(p-1)}||Du||_p^p +\frac{1}{p}\int _{\Omega } [\xi (z)+\beta ]|u|^p dz - \frac{\lambda c_{10}}{q}||u||_q^q \nonumber \\&\qquad - \frac{c_{11}}{r}||u||_r^r - \int _{\Omega }\vartheta (v)|u|dz \nonumber \\&\quad \text{(see } \text{ Corollary } 3\text{) }\nonumber \\&\quad \geqslant c_{12}||u||^p -c_{13}[\lambda ||u||+||u||^r]\nonumber \\&\quad \text{ for } \text{ some }\ c_{12},c_{13}>0\ \text{ and } \text{ all }\ 0<\lambda \leqslant 1\ (\text{ recall } \text{ that }\ \beta >||\xi ||_\infty \ \text{ and }\ 1<q<r)\nonumber \\&\quad =[c_{12} - c_{13}(\lambda ||u||^{1-p}+||u||^{r-p})]||u||^p. \end{aligned}$$

(14)

We introduce the function $\mathfrak {I}_\lambda (t)=\lambda t^{1-p} + t^{r-p},t>0.$ Evidently, $\mathfrak {I}_\lambda \in C^{1}(0,+\infty )$ and since $1<p<r$, we see that

$$\begin{aligned} \mathfrak {I}_\lambda (t)\rightarrow +\infty \ \text{ as }\ t\rightarrow 0^+ \ \text{ and } \text{ as }\ t\rightarrow +\infty . \end{aligned}$$

So, we can find $t_0>0$ such that

$$\begin{aligned} \begin{array}{ll} &{}\mathfrak {I}_\lambda (t_0)=\inf \{\mathfrak {I}_\lambda (t):t>0\},\\ &{}\quad \Rightarrow \mathfrak {I}_\lambda '(t_0) = 0,\\ &{}\quad \Rightarrow \lambda (p-1)t^{-p}_0 = (r-p) t^{r-p-1}_0\\ &{}\quad \Rightarrow t_0 = \left[ \frac{\lambda (p-1)}{r-p} \right] ^{\frac{1}{r-1}}. \end{array} \end{aligned}$$

Since $\frac{p-1}{r-1}<1$, it follows that

$$\begin{aligned} \mathfrak {I}_\lambda (t_0)\rightarrow 0\ \text{ as }\ \lambda \rightarrow 0^+ .\end{aligned}$$

So, we can find $\lambda _0\in (0,1]$ such that

$$\begin{aligned} \mathfrak {I}_\lambda (t_0)\leqslant \frac{c_{12}}{c_{13}} \ \text{ for } \text{ all }\ \lambda \in (0,\lambda _0]. \end{aligned}$$

For $\rho =t_0$, we see from (14) that

$$\begin{aligned} \psi _\lambda |_{\partial \overline{B}_\rho }>0, \end{aligned}$$

(15)

where $\overline{B}_{\rho } = \{u\in W^{1,p}_0(\Omega ):||u||\leqslant \rho \}$ and $\partial \overline{B}_\rho = \{u\in W^{1,p}_0 (\Omega ):||u||=\rho \}$.

We fix $\lambda \in (0,\lambda _0]$. Hypothesis H(a)(iv) implies that we can find $c^*_0 > c^*$ and $\delta >0$ such that

$$\begin{aligned} G(y)\leqslant \frac{c_0^*}{\tau }|y|^{\tau }\ \text{ for } \text{ all }\ |y|\leqslant \delta . \end{aligned}$$

Let $u\in \mathrm{int}\, C_+$ and choose small enough $t\in (0,1)$ such that

$$\begin{aligned} t|Du(z)|\leqslant \delta \ \text{ for } \text{ all }\ z\in \overline{\Omega }. \end{aligned}$$

Then we have

$$\begin{aligned} \psi _\lambda (tu)\leqslant \frac{t^{\tau }c_0^*}{\tau }||Du||_\tau ^\tau + \frac{t^p}{p}\int _{\Omega }[\xi (z)+\beta ]|u|^p dz- \frac{\lambda t^q}{q}||u||_q^q\,. \end{aligned}$$

Since $q<\tau \leqslant p$, choosing $t\in (0,1)$ even smaller if necessary, we have

$$\begin{aligned}&\psi _\lambda (tu)<0,\nonumber \\&\quad \Rightarrow \inf _{\overline{B}_\rho }\psi _\lambda <0. \end{aligned}$$

(16)

The functional $\psi _\lambda (\cdot )$ is sequentially weakly lower semicontinuous and by the Eberlein-Smulian theorem and the reflexivity of $W^{1,p}_0(\Omega )$, the set $\overline{B}_\rho$ is sequentially weakly compact. So, by the Weierstrass-Tonelli theorem, we can find $\overline{u}\in W^{1,p}_0(\Omega )$ such that

$$\begin{aligned} \psi _\lambda (\overline{u}) = \inf \{\psi _\lambda (u): u\in W^{1,p}_0(\Omega )\}\ \ (\lambda \in (0,\lambda _0]). \end{aligned}$$

(17)

From (15), (16) and (17) it follows that

$$\begin{aligned}&0<||\overline{u}||<\rho ,\nonumber \\&\quad \Rightarrow \psi '_\lambda (\overline{u}) = 0\ (\text{ see }\ (17)),\nonumber \\&\quad \Rightarrow \langle A(\overline{u}),h\rangle + \int _{\Omega }[\xi (z)+\beta ]|\overline{u}|^{p-2}\overline{u}hdz = \int _{\Omega } [\vartheta (v)+\hat{k}_\lambda (\overline{u}^+)] hdz \nonumber \\&\quad \text{ for } \text{ all }\ h\in W^{1,p}_0(\Omega ). \end{aligned}$$

(18)

In (18) we choose $h=-\overline{u}^{-}\in W^{1,p}_0(\Omega ).$ Using Lemma 2(c) and since $\beta >||\xi ||_\infty$ we obtain

$$\begin{aligned}&c_{14}||\overline{u}^{-}||^p \leqslant 0\ \text{ for } \text{ some }\ c_{14}>0,\\&\quad \Rightarrow \overline{u}\geqslant 0,\ \overline{u}\ne 0. \end{aligned}$$

Then from (18) we have

$$\begin{aligned}&-\mathrm{div}\, a(D\overline{u}(z)) + \xi (z)\overline{u}(z)^{p-1} = \vartheta (v(z)) + k_\lambda (\overline{u}(z)) \ \text{ for } \text{ almost } \text{ all }\ z\in \Omega , \nonumber \\&\Rightarrow \overline{u}\in W^{1,p}_0 (\Omega )\ \text{ is } \text{ a } \text{ positive } \text{ of } \text{ problem }~(10)_{\lambda }~\text{ for }\ \lambda \in (0,\lambda _0]. \end{aligned}$$

(19)

From (19) and Theorem 7.1 of Ladyzhenskaya and Uraltseva [8, p. 286], we have $\overline{u}\in L^{\infty }(\Omega )$. Hence $k_\lambda (\overline{u}(\cdot ))\in L^\infty (\Omega )$. Recall that $\vartheta (v(\cdot ))\in L^s(\Omega )$ with $s>N$. From Theorem 9.15 of Gilbarg and Trudinger [6, p. 241], we know that there exists a unique solution $y_0\in W^{2,s}(\Omega )$ to the following linear Dirichlet problem

$$\begin{aligned} -\Delta y(z) = \vartheta (v(z))\ \text{ in }\ \Omega ,\ y|_{\partial \Omega } =0 . \end{aligned}$$

By the Sobolev embedding theorem, we have

$$\begin{aligned} W^{2,s}(\Omega ) \hookrightarrow C^{1,\alpha }(\overline{\Omega })\ \text{ with }\ \alpha = 1-\frac{N}{s}>0. \end{aligned}$$

Let $\eta _0(z)=Dy_0(z).$ Then $\eta _0\in C^{\alpha }(\overline{\Omega },\mathbb R^{N})$ and we have

$$\begin{aligned} -\mathrm{div}\,(a(D\overline{u}(z))-\eta _0(z)) + \xi (z)\overline{u}(z)^{p-1} = k_\lambda (\overline{u}(z))\ \text{ for } \text{ almost } \text{ all }\ z\in \Omega . \end{aligned}$$

The regularity theory of Lieberman [11] implies that $\overline{u}\in C_+ \backslash \{ 0 \}$. Moreover, from (19) we have

$$\begin{aligned}&\mathrm{div}\, a(D\overline{u}(z))\leqslant ||\xi ||_\infty \overline{u}(z)^{p-1}\ \text{ for } \text{ almost } \text{ all }\ z\in \Omega ,\\&\quad \Rightarrow \overline{u}\in \mathrm{int}\,C_+ \end{aligned}$$

(from the nonlinear maximum principle, see Pucci and Serrin  [21, pp. 111,120]).

Let $\hat{S_\lambda }$ denote the set of positive solutions of problem $(10)_\lambda$. We have just seen that $\emptyset \ne \hat{S_\lambda }\subseteq \mathrm{int}\,C_+$ for $\lambda \in (0,\lambda _0].$ Moreover, from Papageorgiou et al. [16, Proposition 18], we know that $\hat{S_\lambda }$ is downward directed (that is, if $u_1,u_2,\in \hat{S_\lambda }$, then we can find $u\in \hat{S_\lambda }$ such that $u\leqslant u_1,u\leqslant u_2)$. So, by Lemma 3.10 of Hu and Papageorgiou [7, p. 178], we can find a decreasing sequence $\{ \overline{u}_n \}_{n\geqslant 1} \subseteq \hat{S_\lambda }$ such that

$$\begin{aligned} \inf \hat{S_\lambda } = \inf _{n\geqslant 1}\overline{u}_n. \end{aligned}$$

For every $n\in \mathbb N$ we have

$$\begin{aligned} \langle A(\overline{u}_n),h\rangle + \int _\Omega \xi (z)\overline{u}_n^{p-1} hdz = \int _{\Omega }[\vartheta (v)+ k_\lambda (\overline{u}_n)] hdz\ \text{ for } \text{ all }\ h\in W^{1,p}_0 (\Omega ). \end{aligned}$$

(20)

Choosing $h = \overline{u}_n \in W^{1,p}_0$ and since $0\leqslant \overline{u}_n\leqslant \overline{u}_1$ for all $n\in \mathbb N$, using Lemma 2(c), we see that $\{\overline{u}_n\}_{n\geqslant 1} \subseteq W^{1,p}_0(\Omega )$ is bounded. So, we have

$$\begin{aligned} \overline{u}_n {\mathop {\rightarrow }\limits ^{w}} \overline{u}_\lambda \ \text{ in }\ W^{1,p}_0(\Omega ). \end{aligned}$$

(21)

Next, in (20) we choose $h=\overline{u}_n-\overline{u}\in W^{1,p}_0(\Omega )$, pass to the limit as $n\rightarrow \infty$ and use (21). Then

$$\begin{aligned}&\lim _{n\rightarrow \infty } \langle A(\overline{u}_n),\overline{u}_n-\overline{u}_\lambda \rangle = 0,\nonumber \\&\quad \Rightarrow \overline{u}_n\rightarrow \overline{u}_\lambda \ \text{ in }\ W^{1,p}_0(\Omega ),\ \overline{u}_\lambda \geqslant 0 \nonumber \\&\quad \text{(recall } \text{ that } \ A(\cdot )\ \text{ is } \text{ of } \text{ type }\ (S)_+,\ \text{ see } \text{ Sect. }~2\text{) }. \end{aligned}$$

(22)

We pass to the limit as $n\rightarrow \infty$ in (20) and use (22). Then

$$\begin{aligned}&\langle A(\overline{u}_\lambda ), h\rangle + \int _{\Omega }\xi (z)\overline{u}_\lambda ^{p-1} hdz = \int _{\Omega }[\vartheta (v)+ k_\lambda (\overline{u}_\lambda ) ] hdz\\&\quad \text{ for } \text{ all }\ h\in W^{1,p}_0 (\Omega ),\\&\quad \Rightarrow \overline{u}_\lambda \ \text{ is } \text{ a } \text{ nonnegative } \text{ solution } \text{ of }~(10)_{\lambda } \end{aligned}$$

Note that for all $n\in \mathbb N$, we have

$$\begin{aligned} \begin{array}{ll} -\mathrm{div}\, a(D\overline{u}_n(z)) + \xi ^+(z)\overline{u}_n(z)^{p-1} &{} \geqslant \vartheta (v(z)) + k_\lambda (\overline{u}_n (z)) \\ &{}\geqslant \vartheta (v(z)) = -\mathrm{div}\, a(Dv(z)) + \xi ^{+}(z) v (z)^{p-1}\\ &{}\text{ for } \text{ almost } \text{ all }\ z\in \Omega ,\\ \Rightarrow v\leqslant \overline{u}_n\ \text{ for } \text{ all }\ n\in \mathbb N\end{array} \end{aligned}$$

(by the weak comparison principle, see Damascelli [3, Theorem 1.2])

$$\begin{aligned} \Rightarrow v\leqslant \overline{u}_\lambda \ (\text{ see }~(22)),~\text{ hence }\ \overline{u}_\lambda \ne 0. \end{aligned}$$

(23)

Therefore $\overline{u}_\lambda \in \hat{S_\lambda }\subseteq \mathrm{int}\,C_+$ and $\overline{u}_\lambda = \inf \hat{S_\lambda }$. $\square$

We will use $\bar{u}_\lambda \in \mathrm{int}\,C_+$ from Proposition 6 to show the nonemptiness of $\mathcal {L}$.

Proposition 7

If hypotheses $H(a),H(\xi ),H(\vartheta ),H(f)$ hold, then $\mathcal {L}\ne \emptyset$ and $S_\lambda \subseteq \mathrm{int}\,C_+$.

Proof

From (9) we have

$$\begin{aligned} \lambda x^{q-1}+f(z,x)\leqslant k_\lambda (x)\ \text{ for } \text{ almost } \text{ all }\ z\in \Omega , \text{ and } \text{ all } x\geqslant 0,\, \lambda >0. \end{aligned}$$

(24)

For $\lambda \in \left( 0,\lambda _0\right]$ we have

$$\begin{aligned} -\mathrm{div}\,a(D\bar{u}_\lambda (z))+\xi (z)\bar{u}_\lambda (z)^{p-1}= & {} \vartheta (v(z))+k_\lambda (\bar{u}_\lambda (z))\nonumber \\&(\text{ see } \text{ Proposition }~6)\nonumber \\\geqslant & {} \vartheta (\bar{u}_\lambda (z))+k_\lambda (\bar{u}(z))\nonumber \\&(\text{ see }~(23)~ \text{ and } \text{ hypothesis }~ H(\vartheta )(ii))\nonumber \\\geqslant & {} \vartheta (\bar{u}_\lambda (z))+\lambda \bar{u}_\lambda (z)^{q-1}+f(z,\bar{u}_\lambda (z))\nonumber \\&\text{ for } \text{ almost } \text{ all }\ z\in \Omega \ (\text{ see }~(24)). \end{aligned}$$

(25)

With $\beta >||\xi ||_\infty$ and $\lambda \in \left( 0,\lambda _0\right]$, we consider the following truncation-perturbation of the reaction in problem ($P_{\lambda }$):

$$\begin{aligned}&\gamma _\lambda (z,x)=\left\{ \begin{array}{ll} \vartheta (v(z))+\lambda v(z)^{q-1}+f(z,v(z))+\beta v(z)^{p-1}&{}\quad \text{ if }\ x<v(z)\\ \vartheta (x)+\lambda x^{q-1}+f(z,x)+\beta x^{p-1}&{}\quad \text{ if }\ v(z)\leqslant x\leqslant \bar{u}_\lambda (z)\nonumber \\ \vartheta (\bar{u}_\lambda (z))+\lambda \bar{u}_\lambda (z)^{q-1}+f(z,\bar{u}_\lambda (z))+\beta \bar{u}_\lambda (z)^{p-1}&{}\quad \text{ if }\ \bar{u}_\lambda (z)<x. \end{array}\right. \\ \end{aligned}$$

(26)

This is a Carathéodory function. We set $\Gamma _\lambda (z,x)=\int ^x_0\gamma _\lambda (z,s)ds$ and consider the functional $\hat{\sigma }_\lambda :W^{1,p}_0(\Omega )\rightarrow \mathbb R$ defined by

$$\begin{aligned}&\hat{\sigma }_\lambda (u)=\int _\Omega G(Du)dz+\frac{1}{p}\int _\Omega [\xi (z)+\beta ]|u|^pdz-\int _\Omega \Gamma _\lambda (z,u)dz\\&\text{ for } \text{ all }\ u\in W^{1,p}_0(\Omega ). \end{aligned}$$

Using Proposition 3 of Papageorgiou and Smyrlis [17], we see that $\hat{\sigma }_\lambda \in C^1(W^{1,p}_0(\Omega ))$. Also, from (26), Corollary 3 and since $\beta >||\xi ||_\infty$, we see that $\hat{\sigma }_\lambda (\cdot )$ is coercive. In addition, it is sequentially weakly lower semicontinuous. So, we can find $u_\lambda \in W^{1,p}_0(\Omega )$ such that

$$\begin{aligned}&\hat{\sigma }_\lambda (u_\lambda )=\inf \{\hat{\sigma }(u):u\in W^{1,p}_0(\Omega )\},\nonumber \\&\quad \Rightarrow \hat{\sigma }'_\lambda (u_\lambda )=0,\nonumber \\&\quad \Rightarrow \left\langle A(u_\lambda ,h)\right\rangle +\int _\Omega [\xi (z)+\beta ]|u_\lambda |^{p-2}u_\lambda hdz \nonumber \\&\quad =\int _\Omega \gamma _\lambda (z,u_\lambda )hdz\nonumber \\&\qquad \text{ for } \text{ all }\ h\in W^{1,p}_0(\Omega ). \end{aligned}$$

(27)

In (27) first we choose $h=(u_\lambda -\bar{u}_\lambda )^+\in W^{1,p}_0(\Omega )$. Then we have

$$\begin{aligned}&\left\langle A(u_\lambda ),(u_\lambda -\bar{u}_\lambda )^+\right\rangle +\int _\Omega [\xi (z)+\beta ]u_\lambda ^{p-1}(u_\lambda -\bar{u}_\lambda )^+dz\\&\quad =\int _\Omega [\vartheta (\bar{u}_\lambda )+\lambda \bar{u}_\lambda ^{q-1}+f(z,\bar{u}_\lambda )+\beta \bar{u}_\lambda ^{p-1}](u_\lambda -\bar{u}_\lambda )^+dz\ (\text{ see }~(26))\\&\quad \leqslant \left\langle A(\bar{u}_\lambda ),(u_\lambda -\bar{u}_\lambda )^+\right\rangle +\int _\Omega [\xi (z)+\beta ]\bar{u}_\lambda ^{p-1}(u_\lambda -\bar{u}_\lambda )^+dz\ (\text{ see }~(25)),\\&\quad \Rightarrow u_\lambda \leqslant \bar{u}_\lambda \ (\text{ since }\ \beta >||\xi ||_\infty ). \end{aligned}$$

Next, in (27) we choose $h=(v-u_\lambda )^+\in W^{1,p}_0(\Omega )$. Then we have

$$\begin{aligned}&\left\langle A(u_\lambda ),(v-u_\lambda )^+\right\rangle +\int _\Omega [\xi (z)+\beta ]|u_\lambda |^{p-2}u_\lambda (v-u_\lambda )^+dz\\&\quad =\int _\Omega [\vartheta (v)+\lambda v^{q-1}+f(z,v)+\beta v^{p-1}](v-u_\lambda )^+dz\ (\text{ see }~(26))\\&\quad \geqslant \int _\Omega [\vartheta (v)+\beta v^{p-1}](v-u_\lambda )^+dz\ (\text{ since }\ f\geqslant 0)\\&\quad =\left\langle A(v),(v-u_\lambda )^+\right\rangle +\int _\Omega [\xi (z)+\beta ]v^{p-1}(v-u_\lambda )^+dz\ (\text{ see } \text{ Proposition }~5),\\&\quad \Rightarrow v\leqslant u_\lambda . \end{aligned}$$

So, we have proved that

$$\begin{aligned} u_\lambda \in [v,\bar{u}_\lambda ]\quad (\lambda \in \left( 0,\lambda _0\right] ). \end{aligned}$$

(28)

It follows from (26), (27) and (28) that

$$\begin{aligned}&-\mathrm{div}\,a(Du_\lambda (z))+\xi (z)u_\lambda (z)^{p-1}=\vartheta (u_\lambda (z))+\lambda u_\lambda (z)^{q-1}+f(z,u_\lambda (z))\\&\quad \text{ for } \text{ almost } \text{ all }\ z\in \Omega . \end{aligned}$$

Note that $\vartheta _\lambda (u_\lambda )\leqslant \vartheta (v)$ (see (28) and hypothesis $H(\vartheta )(ii)$) and $\vartheta (v)\in L^s(\Omega )$. So, as before (see the proof of Proposition 6), we infer that

$$\begin{aligned} u_\lambda \in \mathrm{int}\,C_+\,. \end{aligned}$$

Therefore we have seen that

$$\begin{aligned}&\left( 0,\lambda _0\right] \subseteq \mathcal {L},\ \text{ hence }\ \mathcal {L}\ne \emptyset \\ \text{ and }&S_\lambda \subseteq \mathrm{int}\,C_+. \end{aligned}$$

The proof is now complete. $\square$

For $\eta >0$, let $\tilde{u}_{\eta }\in \mathrm{int}\,C_+$ be the unique solution of the following Dirichlet problem

$$\begin{aligned} -\mathrm{div}\,a(Du(z))+\xi ^+(z)u(z)^{p-1}=\eta \ \text{ in }\ \Omega ,\ u|_{\partial \Omega }=0. \end{aligned}$$

By Proposition 9 of Papageorgiou et al. [16], we see that given $u\in S_\lambda \subseteq \mathrm{int}\,C_+$ (that is, $\lambda \in \mathcal {L}$), we can find small $\eta >0$ such that

$$\begin{aligned} \tilde{u}_\eta \leqslant u\ \text{ and }\ \eta \leqslant \vartheta (\tilde{u}_\eta ). \end{aligned}$$

(29)

We will use this to obtain a lower bound for the elements of $S_\lambda$.

Proposition 8

If hypotheses $H(a),H(\xi ),H(\vartheta ),H(f)$ hold and $\lambda \in \mathcal {L}$, then $v\leqslant u$ for all $u\in S_\lambda$.

Proof

Let $u\in S_\lambda \subseteq \mathrm{int}\,C_+$. Then on account of (29) we can define the following Carathéodory function

$$\begin{aligned} e(z,x)=\left\{ \begin{array}{ll} \vartheta (\tilde{u}_\eta (z))&{}\quad \text{ if }\ x<\tilde{u}_\eta (z)\\ \vartheta (x)&{}\quad \text{ if }\ \tilde{u}_\eta (z)\leqslant x\leqslant u(z)\\ \vartheta (u(z))&{}\quad \text{ if }\ u(z)<x. \end{array}\right. \end{aligned}$$

(30)

We set $E(z,x)=\int ^x_0 e(z,s)ds$ and consider the functional $\mu :W^{1,p}_0(\Omega )\rightarrow \mathbb R$ defined by

$$\begin{aligned} \mu (u)=\int _\Omega G(Du)dz+\frac{1}{p}\int _\Omega \xi ^+(z)|u|^pdz-\int _\Omega E(z,u)dz\ \text{ for } \text{ all }\ u\in W^{1,p}_0(\Omega ). \end{aligned}$$

As before, Proposition 3 of Papageorgiou and Smyrlis [17] implies that $\mu \in C^1(W^{1,p}_0(\Omega ))$. The coercivity of $\mu (\cdot )$ (see (30)) and the sequential weak lower semicontinuity guarantee the existence of $\tilde{v}\in W^{1,p}_0(\Omega )$ such that

$$\begin{aligned}&\mu (\tilde{v})=\inf \{\mu (u):u\in W^{1,p}_0(\Omega )\},\nonumber \\&\quad \Rightarrow \mu '(\tilde{v})=0,\nonumber \\&\quad \Rightarrow \left\langle A(\tilde{v}),h\right\rangle +\int _\Omega \xi ^+(z)|\tilde{v}|^{p-2}\tilde{v}hdz=\int _\Omega e(z,\tilde{v})hdz\ \text{ for } \text{ all }\ h\in W^{1,p}_0(\Omega ).\nonumber \\ \end{aligned}$$

(31)

In (31) we choose $h=(\tilde{v}-u)^+\in W^{1,p}_0(\Omega )$. Then we have

$$\begin{aligned}&\left\langle A(\tilde{v}),(\tilde{v}-u)^+\right\rangle +\int _\Omega \xi ^+(z)\tilde{v}^{p-1}(\tilde{v}-u)^+dz\\&\quad =\int _\Omega \vartheta (u)(\tilde{v}-u)^+dz\ (\text{ see }~(30))\\&\quad \leqslant \int _\Omega [\vartheta (u)+\lambda u^{q-1}+f(z,u)](\tilde{v}-u)^+dz\ (\text{ since }\ u\in \mathrm{int}\,C_+,\ f\geqslant 0)\\&\quad \leqslant \left\langle A(u),(\tilde{v}-u)^+\right\rangle +\int _\Omega \xi ^+(z)u^{p-1}(\tilde{v}-u)^+dz\ (\text{ since }\ u\in S_\lambda ),\\&\quad \Rightarrow \tilde{v}\leqslant u. \end{aligned}$$

Similarly, if in (31) we choose $h=(\tilde{u}_\eta -\tilde{v})^+\in W^{1,p}_0(\Omega )$, then we have

$$\begin{aligned}&\left\langle A(\tilde{v}),(\tilde{u}_\eta -\tilde{v})^+\right\rangle +\int _\Omega \xi ^+(z)|\tilde{v}|^{p-2}\tilde{v}(\tilde{u}_\eta -\tilde{v})^+dz\\&\quad =\int _\Omega \vartheta (\tilde{u}_\eta )(\tilde{u}_\eta -\tilde{v})^+dz\ (\text{ see }~(30))\\&\quad \geqslant \int _\Omega \eta (\tilde{u}_\eta -\tilde{v})^+dz\ (\text{ see }~(29))\\&\quad =\left\langle A(\tilde{u}_\eta ),(\tilde{u}_\eta -v)^+\right\rangle +\int _\Omega \xi ^+(z)\tilde{u}_{\eta }^{p-1}(\tilde{u}_\eta -v)^+dz,\\&\quad \Rightarrow \tilde{u}_\eta \leqslant \tilde{v}. \end{aligned}$$

So, we have proved that

$$\begin{aligned} \tilde{v}\in [\tilde{u}_\eta ,u]. \end{aligned}$$

(32)

It follows from (30), (31), (32) that $\tilde{v}$ is a positive solution of (18). Then on account of Proposition 5, we have

$$\begin{aligned}&\tilde{v}=v\in \mathrm{int}\,C_+,\\&\quad \Rightarrow v\leqslant u\ \text{ for } \text{ all }\ u\in S_\lambda \ (\text{ see }~(32)). \end{aligned}$$

The proof is now complete. $\square$

Next, we show a structural property of the set $\mathcal {L}$, namely that $\mathcal {L}$ is an interval. Moreover, we establish a kind of strong monotonicity property for the solution set $S_\lambda$.

Proposition 9

If hypotheses $H(a),H(\xi ),H(\vartheta ),H(f)$ hold, $\lambda \in \mathcal {L},0<\mu <\lambda$ and $u_\lambda \in S_\lambda \subseteq \mathrm{int}\,C_+$, then $\mu \in \mathcal {L}$ and there exists $u_\mu \in S_\mu \subseteq \mathrm{int}\,C_+$ such that $u_\lambda -u_\mu \in \mathrm{int}\,C_+.$

Proof

From Proposition 8 we know that $v\leqslant u_\lambda$. Then with $\beta >||\xi ||_\infty$ we can define the following truncation-perturbation of the reaction in problem ($P_\mu$):

$$\begin{aligned} e_\mu (z,x)=\left\{ \begin{array}{ll} \vartheta (v(z))+\mu v(z)^{q-1}+f(z,v(z))+\beta v(z)^{p-1}&{}\quad \text{ if }\ x<v(z)\\ \vartheta (x)+\mu x^{q-1}+f(z,x)+\beta x^{p-1}&{}\quad \text{ if }\ v(z)\leqslant x\leqslant u_\lambda (z)\\ \vartheta (u_\lambda (z))+\mu u_\lambda (z)^{q-1}+f(z,u_\lambda (z))+\beta u_\lambda (z)^{p-1}&{}\quad \text{ if }\ u_\lambda (z)<x. \end{array}\right. \end{aligned}$$

(33)

Evidently, $e_\mu (z,x)$ is a Carathéodory function. We set $E_\mu (z,x)=\int ^x_0e_\mu (z,s)ds$ and consider the $C^1$-functional $\hat{\psi }_\mu :W^{1,p}_0(\Omega )\rightarrow \mathbb R$ defined by

$$\begin{aligned} \hat{\psi }_\mu (u)&=\int _\Omega G(Du)dz+\frac{1}{p}\int _\Omega [\xi (z)+\beta ]|u|^pdz\\&\quad -\int _\Omega E_\mu (z,u)dz\ \text{ for } \text{ all }\ u\in W^{1,p}_0(\Omega ). \end{aligned}$$

Clearly, $\hat{\psi }_\mu (\cdot )$ is coercive (see (33) and recall that $\beta >||\xi ||_\infty$). It is also sequentially weakly lower semicontinuous. So, we can find $u_\mu \in W^{1,p}_0(\Omega )$ such that

$$\begin{aligned}&\hat{\psi }_\mu (u_\mu )=\inf \{\hat{\psi }_\mu (u):u\in W^{1,p}_0(\Omega )\},\nonumber \\&\quad \Rightarrow \hat{\psi }'_\mu (u_\mu )=0,\nonumber \\&\quad \Rightarrow \left\langle A(u_\mu ),h\right\rangle +\int _\Omega [\xi (z)+\beta ]|u_\mu |^{p-2}u_\mu hdz\nonumber \\&\quad =\int _\Omega e_\mu (z,u_\mu )hdz\ \text{ for } \text{ all }\ h\in W^{1,p}_0(\Omega ). \end{aligned}$$

(34)

In (34) we first use $h=(u_\mu -u_\lambda )^+\in W^{1,p}_0(\Omega )$. Then

$$\begin{aligned}&\left\langle A(u_\mu ),(u_\mu -u_\lambda )^+\right\rangle +\int _\Omega [\xi (z)+\beta ]u_\mu ^{p-1}(u_\mu -u_\lambda )^+dz\\&\quad =\int _\Omega [\vartheta (u_\lambda )+\mu u_\lambda ^{q-1}+f(z,u_\lambda )+\beta u_\lambda ^{p-1}](u_\mu -u_\lambda )^+dz\ (\text{ see }~(33))\\&\quad \leqslant \int _\Omega [\vartheta (u_\lambda )+\lambda u_\lambda ^{q-1}+f(z,u_\lambda )+\beta u_\lambda ^{p-1}](u_\mu -u_\lambda )^+dz\ (\text{ since } \lambda>\mu )\\&\quad =\left\langle A(u_\lambda ),(u_\mu -u_\lambda )^+\right\rangle +\int _\Omega [\xi (z)+\beta ]u_\lambda ^{p-1}(u_\mu -u_\lambda )^+dz\ (\text{ since } u_\lambda \in S_\lambda ),\\&\quad \Rightarrow u_\mu \leqslant u_\lambda \ (\text{ recall } \text{ that }\ \beta >||\xi ||_\infty ). \end{aligned}$$

Next, in (34) we use $h=(v-u_\mu )^+\in W^{1,p}_0(\Omega )$. Then from Proposition 5 and since $f\geqslant 0$, we obtain

$$\begin{aligned} v\leqslant u_\mu \,. \end{aligned}$$

We have proved that

$$\begin{aligned} u_\mu \in [v,u_\lambda ]. \end{aligned}$$

(35)

It follows from (33), (34), (35) that $u_\mu \in S_\mu \subseteq \mathrm{int}\,C_+$ and so $\mu \in \mathcal {L}$.

Let $\rho =||u_\lambda ||_\infty$ and let $\hat{\xi }_\rho >0$ as postulated by hypothesis H(f)(v). We have

$$\begin{aligned}&-\mathrm{div}\,a(Du_\mu )+[\xi (z)+\hat{\xi }_\rho ]u_\mu ^{p-1}-\vartheta (u_\mu )\nonumber \\&\quad =\mu u_\mu ^{q-1}+f(z,u_\mu )+\hat{\xi }_\rho u_\mu ^{p-1}\nonumber \\&\quad \leqslant \lambda u_\lambda ^{q-1}+f(z,u_\lambda )+\hat{\xi }_\rho u_\lambda ^{p-1}\ (\text{ see } \text{ hypothesis }\ H(f)(vi),\nonumber \\&\quad (35)~\text{ and } \text{ recall } \text{ that }\ \mu <\lambda )\nonumber \\&\quad =-\mathrm{div}\,a (Du_\lambda )+[\xi (z)+\hat{\xi }_\rho ]u_\lambda ^{p-1}-\vartheta (u_\lambda ). \end{aligned}$$

(36)

From (36) and Proposition 4 of Papageorgiou and Smyrlis [17], we obtain

$$\begin{aligned} u_\lambda -u_\mu \in \mathrm{int}\,C_+. \end{aligned}$$

The proof is now complete. $\square$

Proposition 10

If hypotheses $H(a),H(\xi ),H(\vartheta ),H(f)$ hold, then $\lambda ^*<+\infty$.

Proof

Recall that by hypotheses H(f)(ii), (iii), we have

$$\begin{aligned} \lim _{x\rightarrow +\infty }\frac{f(z,x)}{x^{p-1}}=+\infty \ \text{ uniformly } \text{ for } \text{ almost } \text{ all }\ z\in \Omega . \end{aligned}$$

So, we can find $M>0$ such that

$$\begin{aligned} f(z,x)\geqslant x^{p-1}\ \text{ for } \text{ almost } \text{ all }\ z\in \Omega ,\ \text{ and } \text{ all }\ x\geqslant M. \end{aligned}$$

(37)

Hypotheses $H(\vartheta )$ imply that we can find small $\delta \in \left( 0,1\right]$ such that

$$\begin{aligned} \vartheta (x)\geqslant \vartheta (\delta )\geqslant 1\geqslant \delta ^{p-1}\geqslant x^{p-1}\ \text{ for } \text{ all }\ x\in \left( 0,\delta \right] . \end{aligned}$$

(38)

Finally, hypotheses H(f)(i), (v) imply that we can find big $\lambda _0>0$ such that

$$\begin{aligned} \lambda _0x^{q-1}+f(z,x)\geqslant x^{p-1}\ \text{ for } \text{ almost } \text{ all }\ z\in \Omega \ \text{ and } \text{ all }\ \delta \leqslant x\leqslant M. \end{aligned}$$

(39)

Combining (37), (38), (39) we have

$$\begin{aligned} \vartheta (x)+\lambda _0x^{q-1}+f(z,x)\geqslant x^{p-1}\ \text{ for } \text{ almost } \text{ all }\ z\in \Omega \ \text{ and } \text{ all }\ x\geqslant 0. \end{aligned}$$

(40)

Let $\lambda >\lambda _0$ and assume that $\lambda \in \mathcal {L}$. Then according to Proposition 7 we can find $u_\lambda \in S_\lambda \subseteq \mathrm{int}\,C_+$. Let $\Omega _0\subseteq \Omega$ be an open set with $\overline{\Omega }_0\subseteq \Omega$ and $C^2$-boundary $\partial \Omega _0$. We have

$$\begin{aligned} 0<m_0=\min \limits _{\overline{\Omega }_0}u_\lambda . \end{aligned}$$

For $\epsilon >0$, let $m^{\epsilon }_{0}=m_0+\epsilon$ and with $\rho =||u_\lambda ||_\infty$, let $\hat{\xi }_\rho >0$ be as postulated by hypothesis H(f)(v). We can always take $\hat{\xi }_\rho >||\xi ||_\infty$. We have

$$\begin{aligned}&-\mathrm{div}\,a(Dm^\epsilon _0)+[\xi (z)+\hat{\xi }_\rho ](m^\epsilon _0)^{p-1}-\vartheta (m^\epsilon _0)\nonumber \\&\quad \leqslant [\xi (z)+\hat{\xi }_\rho ]m^{p-1}_0+\chi (\epsilon )-\vartheta (m_0)\nonumber \\&\qquad \quad \text{ with }\ \chi (\epsilon )\rightarrow 0^+\ \text{ as }\ \epsilon \rightarrow 0^+\ (\text{ see } \text{ hypotheses }\ H(\vartheta ))\nonumber \\&\quad<[\xi (z)+\hat{\xi }_\rho ]u^{p-1}_{\lambda }+u^{p-1}_\lambda -\vartheta (u_\lambda )+\chi (\epsilon )\nonumber \\&\quad<[\xi (z)+\hat{\xi }_\rho ]u^{p-1}_{\lambda }+\lambda _0u^{p-1}_\lambda +f(z,u_\lambda )+\chi (\epsilon )\ (\text{ see }~(40))\nonumber \\&\quad =[\xi (z)+\hat{\xi }_\rho ]u^{p-1}_\lambda +\lambda u^{q-1}_\lambda +f(z,u_\lambda )-(\lambda -\lambda _0)u^{q-1}_\lambda +\chi (\epsilon )\nonumber \\&\quad <[\xi (z)+\hat{\xi }_\rho ]u^{p-1}_\lambda +\lambda u_\lambda ^{q-1}+f(z,u_\lambda )\ \text{ for }\ \epsilon >0\ \text{ small } \text{ enough }\nonumber \\&\quad =-\mathrm{div}\,a(Du_\lambda )+[\xi (z)+\hat{\xi }_p]u^{p-1}_\lambda -\vartheta (u_\lambda )\nonumber \\&\qquad \quad \text{ for } \text{ almost } \text{ all }\ z\in \Omega _0\ (\text{ recall } \text{ that }\ u_\lambda \in S_\lambda ). \end{aligned}$$

(41)

Then from (40) and Proposition 4, we see that for small enough $\epsilon >0$ we have

$$\begin{aligned} u_\lambda -m^\epsilon _0\in \mathrm{int}\,\hat{C}_+(\overline{\Omega }_0), \end{aligned}$$

which contradicts the definition of $m_0$. Hence $\lambda \notin \mathcal {L}$ and so $\lambda ^*\leqslant \lambda _0<+\infty$. $\square$

By Propositions 9 and 10 it follows that

$$\begin{aligned} (0,\lambda ^*)\subseteq \mathcal {L}\subseteq \left( 0,\lambda ^*\right] . \end{aligned}$$

(42)

Proposition 11

If hypotheses $H(a),H(\xi ),H(\vartheta ),H(f)$ hold and $\lambda \in (0,\lambda ^*)$, then problem ($P_{\lambda }$) admits at least two positive solutions

$$\begin{aligned} u_0,\hat{u}\in \mathrm{int}\,C_+,\ u_0\ne \hat{u}. \end{aligned}$$

Proof

Let $0<\mu<\lambda<\eta <\lambda ^*$. We have $\mu ,\eta \in \mathcal {L}$ (see (42)). On account of Proposition 9 we can find $u_\mu \in S_\mu \subseteq \mathrm{int}\,C_+,\ u_0\in S_\lambda \subseteq \mathrm{int}\,C_+,\ u_\eta \in S_\eta \subseteq \mathrm{int}\,C_+$ such that

$$\begin{aligned}&u_0-u_\eta \in \mathrm{int}\,C_+\ \text{ and }\ u_\eta -u_0\in \mathrm{int}\,C_+,\nonumber \\&\quad \Rightarrow u_0\in \mathrm{int}_{C^1_0(\overline{\Omega })}[u_\mu ,u_\eta ]. \end{aligned}$$

(43)

With $\beta >||\xi ||_\infty$, we introduce the Carathéodory function $d_\lambda (z,x)$ defined by

$$\begin{aligned} d_\lambda (z,x)=\left\{ \begin{array}{ll} \vartheta (u_\mu (z))+\lambda u_\mu (z)^{q-1}+f(z,u_\mu (z))+\beta u_\mu (z)^{p-1}&{}\quad \text{ if }\ x\leqslant u_\mu (z)\\ \vartheta (x)+\lambda x^{q-1}+f(z,x)+\beta x^{p-1}&{}\quad \text{ if }\ u_\mu (z)<x. \end{array}\right. \end{aligned}$$

(44)

We set $D_\lambda (z,x)=\int ^x_0 d_\lambda (z,s)ds$ and consider the functional $\varphi _\lambda :W^{1,p}_0(\Omega )\rightarrow \mathbb R$ defined by

$$\begin{aligned} \varphi _\lambda (u)=\!\!\int _\Omega G(Du)dz+\frac{1}{p}\!\int _\Omega [\xi (z)+\beta ]|u|^pdz-\!\!\int _\Omega D_\lambda (z,u)dz\ \text{ for } \text{ all }\ u\in W^{1,p}_0(\Omega ). \end{aligned}$$

We know that $\varphi _\lambda \in C^1(W^{1,p}_0(\Omega ))$ (see Papageorgiou and Smyrlis [17, Proposition 3]). Also, let

$$\begin{aligned} \hat{d}_\lambda (z,x)=\left\{ \begin{array}{ll} d_\lambda (z,x)&{}\quad \text{ if }\ x\leqslant u_\eta (z)\\ d_\lambda (z,u_\eta (z))&{}\quad \text{ if }\ u_\eta (z)<x. \end{array}\right. \end{aligned}$$

(45)

This is a Carathéodory function. We set $\hat{D}_\lambda (z,x)=\int ^x_0\hat{d}_\lambda (z,s)ds$ and consider the $C^1$-functional $\hat{\varphi }_\lambda :W^{1,p}_0(\Omega )\rightarrow \mathbb R$ defined by

$$\begin{aligned} \hat{\varphi }_\lambda (u)=\!\!\int _\Omega G(Du)dz+\frac{1}{p}\!\int _\Omega [\xi (z)+\beta ]|u|^pdz-\!\!\int _\Omega \hat{D}_\lambda (z,u)dz\ \text{ for } \text{ all }\ u\in W^{1,p}_0(\Omega ). \end{aligned}$$

Using (44) and (45) and the nonlinear regularity theory (see the proof of Proposition 7), we show that

$$\begin{aligned}&K_{\varphi _\lambda }\subseteq \left[ u_\mu \right) \cap \mathrm{int}\,C_+, \end{aligned}$$

(46)

$$\begin{aligned}&K_{\hat{\varphi }_\lambda }\subseteq [u_\mu ,u_\eta ]\cap \mathrm{int}\,C_+. \end{aligned}$$

(47)

From (47) we see that we can assume that

$$\begin{aligned} K_{\hat{\varphi }_\lambda }=\{u_0\} \end{aligned}$$

(48)

or otherwise we already have a second positive solution for ($P_{\lambda }$) (see (45)) and so we are done.

Clearly, $\hat{\varphi }_\lambda (\cdot )$ is coercive (see (45)) and sequentially weakly lower semicontinuous. So, we can find $\hat{u}_0\in W^{1,p}_0(\Omega )$ such that

$$\begin{aligned}&\hat{\varphi }_\lambda (\hat{u_0})=\inf \{\hat{\varphi }_\lambda (u):u\in W^{1,p}_0(\Omega )\},\nonumber \\&\quad \Rightarrow \hat{u}_0\in K_{\hat{\varphi }_\lambda },\nonumber \\&\quad \Rightarrow \hat{u}_0=u_0\ (\text{ see }~(48)). \end{aligned}$$

(49)

But from (44) and (45) we see that

$$\begin{aligned} \left. \hat{\varphi }_\lambda \right| _{[u_\mu ,u_\eta ]}=\left. \varphi _\lambda \right| _{[u_\mu ,u_\eta ]}. \end{aligned}$$

(50)

It follows from (43), (49), (50) that

$$\begin{aligned}&u_0\ \text{ is } \text{ a } \text{ local }\ C^1_0(\overline{\Omega })\text{-minimizer } \text{ of }\ \varphi _\lambda ,\nonumber \\&\quad \Rightarrow u_0\ \text{ is } \text{ a } \text{ local }\ W^{1,p}_0(\Omega )\text{-minimizer } \text{ of }\ \varphi _\lambda \ (\text{ see } \text{[5] }). \end{aligned}$$

(51)

On account of (44) and (46), we may assume that

$$\begin{aligned} K_{\varphi _\lambda }\ \text{ is } \text{ finite }. \end{aligned}$$

(52)

Otherwise we already have an infinity of positive smooth solutions. From (51), (52) and Theorem 5.7.6 of Papageorgiou et al. [15], we see that we can find small $\rho \in (0,1)$ such that

$$\begin{aligned} \varphi _\lambda (u_0)<\inf \{\varphi _\lambda (u):||u-u_0||=\rho \}=m_\rho . \end{aligned}$$

(53)

Hypothesis H(f)(ii) and Corollary 3 imply that if $u\in \mathrm{int}\,C_+$, then

$$\begin{aligned} \varphi _\lambda (tu)\rightarrow -\infty \ \text{ as }\ t\rightarrow +\infty . \end{aligned}$$

(54)

Claim 1

$\varphi _\lambda$ satisfies the C-condition.

Consider a sequence $\{u_n\}_{n\geqslant 1}\subseteq W^{1,p}_0(\Omega )$ such that

$$\begin{aligned}&|\varphi _\lambda (u_n)|\leqslant c_{15}\ \text{ for } \text{ some }\ c_{15}>0,\ \text{ and } \text{ all }\ n\in \mathbb N, \end{aligned}$$

(55)

$$\begin{aligned}&(1+||u_n||)\varphi '_\lambda (u_n)\rightarrow \ \text{ in }\ W^{-1,p'}(\Omega )=W^{1,p}_0(\Omega )^*\ \text{ as }\ n\rightarrow \infty . \end{aligned}$$

(56)

From (56) we have

$$\begin{aligned}&\left| \left\langle A(u_n),h\right\rangle +\int _\Omega [\xi (z)+\beta ]|u_n|^{p-2}u_nhdz-\int _\Omega d_\lambda (z,u_n)hdz\right| \leqslant \frac{\epsilon _n||h||}{1+||u_n||}\nonumber \\&\text{ for } \text{ all }\ h\in W^{1,p}_0(\Omega ),\ \text{ with }\ \epsilon _n\rightarrow 0^+. \end{aligned}$$

(57)

In (57) we choose $h=-u^-_n\in W^{1,p}_0(\Omega )$. From (44) and Lemma 2, we have

$$\begin{aligned}&\frac{c_1}{p-1}||Du^-_n||^p_p+\int _\Omega [\xi (z)+\beta ](u^-_n)^pdz\leqslant \epsilon _n+c_{16}||u^-_n||\nonumber \\&\quad \text{ for } \text{ some }\ c_{16}>0,\ \text{ and } \text{ all }\ n\in \mathbb N,\nonumber \\&\quad \Rightarrow \{u^-_n\}_{n\geqslant 1}\subseteq W^{1,p}_0(\Omega )\ \text{ is } \text{ bounded }\ (\text{ recall } \text{ that }\ \beta >||\xi ||_\infty ). \end{aligned}$$

(58)

Next, in (57) we choose $h=u^+_n\in W^{1,p}_0(\Omega )$. Then

$$\begin{aligned}&-\int _\Omega (a(Du^+_n),Du^+_n)_{\mathbb R^N}dz-\int _\Omega [\xi (z)+\beta ](u^+_n)^pdz\nonumber \\&\quad +\int _\Omega [\lambda (u^+_n)^q+f(z,u^+_n)u^+_n]dz\leqslant c_{17}\nonumber \\&\quad \text{ for } \text{ some }\ c_{17}>0\ \text{ and } \text{ all }\ n\in \mathbb N\ (\text{ see }~\ H(\vartheta )(ii)). \end{aligned}$$

(59)

From (55) and (58) we obtain

$$\begin{aligned}&\int _\Omega pG(Du^+_n)dz+\int _\Omega [\xi (z)+\beta ](u^+_n)^pdz-\int _\Omega \left[ \frac{\lambda p}{q}(u^+_n)^q+pF(z,u^+_n)\right] dz\leqslant c_{18}\nonumber \\&\quad \text{ for } \text{ some }\ c_{18}>0\ \text{ and } \text{ all }\ n\in \mathbb N. \end{aligned}$$

(60)

Adding (59) and (60) and using hypothesis H(a)(iv), we obtain

$$\begin{aligned}&\int _\Omega [f(z,u^+_n)u^+_n-pF(z,u^+_n)]dz\leqslant c_{19}+\lambda \left[ \frac{p}{q}-1\right] ||u^+_n||^q_q\nonumber \\&\quad \text{ for } \text{ some }\ c_{19}>0,\ \text{ all }\ n\in \mathbb N. \end{aligned}$$

(61)

From hypotheses H(f)(i), (iii) we see that we can find $\hat{\beta }_1\in (0,\hat{\beta _0})$ and $c_{20}>0$ such that

$$\begin{aligned} \hat{\beta }_1x^{\sigma }-c_{20}\leqslant f(z,x)x-pF(z,x)\ \text{ for } \text{ almost } \text{ all }\ z\in \Omega \ \text{ and } \text{ all }\ x\geqslant 0. \end{aligned}$$

(62)

Using (62) in (61) and recalling that $q<\sigma$ (see hypothesis H(f)(iii)) we obtain that

$$\begin{aligned} \{u^+_n\}_{n\geqslant 1}\subseteq L^{\sigma }(\Omega )\ \text{ is } \text{ bounded }. \end{aligned}$$

(63)

First, suppose that $N\ne p$. It is clear from hypothesis H(f)(iii) that we may assume that $\sigma<r<p^*$ (recall that $p^*=+\infty$ if $N\leqslant p$). Let $t\in (0,1)$ be such that

$$\begin{aligned} \frac{1}{r}=\frac{1-t}{\sigma }+\frac{t}{p^*}. \end{aligned}$$

From the interpolation inequality (see, for example, Papageorgiou and Winkert [18, Proposition 2.3.17, p.116]), we have

$$\begin{aligned}&||u^+_n||_r\leqslant ||u^+_n||^{1-t}_\sigma ||u^+_n||^t_{p^*},\nonumber \\&\quad \Rightarrow ||u^+_n||^r_r\leqslant c_{21}||u^+_n||^{tr}\nonumber \\&\quad \text{ for } \text{ some }\ c_{21}>0\ \text{ and } \text{ all }\ n\in \mathbb N\ (\text{ see }~(63)). \end{aligned}$$

(64)

From hypothesis H(f)(i), we have

$$\begin{aligned} f(z,x)x\leqslant c_{22}[1+x^r]\ \text{ for } \text{ almost } \text{ all }\ z\in \Omega ,\ \text{ all }\ x\geqslant 0\ \text{ and } \text{ some }\ c_{22}>0. \end{aligned}$$

(65)

In (57) we choose $h=u^+_n\in W^{1,p}_0(\Omega )$ and use Lemma 2. Then

$$\begin{aligned}&\frac{c_1}{p-1}||Du^+_n||^p_p+\int _\Omega [\xi (z)+\beta ](u^+_n)^pdz\leqslant \epsilon _n+\int _\Omega d_\lambda (z,u_n)u^+_ndz,\nonumber \\&\quad \Rightarrow \frac{c_1}{p-1}||Du^+_n||^p_p\leqslant c_{23}+\int _\Omega [\lambda (u^+_n)^q+f(z,u^+_n)u^+_n]dz\nonumber \\&\qquad \quad \text{ for } \text{ some }\ c_{23}>0\ \text{ and } \text{ all }\ n\in \mathbb N\ (\text{ see }~(44))\nonumber \\&\quad \leqslant c_{24}[1+\lambda ||u^+_n||^q+||u^+_n||^{tr}]\nonumber \\&\qquad \quad \text{ for } \text{ some }\ c_{24}>0\ \text{ and } \text{ all }\ n\in \mathbb N\ (\text{ see }~(64)~\text{ and }~(65)). \end{aligned}$$

(66)

The hypothesis on $\sigma$ (see H(f)(iii)) implies that $tr<p$. Also we have $q<p$. Therefore it follows from (66) that

$$\begin{aligned} \{u^+_n\}_{n\geqslant 1}\subseteq W^{1,p}_0(\Omega )\ \text{ is } \text{ bounded }. \end{aligned}$$

(67)

If $p=N$, then $p^*=+\infty$ and by the Sobolev embedding theorem, we have that $W^{1,p}_0(\Omega )\hookrightarrow L^s(\Omega )$ for all $1\leqslant s<\infty$. So, we need to replace in the previous argument $p^*$ by $s>r>\sigma$ big enough. More precisely, as before, let $t\in (0,1)$ be such that

$$\begin{aligned}&\frac{1}{r}=\frac{1-t}{\sigma }+\frac{t}{s},\\&\quad \Rightarrow tr=\frac{s(r-\sigma )}{s-\sigma }\rightarrow r-\sigma \ \text{ as }\ s\rightarrow +\infty . \end{aligned}$$

Recall that $r-\sigma <p$ (see hypothesis H(f)(iii)). Hence for large enough $s>r$

$$\begin{aligned} tr=\frac{s(r-\sigma )}{s-\sigma }<p. \end{aligned}$$

Then for such large $s>r$, the previous argument is valid and we again obtain (67).

From (58) and (67) we have that $\{u_n\}_{n\geqslant 1}\subseteq W^{1,p}_0(\Omega )$ is bounded. So, we may assume that

$$\begin{aligned} u_n{\mathop {\rightarrow }\limits ^{w}}u\ \text{ in }\ W^{1,p}_0(\Omega ). \end{aligned}$$

(68)

In (57) we choose $h=u_n-u\in W^{1,p}_0(\Omega )$, pass to the limit as $n\rightarrow \infty$, and use (68). Then

$$\begin{aligned}&\lim \limits _{n\rightarrow \infty }\left\langle A(u_n),u_n-u\right\rangle =0,\\&\quad \Rightarrow u_n\rightarrow u\ \text{ in }\ W^{1,p}_0(\Omega )\\&\quad (\text{ using } \text{ the }\ (S)_+\ \text{ property } \text{ of }\ A(\cdot ),\ see \text{ see } \text{ Sect. }~2\text{) },\\&\quad \Rightarrow \varphi _\lambda (\cdot )\ \text{ satisfies } \text{ the }\ C-\text{ condition }. \end{aligned}$$

This proves Claim 1.

From (53), (54) and Claim 1, we see that we can apply the mountain pass theorem. So, we can find $\hat{u}\in W^{1,p}_0(\Omega )$ such that

$$\begin{aligned} \hat{u}\in K_{\varphi _\lambda }\subseteq \left[ u_\mu \right) \cap \mathrm{int}\,C_+\ (\text{ see }~(46))~\text{ and }\ m_\rho \leqslant \varphi _\lambda (\hat{u})\ (\text{ see }~(53)). \end{aligned}$$

(69)

It follows rom (44) and (69) that

$$\begin{aligned} \hat{u}\in S_\lambda \subseteq \mathrm{int}\,C_+\ \text{ and }\ u_0\ne \hat{u}. \end{aligned}$$

The proof is now complete. $\square$

Proposition 12

If hypotheses $H(a),H(\xi ),H(\vartheta ),H(f)$ hold, then $\lambda ^*\in \mathcal {L}$.

Proof

Let $\{\lambda _n\}_{n\geqslant 1}\subseteq (0,\lambda ^*)$ be such that $\lambda _n\uparrow \lambda ^*$. We know that $\lambda _n\in \mathcal {L}$ for all $n\in \mathbb N$ and so we can find $u_n=u_{\lambda _n}\in S_{\lambda _n}\subseteq \mathrm{int}\, C_+$$(n\in \mathbb N)$ increasing (see Proposition 9).

Let $\hat{\varphi }_{\lambda _n}(\cdot )$ be the functional from the proof of Proposition 11, with $u_\mu =u_{n-1},\ u_\mu =u_{n+1}(n\geqslant 2)$. Then we have

$$\begin{aligned} \hat{\varphi }_{\lambda _n}(u_n)\leqslant & {} \hat{\varphi }_{\lambda _n}(u_{n-1})\nonumber \\= & {} \int _\Omega G(Du_{n-1})dz+\frac{1}{p}\int _\Omega [\xi (z)+\beta ]u^p_{n-1}dz-\int _\Omega [\vartheta (u_{n-1})+\lambda _nu^{q-1}_{n-1}\nonumber \\&+\,f(z,u_{n-1}+\beta u^{p-1}_{n-1})]u_{n-1}dz\nonumber \\\leqslant & {} \int _{\Omega }G(Du_{n-1})dz+\frac{1}{p}\int _\Omega [\xi (z)+\beta ]u^p_{n-1}dz-\int _\Omega [\vartheta (u_{n-1})+\lambda _{n-1}u^{q-1}_{n-1}\nonumber \\&+\,f(z,u_{n-1})+\beta u^{p-1}_{n-1}]u_{n-1}dz\nonumber \\\leqslant & {} \int _\Omega (a(Du_{n-1}),Du_{n+1})dz+\int _\Omega \xi (z)u^p_{n-1}dz-\int _{\Omega }[\vartheta (u_{n-1})+\lambda _{n-1}u^{q-1}_{n-1}\nonumber \\&+\,f(z,u_{n-1})]u_{n-1}dz\ (\text{ see }~(3)~\text{ and } \text{ recall } \text{ that }\ \beta >||\xi ||_\infty )\nonumber \\= & {} 0\ (\text{ since }\ u_{n-1}\in S_{\lambda _{n-1}}). \end{aligned}$$

(70)

Also, we have

$$\begin{aligned}&\left\langle A(u_n),h\right\rangle +\int _\Omega [\xi (z)+\beta ]u^{p-1}_nhdz=\int _\Omega d_{\lambda _n}(z,u_n)hdz\nonumber \\&\text{ for } \text{ all }\ h\in W^{1,p}_0(\Omega )\ \text{ and } \text{ all }\ n\in \mathbb N. \end{aligned}$$

(71)

Using (70), (71) and reasoning as in the proof of Proposition 11 (see Claim 1), we obtain that

$$\begin{aligned} \{u_n\}_{n\geqslant 1}\subseteq W^{1,p}_0(\Omega )\ \text{ is } \text{ bounded }. \end{aligned}$$

From this, as in the proof of Proposition 11, exploiting the $(S)_+$ property of $A(\cdot )$, we obtain

$$\begin{aligned} u_n\rightarrow u_*\ \text{ in }\ W^{1,p}_0(\Omega ). \end{aligned}$$

(72)

Passing to the limit as $n\rightarrow \infty$ in (71) and using (72), we have

$$\begin{aligned} u_*\in S_{\lambda _*}\subseteq \mathrm{int}\,C_+\ \text{ and } \text{ so }\ \lambda ^*\in \mathcal {L}. \end{aligned}$$

The proof is now complete. $\square$

This proposition implies that

$$\begin{aligned} \mathcal {L}=\left( 0,\lambda ^*\right] . \end{aligned}$$

Summarizing the situation for problem ($P_{\lambda }$), we can state the following bifurcation-type result.

Theorem 13

If hypotheses $H(a),H(\xi ),H(\vartheta ),H(f)$ hold, then there exists $\lambda ^*>0$ such that

• (a) for all $\lambda \in (0,\lambda ^*)$ problem ($P_{\lambda }$) has at least two positive solutions

  $$\begin{aligned} u_0,\hat{u}\in \mathrm{int}\,C_+,\ u_0\ne \hat{u}; \end{aligned}$$

• (b) for $\lambda =\lambda ^*$ problem ($P_{\lambda }$) has at least one positive solution $u_*\in \mathrm{int}\, C_+$;

• (c) for all $\lambda >\lambda ^*$ problem ($P_{\lambda }$) has no positive solutions.