Skip to main content
SpringerLink
Log in

Structural optimization of hollow-section steel trusses by differential evolution algorithm

  • Published:
International Journal of Steel Structures Aims and scope Submit manuscript

Abstract

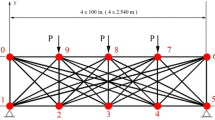
This paper deals with the weight minimization of planar steel trusses by adopting a differential evolution-based algorithm. Square hollow sections are considered. The design optimization refers to size, shape and topology. The design variables are represented by the geometrical dimensions of the cross sections of the different components of the truss, directly involving the size of the structure, and by some geometrical parameters affecting the outer shape of the truss. The topology is included in the optimization search in a particular way, since the designer at different runs of the algorithm can change the number of bays keeping constant the total length of the truss, to successively choose the best optimal solution. The minimum weight optimum design is posed as a single-objective optimization problem subject to constraints formulated in accordance with the current Eurocode 3. The optimal solution is obtained by a Differential Evolutionary (DE) algorithm. In the DE algorithm, a particular combination of mutation and crossover operators is adopted in order to achieve the best solutions and a specific way for dealing with constraints is introduced. The effectiveness of the proposed approach is shown with reference to two case-studies. The analysis results prove the versatility of the optimizer algorithm with regard to the three optimization categories of sizing, shape, topology as well as its high computational performances and its efficacy for practical applications. In particular useful practical indications concerning the geometrical dimensions of the various involved structural elements can be deduced by the optimal solutions: in a truss girder the cross section of the top chord should be bigger than the one of the bottom chord as well as diagonals should be characterized by smaller cross sections with respect to the top and bottom chords in order to simultaneously optimize the weight and ensure an optimal structural behaviour.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  • Adeli, H. and Cheng, N. T. (1993). “Integrated genetic algorithm for optimization of space structures.” J. Aerosp Eng., 6(4), pp. 315–328.

    Article  Google Scholar 

  • Adeli, H. and Cheng, N. T. (1994). “Augmented Lagrangian genetic algorithm for structural optimization.” J. Aerosp Eng., 7(1), pp. 104–118.

    Article  Google Scholar 

  • Ashlock, D. (2006). Evolutionary computation for modeling and optimization. Springer, New York.

    MATH  Google Scholar 

  • Brencich, A. and Gambarotta, L. (2009). “Assessment procedure and rehabilitation of riveted railway girders: The Campasso Bridge.” Engineering Structures, 31, pp. 224–239.

    Article  Google Scholar 

  • British Standards Institution (2006). Eurocode 3: Design of Steel Structures- Part 1-5: Plated structural elements. BSI, London.

    Google Scholar 

  • Coello, C. A. and Christiansen, A. D. (2000). “Multiobjective optimization of trusses using genetic algorithms.” Computers and Structures, 75(6), pp. 647–660.

    Article  Google Scholar 

  • Dauner, H.-G., Oribasi, A., and Wery, D. (1998). “Lully viaduct, a composite bridge with steel tube truss.” Journal of Constructional Steel Research, 46(1–3), pp. 67–78.

    Article  Google Scholar 

  • Deb, K. and Gulati, S. (2001). “Design of truss-structures for minimum weight using genetic algorithms.” Finite Elements in Analysis and Design, 37(5), pp. 447–465.

    Article  MATH  Google Scholar 

  • Fiore, A., Berardi, L., and Marano, G. C. (2012). “Predicting torsional strength of RC beams by using Evolutionary Polynomial Regression.” Advances in Engineering Software, 47, pp. 178–187.

    Article  Google Scholar 

  • Fiore, A., Monaco, P., and Raffaele, D. (2012). “Viscoelastic behaviour of non-homogeneous variable-section beams with post-poned restraints.” Computers and Concrete, 9(5), pp. 375–392.

    Article  Google Scholar 

  • Fiore, A., Marano, G. C., and Monaco, P. (2013a). “Earthquake-induced lateral-torsional pounding between two equal height multi-storey buildings under multiple bidirectional ground motions.” Advances in Structural Engineering, 16(5), pp. 845–865.

    Article  Google Scholar 

  • Fiore, A., Foti, D., Monaco, P., Raffaele, D., and Uva, G. (2013b). “An approximate solution for the rheological behavior of non-homogeneous structures changing the structural system during the construction process.” Engineering Structures, 46, pp. 631–642.

    Article  Google Scholar 

  • Fiore, A., Quaranta, G., Marano, G. C., and Monti, G. (2016). “Evolutionary polynomial regression-based statistical determination of the shear capacity equation for reinforced concrete beams without stirrups.” Journal of Computing in Civil Engineering, ASCE, 30(1), 04014111, doi: 10.1061/(ASCE)CP.1943-5487.0000450.

    Article  Google Scholar 

  • Goldberg, D. (1989). Genetic algorithms in search, optimization and machine learning. Addison-Wesley, New York.

    MATH  Google Scholar 

  • Galante, M. (1996). “Genetic Algorithms as an approach to optimize real-world trusses.” International Journal for Numerical Methods in Engineering, 39(3), pp. 361–382.

    Article  MathSciNet  MATH  Google Scholar 

  • Greco, R., Avakian, J., and Marano, G. C. (2014). “A comparative study on parameter identification of fluid viscous dampers with different models.” Archive of Applied Mechanics, 84, pp. 1117–1134.

    Article  Google Scholar 

  • Guerlement, G., Targowski, R., Gutkowski, W., Zawidzka, J., and Zawidzki, J. (2001). “Discrete minimum weight design of steel structures using EC3 code.” Structural and Multidisciplinary Optimization, 22(4), pp. 322–327.

    Article  Google Scholar 

  • Hajela, P. and Lee, E. (1995). “Genetic algorithms in truss topological optimization.” International Journal of Solids and Structures, 32(22), pp. 3341–3357.

    Article  MathSciNet  MATH  Google Scholar 

  • Kaveh, A. and Kalatjari, V. (2004). “Size/geometry optimization of trusses by the force method and genetic algorithm.” ZAMM-Zeitschrift für Angewandte Mathematik und Mechanik, 84(5), pp. 347–357.

    Article  MathSciNet  MATH  Google Scholar 

  • Kaveh, A., Sheikholeslami, R., Talatahari, S., and Keshvari-Ilkhichi, M. (2014). “Chaotic swarming of particles: A new method for size optimization of truss structures.” Advances in Engineering Software, 67, pp. 136–147.

    Article  Google Scholar 

  • Kawamura, H., Ohmori, H., and Kito, N. (2002). “Truss topology optimization by a modified genetic algorithm.” Structural and Multidisciplinary Optimization, 23(6), pp. 467–473.

    Article  Google Scholar 

  • Klanšek, U. and Kravanja, S. (2006). “Cost estimation, optimization and competitiveness of different composite floor systems-Part 2: Optimization based competitiveness between the composite I beams, channel-section and hollow-section trusses.” Journal of Constructional Steel Research, 62, pp. 449–462.

    Article  Google Scholar 

  • Kripakaran, P., Gupta, A., and Baugh, J. W. (2007). “A novel optimization approach for minimum cost design of trusses.” Computers & Structures, 85(23–24), pp. 1782–1794.

    Article  Google Scholar 

  • Li, L., Huang, Z., and Liu, F. (2006). “An improved particle swarm optimizer for truss structure optimization.” Proc. International Conference on Computational Intelligence and Security, Vol. 1, pp. 924–928.

    Google Scholar 

  • Lamberti, L. (2008). “An efficient simulated annealing algorithm for design optimization of truss structures.” Computers & Structures, 86(19–20), pp. 1936–1953.

    Article  Google Scholar 

  • Li, N. and Ye, F. (2006). “Optimal design of discrete structure with directed mutation genetic algorithms.” Proc. Sixth World Congress on Intelligent Control and Automation, WCICA 2006, Vol. 1, pp. 3663–3667.

    Google Scholar 

  • Marano, G. C., Trentadue, F., and Greco, R. (2006). “Optimum design criteria for elastic structures subject to random dynamic loads.” Engineering Optimization, 38(7), pp. 853–871.

    Article  MATH  Google Scholar 

  • Marano, G. C., Trentadue, F., and Greco, R. (2007). “Stochastic optimum design criterion of added viscous dampers for buildings seismic protection.” Structural Engineering and Mechanics, 25 (1), pp. 21–37.

    Article  Google Scholar 

  • Sgobba, S., and Marano, G. C. (2010). “Optimum design of linear tuned mass dampers for structures with nonlinear behavior.” Mechanical Systems and Signal Processing, 24(6), pp. 1739–1755.

    Article  Google Scholar 

  • Marano, G. C., Greco, R., Quaranta, G., Fiore, A., Avakian, J., and Cascella, D. (2013). “Parametric identification of nonlinear devices for seismic protection using soft computing techniques.” Advanced Materials Research, 639-640(1), pp. 118–129.

    Article  Google Scholar 

  • Monti, G., Quaranta, G., and Marano, G. C. (2010). “Geneticalgorithm-based strategies for dynamic identification of nonlinear systems with noise-corrupted response.” Journal of Computing in Civil Engineering, 24(2), pp. 173–187.

    Article  Google Scholar 

  • Ohsaki, M. and Katoh, N. (2005). “Topology optimization of trusses with stress and local constraints on nodal stability and member intersection.” Structural and Multidisciplinary Optimization, 29(3), pp. 190–197.

    Article  MathSciNet  MATH  Google Scholar 

  • Quaranta, G., Fiore, A., and Marano, G. C. (2014). “Optimum design of prestressed concrete beams using constrained differential evolution algorithm.” Structural and Multidisciplinary Optimization, 49(3), pp. 441–453.

    Article  Google Scholar 

  • Queheillalt, D. T. and Wadley, H. N. G. (2005). “Cellular metal lattices with hollow trusses.” Acta Materialia, 53, pp. 303–313.

    Article  Google Scholar 

  • Xia, Q., Wang, M. Y., and Shi, T. (2013). “A method for shape and topology optimization of truss-like structure.” Structural and Multidisciplinary Optimization, 47(5), pp. 687–697.

    Article  MathSciNet  MATH  Google Scholar 

  • Schumacher, A. and Nussbaumer, A. (2006). “Experimental study on the fatigue behaviour of welded tubular K-joints for bridges.” Engineering Structures, 28, pp. 745–755.

    Article  Google Scholar 

  • Singer, L. (2005). HSS readily available in 2005. Modern Steel Construction, 3.

    Google Scholar 

  • Soh, C. K. and Yang, J. (1998). “Optimal layout of bridge trusses by genetic algorithms.” Computer-Aided Civil and Infrastructure Engineering, 13(4), pp. 247–254.

    Article  Google Scholar 

  • Storn, R. and Price, K. (1997). “Differential evolution-A simple and efficient heuristic for global optimization over continuous spaces.” Journal of Global Optimization, 11(4), pp. 359–431.

    Article  MathSciNet  MATH  Google Scholar 

  • Tsai, L. W. (2001). Mechanism design: enumeration of kinematic structures according to function. CRC Press, New York.

    Google Scholar 

  • Toðan, V. and Daloðlu, A. T. (2006). “Optimization of 3D trusses with adaptive approach in genetic algorithms.” Engineering Structures, 28, pp. 1019–1027.

    Article  Google Scholar 

  • Wang, H. and Ohmori, H. (2013). “Elasto-plastic analysis based truss optimization using Genetic Algorithm.” Engineering Structures, 50, pp. 1–12.

    Article  Google Scholar 

  • Wardenier, J. (2011). Hollow Sections in Structural Applications, 2nd edition. CIDECT Edition.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Technical University of Bari, DICAR, Via Orabona 4, 70125, Bari, Italy

    Alessandra Fiore, Giuseppe Carlo Marano & Erika Mastromarino

  2. Technical University of Bari, DICATECh, Via Orabona 4, 70125, Bari, Italy

    Rita Greco

Authors
  1. Alessandra Fiore
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Giuseppe Carlo Marano
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Rita Greco
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Erika Mastromarino
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Alessandra Fiore.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Fiore, A., Marano, G.C., Greco, R. et al. Structural optimization of hollow-section steel trusses by differential evolution algorithm. Int J Steel Struct 16, 411–423 (2016). https://doi.org/10.1007/s13296-016-6013-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s13296-016-6013-1

Keywords

Search

Navigation