Borrowing Historical Information Across All Concentration Groups with an Application of Potency Estimation in Aquatic Toxicity Assessment

Abstract

Aquatic toxicity tests assess the negative impact of toxicants on survival, reproduction, and growth of organisms. Since the tests are often repeated in the same laboratory, borrowing historical experimental outcomes that are congruent would increase the precision of potency estimation with current data. In this paper, we extend the historical borrowing from control only to historical data from all concentration levels in toxicity assessments with current data using the calibrated power prior. We assume the transportability (i.e., identical concentration–response relationship) between historical and current experimental outcomes while penalizing the historical data borrowing in each concentration group independently with a modified distribution-informed calibration process. This modified calibration process prevents the over/underfitting issues by sufficiently exploring the distribution of congruence level and allows researchers to determine the level of historical information borrowing, either conservatively or aggressively, from a data-driven perspective. The effectiveness and flexibility of our proposed method are demonstrated via simulation studies. As shown in the simulation study, in scenarios when the transportability assumption fails, the proposed method still tremendously aids in the precision of toxicity assessment. The proposed method is applied in a $\textit{Ceriodaphnia dubia}$ test.

1 Introduction

Aquatic toxicology is a field of research that investigates the adverse effect of chemicals on organisms residing in marine and freshwater ecosystems. In an aquatic toxicity test, organisms are assigned to varying concentration levels of a chemical or water effluent. Biological endpoints, e.g., survival rate or reproductive success, are monitored and recorded at the end of the study. The primary objective of such tests is to evaluate the potential risk and potency of chemicals, which serve as critical guidance for the regulation of chemical discharge in aquatic environments. Tests are often carried out in the same laboratory over years following the same standard protocol with the same set of concentrations and the same reference toxicant for regulatory purposes.

Popular statistical tools for potency estimation using toxicity test data include analysis of variance (ANOVA) and regression. Post hoc analysis is used once the ANOVA model is fitted and generates two potency estimates: the highest concentration level without significant difference compared to control (NOEC) and the lowest concentration level associated with statistically significant difference from the control group (LOEC) (Weber et al. 1989). These potency estimates are limited to the tested concentration levels in the experiment. Therefore, when the same chemicals are tested in different experiments, the potency estimates will change correspondingly. Also, the normality assumption in the ANOVA model is not suitable when responses are counts, e.g., number of offspring, or dichotomous, e.g., survival (Crump 1984).

In this regard, the concentration associated with a specified level of inhibition relative to the control is of interest to estimate, i.e., the concentration $c_p$ which leads to a $p\%$ reduction in the mean response $\mu _{c_p}$ relative to the control mean response $\mu _1$,

$$\begin{aligned} \frac{\mu _{c_p}}{\mu _1}=1-\frac{p}{100},\;\;p\in (0,100). \end{aligned}$$

Norberg-King (1993) proposed computing the inhibition concentration ($IC_p$) via a linear interpolation between tested concentrations that bracket the reduction of $p\%$ relative to the mean response in control. $IC_p$ is straightforward to compute, but it has obvious flaws. First, it only uses partial test observations (i.e., observations in control and the two relevant concentrations used for bracketing) and as a mathematical tool it ignores the uncertainty in repeated measured observations. Alternatively, a parametric version of $IC_p$ that accounts for uncertainty in observed data, relative inhibition concentration ($RI_p$), was proposed by Bailer and Oris (1997). $RI_p$ assumes that the logarithm of the mean response is a polynomial function of the concentration, and such a concentration–response relationship can be modeled by fitting a generalized linear regression.

Aquatic toxicity tests are often repeated in the same laboratory for environment monitoring. The availability of historical test data can benefit potency estimation tremendously and improve potency estimation precision. When the historical and current experiment outcomes are transportable, i.e., they share identical concentration–response relationship, it is reasonable to fit models on the pooled data (Lin et al. Lin et al. (1998)). Relaxing the transportability assumption, regularized maximum likelihood estimators with penalties on the discrepancy between subsets of model parameters in current and historical data have been fitted to the combined data (Chatterjee et al. 2016; Tang and Song 2016). However, these methods rely highly on assumptions about how the regression coefficients are associated between historical and current experiments and are an overshoot to small sample-sized data due to overparameterization issues. Also, the analysis of integrated data shifted the focus of potency estimation in the current test to the joint potency estimation of past and current data.

Bayesian framework allows the incorporation of historical information as priors and is a natural way of historical borrowing while focusing on the analysis of current data. Zhang et al. (2012b) proposed using summary statistics from historical tests to inform the analysis of current data. To avoid losing information, it is of interest to explore ways of utilizing the original historical test data, instead of the summary statistics. To serve this purpose, priors informed by historical data likelihood have been proposed and widely applied in clinical trial studies to reduce bias in estimating treatment effects. The power prior (Ibrahim and Chen 2000; Ibrahim et al. 2015) and its extensions (normalized power priors (Duan et al. 2006); calibrated power priors (Pan et al. 2017)) achieve historical information borrowing by raising the historical likelihood to a power parameter. Commensurate prior (Hobbs et al. 2011, 2012) uses a shrinkage parameter to control how much historical information would be borrowed. Mixture prior (Schmidli et al. 2014; Yang et al. 2023) balances between an informative and a vague prior about the historical parameters by imposing weights. Elastic prior (Jiang et al. 2023) discounts historical information by inflating the variance of historical parameter priors via an elastic function. A more complete methodological review can be found in Mikkola et al. (2021) and Suder et al. (2023). In randomized controlled trial (RCT) studies where at least one treatment arm is compared to the control/placebo, most existing literature restricts the historical borrowing solely from the control group (see applications in Viele et al. 2014; Han et al. 2017; Hupf et al. 2021; Shi et al. 2023). When a more sophisticated historical data structure is the target to leverage (i.e., historical dosage–response relationship in identifying the maximum tolerated dose of phase I clinical trials), using aforementioned priors needs more precise modifications and careful designs (Zhang et al. 2023). Among these methods, power prior is particularly favored in practical use due to its intuitive nature and less impact on the model complexity when dealing with the concentration/dosage–response relationship involving covariates or multiple historical datasets. In aquatic toxicology, Zhang et al. (2023) proposed using a calibrated power prior (CPP) to borrow information solely from the control group.

In the present study, we propose incorporating historical data across all concentration levels using CPP for potency estimation in current toxicity tests under the Bayesian generalized linear regression framework. We assume the transportability between historical and current tests while penalizing the historical information via power parameters. This approach differs from Zhang et al. (2023) as we aim to leverage the likelihood of historical concentration–response relationships rather than historical borrowing solely from the control group. Our approach considers historical borrowing from a dose-response structure and hence can be easily generalized to dosage-finding problems in phase I clinical trial studies. Without correctly adjusting between-tests variability, historical information from other concentration groups may not be completely transportable. To mitigate such risk, we developed a modified distribution-informed algorithm to “discount” the historical data in each concentration group independently. Our proposed method evaluates the distribution of congruence measures when data are transportable and allows researchers to calibrate the degree of historical information borrowing, either conservatively or aggressively, from a data-driven perspective. Furthermore, we investigate the case when the transportability assumption fails while the proposed method still improves the precision of $RI_p$ estimations from theoretical and simulation points of view. We also compared the performance of different congruence measures via simulation studies using the proposed approach. The layout of the paper is as follows: in section 2, we introduce the formulation of the modified distribution-informed calibration process under the Bayesian Poisson regression framework; in section 3, we conduct simulation studies to compare the performance of the proposed method to the existing approaches by incorporating either congruent or incongruent historical data; we include the real data analysis using $\textit{Ceriodaphnia dubia}$ reproduction test data; section 5 summarizes our findings and future work.

2 Methodology

2.1 Data Structure and Model

Let $D_c=({\textbf{Y}^c_{1}}^\top ,\ldots ,{\textbf{Y}^c_{K}}^\top )^\top$ denote data from the current experiment. In the context of reproductive aquatic toxicity test, the current experiment contains K distinctive toxicant concentration levels, $c_1,\ldots ,c_K$, to investigate how the toxic emission would affect the reproduction of organisms. $c_1=0$ stands for the control group with zero exposure. $\textbf{Y}^c_k = (y^c_{k1},\ldots ,y^c_{kn})^\top$ denotes a vector of responses from n organisms assigned to the $k^{th}$ concentration level (balanced design assumed). $y^c_{ki}$ is the number of offspring produced by the $i^{th}$ organism in the kth concentration, $i=1,\ldots ,n$ and $k=1,\ldots ,K$. $D_h=({\textbf{Y}^h_{1}}^\top ,\ldots ,{\textbf{Y}^h_{K}}^\top )^\top$ where $\textbf{Y}^h_k = (y^h_{k1},\ldots ,y^h_{kn})^\top$ denotes the data collected in a historical experiment. In this paper, we focus on borrowing information from a single historical test. It is also possible to extend the current methodology to involve multiple external historical studies. Reproduction outcomes in a current test can be modeled via Poisson regression,

$$\begin{aligned} \begin{aligned} y^c_{ki}\mid \mu _k&\sim \text {Poisson}(\mu _k) \\ \log (\mu _k)&= \beta _0 + \beta _1 c_k + \beta _2 c_k^2, \;\; \forall k,i. \end{aligned} \end{aligned}$$

(1)

A second-order polynomial term is flexible enough to model the concentration–response relationship (Bailer and Oris 1997; Zhang et al. 2012a). Note that $\mu _1=e^{\beta _0}$ stands for the control group mean. Let $\varvec{\theta }=(\beta _0,\beta _1,\beta _2)^\top$ denote a vector of the regression coefficient parameters. The posterior distribution of a starting Bayesian model is formulated as

$$\begin{aligned} p(\varvec{\theta }\mid D_c)\propto L(D_c\mid \varvec{\theta })\pi (\varvec{\theta }) \end{aligned}$$

where $L(D_c\mid \varvec{\theta })=\prod _{k=1}^{K} L(\textbf{Y}^c_{k}\mid \varvec{\theta })$ is the likelihood of the current data and $L(\textbf{Y}^c_{k}\mid \varvec{\theta })$ represents the joint distribution of data in the $k^{th}$ concentration group. $\pi (\varvec{\theta })$ is the prior distribution of the regression coefficients. An informative prior on $\beta _0$ can be elicited via summary statistics of historical control group responses and/or the quality control criterion enforced in such tests (mean number of young in control group needs to be at least 15).

2.2 Power Prior

To implement historical borrowing, Ibrahim and Chen (2000) proposed the power prior,

$$\begin{aligned} \begin{aligned} \pi (\varvec{\theta }\mid D_h,\alpha )&\propto L(D_h\mid \varvec{\theta })^{\alpha }\pi (\varvec{\theta }) \end{aligned} \end{aligned}$$

where $\alpha$ is the power parameter for the historical data, ranging from 0 to 1. The ground idea of power prior is straightforward. It raises the historical likelihood function to a power $\alpha$ which reflects the degree of information that we would like to borrow from the historical data. If the underlying biological process of generating historical and current experimental outcomes are identical, then $D_c$ and $D_h$ follow the same probabilistic distribution. The more congruent $D_c$ and $D_h$ are, the higher the power parameter $\alpha$ is expected, and we intend to borrow more information from historical data. Otherwise, the likelihood of $D_h$ needs to be down-weighed in the Markov Chain Monte Carlo (MCMC) sampling process. $\alpha$ can be treated as a random variable with an initial prior (Chen et al. 2000; Ibrahim and Chen 2000) but it violates the likelihood principle and is computationally intractable as model complexity increases (see more details in Duan et al. (2006), Neuenschwander et al. (2009), Ye et al. (2022)). Considering these challenges, we treat $\alpha$ as a known parameter. In the context of toxicology when toxicity data from multiple concentration groups are available, the posterior distribution of an updated Bayesian model with power prior is given by

$$\begin{aligned} \begin{aligned} p(\varvec{\theta }\mid D_c,\alpha _{1},\dots ,\alpha _K)&\propto L(D_c\mid \varvec{\theta })\pi (\varvec{\theta }\mid D_h,\alpha _{1},\dots ,\alpha _K) \\&\propto \prod _{k=1}^{K} L(\textbf{Y}^c_{k}\mid \varvec{\theta })\prod _{k=1}^{K} L(\textbf{Y}^h_{k}\mid \varvec{\theta })^{\alpha _k}\pi (\varvec{\theta }), \end{aligned} \end{aligned}$$

(2)

where $\alpha _k$ is the power parameter for $k^{th}$ concentration group. Note that we assume transportability of $\varvec{\theta }$ between current and historical data but the likelihood of the latter one is discounted by $\alpha _k$. Zhang et al. (2022) suggests pre-selecting a series of $\alpha _k$’s to tailor the sample size determination based on different potential levels of congruence between $\textbf{Y}^c_k$ and $\textbf{Y}^h_k$. When analysis of the current toxicity test is the objective instead of the sample size determination of a future experiment, pre-determining the power parameters based on the estimated congruence level between $Y_k^h$ and $Y_k^c$ is more appealing because it allows the determination of $\alpha _k$ to conform more closely to how $Y_k^h$ and $Y_k^c$ distribute themself.

2.3 Calibrated Power Prior

Calibrated power prior (CPP) proposed by Pan et al. (2017) calibrates the power parameter $\alpha _k$ for $k^{th}$ concentration group by quantifying the similarity between historical data $\textbf{Y}^h_k$ and current data $\textbf{Y}^c_k$ via a congruence measure. Let $S_k \in (0,\infty )$ be the level of congruence between $\textbf{Y}^h_k$ and $\textbf{Y}^c_k$. CPP assumes the power parameter $\alpha _k$ as a two-parameter sigmoid function of $S_k$,

$$\begin{aligned} \alpha _k = \frac{1}{1+\exp (a_k+b_k\log (S_k))}. \end{aligned}$$

$a_k$ and $b_k$ are the hyperparameters for $k^{th}$ concentration groups. $b_k>0$ is explicitly defined to ensure a strict monotone decreasing relationship between $\alpha _k$ and the value of $S_k$. Pan et al. (2017) applied CPP in two-arm randomized clinical trials with normal and binary endpoints to incorporate historical controls. Zhang et al. (2023) applied CPP to incorporate historical controls in toxicity assessment when a Poisson regression is fitted. In this paper, we modified the implementation of CPP and extend this to incorporate historical information from all concentration groups.

2.3.1 Congruence Measure

Congruence measure is a distance metric between historical and current data in the $k^{th}$ concentration group. The “distance” decreases as $\textbf{Y}^h_k$ and $\textbf{Y}^c_k$ are becoming more congruent while the similarity measure alters the opposite.

As proposed in Zhang et al. (2023), we consider 3 congruence measures: (1) Kolmogorov–Smirnov ($\textit{KS}$) test statistic, (2) absolute difference between sample mean ($\textit{ABSmean}$), and (3) sum of absolute difference between ordered samples ($\textit{Sumdiff}$). $\textit{KS}$ statistic is a powerful nonparametric statistical tool that allows researchers to investigate if two data follow the same underlying distribution using the empirical cumulative distribution function. If both groups of data are generated from the Poisson distribution, $\textit{ABSmean}$ can serve as an estimator of the difference in the “mean” parameter which fully specifies the Poisson distribution they follow. $\textit{Sumdiff}$ emphasizes accounting for the individual data difference.

2.3.2 Determination of $\alpha _k$

Pan et al. (2017) proposed using simulation to calibrate $\alpha _k$ values. Two key components are needed: $\gamma ^C_k$, the maximum difference in mean when $\textbf{Y}^c_k$ and $\textbf{Y}^h_k$ are congruent; and $\gamma ^{IC}_k$, the minimum mean difference when they are incongruent. Pan et al. (2017) proposed using subject knowledge input to decide these values, e.g., 0.8$-$1.25 rule, assuming two data sets are congruent if the difference between their log-transformed means is between $(\log (0.8)$ and $\log (1.25))$. This rule of thumb is well established in the context of clinical trials where the biosimilar criterion is rigorously defined. There are no such rule of thumb in aquatic toxicity assessment. Hence, Zhang et al. (2023) proposed a distribution-informed tool instead of using the rule of thumb. In the present study, we extend this approach to identify $\gamma ^C_k$ and $\gamma ^{IC}_k$ for every concentration group (Step 1–3 of the algorithm). The calibration process proposed by Pan et al. (2017) simulates data, both congruent and incongruent compared to the historical one, to study the distributional difference in the estimated congruence levels using the median. Here, we modified this approach to allow more statistical perspectives of the congruence estimates to be incorporated, e.g., variance, percentiles, etc. The complete steps are given below:

• Step 1: Estimate $\mu _k$ by the sample average $\bar{Y}^h_k = \sum _{i=1}^ny^h_{ki}/n$ for $k^{th}$ concentration group.

• Step 2: The additive property of Poisson distribution leads to $X=\sum _{i=1}^ny^h_{ki} \sim \text {Poisson}(n\bar{Y}^h_k)$ such that the sample mean statistics has the same distribution as X/n. Then, derive the distributional mean $\bar{Y}^s$, $5^{th}$ percentiles $\bar{Y}^s_{5}$, $25^{th}$ percentiles $\bar{Y}^s_{25}$, $75^{th}$ percentiles $\bar{Y}^s_{75}$, $95^{th}$ percentiles $\bar{Y}^s_{95}$, and the interquartile range IQR from X/n.

• Step 3: Find $\gamma ^C_k = \max (d_1,d_2)$ where $d_1=|\bar{Y}^s- \bar{Y}^s_{5}|$ and $d_2=|\bar{Y}^s- \bar{Y}^s_{95}|$; Find $\gamma ^{IC}_k = \min (d_3,d_4)$ where $d_3=|\bar{Y}^s-(\bar{Y}^s_{25}-1.5\times IQR)|$ and $d_4=|\bar{Y}^s-(\bar{Y}^s_{75}+1.5\times IQR)|$.

• Step 4: Simulate R data sets with sample size n from Poisson($\bar{Y}^h_k-\gamma ^C_k$) and R data sets with sample size n from Poisson($\bar{Y}^h_k+\gamma ^C_k$). Then, estimate the congruence level $S_k$ between $\textbf{Y}^h_k$ and each of 2R simulated datasets. Find the statistics $T_1,T_2,\ldots ,T_m$ of 2R estimated $S_k$ and denote them by $S^*_1(\gamma ^C_k),S^*_2(\gamma ^C_k),\ldots ,S^*_m(\gamma ^C_k)$. $T_j,j=1,\ldots ,m$ can be mean, variance, confidence bound, etc. The purpose of this step is to sufficiently evaluate the distribution of congruence level $S_k$ when two data sets are genuinely congruent by various perspectives of such distribution using different choices of T statistics.

• Step 5: Repeat Step 4 by replacing $\gamma ^C_k$ with $\gamma ^{IC}_k$. Find the statistics $T_1,T_2,\ldots ,T_m$ of another 2R estimated $S_k$ and denote them by $S^*_1(\gamma ^{IC}_k),S^*_2(\gamma ^{IC}_k),\ldots ,S^*_m(\gamma ^{IC}_k)$.

• Step 6: Derive $a_{k,j}$ and $b_{k,j}$ by solving the equation

  $$\begin{aligned} {\left\{ \begin{array}{ll} \alpha ^{C} = \frac{1}{1+\exp (a_{k,j}+b_{k,j}\log (S^*_j(\gamma ^C_k)))}\\ \alpha ^{IC} = \frac{1}{1+\exp (a_{k,j}+b_{k,j}\log (S^*_j(\gamma ^{IC}_k)))} \end{array}\right. } \end{aligned}$$

  across $j=1,\ldots ,m$ where $\alpha ^{C}$ is a constant close to 1 (i.e., 0.99) and $\alpha ^{IC}$ is a constant close to 0 (i.e., 0.01). In practice, given ${\textbf{Y}^h_{k}}^\top$ and ${\textbf{Y}^c_{k}}^\top$, we end up with a set of estimated power parameters $\alpha _{k,1},\alpha _{k,2},\ldots ,\alpha _{k,m}$ using m heterogeneous statistics. Then, $\alpha _k$ is calibrated by

  $$\begin{aligned} \alpha _k = g(\alpha _{k,1},\alpha _{k,2},\ldots ,\alpha _{k,m}) \end{aligned}$$

  where $g(\alpha _{k,1},\alpha _{k,2},\ldots ,\alpha _{k,m})$ could be the arithmetic mean $\sum _{j=1}^{m}\alpha _{k,j}/m$ or the geometric mean $\root m \of {\prod _{j=1}^{m}\alpha _{k,j}}$. Note that geometric mean is much smaller than arithmetic mean when $\alpha _{k,1},\alpha _{k,2},\ldots ,\alpha _{k,m}$ contains extremely small values.

• Step 7: Repeat Step 1–6 across all K concentration groups independently.

The ground logic of our proposal is concise and easy to implement. For each concentration group of historical data, we firstly identify its probabilistic distribution and summarize the information of the distributional tail using $d_{1},\ldots ,d_4$ in Step 3. Then, we could identify $\gamma ^C_k$ by the absolute difference between $\bar{Y^s}$ and the most extreme distributional quantile $\max (\bar{Y}^s_{5},\bar{Y}^s_{95})$, and evaluate $\gamma ^{IC}_k$ by the absolute difference between $\bar{Y^s}$ and the minimum threshold of outlier detection $\min (\bar{Y}^s_{25}-1.5\times IQR,\bar{Y}^s_{75}+1.5\times IQR)$. Pan et al. (2017) proposed using median to quantify the distributional discrepancy between congruence estimates $S_k$’s in Steps 4–6. Since $\textit{KS}$ statistic only takes discrete values on [0.0, 1.0], $S^*(\gamma ^C_k)$ and $S^*(\gamma ^{IC}_k)$ are oftentimes identical which fails the calibration process. Zhang et al. (2023) used the average between mean and median to alleviate this issue when using $\textit{KS}$ statistic as the congruence measure. This idea inspired us to calibrate $\alpha _k$ by accounting for heterogeneous distributional characteristics of $S_k$’s. Simply, instead of only using median, we choose m statistics to summarize how $S_k$ distributes itself and hence deriving m different power parameters. Then, $\alpha _k$ could be calibrated by the average of $\alpha _{k,1},\ldots ,\alpha _{k,m}$. In this study, we propose using arithmetic mean and geometric mean to calibrate $\alpha _k$. Their pros and cons are extensively studied in the simulation study.

The proposed calibration approach could ensure a close-to-1 power parameter $\alpha _k$ when the difference in the sample averages between two data is at most $\gamma ^C_k$ and a close-to-0 $\alpha _k$ when the difference is at least $\gamma ^{IC}_k$ regardless of the congruence measure we pick. With more statistics being involved (large m), the calibration process turns more conservative due to the increasing possibility of detecting certain degrees of incongruence. Since $\alpha _k$ is calibrated independently using raw data for each concentration group, the congruence in population discrepancy will not be overlooked. Additionally, it is crucial to ensure $b_{k,j}>0$ to make the selection of $T_j$ valid. In aquatic toxicology studies, we are particularly interested in the potency estimation of the relative inhibition concentration ($RI_p$). $RI_p$ (Bailer and Oris 1997) represents a level of concentration where

$$\begin{aligned} \frac{\mu _{RI_p}}{\mu _{1}}=\frac{e^{\beta _0+\beta _1RI_p+\beta _2RI_p^2}}{e^{\beta _0}} = e^{\beta _1RI_p+\beta _2RI_p^2} = 1-\frac{p}{100} \end{aligned}$$

$p\in (0,100)$ is the proportion of inhibition ($\times 100$). $RI_p$ can be interpreted by the toxicant concentration level that leads to a $p\%$ reduction in response (i.e., number of youth of certain organisms) relative to the control group. As observed, $RI_p$ is a function of $\varvec{\theta }$ and hence the estimates of $RI_p$ could be determined simultaneously by the posterior sample at each MCMC iteration. In the present study, we are particularly interested in the estimation of $RI_{25}$ ($RI_{50}$), which represents the concentration with $25\%$ ($50\%$) reduction relative to control.

3 Simulation Studies

In this section, we conduct simulation studies to compare the precision of $RI_{25}$ and $RI_{50}$ estimation when integrating historical information, either congruent or incongruent, from $K=6$ concentration groups, using the modified distribution-informed calibration process ($A_3,A_4$) and 2 competitor methods ($A_1,A_2$). Concentration–response relationships of three different chemicals are assumed to simulate current experiments with $c_k \in \{0,0.25,0.5,1,2,4\%\}, k=1,\ldots ,6$ as shown in Fig. 1. A thorough description of methods $A_1-A_4$ can be found in Table 1.

Fig. 1

3 different response–concentration relationships: case1 (solid, $\log (\mu _k) = \log (32.2) + 0.6 c_k - c_k^2$), case2 (dotted, $\log (\mu _k) = \log (32.2) + 0.05 c_k - 0.3c_k^2$), and case3 (dashed, $\log (\mu _k) = \log (32.2) -0.8 c_k - c_k^2$). The response is the expected number of living youth in the context of aquatic toxicology. The x-axis represents the toxicant concentration level. Case 1 mimics the circumstances when its competitor is more sensitive to the toxicant so that the population of such particular organism would increase at first but decrease later as the toxicant level goes up. Case 2 simulates a situation where the organism is regularly tolerant to the toxicant, while Case 3 shows the organism is sensitive to such toxicant

Table 1 Description of median-based method $A_1$, hybrid mean-median method $A_2$, proposed arithmetic mean method $A_3$, and proposed geometric mean method $A_4$ for calibrating $\alpha _k$ for $k^{th}$ concentration group

Table 2 Case 1: Average $\gamma ^C_{k}$ and $\gamma ^{IC}_k$ across all K concentration groups using 100 simulated $D_h$. The log mean difference is $\log (\bar{\textbf{Y}}^h_k+\gamma ^{C}_k)-\log (\bar{\textbf{Y}}^h_k+\gamma ^{IC}_k)$

To explore the impact of variability among historical experiments on the identification of $\gamma ^C_k$ and $\gamma ^{IC}_k$, we simulate 100 balanced historical experiments ($n=10$) using the first concentration–response relationship (Case 1 in Fig. 1) and calculate the average of $\gamma ^{C}_k$ and $\gamma ^{IC}_k$ as presented in Table 2. Compared to the rule of thumb where data are congruent if the mean difference between $\log (\bar{\textbf{Y}}^h_k+\gamma ^{C}_k)$ and $\log (\bar{\textbf{Y}}^h_k+\gamma ^{IC}_k)$ are within [$-$0.223,0.223], a smaller difference in the log mean elicited by the distribution-informed method guarantees historical information would not be over-borrowed across all concentration groups and hence avoid overfitting issues. Since $\mu _6$ is almost 0, nearly all the simulated responses are zero and therefore we let $\alpha _6=0$ due to the minimal response variability. Figure 2. compares the distribution between $S_k$’s in Step 4 and Step 5 with one historical experiment. They can be separated efficiently with median, mean, variance, or other sensible statistics. The proposed $A_3,A_4$ can jointly capture these meaningful distributional features to calibrate $\alpha _k$. The output for Case 2 and Case 3 is reported in the supplementary materials.

Fig. 2

Case 1: Comparison between $S_{1k}$ and $S_{2k}$ for 3 recommended congruence measures for the first 5 concentration groups $k=1,\ldots ,5$ for one $D_h$, where $S_{1k}$ denote a collection of 2R estimated congruence level of $S_k$ in Step 4 and $S_{2k}$ denote the ones in Step 5

The true regression parameters used to simulate the historical and current data when they are congruent and incongruent are shown in Table 3. We let $n=10$ and set $R=2500$. We generate 100 historical data sets $D_h$ and 400 current data sets $D_c$. Then, for each specific current data, 100 historical data are sequentially incorporated via the calibrated power prior using Bayesian Poisson regression to estimate $RI_{25}$ and $RI_{50}$. We adopt weakly informative priors:

$$\begin{aligned} \beta _0\sim N(3.09,0.5) \;\; \beta _1\sim N(0,10) \;\; \beta _2\sim N(0,10). \end{aligned}$$

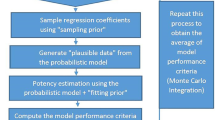
Consequently, this yields $100\times 400$ $RI_p$ estimates. We configure the Markov chain Monte Carlo (MCMC) simulations to run for 6500 iterations, including a 1500 iteration of burn-in, utilizing the rstan package (Stan Development Team 2024) in R. Additionally, we explore alternative potency estimation methods: one using solely current data $D_c$ (no historical borrowing), and the other pooling $D_c$ and $D_h$ altogether without CPP for comparative analysis. To evaluate their performances, we compute the average point estimation bias (Bias), average posterior standard deviation (SD), average coverage probability (CP), and average width (CI width) of the $95\%$ credible interval using $100\times 400$ $RI_p$ estimates. To investigate the information borrowing pattern, we derive the likelihood of completely integrating $D_h$ by the percentage of $\alpha _k<\alpha ^{C}$ across $100\times 400$ power parameter estimates in $k^{th}$ concentration group; and the probability of entirely discarding $D_h$ by the percentage of $\alpha _k>\alpha ^{IC}$.

Table 3 Regression setting of simulation study when $D_h$ and $D_c$ are assumed to be either congruent or incongruent

3.1 Congruence Case

Table 4 compares the efficacy of different historical information borrowing strategies in estimating $RI_{25}$ and $RI_{50}$ under congruence and incongruence scenario 1. Regardless of congruence measures, incorporating historical information by CPP would yield a consistently reduced average point estimation bias compared to solely relying on the current data. This is because CPP manages to incorporate decent amounts of congruent historical information. Our modified method $A_3$ outperforms the competitor method $A_1$ and $A_2$ by a lower average bias, higher coverage probability, and comparably narrow credible interval width. Jointly pooling $D_h$ and $D_c$ results in the most accurate and precise estimation since it fully leverages the correct historical information. However, it is important to highlight that the proposed $A_3$ could achieve similar precision as well with $\textit{Sumdiff}$. This informs us that in practical applications, using partial information from $D_h$ could yield results as accurate as completely pooling, even when $D_h$ and $D_c$ are congruent. However, the concept of “partial”—whether it pertains to the inclusion of historical observations or a partial discounting of historical likelihood—requires careful consideration and analysis. Overall, using $\textit{Sumdiff}$ is more accurate in potency estimation than both $\textit{KS}$ statistic and $\textit{ABSmean}$.

Table 4 Congruence/incongruence Scenario 1: average point estimation bias (Bias), average posterior standard deviation (SD), average coverage probability (CP), and average width of $95\%$ credible interval (CI.width) considering 3 different congruence measures across $100\times 400$ estimated $RI_{25}$ and $RI_{50}$

Based on Table 5, $\textit{ABSmean}$ and $\textit{Sumdiff}$ emerge as more suitable congruence measures than $\textit{KS}$ statistics because they yield higher average power parameters. Since the summation of the percentage of $\alpha _k<\alpha ^{C}$ and $\alpha _k>\alpha ^{IC}$ with $\textit{KS}$ statistics is higher than that of $\textit{ABSmean}$ and $\textit{Sumdiff}$, it implies $\textit{KS}$ statistics either completely borrow or discard historical information. This “only the best or go without” borrowing pattern will lead to a portion of congruent information getting excluded entirely when $D_h$ and $D_c$ are congruent. Similarly, when data are incongruent, parts of incongruent information would be completely kept in the analysis (results are shown in the supplementary material), which explains why $\textit{KS}$ statistics consistently underperform in the accuracy and precision of estimating $RI_p$. It is worth noting that the proposed $A_3$ does not have this undesired feature using $\textit{KS}$ statistic as the congruence measure. Also, the behavior of less frequently dropping the entire $D_h$ using $A_3$ (0$-$3.2% rate of discarding using $\textit{Sumdiff}$ for all k) ensures the integration of congruent information. The other proposed method $A_4$ exhibits a relatively higher complete discard rate (6.3$-$69.4% using $\textit{Sumdiff}$ for all k) than $A_3$. This is due to the sensitivity of geometric mean to small values in $\alpha _{k,1},\alpha _{k,2},\ldots ,\alpha _{k,m}$. If any of the m statistics $T_1,T_2,\ldots ,T_m$ captures a significant degree of incongruence, $\alpha _k$ will be conservatively calibrated and lead to a lower estimation of the power parameter. Therefore, $A_4$ could be viewed as a more cautious approach to $A_3$ when borrowing historical information. With $\textit{Sumdiff}$ as the congruence measure, $A_3$ is a more risk-tolerant method with higher average power parameters compared to $A_4$. Simulation results for congruence scenarios 2, 3 are shown in the supplementary materials.

Table 5 Congruence Scenario 1: Average power parameter (PP), proportion with PP being greater than 0.90, probability of completely borrowing historical information (% of $\alpha _k<\alpha ^{C}$), and probability of completely discarding historical information (% of $\alpha _k>\alpha ^{IC}$) for $k=1,\ldots ,5$ considering different 3 congruence measures for $100\times 400$ simulation outcomes

3.2 Incongruence Case

For incongruence scenario 1 (shown in Table 4), $D_h$ and $D_c$ are simulated with different $\beta _0$, but the same $\beta _1$ and $\beta _2$, i.e., they are not transportable but share the same $RI_p$. With $A_4$, we observe a comparable performance as the strategy of solely modeling current data, particularly when using $\textit{KS}$ statistics and $\textit{ABSmean}$ as congruence measures. This is because the conservative nature of $A_4$ leads to relatively lower power parameters. Note that directly pooling “incorrect” $D_h$ with $D_c$ helps the $RI_p$ estimation in this case, since the true $RI_p$’s are the same for $D_h$ and $D_c$, even though they are incongruent. Further, as shown in the supplementary material, that the theoretical variance of the ${RI_{p}}$ estimator decreases as $\beta _0$ in $D_h$ increases. An elevated $\beta _0$ indicates more optimal culturing conditions. A reduced variance in $RI_{p}$ estimator signifies a more precise estimation. This finding suggests that when historical data are available and the incongruence only comes from the different $\beta _0$, combining $D_h$ and $D_c$ is preferred. Another key insight is when the culturing conditions of current experiments are sufficiently favorable, the necessity to borrow historical information decreases, as the data quality itself would aid in the estimation precision. The supplementary material contains the borrowing pattern for incongruence scenario 1. It also includes the simulation results for incongruence scenarios 2, 3 where $D_h$ and $D_c$ are not transportable and having incongruent $RI_p$. For such scenarios, the simulations demonstrate that CPP with the proposed $A_3$ or $A_4$ can extract congruent information from a particular concentration group of $D_h$ and result in enhanced precision even when the underlying concentration–response relationship used for data generation process between $D_h$ and $D_c$ are totally different.

4 Real Data Analysis

The Ceriodaphnia dubia test studies the decline in reproduction after exposing the organisms to varying effluent concentrations. We treat the most recent test conducted by the laboratory MNEPAD in April 1992 as the current data, and the one from January 1992 as the historical dataset. Both tests include 6 concentration levels $0 (\text {control}),0.25,0.5,1,2,4\%$ with 10 replicates each. Figure 3 shows high variability at level $0,0.25,0.5\%$. This is a sign of sub-optimal culturing that could be attributed to a short acclimation period or individual’s heterogeneous tolerance to the toxicant. In this regard, we intend to borrow partial information from historical tests while still accounting for the presence of outliers in the current toxicity test.

Fig. 3

Concentration level (%) versus the number of living youth between historical (cross) and current (triangle) experiment data

We compared using solely current data $D_c$, the median-based ($A_1$), hybrid mean-median method $A_2$ to the proposed approach $A_3,A_4$ in estimating $RI_{25}$ and $RI_{50}$ with 3 aforementioned congruence measures. Let the number of MCMC iterations be 3500 with 1500 burn-ins. We adopt the same prior in the Simulation section with $\beta _0\sim N(3.09,0.5),\beta _1\sim N(0,10), \beta _2\sim N(0,10)$. We chose $T_1,\ldots ,T_4$ to be the mean, median, variance, and empirical confidence bound. Since the sample mean at $c_6=4\%$ is close to 0 with the smallest variability, we define $\alpha _6=0$. The resulting posterior summary information with estimated power parameters for each concentration is given in Table 6. As Table 6 indicates, relying solely on $D_c$ without CPP leads to the highest posterior standard deviation of $RI_{25}$ and $RI_{50}$. $A_1,A_2$ using $\textit{KS}$ statistic is not suitable since they completely incorporate the historical information at $0,0.25\%$ despite the presence of outliers in current data. Our proposed distribution-informed calibration process, however, captured the desired amount of information either through aggressive ($A_3$) or conservative ($A_4$) risk flavor. We observe the resulting power parameters by $A_3$ are consistently greater than that of $A_4$ across all concentrations, regardless of congruence measures. This finding aligns with the simulation study. In this particular analysis, since the within-test variabilities for each concentration group are not uniformly the same between historical and current test data, determining the amount of information borrowing independently avoids simultaneous exclusions of congruent information. Also, using $\textit{Sumdiff}$ as the congruence measure is advantageous due to lower posterior standard deviation and the fact that the incongruence stems from individual data disparities. In addition, the concern about the low culturing condition in the current experiment motivates us to use a less conservative way of calibrating the power parameter to ensure a robust and data-driven adjustment to potential biases.

Table 6 Posterior summary statistics including posterior mean (pm), posterior standard deviation (SD), 95% highest posterior density interval (HPD) using only current data $D_c$, proposed methods ($A_3,A_4$), and competitors ($A_1,A_2$) via calibrated power parameter with 3 recommended congruence methods ($\textit{KS}$, $\textit{ABSmean}$, $\textit{Sumdiff}$). Estimated power parameters for $k^{th},k=1,\ldots ,6,$ concentration group are listed

5 Conclusion

In this article, we explore the integration of historical information from every concentration level under the Bayesian generalized linear model via the calibrated power prior. The extensive simulation study reveals that this seemingly “riskier” move can actually yield a more precise $RI_p$ estimation using the modified distribution-informed calibration process for CPP. We show in the supplementary material that when $D_h$ and $D_c$ have different underlying concentration–response relationships, there is still a significant amount of congruent information embedded in the raw data at each concentration group worth leveraging. Our proposed approach is capable of capturing such information and hence outperforming the competitor methods in precision. In the context of aquatic toxicology, $\textit{KS}$ statistic as a congruence measure is less favored since it tends to either completely borrow or discard the entire historical information, leading to information abuse or loss. $\textit{Sumdiff}$ is more sensitive to outliers compared to $\textit{KS}$ statistic. In particular, we recommend $\textit{Sumdiff}$ + $A_3$ in calibrating the power parameter because of a consistently more accurate estimation in $RI_p$ than other possible combinations regardless of the congruence level between $D_h$ and $D_c$. The proposed $A_4$ is more conservative in handling historical variability than $A_3$, the most risk-tolerant one, due to the geometric mean’s sensitivity to small values. Both of the proposed methods, if not superior, can yield comparative accuracy compared to the existing approaches. For the concentration level resulting in nearly zero reproductive counts (e.g., $c_k=4\%$ in Fig. 3), calibrating the power parameter becomes unnecessary due to minimal response variability and we suggest setting the power parameter to zero. When overdispersion is present, assuming the reproduction outcomes follow negative-binomial distribution instead of Poisson is recommended, and the proposed calibration method can be easily adapted correspondingly (see supplementary materials for complete steps of algorithms).

Surprisingly, the simulation study shows that pooling $D_h$ and $D_c$ is beneficial in potency estimation when they have strong evidence that supports the transportability in covariate coefficients between $D_h$ and $D_c$ but not the intercept $\beta _0$. We noticed that an increasing $\beta _0$ always results in a reduced estimation bias for $RI_p$. When the response is survival rate or reproduction count in aquatic toxicology tests, an increasing $\beta _0$ is indicative of a more optimal baseline culturing environment. This result suggests that when the control group has high reproduction outcomes, the benefits of borrowing historical information decrease. In addition to the total number of offspring is recorded at the end of experiments, reproductive counts at the daily resolution are available. Modeling daily reproduction and survival responses as functions of time with historical borrowing is also of interest. Borrowing historical information from tests conducted in different laboratories when concentrations are different also requires more flexible techniques to quantify the degree of historical borrowing instead of a simple group-to-group comparison. We leave this for future investigation.