1 Introduction

Zika virus (ZIKV) is an emerging mosquito-borne flavivirus [34]. ZIKV is transmitted to humans through the bites of infected Aedes mosquitoes, including A. aegypti and A. albopictus [2]. Recent studies show that ZIKV can be transmitted between humans via sexual contact or by blood transfusions [32].

ZIKV infection is predominantly a mild or asymptomatic dengue-like disease [29]. ZIKV infection can lead to Guillain–Barré Syndrome, microcephaly and other severe birth defects [37].

There is currently no vaccine, specific treatment, or fast diagnostic test is available to treat, prevent, or diagnose ZIKV infection [33]. ZIKV mitigation is closely associated with the reduction in the presence and abundance of A. aegypti [9]. On the individual level, the best way to control the spread of ZIKV is to reduce sexual transmissions and avoid mosquito bites [62]. This can be achieved by avoiding unprotected sex [14, 59], using mosquito repellents [36], bed nets [57], window screens [42], and air conditioning [62]. The climate changes may be behind the recent rise of ZIKV and other Aedes-borne infections [64,65,66].

ZIKV received considerable attention from mathematical modelers; see for example [2, 3, 11, 17, 26, 43, 45, 47, 52, 61, 71, 73, 74].

Starting with [10], game theory has been increasingly applied to help with the modeling of the prevention of diseases such as African trypanosomiases [24], chikungunya [40], Ebola [13], Hepatitis C [67], meningitis [50], monkeypox [8], toxoplasmosis [70] and others; see [18, 75] for recent reviews.

In this paper, we build on the work of [12, 72]. We show their compartmental ODE model in Sect. 2. The main contribution of this paper is the use game theory to model ZIKV prevention by a voluntary use of insect repellents. The game-theoretical framework is introduced in Sect. 2.3 where we define a population game played by susceptible individuals who repeatedly decide whether to use DEET or not. Our main results, including the game theory analysis, are presented in Sect. 4. We give exact formulas for the minimal DEET coverage needed for ZIKV elimination. We also give numerical values for the Nash equilibria, i.e., the solution of the game and the optimal voluntary use of DEET to prevent the spread of ZIKV through vector bites. We show that the Nash equilibrium is high enough and thus the voluntary use of DEET can significantly contribute to ZIKV elimination.

2 Model

2.1 Compartmental Model

We adapt an SIR-SI compartmental ODE model of ZIKV dynamics originally introduced in [12] and extended in [72].

The total human population at time t, \(N_h(t)\), is divided into susceptible, \(S_h(t)\), infectious, \(I_h(t)\), and recovered, \(R_h(t)\). The mosquito population, \(N_v(t)\), is divided into susceptible, \(S_v(t)\), and infectious, \(I_v(t)\).

The basic model, without any control measures, is as follows. For simplicity, we assume no vertical transmission and thus all humans are recruited, at rate \(\varLambda _h\) as susceptible. The susceptible individuals can be infected in one of the following ways: (1) directly through contact with an infected individual which happens at rate \(\beta _{hh}\), or (2) through a bite by an infected mosquito, the effective mosquito-to-human transmission rate will be denoted \(\beta _{vh}\). The infectious individuals naturally recover at a rate of \(\gamma \). Recovered individuals are assumed to have acquired a permanent immunity. We assume no disease-induced mortality and denote the natural death rate by \(\mu _h\).

The mosquito recruitment rate is \(\varLambda _v\). We again assume that there is no vertical transmission and all mosquitoes are born susceptible. The mosquito natural death rate is \(\mu _v\). Mosquitoes are infected via contact with infected humans at a rate of \(\beta _{hv}\).

There are four control measures:

  1. 1.

    The bite control, \(c_b\), such as using the insect repellent. This control limits the human-to-mosquito and mosquito-to-human contact rate and causes the effective transmission rates to be \(\widetilde{\beta }_{hv}(c_b)= (1-c_b)\beta _{hv}\) and \(\widetilde{\beta }_{vh}(c_b)=(1-c_b)\beta _{vh}\), respectively. Here, we use a linear dependence since, at least in the first approximation, being unprotected for double the time doubles the probability of transmission. We note, however, that other functions may be more appropriate.

  2. 2.

    The human-to-human contact control, \(c_c\), such as the use of condoms. This control causes the effective human-to-human transmission rate to be \(\widetilde{\beta }_{hh}(c_c)= (1-c_c)\beta _{hh}\). As above, we use a linear dependence since, at least in the first approximation, being unprotected in twice as many interactions doubles the probability of transmission. We note, however, that other functions may be more appropriate.

  3. 3.

    The treatment control, \(c_t\), which causes recovery to progress at a faster rate \(\widetilde{\gamma }(c_t)= \gamma + c_t\gamma _{h,t}\).

  4. 4.

    The insecticide control, \(c_i\), which increases the mosquito death rate to \(\widetilde{\mu }_v(c_i)= \mu _v+c_i\mu _{v,i}\).

For simplicity, all control measures are assumed to be constants and in the interval [0, 1].

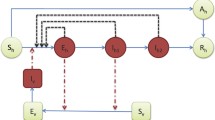
The dynamics of the compartmental ODE model are summarized in Fig. 1. See Table 1 for a summary of the notation and values of the parameters.

Fig. 1
figure 1

Scheme of the ODE model for ZIKV transmission. Full arrows denote transitions between the compartments. The letters next to the arrows specify the per capita rates of the transitions. The dashed arrows show the influence on transmission rates

Full size image

The model in Fig. 1, which is a special case of a system considered in [76], yields the following differential equations.

$$\begin{aligned} \frac{\mathrm{d}S_h}{\mathrm{d}t}&=\varLambda _h - \left( \widetilde{\beta }_{vh}(c_b)\frac{I_v}{N_v} + \widetilde{\beta }_{hh}(c_c)\frac{I_h}{N_h}+\mu _h\right) S_h \end{aligned}$$
(1)
$$\begin{aligned} \frac{\mathrm{d}I_h}{\mathrm{d}t}&=\left( \widetilde{\beta }_{vh}(c_b)\frac{I_v}{N_v} + \widetilde{\beta }_{hh}(c_c)\frac{I_h}{N_h}\right) S_h-(\mu _h+\widetilde{\gamma }(c_t))I_h \end{aligned}$$
(2)
$$\begin{aligned} \frac{\mathrm{d}R_h}{\mathrm{d}t}&=\widetilde{\gamma }(c_t)I_h-\mu _hR_h \end{aligned}$$
(3)
$$\begin{aligned} \frac{\mathrm{d}S_v}{\mathrm{d}t}&=\varLambda _v-\left( \widetilde{\beta }_{hv}(c_b)\frac{I_h}{N_h}+\widetilde{\mu }_v(c_i)\right) S_v \end{aligned}$$
(4)
$$\begin{aligned} \frac{\mathrm{d}I_v}{\mathrm{d}t}&=\widetilde{\beta }_{hv}(c_b)\frac{I_h}{N_h} S_v-\widetilde{\mu }_v(c_i)I_v \end{aligned}$$
(5)
Table 1 Model parameters and notation
Full size table

2.2 Model Calibration

We adopt most of the parameter values from [72] who followed [25] who fit the ZIKV transmission model to data from Brazil.

The recruitment rate, \(\varLambda _h\), in Brazil is 13.92 per year per 1000 people [77]. The life expectancy, \(\mu _h^{-1}\), in Brazil is 74 years [23]. It takes on average 9.9 days for the infected individual to have no detectable virus in blood [46], the infectiousness of ZIKV infection ends 1.5–2 days before the virus becomes undetectable [30]. Thus, an individual stays infectious for \(\gamma ^{-1} = 7.9\) days [25]. The mean duration of the acute ZIKV phase is 5 days [33], which gives \(\gamma _{h,t}=\frac{1}{5}\).

The mosquito recruitment rate, \(\varLambda _v\), is about 3000 a day [4]. The mosquito life expectancy, \(\mu _v^{-1}\), is 11 days [60]. This is in line with the life expectancy for mosquitoes in Rio de Janeiro, Brazil [49], and close to the average of 2–3 weeks considered in biological studies [58].

The time between a mosquito being infected and it infecting a human, \(\beta _{vh}^{-1}\), is 11.3 days [25], while the time between a human infection and a mosquito taking an infectious blood meal, \(\beta _{hv}^{-1}\), is and 8.6 days, respectively [30]. The human-to-human transmission rate, \(\beta _{hh}\), is \(\frac{1}{20}\) [33].

The insecticide related death rate, \(\mu _{v,i}\) is 1, about 10 times the natural mosquito mortality rate, in line with [56].

We estimate the bite control, \(c_b\) as follows. The population of Brazil is about 209 mil people [77]. In 2015, the revenue from mosquito repellent sales in Brazil was $55.7 mil [16]. The revenue for 2016 was expected to rise 120% [16], i.e., to $122.54 mil. The most frequent DEET repellents cost about $4.2 [53], i.e., about 29.17 mil bottles were sold in 2016. One bottle of DEET contains about 400 sprays [28, 54], i.e., lasts about 200 days since, on average, DEET is applied twice a day [53]. At the same time, three applications of DEET per day seem to provide complete protection. We thus get \(c_b = (209\times 10^6)^{-1} \cdot (29.17\times 10^6) \cdot \left( \frac{200}{365}\right) \cdot \left( \frac{2}{3}\right) = 0.051\).

We were not able to obtain values of the controls \(c_i, c_c, c_t\) from the literature, but we calibrated the model as follows. There were 215319 ZIKV infection cases in 2016 [48, 55], i.e., the incidence rate was 103 cases in \(10^5\) people. Setting \(c_c=0.05\), \(c_t=0.05\) and \(c_i = 0.005\) yielded an incidence rate of 106 cases per \(10^5\) people and so we adopted those values. We note that there are many other combinations of values that yield the similar incidence rate. However, the main results are quite robust to a particular choice of this combination since similar incidence rates yield similar risks of infections.

Most ZIKV infections are asymptomatic and do not need any extra costs. The cost of a symptomatic ZIKV infection in the US is around $6355 dollars [45]. The GDP per capita for Brazil is $15600 and for the United States is $59500 [23]. Therefore, the cost of ZIKV infection in Brazil is estimated as $1588.

The cost of mosquito bite prevention by using DEET is estimated as follows. The cost of the most frequently sold DEET is $4.2 per bottle [53]. One bottle of DEET contains 400 sprays and at three sprays a day, the cost is about $0.0315 per day.

2.3 Game-Theoretical Framework of Voluntary Bite Protection

Following [10], we add a game-theoretical component to the compartmental model above. We consider a repeated population game where the payoff to each individual is determined by their own strategy and the average strategy used by the population as a whole.

The players of the game are susceptible individuals who repeatedly choose whether to use DEET or not. We characterize the strategy by a single number \(c_b\) that specifies a proportion of the time the individual uses DEET. The solution of the game, called the Nash equilibrium, is the population-level value \(c_{b,\mathrm {NE}}\) at which no individual can increase their own payoff by deviating from the population strategy.

The payoff to an individual depends on the prevalence of ZIKV in the population, i.e., on the strategies other players are using. To solve for the Nash equilibrium value, we can assume that all players use the same strategy and only the strategy of the focal player may vary. Following [10], we assume that all individuals are provided with the same information such as prevalence of ZIKV in the population, the cost of treatment, and the cost of DEET. We will also assume that they use the information in the same and rational way to assess costs and risks [10].

The probability of getting infected when not using DEET at all while everybody else is using it at frequency \(c_b\) is

$$\begin{aligned} \frac{\beta _{vh}\frac{I_v}{N_v} + \widetilde{\beta }_{hh}(c_c)\frac{I_h}{N_h}}{\beta _{vh}\frac{I_v}{N_v} + \widetilde{\beta }_{hh}(c_c)\frac{I_h}{N_h} + \mu _h} \end{aligned}$$
(6)

which corresponds to the rate moving from \(S_h\) to \(I_h\) (when not using any DEET protection) over the total rate of moving out of \(S_h\). The probability may (and will) depend on \(c_b\), because the formula contains \(I_v\) and \(I_h\) that may (and will) depend on \(c_b\). The average cost of not using DEET, \(C_N\), when everybody else uses it at frequency \(c_b\) is then given by

$$\begin{aligned} C_N(c_b) = C_{\mathrm {Zika}}\frac{\beta _{vh}\frac{I_v}{N_v} + \widetilde{\beta }_{hh}(c_c)\frac{I_h}{N_h}}{\beta _{vh}\frac{I_v}{N_v} + \widetilde{\beta }_{hh}(c_c)\frac{I_h}{N_h} + \mu _h}. \end{aligned}$$
(7)

In order to determine the expected cost of using DEET, let \(C_{\mathrm {DEET}}\) denote the cost of actual use. Because one can still get infected from another human, the probability of infection is

$$\begin{aligned} \frac{ \widetilde{\beta }_{hh}(c_c)\frac{I_h}{N_h}}{\widetilde{\beta }_{hh}(c_c)\frac{I_h}{N_h} + \mu _h}. \end{aligned}$$
(8)

So, the cost of using DEET, \(C_U\), when everybody else is using it at frequency \(c_b\) is given by

$$\begin{aligned} C_U(c_b) = C_{\mathrm {DEET}}+ C_{\mathrm {Zika}}\frac{ \widetilde{\beta }_{hh}(c_c)\frac{I_h}{N_h}}{\widetilde{\beta }_{hh}(c_c)\frac{I_h}{N_h} + \mu _h}. \end{aligned}$$
(9)

To get Nash equilibrium, we have to solve

$$\begin{aligned} C_N(c_b) = C_U(c_b) \end{aligned}$$
(10)

for \(c_b\).

3 Analysis of the ODE System

There are two equilibria of the differential equations given in (1)–(5). The equilibria and the basic reproduction number were derived in [72]; here we summarize the main results.

3.1 Disease-free Equilibrium

The disease-free equilibrium \(E^0 = (S_H^0, I_H^0, R_H^0, S_V^0, I_V^0)\) is given by

$$\begin{aligned} E^0 = \left( \frac{\varLambda _h}{\mu _h}, 0, 0, \frac{\varLambda _v}{\widetilde{\mu }_v(c_i)}, 0\right) . \end{aligned}$$
(11)

The basic reproduction number, \(\mathcal {R}_0\), is given by

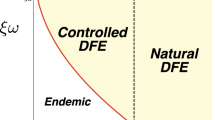
$$\begin{aligned} \mathcal {R}_0= \frac{1}{\mu _h+\widetilde{\gamma }(c_t)} \cdot \left( \widetilde{\beta }_{hh}(c_c)+ \frac{\widetilde{\beta }_{hv}(c_b)\widetilde{\beta }_{vh}(c_b)}{\widetilde{\mu }_v(c_i)}\right) . \end{aligned}$$
(12)

Since system (1)–(5) is a special case of a system considered in [76], Theorems 2.1.1 and 2.1.2 of [76] directly imply that, the disease-free equilibrium is globally asymptotically stable if \(\mathcal {R}_0\le 1\). It is unstable if \(\mathcal {R}_0>1\).

3.2 Endemic Equilibrium

The endemic equilibrium is \(E^*=(S_h^*, I_h^*, R_h^*, S_v^*, I_v^*)\) where \(I_h^*\) is a positive solution of

$$\begin{aligned} a (I_h^*)^2 + b I_h^* + c = 0 \end{aligned}$$
(13)

with

$$\begin{aligned} a&= \left( \frac{\widetilde{\gamma }(c_t)+ \mu _h}{\mu _h}\right) \left( \frac{\widetilde{\beta }_{hh}(c_c)\widetilde{\beta }_{hv}(c_b)}{N_h^2}\right) \end{aligned}$$
(14)
$$\begin{aligned} b&=\frac{\widetilde{\gamma }(c_t)+\mu _h}{\mu _h}\left( \frac{\widetilde{\beta }_{vh}(c_b)\widetilde{\beta }_{hv}(c_b)}{N_h} + \frac{\widetilde{\beta }_{hh}(c_c)}{N_h}\widetilde{\mu }_v(c_i)+\frac{\widetilde{\beta }_{hv}(c_b)}{N_h}\mu _h\right) \nonumber \\&\quad -\frac{\widetilde{\beta }_{hh}(c_c)\widetilde{\beta }_{hv}(c_b)}{N_h} \end{aligned}$$
(15)
$$\begin{aligned} c&=\widetilde{\mu }_v(c_i)\bigl (\widetilde{\gamma }(c_t)+\mu _h-\widetilde{\beta }_{hh}(c_c)\bigr ) - \widetilde{\beta }_{vh}(c_b)\widetilde{\beta }_{hv}(c_b) \end{aligned}$$
(16)

and

$$\begin{aligned} S_h^*&=\frac{\varLambda _h}{\mu _h} - \frac{(\widetilde{\gamma }(c_t)+ \mu _h) I_h^*}{\mu _h} \end{aligned}$$
(17)
$$\begin{aligned} R_h^*&= \frac{\widetilde{\gamma }(c_t)}{\mu _h} I_h^* \end{aligned}$$
(18)
$$\begin{aligned} I_v^*&= \frac{\varLambda _v}{\widetilde{\mu }_v(c_i)} \cdot \frac{\widetilde{\beta }_{hv}(c_b)\frac{I_h^*}{N_h}}{\widetilde{\beta }_{hv}(c_b)\frac{I_h^*}{N_h} + \widetilde{\mu }_v(c_i)} \end{aligned}$$
(19)
$$\begin{aligned} S_v^*&= \frac{\varLambda _v}{\widetilde{\mu }_v(c_i)} - I_v^*. \end{aligned}$$
(20)

If \(\mathcal {R}_0>1\), the endemic equilibrium is unique [72] and locally asymptotically stable [76, Theorem 2.2.1].

4 Results

4.1 Minimal DEET Coverage Needed for ZIKV Elimination

In this section, we determine \(c_{b,\emptyset }\), the minimal coverage at which susceptible individuals should use DEET so that ZIKV is eliminated. It follows from (12) that \(\frac{\partial R_0}{\partial c_b}<0\), i.e., \(\mathcal {R}_0\) is decreasing in \(c_b\). Consequently, ZIKV will be eliminated at the smallest value of \(c_b\in [0,1]\) for which \(R_0\le 1\). Note that if \(\mathcal {R}_0|_{c_b=1}= \frac{1}{\mu _H+\widetilde{\gamma }(c_t)} \cdot \widetilde{\beta }_{hh}(c_c)>1\), then \(\mathcal {R}_0>1\) for all values of \(c_b\) and thus ZIKV will never be eliminated. On the other hand, if \(\mathcal {R}_0|_{c_b=0}<1\), i.e., \(\mathcal {R}_0<1\) even when nobody is using DEET, then ZIKV is not endemic. The only non-trivial critical value of \(c_b\) exists when \(\mathcal {R}_0|_{c_b=0}>1\) and \(\mathcal {R}_0|_{c_b=1}<1\). By (12) it is given as a solution of

$$\begin{aligned} \frac{1}{\mu _h+\widetilde{\gamma }(c_t)} \cdot \left( \widetilde{\beta }_{hh}(c_c)+ \frac{\widetilde{\beta }_{hv}(c_b)\widetilde{\beta }_{vh}(c_b)}{\widetilde{\mu }_v(c_i)}\right) =1. \end{aligned}$$
(21)

Consequently,

$$\begin{aligned} c_{b,\emptyset }= {\left\{ \begin{array}{ll} 0,&{} \text {if } \mathcal {R}_0|_{c_b=0}<1,\\ 1-\sqrt{\frac{\left( \mu _H+\widetilde{\gamma }(c_t)-\widetilde{\beta }_{hh}(c_c)\right) \cdot \widetilde{\mu }_v(c_i)}{\beta _{vh}\beta _{hv}}},&{} \text {if } \mathcal {R}_0|_{c_b=0}>1 \text { and } \mathcal {R}_0|_{c_b=1}<1,\\ \text {Does not exist},&{} \text {if } \mathcal {R}_0|_{c_b=1}>1. \end{array}\right. } \end{aligned}$$
(22)

4.2 Nash Equilibrium

In this section, we are interested in finding \(c_{b,\mathrm {NE}}\). We will consider the situation only under the endemic equilibrium (there is no need to use DEET in the disease-free equilibrium).

Fig. 2
figure 2

The expected cost of not using DEET (solid line) and the expected cost of using DEET as a function of population-level DEET coverage in the population. The parameters are as in Table 1. The solid line reaches 0 at \(c_{b,\emptyset }\), the level needed for ZIKV elimination. The lines intersect at the Nash equilibrium, \(c_{b,\mathrm {NE}}\). While \(c_{b,\mathrm {NE}}< c_{b,\emptyset }\), we can see that \(c_{b,\mathrm {NE}}\approx c_{b,\emptyset }\). In fact, in our model \(c_{b,\emptyset }-c_{b,\mathrm {NE}}<10^{-3}\) even when parameter values differ significantly from the values specified in Table 1

Full size image

The graphical solution of \(C_N(c_b) = C_U(c_b)\) where \(C_N\) and \(C_U\) are given in (7) and (9) is illustrated in Fig. 2. The numerical solutions are shown in Fig. 3.

For the parameter values in Table 1, the resulting social optimum and Nash equilibrium values are \(c_{b,\emptyset }= 0.0886\) and \(c_{b,\mathrm {NE}}=0.0885\), respectively. The annual incidence rate when individuals use the optimal voluntary level of protection, \(c_{b,\mathrm {NE}}\), is 0.2 ZIKV cases per \(10^5\) people. We can thus see that the disease would be almost eliminated by optimal voluntary use of DEET.

We can also consider the annual incidence rate of 0.2 cases per \(10^5\) people to be the price of anarchy as if the social optimum, \(c_{b,\emptyset }\), was enforced, ZIKV would be eliminated, i.e., the incidence rate would be 0.

4.3 Sensitivity Analysis

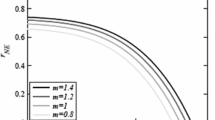
The dependence of \(c_{b,\mathrm {NE}}\) on parameters is shown in Fig. 3 and the sensitivity indices are presented in Table 2. The values of \(c_{b,\emptyset }\) track closely the values of \(c_{b,\mathrm {NE}}\) with only a minimal difference (less than \(10^{-3}\)) between the two.

The optimal voluntary level of protection, \(c_{b,\mathrm {NE}}\), is essentially constant in the human recruitment rate \(\varLambda _h\), the vector recruitment rate \(\lambda _v\), the human natural death rate \(\mu _h\), the cost of the prevention, \(C_{\mathrm {DEET}}\), and the cost of the disease, \(C_{\mathrm {Zika}}\).

Fig. 3
figure 3

Dependence of \(c_{b,\mathrm {NE}}\) on different parameter values. Unless varied, the parameter values are as specified in Table 1. When all parameters are as in Table 1, \(c_{b,\emptyset }= 0.0886\) and \(c_{b,\mathrm {NE}}= 0.0885\). \(c_{b,\mathrm {NE}}\) is constant in \(\varLambda _h, \varLambda _v\) and \(\mu _h\) and these figures are not shown

Full size image

Also, \(c_{b,\mathrm {NE}}\) increases rapidly with the human-to-vector and vector-to-human transmission rates, \(\beta _{hv}\) and \(\beta _{vh}\) and it is also increasing in the human-to-human transmission rate \(\beta _{hh}\). It is rapidly decreasing in the recovery rate \(\gamma \) and the mosquito death rate \(\widetilde{\mu }_v(c_i)\). Correspondingly, \(c_{b,\mathrm {NE}}\) is also decreasing in the treatment control \(c_t\), the insecticide control \(c_i\) and the contact control \(c_c\).

Table 2 The sensitivity index of \(c_{b,\mathrm {NE}}\) on various parameters p calculated as \(\left( \frac{p}{c_{b,\mathrm {NE}}}\right) \cdot \left( \frac{\partial c_{b,\mathrm {NE}}}{\partial p}\right) \), see for example [7]
Full size table

5 Discussion

One of the interesting predictions of this model is that the optimal voluntary use of DEET does not depend in any significant way on the cost of the prevention. This finding is in sharp contrast to other similar game-theoretical models. For example, as shown in [1], the relatively low cost of a typhoid infection (compared to vaccination cost and effectiveness) is the reason why the vaccination coverage is quite low in rural Ghana. Similarly, even for vector-borne diseases such as Chagas disease, the cost of the insecticide-treated nets significantly affects the optimal usage levels and consequently the disease incidence rate [35].

Another interesting prediction is that the optimal voluntary use of DEET brings ZIKV very close to elimination levels. This agrees with predictions for other vector-borne diseases such as malaria [15], dengue [27], chikungunya [40] and visceral leishmaniasis [31] or diseases like Ebola [13]. In all these cases, cost of disease prevention is low relative to the cost of the disease. This is different in vaccination games for diseases like polio [10, 19] and Hepatitis B vaccination [21, 68] where either the real or the perceived vaccination costs are relatively large.

The high cost of ZIKV infection can explain why the ZIKV outbreaks, while serious, are still relatively limited. It has been demonstrated that individuals act in a way that maximizes their self-interests, rather than the interests of the entire group [51]. Vaccination in particular and disease prevention in general is prone to free-riding [38]. The “free-riders” avoid the costs associated with the prevention while benefiting from actions taken by others [18, 69, 75]. However, the risk of severe negative ZIKV complications such as Guillain-Barré Syndrome, microcephaly, and other birth defects means that the cost of ZIKV infection is high and thus the individuals want to protect themselves (and their unborn babies) almost regardless of the cost of the protection.

Our model predicted the optimal voluntary use of the repellents at about 8.8%. On one hand, this number seems quite low. Indeed, in Northern Brazil where the ZIKV outbreak originated, the repellent use during 2016 was 83% among highly educated pregnant women and 56% among pregnant women overall [53]. However, in the very same region, only less than 21% of women of childbearing age (15–49 years) report having used mosquito repellent or insecticides frequently during 2015–2016 [63]. The economic factor was the main justification for the non-use of repellents both in urban and rural areas [53].

6 Conclusions

Mathematical modeling is a useful tool that helps our understandings of how interactions between the population, individuals, and the environment can change the course of a disease [22]. In this paper, we adopted an ODE model of ZIKV transmission dynamics that originated in [12]. We applied a game-theoretical approach, developed by Bauch and Earn [10], and determined the optimal voluntary use of DEET to prevent the spread of ZIKV through vector bites. We also gave formulas for a desired level of DEET usage that leads to ZIKV elimination. Similarly to other recently studied vector-borne diseases, such as dengue [27], malaria [15], visceral leishmaniasis [31] and Chagas [35], we saw that the optimal voluntary use of DEET can significantly contribute to ZIKV elimination. This differs from the predictions for non-vector-borne diseases such as polio [19] and hepatitis B [21] where the optimal voluntary use levels and the levels required for the herd immunity were significantly different.

There are several ways in which our model can be extended. From the game-theoretical perspective, one can apply a multi-agent-simulation (MAS) methodology [5, 39, 44]. This approach may be fruitful for two reasons: (1) the DEET application needs to be repeated as with the influenza [6], typhoid [1] or hepatitis [21, 68] vaccinations, (2) there are multiple ways in which one can get infected and the simulations may provide a more realistic and flexible approach for multiple protective actions. This would also allow the incorporation of game-theoretical component into models like [2, 3, 33] that distinguish between females and males.

There are four control measures that help ZIKV elimination. An individual generally cannot influence the level of hospital care or any large-scale insecticide spraying to substantially increase mosquito death rates; therefore the control measures related to these are not suitable for game-theoretical analysis. At the same time, the reduction in human-to-human transmission through the use of condoms is something an individual can influence directly. However, even this control is still not an individual’s own decision. Unless both individuals agree to use (or not to use) condom, there is no interaction. The proper analysis of the game involving condom use would thus have to take into account a population heterogeneity and contact network structure rather than just simple averages of players’ condom usage.

The analysis of game-theoretical models that deal with two or more prevention measures simultaneously seems to be much harder. So far only specific models for COVID-19 with vaccination or social distancing [20] and cholera with vaccination or clean water usage [41] were considered. It would be of a great interest to develop a general framework.