Introduction

Supercontinuum generation is the formation of an ultra-wideband field spectrum via a complex interplay of several non-linear processes such as four-wave mixing and self phase modulation. A supercontinuum, often referred to as white-light spectrum (Chen et al. 2018), is of interest for various applications such as optical metrology, spectroscopy, fluorescence lifetime imaging, remote sensing, and optical coherence tomography. It is usually attained by the propagation of ultrashort pulses through long optical fibers or via the propagation of relatively longer pulses through optical fibers with high nonlinearity, such as photonic crystal fibers where mode confinement enables non-linear processes to take place at a lower excitation power (Husakou and Herrmann 2002; Mühlschlegel et al. 2005; Liu et al. 2015; Krasavin et al. 2016; Gorbach 2015; Wu et al. 2013; Dasgupta et al. 2018). Currently, a photonic crystal fiber is the most compact choice for generating a supercontinuum. However, as miniaturization of optical devices is under continuous progress to accomplish more complicated and numerous on-chip tasks, supercontinuum generation using micro/nanoscale devices is of significant interest. Miniaturizing optical devices is of critical importance for future applications such as quantum computing and novel metamaterial design, but replacing the existing macroscale optical devices with their nanophotonic versions while maintaining the same performance and functionality is a big challenge (Park et al. 2018; Horiuchi 2020; Bharadwaj et al. 2011; Park 2009; Kullock et al. 2018). Recently, micro- and nanoscale structures that can generate a supercontinuum have been reported or proposed (Chen et al. 2018; Krasavin et al. 2016; Gorbach 2015; Dasgupta et al. 2018). However, these structures have bandwidth limitations and they can generate a supercontinuum either in the infrared (IR) or in the visible (VIS) range depending on the structure. In this study, semiconductor nano-antennas are proposed as energy-storing nanostructures that can generate an ultra-wideband supercontinuum ranging from the far-infrared range to the ultraviolet range of the spectrum and attain a supercontinuum-bandwidth that even surpasses the supercontinuum-bandwidth that is attained via optical fibers. Such a structure is simpler than the previously proposed micro- and nanoscale structures (Chen et al. 2018; Monticone et al. 2017; Hanke et al. 2009; Ünlü et al. 2011; Montesinos-Ballester et al. 2020; Sain et al. 2019), easier to fabricate (Sain et al. 2019), and achieves a wider bandwidth than the previously reported bandwidths (Chen et al. 2018; Husakou and Herrmann 2002; Mühlschlegel et al. 2005; Liu et al. 2015; Krasavin et al. 2016; Gorbach 2015; Wu et al. 2013; Dasgupta et al. 2018; Park et al. 2018; Horiuchi 2020; Bharadwaj et al. 2011; Park 2009; Kullock et al. 2018; Monticone et al. 2017; Hanke et al. 2009; Ünlü et al. 2011; Montesinos-Ballester et al. 2020), paving the way for on-chip spectroscopy, ultrashort pulse generation, and on-chip high-energy density storage. The paper also discusses the potential replacement of photonic crystal fibers with semiconductor nano-antennas for supercontinuum generation, provided that a certain pattern of optical excitation is followed. Latest research suggests that the formation of a supercontinuum is most interesting when: the highest bandwidth is attained at a relatively lower excitation intensity, achieved via a simple structure, attained in an adaptive manner (spectral shaping). Table 1 mentions some of the prominent studies regarding small-scale supercontinuum generation via a comparison with the aim of this study.

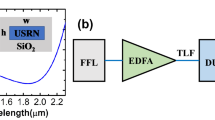
Table 1 Prominent studies regarding small-scale supercontinuum generation
Full size table

The size of the proposed structure is considered to be 10 µm in both width and length, and 300 nm in thickness, with the glass substrate having a thickness of 200 nm and the semiconductor nano-antenna having a thickness of 100 nm. The phenomena of supercontinuum generation from the nano-antenna is numerically investigated. Here, the classical wave equation treatment is followed as the thickness of the nano-antenna is suitable for an accurate classical analysis (Yang et al. 2019). The wave equation that describes the behavior of the electric field, which should have the intended supercontinuum pattern, is coupled with the Lorentz dispersion equation that incorporates the resonance frequency, electron density, and the polarization decay rate of the semiconductor nano-antenna into the wave equation (Zhang et al. 2019; Dubietis et al. 2019; Hilligsøe et al. 2004; Hayat et al. 2021; Aşırım and Yolalmaz 2020; Aşırım et al. 2020; Kim 2021; Taflove and Hagness 2005; Aşırım and Kuzuoğlu 2020a, b; Balanis 2015) The free electron injection dynamics is added into the analysis via coupling with the Lorentz dispersion equation in the form of two seperate differential equations with one describing the free electron injection rate and the other describing the decay rate of the free electron density.

Throughout the study, the pattern of optical excitation of semiconductor nano-antennas is based on the modulation of the electron injection rate. Carrier injection rate modulation allows for high electric energy accumulation in the semiconductor nano-antenna since the electric field of an excitation wave penetrates the nano-antenna when the injection rate and the free electron density is low (lower efffective permittivity), and then gets largely trapped in the nano-antenna as the injection rate and the free electron density increases (higher effective permittivity) (Novotny and Hulst 2011; Merlein et al. 2008; Rahman et al. 1996). As the electric field forms a standing wave pattern within the semiconductor nano-antenna, the gradual increase in the free electron density causes a rapid increase in electric energy density, especially if the injection rate is high and the resulting change in the free electron density is large. Once the free electrons recombine, the accumulated electric energy is transferred to the excitation wave. For bulk semiconductor materials, the free electron density cannot be changed significantly, even with intense optical excitation. However, for semiconductor nano-antennas with a sub-micron width in at least one spatial dimension, the free electron density can be changed drastically as the volume is very small and more fraction of electrons can be raised from the valence band to the conduction band, which also results in a drastic change in the effective permittivity (Saleh and Teich 2007; Boyd 2008; White et al. 1970). Therefore, modulating the free electron density via carrier injection rate modulation is a feasible mechanism for semiconductor nano-antennas to trap the electric field of an excitation wave inside via effective permittivity modulation, and enable electric energy accumulation within the antenna. It is this large increase in electric energy density within the nano-antenna that allows the generation of a supercontinuum (Adamu et al. 2019; Wang and Zhang 2017).

The profile of the carrier injection rate modulation depends on the recombination mechanism of the semiconductor nano-antenna. Since we want to trap the electric field inside a very small thickness, the modulation of the free electron density should be fast. Radiative recombination occurs on the scale of nanoseconds and this rate is not sufficient to trap the electric field of an excitation wave, as the electric field would have disappeared by that time through successive reflections inside the nano-antenna. Therefore, one must resort to the investigation of the nonradiative recombination processes. It is known that when the free electron density is very high, nonradiative recombination occurs on the scale of sub-picoseconds due to Auger recombination (Saleh and Teich 2007; Wang et al. 2007). This makes nonradiative recombination an ideal process for modulating the free electron density through carrier injection rate modulation via intense pulsed excitation of the nano-antenna with a pulse period that is on the same scale with the nonradiative recombination rate of the free electrons. In other words, apart from the excitation wave which is used for supercontinuum generation, one also needs a pump wave for the carrier injection rate modulation process. Essentially, the excitation wave is used to adjust the average intensity of the supercontinuum and the pump wave is used to adjust its bandwidth. A high amplitude for both waves leads to a high gain–bandwidth product. It is important to note that the pump wave frequency must be higher than the bandgap frequency of the semiconductor nano-antenna to raise the electrons to the conduction band. Once the electrons decay to the valence band, the subsequent pump wave pulse should raise them back to the conduction band and this cycle of free electron density modulation should continue until the supercontinuum is fully generated, which takes a few picoseconds. Figure 1 illustrates the side view of the proposed semiconductor nano-antenna with a resonance frequency of \({f}_{1}\), relative permittivity of \({\varepsilon }_{1}\), conductivity of \({\sigma }_{1}\), and a polarization decay rate of \({\gamma }_{1}\).

Fig. 1
figure 1

Side view of the proposed semiconductor nano-antenna (drawing is not to scale)

Full size image

Practical implementation

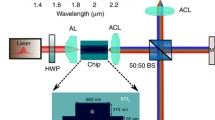
Supercontinuum generation via carrier injection rate modulation process can easily be implemented in experiment. The required setup is illustrated in Fig. 2b. In this configuration, the continuous infrared excitation light is combined with a pulsed-pump light using beam splitters. The pulsed-pump light is used for carrier injection rate modulation, which determines the bandwidth of the generated supercontinuum, such that as the pump wave amplitude is increased so as the bandwidth of the supercontinuum. Whereas the continuous infrared excitation light determines the intensity level of the generated supercontinuum. The recombination rate of the electrons should be in the same timescale with the pulse period of the pump light so that the electrons are immediately re-excited to the conduction band to maintain the modulation cycle. The pump light from the injection source is assumed to have an energy of 500 μJ and a pulse duration of 50 fs. Whereas the excitation pulse is set to have a duration of 5 ps in continuous operational mode. The pump light is coupled to a resonator that consists of an isolator and a beam splitter (see Fig. 2a) that couples approximately 1% of the pump-light power to a 2nd beam splitter. The 2nd beam splitter then fully reflects the pump-light pulse to a focusing lens to be focused on the semiconductor nano-antenna. The rest of the pump light circulates in the resonator and at each round trip another 1% of it is sent to the nano-antenna surface. This allows for a complete pulsed operation of the intense pump beam throughout the duration of the continuous excitation beam and enables an efficient carrier injection rate modulation scheme. The pulse period of the pump light is set by adjusting the distance between the isolator and the 1st beam splitter, i.e., the resonator length d (see Fig. 2b). For example, if the electron recombination time \({\tau }_{r}\) is to be equated to the pulse period of the pump wave, then the round-trip delay that is introduced by the resonator is set to be equal to \({\tau }_{r}\). Hence, the distance relation would be satisfying: \({{2d} \mathord{\left/ {\vphantom {{2d} {\left( {3 \times 10^{8} \,\left( {\frac{{\text{m}}}{{\text{s}}}} \right) } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {3 \times 10^{8} \,\left( {\frac{{\text{m}}}{{\text{s}}}} \right) } \right)}} = \tau_{r}\).

Fig. 2
figure 2

a Transmission configuration of the beam splitters. b Proposed setup for supercontinuum generation via carrier injection rate modulation using a semiconductor nano-antenna. The continuous excitation beam is combined with the intense pump beam pulses using beam splitters.

Full size image

A single pump-light pulse that is coupled out of the resonator, has an energy of 5 μJ. Dividing this value to the pulse duration of a single pump-light pulse yields to the power: 5 μJ/(50 fs) = 1 × 108 W. When focused by a lens onto the semiconductor nano-antenna cross section (the nano-antenna is assumed to have a length and width of 10 µm both), this amount of power yields an intensity of \(I=\frac{P}{A}=\frac{{1 \times 10}^{8} \, \mathrm{ W}}{\pi ({5 \times {10}^{-6 } \, \mathrm{m})}^{2}}\approx 1.28 \times {10}^{18} \, \mathrm{W}/{\mathrm{m}}^{2}\), which corresponds to an electric field intensity of \(E=\sqrt{\frac{I}{0.5 \times \left(3 \times \frac{{10}^{8 } \, \mathrm{m}}{\mathrm{s}}\right){ \times 8.854 \times 10}^{-12} \, \left(\frac{\mathrm{F}}{\mathrm{m}}\right)}}\approx 3 \times {10}^{10} \, \mathrm{ V}/\mathrm{m}\). Therefore, the pump wave electric field has a pulse amplitude on the order of \({10}^{10} \, \mathrm{V}/\mathrm{m}\), whereas the excitation wave amplitude can have an arbitrary value. It is important to mention that in this study the pump wave is assumed to be polarized in the out of plane (orthogonal) direction, while the excitation wave is polarized along the plane (parallel). Hence, as an isotropic nano-antenna is assumed, the two waves do not couple to each other in response to nonlinearity.

The proposed architecture is simple and can be applied for an arbitrary nano-antenna for accomplishing the same purpose, provided that the temporal scale of the electron recombination time matches with the round-trip time of the pump laser pulse in the resonator. Hence, for a given semiconductor, the resonator length d must be adjusted accordingly, so that the optical pumping rate matches with the temporal scale of the electron recombination time, hence the carrier injection rate is controlled. The carrier injection rate can also be arbitrarily modified via modifying the resonator length to control the free electron density in the semiconductor for adaptively shaping the supercontinuum pattern for band-specific emission. This will, to a large extent, eliminate the need for materials with special structures or properties for supercontinuum formation. The suggested system may cause an overheating of the semiconductor when high energy density is accumulated after a long duration of pulsed-pump operation. This can cause the electron recombination time to decrease further due to a higher rate of Auger recombination and may require the resonator length to be shortened to rematch the electron recombination time and the pump-pulse period.

It should also be noted that after a very long duration of pulsed-pump operation, the formation of high energy density within the semiconductor may modify the physical properties of the semiconductor or even lead to a total optical breakdown, thereby disrupting or destroying the operation of the system. For this reason, the amplitude of the pump pulse should be carefully selected, and it should not be selected way beyond the values that are given in this paper.

The excitation source can be selected as any type of near infrared laser source, such as the Nd:YAG laser source (282 THz). The pump laser source on the other hand, has to have a center frequency that is greater than the bandgap frequency of the semiconductor material. Throughout this paper, it is assumed that the semiconductor is GaAs, which has a bandgap frequency of 345 THz. Therefore, the pump laser can be an Alexandrite laser (400 THz) or a ruby laser (445 THz), which is energized enough to generate an electron–hole pair.

Methods

The semiconductor nano-antenna has a very small thickness (100 nm), but a relatively large width (10 µm). Such a large slab width allows for an infinite-slab assumption for the most part of the desired supercontinuum (mainly for frequencies greater than 100 THz). For supercontinuum frequencies below 100 THz, a small relative error in the spectral amplitude is expected to occur (Balanis 2015). However, for the most part of the IR–UV range supercontinuum, one can safely investigate the problem in one dimension, which is along the thickness of the semiconductor nano-antenna.

The electric field wave equation (of the excitation) is solved along with the Lorentz dispersion equation for semiconductors, in other words, the electric field is solved in parallel with the electric polarization density. The electron dynamics is incorporated into the formulation via defining a generation and a recombination rate based on the intensity, duration, period of the pump (injection) pulses, and the electron recombination time respectively. The resulting set of equations are solved using the finite difference time domain method in one dimension. The proposed semiconductor nano-antenna requires the computation of the excitation field along its thickness, which we designate here as the y-direction. The solution of the set of discretized partial differential equations requires the imposition of an absorbing boundary condition from both sides of the computational domain as this is an open boundary problem. The perfectly matched layer described in Taflove and Hagness (2005) is used to absorb the scattered field in order to prevent reflection or re-radiation back into the computational domain which would produce erroneous results. Figure 5 shows the domain of computation, which involves the total field in one sub-domain and the scattered field in the other sub-domain. The two subdomains are seperated by the boundary or axis, known as the total field-scattered field (TF/SF) boundary, where the incident field is excited towards the semiconductor (Fig. 3).

Fig. 3
figure 3

Configuration for the one-dimensional analysis of the supercontinuum generation process using a semiconductor nano-antenna mounted/fabricated on top of a glass substrate

Full size image

Supercontinuum generation is a temporal phenomenon, hence, focusing on a single component of the excitation wave electric field is sufficient. Assuming the domain of analysis lies in the x–y plane, the planar component of the electric field (\({E}_{x})\) will be computed. The TF/SF boundary is defined at the point \(y={y}_{m}\) and the incident excitation wave electric field at the TF/SF boundary is defined as

$${E}_{x, \mathrm{inc}}\left(y{=y}_{m} , t\right)=A \times \mathrm{cos}\left(2\pi vt+\varphi \right); \, A: \mathrm{amplitude} \, \left(\frac{\mathrm{V}}{\mathrm{m}}\right), \, v:\mathrm{excitation} \, \mathrm{frequency}, \varphi :\mathrm{phase \, angle}.$$

In the air and glass regions (apart from the semiconductor region), as the conductivity and the polarization density are negligible, one only needs to solve the homogenous electric field wave equation with a specific value of electrical permittivity in each region:

Air region: (\({\varepsilon =\varepsilon }_{0}\))

$${\nabla }^{2}E-{\mu }_{0}{\varepsilon }_{0}\frac{{\partial }^{2}E}{{\partial t}^{2}}=0 \left({E=E}_{x}\right).$$
(1)

Glass region: (\({\varepsilon =\varepsilon }_{\infty }\))

$${\nabla }^{2}E-{\mu }_{0}{\varepsilon }_{\infty }\frac{{\partial }^{2}E}{{\partial t}^{2}}=0 \left({E=E}_{x}\right).$$
(2)

The real challenge is to solve for the electric field inside the semiconductor region. For a semiconductor, the wave dynamics and the electron dynamics need to be investigated separately. Solving for the full wave dynamics requires the solution of the electric field wave equation (Eq. 3), Lorentz equation for the polarization density of bound charges (Eq. 4), and the Lorentz equation for the polarization density of free electrons (Eq. 5). The density of free electrons is obtained by the addition of Eq. (6), which describes the rate of change of the free electrons in a unit volume via the injection and recombination rates. Equation (5), which is the Lorentz equation for free electrons, is, therefore, coupled with Eq. (6). As the nano-antenna volume is small, injection rate can be considered as very high; therefore, the electron recombination time is also a function of the free electron density (Saleh and Teich 2007) and this makes Eq. (6) a non-linear formulation.

Electric field wave equation: (\({E=E}_{x}\))

$${\nabla }^{2}E-{\mu }_{0}{\varepsilon }_{\infty }\frac{{\partial }^{2}E}{{\partial t}^{2}}={\mu }_{0}{\sigma \frac{\partial E}{\partial t}+\mu }_{0}\frac{{d}^{2}P}{{\partial t}^{2}}.$$
(3)

Lorentz equation for the polarization density of bound charges:

$$\frac{{d}^{2}{P}_{b}}{{dt}^{2}}+{\gamma }_{b}\frac{d{P}_{b}}{dt}+{{\omega }_{0}}^{2}{P}_{b}-\frac{{{\omega }_{0}}^{2}{{P}_{b}}^{2}}{{(Q-Q}_{f})ed}+\frac{{{\omega }_{0}}^{2}{{P}_{b}}^{3}}{{{(Q-Q}_{f})}^{2}{e}^{2}{d}^{2}}=\frac{{{(Q-Q}_{f})e}^{2}E}{m} .$$
(4)

Lorentz equation for the polarization density of free charges:

$$\frac{{d}^{2}{P}_{f}}{{dt}^{2}}+{\gamma }_{f}\frac{d{P}_{f}}{dt}=\frac{{{Q}_{f}e}^{2}E}{m} .$$
(5)

Rate equation for the carrier density

$$\frac{d{Q}_{f}}{dt}=G\left(t\right)-\frac{{Q}_{f}}{{\tau }_{r}}=\frac{c{\varepsilon }_{0}{{(E}_{p}(t))}^{2}}{2h{v}_{p}\Delta w}-A{Q}_{f}-B{{Q}_{f}}^{2}-C{{Q}_{f}}^{3},$$
(6)
$${\tau }_{r}=\frac{1}{\left(A+B{Q}_{f}+C{{Q}_{f}}^{2}\right)}, \, G\left(t\right)= \frac{c{\varepsilon }_{0}{{(E}_{p}(t))}^{2}}{2h{v}_{p}\Delta w},$$
$$P={P}_{b}+{P}_{f}, \, Q={Q}_{b}+{Q}_{f}, \, { Q}_{f}\left(0\right)=0, \, Q\left(0\right)={Q}_{b}\left(0\right).$$

A: Shockley–Read–Hall nonradiative recombination coefficient (trap, impurity, or defect based), B: radiative band-to-band recombination coefficient, C: auger recombination coefficient (Nocedal and Wright 2006), G: carrier density injection rate, \({ \tau }_{r}:\mathrm{electron} \, \mathrm{recombination} \, \mathrm{time}, { \varepsilon }_{0}:\mathrm{free} \, \mathrm{space} \, \mathrm{permittivity}\), \({ E}_{p}: \mathrm{pump} \, \mathrm{electric \, field} (\mathrm{polarized} \, \mathrm{out} \, \mathrm{of} \, \mathrm{paper}), { P}_{b/f}:\mathrm{polarization} \, \mathrm{density} \, \mathrm{of} \, \mathrm{bound}/ \mathrm{free} \, \mathrm{charges}\), \(h:\mathrm{Planck} \, \mathrm{constant}, Q:\mathrm{total} \, \mathrm{electron \, density}, c:\mathrm{speed} \, \mathrm{of} \, \mathrm{light}\), \({\omega }_{0}:\mathrm{transition} \, \mathrm{frequency}\), \(E:\mathrm{electric} \, \mathrm{field} \, \left(\mathrm{excitation}\right), \, {Q}_{b}:\mathrm{bound} \, \mathrm{electron} \, \mathrm{density}, \, d:\mathrm{atom \, diameter}, \, {Q}_{f}:\mathrm{free} \, \mathrm{electron} \, \mathrm{density}\), \(P:\mathrm{total} \, \mathrm{polarization} \, \mathrm{density}, \, \sigma :\mathrm{electrical} \, \mathrm{conductivity}, \, m:\mathrm{electron} \, \mathrm{mass}, \, T:\mathrm{simulation \, duration}\), \({\gamma }_{b/f}:\mathrm{polarization \, damping \, rate \, of \, bound}/ \mathrm{free \, electrons}, \, { \varepsilon }_{\infty }: \mathrm{relative \, permittivity}, \, e: \mathrm{charge}\), \(\Delta w:\mathrm{thickness \, of \, the \, semiconductor \, nanofilm} \left(\Delta w=100 \, \mathrm{nm \, in \, this \, study}\right), {v}_{p}: \mathrm{pump \, frequency}\), \({E}_{p}\left(t\right)={A}_{p} \times \mathrm{cos}\left(2\pi {v}_{p}t+{\varphi }_{p}\right), \, \mathrm{where} \, {hv}_{p}>{E}_{g}, {E}_{g}:\mathrm{bandgap \, energy \, of \, the \, semiconductor}.\)

Notice that in Eq. (6), there is the injection term G(t) which depends on the square of the pump wave electric field. The pump wave electric field \({E}_{p}\) is not included in the wave equation as it is only used to excite the electrons from the valence band to the conduction band and is assumed to be polarized in the z direction so that it is not coupled to the excitation field E. Hence, given that its frequency is greater than the bandgap frequency of the semiconductor nano-antenna, the pump electric field is absorbed by the nano-antenna, and this effect is incorporated by the carrier density injection term G(t) in the semiclassical part of the formulation. There are two basic advantages of using a semiconductor nano-antenna for supercontinuum generation. The first one is the small volume of the nano-antenna, such that the carrier density is easily modulated in high concentrations with a relatively much smaller pump intensity. The second advantage is that the cross-sectional area of a nano-antenna is quite small, therefore, by focusing a laser beam of high power via a lens, a very large intensity can be obtained at the nano-antenna cross section. This allows for ultra-high-intensity supercontinuum generation for well-focused excitation beams.

After reordering the terms for evaluating each quantity at the next time step “j + 1” using the finite difference time domain (FDTD) discretization, the discretized forms of Eqs. (3–6) become:

$$E\left(i,j+1\right)=-\frac{{\Delta t}^{2}}{{\varepsilon }_{\infty }}\left\{\sigma \frac{E\left(i,j\right)-E\left(i,j-1\right)}{{\varepsilon }_{\infty }\Delta t}+\frac{P\left(i,j+1\right)-2P\left(i,j\right)+P\left(i,j-1\right)}{{\varepsilon }_{\infty }{\Delta t}^{2}}-\frac{E\left(i+1,j\right)-2E\left(i,j\right)+E\left(i-1,j\right)}{{\varepsilon }_{\infty }{\mu }_{0}{\Delta x}^{2}}-\frac{2E\left(i,j\right)-E\left(i,j-1\right)}{{\Delta t}^{2}}\right\},$$
(7)
$${P}_{b}\left(i,j+1\right)=2{P}_{b}\left(i,j\right)-{P}_{b}\left(i,j-1\right)-{\gamma }_{b}\Delta t\left({P}_{b}\left(i,j\right)-{P}_{b}\left(i,j-1\right)\right)-{{\omega }_{0}}^{2}{\Delta t}^{2}{P}_{b}\left(i,j\right)+\frac{{{\omega }_{0}}^{2}{\Delta t}^{2}{{P}_{b}}^{2}\left(i,j\right)}{{(Q(j)-Q}_{f}(j))ed} -\frac{{{\omega }_{0}}^{2}{\Delta t}^{2}{{P}_{b}}^{3}\left(i,j\right)}{{{(Q(j)-Q}_{f}(j))}^{2}{e}^{2}{d}^{2}}+\frac{{{(Q(j)-Q}_{f}(j))e}^{2}{\Delta t}^{2}E\left(i,j\right)}{m} ,$$
(8)
$${P}_{f}\left(i,j+1\right)=2{P}_{f}\left(i,j\right)-{P}_{f}\left(i,j-1\right)-{\gamma }_{f}\Delta t\left({P}_{f}\left(i,j\right)-{P}_{f}\left(i,j-1\right)\right)+{\Delta t}^{2}\frac{{{Q}_{f}\left(j\right)e}^{2}}{m}\left(E\left(i,j\right)\right) ,$$
(9)
$${Q}_{f}\left(j+1\right)={Q}_{f}\left(j\right)+\frac{\frac{1}{2}c{\varepsilon }_{0}{{(E}_{p}(j))}^{2}}{e\Delta w}\Delta t-A{(Q}_{f}\left(j\right))\Delta t-B{{(Q}_{f}(j))}^{2}\Delta t -C{{(Q}_{f}(j))}^{3}\Delta t ,$$
(10)

x: spatial coordinate, t: time, \(E\left(x,t\right)=E\left(i\Delta x,j\Delta t,\right)\to E\left(i,j\right), i=\mathrm{1,2},\ldots N , j=\mathrm{1,2},\ldots ,M.\)

To prevent error propagation, it is important to make sure that the temporal and spatial discretization, \(\Delta t\) and \(\Delta x\), are chosen small enough. Although this drastically increases the computational cost, it is required as the problem is non-linear and there is no obvious error criterion to be satisfied. For more information, reference (Taflove and Hagness 2005) can be useful.

Adaptive supercontinuum generation via non-linear programming

It is also possible to control the shape of the generated supercontinuum such that the spectral density of the excitation wave is maximized within a desired frequency interval or bandwidth at a certain time slot. This is done by discretizing Eqs. (3–6) in a recursive manner. To achieve this, the center frequency of the quasi-monochromatic excitation wave, the center frequency of the quasi-monochromatic pump wave, and the pump wave pulse modulation frequency are adaptively tuned within a certain bandwidth based on the constrained gradient descent algorithm as follows (Nocedal and Wright 2006):

$${{\varvec{v}}}^{\left(k\right)}=\left[{\nu }_{\mathrm{excitation}, } {\nu }_{\mathrm{pump}}, { \nu }_{modulation}\right]=\left[{\nu }_{1, } {\nu }_{2}, {\nu }_{3}\right] :\mathrm{ optimization \, parameter \, vector \, at \, the \, }k\mathrm{th \, iteration}.$$

Gradient descent update:

$${{\varvec{v}}}^{\left(k\right)}={{\varvec{v}}}^{\left(k-1\right)}-{\mu }_{k}\frac{f\left({{\varvec{v}}}^{\left(k-1\right)}\right)-f\left({{\varvec{v}}}^{\left(k-2\right)}\right)}{{{\varvec{v}}}^{\left(k-1\right)}-{{\varvec{v}}}^{\left(k-2\right)}}, f\left({{\varvec{v}}}^{\left(k\right)}\right): \mathrm{objective \, function}, { \mu }_{k}:\mathrm{step \, size}.$$
(11)

There are constraints on the tunability of each aforementioned frequency. This is to be set by the designer based on practical constraints. Consequently, each frequency can only be tuned within a certain bandwidth:

$${\nu }_{{\min},1 }<{\nu }_{1 }<{\nu }_{{\max},1}, {\nu }_{{\min},2 }<{\nu }_{2}<{\nu }_{{\max},2}, {\nu }_{{\min},3 }<{\nu }_{3}<{\nu }_{{\max},3}.$$

The objective function in this case, is the spectral density in a desired bandwidth that is bounded by a minimum frequency of \({\omega }_{1}\) and a maximum frequency of \({\omega }_{2}\), plus the penalty functions that quadratically decrease the objective function in cases of constraint violations, where the minimum or maximum frequency value is exceeded:

$$f\left({{\varvec{v}}}^{\left(k\right)}\right)=\left|E\left({\omega }_{1}<\Omega <{\omega }_{2}\right)\right|={\int }_{{\omega }_{1}}^{{\omega }_{2}}{\left|\left\{{\int }_{0}^{T}\{E(y={y}^{^{\prime}},t){e}^{-i\left(2\pi \Omega \right)t}\}dt\right\}\right|}^{2}d\Omega - \left\{{\sum }_{i=1}^{3}{\delta }_{i}{({\nu }_{i}-{v}_{{\max},i})}^{2}\right\}-\left\{{\sum }_{i=1}^{3}{\zeta }_{i}{\left({\nu }_{i}-{v}_{{\min}, i}\right)}^{2}\right\},$$
(12)
$${\delta }_{i}=\left\{\begin{array}{c}0 \, \, \mathrm{if} \,\, { \nu }_{i}<{v}_{{\max},i}\\ >0 \,\, \mathrm{if} \,\, {\nu }_{i}>{v}_{{\max},i}\end{array}\right\}, {\zeta }_{i}=\left\{\begin{array}{c}0 \,\, \mathrm{if} \,\, { \nu }_{i}>{v}_{{\min},i}\\ >0 \,\, \mathrm{if} \,\, {\nu }_{i}<{v}_{{\min},i}\end{array}\right\},$$
(13)
$$\Omega :\mathrm{frequency}, \left\{{\delta }_{i},{\zeta }_{i}\right\}:\mathrm{ penalty \, coefficients}.$$

Hence, the algorithm basically searches for the frequency parameters that shape the generated supercontinuum in such a way that the intensity is maximized at a target bandwidth. Based on the outlined algorithm, Eqs. (3–6) are solved as a function of the parameter vector \({{\varvec{v}}}^{\left(k\right)}\) for adaptive supercontinuum generation:

$${\nabla }^{2}E\left({{\varvec{v}}}^{\left(k\right)}\right)-{\mu }_{0}{\varepsilon }_{\infty }\frac{{\partial }^{2}E{({\varvec{v}}}^{\left(k\right)})}{{\partial t}^{2}}={\mu }_{0}{\sigma \frac{\partial E{({\varvec{v}}}^{\left(k\right)})}{\partial t}+\mu }_{0}\frac{{d}^{2}P{({\varvec{v}}}^{\left(k\right)})}{{\partial t}^{2}} ,$$
(14)
$$\frac{{d}^{2}{P}_{b}{({\varvec{v}}}^{\left(k\right)})}{{dt}^{2}}+{\gamma }_{b}\frac{d{P}_{b}{({\varvec{v}}}^{\left(k\right)})}{dt}+{{\omega }_{0}}^{2}{P}_{b}{({\varvec{v}}}^{\left(k\right)})-\frac{{{\omega }_{0}}^{2}{{P}_{b}}^{2}{({\varvec{v}}}^{\left(k\right)})}{{(Q-Q}_{f})ed}+\frac{{{\omega }_{0}}^{2}{{P}_{b}}^{3}{({\varvec{v}}}^{\left(k\right)})}{{{(Q-Q}_{f})}^{2}{e}^{2}{d}^{2}}=\frac{{{(Q-Q}_{f})e}^{2}E{({\varvec{v}}}^{\left(k\right)})}{m} ,$$
(15)
$$\frac{{d}^{2}{P}_{f}{({\varvec{v}}}^{\left(k\right)})}{{dt}^{2}}+{\gamma }_{f}\frac{d{P}_{f}{({\varvec{v}}}^{\left(k\right)})}{dt}=\frac{{{Q}_{f}e}^{2}E{({\varvec{v}}}^{\left(k\right)})}{m} ,$$
(16)
$$\frac{d{Q}_{f}}{dt}=G\left(t\right)-\frac{{Q}_{f}}{{\tau }_{r}}=\frac{c{\varepsilon }_{0}{{(E}_{p}(t,{{\varvec{v}}}^{\left(k\right)}))}^{2}}{2h{v}_{p}\Delta w}-A{Q}_{f}-B{{Q}_{f}}^{2}-C{{Q}_{f}}^{3}.$$
(17)

The step size \({\mu }_{k}\) is determined at each iteration with respect to the sufficient increase condition, such that

$$f({v}_{k+1})>f({v}_{k})+0.5{\mu }_{k}{\Vert \nabla {f}_{k}\Vert }^{2}.$$
(18)

In this case, Eqs. (14–17) must be solved recursively based on the gradient descent algorithm until the desired spectral density is obtained within a target frequency interval at a given time slot. It is important to note that the excitation frequency should not be tuned beyond the bandgap frequency of the semiconductor nano-antenna to avoid absorption as this might delay the formation of the supercontinuum. The outlined algorithm enables the optimal injection profile to be determined with respect to a given excitation wave frequency, pump wave frequency, and pump wave pulse modulation frequency, such that both the internal electric energy density and the rate of energy transfer to the excitation wave are simultaneously maximized within the desired bandwidth. From this aspect, the carrier injection rate modulation process not only enables the generation of an ultra-broadband supercontinuum, but also enables dynamic control over the shape of the generated supercontinuum.

Numerical simulation

In this section, supercontinuum generation via carrier injection rate modulation will be investigated based on the parameters of Gallum Arsenide (GaAs), which is the material of choice for the semiconductor nano-antenna. The high-intensity infrared (IR) excitation field \(E\) with a frequency of 300 THz, and the pulsed IR 400 THz pump field \({E}_{p}\) (50 pulses) are incident on the semiconductor nano-antenna as in the setting depicted in Fig. 4. Both the excitation and the pump wave are originated at y = 2.5 μm at time t = 0 s. The full configuration of the analysis is as follows (Saleh and Teich 2007; Boyd 2008; Wang et al. 2007):

Fig. 4
figure 4

Excitation of the semiconductor nano-antenna in a one-dimensional setting

Full size image
$$E\left(y=2.5 \, \mu \mathrm{m},t\right)=2 \times {10}^{10}\mathrm{cos}\left(2\pi ({3 \times 10}^{14})t\right)\left(u\left(t\right)- u\left(t-\Delta T\right)\right)\frac{\mathrm{V}}{\mathrm{m}}, \Delta T=5 \, \mathrm{ps}, u\left(t\right):\mathrm{unit \, step \, function},$$
$${E}_{p}\left(y=2.5 \, \mu \mathrm{m},t\right)=\sum_{k=0}^{49}2 \times {10}^{10}\mathrm{cos}\left(2\pi \left({4 \times 10}^{14}\right)t\right)\left(u\left(t-{k\Delta T}_{p}\right)- u\left(t-{k\Delta T}_{p}-0.05 \, \mathrm{ps}\right)\right)\frac{\mathrm{V}}{\mathrm{m}}, { \Delta T}_{p}=0.1 \, \mathrm{ps},$$
$$\mathrm{Spatial \, and \, temporal \, intervals \, of \, the \, simulation}: 0\le x\le 10 \, \mu \mathrm{m}, 0\le t\le 5 \, \mathrm{ ps},$$
$$\mathrm{Resonance \, frequency \, of \, GaAs}: {f}_{r}= 1.1 \times {10}^{15} \, \mathrm{Hz}, \, \mathrm{relative \, permittivity \, of \, GaAs}: \left({\varepsilon }_{\infty }\right)=13,$$
$$\mathrm{GaAs \, bandgap \, frequency}: {f}_{g}=345 \, \mathrm{ THz}, \, \mathrm{GaAs \, polarization \, damping \, rate \, for \, bound \, electrons}: {\gamma }_{b}=10 \, \mathrm{ MHz},$$
$$\mathrm{GaAs \, polarization \, damping \, rate \, for \, free \, electrons}: {\gamma }_{f}=10 \, \mathrm{MHz}, \, \mathrm{modulation \, frequency}:{f}_{p}=10 \, \mathrm{THz}=1/{\Delta T}_{p},$$
$$\mathrm{Spatial \, range \, of \, the \, semiconductor \, nanoantenna} :3 \, \mu \mathrm{m}<x<3.1 \, \mu \mathrm{m},$$
$$\mathrm{Left \, perfectly \, matched \, layer}: 0 \, \mu \mathrm{m}<x<2.25 \, \mu \mathrm{m}, \, \mathrm{ right \, perfectly \, matched \, layer}: 7.5 \, \mu \mathrm{m}<x<10 \, \mu \mathrm{m},$$
$$\mathrm{Electron \, density}: Q=3.5 \times \frac{{10}^{29}}{{\mathrm{m}}^{3}}, \, \mathrm{atom \, diameter}: d=0.3 \, \mathrm{nm},$$
$$\mathrm{Auger \, recombination \, coefficient}: C=\frac{{10}^{-45} \, { \mathrm{m}}^{6}}{\mathrm{s}},$$
$$\mathrm{Shockley}-\mathrm{Read}-\mathrm{Hall \, recombination \, coefficient}: A=\frac{{10}^{9}}{\mathrm{s}},$$
$$\mathrm{Radiative \, recombination \, coef}:B=\frac{{10}^{-18 \, }{\mathrm{ m}}^{3}}{\mathrm{s}} ,$$
$$\mathrm{Relative \, permittivity \, of \, glass}: \left({\varepsilon }_{r}\right)=3.75 \, {(\mu }_{r}=1), \, \mathrm{GaAs \, conductivity}: \sigma ={10}^{-4} \, \mathrm{S}/ \mathrm{m}.$$

Since the total simulation duration is 5 ps, an array of 50 pump-pulses with a pulse period of 0.1 ps and a pulse duration of 50 fs are used. The resulting supercontinuum pattern of the excitation field E is computed at x = 5.6 \(\mu \mathrm{m}\), which is the center point of the distance between the right perfectly matched layer and glass. The density of electrons, which is the number of atoms times the number of valence electrons, and the value of the recombination coefficients are chosen as approximate values for Gallium Arsenide (Saleh and Teich 2007; Boyd 2008; Wang et al. 2007). To solve for the electric field, Eqs. (7–10) are used. Constraints of memory have allowed for a spectral investigation of the generated supercontinuum up to 2000 THz with a resolution of 1 THz. The generated supercontinuum of the excitation wave, which encompasses all spectral regions from Far-IR to Deep-UV, is illustrated in Fig. 5. The reason for this extreme spectral widening is due to the carrier injection rate modulation via pulse modulated pump wave excitation, which enables an extreme accumulation of electric energy density by a sudden drastic increase in free electron density (hence the effective permittivity), while the excitation wave is fully present in the nano-antenna as a standing wave. When the electrons recombine, the electric energy in the nano-antenna suddenly decreases, but the difference in electric energy is transferred to the excitation wave. This transfer of energy to the excitation wave continues for each pump wave pulse period (for each excitation–recombination process) until the spectrum of the excitation wave spans the desired range. The number of the required pump wave pulses is decided based on the total spectral broadening time.

Fig. 5
figure 5

Generated supercontinuum for the excitation wave based on the given parameters

Full size image

If one decides to shape the supercontinuum such that the excitation wave spectrum becomes dominant in the Infra-Red region for example, then one can apply Eqs. (11–18) so that the spectral density is maximized within the infrared bandwidth (10 THz < f < 400 THz). Doing so, it is found that for an excitation frequency of f = 270.3 THz (other parameters are all kept the same), the supercontinuum emits strongly in the infrared region as shown in Fig. 6.

Fig. 6
figure 6

Excitation wave supercontinuum adapted for maximum IR emission

Full size image

Similarly, one can maximize the spectral density of the excitation wave in the ultraviolet range. Tuning the pump wave center frequency at 403.8 THz, the pump wave pulse modulation frequency at 8.86 THz, and the excitation wave frequency at f = 332.1 THz, the spectral intensity between 1200 THz < f < 1800 THz can be maximized as shown in Fig. 7. For the ultraviolet range, it is more challenging to increase the spectral density as the harmonic generation efficiency decreases with increasing frequency in a supercontinuum (Aşırım et al. 2020).

Fig. 7
figure 7

Excitation wave supercontinuum adapted for maximum UV emission

Full size image

It is important to emphasize that once the carrier injection rate modulation effect is removed or overrelaxed, a supercontinuum cannot be generated. An example of this is shown in Fig. 8, where the carrier injection rate is modulated via a much lower pump wave amplitude (\({E}_{p}={2 \times 10}^{7} \, \mathrm{V}/\mathrm{m}, \, \mathrm{ i}.\mathrm{e}., \, \mathrm{ decreased \, by \, a \, factor \, of \, }1000).\) Due to this lower pump wave amplitude, the supercontinuum generation effect subsides due to a negligible number of free electrons being modulated. This is because as more electrons are modulated (generated and recombined), permittivity change becomes greater, and more intensity can be stored/trapped and released in a continuous cycle. Hence, the accumulated field intensity yields to a stronger harmonic generation, and a subsequent wave mixing of different harmonics, resulting in the generation of a broader supercontinuum.

Fig. 8
figure 8

Excitation wave spectrum in the case of significantly decreased carrier injection rate (via decreasing the pump wave amplitude by a factor of 1000) based on the given parameters. The supercontinuum generation effect has subsided and only the excitation frequency and its second harmonic are dominant in the spectrum

Full size image

It should be noted that due to the high-intensity pulsed-pump operation, the noise that is generated by thermal emission via nonradiative electron recombination, is of minor concern. Hence, in this study, the discussion on thermal noise is omitted. Nevertheless, one should act cautiously when a pump wave of relatively low intensity is used, as thermal emission would be more pronounced in such a case.

Electric energy accumulation in the nano-antenna via carrier injection rate modulation

When the injection rate in a semiconductor material is constant, the steady-state operation is reached almost immediately (Saleh and Teich 2007). Therefore, the number of free electrons remains constant, which explains that the change in the electric energy due to free electrons is zero. Hence, no energy can be transferred to the excitation wave for a constant injection rate. However, when the injection rate is modulated, the number of free electrons is continuously changed via an initial increase and a subsequent decrease. Under injection rate modulation, the electrons gain their energy from the pump wave (source of injection) to reach the conduction band. When the electrons lose their energy, they decay back to the valence band where they resume their orbiting around the atom. If there is no excitation wave in the medium, the energy that is released by the recombining electrons can be dissipated as heat or spontaneous photon emission. When there is an excitation wave in the semiconductor medium, that is fully present in the medium as a standing wave pattern, some of the energy that is released by the recombined electrons is transferred to the excitation wave (Saleh and Teich 2007; Boyd 2008). Since, the effective permittivity is frequently increased by the carrier injection rate modulation, the excitation wave is preserved in the semiconductor material and continuously gains energy from the free electron modulation process. The excitation wave keeps on polarizing the free and bound electrons, which increases the energy density even further. The following example with the same structural (material) parameters as given in “Numerical simulation”, investigates this process:

Excitation wave: (pulse amplitude = 1 MV/m, pulse width = 5 ps, excitation frequency is to be tuned)

$$E\left(y=2.5 \, \mu \mathrm{m},t\right)=1 \times {10}^{6}\mathrm{cos}\left(2\pi ({f}_{\mathrm{excitation}})t\right)\left(u\left(t\right)- u\left(t-\Delta T\right)\right)\frac{\mathrm{V}}{\mathrm{m}}, \Delta T=5 \, \mathrm{ps}, u\left(t\right):\mathrm{unit \, step \, function}.$$

Pulse modulated pump wave for carrier injection rate modulation: (pulse amplitude = 30 GV/m, pulse width = 50 fs, pump frequency = 440 THz, pump-pulse period = 0.2 ps)

$${{E}_{p}}^{^{\prime}}\left(y=2.5 \, \mu \mathrm{m},t\right)=\sum_{k=0}^{25}3 \times {10}^{10}\mathrm{cos}\left(2\pi \left({4.4 \times 10}^{14}\right)t\right)\left(u\left(t-{k\Delta T}_{p}\right)- u\left(t-{k\Delta T}_{p}-0.05 \, \mathrm{ps}\right)\right)\frac{\mathrm{V}}{\mathrm{m}} ,$$
$${\Delta T}_{p}=0.2 \, \mathrm{ps}.$$

Pump wave without pulse modulation (no carrier injection rate modulation): (pulse amplitude = 30 GV/m, pump frequency = 440 THz)

$${E}_{p}=3 \times {10}^{10}\mathrm{cos}\left(2\pi \left({4.4 \times 10}^{14}\right)t\right)\left(u\left(t\right)- u\left(t-\Delta T\right)\right)\frac{\mathrm{V}}{\mathrm{m}}, \Delta T=5 \, \mathrm{ps}.$$

Semiconductor (GaAs) material parameters:

$$\mathrm{GaAs \, conductivity}: \sigma ={10}^{-4} \, \mathrm{S}/\mathrm{m},$$
$$\mathrm{Resonance \, frequency \, of \, GaAs}: {f}_{r}= 1.1 \times {10}^{15} \, \mathrm{Hz}, \, \mathrm{relative \, permittivity \, of \, GaAs}: \left({\varepsilon }_{\infty }\right)=13,$$
$${\mathrm{GaAs \, bandgap \, frequency}:f}_{g}=345 \, \mathrm{ THz}, \, \mathrm{GaAs \, polarization \, damping \, rate \, of \, bound \, electrons}: {\gamma }_{b}=10 \, \mathrm{ MHz},$$
$$\mathrm{GaAs \, polarization \, damping \, rate \, of \, \, free electrons}: {\gamma }_{f}=10 \, \mathrm{MHz},$$
$$\mathrm{Electron \, density}: Q=3.5 \times \frac{{10}^{29}}{{\mathrm{m}}^{3}}, \, \mathrm{atom \, diameter}: d=0.3 \, \mathrm{nm}, \, \mathrm{auger \, recombination \, coefficient}: C=\frac{{10}^{-45} \, {\mathrm{m}}^{6}}{\mathrm{s}},$$
$$\mathrm{Schockley}-\mathrm{Read}-\mathrm{Hall \, recombination \, coefficient}: A=\frac{{10}^{9}} {\mathrm{s}}, \mathrm{radiative \, recombination \, coef}:B=\frac{{10}^{-18} \, { \mathrm{m}}^{3}}{\mathrm{s}} ,$$
$${W}_{e}=\mathrm{Electric \, energy \, density}=\frac{1}{2}ED=\frac{1}{2}E\left({\varepsilon }_{0}E+P\right)=\frac{1}{2}{\varepsilon }_{0}{E}^{2}+\frac{1}{2}EP,$$
(19)

\(D:\mathrm{electric \, flux \, density}\), \(P:\mathrm{electric \, polarization \, density}\), \(E:\mathrm{electric \, field \, intensity},\) \({{W}_{e}}^{\mathrm{^{\prime}}}:\mathrm{electric \, energy \, density \, with \, carrier \, injection \, rate \, modulation }\left(\mathrm{measured \, at \, }x=5.6 \, \mu \mathrm{m}\right),\) \({W}_{e}:\mathrm{electric \, energy \, density \, without \, carrier \, injection \, rate \, modulation }\left(\mathrm{measured \, at \, }x=5.6 \, \mu \mathrm{m}\right).\)

The electric energy densities \({W}_{e}\) and \({{W}_{e}}^{^{\prime}}\) are computed in Table 2 with respect to the excitation wave frequency.

  • As seen in Table 2, the electric energy density is much greater for the case of modulated carrier injection rate for each excitation wave frequency.

  • Since the supercontinuum generation phenomena depends on the intra-material electric energy (Park 2009; Hanke et al. 2009; Sain et al. 2019; Adamu et al. 2019; Li et al. 2019), based on this result, it is concluded that the modulation of the carrier injection rate is essential for ultrabroad supercontinuum generation.

Table 2 Electric energy density with and without carrier injection rate modulation versus excitation wave frequency
Full size table

It is very important to state that the accumulation of a gigantic amount of electric energy density may cause optical damage to the semiconductor material under long durations of operation due to excessive heat dissipation. For this reason, a seperate heat monitoring/controlling system can be incorporated to the presented system for long durations of high-energy density operation. Additionally, excessive heat dissipation might also be beneficial for high-rate carrier injection via a higher rate of electron recombination, allowing for a faster operation speed. This can enable high-speed adaptive control over the generated supercontinuum pattern, provided that the degree of heat dissipation does not cause optical dielectric breakdown nor any other sort of serious optical damage.

Concerning the stability of the system, since the supercontinuum is generated within a duration of 5–10 ps based on the given parameters, the system should not be operated way beyond 10 ps for the generation of a single supercontinuum pattern to avoid excess energy accumulation that can harm the material. For adaptive supercontinuum shaping, the duty cycle of supercontinuum generation should be below 0.1% to prevent overheating (Adamu et al. 2019), (Wang and Zhang 2017).

Comparison with semiempirical results

The root of supercontinuum generation via an excitation wave is the second harmonic generation (SHG) process (Montesinos-Ballester et al. 2020; Hilligsøe et al. 2004). Hence for the verification of the analytical and the numerical model presented in this study, the computationally obtained results should be compared with experimental results in the context of second harmonic generation (SHG) efficiency. In the upcoming simulation, the second harmonic generation efficiency is computed via Eqs. (7–10) for different excitation wave intensities ranging from \({10}^{11} \, \mathrm{to} \, {10}^{16} \, \mathrm{W}/{\mathrm{m}}^{2}\)and the results are compared with the well-established semiempirical SHG-effiency formula (Saleh and Teich 2007; Boyd 2008; White et al. 1970) for computational error analysis.

Comparison of numerical and semiempirical second harmonic generation efficiencies

Assume that a 1 μm thick semiconductor slab, which acquires a free electron density via an ultraviolet (UV) pump wave, is stimulated by a high-intensity excitation wave with a frequency of 400 THz and a duration of 5 ps. Both the high-intensity excitation wave and the UV-pump are originated at \(y=2.5 \, \mu \mathrm{m}\) (see Fig. 9). The amplitude of the excitation wave at \(y=2.5 \, \mu \mathrm{m}\) varies as follows:

Fig. 9
figure 9

Time variation of the free and bound electron densities for the given configuration in 6.1

Full size image
$$E\left(y=2.5 \, \mu \mathrm{m},t\right)=A \times \mathrm{cos}\left(2\pi ({4 \times 10}^{14})t\right) \times \left(u\left(t\right)- u\left(t-\Delta T\right)\right)\frac{\mathrm{V}}{\mathrm{m}}, u\left(t\right):\mathrm{unit \, step \, function},$$
$$\Delta T=5 \, \mathrm{ps}, \, \mathrm{where}, \, {10}^{7}\le A\le {1.5 \times 10}^{9} \, \mathrm{V}/\mathrm{m}, \, \mathrm{such \, that} \, A=\{{10}^{7}, 2 \times {10}^{7}, 3 \times {10}^{7},\ldots ,1.5 \times {10}^{9}\}.$$

The UV-pump, which is greater in intensity, has a frequency of 900 THz and a duration of 5 ps:

$${E}_{p}\left(y=2.5 \, \mu \mathrm{m},t\right)=1.5 \times {10}^{11}\mathrm{cos}\left(2\pi ({9 \times 10}^{14})t\right)\left(u\left(t-{\Delta T}_{p}\right)\right)\frac{\mathrm{V}}{\mathrm{m}}, \, \mathrm{where} \, {\Delta T}_{p}=5 \, \mathrm{ps}.$$

The parameters of the simulation are given as follows:

$$\mathrm{Spatial \, and \, temporal \, intervals \, of \, the \, simulation}: 0\le x\le 10 \, \mu \mathrm{m}, 0\le t\le 5 \, \mathrm{ps},$$
$$\mathrm{Resonance \, frequency \, of \, the \, semiconductor \, slab}: {f}_{r}= 1.1 \times {10}^{15} \, \mathrm{Hz}, \, \mathrm{bandgap \, frequency}=500 \, \mathrm{THz},$$
$$\mathrm{Polarization \, damping \, rate \, of \, the \, semiconductor \, slab \, for \, bound}/\mathrm{free \, electrons}: {\gamma }_{b/f}=1 \times {10}^{10} \, \mathrm{ Hz},$$
$$\mathrm{Background \, permittivity \, of \, the \, semiconductor \, slab}: \left({\varepsilon }_{\infty }\right)=13 {(\mu }_{r}=1),$$
$$\mathrm{Spatial \, range \, of \, the \, semiconductor \, slab} :3.1 \, \mu \mathrm{m}<x<4.1 \, \mu \mathrm{m},$$
$$\mathrm{Left \, perfectly \, matched \, layer}:0 \, \mu \mathrm{m}<x<2.25 \, \mu \mathrm{m} , \mathrm{right \, perfectly \, matched \, layer} :7.5 \, \mu \mathrm{m}<x<10 \, \mu \mathrm{m},$$
$$\mathrm{ Density \, of \, valence \, electrons}: Q=2 \times \frac{{10}^{29}} \, {{\mathrm{m}}^{3}}, \, \mathrm{atom \, diameter}: d=0.3 \, \mathrm{nm},$$

\(\mathrm{Slab \, conductivity}: \sigma ={10}^{-4} \, \mathrm{S}/\mathrm{m}\), recombination coefficients: same values as given in “Numerical simulation”.

Based on this setting, the time variations of the free and bound electron densities are plotted in Fig. 9.

The goal is to compute the intensity of the generated second harmonic of the excitation wave (at 800 THz) using Eqs. (7–10, 21) and the experimental SHG efficiency formula that is given in Eq. (20) (Saleh and Teich 2007; Boyd 2008; White et al. 1970)

$${\upeta }_{\mathrm{exp}}={(\mathrm{ tanh}\sqrt{{d}^{2}{\eta }^{3}{\omega }^{2}cn{\varepsilon }_{0}{A}^{2}{L}^{2}} )}^{2} ,$$
(20)
$${\upeta }_{\mathrm{num}}=\frac{\mathrm{Intensity \, of \, the \, second \, harmonic \, at \, }t={t}_{{\max}}}{\mathrm{ Intensity \, of \, the \, first \, harmonic \, at \, }t=0 } ,$$
(21)

d = coefficient of nonlinearity \((\mathrm{C}/\mathrm{V})\), \(\eta\) = impedance of the medium, n = refractive index, A = excitation wave amplitude, L = length of the medium, \(\omega =\mathrm{excitation \, frequency }\left(\mathrm{angular}\right).\)

Since the coefficient of nonlinearity is a parameter that is given in the semiempirical formula (Eq. 20) but not in the analytical model, it must be precisely estimated. The equivalent coefficient of nonlinearity ‘d’ for the semiempirical formula can be accurately estimated by equating Eq. (20) to Eq. (21) at an arbitrary excitation amplitude (sample excitation amplitude). If the implementation of the numerical model is fully correct, then the results should also match for all amplitudes within the investigated set of excitation amplitudes. Here we have a set of 150 different excitation amplitudes. The equivalent coefficient of nonlinearity is estimated as \({d=2.33 \times 10}^{-23} \, \mathrm{C}/\mathrm{V}\) for a sample excitation amplitude of \({A=2 \times 10}^{9} \, \mathrm{V}/\mathrm{m}\). The corresponding numerical results based on Eqs. (7–10, 21) and the experimental results based on the semiempirical formula in Eq. (20) are compared in Fig. 10 and Table 3. From Fig. 10, we can see that the results tend to agree for higher excitation amplitudes, especially for excitation amplitudes that are greater than \(2 \times {10}^{8} \, \mathrm{V}/\mathrm{m}\), in which case the error percentage is less than 1%. The reason for the better agreement of the results for higher excitation amplitudes is that the semiempirical second harmonic generation efficiency (SHGE) formula itself is more accurate for higher excitation amplitudes. For lower excitation amplitudes, the second harmonic generation efficiency is so small that it can yield to very different results for the numerical and the semiempirical formulation. From Table 3, we can see that as the excitation amplitude is increased, the difference between the numerical results and the semiempirical results decreases and the error percentage remains below 0.3%.

Fig. 10
figure 10

Ratio of the semiempirical SHGE results to the numerical SHGE results versus excitation amplitude

Full size image
Table 3 Ratio of semiempirical results to the numerical results versus excitation amplitude
Full size table

Conclusion

A semiconductor nano-antenna is proposed as a nanoscale adaptive ultra-broadband supercontinuum-emitter. The presented structure can be used to dynamically generate a supercontinuum given that the carrier injection rate and hence the free electron density is properly modulated such that the pulse period of the high-power pump wave is at the same timescale with the electron recombination time of the semiconductor. When the free electron density is modulated at this rate, the excitation field induced electric energy can be efficiently accumulated in the semiconductor nano-antenna given that the density of free electrons undergoing modulation is sufficiently high. This is because the effective permittivity of the semiconductor nano-antenna is increased with an increase of the number of free electrons, which raises the captured electric energy density by the nano-antenna and yields to a better confinement of the excitation field intensity. After the accumulated field intensity and the electric energy density exceeds a certain threshold, a supercontinuum can be generated in the nano-antenna. The subsequent drop in the number of free electrons decreases the effective permittivity and leads to the release of the accumulated field intensity as a supercontinuum pattern. The results of this study indicate that semiconductor nano-antennas can be employed in small-scale integrated photonic devices for adaptive ultra-broadband supercontinuum generation.