Introduction

Nano/micro-actuators are wildly utilized in the micro/nanoelectro-mechanical systems (NEMS/MEMS). The resonators are a new type of electronic components which can oscillate in very high frequencies. A double-side resonator is a new type of resonators, composed of a movable electrode, placed between two conductive substrates (Mobki et al. 2013; Azimloo et al. 2014). Applying an external voltage difference between the moveable electrode and the substrates induces an electrostatic field which attracts the moveable electrode into the substrates (Mobki et al. 2013). The moveable electrode and the substrates can be seen as a capacitor (Ansari et al. 2014). The bucking of the moveable electrode does change the capacitive properties of the capacitors, which later can be detected by electronic systems.

Recently, the nano-actuators are applied as sensors for gas detection (Martin et al. 2014) and force measurement (Jóźwiak et al. 2012). They are also applied as gravimetric (Ekinci and Roukes 2005) and the biomolecular fingerprinting (Guthy et al. 2013) sensors. The nano-actuators are good potential candidates for NEMS nonvolatile memories (Choi et al. 2008) and switches (Dumas et al. 2011).

In nanoscale, the influence of the van der Waals attractions on the behavior of the actuator becomes significant when the separation space between the electrode and the substrate is very small (typically in separation spaces below 20 nm) (Mastrangelo and Hsu 1993). The van der Waals attraction is a function of the material properties and is proportional to the inverse cubic power of the separation space (Soroush et al. 2012; Farrokhabadi et al. 2013; Koochi et al. 2013; Sedighi and Daneshmand 2014). It is also demonstrated that the characteristics of the constructive material of miniature structures depend on the size of the structure. As NEMSs are very small in size, the size effect plays a considerable role on the behavior of these devices. Sadeghian et al. (2010) experimentally examined the size-dependent elastic behavior of silicon NEMS, and Beni et al. (2011) utilized the modified couple stress theory to study the size dependency for NEMS.

The presence of van der Waals attraction as well as the size effect inhere nonlinear effects, which can change the oscillating frequency of the nano-resonators. Therefore, analysis of these effects is crucial in sensing applications.

In a recent study, Fu et al. (2011) analyzed the nonlinear oscillation of a double-side micro-resonator subject to electrostatic forces. They found that an increase of the applied voltage difference between the electrode and substrate decreases the oscillating frequency of the system. In the present study, the work of Fu et al. (2011) is extended to a model for nano-resonators, considering the effects of van der Waals attractions and the size effects. The energy balance method is applied to obtain an analytical solution for the nonlinear oscillation of the double-side nano-resonators.

Mathematical model

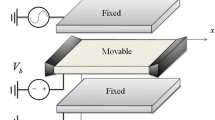
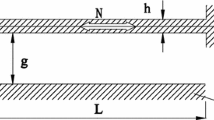
Consider a nano-resonator, composed of a moveable electrode and two fixed substrates. The moveable electrode could be considered as a clamped–clamped or a cantilever beam with a rectangular cross-section, embedded between two fixed substrates. A schematic view of a clamped–clamped resonator is illustrated in Fig. 1. The geometrical details are also shown in the figure.

Fig. 1
figure 1

The schematic view of a clamped–clamped nano-resonator and the geometrical details

Full size image

As seen, the resonator is symmetric, where g 0 is the initial gap space between the electrode and the substrates. There is a total logical applied external voltage difference, V, between the electrode (+V/2) and the substrates (−V/2). The governing equation of the nano-oscillator, considering the size effects, mid-plane stretching effects, and nonlinear forces, is written as (Fu et al. 2011; Noghrehabadi et al. 2013):

$$\left( {\hat{E}I + \mu bh\lambda^{2} } \right)\frac{{\partial^{4} \hat{w}}}{{\partial X^{4} }} + \rho bh\frac{{\partial^{2} \hat{w}}}{{\partial t^{2} }} = \chi_{\text{type}} \left( {N_{p} + \frac{{\hat{E}bh}}{2l}\int_{0}^{l} {\left( {\frac{{\partial \hat{w}}}{\partial X}} \right)^{2} {\text{d}}X} } \right)\frac{{\partial^{2} \hat{w}}}{{\partial X^{2} }} + F_{e} \left( {X,t} \right)$$
(1)

where \(\hat{w}\) is the displacement of the beam. \(\hat{N}\) is the axial force, and F e represents the nonlinear forces. μ is the shear modulus, λ is the length scale parameter, and ρ is the density of the moveable electrode. The effective modulus \(\hat{E}\) simply becomes the Young’s modulus (E) for narrow beams (\(\hat{w}\) < 5 h) and becomes the plate modulus E/(1 − υ 2) for wide beams (\(\hat{w}\) > 5 h) where υ is the Poisson ratio (Ramezani et al. 2007). χ type = 1 for a clamped–clamped beam, and χ type = 0 for a cantilever beam. The boundary conditions for a clamped–clamped beam are written as:

$$\hat{w}\left( {0,t} \right) = 0,\quad \frac{{\partial \hat{w}}}{\partial X}\left( {0,t} \right) = 0,\quad \hat{w}\left( {l,t} \right) = 0,\quad \frac{{\partial \hat{w}}}{\partial X}\left( {l,t} \right) = 0$$
(2a)

and for a cantilever beam as:

$$\hat{w}\left( {0,t} \right) = 0,\quad \frac{{\partial \hat{w}}}{\partial X}\left( {0,t} \right) = 0,\quad \frac{{\partial^{2} \hat{w}}}{{\partial X^{2} }}\left( {0,t} \right) = 0,\quad \frac{{\partial^{3} \hat{w}}}{{\partial X^{3} }}\left( {l,t} \right) = 0$$
(2b)

In Eq. (1), F e is the sum of the electrostatic forces (F elc), the fringing field effects (F fr), and the van der Waals force (F vdW). The electrical force per unit length of the beam can be evaluated as (Fu et al. 2011; Haung et al. 1993):

$$F_{\text{elec}} = \frac{{\varepsilon_{0} bV^{2} }}{2}\left( {\frac{1}{{\left( {g_{0} - \hat{w}} \right)^{2} }} - \frac{1}{{\left( {g_{0} + \hat{w}} \right)^{2} }}} \right)$$
(3)

where ε 0 is the permeability of the vacuum as 8.854187817620 × 10−12 C2 N−1 m−2 (Ramezani et al. 2007). The fringing field effect can also be evaluated as (Haung et al. 1993; Ramezani et al. 2007):

$$F_{\text{fr}} = 0.65\frac{{\varepsilon_{0} V^{2} }}{2}\left( {\frac{1}{{\left( {g_{0} - \hat{w}} \right)}} - \frac{1}{{\left( {g_{0} + \hat{w}} \right)}}} \right)$$
(4)

As mentioned, the van der Waals force per unit length of the beam is a cubic function of distance between the electrode and the substrate as (Ramezani et al. 2007):

$$F_{\text{vdW}} = \frac{Ab}{6\pi }\left( {\frac{1}{{\left( {g_{0} - \hat{w}} \right)^{3} }} - \frac{1}{{\left( {g_{0} + \hat{w}} \right)^{3} }}} \right)$$
(5)

where A is the Hamaker constant. The Casimir force per unit length of the beam is related to the inverse fourth power of distance between the electrode and substrate as (Ramezani et al. 2007):

$$F_{\text{Ca}} = \frac{{\pi^{2} { \rlap{-} h}{cb}}}{240}\left( {\frac{1}{{\left( {g_{0} - \hat{w}} \right)^{4} }} - \frac{1}{{\left( {g_{0} + \hat{w}} \right)^{4} }}} \right)$$
(6)

Invoking the following non-dimensional parameters:

$$\begin{aligned} w = \frac{{\hat{w}}}{g},\quad x = \frac{X}{l},\quad \tau = t\sqrt {\frac{{\hat{E}I}}{{\rho bhl^{4} }}} ,\quad \alpha_{\text{vdW}} = \frac{{Abl^{4} }}{{6\pi g_{0}^{4} \hat{E}I}},\quad \alpha_{\text{Ca}} = \frac{{\pi^{2} {\rlap{-} h}cbl^{4} }}{{240g_{0}^{5} \hat{E}I}}, \hfill \\ \delta = \frac{{\mu bh\lambda^{2} }}{{\hat{E}I}},\quad \gamma = 0.65\frac{g}{b},\quad N = \frac{{\hat{N}l^{2} }}{{\hat{E}I}},\quad \beta = \frac{{\varepsilon_{0} bV^{2} L^{4} }}{{2g_{0}^{3} \hat{E}I}},\quad \alpha = 6\left( {\frac{{g_{0} }}{h}} \right)^{2} . \hfill \\ \end{aligned}$$
(7)

the non-dimensional governing equation is obtained as:

$$\begin{aligned} \left( {1 + \delta } \right)\frac{{\partial^{4} w}}{{\partial x^{4} }} + \frac{{\partial^{2} w}}{{\partial \tau^{2} }} & = \chi_{\text{type}} \left( {N + \alpha \int_{0}^{1} {\left( {\frac{\partial w}{\partial x}} \right)^{2} {\text{d}}x} } \right)\frac{{\partial^{2} w}}{{\partial x^{2} }} \\ & \quad + \alpha_{\text{vdW}} \left( {\frac{1}{{\left( {1 - w} \right)^{3} }} - \frac{1}{{\left( {1 + w} \right)^{3} }}} \right) + \alpha_{Ca} \left( {\frac{1}{{\left( {1 - w} \right)^{4} }} - \frac{1}{{\left( {1 + w} \right)^{4} }}} \right) \\ & \quad + \beta \left( {\frac{1}{{\left( {1 - w} \right)^{2} }} - \frac{1}{{\left( {1 + w} \right)^{2} }}} \right) + \gamma \beta \left( {\frac{1}{1 - w} - \frac{1}{1 + w}} \right) \\ \end{aligned}$$
(8a)

subject to the following non-dimensional boundary conditions:

$$w\left( {0,\tau } \right) = 0,\quad \frac{\partial w}{\partial x}\left( {0,\tau } \right) = 0,\quad w\left( {1,\tau } \right) = 0,\quad \frac{\partial w}{\partial x}\left( {l,\tau } \right) = 0$$
(8b)

where δ and α vdw and α Ca show the non-dimensional size effect parameter, and the non-dimensional van der Waals parameter and the non-dimensional Casmir parameter, respectively. β and γ represent the non-dimensional electrostatic and the non-dimensional fringing field effects; N and α denote the non-dimensional axial load parameter and the non-dimensional stretching parameter, respectively. For a specific nano-resonator with defined design parameters (fixed geometry and material) the value of the non-dimensional voltage parameter (β) is directly a function of cubic value of the applied voltage. The non-dimensional axial load parameter (N) is a direct function of the internal force, which could be controlled by the synthesized method of fabricating the resonator. The values of the size effect parameter (δ) are mostly controlled with the length scale parameter (λ) which is a function of the material and size of the actuator. The values of the non-dimensional fringing field, stretching, Casimir, and van der Waals parameters are mainly a function of the geometry of the resonator and can be controlled by design parameters. The effect of variation of the non-dimensional parameters on the natural frequency of resonator will be analyzed in the present study. A general non-dimensional analysis provides results for understanding the behavior of different sizes and working voltages of nano-resonators.

Now, assuming \(w\left( {x,\tau } \right) = \phi \left( x \right)u\left( \tau \right)\), the solution of Eq. (1) is decomposed into two parts (Fu et al. 2011); where ϕ(x) is the first Eigen mode of the clamped–clamped beam and represents the geometrical shape of the resonator, and \(u\left( \tau \right)\) constricts the time-dependent part of the solution. The first Eigen mode, satisfying the boundary conditions beam, can be expressed by a polynomial as (Batra et al. 2006; Moghimi and Zand 2009):

$$\begin{aligned} \phi \left( x \right) & = 16x^{2} \left( {1 - x} \right)^{2} :{\text{Clamped}} -{\text{clamped}} \\ \phi \left( x \right) & = x^{2} \left( {\frac{1}{2} - \frac{x}{3} + \frac{{x^{2} }}{12}} \right):{\text{Cantilever}} \\ \end{aligned}$$
(9a)

or a harmonic expression as (Moghimi and Zand 2009):

$$\begin{aligned} \phi \left( x \right) & = \cos \,h\left( {\xi x} \right) - \cos \left( {\xi x} \right) - \frac{\cos \,h\left( \xi \right) - \cos \left( \xi \right)}{\sin \,h\left( \xi \right) - \sin \left( \xi \right)}\left( {\sin \,h\left( {\xi x} \right) - \sin \left( {\xi x} \right)} \right):{\text{Clamped}} - {\text{clamped}} \\ \phi \left( x \right) & = \cos \,h\left( {\xi x} \right) - \cos \left( {\xi x} \right) - \frac{\cos \,h\left( \xi \right) + \cos \left( \xi \right)}{\sin \,h\left( \xi \right) + \sin \left( \xi \right)}\left( {\sin \,h\left( {\xi x} \right) - \sin \left( {\xi x} \right)} \right):{\text{Cantilever}} \\ \end{aligned}$$
(9b)

where ξ = 4.730040745 for a clamped–clamped beam, and ξ = 1.8751 for a cantilever beam. Multiplying both sides of Eq. (8a) by \(\left( {1 - w} \right)^{4} \left( {1 + w} \right)^{4}\) and invoking \(w\left( {x,\tau } \right) = \phi \left( x \right)u\left( \tau \right)\) give

$$\begin{aligned} & \left( {1 + \delta } \right)\left( {1 - 4\phi^{2} u^{2} + 6\phi^{4} u^{4} - 4\phi^{6} u^{6} + \phi^{8} u^{8} } \right)\phi^{{\left( {iv} \right)}} u \\ & \quad + \left( {1 - 4\phi^{2} u^{2} + 6\phi^{4} u^{4} - 4\phi^{6} u^{6} + \phi^{8} u^{8} } \right)\phi \textit{\"{u}} \\ & \quad - N\chi_{\text{type}} \left( {1 - 4\phi^{2} u^{2} + 6\phi^{4} u^{4} - 4\phi^{6} u^{6} + \phi^{8} u^{8} } \right)\phi^{{\prime \prime }} u \\ & \quad - \chi_{\text{type}} \alpha \phi^{{\prime \prime }} \left( {1 - 4\phi^{2} u^{2} + 6\phi^{4} u^{4} - 4\phi^{6} u^{6} + \phi^{8} u^{8} } \right)\left( {\int_{0}^{1} {\phi^{{{\prime }2}} {\text{d}}x} } \right)u^{3} \\ & \quad - \alpha_{\text{Ca}} \left( {8\phi u + 8\phi^{3} u^{3} } \right) - \alpha_{\text{vdW}} \left( {6\phi u - 4\phi^{3} u^{3} - 2\phi^{5} u^{5} } \right) \\ & \quad - \beta \left( {4\phi u - 8\phi^{3} u^{3} + 4\phi^{5} u^{5} } \right) - \gamma \beta \left( {2\phi u - 6\phi^{3} u^{3} + 6\phi^{5} u^{5} - 2\phi^{7} u^{7} } \right) = 0 \\ \end{aligned}$$
(10)

Now, applying the Bubnov–Galerkin method (Batra et al. 2006; Moghimi and Zand 2009) gets

$$\int_{0}^{1} {\left( \begin{aligned} & \left( {1 + \delta } \right)\left( {1 - 4\phi^{2} u^{2} + 6\phi^{4} u^{4} - 4\phi^{6} u^{6} + \phi^{8} u^{8} } \right)\phi^{{\left( {iv} \right)}} u \\ & \quad + \left( {1 - 4\phi^{2} u^{2} + 6\phi^{4} u^{4} - 4\phi^{6} u^{6} + \phi^{8} u^{8} } \right)\phi \textit{\"{u}} \\ & \quad - \chi_{\text{type}} N\left( {1 - 4\phi^{2} u^{2} + 6\phi^{4} u^{4} - 4\phi^{6} u^{6} + \phi^{8} u^{8} } \right)\phi^{{\prime \prime }} u \\ & \quad - \chi_{\text{type}} \alpha \phi^{{\prime \prime }} \left( {1 - 4\phi^{2} u^{2} + 6\phi^{4} u^{4} - 4\phi^{6} u^{6} + \phi^{8} u^{8} } \right)\left( {\int_{0}^{1} {\phi^{{{\prime }2}} {\text{d}}x} } \right)u^{3} \\ & \quad - \alpha_{\text{Ca}} \left( {8\phi u + 8\phi^{3} u^{3} } \right) - \alpha_{\text{vdW}} \left( {6\phi u - 4\phi^{3} u^{3} - 2\phi^{5} u^{5} } \right) \\ & \quad - \beta \left( {4\phi u - 8\phi^{3} u^{3} + 4\phi^{5} u^{5} } \right) - \gamma \beta \left( {2\phi u - 6\phi^{3} u^{3} + 6\phi^{5} u^{5} - 2\phi^{7} u^{7} } \right) \\ \end{aligned} \right)} \phi \,{\text{d}}x = 0$$
(11)

Equation (10) can be simplified as:

$$\begin{aligned} & \left( {a_{2} - 4a_{4} u^{2} + 6a_{6} u^{4} - 4a_{8} u^{6} + a_{10} u^{8} } \right)\textit{\"{u}} \\ & \quad + \left( {\left( {1 + \delta } \right)b_{1} - \chi_{\text{type}} Nc_{1} - 8\alpha_{Ca} a_{2} - 6\alpha_{\text{vdW}} a_{2} - 4\beta a_{2} - 2\gamma \beta a_{2} } \right)u \\ & \quad + \left( { - 4\left( {1 + \delta } \right)b_{2} + 4\chi_{\text{type}} Nc_{2} - \chi_{\text{type}} \alpha c_{1} a_{0} - 8\alpha_{Ca} a_{4} + 4\alpha_{\text{vdW}} a_{4} + 8\beta a_{4} + 6\gamma \beta a_{4} } \right)u^{3} \\ & \quad + \left( {6\left( {1 + \delta } \right)b_{3} - 6\chi_{\text{type}} Nc_{3} + 4\chi_{\text{type}} \alpha c_{2} a_{0} + 2\alpha_{\text{vdW}} a_{6} - 4\beta a_{6} - 6\gamma \beta a_{6} } \right)u^{5} \\ & \quad + \left( { - 4\left( {1 + \delta } \right)b_{4} + 4\chi_{\text{type}} Nc_{4} - 6\chi_{\text{type}} \alpha c_{3} a_{0} + 2\gamma \beta a_{8} } \right)u^{7} \\ & \quad + \left( {\left( {1 + \delta } \right)b_{5} - \chi_{\text{type}} Nc_{5} + 4\chi_{\text{type}} \alpha c_{4} a_{0} } \right)u^{9} - \left( {\chi_{\text{type}} \alpha c_{5} a_{0} } \right)u^{11} = 0 \\ \end{aligned}$$
(12)

where the coefficients of a 1–a 10, b 1–b 5, and c 1–c 5 are given in “Appendix”. These coefficients can be evaluated using the first eigenmode ϕ(x) [i.e. either Eqs. (9a) or (9b)]. For convenience, Eq. (12) is rewritten in a more compact form as:

$$\left( {a_{2} - 4a_{4} u^{2} + 6a_{6} u^{4} - 4a_{8} u^{6} + a_{10} u^{8} } \right)\textit{\"{u}} + E_{1} u + E_{2} u^{3} + E_{3} u^{5} + E_{4} u^{7} + E_{5} u^{9} + E_{6} u^{11} = 0$$
(13)

where the coefficients E 1–E 6 are

$$\begin{aligned} E_{1} & = \left( {\left( {1 + \delta } \right)b_{1} - \chi_{\text{type}} Nc_{1} - 8\alpha_{Ca} a_{2} - 6\alpha_{\text{vdW}} a_{2} - 4\beta a_{2} - 2\gamma \beta a_{2} } \right) \\ E_{2} & = \left( { - 4\left( {1 + \delta } \right)b_{2} + 4\chi_{\text{type}} Nc_{2} - \chi_{\text{type}} \alpha c_{1} a_{0} - 8\alpha_{Ca} a_{4} + 4\alpha_{\text{vdW}} a_{4} + 8\beta a_{4} + 6\gamma \beta a_{4} } \right) \\ E_{3} & = \left( {6\left( {1 + \delta } \right)b_{3} - 6\chi_{\text{type}} Nc_{3} + 4\chi_{\text{type}} \alpha c_{2} a_{0} + 2\alpha_{\text{vdW}} a_{6} - 4\beta a_{6} - 6\gamma \beta a_{6} } \right) \\ E_{4} & = \left( { - 4\left( {1 + \delta } \right)b_{4} + 4\chi_{\text{type}} Nc_{4} - 6\chi_{\text{type}} \alpha c_{3} a_{0} + 2\gamma \beta a_{8} } \right) \\ E_{5} & = \left( {\left( {1 + \delta } \right)b_{5} - \chi_{\text{type}} Nc_{5} + 4\chi_{\text{type}} \alpha c_{4} a_{0} } \right) \\ E_{6} & = - \left( {\chi_{\text{type}} \alpha c_{5} a_{0} } \right) \\ \end{aligned}$$
(14)

An initial displacement with the magnitude of A and zero velocity can be assumed as initial conditions for Eq. (13):

$$u\left( 0 \right) = A,\quad \textit{\"{u}} \left( 0 \right) = 0$$
(15)

It is worth noticing that assuming such initial condition for the free vibration does not affect the final solution (Fu et al. 2011; Batra et al. 2006; Moghimi and Zand 2009). In the next section, the energy balance method is applied to obtain an analytical solution for Eq. (13) subject to the initial condition of Eq. (15).

Analytical solution using the energy balance method

The idea of the energy balance method comes from the fact that when θ = 0 the whole energy of the system is in form of the kinetic energy, and when θ = π/2 the whole energy of the system is in the form of the potential energy. Hence, in θ = π/4, a balance between the kinetic and the potential energy of the system can be assumed. The energy balance method utilizes the advantage of this point to collocate a solution at θ = π/4. More details of the energy balance method can be found in Mehdipour et al. (2010). Following the energy balance method, the variational principle of Eq. (13) is obtained as:

$$J\left( u \right) = \int_{0}^{\tau } { - \frac{1}{2} {\textit{\"{u}}^{2}}\left( {a_{2} - 4a_{4} u^{2} + 6a_{6} u^{4} - 4a_{8} u^{6} + a_{10} u^{8} } \right) + F\left( u \right)}$$
(16)

where J is the variational principle of Eq. (13) and F(u) is as follows:

$$F\left( u \right) = \int {\left( {E_{1} u + E_{2} u^{3} + E_{3} u^{5} + E_{4} u^{7} + E_{5} u^{9} + E_{6} u^{11} } \right){\text{d}}u}$$
(17)

The Hamiltonian of Eq. (16) is written as (Mehdipour et al. 2010):

$$H = \frac{1}{2}{\textit{\"{u}}^{2}} \left( {a_{2} - 4a_{4} u^{2} + 6a_{6} u^{4} - 4a_{8} u^{6} + a_{10} u^{8} } \right) + F\left( u \right) = F\left( A \right)$$
(18)

which can be extended as:

$$\begin{aligned} H & = \frac{1}{2}{\textit{\"{u}}^{2}} \left( {a_{2} - 4a_{4} u^{2} + 6a_{6} u^{4} - 4a_{8} u^{6} + a_{10} u^{8} } \right) \\ & \quad + \left( {\frac{1}{2}E_{1} u^{2} + \frac{1}{4}E_{2} u^{4} + \frac{1}{6}E_{3} u^{6} + \frac{1}{8}E_{4} u^{8} + \frac{1}{10}E_{5} u^{10} + \frac{1}{12}E_{6} u^{12} } \right) \\ & = \left( {\frac{1}{2}E_{1} A^{2} + \frac{1}{4}E_{2} A^{4} + \frac{1}{6}E_{3} A^{6} + \frac{1}{8}E_{4} A^{8} + \frac{1}{10}E_{5} A^{10} + \frac{1}{12}E_{6} A^{12} } \right) \\ \end{aligned}$$
(19)

Now, the following trial function is assumed to determine the angular frequency of the system (ω) (Mehdipour et al. 2010):

$$u\left( \tau \right) = A\;\cos \,\left( {\omega \tau } \right)$$
(20)

Substituting Eq. (20) in Eq. (19) yields

$$\begin{aligned} 0 & = \frac{1}{2}\left( { - A\omega \;\sin \left( {\omega \tau } \right)} \right)^{2} \left( {a_{2} - 4a_{4} \left( {A\;\cos \left( {\omega \tau } \right)} \right)^{2} + 6a_{6} \left( {A\;\cos \left( {\omega \tau } \right)} \right)^{4} - 4a_{8} \left( {A\;\cos \left( {\omega \tau } \right)} \right)^{6} + a_{10} \left( {A\;\cos \left( {\omega \tau } \right)} \right)^{8} } \right) \\ & \quad + \left( \begin{aligned} \begin{array}{*{20}l} {\frac{1}{2}E_{1} \left( {\left( {A\cos \left( {\omega \tau } \right)} \right)^{2} - A^{2} } \right) + \frac{1}{4}E_{2} \left( {\left( {A\;\cos \left( {\omega \tau } \right)} \right)^{4} - A^{4} } \right) + \frac{1}{6}E_{3} \left( {\left( {A\;\cos \left( {\omega \tau } \right)} \right)^{6} - A^{6} } \right)} \hfill \\ { + \frac{1}{8}E_{4} \left( {\left( {A\;\cos \left( {\omega \tau } \right)} \right)^{8} - A^{8} } \right) + \frac{1}{10}E_{5} \left( {\left( {A\;\cos \left( {\omega \tau } \right)} \right)^{10} - A^{10} } \right) + \frac{1}{12}E_{6} \left( {\left( {A\;\cos \left( {\omega \tau } \right)} \right)^{12} - A^{12} } \right)} \hfill \\ \end{array} \hfill \\ \end{aligned} \right) \\ \end{aligned}$$
(21)

where solving for ω gives

$$\omega = \sqrt {\frac{{\,\left( {\begin{array}{*{20}l} {\frac{1}{2}E_{1} \left( {\left( {A\;\cos \left( {\omega \tau } \right)} \right)^{2} - A^{2} } \right) + \frac{1}{4}E_{2} \left( {\left( {A\;\cos \left( {\omega \tau } \right)} \right)^{4} - A^{4} } \right)} \hfill \\ { + \frac{1}{6}E_{3} \left( {\left( {A\;\cos \left( {\omega \tau } \right)} \right)^{6} - A^{6} } \right) + \frac{1}{8}E_{4} \left( {\left( {A\;\cos \left( {\omega \tau } \right)} \right)^{8} - A^{8} } \right)} \hfill \\ { + \frac{1}{10}E_{5} \left( {\left( {A\;\cos \left( {\omega \tau } \right)} \right)^{10} - A^{10} } \right) + \frac{1}{12}E_{6} \left( {\left( {A\;\cos \left( {\omega \tau } \right)} \right)^{12} - A^{12} } \right)} \hfill \\ \end{array} } \right)}}{{ - 2A\sin \left( {\omega \tau } \right)^{2} \left( \begin{aligned} a_{2} - 4a_{4} \left( {A\;\cos \left( {\omega \tau } \right)} \right)^{2} + 6a_{6} \left( {A\;\cos \left( {\omega \tau } \right)} \right)^{4} \hfill \\ - 4a_{8} \left( {A\;\cos \left( {\omega \tau } \right)} \right)^{6} + a_{10} \left( {A\;\cos \left( {\omega \tau } \right)} \right)^{8} \hfill \\ \end{aligned} \right)}}} .$$
(22)

Finally, collocating at ωτ = π/4 results

$$\omega = \frac{1}{30}\,\sqrt {\frac{{4725E_{6} A^{10} + 5580E_{5} A^{8} + 6750E_{4} A^{6} + 8400E_{3} A^{4} \, + 10800E_{2} A^{2} + 14400E_{1} }}{{16a_{2} - 32a_{4} A^{2} + 24a_{6} A^{4} - 8A_{8} A^{6} + a_{10} A^{8} }}}$$
(23)

Substituting the obtained value of ω into Eq. (19) leads to the equation of motion of the resonator as:

$$u\left( \tau \right) = A\cos \left( {\frac{1}{30}\,\sqrt {\frac{\begin{aligned} 4725E_{6} A^{10} + 5580E_{5} A^{8} + 6750E_{4} A^{6} \hfill \\ + 8400E_{3} A^{4} \, + 10800E_{2} A^{2} + 14400E_{1} \hfill \\ \end{aligned} }{{16a_{2} - 32a_{4} A^{2} + 24a_{6} A^{4} - 8A_{8} A^{6} + a_{10} A^{8} }}} \tau } \right)$$
(24)

It is worth noticing that ω is a function of the non-dimensional time (τ). The angular frequency in the unit of Hz can be easily obtained as ω(Hz) = ω(τ) × τ.

Validation of the solution

Neglecting the size effect, the fringing field effect, and the van der Waals effect, i.e. δ = γ=α vdW = 0, the present study reduces to the analysis of a micro-resonator, which was examined by Fu et al. (2011). A comparison between the results of the present study and those reported by Fu et al. (2011) is performed in Fig. 2 when δ = 0, γ = 0, α vdW = 0, N = 10, α = 24, A = 0.01 and for two different values β = 25 and β = 100. In addition, the differential Eq. (13) subject to the initial conditions of Eq. (15) is solved using the 4th-order Runge–Kutta method in the present study. The details of the 4th-order Runge–Kutta method have been extensively described in Butcher (2008) and Tan and Chen (2012). The numerical results are also plotted in Fig. 2.

Fig. 2
figure 2

A comparison between the results of the analytical solution, 4th-order Runge–Kutta and Fu et al. Sadeghian et al. (2010) for a clamped–clamped micro-resonator

Full size image

As seen, there is an excellent agreement between the present analytical solution, the 4th-order Runge–Kutta solution, and the results reported by Fu et al. (2011) for a clamped–clamped beam. It is worth noticing that β = 25 and β = 100 correspond to V = 10 and V = 20 in the study of Fu et al. (2011). In practice, the resonators are designed to work with very low amplitudes to save the energy consumption and prevent the mechanical failure of the resonator. Hence, the values of the initial displacement, A, are very small and preferably lower than 10−2.

A comparison between the analytical results, evaluated using Eq. (23), and the results of 4th-order Runge–Kutta method is depicted in Fig. 3 for a nano-resonator when δ = 0.5, γ = 0.65, N = 10, α = 24, β = 25, and A = 0.01. The results are plotted for three selected values of the van der Waals parameter (α vdW).

Fig. 3
figure 3

A comparison between the results of the analytical solution and 4th-order Runge–Kutta method for a clamped–clamped nano-resonator

Full size image

As seen, this figure indicates excellent agreement between the analytical and numerical results in the presence of van der Waals, fringing field effect, and size effects. Therefore, the analytical solution, Eq. (23), is utilized to analyze the influence of the van der Waals, fringing field, and size effects on the resonator frequency.

The results of Figs. 2 and 3 are obtained using the eigenmode proposed in Eq. (9a). The results were also computed using the eigenmode of Eq. (9b). Very slight differences were observed between the results of these two eigenmodes. Thus, for convenience, Eq. (9b) is utilized as the eigenmode to compute the results of the next section. The results in the following section of the paper are evaluated using the analytical solution reported in Eqs. (23) and (24).

Results and discussion

Figure 4 shows the effect of van der Waals parameter (α vdW) on the frequency of the resonator for selected values of the electrostatic parameter (β). This figure indicates that the increase of the applied voltage (electrostatic parameter) or the intermolecular forces (van der Waals parameter) reduces the working frequency of the resonator. Indeed, Fig. 5 depicts the influence of the van der Waals parameter on the frequency of the resonator for different values of the axial force parameter (N), the fringing field effect parameter (γ), the size effect parameter (δ), and the Casimir parameter.

Fig. 4
figure 4

Effect of van der Waals parameter on the frequency of the clamped–clamped nano-resonator for selected values of the voltage parameter

Full size image
Fig. 5
figure 5

The frequency of the clamped–clamped nano-resonator as a function of the van der Waals parameter (α vdW) for different values of the axial force (N) parameter, the fringing field effect parameter (γ), Casimir parameter (α Ca), and the size effect parameter (δ)

Full size image

Figure 5 depicts that the non-dimensional parameters exert significant effects on the prediction of the natural frequency of the resonator. As seen, the variation of natural frequency is a nonlinear function of the van der Waals parameter. This is because of the nonlinear nature of this force. The presence of the fringing field effect reduces the frequency of the resonator (comparison between the curves 1 and 2). The presence of the fringing field increases the magnitude of the acting forces on the electrode, and hence, it decreases the oscillation frequency of the resonator. In contrast, an increase of the axial load parameter increases the oscillation frequency. The presence of an axial load increases the stiffness of the electrode, which results in the augmentation of the oscillation frequency (comparison between the curves 1 and 3). The comparison between curves of 1 and 4 indicates that the presence of the size effect raises the frequency of the system. As the size of the electrode decreases, the size effect increases the stiffness of the system, which leads to the increase of the oscillation frequency. Comparison between the curves of 4 and 5 reveals that the presence of the Casimir force reduces the oscillating frequency of the oscillator. The Casimir force increases the magnitude of the absorption force acting on the actuator, and hence, the oscillating frequency decreases.

Figures 4 and 5 show that for high values of the van der Waals and electrostatic parameters, the resonator frequency suddenly drops to zero, which indicates the occurrence of the pull-in instability. The presence of axial load and size effects tends to postpone the pull-in instability through the increase of the stiffness of the system. In contrast, the presence of external loads tends to unstable the resonator.

Figure 6 depicts the effect of Casimir force (α Ca) on the non-dimensional frequency of the resonator (ω(τ)) for selected values of the van der Waals (α vdW) force. As seen, this figure in agreement with Fig. 5 shows that the increase of the Casimir parameter reduces the natural frequency of the resonator. Comparison between Figs. 5 and 6 shows that the variation of the natural frequency of the actuator with variation of the Casimir parameter is more nonlinear than that of the van der Waals parameter. This is because of the fact that the van der Waals force is related to the cubic inverse of the distance between electrodes, but the Casimir force is a function of the fourth power inverse of the distance between the electrodes.

Fig. 6
figure 6

Effect of Casimir parameter on the frequency of the clamped–clamped nano-resonator for selected values of the van der Waals parameter

Full size image

Figures 7 and 8 show the effect of van der Waals, Casimir, and voltage parameters on the frequency of cantilever nano-resonators. As seen, the increase of the van der Waals, Casimir, and applied voltage parameter reduces the natural frequency of the resonator. However, the magnitude of these parameters is much smaller those for the case of clamped–clamped nano-oscillators. The maximum applicable value of van der Waals, Casimir, and voltage parameters for a cantilever beam resonator, in which the resonator could possibly remain stable, is of order 10. However, attention to Figs. 4 and 6 indicates that the applicable value of van der Waals, Casimir, and voltage parameters for a cantilever beam resonator is order of 100. In addition, the natural frequency of clamped–clamped actuators is also much higher than that of the cantilever ones. These differences are because of the fact that the stiffness of a cantilever beams is much lower than that of the clamped–clamped ones. Hence, the clamped–clamped type resonators are more of interest as resonators in devices with high frequencies and high-voltage systems. The cantilever types are of interest in devices with lower frequencies and low-voltage systems.

Fig. 7
figure 7

Effect of van der Waals parameter on the frequency of a cantilever nano-resonator for selected values of the voltage parameter

Full size image
Fig. 8
figure 8

Effect of Casimir parameter on the frequency of the cantilever nano-resonator for selected values of the van der Waals parameter

Full size image

Conclusion

The resonant frequency of clamped–clamped and cantilever double-side nano-resonator is analyzed in the presence of the van der Waals force, Casimir force, size effects, the electrostatic force, the fringing field effect, the mid-plane stretching effect, and axial loads. The energy balance method is successfully applied to obtain a very compact and accurate analytical solution for resonant frequency of resonators as a function of non-dimensional parameters. The results of the analytic solution and Runge–Kutta method in the present study were compared with those reported in the literature and found in excellent agreement. It is found that an increase of the electrostatic parameter, the van der Waals parameter, Casimir parameter, or the fringing field parameter would reduce the resonant frequency of the nano-resonator. In contrast, an increase of the size effect parameter or the axial load parameter would decrease the resonant frequency of a nano-resonator. The resonant frequency of a cantilever resonator is much lower than that of a clamped–clamped one.