Introduction

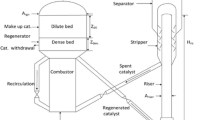
The residue fluid catalytic cracking unit (RFCCU) of Khartoum Refinery Company (KRC) uses conradson carbon residue and metal-contaminated feedstocks (such as atmospheric residue or mixtures of vacuum residue and gas oils) to produce more valuable products (especially gasoline) using active zeolite catalyst in a circulating fluidized bed [1]. In the RFCCU, the oil feed and dispersion steam enter the catalytic riser reactor together with the regenerated catalyst, where cracking of vacuum residue into lighter hydrocarbons starts as it contacts the hot regenerated catalyst from the regenerator. The regenerated catalyst is made to rise by steam introduced at the base of the riser reactor between the regenerator and the feed inlet point. The vaporized feed and the catalyst pass through the riser reactor into disengager for cracked products and catalyst separation. During the cracking process, coke is deposited on the catalyst, and the spent catalyst flows down by gravity into the regenerator, where air is used to burn off the coke deposited on the catalyst in a combustion environment so that it is returned to a stable state for catalysing the cracking reaction. The hot regenerated catalyst is then re-injected into the base of the riser reactor [2]. The complexity of the typical FCCU feed makes it extremely difficult to characterize and describe the inherent kinetics at a molecular level. In this way, similar components are grouped into lumps. Therefore, lumping scheme has been used to study the reactions involved in the catalytic cracking of heavy oil. To give an insight into a comprehensive prediction of products’ distribution, there is an increasing number of lumps of the proposed models for catalytic cracking reactions [3]. In the first kinetic model of Weekman [4, 5] for catalytic cracking of heavy oil, three lumps were identified as gas oil (feedstock), gasoline, and light gas + coke as products, without incorporating diffusion characteristics of solid and gas phases. Lee et al. [6, 7] modified the three-lump model by splitting the light gas + coke lump into two different lumps of C1–C4 gas and coke; therefore, resulting in the four-lump model for catalytic cracking of heavy oil. Corella and Frances [8] developed a five-lump model, in which the gas oil lump was divided into its heavy and light fractions. Different modified versions of five-lump model were developed by Dupain et al. [9], Kraemer et al. [10], and Ancheyta et al. [11]. Other proposed kinetic models for catalytic cracking of heavy oil include: 6-lump [1, 12,13,14,15], 8-lump [16], 10-lump [17, 18], 11-lump [19], 13-lump [20], 14-lump [21], and 19-lump [22], without taking cognisance of diffusion resistance. A comprehensive review was presented by Pinheiro et al. [23] on the subject of fluid catalytic cracking process modelling, simulation, and control. Obviously, the number of lumps of the proposed kinetic models for catalytic cracking of heavy oil may be increased to obtain more detailed descriptions of the catalytic cracking reactions and product distribution [24, 25]. However, sparing kinetic investigations have been carried out with the incorporation of diffusion resistances. Taking into account mass and heat transfer resistances between the reacting fluid and solid phases helps with conceiving the lump concentration on the catalyst surface as well as temperature profiles of the fluid and solid phases. Flinger et al. [26] considered mass transfer between the fluid and solid phases in the FCCU-riser reactor model equation. Gupta and Subba Rao [27] and Nayak et al. [28] applied the relationship for Sherwood number proposed by Ranz and Marshall [29] in their model to demonstrate the effects of mass transfer. The lump concentration within the catalyst is reduced by intraparticle mass transfer. In this way, the presence of an internal concentration gradient reduces the average rate of cracking [30]. Pruski et al. [31] validated adsorption coefficients for the four-lump model of catalytic cracking of gas oil. Bidabehere and Sedran [32] set up a model to investigate the impacts of diffusion, adsorption, and reaction at high temperature inside commercial FCC catalyst pellets and analysed the significance of these phenomenon. Dupain et al. [9] discussed external and internal mass transfer relationships utilised for FCC riser.

Many of the mathematical models in the literature describe the riser reactor with one-dimensional mass, energy, and chemical species balances [33,34,35,36], which was employed in this study to a commercial Khartoum Refinery Company RFCCU using seven-lump kinetics of catalytic cracking of vacuum residue with the incorporation of mass and heat transfer resistances, which is a deviation from the general norm in the literature. The unit is an all continuous process that operates 24 h a day for as long as 3–5 years between scheduled shutdowns for routine maintenance. Table 1 presents KRC–RFCCU feed properties [37].

Table 1 Characteristics of vacuum residue feedstock [37]
Full size table

The modelling of a riser reactor is very complicated owing to the many complex reactions occurring in it, coupled with mass and heat transfer resistances, and catalyst deactivation kinetics. Therefore, a complete model of the riser reactor should include all the important physical phenomena and detailed reaction kinetics. In this study, a one-dimensional adiabatic mathematical model of the riser-type of KRC–RFCCU was developed containing the following components: kinetic model of the catalytic cracking of vacuum residue, catalyst deactivation model, comprehensive hydrodynamic model of the riser reactor, material, force, and energy balances. The simulated results from the model were validated by comparison with industrial RFCCU-riser reactor vacuum residue conversion and yield data. Moreover, the effects of catalyst-to-oil ratio, COR, on catalyst residence time at different input temperatures of catalyst, as well as the effect of different inlet temperatures of catalyst-on-catalyst residence time at different CORs were investigated with a view to providing succinct information on catalyst management and minimizing losses.

Development of mathematical models for riser reactor an industrial residue fluid catalytic cracking unit

Figure 1 shows the schematic diagram of the RFCCU-riser reactor of the Khartoum Refinery Company. The mathematical model of the riser-type RFCCU contains the following components: kinetic model of the catalytic cracking of vacuum residue, material balance, hydrodynamic model of the riser reactor, force balance, deactivation catalyst model and the energy balance.

Fig. 1
figure 1

Schematic diagram of the RFCCU-riser reactor: P represents gas and solid to the stripper and separator

Full size image

Kinetics of catalytic cracking of vacuum residue in the riser reactor of RFCCU

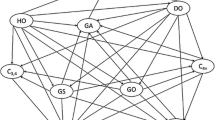
The seven-lump kinetic model for catalytic cracking of vacuum residue, as given by Xu et al. [14], is shown in Fig. 2. The model is divided into VR (vacuum residue, > 500 °C), VGO (vacuum gas oil, 350–500 °C)/HFO (heavy fuel oil, 350–500 °C), LFO (light fuel oil, 200–350 °C), GA (gasoline, ≈ 200 °C), liquefied petroleum gas (LPG), dry gas (DG), and CK (coke) according to their distillation ranges [14]. In the present study, the model was modified to include the formation of coke from gasoline and LPG independently as demonstrated by Xiong et al. [13] and Dasila et al. [39], respectively. However, to modify a kinetic scheme, parameter estimation of the inherent kinetic parameters needs to be performed using a powerful and robust optimization routine owing to differences in the feed and operating conditions, catalyst type etc. Due to the encumbrances involved in setting up of an experiment to determine the kinetic parameters for the formation of coke from gasoline and LPG separately, the kinetic parameters of these reactions were adopted from the work of Xiong et al. [13] and Dasila et al. [39], which entailed the kinetics of the catalytic cracking of vacuum residue in RFCCU-riser reactor. Our work then demonstrated that incorporation of these kinetic parameters led to good agreement between our simulated results and the plant data, giving justification to the fact that these reaction pathways could not be ignored in the catalytic cracking of heavy oil, as done in most works in the literature.

Fig. 2
figure 2

Seven-lump model of vacuum residue catalytic cracking in the riser reactor [14]

Full size image

In Fig. 2, it was assumed that chemical reactions are the rate-determining steps, and that catalytic cracking of vacuum residue and other reactions are irreversible first-order. All reactions take place in the gas phase. Moreover, mass transfer resistance between the reacting fluid and the catalyst are incorporated in the kinetic model, as against previous works in the literature. The specific reaction rate constant, \(k_{\text{r}} ( = k_{i,j} )\), of the reaction from lump i to lump j as depicted in Fig. 2 was modified by multiplying each of them by the effectiveness factor, \(\eta\), and the parallel additive of rate constants and mass transfer coefficient, \(k_{\text{g}}\) was used to determine the overall rate constant for the reaction of lump i to lump j, as given in Eqs. (9) or (10). Equally, heat transfer resistance between the reacting fluid and the solid (catalyst and coke) was considered in the energy balance for the riser reactor, as expressed in Eqs. (63), (64), and (69).

The magnitude of the effectiveness factor, \(\eta\), \(\left( {0\, < \,\eta \, < \,1} \right)\) indicates the relative importance of diffusion and reaction limitations. The internal effectiveness factor of the particle, \(\eta\), is defined as [30]:

$$\eta \,\, = \,\,\frac{{{\text{rate}}\,\,{\text{of}}\,\,{\text{reaction}}\,\,{\text{with}}\,\,{\text{diffusion}}\,\,{\text{resista}}{\text{nce}},\,\,r_{{{\text{p}},i}}^{\prime } }}{{{\text{rate}}\,\,{\text{of}}\,\,{\text{reaction}}\,\,{\text{without}}\,\,{\text{diffusion}}\,\,{\text{resista}}{\text{nce}},\,\,r_{i}^{\prime } }},$$
(1)
$$r_{{{\text{p}},i}}^{\prime } \, = \,\eta r_{i}^{\prime } ,$$
(2)

The particle effectiveness factor, \(\eta\), is a direct measure of the extent to which diffusion resistance reduces the rate of chemical reactions in heterogeneous catalysis and it is a function of Thiele modulus. Thiele modulus, \(\varphi\), is a measure of the ratio of intrinsic reaction rate to diffusion rate and as such Eq. (2) provides a yardstick for determining the rate-determining step in heterogeneous catalysis. The Thiele modulus, \(\varphi\), for an nth-order reaction in a spherical pellet is given by Smith [30]:

$$\phi_{n} = R\sqrt {\frac{{k_{n}^{\prime \prime } S_{\text{a}} \rho_{\text{cat}} c_{A0}^{n - 1} }}{{D_{\text{e}} }}} = R\sqrt {\frac{{k_{n} c_{A0}^{n - 1} }}{{D_{\text{e}} }}} .$$
(3)

However, the internal effectiveness factor for a first-order reaction in a spherical catalyst pellet is given by Smith [30]:

$$\eta = \frac{3}{{\phi_{1}^{2} }}\left( {\phi_{1} \coth \;\phi_{1} - 1} \right).$$
(4)

The rate of reaction of component A based on the interfacial surface area, \(r_{Ai}\), of a fluid reacting on active centres at the surface of a solid for a first-order, irreversible reaction is:

$$r_{Ai} = k_{r} y_{Ai} .$$
(5)

Using Eq. (5) in Eq. (1), we have:

$$r_{{{\text{p}},i}}^{\prime } = \eta k_{\text{r}} y_{Ai} .$$
(6)

The consumption of A at the interface has to be compensated for by transport from the bulk fluid, the flux, \(N_{A}\), of which is given by:

$$N_{A} = k_{\text{g}} \left( {y_{A} - y_{Ai} } \right).$$
(7)

When both diffusion and reaction resistances are significant, at steady state, the two rates in Eqs. (6) and (7) are equal, that is: \(r_{{{\text{p}},i}}^{\prime } = N_{A}\), so we have:

$$y_{Ai} = \frac{{k_{\text{g}} }}{{\eta k_{\text{r}} \, + \,k_{\text{g}} }}y_{A} .$$
(8)

Hence, for a first-order irreversible reaction, the rate of formation of component i, with the incorporation of mass transfer resistance and effectiveness factor, was obtained as [30]:

$$r_{{{\text{p}},i}}^{\prime } = \left( {\frac{1}{{k_{\text{g}} }} + \frac{1}{{\eta k_{i,j} }}} \right)^{ - 1} y_{i} \equiv (k_{0} )_{m} y_{i} ,$$
(9)

where an overall rate coefficient for mass transfer, \((k_{0} )_{m}\), is defined thus [30]:

$$(k_{0} )_{m} = \frac{{\eta k_{i,j} k_{\text{g}} }}{{\eta k_{i,j} \, + k_{\text{g}} }}.$$
(10)

Catalyst deactivation model

In this study, time-on-stream-based catalyst deactivation (or activity) function, \(\phi (t_{\text{c}} ),\) was used to describe RFCCU catalyst deactivation, and is given by Jacob et al. [17] as:

$$\phi (t_{\text{c}} ) = {1 \mathord{\left/ {\vphantom {1 {\left( {1\, + \,\beta t_{\text{c}}^{\gamma } } \right)}}} \right. \kern-0pt} {\left( {1\, + \,\beta t_{\text{c}}^{\gamma } } \right)}},$$
(11)

which is the ratio of the rate of reaction on a catalyst that has been used for a time, \(t_{\text{c}} ,\) \(\left[ { - r_{i}^{\prime } (t_{\text{c}} )} \right],\) to the rate of reaction on a fresh catalyst \((t_{\text{c}} = 0),\) \(\left[ { - r_{i}^{\prime } (t = 0)} \right],\) when there are no diffusion limitations:

$$\phi (t_{\text{c}} ) = \frac{{ - r_{i}^{\prime } (t_{\text{c}} )}}{{ - r_{i}^{\prime } (t_{\text{c}} = 0)}}.$$
(12)

Using Eq. (11) in Eq. (12), we have:

$$- r_{i}^{\prime } (t_{\text{c}} ) = \left[ { - r_{i}^{\prime } (t_{\text{c}} = 0)} \right]\phi (t_{\text{c}} ).$$
(13)

Also, \(f(N)\) and \(f(A)\) are functions describing the poisoning effect of basic nitrogen and the adsorption effect of aromatics, resins, and asphaltene on the reaction rates, respectively, and they are respectively given by Xu et al. [14] as:

$$f(N) = \frac{1}{{1 + K_{N} w_{N} }},$$
(14)
$$f(A) = \frac{1}{{1 + K_{A} w_{A} }}.$$
(15)

Hence, the rate of disappearance of lump i, \(\left[ { - r_{i}^{\prime } (t_{\text{c}} )} \right],\) was obtained by combining Eqs. (13)–(15) thus:

$$- r_{i}^{\prime } (t_{\text{c}} ) = \left[ { - r_{i}^{\prime } (t_{\text{c}} = 0)} \right]\phi (t_{\text{c}} )f(N)f(A).$$
(16)

Continuity equation of component in riser reactor of RFCCU

Mass balance was taken over the elemental volume of the riser reactor depicted in Fig. 1. At the riser entrance, the vacuum residue vaporizes owing to the heat transferred to it by both the dispersion steam and the regenerated catalyst. Each volume element of the riser thus contains both gas phase (i.e., the vaporized gas oil and steam) and solid phase (i.e., the catalyst and coke). The component mass balance taken over an elemental volume of the riser for each lump was obtained using the equation of continuity, thus:

$$\left( {\frac{{\partial \rho_{\text{g}} c_{i} }}{\partial t}} \right)_{z} + G_{\text{v}} \left( {\frac{{\partial c_{i} }}{\partial z}} \right)_{\text{t}} = r_{{{\text{p}},i}}^{\prime } ,\quad i = {\text{VR}},{\text{VGO}},{\text{LFO}},{\text{GA}},{\text{LPG}},{\text{DG}},{\text{CK,}}$$
(17)

where

$$G_{\text{v}} = \frac{{F_{\text{g}} }}{{A_{\text{R}} }} = \frac{{F_{\text{stm}} + \sum\nolimits_{i = 1}^{6} {F_{i} } }}{{A_{\text{R}} }} = \frac{{S_{\text{v}} L\rho_{\text{c}} }}{{ \in_{\text{g}} }},\quad i = {\text{VR}},{\text{VGO}},{\text{LFO}},{\text{GA}},{\text{LPG}},{\text{DG}} .$$
(18)

The assumptions inherent in the model are:

  1. 1.

    Adiabatic and one-dimensional transported ideal plug flow for gas phase and cluster phase (catalyst + coke) but with different velocities, no axial back-mixing and no radial dispersion.

  2. 2.

    Diffusion resistances are significant, and no adsorption within the catalyst particle.

  3. 3.

    There is no heat loss from the riser, and the temperature of the reaction mixture (hydrocarbon vapors and solid particles) falls only because of the endothermicity of the cracking reactions [40].

  4. 4.

    The pressure drop along the riser length is due to the hydrostatic head of catalyst, solid acceleration, solid and gas friction in the riser [41].

  5. 5.

    A variable gaseous superficial velocity with axial position along the riser length is assumed.

  6. 6.

    The catalyst particles are assumed to move as clusters to account for the observed high-slip velocities.

  7. 7.

    The coke exists as solid and its deposition on the catalyst particles does not affect the fluid flow.

  8. 8.

    In each section of riser, the cluster (catalyst + coke) and gas have different temperatures to account for the heat transfer between the fluid and the solid phases.

Since the reactor dynamics is assumed to be fast enough to justify a quasi-steady state model, at steady state, in dimensionless form, Eq. (10) becomes:

$$\frac{{S_{\text{v}} \rho_{\text{c}} }}{{ \in_{\text{g}} }}\left( {\frac{{{\text{d}}c_{i} }}{{{\text{d}}\sigma }}} \right) = r_{{{\text{p}},i}}^{\prime } ,\quad i = {\text{VR}},{\text{VGO}},{\text{LFO}},{\text{GA}},{\text{LPG}},{\text{DG}},{\text{CK}} .$$
(19)

From Eq. (16), the rate of disappearance of lump i, \(( - r_{i}^{\prime } )\), for a first-order reaction is given by Meng et al. [42]:

$$( - r_{i}^{\prime } ) = k_{i} (\rho_{\text{g}} c_{i} )\frac{{\rho_{\text{c}} }}{{ \in_{\text{g}} }}f(N)f(A)\phi (t_{\text{c}} ).$$
(20)

The rate of formation of lump i from lump j, \(r_{ji}\), is directly proportional to the molar concentration of lump j \((\rho c_{j} )\), the stoichiometric coefficient, \(\alpha_{ji}\), for the reaction of lump j to lump i \(\left( { = \,{{M_{j} } \mathord{\left/ {\vphantom {{M_{j} } {M_{i} }}} \right. \kern-0pt} {M_{i} }}} \right)\), and the mass density of solid particle to gas volume fraction \(\left( {{{\rho_{\text{c}} } \mathord{\left/ {\vphantom {{\rho_{\text{c}} } { \in_{\text{g}} }}} \right. \kern-0pt} { \in_{\text{g}} }}} \right)\). The rate of formation of lump i, \((r_{i}^{\prime } )_{\text{f}}\), is the sum of all \(r_{ji}\), and is given by Meng et al. [42]:

$$(r_{i}^{\prime } )_{\text{f}} = \left[ {\sum\limits_{j = 1}^{N} {\alpha_{ji} k_{j} \left( {\rho_{\text{g}} c_{j} } \right)} } \right]\frac{{\rho_{\text{c}} }}{{ \in_{\text{g}} }}f(N)f(A)\phi (t_{\text{c}} ).$$
(21)

So, the net rate of reaction of lump i, \(r_{i}^{\prime }\), without mass transfer is given by Meng et al. [42]:

$$r_{i}^{\prime } = (r_{i}^{\prime } )_{\text{f}} - ( - r_{i} ) = \left[ {\sum\limits_{j = 1}^{N} {\alpha_{ji} k_{j} c_{j} - k_{i} c_{i} } } \right]\frac{{\rho_{\text{g}} \rho_{\text{c}} }}{{ \in_{\text{g}} }}f(N)f(A)\phi (t_{\text{c}} ).$$
(22)

Having modified the specific reaction rate constants according to Eq. (10) to account for mass transfer resistance, the rate of formation, \(r_{{{\text{p}},i}}^{\prime }\), for a lump i involved in the reaction network was obtained, which was used in Eq. (19) to yield the steady-state model of component in riser reactor of RFCCU, thus:

$$\frac{{{\text{d}}y_{\text{VR}} }}{{{\text{d}}\sigma }} = - k_{0,1} y_{\text{VR}} \varPhi ,$$
(23)
$$\frac{{{\text{d}}y_{\text{VGO}} }}{{{\text{d}}\sigma }} = \left\{ {\left( {\frac{1}{{k_{\text{g}} }} + \frac{1}{{\eta k_{1,2} }}} \right)^{ - 1} y_{\text{VR}} - \left[ {\frac{1}{{k_{\text{g}} }} + \frac{1}{{\eta \left( {k_{2,3} + k_{2,4} + k_{2,5} + k_{2,6} + k_{2,7} } \right)}}} \right]^{ - 1} y_{\text{VGO}} } \right\}\varPhi ,$$
(24)
$$\frac{{{\text{d}}y_{\text{LFO}} }}{{{\text{d}}\sigma }} = \left[ {\left( {\frac{1}{{k_{\text{g}} }} + \frac{1}{{\eta k_{1,3} }}} \right)^{ - 1} \alpha_{1,3} y_{\text{VR}} + \left( {\frac{1}{{k_{\text{g}} }} + \frac{1}{{\eta k_{2,3} }}} \right)^{ - 1} y_{\text{VGO}} - k_{\text{LFO}} y_{\text{LFO}} } \right]\varPhi ,$$
(25)
$$\frac{{{\text{d}}y_{\text{GA}} }}{{{\text{d}}\sigma }} = \left[ {\left( {\frac{1}{{k_{\text{g}} }} + \frac{1}{{\eta k_{1,4} }}} \right)^{ - 1} \alpha_{1,4} y_{\text{VR}} + \left( {\frac{1}{{k_{\text{g}} }} + \frac{1}{{\eta k_{2,4} }}} \right)^{ - 1} \alpha_{2,4} y_{\text{VGO}} + \left( {\frac{1}{{k_{\text{g}} }} + \frac{1}{{\eta k_{3,4} }}} \right)^{ - 1} \alpha_{3,4} y_{\text{LFO}} - k_{\text{GA}} y_{\text{GA}} } \right]\varPhi ,$$
(26)
$$\frac{{{\text{d}}y_{\text{LPG}} }}{{{\text{d}}\sigma }} = \left[ {\alpha_{1,5} (k_{1,5} )_{\text{VR}} y_{\text{VR}} + \alpha_{2,5} (k_{2,5} )_{\text{VGO}} y_{\text{VGO}} + \alpha_{3,5} (k_{3,5} )_{\text{LFO}} y_{\text{LFO}} + \alpha_{4,5} (k_{4,5} )_{\text{GA}} y_{\text{GA}} - k_{LPG}^{\prime } y_{\text{LPG}} } \right]\varPhi ,$$
(27)
$$\begin{aligned} \frac{{{\text{d}}y_{\text{DG}} }}{{{\text{d}}\sigma }} & = \Bigg[\alpha_{1,6} (k_{1,6} )_{\text{VR}} y_{\text{VR}} + \alpha_{2,6} (k_{2,6} )_{\text{VGO}} y_{\text{VGO}} + \alpha_{3,6} (k_{3,6} )_{\text{LFO}} y_{\text{LFO}} + \alpha_{4,6} (k_{4,6} )_{\text{GA}} y_{\text{GA}} , \\ & \quad - \alpha_{5,6} (k_{5,6} )_{\text{LPG}} y_{\text{LPG}} \Bigg]\varPhi , \\ \end{aligned}$$
(28)
$$\begin{aligned} \frac{{{\text{d}}y_{\text{CK}} }}{{{\text{d}}\sigma }} & = \Bigg[\alpha_{1,7} (k_{1,7} )_{\text{VR}} y_{\text{VR}} + \alpha_{2,7} (k_{2,7} )_{\text{VGO}} y_{\text{VGO}} + \alpha_{3,7} (k_{3,7} )_{\text{LFO}} y_{\text{LFO}} + \alpha_{4,7} (k_{4,7} )_{\text{GA}} y_{\text{GA}} \\ & \quad - \alpha_{5,7} (k_{5,7} )_{\text{LPG}} y_{\text{LPG}} \Bigg]\varPhi , \\ \end{aligned}$$
(29)

where

$$\begin{aligned} \varPhi & = \frac{{\rho_{\text{g}} }}{{S_{\text{v}} \rho_{\text{cat}} \left( {1 + K_{{N_{2} }} w_{{N_{2} }} } \right)\left( {1 + K_{A} w_{A} } \right)\left( {1 + \beta t_{\text{c}}^{\gamma } } \right)}},\quad \frac{1}{{k_{0,1} }} = \frac{1}{{k_{\text{g}} }} + \frac{1}{{\eta (k_{1,2} + k_{1,3} + k_{1,4} + k_{1,5} + k_{1,6} + k_{1,7} )}} \\ k_{\text{LFO}} & = \left[ {\frac{1}{{k_{\text{g}} }} + \frac{1}{{\eta (k_{3,4} + k_{3,5} + k_{3,6} + k_{3,7} )}}} \right]^{ - 1} ,\quad k_{\text{GA}} = \left[ {\frac{1}{{k_{\text{g}} }} + \frac{1}{{\eta (k_{4,5} + k_{4,6} + k_{4,7} )}}} \right]^{ - 1} \\ (k_{1,5} )_{\text{VR}} & = \frac{{\eta k_{1,5} k_{\text{g}} }}{{\eta k_{1,5} \, + k_{\text{g}} }},\quad (k_{2,5} )_{\text{VGO}} = \frac{{\eta k_{2,5} k_{\text{g}} }}{{\eta k_{2,5} \, + k_{\text{g}} }},\quad (k_{3,5} )_{\text{LFO}} = \frac{{\eta k_{3,5} k_{\text{g}} }}{{\eta k_{3,5} + k_{\text{g}} }},\quad (k_{4,5} )_{\text{GA}} = \frac{{\eta k_{4,5} k_{\text{g}} }}{{\eta k_{4,5} + k_{\text{g}} }} \\ k_{\text{LPG}}^{\prime } & = \left[ {\frac{1}{{k_{\text{g}} }} + \frac{1}{{\eta (k_{5,6} + k_{5,7} )}}} \right]^{ - 1} ,\quad (k_{1,6} )_{\text{VR}} = \frac{{\eta k_{1,6} k_{\text{g}} }}{{\eta k_{1,6} \, + k_{\text{g}} }},\quad (k_{2,6} )_{\text{VGO}} = \frac{{\eta k_{2,6} k_{\text{g}} }}{{\eta k_{2,6} + k_{\text{g}} }} \\ (k_{3,6} )_{\text{LFO}} & = \frac{{\eta k_{3,6} k_{\text{g}} }}{{\eta k_{3,6} + k_{\text{g}} }},\quad (k_{4,6} )_{\text{GA}} = \frac{{\eta k_{4,6} k_{\text{g}} }}{{\eta k_{4,6} \, + k_{\text{g}} }},\quad (k_{5,6} )_{\text{LPG}} \, = \frac{{\eta k_{5,6} k_{\text{g}} }}{{\eta k_{5,6} + k_{\text{g}} }},\quad (k_{1,7} )_{\text{VR}} = \frac{{\eta k_{1,7} k_{\text{g}} }}{{\eta k_{1,7} + k_{\text{g}} }} \\ (k_{2,7} )_{\text{VGO}} & = \frac{{\eta k_{2,7} k_{\text{g}} }}{{\eta k_{2,7} + k_{\text{g}} }},\quad (k_{3,7} )_{\text{LFO}} = \frac{{\eta k_{3,7} k_{\text{g}} }}{{\eta k_{3,7} \, + k_{\text{g}} }},\quad (k_{4,7} )_{\text{GA}} = \frac{{\eta k_{4,7} k_{\text{g}} }}{{\eta k_{4,7} \, + k_{\text{g}} }},\quad (k_{5,7} )_{\text{GA}} = \frac{{\eta k_{5,7} k_{\text{g}} }}{{\eta k_{5,7} + k_{\text{g}} }}, \\ \end{aligned}$$

\(k_{i,j}\) is the specific reaction rate constant for the reaction of lump i generating lump j, expressed using Arrhenius equation, thus:

$$k_{i,j} = (k_{i,j} )_{0} \exp \left( { - \frac{{E_{i,j} }}{{R_{\text{u}} T}}} \right),$$
(30)
$$y_{i} \, = \,c_{i} M_{i} ,\quad i = {\text{VR}},{\text{VGO}},{\text{LFO}},{\text{GA}},{\text{LPG}},{\text{DG}},{\text{CK,}}$$
(31)

and the gas-phase density, \(\rho_{\text{g}}\), is determined using Eq. (41).

Hydrodynamic model of the riser reactor of RFCCU

The hydrodynamics presented herein tries to mimic the real situation in a RFCCU-riser reactor. It is important in describing the behaviour of an industrial FCC riser reactor. The correlation of Patience et al. [43] for slip factor was used in this work, whereby the numerical value of the slip factor, \(\varPsi\), defined as the ratio of the gas interstitial velocity, \(v_{\text{g}}\), to the average particle velocity, \(\bar{V}_{\text{p}}\), is given by:

$$\varPsi = \frac{{v_{\text{g}} }}{{\bar{V}_{\text{p}} }} = \frac{{U_{\text{g}} }}{{ \in_{\text{g}} \bar{V}_{\text{p}} }} = 1 + 5.6Fr^{ - 1} + 0.47Fr_{\text{t}}^{0.41} ,$$
(32)

where the average particle velocity, \(\bar{V}_{\text{p}}\), in the riser is given by:

$$\bar{V}_{\text{p}} = \frac{{G_{\text{s}} }}{{\rho_{\text{c}} \left( {1 - \in_{\text{g}} } \right)}},$$
(33)
$$v_{\text{g}} = \frac{{F_{\text{g}} }}{{\rho_{\text{g}} A_{\text{R}} \in_{\text{g}} }} = \frac{{F_{\text{stm}} + \sum\nolimits_{i = 1}^{6} {F_{i} } }}{{\rho_{\text{g}} A_{\text{R}} \in_{\text{g}} }} = \frac{{G_{\text{v}} }}{{\rho_{\text{g}} \in_{\text{g}} }}.$$
(34)

The gas superficial velocity, \(U_{\text{g}}\), is given by:

$$U_{\text{g}} = \frac{{F_{\text{g}} }}{{\rho_{\text{g}} A_{\text{R}} }},$$
(35)

which thus takes cognizance of the variation of gas velocity along the axial positions in the riser reactor since the catalytic cracking of hydrocarbons is a process with expanding number of moles of species along the riser length.

$$Fr = {{\left( {U_{\text{g}} } \right)_{0} } \mathord{\left/ {\vphantom {{\left( {U_{\text{g}} } \right)_{0} } {\sqrt {gD_{\text{R}} } .}}} \right. \kern-0pt} {\sqrt {gD_{\text{R}} } .}}$$
(36)

Similarly, the Froude number,\(Fr_{\text{t}}\), based on terminal velocity is defined thus:

$$Fr_{\text{t}} = {{U_{\text{t}} } \mathord{\left/ {\vphantom {{U_{\text{t}} } {\sqrt {gD_{\text{R}} } .}}} \right. \kern-0pt} {\sqrt {gD_{\text{R}} } .}}$$
(37)

Many correlations exist in the literatures for calculating the particle terminal velocity, \(U_{\text{t}}\). Generally, the terminal velocity is usually calculated for three zones: Stokes, intermediate, and Newton zones. These are classified according to Archimedes number, \(Ar\), which defines the border amongst the zones. The Stokes regime holds for \(Ar\, < \,32.9\), intermediate regime is valid for \(32.9\, < Ar\, < \,106.5\), and the Newton regime is defined for \(Ar\, > \,106.5\). In this study, the following correlation for intermediate regime was used for calculating Reynolds number based on particle terminal velocity [44,45,46]:

$$Ar = {{\rho_{\text{g}} (\rho_{\text{cat}} - \rho_{\text{g}} )gD_{\text{p}}^{3} } \mathord{\left/ {\vphantom {{\rho_{\text{g}} (\rho_{\text{cat}} - \rho_{\text{g}} )gD_{\text{p}}^{3} } {\mu_{\text{g}}^{2} ,}}} \right. \kern-0pt} {\mu_{\text{g}}^{2} ,}}$$
(38)
$$Re_{\text{t}} = \frac{Ar}{{18 + \left( {2.3348 - 1.7439\varPhi } \right)Ar^{0.5} }},$$
(39)
$$U_{\text{t}} = {{Re_{\text{t}} \mu_{\text{g}} } \mathord{\left/ {\vphantom {{Re_{\text{t}} \mu_{\text{g}} } {\left( {\rho_{\text{g}} D_{\text{p}} } \right)}}} \right. \kern-0pt} {\left( {\rho_{\text{g}} D_{\text{p}} } \right)}}.$$
(40)

However, the gas phase density, \(\rho_{\text{g}}\), is determined by assuming vapors of feed, product hydrocarbons and steam in the riser reactor to be ideal, hence we have:

$$\rho_{\text{g}} = \frac{{p\bar{M}_{\text{g}} }}{{RT_{\text{g}} }} = \frac{{F_{\text{g}} }}{{{{F_{\text{stm}} } \mathord{\left/ {\vphantom {{F_{\text{stm}} } {M_{\text{stm}} }}} \right. \kern-0pt} {M_{\text{stm}} }} + \sum\nolimits_{i = 1}^{6} {{{F_{i} } \mathord{\left/ {\vphantom {{F_{i} } {M_{i} }}} \right. \kern-0pt} {M_{i} }}} }}\frac{p}{{RT_{\text{g}} }},\quad i = {\text{VR}},{\text{VGO}},{\text{LFO}},{\text{GA}},{\text{LPG}},{\text{DG,}}$$
(41)

since coke is not in the gas phase, and \(\bar{M}_{\text{g}}\) is the average vapor-phase molecular weight.

The variation of the vapor-phase mass flow rate,\(F_{\text{g}}\), throughout the riser reactor can be predicted thus:

$$F_{\text{g}} = F_{\text{f}} \left( {y_{\text{VR}} + y_{\text{VGO}} + y_{\text{LFO}} + y_{\text{GA}} + y_{\text{LPG}} + y_{\text{DG}} } \right) + F_{\text{stm}} .$$
(42)

The volume fraction of the gas phase, \(\in_{\text{g}}\), is given by:

$$\in_{\text{g}} = 1 - \in_{\text{c}} ,$$
(43)

where the volume fraction of the cluster phase, \(\in_{\text{c}}\), is determined by:

$$\in_{\text{c}} = \frac{{F_{\text{c}} }}{{\rho_{\text{c}} \nu_{\text{c}} A_{\text{R}} }} = \frac{{G_{\text{c}} }}{{\rho_{\text{c}} \nu_{\text{c}} ,}}$$
(44)

and the cluster density, \(\rho_{\text{c}}\), is calculated by:

$$\rho_{\text{c}} = (1 - \varepsilon_{\text{c}} )\rho_{\text{p}} .$$
(45)

Combining Eqs. (32) and (44) gives an expression for \(\in_{\text{g}}\), thus:

$$\in_{\text{g}} = \frac{{U_{\text{g}} \rho_{\text{c}} }}{{U_{\text{g}} \rho_{\text{c}} + \varPsi G_{\text{c}} }}.$$
(46)

The cluster phase velocity, \(v_{\text{c}}\), in the riser reactor is determined by the momentum equation of Tsuo and Gidaspow [47], and summarized by Han and Chung [36], Gupta et al. [48], Fernandes et al. [49], which is given in dimensionless form, thus:

$$\frac{{{\text{d}}\bar{\nu }_{\text{c}} }}{{{\text{d}}\sigma }} = \frac{L}{{(v_{\text{c}} )_{0} }}\left[ {\frac{{C_{\text{f}} \left( {v_{\text{g}} - \nu_{\text{c}} } \right)A_{\text{R}} }}{{F_{\text{c}} }} - \frac{{2f_{\text{s}} \nu_{\text{c}} }}{{D_{\text{R}} }} - \frac{g}{{\nu_{\text{c}} }}} \right],$$
(47)

where

$$C_{\text{f}} = 0.5\rho_{\text{g}} C_{\text{D}} A_{\text{p}} \left| {v_{\text{g}} - v_{\text{c}} } \right|,$$
(48)
$$C_{\text{D}} = \left\{ {\begin{array}{*{20}l} {\frac{24}{Re}\left( {1 + 0.15Re^{0.687} } \right)} \hfill & {\quad {\text{for}}{\mkern 1mu} {\mkern 1mu} Re{\mkern 1mu} < {\mkern 1mu} 1000} \hfill \\ {0.44} \hfill & {\quad {\text{for}}{\mkern 1mu} {\mkern 1mu} Re{\mkern 1mu} \ge {\mkern 1mu} 1000} \hfill \\ \end{array} ,} \right.$$
(49)
$$Re = \frac{{\rho \varepsilon_{\text{g}} \left| {v_{\text{g}} - \nu_{\text{c}} } \right|D_{\text{c}} }}{{\mu_{\text{g}} }},$$
(50)
$$A_{\text{p}} = {{1.5\varepsilon_{\text{c}} } \mathord{\left/ {\vphantom {{1.5\varepsilon_{\text{c}} } {D_{\text{c}} .}}} \right. \kern-0pt} {D_{\text{c}} .}}$$
(51)

The viscosity of the gas phase, \(\mu_{\text{g}}\), is calculated according to Bromley and Wilke [50], thus:

$$\mu_{\text{g}} = \sum\limits_{\begin{subarray}{l} i = {\text{VR}},{\text{VGO}},{\text{LFO}},{\text{GA}}, \\ {\text{LPG}},{\text{DG}},{\text{stm}} \end{subarray} } {\left( {\frac{{y_{i} \mu_{i} }}{{y_{i} + \sum\nolimits_{\begin{subarray}{l} i = {\text{VR}},{\text{VGO}},{\text{LFO}},{\text{GA}}, \\ {\text{LPG}},{\text{DG}},{\text{stm}} \\ j \ne i \end{subarray} } {\varOmega_{ij} y_{j} } }}} \right)} ,$$
(52)

where

$$y_{i} = {{F_{i} } \mathord{\left/ {\vphantom {{F_{i} } {F_{\text{g}} \quad i = {\text{VR}},{\text{VGO}},{\text{LFO}},{\text{GA}},{\text{LPG}},{\text{DG}},{\text{stm,}}}}} \right. \kern-0pt} {F_{\text{g}} \quad i = {\text{VR}},{\text{VGO}},{\text{LFO}},{\text{GA}},{\text{LPG}},{\text{DG}},{\text{stm,}}}}$$
(53)
$$\varOmega_{ij} = \frac{{\left[ {1 + \left( {{{\mu_{j} } \mathord{\left/ {\vphantom {{\mu_{j} } {\mu_{i} }}} \right. \kern-0pt} {\mu_{i} }}} \right)^{0.5} \left( {{{M_{j} } \mathord{\left/ {\vphantom {{M_{j} } {M_{i} }}} \right. \kern-0pt} {M_{i} }}} \right)^{0.25} } \right]^{2} }}{{\sqrt {8\left( {1 + {{M_{i} } \mathord{\left/ {\vphantom {{M_{i} } {M_{j} }}} \right. \kern-0pt} {M_{j} }}} \right)} }}.$$
(54)

In the above equations, the gas-phase viscosity of the ith component is calculated by the following correlation [51]:

$$\begin{aligned} \mu_{i} & = 18.9943 + 0.061819\theta + 0.017352M_{i} + 9.08118 \times 10^{ - 6} \theta M_{i} - 1.00638 \times 10^{ - 5} \theta^{2} - 1.04832 \times 10^{ - 4} M_{i}^{2} \\ & \quad - 0.136695{\theta \mathord{\left/ {\vphantom {\theta {M_{i} }}} \right. \kern-0pt} {M_{i} }} - 3.20527{\text{In}}M_{i} - 8.35025 \times 10^{ - 3} \theta {\text{In}}M_{i} , \\ \end{aligned}$$
(55)

where \(\theta\) is temperature in °C.

The viscosity of steam, \(\mu_{\text{stm}} ,\) is determined by the correlation of Daubert and Danner [52]:

$$\mu_{\text{stm}} = \frac{{7.6190 \times 10^{ - 8} T^{0.92758} }}{{1 + {{211.6} \mathord{\left/ {\vphantom {{211.6} {T - {{4670} \mathord{\left/ {\vphantom {{4670} {T^{2} }}} \right. \kern-0pt} {T^{2} }}}}} \right. \kern-0pt} {T - {{4670} \mathord{\left/ {\vphantom {{4670} {T^{2} }}} \right. \kern-0pt} {T^{2} }}}},}}$$
(56)

where T is temperature in K.

The catalyst residence time, \(t_{\text{c}}\), can be calculated thus [53]:

$$\frac{{{\text{d}}t_{\text{c}} }}{{{\text{d}}\sigma }} = \frac{{LA_{\text{R}} \rho_{\text{cat}} \varPsi }}{{F_{\text{cat}} \varPsi + {{1.01325 \times 10^{5} F_{\text{g}} \left( {1 - y_{\text{CK}} } \right)\rho_{\text{cat}} RT_{\text{g}} } \mathord{\left/ {\vphantom {{1.01325 \times 10^{5} F_{\text{g}} \left( {1 - y_{\text{CK}} } \right)\rho_{\text{cat}} RT_{\text{g}} } {\left( {p\bar{M}_{\text{g}} } \right),}}} \right. \kern-0pt} {\left( {p\bar{M}_{\text{g}} } \right),}}}}$$
(57)

while the residence time, \(t_{\text{g}}\), of the gas phase was calculated thus:

$$t_{\text{g}} = z/v_{\text{g}} = L\sigma \in_{\text{g}} /U_{\text{g}}$$
(58)

Force balance

As stated in the continuity equation (assumption (4)), the dimensionless pressure drop along the dimensionless length of the riser reactor can be expressed thus:

$$\frac{{{\text{d}}\bar{p}_{\text{R}} }}{{{\text{d}}\sigma }} = - \frac{1}{{p_{\text{in}} }}\left[ {L\rho_{\text{c}} g\left( {1 - \in_{\text{g}} } \right) + \frac{{\rho_{\text{c}} \left( {1 - \in_{\text{g}} } \right)\nu_{\text{c}}^{2} }}{2\Delta \sigma } + \frac{{2Lf_{\text{c}} \rho_{\text{c}} \left( {1 - \in_{\text{g}} } \right)\nu_{\text{c}}^{2} }}{{D_{\text{R}} }} + \frac{{Lf_{\text{g}} \rho_{\text{g}} v_{\text{g}}^{2} }}{{D_{\text{R}} }}} \right],$$
(59)

where the respective pressure drops due to hydrostatic head of solids, solids’ acceleration, solid and gas friction are given by the first, second, third, and fourth expressions in Eq. (59). The expression for solids’ friction factor, \(f_{\text{c}}\), suggested by Konno and Saito [54] was used in this study since it has the widest applicability and it even spills over into dense-phase analysis, and is given by:

$$f_{\text{c}} = \frac{{0.0285(gD_{\text{R}} )^{0.5} }}{{\bar{V}_{\text{p}} }}.$$
(60)

The gas friction factor, \(f_{\text{g}}\), is calculated from Blasius friction factor, which is expressed as:

$$f_{\text{g}} = 0.316Re^{ - 0.25} .$$
(61)

Energy balance for the riser reactor of RFCCU

The inlet temperature, \(T_{\text{g,in}}\), of the fluid phase (vaporized VR + dispersion steam) to the riser reactor was calculated by a consideration of the energy balance, which was obtained at \(z\, = \,0\) of the riser reactor as:

$$T_{\text{g,in}} = T(0) = \frac{{F_{\text{VR}} \left[ {c_{{{\text{p,V}}R}}^{\text{L}} \left( {T_{\text{VR}} - T_{\text{vap}} } \right) + c_{{{\text{p,V}}R}}^{\text{V}} T_{\text{vap}} - \Delta H_{\text{vap}} } \right] + F_{\text{stm}} c_{\text{p,stm}} T_{\text{stm}} }}{{F_{\text{VR}} c_{\text{p,VR}}^{\text{V}} + F_{\text{stm}} c_{\text{p,stm}} }}.$$
(62)

With the assumption of heat transfer between the solid and gas phases, at steady state, the energy balance over an elemental volume of the reactor for the fluid phase in dimensionless form is given by:

$$\left( {F_{\text{VR}} c_{\text{p,VR}} + F_{\text{stm}} c_{\text{p,stm}} } \right)\frac{{{\text{d}}\bar{T}_{\text{g}} }}{{{\text{d}}\sigma }} = \frac{{LA_{\text{R}} }}{{T_{\text{g,in}} }}\left[ {\sum\limits_{i = 1}^{N} {r_{{{\text{p}},i}}^{\prime } \left( { - \Delta H_{\text{rxn}} } \right)_{i} \left( {1 - \in_{\text{g}} } \right)\rho_{\text{cat}} + hA_{\text{gs}} \left( {\bar{T}_{\text{c}} T_{\text{cat}} - \bar{T}_{\text{g}} T_{\text{g,in}} } \right)} } \right].$$
(63)

In dimensionless form, the energy balance for the solid phase is given by:

$$\left( {F_{\text{cat}} c_{\text{p,cat}} + F_{\text{CK}} c_{\text{p,CK}} } \right)\frac{{{\text{d}}\bar{T}_{\text{c}} }}{{{\text{d}}\sigma }} = {{LA_{\text{R}} hA_{\text{gs}} \left( {\bar{T}_{\text{g}} T_{\text{g,in}} - \bar{T}_{\text{c}} T_{\text{cat}} } \right)} \mathord{\left/ {\vphantom {{LA_{\text{R}} hA_{\text{gs}} \left( {\bar{T}_{\text{g}} T_{\text{g,in}} - \bar{T}_{\text{c}} T_{\text{cat}} } \right)} {T_{\text{cat}} }}} \right. \kern-0pt} {T_{\text{cat}} }}.$$
(64)

Two vaporization approaches were considered in this study:

  1. 1.

    Instantaneous vaporization, where the feedstock vaporizes as soon as the catalyst gets in contact with it at the riser inlet. The fluid is thus considered as an ideal gas and the enthalpy balances for the fluid and solid phases are given by Eqs. (62) and (63), respectively.

  2. 2.

    One-dimensional vaporization of the feedstock, where a distillation curve is employed for the fraction of gas oil vaporized, \(X_{\text{vap}} ,\) [17]:

    $$X_{\text{vap}} = 0.0027T - 0.1254,$$
    (65)

    which is valid from 319.5 to 689.8 K. The gas oil liquid and gas phases take place together for a certain period in the riser reactor. Therefore, the enthalpy, \(h_{\text{f}}\), of the mixture is computed by:

    $$h_{\text{f}} = h_{\text{V}} X_{\text{vap}} + \left( {1 - X_{\text{vap}} } \right)h_{\text{L}} .$$
    (66)

By employing the data of Farah [56], the following correlations were obtained [55]:

$$h_{\text{V}} = 0.0022608T^{2} + 1.2518T + 382.81,$$
(67)
$$h_{\text{L}} = 0.0015072T^{2} + 1.8602T + 32.592,$$
(68)

which are valid from 319.5 to 689.8 K.

The fluid-phase temperature is evaluated by the enthalpy balance as follows:

$$\frac{{{\text{d}}h_{\text{g}} }}{{{\text{d}}\sigma }} = \frac{{LA_{\text{R}} }}{{F_{\text{g}} }}\left[ {\sum\limits_{i = 1}^{N} {r_{{{\text{p}},i}}^{\prime } ( - \Delta H_{\text{rxn}} )_{i} (1 - \in_{\text{g}} )\rho_{\text{cat}} } + hA_{\text{e}} (T_{\text{c}} - T_{\text{g}} )} \right],$$
(69)

which can be used in conjunction with Eq. (64) to predict the fluid and solid phases’ temperatures for one-dimensional vaporization of the feedstock.

Hence, the developed model equations consist of a set of twelve coupled, highly non-linear first-order differential Eqs. (23)–(29), (47), (57), (59), (63)/(69), and (64) whose exact analytic solutions are somewhat impossible so, a powerful, robust, numerical method for non-linear differential equations must be used. The initial conditions needed to solve these equations are:

$$\begin{aligned} y_{\text{VR}} (0) & = 1,y_{j} (0) = 0,\left( {j = {\text{VGO}},{\text{LFO}},{\text{GA}},{\text{LPG}},{\text{DG}},{\text{CK}}} \right),\quad \\ \bar{v}_{\text{c}} (0) & = 1,\quad t_{\text{c}} (0) = 5,\quad \bar{p}_{\text{R}} (0) = 1,\bar{T}_{\text{g}} (0) = 1,\bar{T}_{\text{c}} (0) = 1\quad {\text{at}}\quad \sigma = 0. \\ \end{aligned}$$

Computational procedure

The computer program for the numerical solution of the resulting differential equations was written in MATLAB R2017a environment. The program employed semi-implicit Runge–Kutta method with step-size adjustment strategy for the numerical solution of the developed differential equations with a view to predicting the yield of each lump, temperature and pressure profiles and other process parameters in the riser of an industrial RFCCU during the catalytic cracking of vacuum residue. This numerical method is efficient, accurate, and stiffly stable so any unenvisaged problem of instability associated with explicit methods is removed.

Before solving the ordinary differential equations, the required physical parameters of the process must be determined first. The molecular weights of vacuum residue, vacuum gas oil, light fuel oil, gasoline, LPG, dry gas, and coke are 950.0, 386.0, 229.0, 117.8, 46.7, 18.4, and 400.0 kg/kmol [14, 15], while the molecular weight of steam is 18.0 kg/kmol. The dimensions of the industrial riser reactor are \(L\, = \,38\) m and \(D_{\text{R}} = 1.36\) m [1]. The catalytic decay function constants, β and γ, used were 162.15 and 0.76, respectively [14, 15, 17]. The adsorption constant of aromatics, resins, and asphaltenes, \(K_{A}\), was 0.128 [14, 15]. The density of the catalyst was 1700 kg/m3 [1]. The kinetic and thermodynamic parameters used to simulate the RFCCU-riser reactor are presented in Table 2.

Table 2 Kinetic and thermodynamic parameters used for riser reactor-type of FCCU simulation [1]
Full size table

The kinetic parameters for coke formation from gasoline and LPG lumps were obtained from Xiong et al. [13, 39]. The enthalpies of reaction for both reactions were obtained from Dasila et al. [39].

To account for temperature effect in the riser reactor, the specific heat capacity of each lump in the reaction network for the catalytic cracking of vacuum residue was expressed as function of temperature, which was then introduced into the model equations as demanded. This is in variance with previous works in the literature. According to the seven-lump reaction network in Fig. 2, the components obtained from vacuum residue cracking include VGO, LFO, gasoline, LPG, dry gas, and coke. To mimic the reactions and compounds being formed in the reactor as closely as possible, and in the face of dearth of information on VR, VGO, and LFO lumps’ characterization, a pseudo-component was chosen to represent each of these lumps, adopted from the work of Du et al. [18]. Since the higher the molecular weight of a lump, the more paraffinic it is, an alkane of similar molecular weight was therefore chosen to represent VR, VGO, and LFO lumps individually. Approximating the heavy material with paraffins suffices for waxy FCC feedstock, as is the case here with no presence of heteroatoms such as sulphur [1]. Hence, n-octahexacontane, C68H138, was used as a surrogate for VR. n-Heptacosane, C27H56, and n-hexadecane, C16H34, were used as surrogates for VGO and LFO, respectively [18]. Gasoline consists of several hydrocarbons, as revealed in the mass spectrometric analysis of 1 mol of gasoline. For use in the energy balance equation, the specific heat capacities’ constants of the components in gasoline lump were obtained from Sinnott and Towler [57] and ASPEN PLUS/HYSYS 9.0, and are presented in Tables 3 and 4.

Table 3 Constants in the specific heat capacities of components in gasoline [57]
Full size table
Table 4 Constants in specific heat capacities of other components in gasoline, VR (n-octahexacontane) and VGO (n-heptacosane) obtained from ASPEN PLUS/HYSYS 9.0
Full size table

Since ASPEN PLUS/HYSYS 9.0 is a very good software to characterize feedstock and/or product by pseudo-components from an assay, it was used to populate the VR and VGO properties, as presented in Table 4 while those of LFO were obtained from Sinnott and Towler [57]. These give specific heat capacities as functions of temperature to be used in the energy balance equation. However, representing a property of a lump with a surrogate single component may have significant deviations on the simulated results when compared with plant data. In this study, this was not the case as revealed that there was excellent agreement between simulated results and the plant data.

From the experimental analyses of Du et al. [18], LPG lump consisted of propane and butane while dry gas consisted of hydrogen, methane, and ethane, whose properties are given in Table 5.

Table 5 Constants in specific heat capacities of LFO and components in LPG and dry gas
Full size table

In Tables 3 and 5, the specific heat capacity of the individual component is in the form:

$$c_{\text{p}} = a + bT + cT^{2} + dT^{3} ,$$
(70)

which is expressed in J/(mol K).

In Table 4, the specific heat capacities of other components in gasoline and VGO (n-heptacosane) obtained from ASPEN PLUS/HYSYS 9.0 are in the form:

$$c_{\text{p}} = a + b\left\{ {\frac{{\left( {\frac{c}{T}} \right)^{2} \exp \left( {\frac{c}{T}} \right)}}{{\left[ {\exp \left( {\frac{c}{T}} \right) - 1} \right]^{2} }}} \right\} + d\left\{ {\frac{{\left( {\frac{e}{T}} \right)^{2} \exp \left( {\frac{e}{T}} \right)}}{{\left[ {\exp \left( {\frac{e}{T}} \right) - 1} \right]^{2} }}} \right\},$$
(71)

which is expressed in J/(mol K), f and g are the upper and lower temperature limits.

So, the specific heat capacity of gasoline as a lump, \(c_{\text{p,GA}}\), is given by:

$$c_{\text{p,GA}} = \underbrace {{\sum\limits_{j = 1}^{32} {m_{j} c_{{{\text{p}}j}} } }}_{{{\text{using}}\;{\text{equation}}\;(63)}}\, + \,\underbrace {{M_{\text{GA}} \sum\limits_{j = 33}^{37} {m_{j} c_{{{\text{p}}j}} } }}_{{{\text{using}}\;{\text{equation}}\;(64)}},$$
(72)

which is now expressed in J/(mol K).

The specific heat capacity of LPG was computed using:

$$c_{\text{p,LPG}} = m_{{C_{3} H_{8} }} c_{{{\text{p}},C_{3} H_{8} }} \, + \,m_{{C_{4} H_{10} }} c_{{{\text{p}},C_{4} H_{10} }} .$$
(73)

The specific heat capacity of DG was computed using:

$$c_{\text{p,DG}} = m_{{H_{2} }} c_{{{\text{p}},H_{2} }} + m_{{CH_{4} }} c_{{{\text{p}},CH_{4} }} + m_{{C_{2} H_{6} }} c_{{{\text{p}},C_{2} H_{6} }} .$$
(74)

The specific heat capacity of coke was obtained from Smith et al. [58] as:

$$c_{{{\text{p}},{\text{CK}}}} = R_{\text{u}} \left( {1.771 + 7.71 \times 10^{ - 4} T - 8.67 \times 10^{4} T^{ - 2} } \right)\;{\text{J}}/({\text{mol K}}),$$
(75)

while the specific heat capacity of steam is given by Smith et al. [58]:

$$c_{\text{p,stm}} = R_{\text{u}} \left( {3.470 + 1.450 \times 10^{ - 3} T + 1.21 \times 10^{4} T^{ - 2} } \right)\;{\text{J}}/({\text{mol K}}).$$
(76)

The specific heat capacity of catalyst does not change with temperature during reaction such that \(c_{{{\text{p,}}\,{\text{cat}}}} = 1.087\) kJ/(kg K) [59].

The viscosities of VR and VGO were estimated using the correlations obtained from ASPEN PLUS/HYSYS 9.0:

$$\mu_{\text{VR}} = - 8.70 \times 10^{ - 6} + 2.9716 \times 10^{ - 8} T - 1.7952 \times 10^{ - 11} T^{2} + 4.5452 \times 10^{ - 15} T^{3} ,$$
(77)
$$\mu_{\text{VGO}} = - 6.0029 \times 10^{ - 7} + 1.2294 \times 10^{ - 8} T - 1.3150 \times 10^{ - 12} T^{2} + 6.4680 \times 10^{ - 17} T^{3} ,$$
(78)

where T is in K and the viscosities are expressed in Ns/m2.

The other parameter values used in computation are presented in Table 6.

Table 6 Other parameters used in computation
Full size table

Due to the dearth of some data from the Khartoum Refinery Corporation, data were obtained from a similar refinery in Nigeria, Kaduna Refining and Petrochemical Company, Plc., Kaduna, as indicated in Table 6 for computational purposes. Also, the basic nitrogen parameters, \(K_{N}\) and \(w_{N}\) in Table 6 were obtained from Xiong et al. [13], where the feedstock parameters were for the residual fluid catalytic cracking of China National Petroleum Corporation Refinery. Also, as stated earlier, owing to the inability to obtain a complete data for the Khartoum Refinery Company, these parameters were used in computation in this study as the current model is also for a residual fluid catalytic cracking unit and it was assumed that the nitrogen content should be similar.

Estimation of liquid and vapor phase heat capacities of feed, and its enthalpy of vaporization

The enthalpy of vaporization of the feed was obtained from ASPEN PLUS/HYSYS 9.0 as the enthalpy of vaporization of the pseudo-component for vacuum residue, n-octahexacontane, i.e., \(\Delta H_{\text{vap}}\) = 9.21253045 × 107 J/kmol, with its boiling point specified at \(T_{\text{vap}}\) = 930.16 K.

The heat capacity of the feed for both liquid and vapor phases were estimated using \(c_{\text{p}}\) data obtained from ASPEN PLUS/HYSYS 9.0. The liquid-phase heat capacity of the feed, \(c_{\text{p,VR}}^{\text{L}}\), was estimated using the Ruzicka method for temperature ranges between 613 K, which is the inlet temperature of the feed, and the boiling temperature of VR, 930.16 K.

$$c_{\text{p,VR}}^{\text{L}} = 1598930 - 359.131T + 6.18427T^{2} ,$$
(79)

which is expressed in units of J/(kmol K).

The vapor-phase heat capacity of the feed, \(c_{\text{p,VR}}^{\text{V}}\), was obtained via the NIST property estimation as an Aly–Lee heat capacity data, given thus:

$$c_{\text{p,VR}}^{\text{V}} = 1180.74 + 2859.27\left\{ {\frac{{\left( {\frac{ - 827.34}{T}} \right)^{2} \exp \left( {\frac{ - 827.34}{T}} \right)}}{{\left[ {\exp \left( {\frac{ - 827.34}{T}} \right) - 1} \right]^{2} }}} \right\} + 3261.3\left\{ {\frac{{\left( {\frac{ - 24141.2}{T}} \right)^{2} \exp \left( {\frac{ - 24141.2}{T}} \right)}}{{\left[ {\exp \left( {\frac{ - 24141.2}{T}} \right) - 1} \right]^{2} }}} \right\},$$

with temperature limits from 200 to 1000 K and is expressed in units of J/(mol K).

The average heat capacity, \(c_{\text{p}}\), of feed for both liquid and vapor phases was estimated thus:

$$c_{\text{p}} = \frac{\Delta H}{\Delta T} = \frac{{\int_{{T_{\text{L}} }}^{{T_{\text{U}} }} {c_{\text{p}} {\text{d}}T} }}{{\int_{{T_{\text{L}} }}^{{T_{\text{U}} }} {{\text{d}}T} }},$$
(80)

where \(T_{\text{L}}\) and \(T_{\text{U}}\) are the lower and upper temperature limits, 613 K and 930.16 K for the liquid phase and 930.16 K and 1000 K for the vapor phase, respectively.

Estimation of effective diffusivity and mass and heat transfer coefficients

The mass transfer coefficient, \(k_{\text{g}}\), was calculated from the \(j_{\text{D}}\) factor and the Schmidt’s number [30]:

$$k_{\text{g}} = \frac{{j_{\text{D}} G_{\text{V}} }}{{\rho_{\text{g}} \phi_{\text{p}} }}Sc^{{ - {\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 3}}\right.\kern-0pt} \!\lower0.7ex\hbox{$3$}}}} ,$$
(81)
$$Sc = \frac{{\mu_{\text{g}} }}{{D_{\text{k}} \rho_{\text{g}} }}.$$
(82)

The heat transfer coefficient, \(h_{\text{gs}}\), was calculated from the \(j_{\text{H}}\) factor and the Prandtl’s number, Pr, [30]:

$$h_{\text{gs}} = \frac{{j_{\text{H}} c_{\text{p,VR}}^{\text{V}} G_{\text{V}} }}{{\phi_{\text{p}} }}Pr^{{ - {\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 3}}\right.\kern-0pt} \!\lower0.7ex\hbox{$3$}}}} ,$$
(83)
$$Pr = \frac{{c_{\text{p,VR}}^{\text{V}} \mu_{\text{g}} }}{{k_{\text{cat}} }}.$$
(84)

The effective diffusivity, \(D_{\text{e}}\), was calculated from the Knudsen diffusivity [61]:

$$D_{\text{e}} = \frac{{D_{\text{k}} \phi_{\text{p}} \sigma_{\text{c}} }}{\tau }.$$
(85)

The Knudsen diffusivity, \(D_{\text{k}}\), was estimated thus [30]:

$$D_{\text{k}} = \frac{{d_{\text{pore}} }}{3}\sqrt {\frac{{8R_{\text{u}} T_{\text{g}} }}{{1000\pi \overline{M}_{\text{g}} }}} .$$
(86)

In the fluidized-bed catalytic reactor, the j-factors (\(j_{\text{D}}\) and \(j_{\text{H}}\)) are approximately equal and was estimated using the correlation given thus [58]:

$$j_{\text{D}} ,\;j_{\text{H}} = 1.77\left| {\frac{{d_{\text{p}} G_{\text{V}} }}{{\mu_{\text{g}} \left( {1 - \in_{\text{g}} } \right)}}} \right|.$$
(87)

Simulation results and discussion

The API equation of viscosity of lumps was not used for VR and VGO lumps because they ran into negative values for all temperatures studied. Instead, the viscosity equation for the pseudo-components of VR and VGO were obtained from ASPEN PLUS/HYSYS 9.0, as given in Eqs. (77) and (78), respectively.

The unit factors estimated by Xu et al. [14] were adopted to adjust the kinetic parameters to improve correlation of yields with RFCUU-riser reactor plant data, as the kinetic parameters are flexible for use for different feedstocks [1]. The unit factors used were as follows: FU(1) = 1.508 to adjust all reaction constants: \(k_{1,2}\) ~ \(k_{5,7} \,\), FU(2) = 0.5239 to adjust VGO, LFO, and GA lumps’ formation reaction constants from VR (\(k_{1,2} ,k_{1,3} ,\,\) \(k_{1,4}\)) and LFO formation reaction constant from VGO (\(k_{2,3} \,\)); FU(3) = 0.2225 to adjust LPG, DG, and CK lumps’ formation reaction constants from VR: \(k_{1,5} ,k_{1,6} ,\,k_{1,7} \,\); FU(4) = 0.4015 to adjust GA formation reaction constants from VGO and LFO: \(k_{2,4}\) and \(k_{3,4} \,\), FU(5) = 1.676 to adjust LPG and DG formation reaction constants from VGO and LFO: \(k_{2,5} ,k_{2,6} ,\,k_{3,5} \,\) and \(k_{3,6} \,\); FU(6) = 2.267 to adjust CK formation reaction constants from VGO and LFO: \(k_{2,7}\) and \(k_{3,7}\), FU(7) = 0.9756 to adjust LPG, DG, and CK formation reaction constants from GA: \(k_{4,5} ,k_{4,6}\) and \(k_{4,7}\); FU(8) = 0.8245 to adjust DG and CK formation reaction constant from LPG: \(k_{5,6}\) and \(k_{5,7}\). These factors were regressed by the modified Levenberg–Marquardt algorithm with two sets of plant data from Xu et al. [14].

The assignin and evalin MATLAB R2017a functions were used to call out the values of the interstitial gas velocity, while the gas-phase mass flowrate, superficial velocity, average molecular weight, density, and time-on-stream were calculated using the results from the code. The simulated results of the developed mathematical models for riser reactor of RFCCU without mass and heat transfer resistances did not match any of the plant data at all as the results were unrealistic, especially the weight fraction of each lump being negative. Hence the results were not presented here and neither was the discussions made in that respect. Only the simulated results with the incorporation of mass and heat transfer resistances in the developed models were presented and discussed as these results show promising results, as presented in Figs. 3, 4, 5, 6, 7, 8, 9, and 10.

Fig. 3
figure 3

Comparison of predicted yields of VR, VGO, and LFO and conversion with RFCCU-riser reactor

Full size image
Fig. 4
figure 4

Comparison of predicted yields of GA, LPG, DG, and coke with RFCCU-riser reactor

Full size image
Fig. 5
figure 5

Predicted temperature profiles for solid and fluid phases along height of RFCCU-riser reactor

Full size image
Fig. 6
figure 6

Predicted pressure profiles along height of RFCCU-riser reactor

Full size image
Fig. 7
figure 7

Catalyst-and gas-phase residence times against height of RFCCU-riser reactor

Full size image
Fig. 8
figure 8

Velocities of solid and gas phases along height of RFCCU-riser reactor

Full size image
Fig. 9
figure 9

Effect of COR on catalyst-residence time at different input temperatures of catalyst

Full size image
Fig. 10
figure 10

Catalyst-residence time against catalyst-inlet temperature at different CORs

Full size image

From Ahmed et al. [1], Xu et al. [14], Heydari et al. [15], it was stated that the heavy lumps, VR and VGO, could be lumped together as cycle slurry oil (CSO). Thus, the conversion was calculated by the subtraction of the sum of both mass fractions from the total mass fraction i.e., \(X_{\text{VR}} = 1 - \left( {y_{\text{VR}} + y_{\text{VGO}} } \right).\) The conversion results for both instantaneous and one-dimensional vaporization of feedstock were similar with the former being 82.74% and the latter 83.47%. However, the vacuum residue was cracked 96% and 97% for instantaneous and one-dimensional vaporization of feedstock, respectively. The respective yields of each lump at the end of RFCCU-riser reactor after recycling CSO for both instantaneous and one-dimensional vaporizations of feedstock are shown in Table 7.

Table 7 Comparison of predicted yield of lump after recycling CSO (15 wt% of feed) with RFCCU plant data [1]
Full size table

The comparison of the predicted results with RFCCU-riser reactor data in terms of yields of lumps is depicted in Fig. 3 and 4. It can be seen in Fig. 3 that most of the conversion (about 90%) occurs in the first 5 m of the riser reactor. This agrees with the literature findings and it can be inferred that the rate of cracking is fastest at the entrance into the riser reactor [14, 15, 65,66,67,68,69,70]. Also, for both instantaneous and one-dimensional vaporization of feedstock, 95% of the conversion occurs in the first-third of the reaction, while 97% of the conversion occurs in the first half of the reactor, and only 3% of the conversion occurring in the second half of the reactor, implying that the second half of the riser reactor is redundant. Excellent agreements between the predicted results and the plant data were achieved for instantaneous vaporization of feedstock with maximum % error being 3.24 as shown in Table 7, where optimal yields of the cracked products needed to meet market demands and ensuring maximum profit were achieved. The predicted results for one-dimensional vaporization of feedstock yielded poor results. Hence, instantaneous vaporization of feedstock must have occurred at the entrance of the riser reactor.

Figure 5 shows the temperature profile for solid and fluid phases along the height of the RFCUU-riser reactor. There is a rapid increase in the temperature of the gas phase for both models of instantaneous and one-dimensional vaporization of feedstock near the inlet of the riser reactor (at about 2.3 m). This agrees with theory that vaporization occurs towards the inlet of the riser reactor. The solid-phase temperature drops rapidly from 927 K to about 765.5 K for the instantaneous model near the inlet of the riser reactor, and both the solid and gas phases’ temperatures reached a constant value of 765.5 K from 2 m till the end of the riser reactor. The predicted exit temperature of 765.5 K using instantaneous vaporization of feedstock is in excellent agreement with the RFCCU-riser reactor of 755 K, with % error being ± 1.39. However, for the one-dimensional vaporization of the feedstock, the solid and gas phases attained a constant temperature of about 907.5 K near the inlet of the reactor, and afterwards, their temperature profile dropped more evenly across the height of the reactor, reaching a value of 798.15 K at the end of the reactor. This predicted exit temperature is in variance with the plant value of 755 K. For both instantaneous and one-dimensional models, thermal equilibrium of the gas and solid phases occurs in the first 2 m of the riser reactor, which is about 5% of the total riser length, and then drops very gently across the remaining height of the riser reactor for the instantaneous model and a little steep for the one-dimensional vaporization model. Using the heat balance equation for the solid (coke and catalyst), almost 74 MJ and almost 9 MJ of heat was transferred by the solid to the fluid in 1 s within 2 m riser length for instantaneous and one-dimensional vaporization of feedstock, respectively. The point of intersection of the solid and gas phases’ temperature profiles is a direct function of the gas-particulate heat transfer coefficient while the riser reactor exit temperature is a function of the cracking reactions and mass balance between the phases.

Figure 6 shows the pressure profile along the height of RFCCU-riser reactor. The pressure drop for both instantaneous and one-dimensional vaporization of feedstock is gentler towards the entrance of the riser reactor; this can be attributed to the faster reaction rate towards the entrance of the reactor resulting in rapid expansion of the gas-phase. Thus, a more relaxed drop in pressure at the entrance of the reactor is expected. The steeper drop in pressure as the reaction progresses can be attributed to lower rate of reaction and therefore less expansion, thus the pressure drops due to loss in hydrodynamic energy as the products and catalysts are transported along height of the riser reactor. Overall, there is a 26% and 33% drop in pressure in the instantaneous and one-dimensional vaporization models, respectively.

Figure 7 shows the predicted catalyst- and gas-phase residence times along the height of RFCCU-riser reactor. The catalyst spends more time at the inlet of the reactor due to its initial low-velocity, but as reaction occurs, its velocity increases. Averagely, the catalyst residence time increases fairly evenly across the height of the riser reactor. The respective total catalyst residence times for instantaneous and one-dimensional vaporization of feedstock are about 2.03 s and 1.54 s. These are within the plant reaction time of cracking of 1–5 s. The gas spends less time of about 0.65 s and 0.55 s for the respective instantaneous and one-dimensional vaporization of feedstock in the reactor, owing to the higher velocity of the gas phase.

Figure 8 shows the variation of the solid and gas phases’ velocities with height of RFCCU-riser reactor for instantaneous and one-dimensional vaporization of feedstock. For both models, the velocity of solid and vapor phases increases along the height of the riser reactor. The cluster-phase velocity is lower than that of the gas superficial velocity owing to the high momentum of the gas particles moving the solid phase. The cluster-phase velocity increases from 0.69 to 39 m/s and to 47 m/s for instantaneous and one-dimensional vaporization of feedstock, respectively. The gas superficial velocity increases from 0.41 to 3.00 m/s and to 3.06 m/s for instantaneous and one-dimensional vaporization of feedstock, respectively, while the gas interstitial velocity from 4 m/s to 58.5 m/s and from 9 to 68.5 m/s, respectively. These high values of velocities may be attributed to the pressure at which the RFCCU is operating. The inlet pressure being almost twice and the exit pressure being similar to that of commercial RFCCU. The slip factor between the solid and vapor phases was seen to drop to about 1.5; however, the slip factor at the outset of cracking is about 1.9 for both models which agrees with theoretical range from 1.2 to 4, where 2 is considered typical in a commercial FCCU [40].

Figure 9 shows the effect of COR on catalyst residence time at different input temperatures of catalyst, \(T_{\text{cat}}\). It was observed that for both instantaneous and one-dimensional vaporization of feedstock, the catalyst residence time reduced as COR increased for all input temperatures of catalyst as a result of higher flow rate of catalyst, thus higher velocity of catalyst.

Figure 10 shows the effect of different inlet temperatures of catalyst on catalyst residence time at different CORs. It was observed that, an increase in the inlet temperature of catalysts also reduced catalyst residence time at different catalyst oil ratios. A higher input temperature of catalyst, resulted in higher temperatures of reaction mixture, thus resulting in faster reaction rates, and ultimately in higher velocities of the gas phase and thus the catalysts. However, the COR has a greater effect on catalyst residence time than catalyst inlet temperature.

Conclusion

A comprehensive one-dimensional adiabatic mathematical model was developed for RFCCU-riser reactor using modified version of the seven-lump kinetics of vacuum residue cracking. Also, the model incorporated material balance, energy balance, mass and heat transfer resistances, adsorption characteristics of asphaltenes, resins, and aromatics, and of basic nitrogen, and coking characteristics based on time-on-stream of catalyst. The resulting coupled ODEs were numerically integrated using MATLAB built-in function of ode23t. It was found that most of the cracking reaction occurs toward the inlet of the riser reactor, with 90% of the final conversion occurring in the first 5 m, 95% and 97% of the conversion occurring in the first half and third of the riser reactor, respectively. With the other half of the reactor accounting for only 3% of the conversion, it could be inferred that this half is relatively redundant. Comparison was made between the KRC–RFCCU data and the simulated results for both instantaneous and on-dimensional vaporization of feedstock, where an excellent agreement was achieved with AAD < ± 5% in the former for all cases investigated.