Introduction

Hydraulic fracturing has become a widespread stimulation technology to enhance hydrocarbon production from low-permeability reservoirs (Montgomery & Smith 2010). Fracturing the zone around the wellbore will increase access to the reservoir by creating a higher permeability zone and, more importantly, by increasing the contact area between the reservoir and the well system. Over the last two decades, hydraulic fracturing treatments have been widely applied in the development of unconventional hydrocarbon resources (Ostojic et al. 2012; Tiab & Donaldson 2015), characterized by ultra-low permeability, low porosity, and high heterogeneity (Khan & Al-Nakhli 2012). The production from such unconventional reservoirs cannot be economic unless hydraulic fracturing is used to stimulate production (Medavarapu et al. 2017; Taha et al. 2013).

Hydraulic fracturing treatment involves injecting fluid to apply hydraulically enhanced pressure that opens up new fractures initiated from perforations in the wellbore. Proppants are added to the fracturing fluid to maintain some residual aperture in the newly created fractures. The proppant will assist in keeping the fractured region around the wellbore open and increases the hydrocarbon recovery (Khan & Al-Nakhli 2012). Crucially, the hydrocarbon production from hydraulically fractured well-systems will primarily depend on the fracture-length and fracture-height created by the engineering intervention, given that all other reservoir properties are predetermined by nature.

In our study, the effective fracture half-length is assumed to be comprised of those fracture sections that are characterized by infinite conductivity, which effectively conduits reservoir fluid via the wellbore for harvesting at the surface. In the design of fracturing treatments, considerations are made to have the optimum fracture half-length because the longer the fracture half-length, the greater the recovery (Guo 2007; Muther et al. 2020). However, analysis of well performance after a fracturing treatment frequently shows that the effective fracture half-length tends to be less than the designed or simulated length (Barree et al. 2005; Cipolla et al. 2008). This difference between real and planned fracture half-lengths appears to result from two capacity gaps (1) still limited engineering success in fracturing from every perforation cluster and delivering proppant far into the formation to keep fractures open with long effective half-lengths (Nandlal & Weijermars 2022a, b; Waters & Weijermars 2021), and (2) fracture modeling with reliable predictive capacity is still wanting (Tugan & Weijermars 2022a, b). The gap in the model estimations of fracture half-length and the actual fractures created is commonly attributed to a ‘complex fracture geometry’ (Elbel & Ayoub 1992).

Reliable estimations of post-fracturing fracture half-length are fundamental to enter on a learning curve for the improvement of future fracturing treatments in shale acreage. Rate-transient analysis (RTA) and pressure-transient analysis (PTA) models are the classical methods used to estimate the effective fracture half-length (Cipolla & Mayerhofer 1998; Bahrami et al. 2015). However, these methods are most accurate when the permeability is already well-constrained. For unconventional resources, it takes a very long time for the pressure to build up to estimate the permeability, rendering results subject to significant uncertainty. Other tools, such as production data analysis (PDA), can compute fracture half-length without shutting in the well (Rushing & Blasingame 2003). However, a disadvantage of PDA is that it is highly affected by the quality of production data, which could again result in estimations with high uncertainty. Micro-seismic mapping is a practical field tool that can provide images to estimate the hydraulic fracture geometry (Gutierrez et al. 2010). A limitation of this mapping tool is that it gives the maximum fracture half-length, not the effective half-length that contributes to hydrocarbon production (Ibrahim et al. 2020).

The present study assesses whether a physics-based Gaussian solution of the diffusivity equations (Weijermars 2021, 2022a) can be applied to provide reliable estimations of the fracture half-lengths. Based on a new solution to the pressure diffusion equation, three application modes were proposed, such as Gaussian decline curve analysis (DCA), Gaussian pressure transient model (PTA), and Gaussian reservoir models (Weijermars 2022a). For the Gaussian PTA model, to estimate the fracture half-length, it is helpful to first obtain a reliable value of the hydraulic diffusivity (Weijermars & Afagwu 2022). The Gaussian DCA method can be used to obtain the required hydraulic diffusivity by history-matching historical production data using the following Gaussian DCA equation (Weijermars 2022a, b):

$$ q\left( t \right) = q_{i} \frac{1}{t}e^{{\left( \frac{1}{4Dh} \right)\left( {1 - \frac{1}{t}} \right)}} $$
(1)

Equation (1) can be applied using daily production data. For oil wells, the initial well rate \({q}_{i}\) (for the first day of production) is set at 1 bbl/day; for gas wells use of 1 Mscf/day is recommended (Weijermars 2022a). The term \(\frac{1}{t}{e}^{\left(\frac{1}{4Dh}\right)\left(1-\frac{1}{t}\right)}\) is non-dimensional, but normalization of its parameters was achieved using unit measures, such that substitution of t in dimensionless units (e.g., t = 1 for tdimensional = 1 day, or 10 for 10 days, etc.) and using dimensionless Dh (such that Dh = 1 equals to a dimensional input Dh_dimensional of 1 ft2/day).

The primary novelty of present study resides in the estimation of fracture half-length from well production data, which traditionally requires specialized knowledge and the utilization of RTA. In contrast to conventional methods, the newly proposed Gaussian PTA-method demonstrates enhanced versatility in swiftly generating probabilistic estimations of the fracture half-length. This investigation demonstrates the capabilities of the Gaussian PTA-model in providing both deterministic and probabilistic estimations for the fracture half-length. The analysis focuses on the examination of production data obtained from two Wolfcamp wells, namely Well 4H and 31H, located in the Midland Basin of West Texas. The results acquired from the RTA model are compared with the half-length estimates derived through independent rate-transient analysis and microseismic mapping. Consequently, this paper presents an innovative approach based on a previously unexplored analytical solution for estimating fracture half-length, offering supplementary evidence through a comprehensive comparative analysis between the novel method and the traditional RTA solution.

Methodology

Our team conducted this research to examine the applicability of a recently developed GPT-method for determining hydraulic fracture half-lengths (Weijermars 2022a). This study evaluates hydraulic fracture half-length in shale reservoirs using Gaussian pressure transient analysis (PTA), and the results obtained were benchmarked against the traditional RTA-method. Widely used in the oil and gas industry for calculating hydraulic fracture half-lengths, the classic RTA-method was chosen as the benchmark technique. The workflow presented in the first part of this section was applied to two shale wells (Wells 4H and 31H) located in the Wolfcamp Formation (Midland Basin, West Texas, US).

Workflow

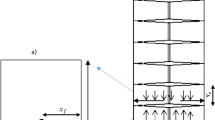
Figure 1 depicts the workflow adopted to evaluate hydraulic fracture half-length, using Gaussian Pressure-Transient (GPT) solutions, deterministically and probabilistically, for two wells drilled in the Wolfcamp Shale Formation.

Fig. 1
figure 1

Workflow to evaluate hydraulic fracture half-length using the GPT method (deterministically and probabilistically)

Full size image

The workflow begins with gathering all the necessary input data, including fluid and rock properties, historical production data, and microseismic survey data that were recorded during the hydraulic fracturing of the stages. The Gaussian DCA-method is then used to obtain the hydraulic diffusivity parameter, which is an essential input for the GPT-model’s application to determine the deterministic and probabilistic half-length of the hydraulic fractures. The results of the GPT-based PTA-model were validated using traditional RTA and microseismically interpreted fracture half-lengths.

Input data

This study estimates hydraulic fracture half-length using a combination of well data, including fluid analysis, petrophysical core analysis, micro-seismic monitoring during hydraulic fracturing, and subsequent historical production data. The uncertainty range of critical parameters is captured through probabilistic sampling from the input data distributions generated for the pertinent data sets. The pertinent data sets used are briefly described below.

PVT analysis

The data utilized from PVT-tests for shale oil reservoirs are viscosity and oil formation volume factors. An average value was used for oil viscosity between reservoir and wellbore conditions. The oil formation factor accounted for the volume change when oil from reservoir conditions (reservoir bbls) is lifted to the surface stock-tank conditions (STB). Table 1 shows mean values available for each well from PVT reports.

Table 1 PVT mean values for Well 4H and 31H
Full size table

Shale core analysis

The crushed shale permeability was measured during shale core analysis, which is an essential input for the subsequent estimation of the fracture half-lengths. Pressure decay on the fresh, crushed, 20/35 mesh size equivalent sample was used by a service company to calculate the matrix permeability. In our study, the permeability data sets for both wells were fitted with probability distribution functions, with best-fitting distributions determined using @Risk. According to the Akaike information criterion (AIC), a Weibull probability distribution function gave the best fit to the primary data for both wells Fig. 2a, b.

Fig. 2
figure 2

Permeability probability density functions (a) 4H (118 sample size) and (b) 31H (95 sample size)

Full size image

History matching production data

Both study wells analyzed were hydraulically fractured and produced from the Wolfcamp Shale Formation for over two years. The production data was history-matched using Gaussian DCA (according to Eq. 1) to estimate reservoir hydraulic diffusivity (Dh), the only unknown parameter, the initial production rate qi is assumed to be 1 STB/day. The history matching was performed using the Solver plug-in of Microsoft Excel to obtain the hydraulic diffusivity regressing with the least sum of square errors of the daily production rates residual:

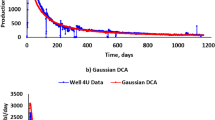
$$ daily \;rate\; residual = \sum {\left( {q_{Gaussian DCA \bmod el} - q_{historical data} } \right)^{2} } $$
(2)

Well 4H was completed with 33 stages and three perforation clusters per stage. The original reservoir pressure was 4680 psi, and the bottom-hole reservoir pressure was kept at 1000 psi. The assumed reservoir thickness is 100 ft. Daily production rates for four years were used in the history-matching to establish the diffusivity parameter that best fitted the historical production data (Chakra & Saraf 2015). The 48 months of daily production data for Well 4H were history matched with the Gaussian DCA model; the obtained best-fitting DCA-curve is illustrated in Fig. 3a. The hydraulic diffusivity for this well is approximately 0.02267 ft2/day.

Fig. 3
figure 3

History matching of production rates on Gaussian DCA model (a) Well 4H (and (b) Well 31H

Full size image

Well 31H has 23 months of daily production data, which was also utilized to estimate the hydraulic diffusivity. The original reservoir pressure was 5850 psi, while the bottom-hole pressure was kept at 1000 psi. The well is assumed to be produced from a 100 ft thick payzone and was completed with 36 fracturing stages, with 5 clusters per stage. The 23 months of daily production data were fitted with the Gaussian DCA model, providing the minimum square error for the best history matching; the corresponding hydraulic diffusivity is 0.02178 ft2/day. The diffusivity parameters listed in Table 2 are essential for the subsequent estimating of the fracture half-lengths using the GPT model.

Table 2 Main well characteristics for both case study wells
Full size table

Microseismic mapping

Microseismic monitoring is a technique that uses microseismic phenomena caused by fracturing caused by water injection. It is similar to natural earthquakes but has low intensities. Microseismic monitoring gives real-time measurements of the heights, lengths, orientations, geometries, and spatial configurations of fractures created during the fracturing treatment (Zou 2017). Three offset wells recorded microseismicity near Well 31H, and direct monitoring was acquired on Well 4H.

The micro-seismic monitoring occurred as fractures formed and propagated to their maximum value. Fracture-length of Well 4H is depicted in Fig. 4 on histograms created from the microseismic profiles of the monitored well. A side view of the stimulated rock volume during Well 4H’s fracturing is depicted in Fig. 5. The fluid drainage around Well 4H was previously analyzed in detail using complex-analysis-based flow models (Weijermars et al. 2017a, b). Figure 6 displays a Gunbarrel view of the offset wells for Well 31H. These wells are located only 3.5 miles from the wellhead of Well 31H.

Fig. 4
figure 4

Histogram view of microseismic fracture lengths on each stage for Well 4H (a) Length Asymmetry (b) Total Microseismic Lengths

Full size image
Fig. 5
figure 5

Microseismic side view of the stimulated volumes for Well 4H. The left image (a) shows signals colored by stage; the right image (b) cloud-colors the stages

Full size image
Fig. 6
figure 6

Gunbarrel view surveyed offset wells (Wells 44H, 45H, and 46H)

Full size image

The laterals of Well 31H and Wells 44H, 45H, and 46H are located in the same landing zone (Wolfcamp C-D), with toes only 1.5 miles apart. Wells 44H, 45H, and 46H have a 350 ft vertical offset, and the horizontal wells offset 375 ft. Fracture-lengths for Wells 44H, 45H, and 46H are depicted in Fig. 7 on histograms interpreted from the microseismic profiles of the monitoring wells.

Fig. 7
figure 7

Histogram view of micro seismic monitored fracture lengths for surveyed 31H offset wells (44H, 45H, and 46H)

Full size image

The 3-D drained rock volume around five hydraulic fractures in a single stage of Well 46H was previously regenerated from history-matched production data in (Parsegov et al. 2018). The fracture half-lengths estimated from the micro-seismic surveys are summarized in Table 3. Only the average fracture half-lengths from Well 45H and Well 46H were used because of the limited number of stages monitored for Well 44H (Fig. 7).

Table 3 Average fracture half-length Yf from microseismic for Wells 4H, 44H, 45H, and 46H
Full size table

GPT-equations

The Gaussian pressure-transient solution for fluid flow in porous media was derived by Weijermars (2021) and used as a decline curve analysis method. In the context of this study, the GPT-model can be applied to estimate hydraulic fracture half-lengths by regression using historical production rates:

$$ {\textit{q}}_{{\textit{r}}} \left( {\textit{t}} \right) = \frac{{2{\textit{Ak}}\left( {{\textit{P}}_{0} - {\textit{P}}}_{BH} \right)}}{{{\mu D}_{{\textit{h}}} {\textit{t}}}}{\textit{xe}}^{{\left( {\frac{{ - {\textit{x}}^{2} }}{{4{\textit{D}}_{{\textit{h}}} {\textit{t}}}}} \right)}} $$
(3)

where qr(t) denotes the production rate at time t, Dh is the hydraulic diffusivity, 2A is the area of both sides around the fracture, k is the matrix permeability, \(\mu \) is fluid viscosity, P0 original reservoir pressure, PBH represents bottom hole pressure, x is a fixed distance to the fracture plane (set at 1 ft if using field units)

$$ {\textit{q}}_{{\textit{w}}} \left( {\textit{t}} \right) = \frac{{{\textit{q}}_{{\textit{r}}} \left( {\textit{t}} \right)}}{{\textit{B}}}\,\& \,{\textit{Y}}_{{\textit{f}}} = \frac{{\textit{A}}}{{2{\textit{nh}}}} $$
(4)

By applying Eq. (4a,b), which accounts for both produced fluid compressibility and substitutes fracture half-length Yf, Eq. (3) can be rewritten as:

$$ {\textit{q}}_{{\textit{w}}} \left( {\textit{t}} \right) = \frac{{{\textit{C}}1{\textit{C}}2}}{{{\textit{C}}3}} \cdot \frac{{2{\textit{nhkY}}_{{\textit{f}}} \left( {{\textit{P}}_{0} - {\textit{P}}}_{BH} \right)}}{{{\mu B}_{0} {\textit{D}}_{{\textit{h}}} {\textit{t}}}}{\textit{xe}}^{{\left( {\frac{{ - {\textit{x}}^{2} }}{{4{\text{D}}_{{\text{h}}} {\text{t}}}}} \right)}} $$
(5)

Equation (5) relates well flow rate and hydraulic fracture half-length and can be applied as an RTA-method to estimate linear flow parameters. The conversion factors C1, C2, and C3 are needed when working in field units, with qr(t) in bbl/day, t in days, Dh in ft2/day, 2A in ft2, k in mD, P0 and PBH in psi, x is 1ft and \(\mu \) is in cPoise (which equals mPa.s), where B is the oil formation volume factor in reservoir bbl/STB, n is the total number of fractures, h represents the reservoir thickness in ft, and C1, C2, and C3 are conversion factors to field units 0.178108 bbls/ft3, 1.06235E-14 ft2/mD and 1.67868E-12 psi.day/cPoise, respectively.

Rearranging Eq. (5) yields Eq. (6), which was used in this study to stochastically model the fracture half-length:

$$ {\textit{Y}}_{{\textit{f}}} = \frac{{{\textit{C}}3}}{{{\textit{C}}1{\textit{C}}2}} \cdot \frac{{{\textit{q}}_{{\textit{w}}} \left( {\textit{t}} \right).{\mu B}_{0} {\textit{D}}_{{\textit{h}}} {\textit{t}}}}{{2{\textit{nhk}}\left( {{\textit{P}}_{0} - {\textit{P}}}_{BH} \right)}}{\textit{xe}}^{{\left( {\frac{{{\textit{x}}^{2} }}{{4{\text{D}}_{{\text{h}}} {\text{t}}}}} \right)}} $$
(6)

GPT-Approaches

Two Approaches (A,B) were evaluated to estimate the hydraulic fracture half-length, based on the GPT-model explained in the previous sections. Approach A is deterministic, while Approaches B uses Monte Carlo simulation to probabilistically sample input parameters and history-match the fracture half-lengths. A Monte Carlo simulation was used to stochastically samples the input data (performed using the Palisade@Risk plug-in for Microsoft Excel) to account for uncertainties in determining the fracture half-length.

Approach A: Deterministic estimation of hydraulic fracture half-length

In this approach, fracture half-length was history-matched using historical production rates and Eq. (6). From the probabilistic distribution functions, the mean values of all equation parameters were compared to those obtained from the deterministic values of fracture half-length. The parameters utilized in history matching in this approach are listed in Table 4. Please note viscosity and formation volume factor are averaged from subset of data in Table 5 and 6 which covers data from bottom hole pressure to reservoir pressure, resulting in values being slightly different from those in Table 1. In Approach A, we never used the full cluster numbers; we assume only 70% of the perforations to create hydraulic fractures, which is 69 for Well 4H and 95 for Well 31H (Table 4).

Table 4 The property values applied in history matching in approach A for both wells
Full size table
Table 5 FVF and viscosity data obtained from PVT tests for Well 4H
Full size table

Approach B: probabilistic estimation of hydraulic fracture half-length

Equation (6) was used to stochastically samples the input values to estimate fracture half-lengths using historical production rates. Since production rates and corresponding times are strongly interrelated, a correlation between them was considered during sampling. For all wells, the permeability is considered as 100 nD. The mean of the resulting probability distribution function for fracture half-length was compared to traditional RTA analysis and microseismic monitored fracture half-length. The input parameters PDF characteristics used in this scenario are listed in Table 7.

Table 6 FVF and viscosity data obtained from PVT tests for Well 31H
Full size table
Table 7 The properties of PDF used in approach B for both wells
Full size table

In Approach B, a success ratio of 70–100% for the total cluster numbers was used when sampling input data; we effectively used a probability distribution between 70 and 100%. We assumed 70% as a minimum number of perforations to create hydraulic fractures and considered a range of better success rates in the probabilistic model. For Approach A, we use 69–99 fractures for Well 4H and 95–136 for Well 31H.

Results

Fracture half-lengths were estimated with the GPT-method using the proposed approaches (GPT-Approaches). Results of GPT-methods will be presented first, followed by micro-seismic and RTA-methods. The results of Approach A will be shown for both wells, and then Approach B outcomes will be displayed.

Approach A: deterministic estimation of hydraulic fracture half-length for well 4H

This approach estimates hydraulic fracture half-length deterministically using two scenarios. Equation (5) was employed to match daily rate data to the Gaussian model Fig. 8 shows the history-matched decline rate and cumulative. The history match is used to calculate for hydraulic fracture half-length by using lab measurement data. It can be seen that history matching is quite acceptable, considering the noisy production data. Production data from specific days were excluded from the history matching due to their long shutdown time (more than 10 h). Almost 48 days with production outliers were omitted from history matching for this Well 4H.

Fig. 8
figure 8

History matching of daily rates and cumulative production using the GPT-method for Well 4H

Full size image

Firstly, PVT data were obtained from available reports to address suitable formation volume factor (FVF) and viscosity values. Since the measured flow rate is at surface conditions and must be converted to reservoir conditions, FVF at reservoir conditions was considered in this approach, as shown in Table 5. An average value between the reservoir and bottom-hole pressure conditions will be considered for viscosity since we only focus on the flow from the reservoir to the bottom hole. Accordingly, two values of Yf were estimated using the reservoir condition’s FVF coupled with the viscosity at the reservoir and bottom hole conditions. The results of fracture half-length values using Approach A for Well 4H are summarized in Table 8.

Table 8 Deterministic fracture half-length Yf -values estimated using Approach A for Well 4H
Full size table

The two deterministic Yf-values (Table 8) were averaged to get one reference value that will be used later for comparison purposes. The average fracture half-length for Well 4H is 217 ft.

Approach A: deterministic estimation of hydraulic fracture half-length for well 31H

The same procedures were applied to Well 31H. Figure 9 depicts history-matching plots for the daily production rate and cumulative. In this case, history matching is not as good as the previous well due to irregular operational shutdowns related to technical interventions, as stated in production reports. For instance, the well was not producing from day 307 to day 339, as noted from the historical production rates in Fig. 3b. Additionally, days with production outages above 10 h were not considered in our history-matching. For Well 31H, 78 days from the production history were omitted.

Fig. 9
figure 9

History matching of daily rates and cumulative production using GPT-method for Well 31H

Full size image

For this well, multiple viscosity values (e.g., bottom-hole and reservoir condition values). The complete set of FVF and viscosity records for different pressures are listed in Table 6. Table 9 displays the summary of the Yf outcomes by using reservoir FVF, and viscosity at both reservoir and bottom-hole conditions. For the upcoming comparison, two Yf-values were averaged, and the deterministic reference value is 177 ft.

Table 9 Facture half-length values using deterministic approach for Well 31H
Full size table

Approach B: Probabilistic estimation of hydraulic fracture half-length for Well 4H

This approach estimates the hydraulic fracture half-length probabilistically using input distributions. Equation (6) was applied to estimate a probabilistic distribution of Yf using the best fit distributions for the inputs. For Yf to be estimated probabilistically, some input parameters were fitted to distributions using an excel @Risk plug-in. For correlation consideration between the inputs, a correlation matrix was defined for the flow rate (qw) and time (t) since they are considerably related (as seen in the decline curve of Fig. 8). In addition, the FVF and viscosity data were used to determine the distribution range between the reservoir and bottom-hole conditions. Table 10 shows the best-fitted distributions for the concerned input parameters.

Table 10 Best fit distributions for input parameters in Eq. (6) for Well 4H
Full size table

The @Risk Output function was now defined with some discrete and some probabilistic values based on Eq. (6). The final Yf was probabilistically estimated and is shown in Table 10. Additionally, the values reported from this approach include P10, P50, P90, and the mean for comparison purposes, as can be observed in Table 11.

Table 11 Probabilistic Yf values from Approach B for Well 4H
Full size table

Approach B: probabilistic estimation of hydraulic fracture half-length for Well 31H

The same procedure was applied to Well 4H. However, the fitted distributions of input parameters are quite different since we are dealing with various well records (Fig. 10). The used input parameters’ distributions are summarized in Table 12.

Fig. 10
figure 10

Probability distribution function of fracture half-length using probabilistic approach for well 4H

Full size image
Table 12 Best fit distributions for input parameters of Eq. (6) for Well 31H
Full size table

Furthermore, a correlation matrix employing @Risk was created for time and production rate. Figure 11 shows the PDF of Yf obtained from applying Approach B to Well 31H. Similar to Well 4H, the P10, P50, P90, and mean-values were reported for the Yf distribution, as shown in Table 13.

Fig. 11
figure 11

Probability distribution function of fracture half-length using probabilistic approach for well 31H

Full size image
Table 13 Probabilistic Yf values from Approach B for Well 31H
Full size table

Micro-Seismic results

This section will summarize the micro-seismic data to validate GPT approaches. Table 14 contains the averaged Yf values for both wells. It is vital to highlight that the recorded micro-seismic values overestimate the actual fractured length and are regarded as upper limits for other approaches.

Table 14 Average fracture half-lengths reported from Micro-seismic measurements
Full size table

RTA-Results

Rate transient analysis (RTA) is a method used to analyze the production behavior of shale gas wells over time. It involves using pressure, flow rate, and production data to create a mathematical model that describes the well’s performance. The model is then used to predict future well behavior, such as how long the well will continue to produce at a certain rate, and how much gas will be recovered over the life of the well. RTA is considered a valuable tool for optimizing production and making decisions about well completion and stimulation.

Rate-transient analysis (RTA) is based on the conventional well-testing solution of the pressure diffusivity equation for the pressure transient, which assumes a constant well-rate and provides for a vertical well. When applying RTA to hydraulically fractured wells, the Wattenbarger et al. (1998) solution, which assumes linear flow and infinite fracture conductivity, can be used. When applying RTA, the production rate was used to normalize the pressure drop (p-pwf) between the reservoir and the bottom hole pressures. The normalized pressure drop and material balance time (tmb) are then used in an RTA-plot for Ac characterization (Nashawi and Malallah 2006). To identify the different flow regimes, log–log diagnostic plots of \(\left[{p}_{i}-{p}_{wf}\right]/{q}_{o}\) and the drop-pressure/oil rate derivative function, \(\textit {t}\hspace{0.33em}[\Delta (p)/{q}_{o}]{\prime}\), are recommended. Typically, a linear flow regime, with ½ slope in the diagnostic plot, is the dominant flow regime in infinite conductivity hydraulically fractured well. This requires the construction of (1) a diagnostic log–log plot of (\(\Delta \) p)/qo versus (tmb), and (2) a log–log plot of \(t\;[\Delta (p)/q_{o} ]^{\prime}\) versus t (Fig. 12b). The flow regimes can then be determined as a function of the tangent slopes to the plotted data (Ibrahim and Wattenbarger 2005; Dheyauldeen et al. 2022). Finally, a specialized plot for the linear flow regime needs to be constructed by plotting the normalized pressure difference versus the square root of the material balance time. In the Cartesian plot, a straight line with a slope (m) can be estimated. Then, from the line slope (m), \(\sqrt{k}{A}_{c}\) can be calculated (Wattenbarger et al. 1998):

$$\sqrt{k}{A}_{c}=\frac{79.65B\mu }{\sqrt{\hspace{0.33em}(\varnothing \mu {c}_{t}{)}_{i}}}\left(\frac{1}{m}\right)$$
(7)

where Ac is the total fracture surface area, which reflects the effective area for the fluid production, \(\varnothing ,\mu ,{c}_{t}\) are the formation porosity, fluid viscosity, and total compressibility, respectively. T is temperature, and k is the formation permeability. By knowing the number of fractures (nf) and the fracture height (hf), the average fracture half-length (Yf) can be estimated using the following equation.

Fig. 12
figure 12

RTA-analysis for 31H and 4H wells, left column, (a) and (c), represent the diagnostic plots of normalized pressure difference divided by rate, \(\left[{{p}}_{{i}}-{{p}}_{{wf}}\right]/{{q}}_{{o}}\), versus material balance time, and the right column, (b) and (d), represent RTA specialized plots for linear flow regime

Full size image
$${A}_{c}=4n_f Y_f h_f$$
(8)

These RTA methodologies were applied for both wells under investigation. Figure 12 shows the RTA analysis for both wells through the log–log diagnostic plot and the specialized Cartesian plots. The results showed that well 4H has a slightly longer fracture half-length compared to 3H. The fracture half-length was estimated to be 293 ft for Well 31H, and 200 ft for Well 4H.

Discussion

The introduction of this publication said that the standard RTA-method had been the only focus of well-testing literature up until this point in estimating hydraulic fracture half-length. Of course, this conventional method has advantages of its own. What is provided here, however, is a supplementary practical tool that can be utilized to calculate hydraulic fracture half-length using historical production rates and hydraulic diffusivity. The Gaussian Pressure Transient Method, which allows for quick estimation of fracture half-length, emphasizes hydraulic diffusivity as a critical factor influencing fluid mass transfer in hydraulically fractured reservoir regions. Additionally, the novel Gaussian Method is ideally suited for estimating fracture half-length deterministically and probabilistically because the simple analytical solution of Eq. (6) allows for quick iteration of inputs to quickly estimate modify fracture half-length and test the influence on the well rate.

Comparison between GPT approaches, RTA, and Micro-seismic (MS)

In this section, a comprehensive comparison of Yf values for Well 4H and 31H obtained from new GPT approaches will be weighed against micro-seismic values and compared to RTA results in Table 15. For Well 4H, GPT-Approach B successfully simulated a range of distribution of Yf –values between 37 and 1011 ft, using @Risk, which is considered a good result for the probabilistic distribution. Moreover, it appears that the Yf -value obtained from P50 in GPT-Approach B has the lowest relative error to RTA-method compared to GPT-Approach A.

Table 15 Comparison of Yf estimations from GPT, RTA, and MS methods for Well 4H and Well 31H
Full size table

Additionally, Micro-Seismic (MS) result has a 185% relative error to the classic RTA-method, which is considered an upper limit of Yf. Table 15 depicts the comparison between Yf values obtained for Well 4H. For Well 31 H, GPT-Approach A simulated a closer match to the result of the traditional RTA-method as compared to P50 GPT-Approach B. However, the mean value of probabilistic GPT-Approach B has only a 2% relative error to the RTA-method which had the lowest error when compared to GPT Approach-A while still maintaining a Yf value lower than the upper limit of the Yf, Micro-Seismic (MS) result. The comparison of two Wolfcamp case-study wells thus was successfully demonstrated with practical work-flows to test the robustness of the recently developed GPT-method for estimating fracture half-length deterministically and probabilistically. The outcomes were in reasonable agreement with the independent RTA result.

Strengths and limitations

The current study offers concrete applications of how a new Gaussian method can be used for estimating hydraulic fracture half-lengths. The method has two obvious advantages: (1) time savings due to its simplicity, and (2) uncertainty can be readily captured using probabilistic inputs. The Gaussian solution approach is a novel and original approach to estimate fracture half-length and improve well performance. Although still in its infancy and highly dependent on hydraulic diffusivity and permeability inputs, the Gaussian approach can estimate hydraulic fracture half-length probabilistically with reasonable accuracy while saving time due to its simplicity. The proposed approaches are thought to become part of standard operating procedures for petroleum engineering projects because, as of the study’s completion date, no glaring flaws in the practical approaches have emerged.

Fig. 13
figure 13

Hydraulic fracture half-length with time for Well 4H

Full size image

Time-dependency

Fracture half-lengths estimated with the Gaussian method using Eq. (6) are time-dependent. The same would appear in traditional RTA, but is commonly not assessed because the latter method conveniently assumes a constant well rate. Using the Gaussian method, the time-dependent Yf can be computed for each day, based on the available daily production rates for Well 4H (Fig. 13). The calculated Yf initially exhibits considerable variation with outliers (e.g., above 1000 ft). Finally, we successfully reach a stable fracture half-length; the mean value for Well 4H is 281 ft (141% of RTA benchmark for Well 4H in Table 15), as recorded from this approach. Similarly, Yf for Well 31H was determined for each time step using Eq. (6) (Fig. 14). Again early data reach above 1000 ft, but a stable fracture half-length with a mean value of 167 ft (57% of RTA benchmark for Well 31H in Table 15) was eventually reached.

Fig. 14
figure 14

Hydraulic fracture half-length with time for Well 31H

Full size image

The variation of fracture half-length over time suggested by Figs. 13 and 14 needs clarification, with a focus on the physical meaning, especially of (1) the high fracture half-lengths early in the well life and (2) the occasional high outliers later in the well life. The outliers seen later in the well-life are easy to explain. These are caused by brief periods of well shut-in related to workovers, due to which the daily production rates spike once the wells are turned on again. However, these enhanced rates are not representative of the long-term behavior of the well system. Separately, the early, high well-rates are known to occur before pressure interference starts, and the rates become relatively steady after transitioning from primary-transient to apparent boundary-dominated flow (Weijermars et al. 2019). We attribute the early enhanced flow-rate and its brief impact on large effective fracture half-lengths to initial wider fracture apertures at the distal end of newly created hydraulic fractures before closing as pressures near the well system drop.

Future work

The novel practical techniques for estimating fracture half-lengths that are provided in this paper can be used in a wide variety of intricate subsurface reservoirs because they are derived from the original GPT technique solutions. The author and his research team intend to use more case study examples in their upcoming work to understand better the time dependency of hydraulic fracture half-lengths, which will help pave the way for such an application. The time-dependent estimation of the hydraulic fracture half-length method uses input distributions with a time-dependent design to predict the hydraulic fracture half-length. Apart from production rate and time, which were explicitly entered into the Equation from production data, Eq. (6) can be used to estimate the hydraulic fracture half-length using the best fit distributions for the inputs using @Risk. In order to determine the impact of time elapsed on the hydraulic fracture half-length based on the available daily production rates, the Yf calculation is carried out for each flow rate and time step. Separately, a business may be established to provide a valuable set of tools for a simple application in real-world implementations based on the numerous applications of the Gaussian approach.

Conclusions

This study presents a novel approach to assessing the performance of the Gaussian Pressure Transient (GPT) method in the Wolfcamp Shale Formation. The effectiveness of this method is validated by comparing it to the traditional RTA-method. The GPT-method was compared to the RTA-method for estimating the hydraulic fracture half-length, using both deterministic and probabilistic models. The GPT-method offers simplicity and user-friendliness, making it accessible to individuals without specialized expertise. Despite its simplicity, the GPT-method maintains high reliability and closely aligns with the results obtained from the RTA-method for determining the hydraulic fracture half-length. The study successfully demonstrates how to use the newly developed GPT-method for deterministic and probabilistic estimation of fracture half-length through a comparison of two Wolfcamp case-study wells, with the results verified independently by the RTA-method. Additionally, the Gaussian method allows for time-dependent estimation of fracture half-lengths, enabling daily calculations based on provided production rates. Ultimately, this research attains stable fracture half-length values for both wells, validating the relevance of the innovative Gaussian method.

The following highlights were concluded:

  • The novel Gaussian Method is a supplementary practical approach tool that can be utilized to calculate hydraulic fracture half-length deterministically and probabilistically.

  • The new Gaussian method closely matches micro-seismic fracture half-lengths and is separately confirmed by the classic RTA-method.

  • The advantages of the Gaussian method are time savings due to its simplicity, and uncertainty can be readily captured using probabilistic inputs.

  • The Gaussian Pressure Transient Method emphasizes hydraulic diffusivity as a critical factor influencing fluid mass transfer in hydraulically fractured well systems.

  • Fracture half-lengths estimated with the Gaussian method are time-dependent and reach a stable fracture half-length for two Wolfcamp case-study wells.