Simulation of nuclear magnetic resonance response based on 3D CT images of sandstone core

Abstract

In recent years, nuclear magnetic resonance (NMR) logging has become increasingly prevalent in the characterization of rock properties such as porosity, permeability, saturation, and pore size distribution. However, interpreting such properties accurately from NMR logging data is challenging for some reservoirs. In particular, the impact of salinity, viscosity, and saturation on NMR measurements is not always clear, which can lead to inaccuracies in the resulting data interpretation. Properly accounting for these factors is essential in order to obtain accurate and reliable measurements for effective characterization of subsurface formations. This study utilized a random walk technique to simulate the NMR response of homogeneous sandstones using 3D CT images and conducted a sensitivity analysis under various salinity, crude oil viscosity, and water saturation conditions. The results indicate that the T₂ relaxation time slightly shifts toward the short relaxation direction as the salinity of the formation water increases. In addition, longer echo intervals result in a more significant forward shift in the T₂ value than shorter intervals. Whereas, for crude oil, the T₂ relaxation time becomes shorter as its viscosity increases. Furthermore, the effect of echo interval on the forward T₂ shift is less pronounced for crude oil than it is for formation water. Under water wet conditions, the T₂ spectrum of crude oil exhibits a peak at the volume relaxation position. As the water saturation decreases, the left two peaks in the T₂ spectrum shift toward shorter relaxation times. Under oil wet conditions, the T₂ spectrum exhibits a complex three-peak structure. The method provides a physical basis for interpreting NMR macroscopic responses, and the simulated NMR responses can help identify fluids in reservoirs.

Introduction

Nuclear magnetic resonance (NMR) technology has significantly improved petrophysics and reservoir evaluation in the petroleum industry over the past 30 years (Cannon et al. 1998; Brown et al. 2001; Freedman 2006). Researchers can determine the size and distribution of the pores, calculate water saturation, porosity, and permeability, and identify fluid types using two-dimensional NMR logging (Xu et al. 2013; Tan et al. 2015a, b; Rick 2004; Tutuncu et al. 2016). Additionally, low-field NMR can be used to quantify the rock wettability and observe hydrate behavior in geologic sediments (Ghazanfer et al. 2021). NMR experiments provide the physical basis for interpreting NMR logging data and establishing a petrophysical model (Kleinberger et al. 1996; Appel et al. 2000; Horkwitz et al. 1995). However, saturation with different fluids can lead to changes in volume relaxation T₂, hydrogen content index HI, and diffusion coefficient D. These are important parameters in nuclear magnetic resonance (NMR) logging technology. Experimental research on them is the physical basis for setting NMR logging measurement parameters, interpreting data processing, and forming new logging techniques (Akkurt et al. 1996, 1998; Morriss et al. 1996).

According to the principle of nuclear magnetic resonance logging, when the rock is water wet and 100% saturated with water, the morphology of nuclear magnetic resonance T₂ spectrum corresponds to the distribution of pore radius of the rock. At this point, the pore structure of the rock can be characterized using nuclear magnetic resonance T₂ spectroscopy (Coates et al. 2000; Dunn et al. 2002; Xiao et al. 2016a, b; Lai et al. 2018). However, this relationship is only effective for water or dry layers (Volokitin et al. 2001; Xiao et al. 2016a, b). When the pore space is saturated with different fluids, such as oil, the shape of the NMR T₂ spectrum changes significantly (Mao et al. 2007; Xiao et al. 2013), making it difficult to distinguish irreducible water and mobile oil in the T₂ distribution. To make NMR logging applicable to evaluating the pore structure of both water-bearing and oil-bearing formations, it is necessary to understand the influence of oil on NMR T₂ maps (Zhao et al. 2017; Niu et al. 2008). Although some conventional physical experimental methods have been proposed to study this effect (Zhao et al. 2017; Tan et al. 2015a, b), the small range of fluids used in these studies and the lack of analysis of mechanisms for different wettability and fluid types limit their usefulness.

Digital core technology is a combination of 3D CT images and numerical simulations to simulate the properties of rock formations at a microscopic level. The process involves scanning a rock sample with a high-resolution CT scanner, which is reconstructed into a digital model that captures the spatial distribution and connectivity of the pores. Numerical simulations are then used to predict the flow of fluids or solutes, as well as other properties such as mechanical strength, electrical conductivity, and thermal conductivity. Digital core technology allows for non-invasive analysis of rock samples and eliminates the need for expensive laboratory experiments, which could be time-consuming and require significant resources. Also, Digital core technology can be used to better understand how rock formations behave under different conditions such as stress or pressure, which has the potential to provide a cost-effective solution for studying NMR response. Various numerical methods have been used to simulate the NMR response based on 3D CT images, such as the random walk, finite element, or finite difference methods (Toumelin et al. 2003; Tan et al. 2014; Zientara et al. 1980; Arns et al. 2011; Wang et al. 2019). The random walk method is commonly used in the simulation of NMR response due to its ability to accurately reproduce the relaxation behavior of fluids in porous media. This method randomly distributes a large number of particles in the pores to represent fluid molecules and simulates the Brownian motion of fluid in the pores through diffusion equations. However, the accuracy of the random walk method depends on the quality of the digital core model and the appropriate selection of parameters such as the diffusion coefficient and surface relaxation rate.

The objective of this study was to assess the viability of utilizing 3D digital core technology and the random walk method to simulate the influence of oil on the NMR T₂ spectrum. The focus was to investigate the impact of oil on the NMR T₂ spectrum with the aim of gaining a deeper understanding of the underlying physics.

Method

Image acquisition by CT

The nanoVoxel-3502E, manufactured by QingNengSanying in China, was used for micron CT scanning in this study. The equipment boasts an industry-leading view field of 1920 × 1920 × 1920 and is equipped with a microfocus ray source capable of up to 300 kV, ensuring high-precision detection capability. As shown in Fig. 1, the scanner features a ray source on one side and a signal receiver on the other side. During the scanning process, samples are fixed on the middle turntable and rotate at low speed. Image reconstruction of hundreds of sample images taken from different angles is carried out to obtain three-dimensional structures (Vinegar 1995). The scanning resolution is limited to 0.5 μm. After the 3D imaging experiment of the core is completed, a 2D median filtering algorithm is used to filter the gray image of the core.

Fig. 1

Samples and internal structure of micro-CT

Segmentation of CT images into their respective components is a crucial step in building 3D digital cores. The gray-scale images of rocks need to be divided into pores and matrices in order to characterize the microscopic pore structure within them, including the size, morphology, and connectivity of pore throats. This process of digitization and segmentation of rock gray images into pores and rock skeletons is essential when simulating the quantitative aspects of the pore-scale rock physical properties. Different gray values in CT images represent different minerals in the rock matrix and fluids in pores. Brighter colors represent the rock matrix, while darker colors represent pores. The CT images can be used to divide the rock matrix and porosity using a threshold method. The best threshold value is selected and used to binarize the two-dimensional gray image. A value of 1 represents a rock pore, and 0 represents the rock skeleton. In this paper, a sandstone with a porosity of 13.218% and a resolution of 1.5 μm was selected, with 8003 voxels. Its digital core model is shown in Fig. 2, with the white part representing the particle framework and the blue part representing the pores. Table 1 shows the pore parameters obtained from micron CT images.

Fig. 2

Sandstone data volume obtained by CT

Table 1 Attributes of micron CT extraction

Simulation of oil–water distribution based on 3D images

A digital core is a three-dimensional image composed of solid and pore space, with the rock skeleton represented by 0 and the pore space represented by 1. Mathematical morphology calculation of the pore space using different structural elements is used to simulate oil–water two-phase displacement and obtain digital cores under different water saturations (Jin et al. 2009). The open operation is typically used to construct digital cores with different saturations, as it expands and shrinks the image like fluid displacement in core petrophysical experiments. However, as shown in Fig. 3a, using the water wettability condition as an example, the open calculation results often lead to contact between the oil phase in the pores and the rock surface, while in actual rock interiors, the water phase forms a film on the rock pore surface to block oil phase contact. Therefore, in this paper, corrosion calculation is first used to erode voxels inward along the pore surface, and the corroded part of the pore is taken as the water phase, as shown in Fig. 3b, forming the “oil in water” state.

Fig. 3

Comparison before and after water film construction

Different oil and water distributions in rock pore space can be obtained by mathematical morphology calculation of the rock pore space. Figure 4 shows the distribution of oil and water with different saturations in the pore space. In the figure, the black part represents the rock skeleton, the blue represents water, and the red represents oil.

Fig. 4

Oil and water distribution in pore space at different saturations

During displacement experiments on rocks, the non-wetting phase flow will first occupy the middle of the macropores, and as the displacement pressure increases, the non-wetting phase fluid will invade the pores in the order of large to small and diffuse from the center to the edge of the pores (Looyestijn et al. 2006; Zhao et al. 2010). Therefore, mathematical morphology can be used to simulate the displacement process of rocks and then, determine the distribution of oil and water in the pore space under different water saturation.

Random walk simulation of NMR response based on 3D images

According to NMR logging theory, the lateral relaxation time (T₂) of NMR is determined by the volume relaxation time (T_2B), surface relaxation time (T_2S), and diffusion relaxation time (T_2D). The relationship between these relaxation times is given by the following equations (Coates et al. 2000; Dunn et al. 2002):

$$\frac{1}{{T}_{2}}=\frac{1}{{T}_{2B}}+\frac{1}{{T}_{2S}}+\frac{1}{{T}_{2D}}$$

(1)

$$\frac{1}{{T}_{2S}}=\rho \frac{S}{V}$$

(2)

$$\frac{1}{{T}_{2D}}=\frac{D{(\gamma G{T}_{E})}^{2}}{12}$$

(3)

where ρ is the surface relaxation rate, S is the pore surface area, V is the pore volume, γ is the rotational magnetic ratio, D is the fluid diffusion coefficient, T_E is echo interval, and G is magnetic field gradient. T_2B is determined by the chemical composition and inherent properties of the fluid in the pores, T_2S is related to the aperture, and T_2D is mainly related to D, T_E and G. The change in NMR magnetization strength, M(t), with time t can be calculated using the following formula:

$$M\left(t\right)={M}_{0}\mathrm{exp}\left(\frac{-t}{{T}_{2}}\right)$$

(4)

where M₀ is the magnetization strength at the initial time. The random walk method is used to simulate the surface relaxation signal strength M_S(t) of the fluid in rock pores. The specific steps of this method are as follows:

• (1) A fixed number of protons are randomly distributed in rock pores;where r is the diffusion radius and ∆t is the time step.

• (2) Calculate the diffusion radius r = (6D∆t) ^0.5 (Zheng et al. 1989); where r is the diffusion radius and ∆t is the time step.

• (3) After each time step, the new position of the proton [x(t + ∆t), y(t + ∆t), z(t + ∆t)] is given by the following equation:

  $$\left\{\begin{array}{c}x(t+\Delta t)=x(t)+r\cdot sin\theta \cdot cos\varphi \\ y(t+\Delta t)=y(t)+r\cdot sin\theta \cdot cos\varphi \\ z(t+\Delta t)=z(t)+r\cdot cos\theta \end{array}\right.$$

  (5)

  where the angles θ and φ are randomly selected in the range 0 ≤ θ ≤ 2π, and [x(t), y(t), z(t)] is the position of the proton at the current time.

• (4) Determine whether the proton collides with the solid surface. If the proton does not disappear, it bounces back (Talabi et al. 2009). If it does, the proton disappears with probability δ:

  $$\delta =\frac{2\rho r}{3D}$$

  (6)

• (5) If the proton survives, it will simply bounce back from the interface and return to its previous position (Ramakrishnan et al. 1998, Oren et al. 2002, Hidajat et al. 2003), and the time will advance according to the time step given in step (3). At each time step, the ratio of the number of surviving protons to the number of initial protons is recorded, which is the surface relaxation magnetization strength M_S(t):

  $${M}_{S}\left(t\right)=\frac{{N}_{t}}{{N}_{0}}$$

  (7)

  where N_t is the number of protons alive at time t, and N₀ is the initial number of protons at time t = 0.

• (6) Calculate the diffusion magnetization strength, M_D(t):

  $${M}_{D}\left(t\right)=\mathrm{exp}\left[\frac{-tD{\left(\gamma G{T}_{E}\right)}^{2}}{12}\right]$$

  (8)

• (7) Since all relaxation mechanisms occur at the same time, the normalized magnetization strength, M(t), as a function of time is:

  $$M\left(t\right)={M}_{0}\mathrm{exp}\left(\frac{-t}{{T}_{2B}}\right)\frac{{N}_{t}}{{N}_{0}}\mathrm{exp}\left[\frac{-tD{\left(\gamma G{T}_{E}\right)}^{2}}{12}\right]$$

  (9)

• (8) When the pore contains two-phase fluid, the total echo data amplitude at time t simulated by random walk method can be expressed as follows:

  $$M\left(t\right)=\frac{{S}_{w}{HI}_{w}{M}_{w}\left(t\right)+{S}_{o}{HI}_{o}{M}_{o}(t)}{{S}_{wi}{HI}_{w}+{S}_{o}{HI}_{o}}$$

  (10)

  where: M_w(t) is the magnetization strength of water; M_o(t) is the magnetization strength of oil; S_w is water saturation; S_o is oil saturation; HI_w is the hydrogen index of water; HI_o is the hydrogen index of the oil (Fig. 5).

  Fig. 5

  

  Spherical pore structure with a radius of 5 μm

Water-saturated spherical pores with a radius of 5 µm were subjected to a gradient field of 0.3 T/m. The surface relaxation rate was 30 µm/s, and the diffusion coefficient of water was 2 × 10⁻⁹m²/s. Numerical simulation was conducted and compared with the theoretical solution presented in Eq. (4). Figure 6 illustrates a comparison between the simulated magnetic field attenuation (black line) and the theoretical one (red line). It can be seen from the figure that the two are completely coincident, with a maximum error that is very small. This verifies the effectiveness of the random walk method in simulating NMR.

Fig. 6

Comparison between simulated value and theoretical value of random walking method

The following parameters in the random walk model are used in this study:

• (1) Hydrogen index

The hydrogen content index of pure water and aqueous solution is generally independent of temperature and pressure. However, the salinity of formation water has a significant effect on the hydrogen index of the solution. When the salinity is low, the hydrogen index of the aqueous solution is close to 1. The hydrogen index of high salinity solutions can be reduced by up to 10%.

Crude oil is typically composed of various hydrocarbons, and its exact chemical composition is often difficult to determine. In general, the API relative density of crude oil can be used to indicate its hydrogen index. The hydrogen index of light crude oil with an API relative density greater than 25 is close to 1.

• (2) Diffusion coefficient

The diffusion coefficients of brine and oil used in the simulation are determined based on the following correlations (Vinegar 1995):

$${D}_{o}\cong 1.3\times \left(\frac{{T}_{K}}{298\eta }\right)\times {10}^{-12}$$

(11)

$${D}_{w}\cong 2\times \left(\frac{{T}_{K}}{298\eta }\right)\times {10}^{-12}$$

(12)

where D_o and D_w are the diffusion coefficients of oil and water, respectively, in m²/s, T_K is temperature in Kelvin (K), and η is the fluid viscosity in Pa·s. Similarly, their respective volume relaxation times are determined by the following formula:

• (3) Volume relaxation

$${T}_{2Bo}\cong 0.00713\frac{{T}_{K}}{\eta }\times {10}^{-3}$$

(13)

$$T_{2Bw} \cong 3\frac{{T_{K} }}{298\eta } \times 10^{ - 3}$$

(14)

T_2Bo and T_2Bw are the volume relaxation time (s) of oil and water, respectively.

• (4) Surface relaxation

A surface relaxation ratio of 0.33 was used in all simulations (ρ_o/ρ_w), where ρ_o and ρ_w are the surface relaxation rate of porous media to oil and water, respectively.

Results and discussion

NMR characteristics of single-phase fluid

Simulation of NMR response under various salinity

Understanding the nuclear magnetic resonance properties of reservoirs and fluids is important for interpreting nuclear magnetic resonance logging data and improving the application effect of nuclear magnetic resonance logging data in complex reservoir evaluation. It is also an important basis for well logging acquisition and pre logging design.

In order to analyze the influence of salinity of reservoir formation water on NMR porosity and T₂ spectrum, water solutions with salinity of 0 ppm, 50,000 ppm, 100,000 ppm, 150,000 ppm, 200,000 ppm and 250,000 ppm were used for NMR simulation. The input parameters are: echo interval T_E = 0.2 ms, number of echoes N_E = 4096, external magnetic field gradient G = 0.3 T/m (the internal gradients are not considered), and the ambient temperature of the simulated fluid is 35 ℃. The relevant fluid relaxation properties are calculated by Eqs. (12) and (14) as shown in Table 2.

Table 2 Physical parameters of aqueous solutions with different salinity

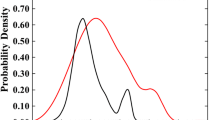
Figure 7 shows the T₂ relaxation time distribution of aqueous solutions only (no core) with different salinities at 35 °C. The simulation results show that salinity has little effect on the T₂ relaxation characteristics of the solution. As the salinity increases, the T₂ relaxation distribution of the solution shifts slightly to the short T₂ direction, and its average T₂ value decreases slightly. Additionally, the peak value and area of the T₂ distribution spectrum of the solution decreased slightly with increasing salinity. This is due to the reduction in the hydrogen content index in high salinity solutions, which leads to a reduction in signal amplitude.

Fig. 7

T₂ spectrum of aqueous solutions with different salinity

This result shows that in a reservoir with high salinity formation water, the porosity from NMR logging may be underestimated due to the decrease in the hydrogen index of the formation water solution.

Figure 8 shows the T₂ spectrum of a pure water solution with 0 salinity at different echo intervals T_E. The simulation results show that as the echo interval increases, the T₂ wave of free fluid moves toward the small T₂ direction and the distribution width narrows. This is because as the echo time interval increases, the volume relaxation remains unchanged while the role of diffusion relaxation increases, leading to the shortening of T₂ relaxation time and the shift of the T₂ spectrum toward smaller values (Yan et al. 2018).

Fig. 8

T₂ spectrum of aqueous solution with 0 Salinity at different echo interval

Figure 9 shows the T₂ spectrum diagrams of aqueous solutions saturated in the digital cores with different salinity levels. The fluid is affected by the relaxation of the rock surface, which is significantly different from the fluid relaxation properties shown in Fig. 7. The surface relaxation rate of water was set to 30 μm/s; the echo interval is set to 0.2 ms, while the other simulation conditions were kept consistent. The simulation results show that as the salinity of the aqueous solution increases, the T₂ spectrum distribution becomes narrower and sharper, with a clear spectral shift, particularly at the short T₂ end of the spectrum. The front end of the T₂ spectrum for the sandstone moves backwards significantly, while the back end moves slightly forward or remains unchanged. The backward shift of the front end of the T₂ spectrum is due to diffusion. According to NMR rock physics theory, in a gradient magnetic field, the pore fluid in the rock is affected by three relaxation mechanisms: volume relaxation, surface relaxation, and diffusion relaxation [Eq. (1)]. As the salinity of the formation water solution increases, the viscosity of the solution increases and the diffusion coefficient decreases, leading to a decrease in the role of diffusion relaxation and a slower relaxation of the sample T₂, especially in small pores. The bound water peak moves backwards. The backward shift of T₂ spectrum is mainly due to the left shift of water volume relaxation as the salinity of formation water increases. However, as shown in Fig. 5, the overall position does not change significantly, and the peak position is still located at a longer relaxation time. Only under higher salinity conditions can certain effects be produced, leading to an apparent forward movement of the spectrum.

Fig. 9

T₂ spectrum of water solution filled with different salinity

Simulation of NMR response under various oil viscosity

Table 3 shows the physical parameters of crude oil samples with different viscosities calculated by Eqs. (11) and (13), and other parameters are consistent with the above. Figure 10 shows the T₂ spectrum simulation results of crude oil with different viscosities. The simulation results indicate that the peak value of the T₂ distribution of crude oil is related to viscosity. As the viscosity decreases, the T₂ relaxation time increases. The T₂ relaxation time of high viscosity crude oil is very short, and its value is equivalent to the bound water relaxation time. Therefore, when analyzing the T₂ spectrum of an actual oil-bearing reservoir, it is important to consider the T₂ relaxation properties of crude oil viscosity.

Table 3 Physical parameters of crude oil samples with different viscosity

Fig. 10

T₂ spectrum of crude oil samples with different viscosity

Figure 11 shows the T₂ spectrum simulation results of a 1.86 mPa·s crude oil sample with different echo intervals (T_E). The simulation results show that the spectrum shift of the crude oil in a free state is significant, which mainly indicates that the relaxation spectrum of the crude oil moves forward with an increase in the echo interval (the relaxation time decreases). This is because with an increase in the echo time interval, the volume relaxation remains unchanged, while the role of diffusion relaxation increases, leading to the shortening of the T₂ relaxation time and the forward shift of the T₂ spectrum. Compared to Fig. 7, the spectrum shift amplitude of the crude oil sample is slightly lower than that of pure water, mainly due to the difference in viscosity (Yan et al. 2018). It should be noted that the results shown in Fig. 10 are the relaxation results of the crude oil itself, which is equivalent to the volume relaxation of the crude oil. The analysis of T₂ relaxation spectra of actual oil-bearing rocks also needs to consider rock wettability and pore structure, which will be discussed below. Additionally, the T₂ relaxation time of actual crude oil is not a single value, but a spectrum. The simulated oil sample in this study is more similar to refined oil (such as kerosene) due to its single component, resulting in a narrow T₂ spectrum distribution. In contrast, the T₂ spectrum of actual crude oil often has a wide distribution due to the complexity of hydrocarbon types and components.

Fig. 11

T₂ spectrum of 1.86 mPa·s crude oil samples with different echo intervals

Due to the presence of bound water, there is no completely saturated oil core sample. Therefore, the results of core samples in different saturation states will be discussed in the next section.

The technical advantage of nuclear magnetic resonance logging is that it can reflect the occurrence state and fluid type of reservoir pore fluid. Understanding the relaxation characteristics of various reservoir fluids are very important for correctly understanding nuclear magnetic logging data. In addition, understanding the impact of different acquisition parameters (such as T_E) of the instrument on measurement results is of great significance to guide the design of nuclear magnetic resonance logging and the application of nuclear magnetic resonance logging data.

Simulation of NMR response under various saturations

Water wet condition

When the pore saturation state of the experimental sample is different, such as completely water-bearing and oil–water two-phase, the relaxation properties of the sample are greatly different from the fluid relaxation properties shown in the previous section due to the influence of surface relaxation. This section briefly introduces the simulation results of nuclear magnetic resonance T₂ spectra of sandstone samples under different saturation states. These results have certain guiding significance for in-depth understanding of the relevant theories of nuclear magnetic resonance logging data evaluation.

Assuming that the sandstone is completely hydrophilic, the water phase in the rock has 0 ppm salinity. The surface relaxation rate of water is set to 30 μm/s, the echo interval is set to 0.2 ms, and the remaining parameters remain unchanged. Then, the NMR response is simulated using the random walk method based on the 3D images of the sandstone under various saturations. When in a gradient magnetic field and using a shorter echo interval (T_E value), the diffusion effect of other formation fluids, except for hydrocarbon gases, becomes very small. Echo interval is a parameter that can be selected by engineers during NMR operations. Depending on the need, diffusion can be enhanced or reduced by selecting appropriate echo intervals. For example, shortening the echo interval to highlight surface relaxation is used to evaluate the pore size of saturated wetting phase fluid porous media; Enhanced diffusion relaxation can be used to identify hydrocarbon gases. In this paper, when the core is saturated with water and oil, a shorter echo interval of 0.2 ms is used to reduce the impact of diffusion relaxation. Therefore, the following article mainly discusses the impact of surface relaxation and volume relaxation.

Figure 12 shows T₂ spectra of sandstone cores saturated with crude oil of different viscosities under different saturation conditions. When the pore space is fully saturated with water, the T₂ spectrum exhibits a bimodal distribution dominated by macropore relaxation. However, when the pore space contains non-wetting crude oil, the T₂ spectrum morphology changes completely. In comparison with the T₂ distribution in the fully saturated water state, there will be a peak at the volume relaxation position of crude oil, which mainly reflects the volume relaxation characteristics of crude oil. In this oil-bearing state, T₂ distribution can no longer accurately reflect the pore structure of the rocks (Liang et al. 2018). In sandstone saturated with oil and water, as the water saturation decreases, the positions of the two water peaks in the NMR T₂ spectrum gradually move toward the direction of short relaxation times, while the positions of the oil peaks remain unchanged. This is because water is in a wetting phase, meaning that its surface relaxation plays a dominant role. As the water saturation decreases, the ratio of the surface area and volume of rock pores occupied by water becomes larger, leading to a stronger surface relaxation of water, resulting in a shorter relaxation time for water. Oil, on the other hand, is a non-wetting phase and is not subject to surface relaxation, so changing oil saturation does not affect its transverse relaxation time. When the crude oil sample is a light oil (1.86 mPa·s and 4.77 mPa·s), as shown in Fig. 12a and b, the volume relaxation time of oil is longer than the surface relaxation time of water, resulting in a triple peak structure in the T₂ spectrum. The volume relaxation peak of oil is located on the right side of the spectrum, which leads to an overestimation of movable water. When the volume relaxation of crude oil samples is similar to that of water surfaces, their morphology remains a bimodal structure, and a low viscosity (58.1 mpa·s) can lead to an overestimation of movable water, as shown in Fig. 12c; High viscosity (624.5 mpa·s) can lead to an overestimation of bound water, as shown in Fig. 12d. When the crude oil sample is heavy oil (5584 mpa·s), it can be seen from Fig. 12e that the volume relaxation of oil is much smaller than the surface relaxation of water, resulting in a three-peak structure in the T₂ spectrum. The volume relaxation peak of oil is located at the far left of the spectrum, resulting in overestimation of bound water.

Fig. 12

T₂ spectrum of core filled with crude oil of the same viscosity at different saturations

Figure 13 shows the T₂ spectrum simulation results of sandstone cores saturated with crude oils of different viscosities under the same saturation state. These simulation results are in good agreement with Eq. (13), which shows that the peak value of the T₂ distribution of crude oil is related to its viscosity. The T₂ relaxation time of crude oil tends to increase with decreasing viscosity. High viscosity crude oil has a very short T₂ relaxation time. When analyzing the T₂ spectrum of actual reservoirs, it is important to consider the T₂ relaxation properties of crude oil viscosity in addition to rock wettability and pore structure. Additionally, Fig. 13 shows that under the same saturation, the positions of the water peaks are basically the same. This is because this is a static NMR simulation. At the same saturation, the distribution of oil and water with different viscosities in the digital core is the same, resulting in the same surface relaxation signal for water. However, oil provides mainly volume relaxation, leading to differences in T₂ spectra. As shown in Figs. 12 and 13, when the reservoir rocks are hydrophilic, the relaxation characteristics of crude oil in the pores are basically volume relaxation characteristics, independent of the pore structure of the rocks.

Fig. 13

T₂ spectrum of core filled with crude oils of different viscosities at the same saturation

Oil wet condition

Under oil wet conditions, according to the formation principle of the reservoir, the oil drives away part of the water in the large pores of the formation, while the unconnected small pores are always full of immovable bound water. As demonstrated in Fig. 14a, it is advisable to separate and maintain the disconnected, isolated pores as always water wet when partitioning the oil and water distribution in digital cores. The remaining connected holes adopt the same method as the water wet condition to form “water in oil” in the pore space, as shown in Fig. 14b. The simulation parameters and water wet conditions were kept unchanged, and the NMR simulation was carried out.

Fig. 14

Sandstone with 55.58% oil saturation

The T₂ spectrum of sandstone cores saturated with crude oils of varying viscosities under oil wet conditions is depicted in Fig. 15, revealing a three-peak structure at different saturations. The sandstone sample used in this experiment exhibits good connectivity, with isolated pores constituting only 1.3% of the total pores, thereby providing limited information on bound water relaxation. The simulation employs an echo interval of 0.2 ms, and the diffusion relaxation has a minimal effect (as shown in Figs. 8 and 10), thus implying that the T₂ spectrum is mainly determined by surface relaxation, oil volume relaxation, and water volume relaxation. For light oil conditions illustrated in Fig. 12a, the first and second peak reflect the surface relaxation of oil since the physical properties of the oil are analogous to those of water. Hence, the volume relaxation of water and oil jointly impacts the third peak. As the oil viscosity increases, the volume relaxation also increases. Consequently, for increased viscosity, the second peak reflects only the volume relaxation of oil, while the third peak reflects the relaxation of water. This effect is clearly depicted in Fig. 12b–e.

Fig. 15

T₂ spectrum of core filled with crude oil of the same viscosity under different saturations

From Fig. 15, it is evident that the NMR T₂ distribution shifts gradually to the left as the oil saturation decreases. This phenomenon is more pronounced for oils with lower viscosity, where the specific surface area of the oil increases, causing an improved surface relaxation effect [Eq. (2)]. In the case of high oil viscosity, the volume relaxation time is relatively short, and the oil is primarily affected by the volume relaxation even at low saturation levels. Here, saturation mainly influences the amplitude of the volume relaxation peak for oil and the volume relaxation peak for water. Incomplete parts in the figure are related to the incomplete attenuation or the decay. The SVD singular value decomposition method for the inversion algorithm is used in this study (Hughes et al. 1996).

The T₂ spectrum simulation results of sandstone cores saturated with crude oils of varying viscosity at the same saturation level are represented in Fig. 16 and can be compared to the water wet results. The left oil peak position has a correlation with viscosity—the higher the viscosity, the shorter the T₂ relaxation time. The water peak position on the right side is remarkably similar at the same saturation level, indicating that it primarily reflects the volume relaxation of water in the oil wet state. Therefore, to analyze the T₂ spectrum of actual oil-bearing reservoirs, it is vital to consider both the T₂ relaxation property of crude oil viscosity and the rock's wettability. The simulation results suggest that when the reservoir rock is oil wet, the relaxation characteristics primarily correspond to the volume relaxation characteristics of oil and water, irrespective of the rock's pore structure.

Fig. 16

T₂ spectrum of core filled with crude oil with different viscosity under the same saturation

Conclusions

This study employed the mathematical pore morphology method to establish the oil–water distribution and used the random walk method to simulate the NMR response based on 3D CT images. Various factors affecting the NMR responses of formation water were investigated, including differences in salinity and crude oil viscosity. The following observations and conclusions were made:

• 1. The T₂ relaxation time of formation water increases with an increase in salinity, shifting toward a short relaxation direction. The T₂ value of formation water is highly sensitive to the echo interval, with a leftward shift as the interval increases. Furthermore, the high salinity of formation water results in a slight shift or no change in the end position of the active water peak value, and a shift to the right in the bound water peak value. These changes are attributed to the combined effect of volume and diffusion relaxation.

• 2. Crude oil T₂ distribution is linked to viscosity, with shorter relaxation times for higher viscosity oils. Additionally, crude oil and formation water have different echo interval sensitivity, with crude oil showing less of a shift with increasing echo interval due to its viscosity and low diffusion coefficient.

• 3. The influence of saturation on the T₂ spectrum varies under different wettability conditions. In strong water wet conditions, there is a peak at the volume relaxation position of crude oil, whereas in strong oil wet conditions, the T₂ spectrum has a triple peak structure reflecting surface and volume relaxation of oil and water under varying viscosity conditions.

• 4. The T₂ distribution in oil-bearing states does not accurately reflect the pore structure of rocks due to the influence of wettability and volume relaxation. To assess the pore structure of formations using onsite NMR logging, it is essential to consider the impact of wettability and volume relaxation.

• 5. It should be noted that this study used a convenient pore morphology model that does not include the wetting angle as input, limiting simulations to strong water wet and strong oil wet conditions. Additionally, the digital core technique has a 1.5 μm limit of CT resolution, resulting in fewer calculations of bound water through disconnected pores. Further research is necessary to address these limitations.

• 6. Even through such findings can improve the accurate interpretation of the NMR logging, the NMR response in the real rock is much more complicated than the simplified geometry. Thus, the laboratory NMR experiments on the actual fractured sandstone needs to be performed to validate the three peaks observation from the digital analysis.

• 7. Scaling up from the pore-scale simulations in this study to the core-scale measurements performed in the laboratory is currently challenging (Zhang 2015), and there is limited research on NMR. Further investigation, including scale-up and comparison to laboratory results, is necessary.