Introduction

Since Euclidean geometry cannot express most of the complexities in nature, expressing these complexities requires the geometry of nature, especially fractal geometry (Mandelbrot 1983). As their great advantage, fractals describe real nature, especially geological parameters (Mandelbrot 1983; Turcotte 1989; 1997; Goncalves et al. 2001; Afzal et al. 2010; Deng et al. 2010). Many fractal models have been proposed and developed for this purpose, such as number–size (Mandelbrot 1983), concentration–area (Cheng et al. 1994), spectrum–area (Cheng 1999), concentration–volume (Afzal et al. 2011), concentration–number (Hassanpour and Afzal 2013), concentration–concentration (Sadeghi 2021). These models are used for hydrocarbon reservoir simulation and modeling because of their ability to deal with complex issues and the complications in geological and petrophysical parameters’ distribution of the reservoir rock in the static modeling of the reservoir. Geostatistics and fractal methods are used to describe and identify reservoir rock properties, including porosity, permeability, and degree of saturation (Amanipoor 2013; Kianersi et al. 2021).

The results of conventional methods, especially those based on classical statistics, have disadvantages concerning the normal distribution, removing several data as outliers, not paying attention to the spatial distribution of the data, and the geometrical shape of the anomalies (Davis 2002; Afzal et al. 2010; 2017; Daya 2015; Agterberg 1995; Habib et al. 2017; Saadati et al. 2020; Farhadi et al. 2022; Kianoush et al. 2022; Pourgholam et al. 2022).

Subsurface data of hydrocarbon reservoirs have multi-fractal behavior (Ebrahim et al. 2018; Kianersi et al. 2021). These data indicate the number of geological characteristics, porosity, permeability, degree of fluid saturation, and the properties of reservoir rocks.

The production index (PI) is among the proper data showing the reservoir rock quality. This index presents the production potential of each well based on rock and reservoir fluid properties, such as porosity, permeability, and reservoir rock pressure (Amanipoor 2013).

Most of the past researches in the field of fractals have been carried out in the field of mineral resources. These studies are mainly carried out on the geochemical parameters of mineral rocks with the aim of separating anomalies of valuable elements from the chemical background of rocks (Daya 2015).

Fractal modeling has been proposed in recent decades mainly related to the exploration of promising areas of metal minerals such as lead, zinc and iron (Mahdizadeh et al. 2022).

In the present study, by taking ideas from past researches, it has been tried to use the principles of fractal modeling to identify more potential parts of reservoir rocks in order to increase production.

Obviously, due to having two environments with different static and dynamic behaviors, naturally fractured reservoirs have the best characteristics for testing fractal concepts and theorizing its application in reservoir studies.

Naturally fractured reservoirs contain natural fractures and have positive or negative effects on fluid flow. These reservoirs have two different types of environments. One is the matrix, which has high storage and low current capacity, and the other is cracks (fractures), which provide a high current path but have low storage. Production from naturally fractured reservoirs has many complications and challenges. These reservoirs can be characterized by image logs, outcrop, and core analysis. In this study, an attempt has been made to present a method for classifying production parameters in naturally fractured reservoirs using fractal methods.

In this study, PI data were analyzed from 260 wells related to one of the oil fields in southwest Iran. Reservoir PI zones were separated after geostatistical modeling by ordinary kriging method and concentration–area (C–A) and concentration–number (C–N) fractal models. This study aimed to introduce high-quality and promising parts of this oil field for drilling future wells and ultimately increasing oil and gas production.

Geographical and geological setting of the case study

The Gachsaran oil field is located 223 km southeast of Ahvaz (SW Iran). This oilfield includes the Asmari and Bangestan fractured formations, located in the general northwest-southeast direction of anticlines oil fields in southern Iran. This anticline is about 75 km long and 5–13 km wide. Most of the oil production is done in the Asmari formation in this field, which is mainly composed of carbonate rocks (Fig. 1).

Fig. 1
figure 1

The geographical location of the Gachsaran oil field (Hosseini et al. 2015)

Full size image

The Asmari reservoir is composed of dolomite and limestone and is one of the most famous fractured reservoirs in the world. The Asmari and Bangestan reservoirs contain oil and gas. This reservoir is about 56 km long, and its width varies between a minimum of 1 km and a maximum of 13 km. The northwest part of this area is the widest and is known as Lishtar. The layer thickness of the Asmari formation is 633 m, which is about the slope of the formation. The drilling thickness of areas where the slope of the formation is high reaches 153 m. The data from the wells show that the dense rocks of the northeastern area are more widespread. The production rate of wells in some parts of the Gachsaran field indicates the development of cracks in these areas. Several faults with an approximate east–west extension have been identified in this reservoir. The results show the seismic activity of a reverse fault with a high dip angle in the southeast of the field (Motamedi et al. 2012). In the same fault area, the layer thickness and drilled thickness maps are predicted based on the different gas and oil levels. The useful thickness of the reservoir rocks and the average porosity maps for some parts of the reservoir shows that other faults may have sheared the reservoir (Motamedi et al. 2012).

Fractured reservoirs’ behavior and production performance are much more complex than conventional reservoir rocks (Sarkheil et al. 2021). Production in fractured reservoirs is controlled by the matrix of the main rock body and the network of fractures (Fig. 2). Obviously, due to the high permeability of the rock matrix gap, the reservoirs with more fractures have a much higher production rate.

Fig. 2
figure 2

Fractured reservoir framework, including matrix and fracture network

Full size image

Methodology

This study is divided into three separate steps. First, the PI parameter data related to 260 wells from the Gachsaran oil field in Iran were obtained, and classical statistical evaluations were performed on these data. In this step, parameters such as variance, mean, and median were calculated, and a histogram was prepared. The results of the models obtained in the first part are based on the analyses carried out in the next stages and played a key role in the interpretation.

In the second step, the PI parameter distribution is used for the entire reservoir layer by geostatistical estimation by the ordinary kriging method. In this respect, Kriging is the best linear unbiased estimator with the lowest estimation variance (Khaled et al. 2007). However, it gives its error value along with each estimate. As a result, not only can the average value of errors be calculated, but it is also possible to obtain the distribution of errors in the entire investigated range. Kriging is an estimation method based on weighted moving average logic (Afzal et al. 2012). The ordinary kriging method is one of the proper methods for preparing distribution maps.

In the final step, the data derived via the previous estimates were classified based on C–A and C–N fractal models. Then, various rock areas with different production qualities (rock types) were recognized based on the log–log plots obtained by both fractal models. The flowchart of this methodology is depicted in Fig. 3.

Fig. 3
figure 3

Study method flowchart

Full size image

Fractal model of C–A and C–N

Mathematics is a powerful tool for describing processes related to nature, especially geology. Since Euclidean geometry is not able to express most of the complexities in nature, scientists were looking for a geometry that could describe all the processes in nature. In this regard, Mandelbrot (1983) introduced fractal geometry as an appropriate tool for this purpose.

The C–A method proposed by Cheng (1994) is based on the area occupied by each specific concentration (PI in this scenario). When the parameter concentration increases, the area occupied by it decreases. C–A is one of the most common models to illustrate the distribution of the concentration of a parameter in an area to generate a contour map of the value of the corresponding parameter in the studied area (Cheng et al. 1994; Daya and Afzal 2015; Daya et al. 2016). If the value of each counter is considered ρ, a power equation can be presented for the concentration of materials with fractal properties:

$$A( \ge \rho ) \infty \rho ^{{ - D}}$$
(1)

A: Area where D represents the fractal dimension related to different ρ domains. A population’s dimension is calculated through the slope of the fitted line by plotting the area changes against the value in a logarithmic diagram. The breaking points (i.e., change in the slope of the fitted line) in this graph indicate the change from one population to another. In addition to separating the background, it is possible to distinguish the different zones of a parameter. Even in some cases, it allows distinguishing the porosity related to the rock background from the porosity resulting from the fracture.

The exchange from one population to another indicates the change in reservoir geological, tectonic, and lithological conditions. This special feature, which is due to the fractal nature of the distribution of elements in nature, obviates the need to remove outlier values because these data are automatically discarded due to the fractal nature of the data (Hassanpour and Afzal 2013; Shafieyan and Abdideh 2019; Torshizian et al. 2021; Mahdizadeh et al. 2022; Nabilou et al. 2022).

The theory of multi-fractal modeling is based on the nature of the fractal distribution of rock parameters and also the type of relationship between the value and the area it covers. This power-form function represents the number of formation stages of the rock properties of the reservoir, such as porosity, and the secondary distribution of these parameters in a study area.

The C–N method is based on the inverse relationship between the studied parameter and the cumulative frequency of its value and higher concentrations (Nazarpour et al. 2015). This method is proposed based on the following formula (Hassanpour and Afzal 2013):

$${\text{N }}\left( { \ge {\text{ C}}} \right) \, \infty \, \rho^{ - \beta }$$
(2)

N: Number where C is equal to the number of samples whose concentration is equal to and higher than N(≥ C), β is equal to the fractal dimension of concentration, and ρ is equal to concentration. Using this equation may provide more about the geological situation in the studied reservoir. Certainly, a proper interpretation of the static modeling of a studied reservoir is obtained by multi-fractal modeling and combining its results with geological data.

Discussion of results

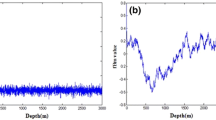
In this study, PI values related to 260 wells from the Gachsaran oil field in southwest Iran and the wells’ coordinates (Fig. 4) were analyzed. The spatial relationship between the values of a quantity in the community of samples collected in mathematical formats is called spatial structure. This relationship is examined in terms of distance and direction. Geostatistics is a branch of statistics that investigates the variables with a spatial structure. In other words, if the reservoir data have a mathematical relationship with each other in a specific distance and direction, this data series is called structured data and is interpreted by variogram (Davis 2002; Shahbeik et al. 2014). Figure 5 presents variograms and anisotropic ellipsoids generated for PI. As can be seen, there is a clear anisotropy with main and minor directions at NE-SW and NW-SE, respectively.

Fig. 4
figure 4

Location of each well in the studied oil field

Full size image
Fig. 5
figure 5

Variogram and anisotropic ellipsoid of PI data, Variogram specifications, anisotropic ellipsoid, and Variogram chart

Full size image

This step estimates the parameter PI in the entire reservoir layer after specifying the spatial structure by variogram analysis. The PI distribution was estimated using the ordinary kriging method (Fig. 6). As can be seen, the highest amount of PI is located in the northwest and southeast of the oil field (Fig. 5). In other words, the center of this field does not have good quality and capacity in terms of oil production. The noteworthy point is the coincidence of places with high PI despite the faults and the accumulation of fractures in the reservoir.

Fig. 6
figure 6

PI distribution estimation by ordinary kriging method

Full size image

PI data can be used to separate several populations based on fractal models of C–A and C–N log–log plots, as depicted in Figs. 7 and 9. In general, fractal modeling categorizes PI data based on different conditions of their formation and control. These conditions depend on lithology, petrophysical changes, or secondary geological parameters such as the effect of fractures (Kianersi et al. 2021). This modeling provides a platform for separating an important concept, such as porosity, from the rock matrix or cracks. The iso-intensity of PI distribution is prepared by ordinary Kriging (Fig. 6). Next, from this iso-intensity map, the enclosed area is calculated at any value to achieve the correct pattern of PI regional distribution. First, the data are gridded to calculate the area corresponding to each value. In the following, according to the calculated areas for each concentration, the C–A and C–N curves are generated cumulatively, and lines are built up on the fractal C–A and C–N log–log plots (Figs. 7 and 9).

Fig. 7
figure 7

C–A log–log plot of PI and related threshold values, The blue line near the horizon represents the PI data related to the rock matrix, and the other colored lines represent the PI data under the control of reservoir rock fractures

Full size image

Populations and zone’s thresholds were determined from the context by fitting straight lines to a series of points and identifying the breaking points of these lines (Figs. 7 and 9). This context is the concentration of production corresponding to the rock matrix. Overall, these zones present the amount of production resulting from secondary geological processes such as a fracture. Figures 8 and 9 present PI parameter separation maps based on the C–A and C–N modeling.

Fig. 8
figure 8

Zones’ distribution map of the PI based on the C–A method in the Gachsaran oil field

Full size image
Fig. 9
figure 9

C–N log–log of PI and related threshold values, the blue line near the horizon represents the PI data related to the rock matrix, and the other colored lines represent the PI data under the control of reservoir rock fractures

Full size image

Figures 7 and 9 present log–log plots for this reservoir rock, indicating the multi-fractal nature of the PI. There are six and four populations based on C–A and C–N models, respectively, resulting from the exchange in the slope of the straight lines (Figs. 7 and 9).

The geological concepts of the studied reservoir can be determined by examining the slope of the lines resulting in the multi-fractal diagram of C–A and C–N related to the PI parameter.

In Figs. 7 and 9, the line with the lowest slope (almost horizontal) corresponds to the diagram’s context-dependent PI (matrix). The limit of this horizontal line is marked with other steep lines in Figs. 6 and 8. Other steep lines might be related to secondary diagenesis processes affecting the reservoir rock quality. Dissolution, substitution, and fracture are among the noteworthy diagenesis processes. The existence of other communities can be explained by the PI parameter, as the lithology of the studied reservoir rock is carbonate, and southwestern Iran has an active tectonic setting.

The blue segment in Figs. 7 and 9, which has a very low slope, indicates the community related to the rock matrix, and the segments with other colors show communities related to secondary parameters such as fracture. Now, by carefully looking at the maps in Figs. 8 and 10 and the color changes on the maps, it is easy to recognize the areas where the increase in the PI parameter is dependent on secondary processes such as the presence of fractures (such as the orange and red parts in Figs. 8 and 10). Obviously, these areas are promising areas for drilling future wells for production.

Fig. 10
figure 10

Zones’ distribution map of the PI based on the C–N method in the Gachsaran oil field

Full size image

Field studies show that the Asmari formation in southwest Iran is highly fractured in many parts. It has been replaced and dolomitized by the diagenesis process due to tectonic action (Bahroudi et al., 2004). These concepts are evident in the maps of the zones’ separation of C–A and C–N of the PI parameter of the Asmari reservoir rock in southwest Iran (Figs. 8 and 10). As a result, the types of rocks in the reservoir can be separated.

According to Figs. 8 and 10, based on the C–N and C–A models, the parts with PI ≤ 44 and PI ≤ 63, respectively, correspond to the production of wells from the reservoir rock matrix in this oil field. Most of these parts occurred in this oil field’s central and SE sections. However, zones with PI ≥ 223 include the production of wells at the fracture network of the reservoir rock, which existed in the NW part of this area (Figs. 8 and 10). Image logs are among the efficient tools to identify fractures in reservoir rock. According to Fig. 11, the Asmari reservoir rock in the Gachsaran oil field has a network of open fractures that control the high production rate.

Fig. 11
figure 11

Open fractures in the Asmari reservoir rock of the NW part of the Gachsaran oil field observed in the image log (Dark colored areas indicate open fractures)

Full size image

Conclusions

This study presented that the concentration–area (C–A) and concentration–number (C–N) multi-fractal methods are proper methods for separating different rock types in the reservoir. The resulting zones identified for the PI parameter with these methods are well confirmed by geological evidence, especially the impact of fractures, faults, and other diagenesis factors in the reservoir rock.

The main results of this study are as follows:

  1. 1.

    The spatial distribution of the desired variable is observed by plotting the map. The highest value of PI is in the southeast and northwest parts of the oil field. This result indicates better quality of reservoir rock in this area. The reason is the presence of faults and the accumulation of fractures in these areas, increasing the reservoir rock’s permeability and PI.

  2. 2.

    The fractal analysis of the C–A method shows six different rock types and zones, and the C–N fractal method indicates four zones based on PI data in the studied reservoir rock. Comparing the fractal methods indicates that resulted zones have a relative overlap.

  3. 3.

    The anomaly obtained by the C–A method is more extensive than the C–N method. In addition, the PI data of the reservoir rock show a multi-fractal mode.

  4. 4.

    The change in the slope of the lines in the multi-fractal diagrams of C–A and C–N is attributed to the variation in geological conditions, lithology, or diagenesis factors. The reason for the separation of rock types in the studied reservoir rock is the effect of fracturing and diagenesis processes.

  5. 5.

    The present study exhibited the efficiency of fractal models to separate and determine the production capacity of the reservoir rock. It also recognized areas with high production potential for developing oil and gas fields.

  6. 6.

    Based on the C–N and C–A models, the parts with PI ≤ 44 and PI ≤ 63, respectively, correspond to the production of wells from the reservoir rock matrix in this oil field and PI ≥ 223 include the production of wells at the fracture network of the reservoir rock.