Introduction

Hydraulic fracturing technology was introduced in the 1940s as a secondary recovery method for conventional reservoirs. During the last few decades, however, this technology has become the primary recovery method for extracting hydrocarbons from low-permeability formations because of increased drilling in unconventional shale and tight gas reservoirs. The hydraulic fracturing process follows complex physical laws, and an appropriate model is necessary to capture at least the fundamental mechanisms of viscous fracturing fluid flow, the rock deformation in response to the fracturing fluid pressure, the propagation condition, and the overall mass conservation. Normally, the rock deformation response is controlled by linear elasticity theory, which describes, via an integral equation, the relationship between the fracture opening and the fracturing net pressure. The viscous flow is governed by lubrication theory, which is characterized by a nonlinear partial differential equation related to the viscous flow rate, fracture opening, and fluid pressure. Moreover, based on linear elastic fracture mechanics (LEFM), the crack propagating criterion is modeled using strain energy release theory. Note that in this article, any related terms containing the words “fracture” or “fracturing” imply “hydraulic fracture” and “hydraulic fracturing,” respectively, unless specified differently in the context.

A lot of effort has been invested over the past decades to develop hydraulic fracture models with greater accuracy, as categorized by two-dimensional (2D), pseudo-three-dimensional (P3D), and planar three-dimensional (PL3D) models. These models vary in their assumptions for formulating governing equations, flexibility of required input–output data, and difficulty of the solution method and algorithms. The 2D models in widest usage are Perkins–Kern–Nordgren (PKN) (Perkins and Kern 1961; Nordgren 1972; Kemp 1990) and Khristianovic–Geertsma–de Klerk (KGD) (Zheltov 1955; Geertsma and De Klerk 1969). Although these models are not meant for industrial use owing to their simplified assumptions, they serve as a basis for validating numerical algorithms of higher sophistication. In particular, such sophisticated PL3D models solve the full 3D elastic rock deformation problem coupled with a 2D viscous fluid flow field. Although these generations of PL3D models (Clifton and Abou-Sayed 1979, 1981; Cleary et al. 1983a) provide the most comprehensive capabilities for hydraulic fracturing analysis and design, they require excessive central processing unit resources and lack the ease of operation required for practical use. However, P3D models have become popular owing to their prefracture design and post-fracture analysis coupled with efficiency in computation and time requirements. Moreover, P3D models enable on-site evaluation and analysis at the faster rates than those in real time because they use as inputs the actual measured field data such as fluid viscosity, flow rate, and wellbore pressure during the hydraulic fracture treatment. The result, in turn, instantly modifies the treatment schedule for more accurate estimation of final fracture configurations.

The P3D models have been developed from the PKN model by allowing the fracture height to vary in time and space. The complete 3D elastic rock response is decreased to a 2D deformation problem by assuming elastic plane strain for each vertical cross section. This indicates that the fracture opening at one point is directly associated with the local net pressure at that given point and does not depend on the net pressure in the neighboring cells, which significantly simplifies the elasticity equation. The fluid flow is assumed to be 1D in the vertical or horizontal direction or in both directions. The dimensional reduction technique thus decreases the computational cost. However, P3D models are valid only for fracture configurations that do not significantly differ from their essential assumptions [e.g., an elongated fracture with length/height ratio ≥ 5 (Palmer and Craig 1984,)]. For relatively unconfined fracture growth (i.e., in which the pay zone horizontal minimum stress is higher than the bounding stresses), the fracture height growth tends to become unstable, and the model becomes invalid. This occurs in sandstone reservoirs with thin and weak interlayers. The fracture is significantly propagated in the vertical direction, leading to a length/height ratio < 5. For better agreement between the model and actual shape in this condition, the vertical fluid flow effect requires to be considered.

This work reviews P3D models from their early development in the 1980s to the present. In the literature, as shown in Fig. 1, these models are divided into lumped and cell-based models (Mack and Warpinski 2000). This division can be confusing because the former indicates fracture geometry, which often comprises two half-elliptical shapes connected at the middle. However, the latter indicates the method of solution. The lumped models often refer to generalized PKN or KGD models or their combination, which is referred to a P3DH-type model (Cleary 1980; Keck et al. 1984). In the latter, the PKN type used for estimating height growth is coupled with the KGD type for estimating fracture length. Some studies refer to the P3DH-type model as a cell-based model owing to its method of solution, whereas the original authors considered it to be a lumped model (Keck et al. 1984). The cell-based models divide the fracture into vertical plane strain cross sections in which each cell deforms independently. In such cases, the fracture geometry is not specified a priori, and the vertical fluid flow is not fully integrated into the fracture geometry computation. However, the lumped models can be discretized and solved for each pointwise at each time step.

Fig. 1
figure 1

Schematic of the two types of P3D models (Guo et al. 2017)

Full size image

All of the P3D models reviewed in this work are chronologically divided into the early modeling stage during the 1980s–1990s and the current modeling stage during the 2000s to the present. The prominent modeling approach in the early stage considers the lumped shape of the fracture. Since the 2000s, the focus has shifted to the cell-based modeling approach, which began with the employment of the equilibrium fracture height growth concept introduced by Simonson et al. (1978). This simple division provides transparency and efficiency in analyzing the progress of P3D modeling approaches, which is the primary objective of this review. The P3D modeling evolution through time is illustrated by the differences in formulating the governing equations under different assumptions and various propagation regimes as well as the computation of height growth based on the equilibrium or non-equilibrium height concept (i.e., whether to account for the pressure loss caused by vertical viscous flow). Moreover, P3D models serve as a basis for modeling complex fracture networks that interact with preexisting natural fractures observed in shale and oil gas reservoirs (Weng et al. 2011; Kresse et al. 2012; Chuprakov and Prioul 2016). This application of P3D modeling is an economical tool for hydraulic fracture design and the analysis of shale gas reservoirs and is thus discussed in detail here. Furthermore, this study highlights the importance of three studies in particular. Mendelsohn (1984) discussed early attempts to develop P3D and PL3D models, and a thorough review of the evolution of 2D PKN-type modeling from the beginning stages until the present has been presented by Nguyen et al. (2020). Moreover, Adachi et al. (2007) provided a comprehensive discussion on the challenges faced in numerical implementation of hydraulic fracture modeling such as scaling laws, propagation regimes, tracking of fracture footprints, and coupling of the governing equations.

The rest of this study is structured as follows. The next section summarizes the P3D models by dividing them into two groups of early and the modern stages. Then the P3D-based complex fracture network models that consider the interaction between existing natural fractures and induced hydraulic fractures are presented. The application section reports several simulation results for illustrating the validation of P3D numerical algorithms. Finally, certain research gaps are discussed for further study.

P3D model summary

Group I: early modeling stage of the 1980s–1990s

In this early phase of P3D modeling development, the primary focus was on lump-shaped fractures owing to the increased demand for a compromise between fast but simple 2D models and sufficient but time-consuming PL3D models. At that time, the lumped models reduced the computational complexity and could be implemented using a pocket calculator. The starting point of the lumped models is represented by the general governing equations that describe the fundamental hydraulic fracturing process such as mass conservation, conservation of momentum, and the relation between fracture opening and net pressure based on the vertical plane strain condition in a linear elastic manner. A predefined elliptical fracture geometry and a spatial averaging technique were then employed to reduce the governing system into a set of ordinary differential equations. This approach implicitly requires the self-similarity condition such that the fracture geometry remains the same as time evolves; only the length scale increases. Cleary (1980), Cleary et al. (1983b), and Settari and Cleary (1986) developed closed-form solutions for generalized versions of PKN and KGD models which enabled variation in height at any cross section. The self-similar feature enabled approximation of the time derivative of the fracture volume, and the governing equations were averaged over the fracture length. The solutions were decreased to functions of known constants and time-dependent coefficient terms. Then, a combination of the generalized PKN and KGD solutions for lateral extension and height growth, respectively, was presented as the P3DH model for more realistic modeling of a reasonably contained hydraulic fracture (Fig. 2).

Fig. 2
figure 2

Concept of P3DH modeling (Settari and Cleary 1984)

Full size image

The rate of height growth \(\dot{h}\) derived from the generalized KGD formulation for each vertical cross section is given as follows:

$$\dot{h} = \lambda h/\tau_{{\text{c}}} ,$$
(1)

where the characteristic time \(\tau_{{\text{c}}}^{m} = (\mu E^{2n + 2 - m} )/(p^{2n + 2 - m} H^{2n - 2m} )\); λ is vertical propagation rate coefficient; n is the flow behavior index; m is a power describing channel flow (m = n for laminar flow); and μ is effective viscosity. Similarly, the rate of length growth \(\dot{l}\) derived from the generalized PKN formulation is given as follows:

$$\dot{l} = \lambda_{{\text{L}}}^{m} h_{{\text{w}}}^{m + 1} /l\tau_{{{\text{cw}}}}^{m} ,$$
(2)

where the characteristic time evaluated at wellbore \(\tau_{{{\text{cw}}}}^{m} = (\mu E^{2n + 2 - m} )/(p^{2n + 2 - m} h_{{\text{w}}}^{2n - 2m} )\); hw is the fracture height evaluated at the wellbore; λL is the lateral propagation rate coefficient; and p is the net pressure inside the fracture. Theoretically, the lumped governing equations are general and transparent; however, the difficulty lies in the choice of coefficients that affect the accuracy under different conditions. The values of the coefficients have been determined by elaborate simulations, experiments, and field-based studies. Keck et al. (1984) presented the vertical lumped version of the P3DH model using a generalized KGD model for estimating the fracture length and a generalized PKN model for evaluating the height growth. Their model is suitable for poorly contained fractures. Settari and Cleary (1984) integrated heat transfer and proppant transport models into the P3DH model to create a more comprehensive P3D simulator. Settari (1988) presented a quantitative evaluation of vertical extension and extended the PKN and CGD models for more practical variable field problems. By using the finite element method, Advani et al. (1985) and Advani et al. (1986) solved an elliptical lumped model similar to the generalized PKN model presented by Cleary (1980). Their model considered the fluid flow in both the vertical and pay zone directions in the form of continuity equations. Fluid leak-off in the formation was included for both vertical and horizontal cross sections; however, LEFM was not considered. This model was limited to fractures with a length/height ratio < 2.5. Palmer and Carroll Jr (1983), Palmer and Craig (1984) and Palmer and Luiskutty (1985) solved simple P3D models for three-layer symmetrical and asymmetrical formation that did not consider vertical fluid flow. However, leak-off with spurt loss was considered and the fracture propagation followed LEFM such that the stress intensity factor at the tip is equal to the fracture toughness (i.e., KI = KIC). Such models are applicable to elongated fractures in which the vertical height growth rate is negligible with (i.e., \(\frac{{{\text{d}}h}}{{{\text{d}}t}} \ll \frac{{{\text{d}}l}}{{{\text{d}}t}}\)).

For each vertical fracture cross section, the vertical pressure drop is more significant than that in the central part owing to its narrower width and hence has greater influence on the height growth rate. The fracture boundary moving away from the center during the fracture propagation leads to the streamlines near the crack boundary approximately perpendicular to the boundary. Therefore, P3D models that consider vertical viscous flow tend to overestimate the height extension for a poorly contained fracture. Weng (1992) improved the representation of a realistic 2D flow in a fracture by dividing the fracture into two domains: an inner part with a relatively horizontal flow direction and an outer part in which the fluid flow is estimated by radial flow from an imaginary source. The continuity equation and the relation between the pressure gradient and the flow rate are modified as follows:

$$\frac{{\partial rq_{{\text{r}}} }}{\partial z} + zq_{{\text{L}}} + z\frac{\partial w}{{\partial t}} = 0,$$
(3)
$$- \frac{\partial p}{{\partial z}} = 2k\left( {\frac{4n + 2}{n}} \right)^{n} \frac{{q_{{\text{r}}}^{n - 1} q_{{\text{z}}} }}{{w^{2n + 1} }},$$
(4)

where r is radial distance from the imaginary source; qz and qr are vertical and radial flow rates, respectively; qL is the leak-off rate; n is the fluid flow index; k is the fluid consistency index; and w is the fracture width. The modified governing system was solved using the same collocation method with a suitable set of Chebyshev points as that used in the P3DH model (Settari and Cleary 1986). The result showed a better agreement in height calculation between this model and a complete 3D model.

Group II: later modeling stage from the 2000s to the present

The cell-based modeling approach has drawn considerable attention in the later years, especially for more reasonably contained fractures where the vertical viscous flow can be neglected. However, for improving the accuracy of P3D modeling, the original concept of using KGD-type modeling for viscous vertical growth in lumped fracture modeling is still invaluable. Increased oil prices in the late 1970s necessitated oil production from low-permeability reservoirs. The existing 2D models often used for massive treatment became inefficient and unfeasible for layered formations in which fracture geometry is dependent on variable confining stresses between layers. Such conditions inspired Simonson et al. (1978) to develop a symmetric three-layer height growth solution for computing the fracture height penetrating higher-confining-stress zones as a function of pressure. This fundamental work, which is often referred to as the equilibrium height concept, was instrumental for cell-based P3D modeling. Fung et al. (1987) later improved Simonson’s concept for non-symmetrical multilayer cases. The equilibrium height condition requiring the vertical extension to be small compared with the lateral growth in turns suits the vertical plane strain assumption of P3D modeling. Its computation does not consider the effect of variable elastic modulus because such variation is associated with the presence of a significant pressure drop in the height growth direction. This so-called equilibrium height calculation is valid, given that the vertical viscous fluid rate is relatively low so that the vertical pressure loss owing to the vertical viscous flow is insignificant. This condition is invalid in highly permeable layers or weak layers with insufficient in situ stress for confining the fracture. For such cases, the vertical fluid rapidly moves into these zones, which causes notable pressure loss.

Classical P3D model

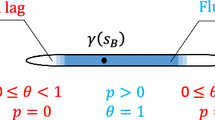
The so-called classical P3D (Fig. 3) model was reexamined by Adachi et al. (2010). In the classical P3D model, the fracturing fluid follows Poiseuille’s law, indicating a steady, viscous flow between parallel plates. The fracture equilibrium height growth is controlled by the criterion of LEFM, i.e., crack advance occurs when the stress intensity factor (i.e., the strength of the inverse square root stress singularity) near the crack tip matches the formation fracture toughness. This propagation criterion implies a fracture toughness-dominated regime in the vertical direction.

Fig. 3
figure 3

Schematic of the classical P3D model including partial views (Dontsov and Peirce 2015a)

Full size image

The formulation scaling rigorously accounts for storage or leak-off-dominated asymptotic solutions in the fracture tip region. The scaled analysis shows that the solutions of this classical model depend on only two dimensionless coefficients representing toughness κ and leak-off c:

$$\kappa = \sqrt {\frac{2\pi }{H}} \frac{{K_{{{\text{IC}}}} }}{\Delta \sigma },$$
(5)
$$c = \frac{{2CH^{2} \Delta \sigma^{3/2} }}{{\mu^{1/2} E^{\prime } Q_{0} }},$$
(6)

where E is Young’s modulus; \(E^{\prime} = \frac{E}{{1 - \nu^{2} }}\) is plane strain modulus; ν is Poisson’s ratio; Δσ is stress jump; H is pay zone thickness; C is Carter’s leak-off coefficient; Q0 is the injection rate at the wellbore; and μ is dynamic viscosity. Moreover, the scaled formulation enables additional analysis in the quantitative condition when the equilibrium height condition becomes invalid (i.e., when the fracture height becomes unstable as the vertical growth rate increases rapidly). The model fails to be valid when the dimensionless fracture height λ ≥ λu where λu is a dimensionless critical value of fracture height, calculated as

$$\lambda_{{\text{u}}} = \frac{{8 + \sqrt {\kappa^{4} + 64} }}{{\kappa^{2} }}.$$
(7)

Enhanced P3D models

Although the computational time is not an issue for the classical P3D model, its applicable range is extremely limited. The problem lies in the primary assumptions of the classical model. The model considers only the toughness regime and completely ignores the viscous resistant effect in the height growth direction, which leads to overestimation of the height growth for small or zero fracture toughness. Furthermore, the model considers only the viscous regime in the height growth direction; the plane strain (local) elastic condition rules out considering lateral growth resistance caused by fracture toughness. Therefore, the fracture length growth is overestimated when the fracture toughness is large and the horizontal flow becomes toughness-dominated. Based on this analysis, Dontsov and Peirce (2015a) developed an enhanced pseudo-3D model (EP3D) to consider the vertical viscous flow effect, non-local elasticity, and lateral toughness. The EP3D model can capture toughness, viscous, and viscous-to-toughness transitional propagation regimes by incorporating asymptotic solutions for the tip elements of each regime correspondingly (Dontsov and Peirce 2015b). The apparent fracture toughness (ΔKIC) is introduced to compensate for the vertical viscous loss by matching the toughness and viscous asymptotic solutions (wK and wM) at distance d:

$$w_{{\text{K}}} \equiv \sqrt {\frac{32}{\pi }} \frac{{\Delta K_{{{\text{IC}}}} }}{{E^{\prime } }}d^{1/2} = \beta_{{\text{m}}} \left( {\frac{{\mu^{\prime } V}}{{E^{\prime } }}} \right)^{1/3} d^{2/3} \equiv w_{{\text{M}}} ,$$
(8)

where \(V = \frac{1}{2}\frac{\partial h}{{\partial t}}\); \(\beta_{{\text{m}}} = 2^{1/3} .3^{5/6}\); \(d = \frac{{\Delta K_{{{\text{IC}}}}^{6} }}{{\mu^{\prime } E^{\prime 4} V^{2} }}\); \(\mu^{\prime } = 12\mu\).

The apparent fracture toughness is then obtained as follows:

$$K_{{{\text{IC}}}} = \sqrt {\frac{\pi }{32}} \beta_{{\text{m}}} E^{\prime 2/3} \mu^{\prime 1/3} V^{1/3} d^{1/6} .$$
(9)

The non-local elasticity equation accounting for full elastic interaction and lateral growth resistance is given as follows:

$$p(x) = - \frac{{E^{\prime } }}{8\pi }\int_{ - l(t)}^{l(t)} {\int_{{ - \frac{1}{2}h(x,t)}}^{{\frac{1}{2}h(x,t)}} {\frac{{w(x,z)dz^{\prime } dx^{\prime } }}{{((x - x^{\prime } )^{2} + z^{\prime 2} )^{3/2} }}} } ,$$
(10)

where the integral is singular in the Cauchy principal value sense and takes its Cauchy principal value at (x, z) = (x′, z′). The third modification of this EP3D model replaced the classical P3D flat fracture tip with a curved tip to resemble the fully PL3D geometry presented by Peirce and Detournay (2008). This improved the overall estimate of the model. The curved fracture tip was introduced by equating it with the analytical solution for a radial fracture. The fracture opening and the corresponding fracture height for the radial solution are given as follows:

$$w_{{{\text{rad}}}} = \frac{{4K_{{{\text{IC}}}} }}{{\sqrt {\pi l} E^{\prime } }}\sqrt {l^{2} - x^{2} - z^{2} } ,$$
(11)
$$h_{{{\text{rad}}}} = 2\sqrt {l^{2} - x^{2} } ,$$
(12)

where the fracture length l is its radius. Attempts have been made to add a proppant transport model for a completely integrated P3D simulator during that time. Dontsov and Peirce (2015c) added a 2D transport model with a gravitational settling effect into the classical P3D model. Skopintsev et al. (2020) coupled a proppant transport model with the EP3D model to include a leak-off rate following Carter’s theory (Carter 1957), which is a critical component for proppant transport. The gravitational settling effect, however, was not considered.

One limitation of the classical P3D model is that the fracture is initiated and propagated from the layer with lower stress into the bounding layers. In practice, this is not always the case. For hydraulic fracturing operation in shale reservoirs characterized by a complex stress field and vertically heterogeneous mechanical properties, the perforations in a horizontal wellbore are not always placed in the lower-stress layer. This could lead to inaccuracy and instability of the fracture height growth. Cohen et al. (2015b, 2017) enhanced the P3D model to relax this assumption and enable more accurate fracture height prediction. Their model, referred to as the stack height growth model (SHG), states that a stack of fracture cells is created when a cell propagates into a lower-stress zone and the cell is vertically split into a stack of two cells connected, as shown in Fig. 4. This enabled the fracture to have multiple fronts at different depths and the stress intensity factors at the top and bottom tips to include all of the stacked cells of the cross section.

Fig. 4
figure 4

Illustration of fracture cell splitting (Cohen et al. 2015a)

Full size image

Markov and Linkov (2018) and Linkov and Markov (2020) improved the P3D model for multilayer formations with arbitrary stress contrasts. The improvement was established on a correspondence principle based on the similarities between a P3D model with uniform vertical fluid pressure and the KGD model. The principle suggests that if these two plane strain models have the same fracture height and fluid volume, the fracture tip speed in the KGD model is equal to the height growth rate of the corresponding P3D model. This model is applicable to the viscosity-dominated regime and the transitional toughness to viscosity-dominated regime in the height growth direction. Recent hydraulic fracturing operations in coal seam gas reservoirs containing significant elastic contrast between thin layers (Pandey et al. 2017) motivated Zhang et al. (2017) to introduce a cell-based P3D model that considers the effects of variable elastic layers on the vertical fracture growth. To capture the non-equilibrium height growth, the fluid flow in each cell is divided into horizontal flow in the central region and vertical flow in the filling region. For both height and lateral fracture growth, the LEFM propagation criterion is applied. When stress interaction opens a new fracture element, the filling part is first assigned with no fluid pressure. The fluid pressure inside will gradually increase and can become a portion of the central part. A criterion for transforming a filling part into the central domain is given as follows:

$$K_{{{\text{Il}}}} = \chi K_{{{\text{IC}}}} ,$$
(13)

where KIl is the stress intensity factor in the length direction and the correlation factor χ is assumed to be a constant for a specific problem. By comparing this model with the full 3D model presented by Peirce (2015), Zhang et al. (2018) reported that the value of χ should be a function of material, loading, and computational parameters to be given as the following formula using the following regression method:

$$\chi = 0.42 - 0.024 \times K^{\prime } ,$$
(14)

where the dimensionless factor K′ is computed as follows:

$$K^{\prime } = \frac{{K_{{{\text{IC}}}} \sqrt d }}{{E^{\prime 2/3} \mu^{1/3} Q_{0}^{1/3} }},$$
(15)

This model considered toughness-dominated regimes in both the vertical and lateral directions, which is not often the case in hydraulic fracturing where viscous fluid flow tends to be a predominant factor for propagation (Savitski and Detournay 2002). Therefore, additional study to properly quantify the applicable range for this model is recommended. Furthermore, for highly permeable coal seam stimulation, the pressure-dependent leak-off should be considered because it significantly affects the hydraulic fracture growth. Table 1 provides a summary of the P3D models discussed in this review. The significant enhancements and assumption differences are listed to illustrate the overall evolution in P3D modeling approaches over time.

Table 1 Summary of cell-based P3D modeling evolution
Full size table

P3D-based complex fracture network modeling

In the last few decades, shale oil and gas operations have increased rapidly worldwide after the success of multistage hydraulic fracturing technologies in horizontal wells. Microseismic data have demonstrated that hydraulic fracturing in shale gas reservoirs tends to result in complicated fracture networks owing the preexisting natural fractures and vertically heterogeneous mechanical characteristics (Maxwell et al. 2002; Fisher et al. 2005; Gale et al. 2007). This condition makes the bi-wing-shaped fracture in conventional reservoirs unsuitable for modeling the complex geometry of shale gas formations. As an alternative, complete 3D models that consider the mechanical interference between the induced and natural fractures in an elaborate heterogeneous 3D stress field have been developed (Fu et al. 2011; Nagel et al. 2011; Nagel and Sanchez-Nagel 2011). However, solving a full 3D non-planar fracture problem requires a full 3D numerical method such as the finite element, which is computationally expensive and more suitable as a research tool than for general engineering use. Therefore, a conventional bi-wing P3D-based model for simulating complex fracture networks in unconventional formations has been developed and adopted. Moreover, the P3D approach increases the computational efficiency and reduces the time expended for routine design activities, which makes it a convenient tool for the study of various scenarios to evaluate feasible simulation results for a given range of reservoir parameters.

Lumped fracture network models

Similarly, P3D complex fracture network models can be classified as lumped (elliptical) and cell-based models. The lumped complex network has been modeled by Xu et al. (2009) and Meyer and Bazan (2011) in which the network pattern predefined two orthogonal sets of parallel evenly distributed fractures in the maximum and minimum horizontal stress directions. Furthermore, because the primary fractures are propagated in the plane normal to the minimum horizontal stress, the discrete fracture network (DFN) can include secondary fractures in all three planes. The governing equations comprise elastic and fluid flow equations and overall mass balance calculation. The interfering effect among collateral fractures and proppant transport is considered; however, this model does not consider the interaction between the hydraulic fractures and preexisting natural fractures. Therefore, this simplified model is limited to cases in which the existing DFN comprises two normal sets of natural fractures, and the hydraulic fractures straightforwardly open into the DFN.

Cell-based fracture network models

Kresse et al. (2011), Weng et al. (2011) and Kresse et al. (2012, 2013) presented a cell-based unconventional fracture model (UFM) to account for the complex hydraulic fracture network present in naturally fractured reservoirs. Both the preexisting natural fractures and the induced hydraulic fractures are assumed to be vertical. Therefore, the UFM is suitable only for reservoirs with nearly vertical natural fractures. The coupled problems of elastic rock response, viscous flow, and proppant transport are solved in this model similar to that in the conventional bi-wing P3D model. Correspondingly, the fracture height growth is calculated on the basis of the equilibrium height concept and is then extended to the non-equilibrium height growth, in which the pressure resistance caused by the vertical viscous flow is considered in the form of apparent fracture toughness (Mack and Warpinski 2000). The UFM solves the governing system using the Newton–Raphson method for the entire network rather than only one hydraulic fracture in a single plane.

The interaction between induced hydraulic fractures and natural fractures was first considered using an analytical crossing criterion adopted from Renshaw and Pollard (1995), which agreed with the experiments. The criterion is based on a solution of LEFM for stresses in the fracture tip region to predict whether a fracture will terminate at or propagate across a frictional interface at a perpendicular intersection. The fracture crosses if

$$\frac{{ - \sigma_{xx} }}{{T_{0} - \sigma_{yy} }} > \frac{{0.35 + \frac{0.35}{{k_{{{\text{fric}}}} }}}}{1.06},$$
(16)

where σxx and σyy are the in situ stress parallel and normal to an approaching hydraulic fracture, respectively; T0 is the tensile strength of the rock; and kfric is a frictional coefficient. Renshaw and Pollard’s criterion was modified for a non-orthogonal intersection between a fracture and a frictional interface by Kresse et al. (2012). This simplified crossing criterion does not consider the interaction between the fluid and the frictional interface and cannot assess the decisive role of the horizontal interface for fracture containment in most field cases. Subsequently, a more sophisticated model, OpenT, was developed by Chuprakov et al. (2013) to consider the mechanical effects of the hydraulic fracture opening and the preexisting natural fracture permeability. However, the OpenT model assumes constant permeability for the natural fractures and a uniform opening of the hydraulic fracture approaching a discontinuity. The OpenT model was later improved into the FracT model by relaxing the uniform opening and making the fracture opening profile part of the problem solution (Chuprakov and Prioul 2015, 2016; Weng et al. 2018). Moreover, the UFM model accounts for the mechanical interference between neighboring fractures, which is referred to as the stress shadow effect, and is computed on the basis of the 2D displacement discontinuity solution (Crouch et al. 1983). This model states that the opening and shearing displacement discontinuities (Dn and Ds) of nearby fractures cause normal stress (σn) and shear stress (σs) on one fracture as follows:

$$\sigma_{{\text{n}}}^{i} = \sum\limits_{j = 1}^{N} {A^{ij} C_{{{\text{ns}}}}^{ij} D_{{\text{s}}}^{j} } + \sum\limits_{j = 1}^{N} {A^{ij} C_{{{\text{nn}}}}^{ij} D_{{\text{n}}}^{j} } ,$$
(17)
$$\sigma_{{\text{s}}}^{i} = \sum\limits_{j = 1}^{N} {A^{ij} C_{{{\text{ss}}}}^{ij} D_{{\text{s}}}^{j} } + \sum\limits_{j = 1}^{N} {A^{ij} C_{{{\text{sn}}}}^{ij} D_{{\text{n}}}^{j} } ,$$
(18)

where \(C_{{{\text{ns}}}}^{ij}\) is a plane strain elastic influence coefficient and Aij is a 3D correction factor for the influence coefficients of the interaction decay occurring when the distance between any two fractures increases, as suggested by Olson (2004).

Application

This section presents two simulation examples to illustrate several important aspects of P3D modeling. The MATLAB algorithm employed was published by Peirce et al. (2010) for a classical P3D model (Adachi et al. 2010) that considers fracture tip asymptotic solutions. A scaling scheme is included to reduce the governing equations into a system of ordinary differential equations, which is then solved using an implicit fourth-order collocation method.

The first simulation was conducted to illustrate the validation of a P3D numerical method by comparing the P3D simulation results under confined fracture growth (i.e., constant fracture height) with the 2D PKN small-time regime (i.e., storage-dominated) and large-time regime (i.e., leak-off-dominated) asymptotic solutions (Kovalyshen and Detournay 2009). These computations were designed to sufficiently cover small-time τ = 10−6 to large-time τ = 104 solutions with an initial time step τ = 10−7. The comparisons are shown in Figs. 5 and 6. The charts show an almost identical agreement between the computed P3D solution and the asymptotic solutions of PKN storage (small-time) and leak-off (large-time) dominations. This result indicates that under confined vertical extension, the fracture initially propagates with the storage regime and continues as a leak-off regime at the end of the process.

Fig. 5
figure 5

P3D fracture width versus PKN small-time (left) and large-time (right) width asymptotic solutions

Full size image
Fig. 6
figure 6

Comparison of fracture length evolution between P3D and PKN asymptotic solutions

Full size image

The injection rate is a controlling parameter in the success of hydraulic fracture treatment. Most P3D models have been developed for a constant injection rate only. In certain field applications, however, the injection rate at the wellbore cannot be kept constant or is expected to vary. To gain insight into the impact of variable rates on the fracture propagation process, the second simulation was conducted with the wellbore injection rate modified to vary in time, assuming as power-law time-dependent function \(Q(0,t) = Q_{0} t^{\alpha }\) where Q0 is a constant nominal rate and α ≥ 0. Correspondingly, the dimensionless form of the injection rate is \(\overline{\Psi }(0,\tau ) = \tau^{\alpha }\). The MATLAB code was accordingly edited for this injection rate change.

The modified P3D model was run for three cases of non-dimensionalized injection rates with α = 1/9, α = 1/20, and α = 0 (i.e., constant injection rate). Figure 7 shows the resulting dimensions of the fracture in the three cases. In the cases of time-varying rates (α = 1/9 and α = 1/20), the injection rate slightly increased the vertical extension and the fracture opening evolution yet remarkably slowed the fracture length. This result indicates that the fluid injection rate in the wellbore has a significant effect on the fracture length evolution.

Fig. 7
figure 7

Varied injection rate versus fracture height (upper left panel), fracture width (upper right panel), and fracture length (bottom panel)

Full size image

Conclusion

This study reviewed the evolution of P3D modeling approaches applied to hydraulic fracturing since the 1980s. The limitations of the classical P3D were analyzed, which led to the conclusion that vertical viscous resistance should be considered to improve the accuracy of height growth estimation. The viscous loss can be compensated in the form of apparent fracture toughness, and the vertical propagation rate can be more directly computed by matching each vertical fracture cross section with the KGD-type solution. The non-local elasticity equation is considered for improved prediction of the lateral growth for large fracture toughness in the horizontal direction. The P3D-based unconventional fracture models are efficient engineering tools for shale gas–oil reservoir applications, which were discussed in detail.

One major limitation with the P3D models is that their applicable range is not accurately quantified. The majority inherited PKN length/height ratios ≥ 5; therefore, more applicable analyses should be directly conducted on such models to determine their precise ranges of field application. As a more comprehensive integrated simulator for industrial applications, the EP3D model should be extended to asymmetric formations of more than three layers and should include complete proppant and heat transfer models. Furthermore, P3D models developed primarily for highly permeable shale gas reservoirs should include a more elaborate leak-off rate sensitive to the fluid pressure rather than a simple Carter leak-off term.