Evaluating different energized fracturing fluids using an integrated equation-of-state compositional hydraulic fracturing and reservoir simulator

Abstract

Horizontal wells are often drilled and hydraulically fractured in tight reservoirs to produce hydrocarbons or heat. Different fracturing fluids such as slick water, gas, foam, gel, or a combination can be used with slick water being the most common fracturing fluid. In this paper, we study the impacts of different fracturing fluids on fractured well productivity using an in-house integrated hydraulic fracturing and reservoir simulator with an equation-of-state compositional model. We analyzed the fracture geometry, stress interference, proppant placement, and the subsequent well productivity using different fracturing fluids. The results clearly show that different fracturing fluids result in very different fracture shape, sand distribution, and water and hydrocarbon production. By conducting fracturing and production simulations in one simulator, we ensure that no physics and data loss occurs due to data migration between two different software packages for hydraulic fracturing and reservoir simulation. To the best of the authors’ knowledge, this is the first time that a single integrated equation-of-state compositional hydraulic fracturing and reservoir simulator has been presented and applied for well lifecycle simulation.

Introduction

Horizontal drilling and hydraulic fracturing are the two main technologies required to unlock oil and gas resources from tight formations. Multi-stage hydraulic fracturing treatment design is challenging as it has to overcome large stress shadow effects and non-uniform fracture growth in the subsurface to achieve the maximum oil and gas recovery (French et al. 2019). Hydraulic fracturing design parameters such as cluster spacing, proppant type, fracturing fluid type, and injection rates affects the fracturing process in terms of proppant placement, fracture conductivity, stimulated reservoir volume (SRV), fracture half-length, propped length, and interaction between hydraulic fractures and natural fractures (Kolawole et al. 2020; Kolawole and Ispas 2020). Field evidence shows a large pressure drop in the completion caused by non-uniform proppant distribution (Daneshy 2007). Proppant selection can have a big impact on the well production (Terracina et al. 2010). It is important to correctly predict fracture width and proppant distribution when history matching the well production.

Different fracturing fluids have been developed and used in the past for various purposes, e.g., fracture initiation, fracture propagation, proppant carrying, and wellbore flushing. Most hydraulic fracturing simulators developed in the past (Wang 2015; Wu and Olson 2015; Settgast et al. 2017; Ouchi et al. 2017; Wang et al. 2017; Hirose and Sharma 2018; Agrawal et al. 2020) assume single-phase flow and cannot model different fracturing fluids. None of the above simulators can be applied for post-fracturing reservoir simulation purposes either. To evaluate fractured well productivity, one has to export the fracture geometry to other stand-alone reservoir simulators, during which important information such as pore pressure and stress change, proppant distribution, fracture conductivity, and fracture width may be lost. Fracture closure, fracture tip extension, and proppant settling during the shut-in period are usually not considered (Zheng et al. 2020).

Friehauf (2009) developed the first compositional 2-D hydraulic fracturing model and incorporated thermal and compositional effects in addition to fracture mechanics and proppant transport in the fracture. Gu (2013) also developed a 2-D fracturing model for one fluid phase (e.g., foam) and one solid phase (proppant). The main limitation of both the models arises from the simplified fracture mechanics. Their models assume that the fractures are contained and follow the shape prescribed by Perkins–Kern–Nordgren analytical fracture model. Thus, their models are not suitable for fracture propagation and containment in real field cases. A 3-D compositional fracture propagation model was developed by Ribeiro and Sharma (2013a, b). The model was used to simulate and optimize different fracturing fluids such as, slick water, gel, gas, and foam (Ribeiro and Sharma 2013b). This model coupled a compositional 3-D fracturing model with a wellbore and a simplified well productivity model. This has been by far the most comprehensive effort to handle various fracturing fluids and compare their flowback performance using a simplified productivity model. However, there are several limitations inherent to this model: (a) The fracture modeling is limited to single planar fracture propagation; (b) The model does not calculate stress and strain in the near-fracture region but uses far field stresses instead for fracture propagation; (c) A single leak-off coefficient is assumed for multi-phase leak-off and it is hard to estimate the leak-off coefficients for phases other than water; (d) On the phase behavior side, the phase behavior is analyzed based on equilibrium values (K-value) rather than an equation of state. The well productivity model is simplified too. It does not consider the effects of phase behavior, fracture geometry, proppant distribution, fracture width, production schedule, and completion design on fractured well productivity. Cai et al. (2021) propose a new hydro-mechanical-chemical model with the capillary-confined effect to simulate multi-phase compositional problems in high precision and computational efficiency. The coupled response of confined phase equilibrium, rock deformation, reaction-controlled porosity evolution, and hydraulic flow are analyzed in detail to reveal the constraints of hydrocarbon production and CO₂ trapping in tight reservoirs, which is essential for successfully deploying carbon capture, utilization, and storage in deep reservoirs. However, their model does not consider fracture propagation problems.

In this paper, we introduce an integrated equation-of-state compositional fracturing and reservoir simulator and apply it to study fracture propagation and the well productivity using different kinds of water-based and energized fracturing fluids. We apply the hydraulic fracturing and reservoir simulator to model hydraulic fracturing treatment using fracturing fluids such as slick water, pure CO₂, cross-linked gel, N₂ foam, and hybrid CO₂/slick water. This simulator solves fully coupled physics within and in-between three solution domains: reservoir domain (solid deformation, multi-phase compositional porous flow, leak-off, poro-thermo-elasticity), fracture domain (multi-phase compositional slurry flow, proppant advective transport and gravitational settling, fracture propagation, opening and closure), and wellbore domain (slurry distribution among perforation clusters, wellbore storage, wellbore friction pressure drop, production). Peng–Robinson equation of state is used to model the phase behavior of reservoir hydrocarbon and injected non-aqueous fracturing fluids. Fracture geometry, proppant placement, and changes in pressure, stress, and reservoir fluid composition using different fracturing fluids are obtained from the fracture propagation simulations (Zheng et al. 2021b). The simulations are then seamless transferred into compositional reservoir simulation with the information from the fracturing simulation.

Observations from simulation results clearly show that different types of fracturing fluids have significantly different properties such as compressibility, viscosity, and density. These properties affect the flow in the fracture and wellbore, leak-off into the reservoir, and the capability to carry the sand, which play an important role in determining the fracture geometry and sand placement. Fluids with lower viscosity (e.g., slick water) tend to create longer, thinner, and more unpropped fractures. Fluids with higher viscosity or higher compressibility (e.g., N₂ foam and cross-linked gel) tend to create shorter, thicker, and better propped fractures. Fluids with low viscosity and higher compressibility (CO₂) reduce the breakdown pressure owing to the more pronounced leak-off and wellbore storage effects. Wells treated with CO₂ show a higher initial hydrocarbon production and lower water production due to the pressurization, viscosity reduction, volume expansion, and improved oil relative permeability whereas water-based fracturing fluids yield a lower oil/gas rate and a higher water rate because of the damaged oil/gas relative permeability and potential water blocking in the reservoir and fractures. Wells treated with energized fracturing fluids clearly show higher hydrocarbon production and lower water production taking the created fracture surface area into consideration.

The remaining sections are organized as follows: The fully integrated fracturing and reservoir simulator is introduced in Sect. 2. Case setup including computation mesh, rock and fluid properties, completion design, and production schedule are presented in Sect. 3. The results for fracture propagation simulation and production simulation are summarized and discussed in Sect. 4 and  5, respectively. Key findings and conclusions are presented in Sect. 6.

Model description

An integrated hydraulic fracturing and reservoir simulator has been developed by researchers at the University of Texas at Austin. The simulator was initially developed for pad scale fracture propagation simulation (Zheng et al. 2019; Manchanda et al. 2020) and flowback simulation (Manchanda et al. 2019) with a single-phase flow model. The single-phase flow model in the simulator was then extended to a non-isothermal, multi-phase black-oil flow in reservoir, fracture, and wellbore domains (Zheng et al. 2021a; Hwang et al. 2020). A general proppant transport model was then added to include proppant convective flow, gravitational settling, and embedment coupled with fracture closure during the lifecycle of wells (Zheng et al. 2020). The single-phase fracturing simulator was also extended to an integrated equation-of-state (EOS) compositional fracturing and reservoir simulator (Zheng et al. 2021b), and this fully compositional model will be utilized in this paper.

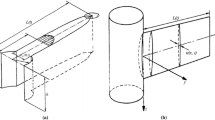
Figure 1 shows the coupled reservoir-fracture-wellbore domains and the coupled physics in the three domains. Multiple physics in the reservoir domain (solid deformation, multi-phase compositional porous flow, leak-off, poro-thermo-elasticity), fracture domain (multi-phase compositional slurry flow, proppant advective transport and gravitational settling, fracture propagation and closure), and wellbore domain (slurry distribution among perforation clusters, wellbore storage, production) are tightly coupled.

Fig. 1

The coupled reservoir-fracture-wellbore domains and the coupled physics within the three domains in the fully integrated simulator

The key governing equations are summarized in this paper and readers are encouraged to refer to the previous publications as cited above for the derivation of the governing equations and other numerical details of this simulator. In the reservoir domain, the solid deformation equation in the internal reservoir cells and fracture boundary faces is shown in Eqs. (1) and (2). The mass conservation equation for component $i$ is shown in Eq. (3). The pore pressure equation is shown in Eq. (4).

$$\mathop \oint \limits_{\Gamma }^{{}} \left[ {\left( {2\mu + \lambda } \right)n \cdot \nabla u_{n} + \lambda ntr\left( {\nabla_{t} u_{t} } \right) + \mu n \cdot \nabla u_{t} + \mu \nabla_{t} u_{n} + \sigma_{0} + \alpha pI} \right]{\text{d}}\Gamma = 0$$

(1)

$$\mathop \smallint \limits_{{\Gamma_{b} }}^{{}} \left[ {\left( {2\mu + \lambda } \right)n \cdot \nabla u_{n} + \lambda ntr\left( {\nabla_{t} u_{t} } \right) + \mu n \cdot \nabla u_{t} + \mu \nabla_{t} u_{n} + \sigma_{0} - \alpha pI} \right]{\text{d}}\Gamma + np_{{\text{f}}} \left| {\Gamma_{b} } \right| = 0$$

(2)

$$\frac{{\partial N_{i} }}{\partial t} - V_{b} \nabla \cdot \mathop \sum \limits_{j = 1}^{{n_{p} - 1}} \left[ {\xi_{j} x_{ij} \frac{{k_{rj} }}{{\mu_{j} }}k \cdot \nabla \left( {p + p_{crj} - \rho_{j} gD} \right) + \phi \xi_{j} S_{j} K \cdot \nabla x_{ij} } \right] - q_{i} = 0$$

(3)

$$\begin{gathered} \left( {\frac{1}{N}\frac{\partial p}{{\partial t}} + \alpha \nabla \cdot \frac{\partial u}{{\partial t}}} \right) - \frac{{\partial V_{t} }}{\partial p}\frac{\partial p}{{\partial t}} - \frac{1}{{V_{b} }}\mathop \sum \limits_{k = 1}^{{n_{c} + 1}} V_{tk} q_{k} - \hfill \\ \nabla \cdot \mathop \sum \limits_{k = 1}^{{n_{c} + 1}} V_{tk} \nabla \cdot \mathop \sum \limits_{j = 1}^{{n_{p} }} \left[ {\xi_{j} x_{ij} \frac{{k_{rj} }}{{\mu_{j} }}k \cdot \nabla \left( {p + p_{crj} - \rho_{j} gD} \right) + \phi \xi_{j} S_{j} K \cdot \nabla x_{ij} } \right] = 0 \hfill \\ \end{gathered}$$

(4)

Equations (5) and (6) are the mass conservation and pressure equations in the fracture domain. Equation (7) is the proppant mass conservation equation in the fracture domain. During fracture propagation period, the fracture permeability is modeled using the cubic law and calculated using $\frac{{w}^{2}}{12}$. During production, the fracture permeability is calculated by Eq. (8) in which the proppant concentration, proppant diameter, fluid density, velocity, and viscosity effects are considered.

$$\frac{{\partial N_{i} }}{\partial t} - \nabla \cdot \mathop \sum \limits_{j = 1}^{{n_{p} }} \left[ {\xi_{j} x_{ij} \frac{{k_{rj} }}{{\mu_{j} }}\frac{{w^{2} }}{12}\left( {wS} \right) \cdot \nabla p} \right] = q_{Ini} - q_{{{\text{Leaki}}}}$$

(5)

$$\frac{1 - c}{V}\frac{\partial V}{{\partial t}} - \frac{\partial c}{{\partial t}} - \frac{1}{V}\frac{{\partial V_{t} }}{{\partial p_{f} }}\frac{{\partial p_{f} }}{\partial t} - \mathop \sum \limits_{i = 1}^{{n_{c} + 1}} \left[ {\frac{{\partial V_{t} }}{{\partial N_{i} }}\nabla \cdot \left( {\mathop \sum \limits_{j = 1}^{{n_{p} }} \xi_{j} x_{ij} \frac{{k_{rj} }}{{\mu_{j} }}\frac{{w^{2} }}{12}\nabla p_{{\text{f}}} } \right)} \right] = \mathop \sum \limits_{i = 1}^{{n_{c} + 1}} \frac{{\partial V_{t} }}{{\partial N_{i} }}\frac{{q_{Ini} - q_{{{\text{Leaki}}}} }}{V}$$

(6)

$$\frac{{\partial V_{pi} }}{\partial t} + \mathop \sum \limits_{j = 1}^{{n_{p} }} \nabla \cdot \left( {u_{pij} \gamma_{ij} V_{pi} } \right) = q_{pi}$$

(7)

$$k_{f} = \frac{{d_{p}^{2} \left( {1 - c} \right)^{3} }}{{150c^{2} + 4.2c^{2} \left( {\frac{{d_{p} \rho_{f} u_{f} }}{{\mu_{f} c}}} \right)^{\frac{5}{6}} }}$$

(8)

In the wellbore domain, Eqs. (9) and (10) model the wellbore storage effects and slurry distribution among different perforation clusters during hydraulic fracturing. During flowback or production, a modified Peaceman well model is applied to calculate the well productivity index of a fractured well as shown in Eq. (11).

$$P_{{{\text{BHP}}}} - P_{{{\text{BHP}}}}^{{{\text{old}}}} - \frac{{K_{{\text{f}}} }}{{V_{{{\text{well}}}} }}\left( {q_{in} - \mathop \sum \limits_{i = 1}^{n} q_{i} } \right)\Delta t = 0$$

(9)

$$p_{{\text{f}}} = p_{{{\text{BHP}}}} - {\Delta }p_{{{\text{section}}}} - {\Delta }p_{{{\text{perf}}}}$$

(10)

$$WI_{{\text{f}}} = \frac{{k_{{\text{f}}} w}}{{0.5{\text{ln}}\left( {L_{{\text{f}}}^{2} + h_{{\text{f}}}^{{2}} } \right) - {\text{ln}}\left( {r_{w} } \right) - 1.966}}$$

(11)

The coupled nonlinear system of equations shown in Fig. 1 is solved using the Newton–Raphson method. An implicit pressure, explicit composition solution algorithm of this fully compositional model is shown in Fig. 2. Three loops are included in the solution algorithm: the inner Newton loop, the middle failure loop, and the outer time loop. After a new time step is initiated, the Jacobian matrix and residual vector are constructed and the block-coupled governing equations solved within the inner Newton loop. Then fracture propagation is checked against the fracture propagation criterion (stress intensity factor method) and if fractures were to propagate within the current time step, mesh change or dynamic mesh refinement will be performed and iterated within the middle failure loop until no more mesh topological changes are required. Then different conservation equations (e.g., component mass, proppant volume, temperature) in the reservoir, fracture, and wellbore domains are solved. A phase behavior analysis based on EOS and other correlations is performed at the end of each timestep using the converged solutions.

Fig. 2

The implicit pressure, explicit composition solution algorithm for the fully integrated simulator

The integrated hydraulic fracturing and reservoir simulator has been validated with various analytical results, experimental data, and field data. The validations related to the compositional fracturing and reservoir model include:

• The fracture propagation has been validated against the analytical solutions for Kristianovich–Geertsma–de Klerk, Perkins–Kern–Nordgren, and radial fracture problems in Zheng et al. (2019) and Manchanda et al. (2020).

• Validation with an unconventional oil well which was fractured using CO₂, slick water, and cross-linked gel was presented in Zheng and Sharma (2020). The surface treating pressure and oil/gas/water/CO₂ flow back have been matched between the simulation results and field data.

• The phase behavior modeling of hydrocarbons using the Peng–Robinson equation of state has been validated with experimental data and the production simulation using the compositional model has been compared with a commercial simulator in Gala (2019).

Case setup

The reservoir domain size in the x, y, and z directions are set to $1920 \mathrm{m}$, $1920 \mathrm{m}$, and $50 \mathrm{m}$, respectively (Fig. 3). In this paper, we ran 2-D simulations with a constant fracture height ($50 \mathrm{m}$). It is worth noting that our model has the full capability to run 3-D simulations as well (Zheng and Sharma 2020). A horizontal slice of the reservoir mesh which penetrates the wellbore is shown in Fig. 3. The horizontal wellbore is set to be along the x-axis ($y=960$, $z=0$) and the treating stage is placed in the center of the reservoir domain ($x=960$, $y=960$, $z=0$). The maximum grid size (in the far field) in the reservoir domain is $40\times 40 {\mathrm{m}}^{2}$ and the smallest grid size (near the fractures) after a 2-level static refinement in the x direction and a 4-level dynamic refinement in x and y direction is $0.625\times 2.5 {\mathrm{m}}^{2}$.

Fig. 3

A horizontal slice view of the reservoir domain mesh which penetrates the wellbore (y = 960, z = 0)

During the fracturing treatments, hydraulic fractures may interact with existing natural fractures and barriers in the formation, which may significantly alter the geometry of the main hydraulic fractures and even form a fracture network (Kolawole and Ispas 2020). Hydraulic fracturing using different fracturing fluids with different rheology properties will result in different interactions between the hydraulic fractures and natural fractures. There are two methods to consider the effect of natural fractures and barriers in the fracture propagation. One method is to build a discrete fracture network (DFN) and simulate the complex interaction between the hydraulic fractures and natural fractures. Displacement discontinuity method and extend finite element method-based models are usually used with DFN. In the other method, instead of modeling the natural fractures explicitly, a Stimulated Rock Volume (SRV) is set around the main hydraulic fractures. As in this paper, we focus on the compositional and phase behavior effect of different fracturing fluids on fracture propagation and the following production instead of the hydraulic fractures-natural fractures interaction, we adopted the second method to avoid the meshing complexity and uncertainty in fracture propagation caused by the DFN.

The reservoir hydrocarbon fluid consists of six pseudo-components: CO₂, N₂–C₁, C₂–C₃, C₄–C₆, C₇–C₁₄, and C₁₅–C₃₀. The PVT properties including critical pressure ($P_{{\text{c}}}$,), critical temperature ($T_{{\text{c}}}$), critical volume ($V_{{\text{c}}}$), acentric factor ($\omega$), molar weight ($M_{w}$), volume shift ($V_{{\text{s}}}$), as well as the composition ($z$) are shown in Table 1. The binary interaction parameters (BIP) are shown in Table 2.

Table 1 PVT properties and composition for the reservoir hydrocarbon fluid

Table 2 Binary interaction parameters between components for the reservoir hydrocarbon fluid

The water/oil/gas three-phase relative permeability is modeled using the Stone-II relative permeability and the parameters are shown in Table 3. Hydraulic fracturing treatment of half an hour is simulated. The pumping schedule is shown in Fig. 4. The injection rate is fixed at $0.15 {\mathrm{m}}^{3}/\mathrm{s}$ and injection proppant concentration includes a ramping up and ramping down period. Other input parameters including porous properties, mechanical properties, and completion design parameters are shown in Table 4.

Table 3 Stone-II relative permeability parameters used in the simulation

Fig. 4

Pumping schedule (slurry injection rate and proppant concentration) used in the simulation

Table 4 Porous properties, mechanical properties, and completion design parameters used in the simulation

Five fracturing fluids are studied in this paper, including water-based fracturing fluids (slick water, cross-linked gel), energized fracturing fluids (0.95 quality N₂ foam, CO₂), and hybrid fluids (CO₂/slick water). The fracturing fluid viscosity for slick water, cross-linked gel, 0.95 quality N₂ foam are set to be $5 \mathrm{cP}$, $30 \mathrm{cP}$, and $100 \mathrm{cP}$ whereas the viscosity for CO₂ is determined using EOS and Lohrenz–Bray–Clark correlations (Zheng and Sharma 2020). The compressibility and density for CO₂ and N₂ are also determined using EOS. An SRV region with a permeability enhancement of 10 times within 10 m to the fracture surfaces is assumed, which grows dynamically with the propagating fractures. After the fracturing simulation, the simulation is seamlessly transferred to production simulation using the fracture geometry, proppant placement, stress change, leak-off induced pressure, and composition change in the reservoir, etc. The production duration is set to 5 years and the production bottom-hole pressure is fixed at $10 \mathrm{MPa}$. The surface pressure and temperature are fixed at $0.1 \mathrm{MPa}$ and $293 \mathrm{K}$ for surface oil/gas/water production calculation.

Fracture propagation simulation results

Five hydraulic fracturing simulations have been run using (a) slick water, (b) cross-linked gel, (c) hybrid CO₂/slick water, (d) 0.95 quality N₂ foam, and (e) CO₂. Since CO₂ is a poor sand carrier, in the CO₂ case, we do not inject any proppant and just intend to see how the fracture propagates during CO₂ injection. In the hybrid CO₂/slick water case, CO₂ is used before proppant is injected in the first 400 s and proppant is carried by slick water in the last 1400 s. The fracture geometries generated using the five fracturing fluids are shown in Fig. 5. The color scale on the fracture surfaces represents the fracture width at the end of injection phase. By comparing the water-based fracturing fluid cases (a) and (b), one can observe that cross-linked gel which has a higher viscosity fluid creates shorter fracture length and larger fracture width than slick water which has a lower viscosity. Larger stress shadow effect is also expected if the fluid viscosity is larger as the fracture turning angle in case (b) is larger than that in case (a). By comparing the energized fracturing fluid cases (d) and (e), one can observe that pure gas fracturing fluid creates fractures with much smaller length and width compared to a water-based fracturing fluid. This is because the higher leak-off and high compressibility of the gas fracturing fluid make it more difficult to create hydraulic fractures. If a foam were to be formed, the water and gas phases will travel together as one pseudo-phase with a much higher viscosity and the leak-off of foam is the lowest among all the fracturing fluids. Similar to the highly compressible gas, foam creates a short fracture which is only longer than the pure CO₂ case and the largest fracture width. No significant difference in fracture geometry is observed between the slick water case (case (a)) and the hybrid CO₂/slick water case (case (c)) but the fracture length in the hybrid case is slightly smaller than the slick water case.

Fig. 5

Fracture geometry and width distribution after the hydraulic fracturing simulation. a slick water b cross-linked gel c hybrid CO₂/slick water d 0.95 nitrogen foam e CO₂

Figure 6 plots the stress distribution (compression negative) in the direction of the in-situ minimum horizontal stress for the five cases with different fracturing fluids at the end of the injection period. A tensile region is observed in all the cases because of the opening effect at the fracture tip. The slick water and cross-linked gel cases show a smaller stress shadow effect (smaller increase in the compressive stress) compared to other cases because of its relatively low viscosity. The nitrogen foam case shows higher stress (large compressive stress around the fractures) because of the high viscosity and low leak-off of the nitrogen foam. For the CO₂ and hybrid CO₂/slick water cases, it shows large compressive stress near the CO₂ leak-off region, which is mainly because of the poro-elastic effects caused by CO₂ leak-off into the reservoir.

Fig. 6

Stress distribution after the hydraulic fracturing simulation. a slick water b cross-linked gel c hybrid CO₂ and slick water d 0.95 nitrogen foam e CO₂

Figure 7 shows the well bottom-hole pressure changing as a function of the injection time for cases using different fracturing fluids. The cross-linked gel case is found to have the largest breakdown pressure ($53.8 \mathrm{MPa}$) and net pressure because of the low compressibility and high viscosity of cross-linked gel. Similarly, N₂ foam has a high viscosity but high compressibility, which partially offsets the effect of high viscosity, making the net pressure lower than the cross-linked gel case. On the contrary, CO₂ shows both low viscosity and high compressibility, giving the lowest net pressure and least obvious break down, because of the large wellbore storage and leak-off effects. In the hybrid CO₂/slick water case, the net pressure follows the CO₂ trend during the CO₂ injection period and gradually switches to the slick water trend when the slurry of slick water and proppant starts to be injected into the wellbore and eventually coincides with the slick water case.

Fig. 7

Bottom-hole pressure change versus time during hydraulic fracturing using different fracturing fluids

Fracture propagation is mainly controlled by the fluid viscosity and compressibility from a phase behavior point of view. Figure 8 depicts the created fracture surface area increasing with time using different fracturing fluids. The results show that water-based fracturing fluids tend to create longer fractures than energized fracturing fluids. It also shows that fracturing fluids of low viscosity and low compressibility create longer fractures than any other combination of fluids.

Fig. 8

Created fracture surface area versus time during hydraulic fracturing using different fracturing fluids

Figure 9 shows the fracture geometry and proppant distribution at the end of well completion. A non-uniform proppant distribution is observed in the fractures. As Fig. 9a, b, d depicts, since the proppant is not injected from the beginning, the fracture tip regions are left unpropped. It is visually obvious that the hybrid CO₂/slick water case (case (c)) achieved the best proppant placement with the most propped fracture area and least unpropped fracture area. CO₂ has a poor capability of creating fractures as compared to slick water and thus creates shorter fractures than the slick water case within the first $400 s$ before the proppant slurry is injected into the wellbore. Fracturing fluids with higher viscosity are used in case (b) and case (d) in which the slurry flows slower inside the fractures and thus the proppant mass is larger locally, compared to the lower viscous fluid cases. The remaining fracture width and permeability correlates positively with the proppant placement. Better propped fractures show a higher fractured well productivity (Zheng et al. 2020). The impacts of fracture geometry, proppant distribution, and leak-off on well productivity will be evaluated and analyzed in the following section.

Fig. 9

Fracture geometry and proppant distribution after hydraulic fracturing. a slick water b cross-linked gel c hybrid CO₂/slick water d 0.95 nitrogen foam

Production simulation results

Once the hydraulic fracturing simulation phase is completed, the simulation continues to the production simulation phase seamlessly. In the production simulation, the fractured well is produced for 5 years under a constant bottom-hole pressure$(10 \mathrm{MPa}$). The leak-off induced pressure increase, fluid composition change in the near-fracture region, the effect of fracture geometry, width and non-uniform proppant placement are all inherited from the previous fracture propagation simulation. For unpropped fractures, a minimum fracture width of $0.01 mm$ is assigned to calculate the fracture permeability using the cubic law. Figures 10, 11 and 12 show the distributions of pressure, CO₂ mole fraction and water saturation in the reservoir after the hydraulic fracturing treatment in the hybrid CO₂/slick water case. As shown in figure, the pore pressure near the created fractures increases because of CO₂ and water leak-off. The pressure increase near the wellbore is higher than other regions because the CO₂ leak-off rate is much larger than the slick water leak-off rate. Significant CO₂ mole fraction increase (up to 10%) due to the CO₂ injection period is observed from Fig. 11. The water saturation decreases in the near wellbore region displaced by CO₂ and water saturation increase in the region far away from the wellbore because of the water leak-off are observed in Fig. 12. All of the changes happen to the reservoir during the fracturing has been preserved and used in the reservoir simulation.

Fig. 10

Pore pressure distribution in the reservoir for the hybrid CO₂/water case after the hydraulic fracturing simulation

Fig. 11

CO₂ mole fraction distribution in the reservoir for the hybrid CO₂/water case after the hydraulic fracturing simulation

Fig. 12

Water saturation distribution in the reservoir for the hybrid CO₂/water case after the hydraulic fracturing simulation

Figure 13 shows the pore pressure distribution at the end of the 5-year production. The shape of depleted zones in different cases roughly follows the fracture geometry: larger fracture surface area results in larger depleted region.

Fig. 13

Pore pressure distribution in the reservoir after the 5-year production. a slick water b cross-linked gel c hybrid CO₂ and slick water d 0.95 nitrogen foam

Figures 14, 15, and 16 plot the cumulative oil, gas, and water production (at surface conditions) for cases with different fracturing fluids. Generally speaking, larger created and propped fracture surface areas result in larger cumulative surface production. It is worth pointing out that the initial surface oil and gas rate is higher and the initial water rate is lower in the hybrid case as compared to the slick water case. The benefits of CO₂ used in the hybrid case include: dissolving in the subsurface oil phase, reducing the oil viscosity, swelling the oil phase, and pressurizing the reservoir. On the contrary, slick water used in the hybrid case increases the water saturation and decreases the oil and gas relative permeability in the near-fracture region. The other thing to point out is that the increased or decreased water saturation is expressed in a more “averaged manner” in the reservoir grids near the fractures. In field applications, the effect of CO₂ used during hydraulic fracturing will be even larger because the numerical model tends to underestimate the relative permeability improvements in the near-fracture reservoir region.

Fig. 14

Cumulative oil production per stage (at surface conditions) using different fracturing fluids

Fig. 15

Cumulative gas production per stage (at surface conditions) using different fracturing fluids

Fig. 16

Cumulative water production per stage (at the surface conditions) using different fracturing fluids

The production results shown in Figs. 14, 15, and 16 are the results for one stage. Figures 17, 18, 19 show the surface oil, gas, and water production per unit created fracture surface area. Energized fracturing fluids including hybrid CO₂/slick water and nitrogen foam show a slightly higher oil/gas and lower water production per unit fracture surface area. Water-based fracturing fluids including slick water and cross-linked gel show lower oil/gas and higher water production per fracture surface area.

Fig. 17

Cumulative surface oil production per unit fracture surface area using different fracturing fluids

Fig. 18

Cumulative surface gas production per unit fracture surface area using different fracturing fluids

Fig. 19

Cumulative surface water production per unit fracture surface area using different fracturing fluids

When we translate these findings to actionable field decisions, we can conclude that a smaller well spacing can be used for energized fracturing fluids (which tend to create shorter but better propped fractures). The same reservoir volume will yield a higher recovery factor and lower water production. Placing more stages in a well will also result in faster recovery of hydrocarbons, and therefore, a higher net present value (NPV) for the well.

Conclusions

In this paper, we utilized an integrated compositional hydraulic fracturing and reservoir simulator to evaluate the effectiveness of different fracturing fluids in unconventional wells. We simulated the simultaneous propagation of multiple fractures using slick water, cross-linked gel, CO₂, 0.95 quality N₂ foam and hybrid CO₂/slick water. The fracture geometries, proppant placement, and complex phase behavior changes in the reservoir were then used for production simulation. Based on the simulation results, the following conclusions can be reached:

• The viscosity, compressibility, and miscibility with reservoir fluids are the key fracturing fluid properties that control the well productivity and hydrocarbon recovery from hydraulically fractured wells.

• Different fracturing fluids lead to very different fracture geometry, proppant placement, and near wellbore phase behavior changes (saturation, fluid composition, viscosity, compressibility, relative permeability) in the reservoir.

• Gas has to be used in combination with other fracturing fluids to achieve well propped fractures because of its limited ability to carry sand.

• The leak-off of the fracturing fluid into the reservoir matrix has a significant impact (positive or negative) on the primary production from the well.

• The fractured well productivity is controlled by propped fracture surface area and the near-fracture hydrocarbon permeability at bottom-hole conditions.

• Energized fracturing fluids are likely to deliver higher oil and gas production and lower water production. The incremental costs of these fluids must be weighed against the improved well productivity to quantitatively evaluate the cost effectiveness of these fluids for a particular application. This important fracturing fluid selection decision can be made using the integrated model presented in this paper.