Introduction

Rock mechanics, as a sub-branch of geomechanics, uses the concepts of continuity, solid mechanics, and geology to determine the behavior of rock environments against environmental stresses. In petroleum geomechanics, a prediction of rock behavior, compaction, failure, and fault in oil and gas reservoirs due to exploitation drilling is investigated. Although almost a century has passed since the beginning of the exploration drilling industry, the science of geomechanics has recently entered the industry.

The importance of drilling planning and operation of hydrocarbon reservoirs is becoming increasingly apparent due to the decline in oil prices and competitive production of hydrocarbon resources. One of the problems occurring in most drilling wells is the instability of the wellbore, which leads to sticking pipes to the well, decreasing well diameter, losing mud, increasing well diameter, and flowing well. In some cases, the costs are increased by up to 1 billion$ a year (Al-Ajmi 2006). The stability of the wellbore is not only influenced by drilling but also by reducing pore pressure during the operation in the fields.

Instability of wellbore can occur at various stages of a well’s life, including drilling, completion, as well as flow and production tests (Fjar 2008). These instabilities are the main source of drilling problems, leading to high cost and time waste and sometimes loss of the entire well (Zoback 2010). Oil companies spend a lot of time and money dealing with the problems caused by the wellbore instability in drilling operations. There are various opinions about the cost due to the instability of the wellbore, which is estimated to be about $ 1 billion per year (Zeynali 2012). Therefore, it seems necessary to investigate this issue in order to reduce such costs.

Many parameters influence the instability of the wellbore. Some of these parameters are related to the properties of drilling mud and its interaction with formation, and some are related to mechanical properties of formation and the amount of stress direction around the well. In general, the instability of wellbore can be related to physicochemical and mechanical factors or their combination (Maleki 2014).

It is necessary to build a geomechanical model to predict the safe and stable weight range of drilling mud windows in future wells and better understand the parameters influencing the wellbore instability (Kidambi and Kumar 2016). Geomechanical model is a logical set including information related to geology, regional stresses, rocks’ mechanical properties, and pore pressure; it is used to quickly update information used in drilling operation and reservoir management (Moos 2003).

The wellbore instability is predicted using failure criteria and models that calculate the stresses around the well. Failure criteria used in stability analysis include Mohr–Coulomb, Drucker–Prager, Mogi–Coulomb, modified lead, and three-dimensional Hoek–Brown models.

Each of these failure criteria predicts different values for rock strength and minimum mud weight required for wellbore stability; therefore, choosing failure criterion is difficult and controversial for analysis of wellbore stability (Amiri et al. 2019).

Many researchers have studied the application of geomechanics to analyze wellbore stability, some of which are introduced below.

Al-Ajmi presented the Mogi–Coulomb criterion to analyze shear failures in rocks (2006). Due to the ability of this criterion to model failure in rocks, in 2009, a model of vertical, directional, and horizontal wellbore stability was presented (Ameen et al. 2009).

Poisson’s ratio and Young’s modulus could be predicted through vertical seismic profiles determining shear and compression wave velocity and using some experimental equations (Rutqvist et al. 2009). Also, Ameen et al. investigated the relationship between porosity and elastic parameters of rock and could provide elastic logs of rock based on empirical relationships (2009).

Zhang et al. performed five failure measurement experiments on five different rock samples and showed the best failure criteria for wellbore stability analysis to be the three-dimensional Hoek–Brown and Mogi–Coulomb criteria based on the evaluated samples (2010).

Younesi and Rasouli also studied the effect of landslides along fractures on the wellbore stability and provided an index to investigate landslide potential. They showed that using the presented method, the instability of wellbore could be investigated based on the reactivation mechanism of faults and fractures (2010).

In addition, Rajabi et al. used well logs to determine the velocity of compression and shear waves (2010).

Mirzaghorbanali and Afshar determined mud weight window based on the Mogi–Coulomb refractive index and elastoplastic model (2011). They showed that such models offer better results than those conventional ones. Maleki (2014), at an oil field near Khark Island, applied the three Mohr–Coulomb, Mogi–Coulomb, and Hoek–Brown failure criteria in analyzing the wellbore stability. According to the studied environment (Burgan sandstone reservoir), the Mogi–Coulomb failure criterion provided more accurate results (Maleki 2014). In the same year, Gholami et al. used the Mohr–Coulomb, Hoek–Brown, and Mogi–Coulomb failure criteria to determine safe window and mud weight for drilling one well in the Khuzestan Oil Field in Iran (2014). They showed that the wellbore stability analysis using the Mogi–Coulomb failure criterion was in better agreement with diametric diagram data.

Shen et al. presented a flowchart for one-dimensional analysis of pore pressure and safe mud window estimates in high-angle wells (Shen et al. 2015). Also, Ma et al., in collaboration with the just mentioned team, analyzed stability and optimization of the well path based on the Mogi–Coulomb failure criterion and the breakout width model. It was concluded that this hybrid model could produce the lowest amount of safe mud window in agreement with its actual amount (Ma et al. 2015).

The mechanical earth model (MEM) represents mechanical stress, pore pressure, and properties of a particular section in a field or basin. This model includes all geomechanical information to analyze any geomechanical applications, including wellbore stability analyzing, sand production forecasting, hydraulic fracture reservoir designing, compacting, and reservoir subsiding. The best necessary method can be achieved for drilling operations and safe completion in a well and the well field by constructing a geomechanical model (Amiri et al. 2018).

The ultimate goal of this study was to develop a one-dimensional geomechanical model in the well APP2 in one of the oil fields in southern Iran. Accordingly, core samples and interpretation of various logs were used in modeling. Rock mechanics tests were performed on core samples taken from the well. The tests were as follows:

Uniaxial compression resistance test uses the ASTM-C170 ISRM and ASTM-D2938 standards, the results of which were analyzed and processed to construct a geomechanical model.

In this research, petrophysical logs were used along with the calibrated core mechanical results obtained from the laboratory to construct a geomechanical model and perform wellbore stability analysis.

Geological setting

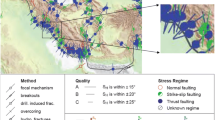
The studied oil field is located in Khuzestan Province and Abadan Plain (southwest of Iran). Its length is 20 km and its width is 2.5 km, in the N-S direction with an approximate area of 52 square kilometers. In other words, this field is located along the Iranian–Iraqi border.

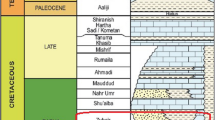
Based on the available information from the wells, the four main production horizons in this field include Sarvak, Kajdomi sandstone, Gadvan, and limestone layers in Fahliyan Formation. It should be noted that there are no geological outcrops in this field at ground level, and the obtained information is based on the results of the 3D seismic method.

The formations and lithological characteristics of this oil field are presented in Table 1.

Table 1 Underground formations with their lithological characteristics in the studied oil field
Full size table

Materials and methods

In general, the instability of the wellbore is classified into the following two categories:

  1. (A)

    Chemical origin instability: The most common instability of chemical origin is related to water absorption by shale formations and leaching of salt formations by the aqueous phase of drilling fluid. Absorption of water in shale causes swelling and loss of formation, leading to more or less well diameter. Leaching of salt formations may cause large cavities around the wellbore, or it may contaminate drilling fluid. This type of instability can be counteracted by changing the chemical composition of the drilling fluid (Gao 2019).

  2. (B)

    Mechanical origin instability: Before drilling, rocks of the formation are less than the strength of the rock, and chemical conditions in the formation are in equilibrium. With the start of drilling, load on the rocks around the well is removed, and the stresses left around the well are increased, showing stress concentration. Depending on the strength of the rock, stress concentration can cause the wellbore to break. Mechanical stability manages the stresses preventing shear and tensile failure in the rock. Typically, these stresses are compact and create shear stresses in the rock. The more closely these stresses (equal to each other), the more stable the rocks are (Zoback 2003).

The MEM is actually a numerical representation of the geomechanical information available for a field or basin. Planning for drilling high-risk wells without using a MEM can dramatically increase the costs. For example, in the absence of a MEM and the presence of the wellbore instability, it is not possible to correctly decide whether to reduce or increase the weight of drilling mud.

  • One-dimensional MEM

A one-dimensional MEM includes all geomechanical parameters against depth. In this model, drilling data against depth can also be provided. Geomechanical parameters involved in the one-dimensional mechanical model of stratigraphy referred to as hard data are as follows (Lund and Zoback 1999):

  • Poisson’s ratio

  • Young’s modulus

  • Uniaxial compressive strength

  • Friction angle

  • Pore pressure

  • Minimum horizontal stress

  • Maximum horizontal stress

  • Vertical stress

  • Horizontal stresses direction

The above data are used to determine the safe mud window (the amount of mud weight if used, minimizing the number of tensile and shear failures).

  • Three-dimensional MEM

In this model, the two-dimensional plates of fracture, fault, and head of formations are interpreted according to seismic data; they are used together with well log data.

Estimation of safe mud window

Instability of wellbore occurs due to rock failure from two main types of tensile and shear failure. Shear failure usually occurs due to low mud weight, and tensile failure occurs due to high mud weight. There are several methods to predict rock failure and instability of wellbore, such as using failure criteria.

Safe mud window is one of the outputs regarding analysis of wellbore stability, the concept of which is shown in Fig. 1. In defining a safe mud window, four points are essential:

  • Pore pressure

Fig. 1
figure 1

Safe mud weight window

Full size image

If the amount of mud weight and, consequently, the pressure inside the well is less than pore pressure, one can expect a washout and well flow. Of course, it should be noted that the swabbing process, causing a sudden decrease in the pressure inside the well to the extent less than the formation pressure, can have a similar effect. (In the pipe-raising operation, separation of the drill from bottom of the well reduces the pressure inside. This phenomenon is called swab.)

  • The minimum amount of mud weight to prevent breakout failure

At mud weight less than safe mud weight, the rock breaks, and the lower the mud weight, the more severe the breakout fracture; the swabbing process can have a similar effect (Kanfar et al. 2017).

  • The minimum main stress level (herein, the minimum horizontal stress)

If there are natural fractures or any other conductive properties around the wellbore or in the high permeability zone, then mud weight pressure more than the original stress is expected to open the natural fractures and cause loss of the drilling mud. In formations with high fractures, any pressure greater than horizontal stress can at least cause geometric fractures, propagating them toward the wellbore. Excessive mud or surge in the pipe-lowering operation can have similar effects. (In this operation, the pressure of the drill bit on the mud in the well increases the pressure inside the well, called the surge phenomenon.)

  • Formation of fracture pressure

When the failure pressure of the mud is higher than that of the formation, it leads to developing tensile failures. Tensile failures are also called hydraulic and inductive failures. If the rate of failure pressure exceeds the original minimum stress (here, the minimum horizontal stress), loss of circulation will occur.

In general, it can be said that the ideal mud weight should be more than the pore pressure. The minimum mud weight to prevent breakout should be less than the horizontal stress and failure pressure of the formation, as shown in Fig. 1.

In this study, the information of in-well logs of sonic (DT), gamma ray (GR), neutron porosity (NPHI), bulk density (RHOB), and caliper (CAL) from the depth of 1930—4263 was used to estimate elastic properties of the rock (elastic deformation and strength parameters) in the APP2 well after revision (Fig. 2). Overall, different types of data, such as in-well tests, drilling data, in-well logs, and rock mechanics tests, were used in the study.

Fig. 2
figure 2

Log data of the APP2 well

Full size image

In this research, Techlog software, as one of the unique software applications in the world used in petroleum engineering, was applied. It has various analyses; definite and non-definite petrophysical analyses; image log analysis, texture analysis, dip log analysis, and core analysis (included in geology section); the analysis of wellbore stability, estimation of overburden stress, and study of fracture gradient (included in drilling section); the analysis of hydrostatic pressure, analysis of pressure gradient, and PC modeling (included in pressure engineering section); time-to-depth conversion, quality control (QC) plots, Delta-T processing, and reservoir that are unconventional (included in geophysics section).

Results and discussion

The well stability model in the studied oil field was based on geological information, in-well log information, rock mechanics laboratory data, as well as drilling and reservoir experiments.

In this study, the data obtained from the image log (FMI) were used to determine the direction of the main stresses in the region. These stresses were also calibrated using the wells’ leak-off test (LOT) information.

Construction of geomechanical model (MEM) and its calibration

Various steps are performed to construct a geomechanical model for one- or two-dimensional geomechanical analysis in a well or three-dimensional analysis in an oil field. Figure 3 shows a general flowchart of the steps for constructing a geomechanical model using in-well data and logs.

Fig. 3
figure 3

Flowchart of the steps to construct a geomechanical model

Full size image

Uniaxial compressive strength (UCS) is the most common criterion in calculating the rocks’ strength. This parameter is the primary criterion in estimating the stability of the wellbore due to the formation failure pressure.

In this study, multistage triaxial compressive tests performed on core components were used to calibrate UCS calculated from in-well logs.

Determining the formation tensile strength is vital to evaluate the tensile strength caused by stress concentration in the wellbore. This parameter was obtained from the results of the Brazilian test. Table 2 provides the values obtained in the Brazilian and uniaxial tests for the studied well. Based on this, a graph sequence was obtained for the values of static Young’s modulus, uniaxial strength, and tensile strength along the well (Fig. 4).

Table 2 Rocks’ strength parameters obtained from Brazilian laboratory and triaxial tests
Full size table
Fig. 4
figure 4

Interpolation of uniaxial and tensile strength values with static Young’s modulus in the studied well

Full size image

Figure 5 shows the elastic parameters calculated in the well. As shown, a good agreement was observed between the static Young’s modulus calculated from the in-well logs and that calculated in the laboratory tests, indicating the validity of the calculated elastic properties. This finding was also true for Poisson’s ratio.

Fig. 5
figure 5

Elastic parameters of the rock in the well

Full size image

The internal coefficient of friction (µ) and cohesion (C) along the well path were both calculated using a sonic log (DT) (Fig. 6). Also, a good correlation was observed between the rocks’ strength calculated from the in-well logs and core data, indicating a suitable calibration in the design of the geomechanical model.

Fig. 6
figure 6

a Correlation between rocks’ cohesion and DT, b correlation between rocks’ friction coefficient and DT

Full size image

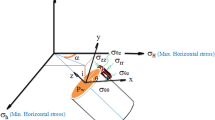
Magnitude of in situ stresses

Normally, one of the main stresses is vertical, and the other two stresses are horizontal. Vertical stress is obtained through the following equation. Of the two horizontal stresses, the minimum horizontal stress (σh) is obtained indirectly using the mini-fracture test with a reasonable estimate.

$$\sigma_{v} = \int\limits_{0}^{z} {\rho_{b} (z) \cdot g\;{\text{d}}z}$$

Irrespective of temperature, the minimum and maximum horizontal stress values can be achieved using the following prolastic relations:

$$\sigma_{h} = \frac{v}{1 - v}\sigma_{v} - \frac{v}{1 - v}P_{p} + \frac{E}{{1 - v^{2} }}\varepsilon_{x} + \frac{vE}{{1 - v^{2} }}\varepsilon_{y}$$
$$\sigma_{H} = \frac{v}{1 - v}\sigma_{v} - \frac{v}{1 - v}P_{p} + \alpha P_{p} + \frac{E}{{1 - v^{2} }}\varepsilon_{x} + \frac{vE}{{1 - v^{2} }}\varepsilon_{y}$$

where σv, σh, Pp, and σH are the vertical–horizontal minimum stresses, pore pressure, and maximum horizontal stresses in meg pascal, respectively; Young’s modulus is in Giga pascal, and α is the Biot’s coefficient.

The values Ɛx and Ɛy are horizontal strains in the region that can be compressive or tensile depending on the region’s tectonics. These values are calibrated using the LOT data in the well. Due to the lack of information on the rock particles, bulk modulus which is used to calculate the Biot’s coefficient is considered equal to 0.7 along the well, a common value in carbonate lithology (Abdollahipour 2015).

Joint opening (pressure drop in LOT) occurs when the inlet pressure reaches a critical level called the formation failure pressure. In this case, the tangential stress around the well (σθmax) equals tensile stress (σt).

$$\sigma_{\theta \max } = - \sigma_{t}$$

The maximum horizontal stress value is calculated as follows by placing the above equation in the hydraulic failure equations:

$$\sigma_{H} = 3\sigma_{h} - {\text{FBP}} + \sigma_{t}$$

The maximum stress obtained from the above relation is applied only to non-porous rocks, thus for those without pore pressure. Given the pore pressure of the formation, the above relation is written as follows:

$$\sigma_{H} = 3\sigma_{h} - {\text{FBP}} + \sigma_{t} - P_{p}$$

Figure 7 shows the LOT and formation breakdown pressure (FBP) values obtained from the diagram. The LOT value is equal to the main stress, at least around the well. Thus,

$$\sigma_{h} = {\text{LOT}} = {2}0{8}0 + {3818} = {\text{5898 psi}} = {4}0.{\text{66 Mpa}}$$
Fig. 7
figure 7

Results of LOT of the well at a depth of 2205 m (pressures are inside the well)

Full size image

It should be noted that the pressure shown in Fig. 7 is the one at the end of the well. In order to calculate the total pressure, the pressure from the drilling mud column must be added to the above value. The input parameters for calculating the horizontal stress at a maximum depth of 2205 m are given in Table 3.

Table 3 Input parameters for calculating the maximum horizontal stress at a depth of 2205 m
Full size table

The maximum horizontal stress value at this depth was calculated as 57.19 MPa by placing the information in Table 3 in the above equation.

This calculation is used to calibrate the prolastic stress equations; the values of Ɛx and Ɛy were calculated as 0.9635 and 2.7091, respectively, by placing the main stresses obtained in the prolastic relations; therefore, the values of the main stresses are calibrated by these values.

The square symbol in the stress column in Fig. 8 represents the maximum horizontal stress value in calibrating the maximum horizontal stress graph, and the circle symbol represents the minimum horizontal stress value obtained from LOT to calibrate the maximum horizontal stress graph. According to the stress diagram in Fig. 8, the stress regime is defined in a normal and strike-slip zone. In the lower parts of the well, as well as in the Gadvan Formation and many parts of the Fahliyan Formation, the stress regime becomes normal. In the following, information is presented regarding how the outcome of the main stresses and mud column pressure determines the stability of the wellbore using parameters derived from the data of drilling reports and changes in the well radius measured by the caliper tool.

Fig. 8
figure 8

Stress profile in the well (σH value is estimated based on LOT data and hydraulic failure theory relations)

Full size image

Determining direction of the horizontal stresses

Determining the direction of the main stresses is the first step to analyze the geomechanical model. Identifying the main stresses leads to designing the correct direction to drill the well with greater stability. Also, their direction design helps to improve perforation operation or complete the well and production planning.

There are various methods, such as breakout orientation, hydraulic fracturing, shear sonic anisotropy, and three-component vertical seismic profile (VSP), to determine the direction of the main stresses in an area. Breakouts are generally formed along the direction of the main stress, at least around the opening of the well where the stress concentration is at the greatest level. Thus, in a vertical well, the created breakout orientation determines the direction of the minimum main stress around the well (Fig. 9).

Fig. 9
figure 9

Relationship of the main stresses with breakout and tensile fractures

Full size image

The created breakout orientation around the well can be determined using image logs or by analyzing the oriented multi-arm caliper data.

In a hydraulic fracturing operation, the main fracture usually occurs along the direction of the maximum main stress where the hoop stress is in a tensile state. Therefore, hydraulic fracturing in a vertical well indicates the direction of the maximum main stress. The direction of the induced fracture due to drilling, which is in the direction of the mentioned fractures, can be identified by interpreting the image logs’ data. In this study, well graph data were used to determine breakout orientation. In this well, breakouts were observed in almost all dense or low-porosity parts of the Fahliyan Formation, especially in the interlayer areas. Figure 10 shows the breakout observed in the interval of a well from the lower Gurpi to the Sarvak Formation.

Fig. 10
figure 10

Breakout orientation in the well

Full size image

Analysis of the data obtained from the orthogonal caliper diagram and their azimuth identified a large number of breakouts with a predominant northwest–southeast direction (NW–SE) (Fig. 11), indicating that the minimum main stress direction (σh) around the well is approximately NW–SE; therefore, the maximum main stress direction (σH) is NE–SW.

Fig. 11
figure 11

a Rose diagram of breakout orientation, b breakout orientation in the wells’ top schematic

Full size image

Wellbore stability analysis

The geomechanical model and well path are used to calculate the concentration of the stresses around the well; further, by comparing them with the rupture criteria in the rock, it can be concluded whether the desired part of the wellbore is stable or not. Rock fractures causing wellbore instability are divided into two general categories: shear and tensile. The former usually occurs due to low mud weight, while the latter is caused by high mud weight. There are various criteria to predict rock fracture and well stability, of which the Mohr–Coulomb failure criterion is the most common. This criterion is widely used to determine shear failure, and the maximum tensile stress criterion is used to determine tensile failure.

Flow pressure, loss, breakout, and tensile fractures are shown in Fig. 12. Depending on the type of pressure, movement of the black line in the pressure column toward each of the colored areas indicates the risk of developing flow, loss, breakout, or tensile fractures.

Fig. 12
figure 12

Analysis of mud window and APP2 well stability

Full size image

Since a very high mud weight has been used while drilling the Fahliyan Formation, it is the most problematic formation in the drilling according to the mud window introduced in this well.

The key findings related to stability analysis and the events occurring during drilling in the APP2 well are as follows:

In the 12.25-inch well, the model predicted several breakouts for depths of 2500–2570 (Ilam Formation), 3080–3109 (Sarvak), and 3580–3760 (Gadvan); also, the data from the caliper tool showed several openings at these points (Fig. 12).

At depths of 3415–3450 m, no problem was reported with the well instability, and the model did not predict any failure at these depths. The openings observed in the well were related to the suction created during the pipe-raising operation.

In the 12.25-inch well, mud pressure was very close to drilling mud pressure, at least to prevent breakout and surge; also, swabbing phenomena should be avoided during the well path.

In the 8.375-inch well, the caliper tool showed several breakouts at depths of 3830–3880 m (above Fahliyan Formation), and the model also predicted shear failures for these depths.

No problem was reported at a depth of 3950 m during drilling, and the model did not predict any specific failure at this depth. Also, the data obtained from the caliper tool showed appropriate well conditions at this depth (Fig. 12).

In the 8.375-inch well, the weight of drilling mud was greater than that needed to prevent loss; therefore, it is recommended to reduce the weight of the mud in this hole. Although traveling in the well should be done with caution; also, surge and swabbing phenomena should be avoided.

Sensitivity analysis in the surrounding wells

In this section, a sensitivity analysis is presented regarding the effect of borehole orientation and azimuth drilling on the mud window. This analysis can include both a specific point and a depth interval. Output is derived from the results of the Mechanical Earth Model (MEM), especially the rocks’ strength and stress data. With the explanations provided, sensitivity analysis was performed at depths of 2850–3700 m with different angles and azimuths. Figures 13 and 14 show the minimum and maximum mud weights required for safe drilling.

Fig. 13
figure 13

Stereonet plot of sensitivity analysis of the well stability at a depth of 2850 m: a minimum required mud weight (left), b maximum allowable mud weight (right)

Full size image
Fig. 14
figure 14

Stereonet plot of sensitivity analysis of the well stability at a depth of 3700 m: a minimum required mud weight (left), b maximum allowable mud weight (right)

Full size image

Also, the minimum mud weight required to prevent breakout and the maximum allowable mud weight in order to avoid hydraulic fracture in the formation are both shown. The center of the stereonet represents a vertical well, and the angle of the well increases as it moves toward the circle’s boundary. As shown in Figs. 13 and 14, at a depth of 2850 m, drilling in a vertical well or a directional well (with a dip angle of fewer than 50 degrees) to the maximum horizontal stress direction and, at a depth of 3700 m, drilling a directional well in a direction parallel to the maximum horizontal stress (azimuth of 45 degrees) are the worst options.

While drilling in the direction parallel to the main stress is minimal, it is considered the most stable drilling mode. According to Figs. 13a and 14a, drilling in a relatively horizontal position with a low angle to the minimum horizontal stress is the most stable position for a depth of 2850 m. While at a depth of 3700 m, drilling vertically (up to 15 degrees) with a low angle to least horizontal stress (135 degrees) has the slightest instability problem. According to stereonet, at a depth of 2850 m, the minimum weight of breakout mode decreases by increasing the well angle.

This means that for this drilling depth, a horizontal well along the direction of the minimum stress is more stable than a vertical well, or a horizontal well drilled along the direction of main stress is more stable. At a depth of 3700 m, the situation is the opposite; this means that the mud weight required for the occurrence of breakout increases by increasing the well angle. Therefore, at this depth (in Gadvan and Fahliyan Formations), drilling a vertical well or a well with a low angle is more stable than drilling a horizontal well.

Figures 13b and 14b show the maximum mud weight allowed for preventing tensile cracks in the formation. The results in this section are the same as those presented in Fig. 13a. At this depth, digging a horizontal well along the main stress direction is at least more stable. Also, at a depth of 3700 m, a relatively horizontal well (with a dip angle of about 60 degrees) is at least more stable along the main stress direction.

As the stress regime in the well is changed from normal to strike-slip length, stable drilling directions are also changed. Further, the mud window obtained at a depth of 3700 m (ppg16.04–10.35) is narrower than that at a depth of 2850 m (ppg33.42–10.61).

Conclusion

In this research, a geomechanical model (MEM) was constructed for the APP2 well. Also, the existing data were used in the best possible way, being confirmed by laboratory results. Some problems reported while drilling with the mud window built into the geomechanical model confirmed the accuracy of the analysis. The following results were obtained from the stability analysis of the APP2 well:

  • Based on the geomechanical model (MEM), breakouts were identified at the depths of 2500-2570 m (Ilam), 3080–3109 m (Sarvak), and 3580–3760 m (Gadvan). At the depths of 3415–3450 m, no problem was reported with the well instability, and the model did not predict any failure. The openings observed in the well were related to suction, as well as surging and swabbing phenomena that occurred during pipe-raising and lowering operations.

  • The MEM was calculated with the help of the available data for the reservoir area in this field, and relationships were presented for mechanical properties of source rock (Fahliyan Formation) in the area.

  • At the depths of 3830–3880 m (upper Fahliyan), several breakouts occurred. In the 8.375-inch well, drilling mud weight was more than that needed for preventing wastage; thus, it is recommended to reduce the mud weight in the well. Also, traveling in the well should be done with caution, and pinching should be avoided.

  • Based on calculations of the minimum mud weight required for a depth of 2850 m, the most stable possible drilling position was an almost horizontal well in the direction closest to the minimum main stress. Also, for a depth of 3700 m, drilling in the azimuth of about 135 degrees with an angle of about 15 degrees was the most stable drilling position. It should be noted that the optimal direction and angle of the well may be different due to changes in the stress regime in different layers. According to the calculations related to the maximum allowable weight for the well at a depth of 2850 m, horizontal drilling along the main stress direction was the least stable state possible. For a depth of 3700 m, digging a well with an angle of about 60 degrees along the main stress direction was at least more stable.