Introduction

Drilling fluid design plays the most significant role in the whole drilling process. Drilling fluid behaves as a non-Newtonian fluid, and it demonstrates shear thinning behaviour (Rasool et al. 2021a). For a drilling fluid, apart from having necessary yield point and gel strength, the high viscosity is required when cuttings are transported to the surface, and low viscosity is needed when mud is passing through the drill string (Ofei et al. 2017).

Different kinds of additives are added in the drilling mud to enhance the rheological properties of the drilling mud (Rasool et al. 2021b). These additives mainly alter the chemical properties (related to hydrates inhibition and shale swelling) or mechanical properties which are related to the flow behaviour of the mud such as yield point and gel strength which govern the cutting transportation ability of the drilling mud (Ekeinde et al. 2019, Abbas et al. 2021).

Lately, ionic liquids are used as drilling fluid additives to enhance the rheological and improve the filtration properties of the drilling mud. Ionic liquids are low melting point liquids possessing negligible vapour pressure (Bavoh et al. 2020; Bera et al. 2020). Research has shown the addition of ionic liquids affects the clay structure which in turn alters its wettability which results into the modification of the mud rheology and its filtration behaviour (Ahmad, et al. 2019; Ahmed Khan et al. 2020).

Though ionic liquids have a lot of applications in drilling industry, there are certain disadvantages associated with the usage of ionic liquids which puts a question mark for its industrial usage. Ionic liquids are expensive, non-biodegradable and hard to prepare as it requires sophisticated techniques and equipment for its preparation (Kunz and Häckl 2016). Moreover, study has shown that the most popular class of ionic liquids being used in drilling fluids, i.e. imidazolium-based ionic liquids, is toxic (Zhao et al. 2007; Romero et al. 2008; Pham et al. 2010; Egorova and Ananikov 2014). An alternative solvent is needed that holds all the required traits of ionic liquids and can be used as a drilling fluid additive.

Deep eutectic solvents (DES) are fourth-generation ionic liquids which are formulated by the combination of a hydrogen bond donor (HBD) and a hydrogen bond acceptor (HBA) (Naser et al. 2013). These HBA and HBD are mostly easily available salts or alcohols which are non-toxic and which on mixing together at a particular ratio and temperature gives a low melting point solvent which retains its physical state at broad range of temperature (Hansen et al. 2020).

Previous study

In our previous work, potassium carbonate (PC) and glycerol (Gly)-based deep eutectic solvent (DES) has been prepared in-house and its rheological properties have been measured (Rasool et al. 2021a). It has been observed that the addition of DES resulted into improving the yield point/plastic viscosity (YP/PV) of the mud nearer to the acceptable range of 0.75–1 lbm/100ft2/cp. YP/PV is considered as one of the important indicators of mud rheology. Moreover, the DES-based mud also reduced the filtrate volume by 24% and mudcake thickness by 36% (Rasool et al. 2021b).

Current study

Structural characterizations

This research work focusses on the characterization of the DES-based drilling mud to understand the underlying mechanism behind DES as a rheology modifier. The characterizations are conducted to find the answers of the following questions.

  1. 1.

    Which mineral of clay will show more affinity towards DES?

  2. 2.

    What will be the effect of DES on d-spacing and mean crystalline size of clay?

  3. 3.

    What will be the effect of DES on stability of colloidal?

To answer the above-mentioned questions, FTIR, XRD and zeta potential of DES -WBM (water-based mud) are conducted.

Rheological modelling

The rheological models are essential for drilling mud rheology analysis because they are employed to stimulate the behaviour of drilling mud under different dynamic conditions (Skadsem et al. 2019). The rheological models can help us to predict and estimate the following applications/behaviour (Wiśniowski et al. 2020):

  • Frictional pressure losses in pipes and annuli

  • Flow regimes

  • Swab and surge pressure

  • Hole cleaning efficiency

  • Equivalent circulation density (ECD)

In this study, the best fit rheological model will be found out that best describes the behaviour of DES-WB.

Shear thinning behaviour

It is important for drilling mud to show shear thinning behaviour during its circulation for better hole cleaning and cutting transportation (Tchameni et al. 2021). This research will also focus on studying the shear thinning behaviour of mud at room temperature as well as at elevated temperature.

Materials and methods

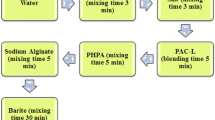
The method to prepare in-house DES, DES-WBM and finding the rheological and filtration properties of the drilling mud have been given in detail in our previous work (Rasool et al. 2021a).

Characterization techniques

FTIR

Fourier-transform infrared spectra (FTIR, Perkin Elmer) of DES-WBM (prepared under API 13B/1 guidelines) have been done to assess the interaction of DES with the clay.

XRD

The wet drilling mud samples with varying concentrations of DES have been used to investigate the intercalation of DES into the clay layers by using X-ray diffraction (XRD) analysis. The XRD peaks have been obtained by utilizing Benchtop X-ray diffractometer (D2 phaser) operating at 45 kV and 40 mA with Cu Kα radiation (λ = 1.54059 Å). Bragg’s equation was then applied to find the d-spacing. Moreover, the minerology of dry sodium bentonite as well as its d-spacing is also found out by using XRD analysis.

Mean crystalline size analysis

The broadening of peak in XRD analysis can also be used to estimate the ordered mean crystalline size using Scherrer equation

$${\varvec{\tau}}=\frac{{\varvec{K}}{\varvec{\lambda}}}{{\varvec{\beta}}{\varvec{cos}}{\varvec{\theta}}}$$
(1)

where \({\varvec{\tau}}\) is mean ordered crystalline size which may be equal or smaller than the grain size, K = Scherrer’s constant which is equal to 0.9, \({\varvec{\beta}}\) is FWMH, i.e. the line broadening at half the full intensity, and \({\varvec{\theta}}\) is the Bragg’s angle.

The crystalline size obtained from Eq. (1) may not be the true representation of numerical value of particle size, but it gives a generic idea about the trend in the overall size of the particle (Miranda and Sasaki 2018).

Zeta potential

The diluted drilling mud samples were used to measure zeta potential. ZP (zeta potential) of the dispersion was computed by Malvern Zetasizer Nano ZSP.

Rheological modelling and shear thinning behaviour

Rheological modelling is very significant in drilling fluid calculations because it helps in anticipating the behaviour of drilling fluid in dynamic conditions.

In this study, rheometer (DHR1) has been used to find shear stress and dynamic viscosity of DES-WBM at shear rates between 1.48 and 1200 s−1 at 25 °C, 100 °C. Drilling fluid shows non-Newtonian behaviour in which the viscosity changes with shear rate. There are three main models that are generally used to model the behaviour of the drilling mud (Moghaddam and Saadatabadi 2020).

  1. 1)

    Bingham Plastic Law (B.P.L)

  2. 2)

    Power Law (P.L)

  3. 3)

    Herschel–Buckley Model or Yield Power Law (Y.P.L)

The details and mathematical calculation of all these models can be found in the work of Folayan (2017) (Folayan et al. 2017). The best fit model is determined by curve fitting using two parameters mentioned below as Eqs. (2) and (3):

  • M.P.E. (Mean percentage error) 2. Standard deviation (S.D)

$${\varvec{M}}.{\varvec{P}}.{\varvec{E}}.=\frac{100}{n}\sum_{t=1}^{n}\frac{At-Ft}{At}$$
(2)

where At is the actual value where \({F}_{t}\) is the forecasted value.

$${\varvec{\sigma}}=\sqrt{\frac{\sum {\left({x}_{i}-{\overline{x} }_{i}\right)}^{2}}{N}}$$
(3)

where \(\sigma \) is standard deviation, \({x}_{i}\) is each value from the data set, \({\overline{x} }_{i}\) is mean of the whole population and N is the size of the population.

Results and discussion

Minerology of dry sodium bentonite (Clay)

The X-ray diffraction analysis was used to find the mineralogical composition of clay. Table 1 shows the mineralogical quantification of clay. The clay contains 47% smectite group which further had 88.6% of Montmorillonite. The Montmorillonite is mainly comprised of tetrahedral and octahedral sheets alumina and silica which has the dominant percentage of silica (Uddin 2018).

Table 1 Bentonite composition
Full size table

FTIR analysis of DES based mud

In FTIR spectrum, the y-axis represents % transmittance which shows the intensity of the Infrared radiation with respect to the reference. Low transmittance percentage means that there are huge number of bonds whose vibrational energies correspond to the incident light and reverse is true for high transmittance percentage. Also, the x-axis shows wave number which corresponds to a particular functional group. The change in wave number corresponds to the change in electronegativity difference which depicts the formation of a bond (Nandiyanto et al. 2019). Generally, the clay (Na-MMT) contains dominant percentage of silica and alumina in its composition which are represented by peaks 1032 cm−1 and 634.3 cm−1, respectively (Majdan et al. 2005).

FTIR spectrum of blank/base mud sample and DES-based samples shows DES didn’t show any affinity towards silica mineral as there hasn’t been any change in wave number 1032 cm−1 (silica) for base sample as well as DES-based samples. The change in wavenumbers from 634.3 to 648.4 cm−1 (0.1% DES), 632.3 cm−1 (0.5% DES) and 605 cm−1 (1% DES) shows the interaction between clay (alumina mineral) and added DES as shown in Fig. 1. The irregular decrement and increment are due to the different population of bonds present in different percentages of DES.

Fig. 1
figure 1

FTIR spectra DES-PC:Gly-based mud at various conc

Full size image

This FTIR confirms that DES has shown affinity towards clay surface by bonding onto it. However, the phenomenon of intercalation will be confirmed by XRD analysis (Seidl et al. 2017).

D-spacing analysis of DES based mud

XRD analysis of dry Na-Bt (sodium bentonite), base mud (hydrated Na-Bt) and DES-based mud samples in terms of d-spacing proved to be very conclusive. D-spacing is an important factor in deciding if any added solvent will have any affinity towards clay or not (Manoratne et al. 2017). D-spacing is a function of clay layer and interlayer cations, e.g. kaolinite has no interlayer cations; thus, its d-spacing value will be less than smectite which has inter-layer cations present (Ahmad et al. 2019). The addition of water hydrates the cation, thus causing an increase in d-spacing values (Moore and Hower 1986).

For wet drilling mud samples, water is present between the alumino-silicate layers, and if the added solvent possesses more affinity towards clay than water, it will expel the water and hydrated cations out of the clay layers while decreasing the d-spacing (Jia et al. 2019; Weichao et al. 2021).

XRD results show d001 of the dry Na-Bt came out to be 9.92 Ao which increased to 18.01 Ao after adding water (base sample) as shown in Fig. 2. The addition of DES decreased the d-spacing to 14.756 Ao at 0.1%. This further decreased to 13.45 Ao at 0.5%. It became nearly constant at 1% DES which means that DES can’t replace the water from between alumino-silicate layers anymore.

Fig. 2
figure 2

d-spacing analysis of Dry Na-Bt, base sample and DES-based mud

Full size image

Effect of DES on average grain size of clay

The average grain size of the clay particles has been found to understand the effect of DES on clay granules using method mentioned in Sect. 2.1.2.1. From Table 2, it can be seen that the average grain size of the clay increases from 336 to 434.81 nm when it is hydrated which grdually decreases on addition of DES. The base sample conatins water present between the alluminio-silicate layers which is explelled on the addition of DES into the mud slurry. This expulsion of water between the clay layers indicates that DES shows more affinity towards clay than water, hence expelling water from the clay layers.

Table 2 Effect of DES on mean clay size
Full size table

The results of avegare grain size are in accordance with the d-spacing calculated for dry Na-Bt, wet mud slurry and DES-based mud samples.

Zeta potential

Zeta potential is an important parameter in dictating the stability of the dispersion in any colloidal. The magnitude of the zeta potential shows the electrostatic repulsion between same sizes particles in any colloidal. When the zeta potential is small, the attractive forces may overcome the repulsive forces which will result into the flocculation of the dispersion, thus disrupting the stability of the colloidal. So, the dispersions with small zeta potential values tend to flocculate while the higher values of Z.P. will tend to avoid the flocculation thus making the colloidal more stable.

In this research, zeta potential of the base mud and DES-based mud samples has been measured. The colloidal is said to be stable when its zeta potential value is higher than 30 mV as tabulated in Table 3. From the results, it can be seen that the base mud sample is stable.

Table 3 Relation between zeta potential values and stability (Kumar and Dixit 2017)
Full size table

For potassium carbonate-based DES, it can be seen that the dispersion becomes more stable with the addition of DES. However, at 0.5%, the zeta potential value rose to −42.9 mV which indicates at this higher value the solution of dispersion will suppress aggregation thus conferring good stability to the colloidal as shown in Fig. 3.

Fig. 3
figure 3

Zeta potential of PC:Gly-based mud at various conc

Full size image

Discussion on mechanism behind DES as a drilling fluid additive

Mechanism behind improvement in rheological properties

Sodium bentonite (Na-Bt) possesses a specific face to edge structure in which face is attracted to the edge giving rise to a special ‘house of card’ structure. This structure is responsible to grant specific properties to the drilling mud suspension. The DES attaches/bonds to the clay surface and intercalates into clay layers decreasing the d-spacing as shown in Fig. 4 which hinders the so-called face and edge surfaces to attract each other and formulate the ‘house of card’ structure.

Fig. 4
figure 4

Illustration of effect of PC:Gly-DES on intercalation and average gran size of mud

Full size image

From Fig. 4, it can be seen that the d-spacing increases when dry Na-Bt is added into water as water intercalates between clay layers increasing the d-spacing. The addition of DES expels water between the hydrated clay layers and keeps on intercalating till the maximum exchange has occurred causing a decline in d-spacing values.

This attraction between Na-Bt and DES disturbs the inherent structure of Na-Bt dispersion which changes the yield point and viscosity of the mud (Rasool et al. 2021b).

Mechanism behind improvement in filtration properties

It is desirable to design a mud slurry which will give low permeable mud cakes which indicates good filterability. Relatively, smaller grain particles give good filtration properties because their compacted structure offers less permeability which improves the filtration behaviour (Zhang 2017). Moreover, the filtration behaviour of drilling mud is strongly controlled by its ability to flocculate, dispersed and deflocculated. The advantageous scenario is when the Na-Bt particles in the slurry are dispersed and deflocculated as the small clay particles will offer low porosity and permeability (Kelessidis et al. 2007).

From Table 2 and Fig. 4, it can be seen that the addition of DES in the mud slurry decreases the average grain size of bentonite. Moreover, Fig. 3 shows how the addition of DES increases the zeta potential on clay surface which hinders its ability to flocculate, thus giving a good dispersion. Thus, the addition of the DES in the mud slurry disperses the clay particles which reduce the permeability and porosity of the filter cake, thus improving the overall filtration behaviour of the drilling mud (Feng et al. 2021).

Rheological modelling and shear thinning behaviour of mud

It is very important to find the right rheological model to exactly simulate the behaviour of drilling mud under dynamic conditions. M.P.E. and standard deviations (Eqs. 2 and 3) of all three rheological models have been determined for curve fitting as shown in Figs. 5, 6, 7, 8, 9, 10, 11, 12. Table 4 shows that the base sample follows power law while DES-based mud follows Y.P.L (Herschel–Buckley model) at 25 °C and 100 °C which is the best model because it incorporates the yield stress even at lower shear rates.

Fig. 5
figure 5

Shear rate vs shear stress for base sample at 25 °C

Full size image
Fig. 6
figure 6

Shear rate vs shear stress for 0.1% PC:Gly-based sample at 25 °C

Full size image
Fig. 7
figure 7

Shear rate vs shear stress for 0.5% PC:Gly-based sample at 25 °C

Full size image
Fig. 8
figure 8

Shear rate vs shear stress for 1% PC:Gly-based sample at 25 °C

Full size image
Fig. 9
figure 9

Shear rate vs shear stress for base sample at 100 °C

Full size image
Fig. 10
figure 10

Shear rate vs shear stress for 0.1% PC:Gly-based sample at 100 °C

Full size image
Fig. 11
figure 11

Shear rate vs shear stress for 0.5% PC:Gly-based sample at 100 °C

Full size image
Fig. 12
figure 12

Shear rate vs shear stress for 1% PC:Gly-based sample at 100 °C

Full size image
Table 4 Rheological curve fitting
Full size table

Shear thinning behaviour

It is important for drilling mud to show thixotropic behaviour such as varying viscosity with time in order to perform certain functions such as circulation and cutting transportation. The current research shows that DES-based mud exhibits predictable shear thinning behaviour as shown in Figs. 13 and 14. The effect of elevated temperature on shear thinning behaviour of the mud is shown in Fig. 14.

Fig. 13
figure 13

Shear thinning behaviour of DES-based mud at 25 °C

Full size image
Fig. 14
figure 14

Shear thinning behaviour of DES-based mud at 100 °C

Full size image

The elevated temperature causes a decrement in dynamic viscosity due to decrease in intermolecular attraction. However, the DES-based mud retains its shear thinning behaviour at elevated temperature.

Conclusion

  1. 1.

    Potassium carbonate-based DES is successful in improving rheology as well as the filtration behaviour of the mud.

  2. 2.

    Potassium carbonate-based DES interacted with clay and successfully intercalated between clay layers, reducing d-spacing which modified its rheology.

  3. 3.

    XRD showed that average grain size decreases with the addition of DES.

  4. 4.

    The smaller grain size will result into lesser permeable and porous mud cake. Moreover, the higher zeta potential values will hinder the clay particles to flocculate which will result into a better dispersion and thus improved filtration behaviour.

  5. 5.

    PC-based DES follows Herschel–Buckley’s model and exhibits good shear thinning behaviour even at an elevated temperature of 100 °C.