Introduction

The oil density at the bubble point is an important property that is required in reservoir engineering calculations and in engineering design for oil production, fluid transportation, surface processing and material balance calculations. The oil density is defined as the mass per unit volume at a specified pressure and temperature.

$$ \rho_{{\text{o}}} = \frac{{m_{{\text{o}}} + m_{{\text{g}}} }}{{v_{{\text{o}}} + v_{{\text{g}}} }} $$
(1)

The gas-saturated oil density or bubble point oil density, ρob, is defined as the mass per unit volume at the bubble point pressure. It is usually expressed in terms of lb/ft3 or g/cm3. Oil specific gravity or oil relative density relates the density of oil to that of the density of water. The conversion of oil specific gravity to oil density is:

$$ \rho_{{{\text{ob}}}} = \gamma_{{{\text{ob}}}} *\rho_{{\text{w}}} $$
(2)

For practical purposes, the water density ρw is approximately 1 g/cm3. In the oil industry, the terms density and specific gravity are often used interchangeably in absolute values even though their units are not the same.

Under a given condition, the oil density at the bubble point is calculated by the material balance equation. The material balance equation is expressed as a function of the oil specific gravity at stock tank conditions, a total solution gas oil ratio, the gas gravity and the oil formation volume factor at the bubble point pressure.

$$ \gamma_{{{\text{ob}}}} = \frac{{\gamma_{{\text{o}}} + 2.18 \times 10^{ - 4} R_{{\text{s}}} \gamma_{{\text{g}}} }}{{B_{{{\text{ob}}}} }} $$
(3)

The four parameters (γo, Rs, γg, Bob) are obtained either from separator tests of reservoir fluids or from differential gas liberation tests.

The classic works of gas-saturated oil density determination are derived mainly from the material balance equation. Standing (1947), Ahmed (1989) and McCain (1991) presented correlations for calculating the oil density at the bubble point pressure based on a material balance as described by Eq. 3, with the replacement of the bubble point oil formation volume factor, Bob by an estimate from empirical correlations. Standing and Katz (1942) presented a method to calculate the oil density at the bubble point based on the principle of an ideal solution. Rostami et al. (2012, 2013) used neural networks and Gaussian process regression to estimate the oil density.

Under the same conditions of reservoir temperature, pressure and fluid compositions, the oil density at the bubble point is unique regardless of the method used to determine its value. The bubble point oil density obtained from separator tests or from differential gas liberation tests is not the same. Therefore, to obtain trustworthy fluid properties, the need to have an optimum accurate value of oil density for data consistency is inevitable. Current industrial practice is to average oil density values obtained from differential liberation expansion and all separator tests available. No adjustment or correction is made to other PVT properties that are influenced by the selected average oil density. This practice leads to inconsistency in reservoir calculations, well testing and other calculated physical properties.

This paper presents a new calculation method that depends on the material balance for finding the oil density at the bubble point pressure. The material balance equation is mathematically manipulated to produce a straight line that passes through the origin point (0, 0). A linear least-squares regression is used to develop the optimum unique value for the oil density at the bubble point utilizing the data from all separator and differential gas liberation tests.

A consistent correction procedure of other PVT properties is introduced to reflect the unique density value. A quantitative quality control index is defined to measure the quality of PVT laboratory reports. This is achieved by utilizing the unique value of oil density at the bubble point, which is usually ignored.

Data acquisition

Experimental data of two oil samples, volatile oil and black oil, were collected. Detailed data analysis and calculation of the volatile oil sample are presented, while the black oil data analysis and calculation are only briefly illustrated to avoid repetition.

For the volatile oil sample, experimental data from a single differential gas liberation test and three separator tests of reservoir fluid are collected. In the differential liberation experiment, reservoir liquid is brought to the reservoir temperature and bubble-point pressure. Then, the pressure gradually decreases in steps, any liberated gas is removed from the oil, and the incremental liberated gas volume and its specific gravity are recorded at each step or stage. Table 1 presents the laboratory data for the experimental differential gas liberation test.

Table 1 Experimental differential gas liberation test
Full size table

To convert the experimental differential gas liberation test data, Table 1, to differential dissolved gas data, Table 2, Eqs. 4 and 5 are used to calculate each separation stage gas/oil ratio and gas specific gravity, respectively, as shown in columns 2 and 3. The stock tank oil specific gravity, column 6, is calculated from Eq. 6, and the oil specific gravity at each pressure, column 7, is calculated from Eq. 3:

$$ R_{{{\text{s}}j}} = \mathop \sum \limits_{i} \check{R}_{{{\text{s}}_{i} }} $$
(4)
$$ \gamma_{{{\text{g}}j}} = \frac{{\mathop \sum \nolimits_{i} \check{R}_{{{\text{s}}_{i} }} \tilde{\gamma }_{{{\text{g}}_{i} }} }}{{\mathop \sum \nolimits_{i} \check{R}_{{{\text{s}}_{i} }} }} $$
(5)
Table 2 Experimental differential dissolved gas presentation
Full size table

i = j:n and j = 1:n, where Ř is the stage gas/oil ratio, γ͂ is the gas gravity, and j is the separation stage number.

$$ \gamma_{{\text{o}}} = \frac{141.5}{{{\text{api}} + 131.5}} $$
(6)

In the separator test, reservoir liquid is brought to the reservoir temperature and bubble-point pressure. Then, the liquid is flashed through one or two or three stages of separation, with the last stage at 14.7 psi and 60 °F. For the purpose of this study, the multistage separator tests are collapsed to one stage for simple illustration by utilizing the following equations, where ‘i’ indicates the separator stage:

$$ R_{{\text{s}}} = \mathop \sum \limits_{i} R_{{{\text{s}}_{i} }} $$
(7)
$$ \gamma_{{\text{g}}} = \frac{{\mathop \sum \nolimits_{i} R_{{{\text{s}}_{i} }} \gamma_{{{\text{g}}_{i} }} }}{{\mathop \sum \nolimits_{i} R_{{{\text{s}}_{i} }} }} $$
(8)

Table 3 presents the laboratory data for three separator tests of volatile oil sample fluid collapsed into a single-stage test and summarizes differential data at the bubble point pressure.

Table 3 Experimental data of separator and differential tests of the volatile oil sample
Full size table

For the black oil sample, experimental data from a single differential gas liberation test and a single separator test of reservoir fluid are collected. The choice of oil sample is dictated by the fact that in a large number of recent PVT laboratory reports, only a single flash test and a single differential liberation test are described. Table 4 presents summarized laboratory data at the bubble point pressure.

Table 4 Experimental data of separator and differential tests of the black oil sample
Full size table

Current correction procedure for oil density at the bubble point

For any separator or differential test, the following material balance equation holds:

$$ \gamma_{{{\text{ob}}_{i} }} = \frac{{\gamma_{{{\text{o}}_{i} }} + 2.18 \times 10^{ - 4} R_{{{\text{s}}_{i} }} \gamma_{{{\text{g}}_{i} }} }}{{B_{{{\text{ob}}_{i} }} }} $$
(9)

The current industry procedure for estimating the global oil density at the bubble points under reservoir conditions is one of the following two methods:

  1. 1.

    the average of all bubble point densities calculated from all separators and differential tests:

    $$ \gamma_{{{\text{ob\_global}}}} = \frac{1}{n}\mathop \sum \limits_{1}^{n} \gamma_{{{\text{ob}}_{i} }} ,\quad i = 1,2, \ldots ,n $$
    (10)
  2. 2.

    the weighted average of 50% of all separator tests and 50% of all differential tests even if there is only one differential test:

    $$ \gamma_{{{\text{ob\_global}}}} = \frac{1}{{2n_{1} }}\mathop \sum \limits_{1}^{{n_{1} }} \gamma_{{{\text{ob}}_{i} }} + \frac{1}{{2n_{2} }}\mathop \sum \limits_{1}^{{n_{2} }} \gamma_{{{\text{ob}}_{j} }} $$
    (11)

where separator tests: \(i = 1,2,\ldots ,n_{1}\), differential tests: \(j = 1,2,\ldots ,n_{2}\).

The correction method used in the industry as outlined is inconsistent with other PVT properties that were influenced by the corrected oil density, such as \(\gamma_{{\text{o}}}\) and \(\gamma_{{\text{g}}}\).

The new correction method for oil density at the bubble point

Under the same conditions of reservoir temperature, pressure and fluid compositions, the oil density at the bubble point is calculated by the material balance equation, where the total mass of oil and gas is divided by the total volume. Therefore, for any separator or differential test, the material balance equation, Eq. 9, holds. The material balance equation is mathematically manipulated to produce a straight line that passes through the origin. Equation 9 can be written as

$$ \gamma_{{{\text{o}}_{i} }} + 2.18 \times 10^{ - 4} R_{{{\text{s}}_{i} }} \gamma_{{{\text{g}}_{i} }} = \gamma_{{{\text{ob}}_{i} }} B_{{{\text{ob}}_{i} }} $$
(12)

Or

$$ y_{i} = bx_{i} $$
(13)

where

$$ y_{i} = \gamma_{{{\text{o}}_{i} }} + 2.18 \times 10^{ - 4} R_{{{\text{s}}_{i} }} \gamma_{{{\text{g}}_{i} }} $$
(14)
$$ x_{i} = B_{{{\text{ob}}_{i} }} $$
(15)
$$ b = {\text{slope}} = \gamma_{{{\text{ob}}_{i} }} $$
(16)

The objective of this study is to develop a method to determine the optimum value for oil density at the bubble point by utilizing all values of oil density obtained from all available separators and differential tests. Therefore, least-squares regression is used to find the best fit.

We minimize the sum of squares of the errors or differences between measured and predicted values:

$$ \Sigma \varepsilon^{2} \left( b \right) = \mathop \sum \limits_{i} \left( {y_{i} - bx_{i} } \right)^{2} $$
(17)

Taking the derivative with respect to the unknown variable b and setting it equal to zero, we obtain

$$ \begin{aligned} \frac{{\partial \varepsilon^{2} }}{\partial b} & = \frac{\partial }{\partial b}\mathop \sum \limits_{i} \left( {y_{i} - bx_{i} } \right)^{2} = - 2\mathop \sum \limits_{i} x_{i} \left( {y_{i} - bx_{i} } \right) = 0 \\ \mathop \sum \limits_{i} x_{i} y_{i} & = b\mathop \sum \limits_{i} x_{i}^{2} \\ b & = \frac{{\mathop \sum \nolimits_{i} x_{i } y_{i} }}{{\mathop \sum \nolimits_{i} x_{i}^{2} }} \\ \end{aligned} $$

Therefore, the optimum and best value for oil density at the bubble point are

$$ \gamma_{{{\text{ob\_global}}}} = {\text{Slope}} = \frac{{\mathop \sum \nolimits_{i} x_{i } y_{i} }}{{\mathop \sum \nolimits_{i} x_{i}^{2} }} $$
(18)

Correction of oil and gas gravities at standard conditions

PVT properties that were influenced by the modification of the value of oil density at the bubble point, such as \(\gamma_{{\text{o}}}\) and \(\gamma_{{\text{g}}}\), are corrected for each separator test by introducing a correction factor as follows:

$$ \alpha_{i} = \frac{{\gamma_{{{\text{ob}}_{{\text{g}}} {\text{lobal}}}} }}{{\gamma_{{{\text{ob}}_{i} }} }}\quad i = 1,2, \ldots \left( {{\text{number}}\,{\text{of }}\,{\text{separator}}\,{\text{tests}}} \right) $$
(19)

The corrected values are

$$ \gamma_{{{\text{o}}_{i} \left( {{\text{corrected}}} \right)}} = \alpha_{i} \gamma_{{{\text{o}}_{i} }} \quad i = 1,2, \ldots \left( {{\text{number}}\,{\text{of}}\,{\text{ separator}}\,{\text{ tests}}} \right) $$
(20)
$$ \gamma_{{{\text{g}}_{i} \left( {{\text{corrected}}} \right)}} = \alpha_{i} \gamma_{{{\text{g}}_{i} }} \quad i = 1,2, \ldots \left( {{\text{number }}\,{\text{of}}\,{\text{ separator}}\,{\text{tests}}} \right) $$
(21)
$$ \gamma_{{{\text{ob}}_{{\text{g}}} {\text{lobal}}}} = \frac{{\gamma_{{{\text{o}}_{i} \left( {{\text{corrected}}} \right)}} + 2.18x10^{ - 4} R_{{{\text{s}}_{i} }} \gamma_{{{\text{g}}_{i} \left( {{\text{corrected}}} \right)}} }}{{B_{{{\text{ob}}_{i} }} }}\quad i = 1,2, \ldots \left( {{\text{number }}\,{\text{of}}\,{\text{ separator}}\,{\text{tests}}} \right) $$
(22)
$$ {\text{api}}_{{i \left( {{\text{corrected}}} \right)}} = \frac{141.5}{{\gamma_{{{\text{o}}_{i} \left( {{\text{corrected}}} \right)}} }} - 131.5\quad i = 1,2, \ldots \left( {{\text{number}}\,{\text{ of }}\,{\text{separator}}\,{\text{ tests}}} \right) $$
(23)

For the differential gas liberation test, the correction factor is

$$ \alpha_{{{\text{dif}}}} = \frac{{ \gamma_{{{\text{ob}}_{{{\text{global}}}} }} }}{{\gamma_{{{\text{ob}}_{{{\text{dif}}}} }} }} $$
(24)

The corrected values are

$$ \gamma_{{{\text{o}}\_{\text{dif}} \left( {{\text{corrected}}} \right)}} = \alpha_{{{\text{dif}}}} \gamma_{{{\text{o\_dif}}}} $$
(25)
$$ \gamma_{{{\text{g}}_{j} \left( {{\text{corrected}}} \right)}} = \alpha_{{{\text{dif}}}} \gamma_{{{\text{g}}_{j} }} \quad j = 1,2, \ldots \left( {{\text{number }}\,{\text{of }}\,{\text{differential}}\,{\text{stages}}} \right) $$
(26)
$$ {\text{api}}_{{{\text{dif }}\left( {{\text{corrected}}} \right)}} = \frac{141.5}{{\gamma_{{{\text{o\_dif }}\left( {{\text{corrected}}} \right)}} }} {-}131.5 $$
(27)
$$ \gamma_{{{\text{op}}_{j} }} = \frac{{\gamma_{{{\text{o}}_{{{\text{dif }}\left( {{\text{corrected}}} \right)}} }} + 2.18x10^{ - 4} R_{{{\text{s}}_{j} }} \gamma_{{{\text{g}}_{j} \left( {{\text{corrected}}} \right)}} }}{{B_{{{\text{op}}_{j} }} }}\quad j = 1,2, \ldots \left( {{\text{number}}\,{\text{of}}\,{\text{differential}}\,{\text{stages}}} \right) $$
(28)

Development of a quality control index for separator and differential tests

The fitted line of oil density at the bubble point is forced to pass through the origin point (0, 0). The assumption here is that a mass of zero volume should have a density of zero. This assumption leads to devising a quality control index by calculating how far the test coordinates are from the fitted line. The following equation represents the quality control index for test i:

$$ {\text{QCI}}_{i} = 100\left( {1 - \frac{{\left( {\frac{{ y_{i} - \hat{y}_{i } }}{{y_{i} }}} \right)^{2} }}{{\mathop \sum \nolimits_{j = 1}^{n} \left( {\frac{{ y_{j} - \hat{y}_{j } }}{{y_{j} }}} \right)^{2} }}} \right) $$
(29)

where ŷ is the predicted value of the dependent variable y in the regression equation. It is the average value of the response variable.

$$ \hat{y}_{j } = bx_{i} , \quad i = 1,2, \ldots ,n $$
(30)

A quality control index, QCI, of 100 is a perfect test (separator or/and differential). The index is relative to all tests performed on the same sample anchored at the point of zero–zero origin.

Results and discussion

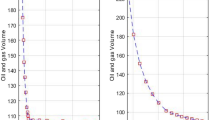
For the volatile oil sample, the optimum value for oil density at the bubble point is obtained by least-squares regression of the separator and differential test data, as shown in Table 5 and Fig. 1. The optimum value for oil specific gravity at the bubble point is calculated by Eq. 18 as follows:

$$ b = {\text{Slope}} = \frac{14.1491 }{{30.9232 }} = 0.45755594 $$
Table 5 Optimum global oil specific gravity calculation for the volatile oil sample
Full size table
Fig. 1
figure 1

Linear least-squares fit for the bubble point oil specific gravity

Full size image

The original data of the separator and differential tests at the bubble point are summarized in Table 3. The corrections after determining the optimum oil specific gravity at the bubble point are presented in Table 6.

Table 6 Modified data of separator and differential tests at the bubble point for the volatile oil sample
Full size table

Figure 2 presents the original oil specific gravity data obtained from the separator and differential tests. The current methods and the new method are also shown in the figure for comparison purposes.

Fig. 2
figure 2

Oil density at the bubble point for the volatile oil sample

Full size image

Columns 3, 5, 6 and 7 of Table 2 are modified by Eqs. 26, 27, 6, and 28, respectively, to generate the corrected differential dissolved gas data (Table 7).

Table 7 Corrected differential dissolved gas data
Full size table

Equation 29 is applied to calculate the quality index for every separator and differential test, where Fig. 3 and Table 6 show their numerical values.

Fig. 3
figure 3

Quality control index for the volatile oil sample

Full size image

For the black oil sample, the optimum value for oil density at the bubble point is obtained by least-squares regression. The original data of the separator and differential tests at the bubble point are summarized in Table 4. The correction after obtaining the optimum oil specific gravity at the bubble point is presented in Table 8.

Table 8 Modified data of separator and differential tests at the bubble point for the black oil samples
Full size table

Figure 4 presents the original oil specific gravity data obtained from the separator and differential tests. The current methods and the new method are also shown in the figure for comparison purposes.

Fig. 4
figure 4

Oil density at the bubble point for the black oil sample

Full size image

The correction of the oil density at the bubble point is inevitable whether the oil sample is black or volatile and whether the available tests are single or multiple. A comparison of the correction methods of the bubble point oil density for the two oil samples investigated is shown in Table 9.

Table 9 Comparison of correction methods
Full size table

In summary, a new smoothing method for the oil density at the bubble point based on a material balance is presented. This method yields an optimum unique oil density value at the bubble point. This method reflects other PVT properties; therefore, the PVT report becomes consistent across all experimental tests, namely differential, separators, liquid phase density, mixture density and specific volume. After adjustments, all separator and differential tests produce exactly the same value of density at the bubble point, whereas current methods fail to achieve a unique value for bubble point oil density. A major enhancement for quality control is performed within each PVT experiment and consequently observed among all tests.

Conclusion

The following conclusions were drawn from this study.

  • A new method based on material balance is introduced to determine the best value for oil density at the bubble point.

  • A new correction procedure is introduced to adjust PVT properties that are influenced by the correction of oil density at the bubble point, such as gas specific gravity and oil specific gravity. This correction guarantees that the oil density at the bubble point is the same whether separator or differential data are used for calculation.

  • A quantitative quality control index is defined and applied to measure the quality of the separator and differential tests of the PVT laboratory report.