Integrated optimum design of hydraulic fracturing for tight hydrocarbon-bearing reservoirs

Abstract

Although hydraulic fracturing is not a new technology, it has not yet been implemented in the United Arab Emirates. Abu Dhabi National Oil Company (ADNOC), the regional producer in United Arab Emirates, has set out to initiate the utilization of this treatment during year 2019. In this work, a systematic design procedure for hydraulic fracturing in tight petroleum-bearing reservoirs is proposed. The design caters for surface and subsurface flow parameters, and it is hoped to provide basic guidelines for ADNOC in this respect. The proposed design process incorporates both unified fracture design (UFD) methodology and the fracture geometry (PKN) model. Excel spreadsheets were developed and utilized to run sensitivity analysis for optimal performance and predict long-term production profiles before and after fracturing. The excel spreadsheets made are flexible in use, in the sense that they resolve issues with infinite/finite fractures, high/low surface injection rate as well as investigate for non-Darcy flow effects. Reliable published data were used to perform the necessary calculations. The results of the performance calculations have shown that it is possible to access commercial quantities of hydrocarbons from a tight reservoir. In addition, improved productivity by 15-folds and increased gas recovery of 1.02 MMMscf over the first 8 years of production can be achieved by proper hydraulic fracturing design and implementation in tight gas reservoirs. The results of calculations of non-Darcy effect revealed a threshold velocity of approximately 0.2 fps above which these effects could become significant in predicting the overall flow efficiency inside the fracture. To the authors’ knowledge, the literature has not fully addressed the hydraulic fracturing design analytically, and the methodology proposed in this work provides a complete design package which incorporates the UFD concept, the PKN model, the non-Darcy model, and long-term prediction of post-fracturing production performance, and applying the proposed approach in a case study.

Introduction

Tight carbonate reservoirs, although less well understood and believed to require higher development costs and risks than conventional reservoirs, have become an important hydrocarbon resource. Historically, tight reservoirs have been unpopular and unfavorable for geologists and reservoir engineers mainly due to difficulty associated with their development with limited commercial productive value. Well stimulation is commonly applied to boost oil or gas production and, consequently, revenues therefrom. Hydraulic fracturing is a well-stimulation technique used commonly in low-permeability rocks like tight sandstone, shale, and some coal beds to increase oil and gas flow to a well from petroleum-bearing rock formations. Hydraulic fracturing has become a critical component in the successful development of unconventional reservoirs; including tight gas, oil and gas-producing shales, and coal bed methane, such resources rely on hydraulic fracturing for commercial viability (Al-Attar and Barkhad 2018). By 2012, hydraulic fracturing had merged as $20 billion annual activity, second only to drilling budgets (Economides et al. 2015). The execution of a hydraulic fracture involves the injection of fluids at a pressure sufficiently high to cause tensile failure of the rock. At the fracture initiation pressure, often known as the “breakdown pressure,” the rock opens. As additional fluids are injected, the opening is extended, and the fracture propagates to the design fracture half length.

In recent years, new fracturing designs and techniques have been developed to enhance production of trapped hydrocarbons (Lin and Zhu 2010; Nolte and Economides 1991; Song et al. 2011). Garavand and Podgornov 2018 proposed a modified pseudo-3D model, suggesting a combination of unified fracture design (UFD), 2D fracture propagation models (PKN or KGD) and linear elastic fracture mechanic (LEFM) principle to achieve optimized fracture geometry. Based on two field studies, these authors concluded that their model is applicable to broad spectrum of multilayered oil and gas reservoirs with more accurate estimation of final fracture height and treating pressure.

A primary goal in unconventional reservoirs is to contact as much rock as possible with a fracture or a fracture network of appropriate conductivity. In designing a hydraulic fracture treatment, fracture length, width, and proppant pack permeability must be suited to the formation properties, especially formation permeability. For tight gas reservoirs specifically, which are the target formations of this work, long and narrow fractures are the most appropriate (Economides and Martin 2007). Justification of the previous statement in simple terms is as follows; in such reservoirs, the well would not produce at an economic rate without the hydraulic fracture, and thus it is not a matter of relatively improving the permeability of the matrix system, but rather creating a channel long enough to free as much trapped hydrocarbon as possible, that would otherwise have no means to flow to the well. Tight carbonate reservoirs, although less well understood and believed to require higher development costs and risks than conventional reservoirs, have become an important hydrocarbon resource. The majority of oil and gas fields in the UAE are carbonates of low matrix permeability, and hydraulic fracturing seems to be the most effective technique to develop such reservoirs.

The design of hydraulic fracturing is strongly dependent on reservoir permeability. In high-permeability reservoirs, the fracture accelerates production without impacting the well reserves, and therefore, fracturing relies on net present value economics. The characteristic curves of such reservoirs are shown in Fig. 1. In reservoirs of low or extremely low permeability (less than 1 md for oil and 0.01 md for gas), the hydraulic fracture significantly contributes to well productivity and to the well reserves, as illustrated in Fig. 2. In such reservoirs, the well would not produce an economic rate without induced fracturing. Comparing the two cases yields the following conclusion: Whether our reservoir is of moderate permeability or low permeability, there will be an increase in production rate following the treatment; as can be observed from Figs. 1 and 2 of production versus time. The difference between the two scenarios is the following; in reservoirs of moderate permeability (up to 50 md for oil and 1 md for gas), the amount of recoverable hydrocarbons remains unaffected. However, in low-permeability reservoirs, ultimate recovery will be significantly increased post-fracturing (Economides et al. 2015). Depending on the original reservoir permeability, the objective of our design would vary.

Fig. 1

The concept of production and recovery acceleration, high-permeability reservoirs (Holditch 2006)

Fig. 2

The concept of production and reserves enhancement from hydraulic fracture, low-permeability reservoirs (Holditch 2006)

In the past, hydraulic fracturing was limited to low-permeability reservoirs only, but nowadays fracturing has become an integral part of well and reservoir management rather than a decision. Every hydraulic fracture is characterized by its fracture half conductive length (x_f), dimensionless fracture conductivity (C_fD), and equivalent skin factor (S_f). Agarawal et al. (1979) and Cinco-Ley and Samaniego (1981) introduced the fracture dimensionless conductivity as

$$C_{\text{fD}} = k_{\text{f}} w/kx_{\text{f}}$$

(1)

A graphical presentation of the relationship between C_fD and S_f was presented by Cinco-Ley and Samaniego (1981) that can be used to estimate the folds of increase in productivity post-fracturing treatment. The concept of equivalent skin effect, however, only applies after pseudoradial flow is established. When pseudoradial flow emerges after bilinear and/or linear flow, the skin determined from a pressure buildup test will be the equivalent skin effect indicated in the graphical presentation of Cinco-Ley and Samaniego (1981). The same authors plotted [S_f + ln (x_f/r_w) + 0.5 ln (C_fD)] versus C_fD on a semi-log graph paper and their plot shows a minimum that appears at exactly C_fD = 1.6. They concluded that there exists one optimum conductivity that maximizes the productivity index, and this conductivity corresponds to a particular fracture width and length. It should be emphasized at this point that such hypothesis applies whenever x_f ˂˂ r_e that pseudoradial flow can occur. A methodology provided by Economides, Oligney and Valkó (2002), which assumes that for a given proppant volume, well drainage area and shape there is a fracture half length, width and conductivity that maximizes well productivity. They provided the concept of unified fracture design (UFD) which expands the above optimum productivity approach to include fracture and well drainage dimensions that will not reach pseudoradial flow before the onset of pseudosteady state. These authors developed correlations for optimum fracture dimensions in square drainage areas which will yield maximum dimensionless pseudosteady-state productivity index and as presented in Eqs. 2 through 7.

$$\begin{aligned} J_{{D\,\hbox{max} \,{\text{pss}}}} \left( {\text{Np}} \right) & = 1/\left[ {0.990{-}0.5{ \ln }\left( {\text{Np}} \right)} \right] \quad {\text{for}}\;{\text{Np}} \le 0.1 \\ & = 6/\pi {-}{ \exp }\left\{ {\left[ {0.423{-}0.311{\text{Np}}{-}0.089\left( {\text{Np}} \right)^{2} } \right]} \right. \\ & \quad /\left. {\left[ {1 + 0.66{\text{Np}} + 0.015\left( {\text{Np}} \right)^{2} } \right]} \right\} \quad {\text{for}}\;{\text{Np}} > 0.1 \\ & = 6/\pi \quad {\text{for}}\;{\text{Np}} \ge 100 \\ \end{aligned}$$

(2)

$$\begin{aligned} C_{{f\,{\text{Dopt}}}} & = \, 1.6 \quad {\text{for}}\;{\text{Np}} < 0.1 \\ & = 1.6 + \exp \left[ {\left( { - 0.588 + 1.48\,{ \ln }\,{\text{Np}}} \right)/\left( {1 + 0.142\,{ \ln }\,{\text{Np}}} \right)} \right] \\ & \quad {\text{for}}\;0.1 \le {\text{Np}} \le 10 \\ & = {\text{Np}}\quad {\text{for}}\;{\text{Np}} > 10 \\ \end{aligned}$$

(3)

$${\text{Np}} = \left( {2k_{\text{f}} V_{\text{f}} } \right)/\left( {kV_{\text{r}} } \right)$$

(4)

$$x_{{{\text{f}}\,{\text{opt}}}} = \left[ {\left( {k_{\text{f}} V_{\text{f}} } \right)/\left( {2C_{{{\text{f}}\,{\text{Dopt}}}} kh} \right)} \right]^{0.5}$$

(5)

$$w_{\text{opt}} \, = \,\left( {C_{{{\text{f}}\,{\text{Dopt}}}} k\,V_{\text{f}} /2k_{\text{f}} h} \right)^{0.5}$$

(6)

$$J_{\hbox{max} } = \left( {kh/141.2\,B\mu } \right)J_{{D\,\hbox{max} \,{\text{pss}}}}$$

(7)

where Np is dimensionless proppant number defined by Eq. 4. For non-square drainage areas, productivity optimization was presented by Daal and Economides (2006). They presented a set of equations similar to Eqs. 2 through 7 but modified to accommodate the drainage shapes other than the square drainage area. Their approach is appropriate for multiple hydraulic fractures intersecting a horizontal well transversely. Perkins and Kern (1961) developed a model for predicting fracture width for a fixed height vertical fracture. This model was later adjusted for laekoff and storage within fracture by Nordgren (1972) and is now known as the PKN model. The average width of the PKN fracture is expressed in Eq. 8.

$$w_{\text{avg}} = 0.3\left[ {q_{i} \mu \left( {1 - v} \right)x_{\text{f}} /G} \right]^{0.25} \left( {\pi \gamma /4} \right)$$

(8)

The PKN model is applicable for cases in which the fracture length is much larger than the fracture height (x_f≫ h_f) and fracturing fluid is Newtonian. This is ideal for the target formation which has an extremely low permeability, thus requiring long and narrow fractures that would create sufficient conductivity to maximize performance and justify cost. In Eq. (8), the term (πγ/4) is approximately equal to 0.59 and γ is a factor equal to 0.75. For non-Newtonian fracturing fluids, Eq. 9 can be used to estimate maximum fracture width.

$$ \begin{aligned} w_{\hbox{max} } = & 12\left\{ {\left( {128/3\pi } \right)\left( {n^{{\prime }} + 1} \right)\left[ {\left. {\left( {2n^{{\prime }} + 1} \right)/n^{{\prime }} } \right)} \right]^{{n^{{\prime }} }} \left( {0.9775/144} \right)\left( {5.61/60} \right)^{{n^{{\prime }} }} } \right\}^{{[1/(2n^{{\prime }} + 2)]}} \\ & \quad \times \left[ {q_{i}^{{n^{{\prime }} }} K^{{\prime }} x_{\text{f}} h_{\text{f}}^{{(1 \, - n^{{\prime }} )}} /E} \right]^{{[1/(2n^{{\prime }} + \, 2)]}} \\ \end{aligned} $$

(9)

The quantities n′ and K′ are the power-law rheological properties of the fracturing fluid. The average fracture width can be calculated by multiplying w_max by 0.628 (Economides et al. 2015).

Other important design parameters include total injection time (t_i) and volume of treatment (V_i). The approximate relationship between the volume of treatment, and the pad volume, V_pad, was provided by Nolte (1986) and Meng and Brown (1987), as expressed in Eq. 10.

$$V_{\text{pad}} = V_{i} \left[ {\left( {1 - \eta } \right)/\left( {1 + \eta } \right)} \right]$$

(10)

where η is the fluid efficiency and is determined by iterative scheme of calculations as follows. A material balance between total fluid injected, created fracture volume, V_f, and fluid leakoff, V_L, can be expressed as

$$V_{i} = V_{\text{f}} + V_{\text{L}}$$

(11)

Equation (11) is expanded to yield:

$$q_{i} t_{i} \, = \,A_{\text{f}} w_{\text{bar}} \, + \,K_{\text{L}} C_{\text{L}} \left( {2A_{\text{f}} } \right)r_{\text{p}} \sqrt {t_{i} }$$

(12)

where q_i is the injection rate in bpm, t_i is the total injection time in minutes, A_f is the fracture area in sq.ft, C_L is the leakoff coefficient in ft/min^0.5, and r_p is the ratio of the net to fracture height (h/h_f). The variable K_L is known as opening time distribution factor and defined by Nolte (1986).

$$K_{\text{L}} = 0.5\left[ {\left( {8/3} \right)\eta + \pi \left( {1 - \eta } \right)} \right]$$

(13)

$$\eta \, = \,V_{f} /V_{i}$$

(14)

Thus, the value of K_L is between 1.33 and 1.57. For a given x_f, the average hydraulic fracture width, w_bar, can be calculated using the PKN model. Equation (12), which is a quadratic equation, can be solved for t_i by trial and error. The product q_it_i is equal to the volume of treatment (pad volume plus slurry volume), V_i, and

$$t_{\text{pad}} \, = \,V_{\text{pad}} /q_{i}$$

(15)

$$t_{\text{slurry}} \, = \,t_{i} \,{-}\,t_{\text{pad}}$$

(16)

The leakoff coefficient, C_L, can be obtained from the laboratory or from a fracture calibration treatment as described by Nolte and Economides (1989). During the slurry stage of the fracturing treatment, propping agent is continuously added to the fracturing fluid at time-dependent concentrations until the total injection time is achieved. Therefore, the fracturing design should solve for proppant schedule which depends on the fluid efficiency. Nolte (1986) has shown that

$$c_{\text{p}} \left( t \right) = c_{\text{f}} \left[ {\left( {t\,{-}\,t_{\text{pad}} } \right)/\left( {t_{i} \,{-}\,t_{\text{pad}} } \right)} \right]^{\varepsilon }$$

(17)

$$\varepsilon = \left( {1 - \eta } \right)/\left( {1 + \eta } \right)$$

(18)

where c_p(t) is the slurry concentration for any time greater than t_pad, in pounds per gallon in ppg, c_f is the final slurry concentration in ppg, and the variable ε depends on the fluid efficiency defined in Eq. (18). At this point, it should be emphasized that the average fracture width predicted by the PKN model is the width created during the propagation of the fracture, and is known as hydraulic width. At the end of the fracturing job and when the surface pumps are switched off at the surface, the fracture tends to close due to the natural stresses in earth. The placement of propping agent, however, inside the fracture will only allow partial closing of the fracture which results in a final fracture width, known as propped fracture width denoted by w_p, that is a little narrower than the hydraulic fracture width. Assuming that a mass of proppant, M_p, has been injected into a fracture of half length x_f and height h_f and the proppant is uniformly distributed, then

$$M_{\text{p}} = 2x_{\text{f}} \,h_{\text{f}} \,w_{\text{p}} \left( {1 - \phi_{\text{p}} } \right)\rho_{\text{p}}$$

(19)

where the product 2x_f h_f w_p (1 − ϕ_p) represents the volume of the proppant pack and ρ_p is the density of the propping agent in lbm/cu.ft. The proppant concentration in the fracture, C_p in lb/sq.ft., may be defined as

$$C_{\text{p}} = M_{\text{p}} /2x_{\text{f}} h_{\text{f}}$$

(20)

$$w_{\text{p}} = C_{\text{p}} /\left[ {\left( {1 - \phi_{\text{p}} } \right)\rho_{\text{p}} } \right]$$

(21)

In the present work, the proposed design targets low-permeability reservoirs since they pose a challenge to the UAE oil and gas industry. The design combines the concept of UFD, total injection time, volume of treatment, proppant schedule, propped fracture width, non-Darcy flow, and long-term production behavior for a hydraulically fractured in one package.

Proposed design methodology

Design criteria and specifications

The following conditions represent the foundation of the proposed design:

• 1. Vertical well completion.

• 2. Square drainage area.

• 3. Unified fracture design is utilized to optimize the following: fracture half length, fracture width, fracture conductivity, and skin effect.

• 4. PKN model is used to estimate injection flow rate of fracturing fluid.

• 5. If dimensionless fracture conductivity is greater than 50: infinite fracture conductivity, i.e., linear flow (Poe and Economides 2000).

• 6. If dimensionless fracture conductivity is less than 50: finite fracture conductivity, i.e., bilinear flow (Poe and Economides 2000).

• 7. Infinite fracture conductivity:

  • Target: large surface area

  • Dominant parameter: x_f

• 8. Finite fracture conductivity:

  • Target: wide fracture

  • Dominant parameter: w and k_f

• 9. Computation of surface injection pressure depends on the value of injection rate. (whether it is greater than 9 bpm)

• 10. Maximum allowed injection time for efficiency purposes: 24 h.

• 11. Maximum allowed surface injection pressure for safety purposes: 5000 psi.

• 12. Maximum possible skin effect due to stimulation: − 8.5 (Flow efficiency goes to infinity at this value).

• 13. The fracturing fluid efficiency should be greater than 0.5.

• 14. The following relates formation permeability and fracture width:

  • Average fracture width is inversely proportional to the shear modulus of elasticity.

  • Shear modulus of elasticity is directly proportional to Young’s modulus of elasticity.

  • Young’s modulus of elasticity is dependent on depth.

  • As the depth increases, the rock is more consolidated thus matrix permeability decreases.

Assumptions

The following assumptions were made to simplify the construction of the design and cater for the conditions of the target formation (carbonate tight gas reservoirs):

• 1. Assumed fracture height equals reservoir height. Height containment is due to the natural stress contrast resulting from the difference in Poisson ratio between the investigated tight carbonate formation and surrounding shale formations.

• 2. The following range is assumed for Young’s modulus of elasticity: (a) 2E05 ˂ E ˂ E07 psi, (b) E ≈ E07 psi in deep reservoirs (narrow fracture), and (c) E ≈ 2E05 psi in shallow reservoirs (wide fracture).

• 3. For infinite fracture conductivity, pressure drop in the fracture is assumed negligible.

• 4. Assumed very low value of liquid leak-off coefficient to improve design efficiency. [C_L = 0.0001 ft/(min)^1/2]

• 5. Formula of skin effect used is based on radial flow assumption. This parameter, however, is best obtained from post-fracture test analysis.

• 6. Skin effect before stimulation assumed zero. Hydraulic fracture bypasses the near-wellbore damage zone. Thus, the pretreatment skin effect has little or no impact on the post-fracture equivalent skin effect value.

• 7. Constant-percentage decline rate.

• 8. Vertical fractures are induced at depths greater than 3000 ft.

• 9. The following flow pattern is assumed for each of the mentioned cases (Figs. 3, 4):

  Fig. 3

  

  Infinite fracture conductivity [ETR → LTR]

  Fig. 4

  

  Finite fracture conductivity [ETR → MTR → LTR]

where ETR: early time region (reflecting wellbore storage and skin effects), MTR: middle time region (infinite-acting system behavior reflecting reservoir properties), LTR: late time region (reflecting boundary effects). Both figures are top views showing fracture extension into the formation. In Fig. 3, the fracture is of infinite conductivity and half-fracture length is equal to the drainage radius of the formation and thus, the pressure transient moves from ETR into LTR without going through MTR. The flow geometry is basically linear from the formation into the fracture. In Fig. 4, the fracture is of finite conductivity and half-fracture length is less than the drainage radius of the formation and thus, the pressure response exhibits ETR then MTR and finally LTR. The flow geometry is bilinear between the wellbore and fracture tip and pseudoradial between fracture tip and formation outer boundary.

Detailed proposed design procedures

• 1. Calculate formation in situ stresses, breakdown pressure, and fracture propagation pressure. The necessary equations can be found in Economides et al. (2015).

• 2. Assume values for proppant mass (M_p) for a fixed value fracture permeability (k_f) and reservoir permeability (k). Solve Eq. (18) for propped volume in the pay, V_f.

• 3. Estimate V_r using available well drainage area and formation thickness.

• 4. Calculate dimensionless proppant number; Np by Eq. (4).

• 5. Calculate maximum pseudosteady-state productivity index by Eq. (2)

• 6. Calculate C_fDopt(Np) using Eq. (3).

• 7. Calculate optimum fracture half length and width by Eqs. (5) and (6).

• 8. Verify C_fDopt(Np) value and calculate skin effect: (Cinco-Ley and Samaniego 1981).

Infinite dimensionless fracture conductivity: C_fDopt(Np)>50

$$S_{\text{f}} \approx 0.7{-}\ln \left( {x_{\text{f}} /r_{\text{w}} } \right)$$

(22)

• 9. Finite dimensionless fracture conductivity: C_fDopt(Np)≤50

  $$S_{\text{f}} \approx 1.52 + 2.31\;\log \left( {r_{\text{w}} } \right){-}1.545\;\log \left( {k_{\text{f}} w/k} \right){-}0.765\;\log \left( {x_{\text{f}} } \right)$$

  (23)

• 10. Solve PKN geometry model, Eq. (8) for injection rate, q_i.

• 11. Calculate surface injection pressure, p_si.

  $$p_{\text{si}} = p_{\text{bd}} {-}\Delta p_{\text{h}} + \Delta p_{\text{f}}$$

  (24)
  $$\Delta p_{\text{f}} = \left( {518\gamma_{{{\text{frac}}\,{\text{fluid}}}}^{0.79} q_{i}^{1.79} \mu_{{{\text{frac}}\,{\text{fluid}}}}^{0.207} /1000D^{4.79} } \right)H$$

  (25)
  $$\Delta p_{\text{h}} = 0.433\left( {\gamma_{{{\text{frac}}\,{\text{fluid}}}} } \right)H$$

  (26)

• 12. Construct detailed proppant schedule using Eq. (16).

• 13. Apply Eqs. (12, 13, and 14) to determine t_i by trial and error.

• 14. Investigate non-Darcy flow effects; Cooke (1993), Miskimins et al. (2005), Holditch and Morse (1976), Frederick and Graves (1994).

  $$q_{\text{g}} = \left\{ {\left[ {m\left( {p_{\text{avg}} } \right) - m\left( {p_{\text{wf}} } \right)} \right]kh/1424T} \right\}J_{{D\,\hbox{max} \,{\text{pss}}}}$$

  (27)
  $$B_{\text{g}} = 0.0283\,ZT/p$$

  (28)
  $$\beta = 7.89 \times 10^{10} /k_{\text{f}}^{1.6} \phi_{\text{prop}}^{0.404}$$

  (29)
  $$v = B_{\text{g}} q_{\text{g}} /2h\,w_{\text{opt}}$$

  (30)
  $$\rho_{\text{g}} = 28.96\gamma_{\text{g}} p_{\text{wf}} /RT$$

  (31)
  $$N_{{\text{Re} ,nD}} = \beta k_{\text{f}} v\rho_{\text{g}} /\mu$$

  (32)
  $$\begin{aligned} J_{nD} /J_{Do} & = \left[ {{ \ln }\,\left( {r_{\text{e}} /r_{\text{w}} } \right){-}0.75{-}{ \ln }\,\left( {0.28k_{\text{f}} w/k_{\text{r}} w} \right)} \right]/ \\ & \quad \left\{ {{ \ln }\,\left( {r_{\text{e}} /r_{\text{w}} } \right){-}0.75{-}{ \ln }\,\left[ {0.28k_{\text{f}} w/k\,r_{\text{w}} \left( {1 + N_{{\text{Re} ,nD}} } \right)} \right]} \right\} \\ \end{aligned}$$

  (33)

Equation (33) can reduced to:

$$J_{nD} /J_{\text{o}} = J_{Do} /\left[ {J_{Do} + { \ln }\,\left( {1 + N_{{\text{Re} ,nd}} } \right)} \right]$$

(34)

• 15. Based on the results, choose the best M_p value.

• 16. Repeat process, vary k_f for chosen M_p and fixed k.

• 17. Conclude the most productive and cost-effective M_p and k_f values for the design.

• 18. Predict long-term production performance as presented in the following section.

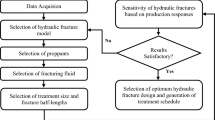
A flowchart of the proposed design methodology is presented in Fig. 5. In this chart, Chen equation provides a direct solution for the friction factor in terms of Reynolds number and pipe relative roughness. Equation 25 is used to estimate pressure drop due to friction across pipe length. It has been found that this equation loses its accuracy when the fluid injection rate exceeds 9 bpm (Economides et al. 2015).

Fig. 5

Block diagram of proposed design methodology

Applying Eqs. (27 through 32), a series of calculations were performed to investigate the effect of non-Darcy flow in hydraulically induced fractures. The results of these calculations are presented in Figs. 6 and 7, in which the flow velocity in fps is plotted versus pressure drop in psi with correlating parameters x_f and k_f, respectively. It can be observed that in both plots and regardless of the value of correlating parameter, the relationship is nonlinear and that the dramatic increase in flow velocity takes place at pressure drop approximately equals to 3700 psi. The inflection point in both plots designates threshold conditions in terms of flow velocity and corresponding pressure drop. The threshold velocity is estimated by drawing an asymptote through the higher velocity data points and it begins at approximately 0.2 fps. At velocities higher than 0.2 fps, the non-Darcy flow effects become significant and ignoring these would result in significant errors in the calculations of fracture conductivity.

Fig. 6

Threshold velocity: flow velocity versus. pressure drop; x_f as a correlating parameter

Fig. 7

Threshold velocity: flow velocity versus pressure drop; k_f as a correlating parameter

Predicting long-term production behavior

For an infinitely conductive fracture, with the fractured well in the middle of a rectangular bounded reservoir, Wattenbarger et al. (1998) provided a general formula for the dimensionless production rate:

$$1/q_{\text{D}} = \left( {\pi /4} \right)\left( {y_{\text{e}} /x_{\text{f}} } \right)/\left\{ {\sum_{n \, = 1 \to \infty } \exp \left[ {{-}\left( {2n{-}1} \right)^{2} \pi^{2} t_{\text{Dye}} /4} \right]} \right\}$$

(35)

where y_e is the distance from the fracture to the drainage boundary in the direction perpendicular to the fracture, and the dimensionless time is

$$t_{\text{Dye}} \, = \,\left( {x_{\text{f}}^{2} /y_{\text{e}} } \right)^{2} t_{Dxf}$$

(36)

$$t_{Dof} \, = \,0.000 2 6 3 7kt/\phi \,\mu \,c_{\text{t}} x_{\text{f}}^{ 2}$$

(37)

Equation (35) can be replaced by two equations and as follows:

• (a) For t_Dye ˂ 0.25: Transient (early time region; ETR);

  $$1/q_{\text{D}} \, = \,\left( {\pi /2} \right)\,\left( {\pi t_{Dxf} } \right)^{0.5}$$

  (38)

• (b) For t_Dye > 1.25: Pseudosteady state (late time region; LTR-Exponential Depletion)

  $$1/q_{\text{D}} = \left( {\pi /4} \right)\left( {y_{\text{e}} /x_{\text{f}} } \right)\,\exp \,\left( {\pi^{2} t_{\text{Dye}} /4} \right)$$

  (39)

For 0.25 > t_Dye > 1.25 Eq. (35) must be used.

The relationship between q_g in Mscf/d and q_D is:

$$q_{\text{g}} = kh\left[ {m\left( {p_{i} } \right){-}m\left( {p_{\text{wf}} } \right)} \right]/\left[ {1424 \, \left( {1/q_{D} } \right)} \right]$$

(40)

Detailed design calculations

The design methodology described earlier and illustrated in Fig. 5, was implemented in a vertical gas well completed in a carbonate reservoir with low permeability. The data pertinent to the well and the reservoir are listed in Table 1. A complete sample of calculations is presented in “Appendix A” including schedule of proppant as illustrated in Fig. 8. Three scenarios were considered and as listed in Table 2. The last five columns in Table 2 highlights the optimum values of design parameters for each scenario which meet all design criteria. The relationship between optimum design parameters and formation permeability can be deduced from Table 2. A sample of calculations for predicting long-term production profile before and after fracturing is shown in “Appendix B”. Since the fracture half length (x_f) and half of the length (0.5 x_e) of square drainage area are approximately equal, therefore the flow geometry is basically linear (for C_fD > 50).

Table 1 Stimulation data

Fig. 8

Proppant schedule

Table 2 Implementation of proposed design in the selected three scenarios

The time this flow geometry lasts is calculated by Eq. (41), and the production profile is predicted by Eq. (42) (Kelkar 2008).

$$t_{{{\text{lf}}\,{\text{end}}}} = 438\,\phi \,\mu \,c_{\text{t}} x_{\text{f}}^{2} /k$$

(41)

$$Q_{\text{gsc,L}} = \left\{ {\left. {\left[ {m\left( {p_{i} } \right){-}m\left( {p_{\text{wf}} } \right)} \right]\left( {h/T} \right)\left( {x_{{{\text{f}}\,{\text{op}}t}} } \right)\left( {k\phi \mu c_{\text{t}} } \right)^{0.5} \left( t \right)^{{{-}0.5}} } \right\}} \right./64.35$$

(42)

The results of calculations of production profile over this period when linear flow geometry dominates are listed in Table 3. For the same reason, there will be no middle time region and pressure transient enters directly into pseudosteady state without going through infinite-acting system behavior. Predicting long-term production profile for times greater than t_{lf end} is achieved by Eq. (43) (Kelkar 2008) and the results of calculations are illustrated in Table 4.

Table 3 Results of calculations of long-term post-fracturing production profile; early time linear flow transient state

Table 4 Results of calculations of long-term post-fracturing production profile; late time radial flow pseudosteady state

$$ Q_{\text{gsc,pss}} = \left\{ {703*10^{{{-}6}} \left[ {m\left( {p_{\text{avg}} } \right){-}m\left( {p_{\text{wf}} } \right)} \right]kh} \right\}/T\left[ {0.5\;\ln \,\left( {10.06A/C_{\text{A}} r_{\text{w}}^{2} } \right)\,{-}\,0.75 + S} \right] $$

(43)

Results and discussion

The proposed design methodology was implemented in three scenarios representing three reservoir permeabilities of 0.01, 0.1, and 1 md, respectively. The data used in all calculations are listed in Table 1. For each scenario, the proppant mass (M_p) was varied between 50,000 lbm and 500,000 lbm, and for each proppant mass, 11 key design parameters were calculated. These parameters include: maximum dimensionless pseudosteady-state productivity index, optimum fracture half length, optimum propped fracture width, optimum fracture conductivity, equivalent skin factor, fracturing fluid injection rate, total injection time, maximum surface injection pressure, fluid efficiency, gas production rate, and dimensionless productivity ratio with and without non-Darcy flow effects. The results of one scenario are presented in Table 5 and it can be observed that the best choice would be for M_p= 200,000 lbm because corresponding surface injection pressure, total injection time, fracturing fluid efficiency, and fluid injection rate meet the design criteria set out earlier in this paper. Qualitatively, this value of M_p is cost effective in comparison with the higher values in Table 5 (figures highlighted in red color do not meet design criteria). Similarly, the best choices of M_p for the other two scenarios were concluded and the results are listed in Table 2. The last column in Table 2 illustrates the ratio J_{Dmax pss post-frac}/J_{D pss pre-frac} for the three selected scenarios and it can be observed that this ratio is highly dependent on the reservoir permeability. A maximum value of 15 for this ratio has been obtained for k = 0.01 md, which is indicative of the effectiveness of hydraulic fracturing treatment in tight reservoirs. The results of the three selected scenarios also show that hydraulic fracturing is less effective in higher permeability reservoirs. The effect of non-Darcy flow was included in the proposed design methodology using Eqs. (26 through 33). To confirm whether non-Darcy effect is important, sensitivity analysis was performed in terms of flow velocity versus pressure drop inside the fracture with fracture half length and fracture permeability as correlating parameters as shown in Figs. 6 and 7, respectively. The resulting relationships shown in both figures exhibit a deflection from linear to nonlinear behavior which takes place at flow velocity of nearly 0.2 fps. In this paper this velocity is called threshold velocity above which neglecting non-Darcy effects in the calculations of gas flow rate can result in serious errors. In addition, non-Darcy effects can be evaluated by either Eq. (32) or its equivalent Eq. (33), through the calculation of the ratio J_nD/J_o. A ratio of one indicates negligible non-Darcy effects, while a ratio less than one is indicative of some degree of non-Darcy flow effects. These two criteria, namely, threshold velocity and J_nD/J_o, have been considered in the proposed design methodology. The last part of the discussion addresses the prediction of long-term production profiles. The results of calculations of this part are presented in Tables 3 and 4 for early time linear flow geometry-transient state and late-time radial flow geometry pseudosteady state, respectively. Detailed calculations can be found in “Appendix B”. Low-permeability reservoirs are commonly produced with p_wf held constant, so that the well boundary condition for the well production models illustrated in Eqs. (34 through 42) apply (Economides et al. 2015). Consequently, in this work, the bottom-hole flowing pressure was held constant at 2500 psi. The pre-fracturing predictions of production profile over a period of 8 years have shown a significant drop in gas production rate from 92.57 to 8.45 Mscf/d (Fig. 9) and cumulative gas recovery of 0.23 MMMscf at the end of the eighth year. Since there has been no production history available for this case, a constant nominal daily decline rate D_d = 0.000417 day⁻¹ was assumed to perform these predictions. The results of post-fracturing predictions for the same period of 8 years indicated a significant drop of gas flow rate from 1500 to 200 Mscf/d (Fig. 10) and a cumulative gas recovery of 1.25 MMMscf. These results are in line with the qualitative field observations shown in Figs. 1 and 2 (Holditch 2006), and that hydraulic fracturing increased the productivity of this particular case 15-folds and increased the cumulative gas recovery by 1.02 MMMscf.

Table 5 Summary of results for k = 0.01 md

Fig. 9

Long-term pre-fracturing production profile

Fig. 10

Long term post-fracturing production profile

Summary and conclusions

The design methodology proposed in this work encompasses the UFD concept and PKN geometry model. Spread sheets have been prepared to accommodate the necessary design calculations using published data. Three scenarios of reservoir permeability have been selected to investigate the effectiveness of hydraulic fracturing in tight formations. Based on the results obtained in this work, the following conclusions may be drawn.

• 1. A simple design methodology is presented which makes it possible to compute key parameters in hydraulic fracturing treatment with the limited tools and data.

• 2. Application of the proposed design package to three scenarios of tight gas reservoirs have shown that hydraulic fracturing is most effective when k = 0.01 md and corresponding optimum M_p and maximum ratio J_{Dmax pss post-frac}/J_{Dpss pre-frac} have been found equal to 200,000 lbm and 15, respectively. Certainty in enhancement of gas production justifies initial investment considering the folds of increase in production.

• 3. Sensitivity analysis of non-Darcy flow effects revealed a threshold flow velocity of 0.2 fps. For any flow velocity below this limit, the non-Darcy flow effects can be neglected from the calculations of gas flow rate and J_nD/J_o = 1.0.

• 4. Predictions of production profiles have shown significant improvement in gas production rate and gas recovery over the 8 year time period at 15 folds and 1.02 MMMscf, respectively.

Appendices

Appendix A

See Table 5 and Fig. 8.

Sample Calculations

$$M_{\text{p}} = 200,000\,{\text{lbm}};k_{\text{f}} = 220\,{\text{Darcy}};k = 0.01\,{\text{md}}.$$

$$\sigma_{\text{v}} = \left( {\rho_{\text{ovbd}} H} \right)/144 = 165H/144 = 1.15H\,{\text{psi}}$$

$$G_{\text{w}} = \rho_{\text{w}} /144 = 64/144 = 0.43\,{\text{psi/ft}}$$

$$p_{\text{p}} = G_{\text{w}} *H = 0.43H\,{\text{psi}}$$

$$\sigma_{\text{v}}^{{\prime }} = \sigma_{\text{v}} {-}\alpha \,p_{\text{p}} = 1.15H{-}0.72*0.43H = 0.84H\,{\text{psi}}$$

$$\sigma_{\text{H}} = v/\left( {1 - v} \right)\sigma_{\text{v}} = 0.25/\left( {1 - 0.25} \right)\left( {0.84H} \right) = 0.28H\,{\text{psi}}$$

$$\sigma_{H,\hbox{min} } = \sigma^{{\prime }}_{H} + \alpha \,p_{\text{p}} = 0.28H + 0.72*0.43H = 0.59H\,{\text{psi}}$$

$$\begin{aligned} \sigma_{H\hbox{max} } & = \sigma_{H\hbox{min} } + \sigma_{\text{tect}} = 0.59H + 2000 \\ & = 0.59\left( {10,000} \right) + 2000 = 7,900\,{\text{psi}} \\ \end{aligned}$$

$$\begin{aligned} p_{\text{bd}} & = 3\sigma_{H\hbox{min} } {-}\sigma_{H\hbox{max} } + T{-}p_{\text{p}} = \left( 3 \right)0.59\left( {10,000} \right) \\ & \quad {-}7900 + 1000 - 0.43\left( {10,000} \right) = 6,500\,{\text{psi}} \\ \end{aligned}$$

$$p_{\text{pg}} = p_{\text{bd}} {-}T = 6500{-}1000 = 5,500\,{\text{psi}}$$

$$\sigma^{{\prime }}_{{H({\text{shale}})}} = v/\left( {1 - v} \right)\sigma^{{\prime }}_{\text{v}} = 0.27/\left( {1 - 0.27} \right)\left( {0.84H} \right) = 3,107\,{\text{psi}}$$

$$\sigma_{{H,\hbox{min} ({\text{shale}})}} = \sigma^{{\prime }}_{H} + \alpha \,p_{\text{p}} = 3106.85 + \left( {0.72} \right)0.43H = 6,203\,{\text{psi}}$$

$$\Delta p = \sigma_{{H,\hbox{min} ({\text{shale}})}} - \sigma_{H,\hbox{min} } { = }6202.85{-}5900 = 303\,{\text{psi}}$$

$$G_{\text{ov}} = \rho_{\text{ovbd}} /144 = 265/144 = 1.15\,{\text{psi/ft}}$$

$$\begin{aligned} H_{\text{critical}} & = \left. {\left( { - G_{\text{ov}} *\Delta H} \right)/\left( {\left( {\sigma_{H,\hbox{min} } } \right) - \sigma_{\text{v}} } \right)/H} \right) \\ & = \left( { - 1.15*2,000} \right)/\left( {\left( {5900 - 11,500} \right)/10,000} \right) = 4107\,{\text{ft}} \\ \end{aligned}$$

$$p_{\text{prpt}} = \gamma_{\text{prpt}} \times \rho_{\text{w}} = 2.65 \times 62.4 = 165.36\,{\text{lb/cf}}$$

$$\begin{aligned} V_{f} & = \left( {h/h_{\text{f}} \left( {M_{\text{p}} } \right)} \right)/\left( {\rho_{\text{prpt}} \left( {1 \, - \emptyset_{\text{prpt}} } \right)} \right) \\ & = \left( {100/100\left( {200,000} \right)} \right)/\left( {165.36\left( {1 - 0.38} \right)} \right) = 1950.78\,{\text{ft}}^{3} \\ \end{aligned}$$

$$V_{\text{r}} = Ah = 320 \times 43560 \times 100 = 1.39 \times 10^{9} \,{\text{ft}}^{3}$$

$$\begin{aligned} N_{\text{p}} & = \left( {2k_{\text{f}} V_{\text{f}} } \right)/\left( {kV_{\text{r}} } \right) = \left( {2 \times 220,000 \times 1950.78} \right)/\left( {0.01\left( {1.39 \times 10^{9} } \right)} \right) \\ & = 61.75\left( {0.1 < N_{\text{p}} < 100} \right) \\ \end{aligned}$$

$$\begin{aligned} J_{\text{Dmax,pss}} & = 6/\pi - \exp \left\{ {\left[ {0.423{-}0.311N_{\text{p}} {-}0.089\left( {N_{\text{p}} } \right)^{2} } \right.} \right./ \\ & \quad \left. {\left[ {1 + 0.667N_{\text{p}} + \, 0.015 \, \left( {N_{\text{p}} } \right)^{2} } \right]} \right\} \\ & = 6/\pi {-}\exp \left( {\left( {0.423 - 0.311\left( {61.75} \right) - 0.089\left( {61.75} \right)^{2} } \right)} \right./ \\ & \quad \left. {\left( {1 + 0.667\left( {61.75} \right) + 0.015\left( {61.75} \right)^{2} } \right)} \right) = 1.883 \\ \end{aligned}$$

$$A = x_{\text{e}}^{2} ;x_{\text{e}} = 2r_{\text{e}}$$

$$A = 320 \times 43560 = 13.94 \times 10^{6} \,{\text{ft}}^{2}$$

$$x_{\text{e}} = y_{\text{e}} = \surd A = \surd \left( {13.94 \times 10^{6} } \right) = 3,734\,{\text{ft}}$$

$$r_{\text{e}} = x_{\text{e}} /2 = 1867\,{\text{ft}}$$

$$N_{\text{p}} > 10$$

$$C_{{{\text{fD}}\,{\text{opt}}}} = N_{\text{p}} = 61.75$$

$$\begin{aligned} x_{{{\text{f}}\,{\text{opt}}}} & = \left( {\left( {k_{\text{f}} V_{\text{f}} } \right)/\left( {2C_{{{\text{fD}}\,{\text{opt}}}} k\,h} \right)} \right)^{0.5} = \left( {\left( {220,000 \times 1950.78} \right)} \right./ \\ & \quad \left( {\left( {2 \times 61.75 \times 0.01 \times 100} \right)} \right.^{0.5} = 1864\,{\text{ft}} \\ \end{aligned}$$

$$\begin{aligned} w_{\text{opt}} & = \left( {\left( {C_{{{\text{fD}}\,{\text{opt}}}} kV_{\text{f}} } \right)/\left( {2k_{\text{f}} h} \right)} \right)^{0.5} = \left( {\left( {61.75 \times 0.01 \times 1950.78 } \right)/} \right. \\ & \quad \left( {2 \times 220,000 \times 100} \right)^{0.5} = 5.23 \times 10^{ - 3} {\text{ft}} = 0.0628\,{\text{in}} \\ C_{{{\text{fD}},{\text{opt}}}} & = \left( {k_{\text{f}} w_{\text{opt}} } \right)/\left( {kx_{{{\text{f}},{\text{opt}}}} } \right) = \left( {220,000 \times 5.23 \times 10^{ - 3} } \right)/ \\ & \quad \left( {0.01 \times 1864 \, } \right) = 61.73 \\ C_{{{\text{fD}},{\text{opt}}}} & > 50 \\ \end{aligned}$$

$$S_{\text{f}} = 0.7 - \ln \left( {x_{{{\text{f}},{\text{opt}}}} /r_{\text{w}} } \right) = 0.7 - \ln \left( {1864/0.328} \right) = - 7.95$$

$$G = E/\left[ {2\left( {1 + v} \right)} \right] = 10^{7} /\left[ {2\left( {1 + 0.25} \right)} \right] = 4 \times 10^{6} \,{\text{psi}}$$

$$w_{\text{opt}} = 0.3\left[ {\left. {q_{i} \mu_{{{\text{frac}}\,{\text{fluid}}}} \left( {1 - \nu } \right)x_{f} } \right)/G} \right]^{1/4} \left( {\pi /4\gamma } \right)\left[ {\text{in}} \right]$$

$$0.0628 = 0.3\left[ {\left( {q_{i} } \right)\left( {10} \right)\left( {1 - 0.25} \right)\left( {1864} \right)/\left( {4 \times 10^{6} } \right)} \right]^{1/4} \left( {\pi /4*0.75} \right)$$

$$q_{i} = 4.56\,{\text{bpm}} \times 1440 = 6566.4\,{\text{bpd}} < 9\,{\text{bpm}}$$

$$\begin{aligned} \Delta p_{\text{f}} & = \left\{ {\left[ {518\left( {\rho_{\text{w}} } \right)^{0.79} \left( {q_{i} } \right)^{1.79} \left( {\mu_{{{\text{frac}}\,{\text{fluid}}}} } \right)^{0.207} } \right]/\left( {1000*D^{4.79} } \right)} \right\}H \\ & = \left\{ {\left[ { 5 1 8 { }\left( { 1. 2} \right)^{0. 7 9} ( 4. 5 6)^{ 1. 7 9} ( 10)^{0. 20 7} } \right] /\left[ { 1000 \, \left( 3\right)^{ 4. 7 9} } \right]} \right\} \\ & \quad 10,000 \, = 7 5 5 {\text{ psi}} \\ \end{aligned}$$

$$\Delta p_{\text{h}} = \left( {\rho_{{{\text{frac}}\,{\text{fluid}}}} } \right)\left( {G_{\text{w}} } \right)H = \left( { 1. 2} \right)\left( {0. 4 3} \right)\left( { 10,000} \right) = 5, 1 60\,{\text{psi}}$$

$$p_{\text{si}} = p_{\text{bd}} {-}\Delta p_{\text{h}} + \Delta p_{\text{f}} = 6500{-}5160 + 755 = 2095\,{\text{psi}}$$

$$A_{\text{f}} = 2x_{\text{f}} h_{\text{f}} = 2\left( {1864} \right)\left( {100} \right) = 372,800\,{\text{ft}}^{2}$$

$$\begin{aligned} V_{\text{f}} & = A_{\text{f}} w_{\text{opt}} = \left( {372800} \right)\left( {5.23 \times 10^{{{-}3}} } \right) \\ & = 1949.7\,{\text{ft}}^{3} \times 7.48 = 14583.7\,{\text{gal}} \\ \end{aligned}$$

$$r_{\text{p}} = h/h_{\text{f}} = 100/100 = 1$$

$$V_{\text{inj}} = V_{\text{f}} + V_{\text{leak - off}}$$

$$K_{\text{L}} = 1.5\left( {\text{assumed}} \right)$$

$$\begin{aligned} q_{i} t_{i} & = A_{\text{f}} w_{\text{opt}} + 2K_{\text{L}} C_{\text{L}} A_{\text{f}} r_{\text{p}} \surd t_{i} \\ & \quad \left( {4.56 \times 5.615} \right)t_{i} = 1949.7 + 2\left( {1.5} \right)\left( {0.0001} \right)\left( {372,800} \right)\left( 1 \right)\surd t_{i} \\ t_{i} & = 125 \, \hbox{min} \\ \end{aligned}$$

$$\begin{aligned} V_{\text{inj}} & = q_{i} t_{i} = \left( {4.56} \right)\left( {5.615} \right)\left( {125} \right) \\ & = 3200.5\,{\text{ft}}^{3} \times 7.48 = 23936\,{\text{gal}} \\ \end{aligned}$$

$$h = V_{\text{f}} /V_{\text{inj}} = 14583.7/23936 = 0.609$$

$$\begin{aligned} K_{\text{L}} & = 1/2\left[ {\left( {8/3} \right)\eta + \pi \left( {1{-}\eta } \right)} \right] \\ & = 1/2\left[ {8/3\left( {0.609} \right) + \pi \left( {1 - 0.609} \right)} \right] = 1.43 \\ \end{aligned}$$

Itirate:

$$ V_{\text{inj}} = V_{\text{f}} + V_{\text{leak - off}} $$

$$ \begin{aligned} q_{i} t_{i} & = A_{\text{f}} w_{\text{opt}} + 2K_{\text{L}} C_{\text{L}} A_{\text{f}} r_{\text{p}} \surd t_{i} \\ & \quad \left( {4.56 \times 5.615} \right)t_{i} = 1949.7 + 2\left( {1.43} \right)\left( {0.0001} \right)\left( {372,800} \right)\left( 1 \right)\surd t_{i} \\ t_{i} & = 122\,\hbox{min} \\ \end{aligned} $$

$$ V_{\text{inj}} = q_{i} t_{i} = \left( {4.56} \right)\left( {5.615} \right)\left( {122} \right) = 3123.7\,{\text{ft}}^{3} \times 7.48 = 23365\,{\text{gal}} $$

$$ h = V_{\text{f}} /V_{\text{inj}} = 14583.7/23365 = 0.624 $$

$$ K_{\text{L}} = 1/2\left[ {\left( {8/3} \right)\eta + \pi \left( {1{-}\eta } \right)} \right] = 1/2\left[ {8/3\left( {0.624} \right) + \pi \left( {1 - 0.624} \right)} \right] = 1.42 $$

Itirate:

$$ V_{\text{inj}} = V_{\text{f}} + V_{\text{leak - off}} $$

$$ \begin{aligned} q_{i} t_{i} & = A_{\text{f}} w_{\text{opt}} + 2K_{\text{L}} C_{\text{L}} A_{\text{f}} r_{\text{p}} \surd t_{i} \\ & \quad \left( {4.56 \times 5.615} \right)t_{i} = 1949.7 + 2\left( {1.42} \right)\left( {0.0001} \right)\left( {372,800} \right)\left( 1 \right)\surd t_{i} \\ t_{i} & = 121.8\,\hbox{min} \\ \end{aligned} $$

$$ V_{\text{inj}} = q_{i} t_{i} = \left( {4.56} \right)\left( {5.615} \right)\left( {121.8} \right) = 3118.6\,{\text{ft}}^{3} \times 7.48 = 23327\,{\text{gal}} $$

$$ h = V_{\text{f}} /V_{\text{inj}} = 14583.7/23327 = 0.625 $$

$$ K_{\text{L}} = 1/2\left[ {\left( {8/3} \right)\eta + \pi \left( {1{-}\eta } \right)} \right]{ = }1/2\left[ {8/3\left( {0.625} \right) + \pi \left( {1 - 0.625} \right)} \right] = 1.42 $$

$$ V_{\text{pad}} = V_{\text{inj}} \left[ {\left( {1{-}\eta } \right)/\left( {1 + \eta } \right)} \right] = 23327\left[ {\left( {1 - 0.625} \right)/\left( {1 + 0.625} \right)} \right] = 5383\,{\text{gal}} $$

$$ t_{\text{pad}} = V_{\text{pad}} /q_{i} = 5383/4.56\left( {42} \right) = 28\,\hbox{min} $$

$$ \varepsilon = \left( {1{-}\eta } \right)/\left( {1 + \eta } \right) = \left( {1 - 0.625} \right)/\left( {1 + 0.625} \right) = 0.23 $$

$$ \left( {c_{\text{p}} } \right)_{\text{bar}} = M_{\text{p}} /\left( {V_{\text{inj}} {-}V_{\text{pad}} } \right) = 200,000/\left( {23327{-}5383} \right) = 11\,{\text{ppg}} $$

$$ c_{\text{f}} = \left( {c_{\text{p}} } \right)_{\text{bar}} (1 + e) = \left( {11} \right)\left( {1 + 0.23} \right) = 13.53\,{\text{ppg}} $$

$$ C_{\text{p}} = M_{\text{p}} /2x_{\text{f}} h_{\text{f}} = 200,000/2\left( {1864} \right)\left( {100} \right) = 0.536\,{\text{lbm/ft}}^{2} $$

$$ \begin{aligned} w_{\text{propped}} & = C_{\text{p}} /\left( {1{-}f_{\text{prpt}} } \right)\rho_{\text{prpt}} = 0.536/\left( {\left( {1 - 0.38} \right)\left( {165.36} \right)} \right) \\ & = 5.23 \times 10^{ - 3} {\text{ft}} = w_{\text{opt}} \\ \end{aligned} $$

$$ \begin{aligned} c_{\text{p}} \left( t \right) & = c_{\text{f}} \left[ {\left( {t{-}t_{\text{pad}} } \right)/\left( {t_{i} {-}t_{\text{pad}} } \right]^{\varepsilon } } \right. \\ & = 13.74\left[ {\left( {t - 28} \right)/\left( {121.8 - 28} \right)} \right]^{0.23} \\ \end{aligned} $$

$$ \begin{aligned} q_{\text{g}} & = \left\{ {\left[ {m\left( {p_{\text{avg}} } \right){-}m\left( {p_{\text{wf}} } \right)} \right]{\text{kh}}/1424T} \right\}J_{{{\text{D}},\hbox{max} ,{\text{pss}}}} \\ & { = }\left( {1.22E + 09{-}4.65E + 06} \right)\left( {0.01} \right)\left( {100} \right)\left( {1.883} \right)/\left( {1424\left( {640} \right)} \right) \\ & = 1560\,{\text{Mscf/d}} \\ \end{aligned} $$

$$ m_{\text{g}} = 0.0249\,{\text{cp}} \times 6.719689 \times 10^{ - 4} = 1.67 \times 10^{ - 5} {\text{lb/ft}} . {\text{s}} $$

$$ \begin{aligned} r_{\text{g}} & = \left( {28.96\gamma_{\text{g}} p_{\text{wf}} } \right)/10.73T = \left( {28.96 \times 0.7 \times 2500} \right)/\left( {10.73 \times 640} \right) \\ & = 7.38\,{\text{lb/ft}}^{3} \\ \end{aligned} $$

$$ \begin{aligned} b & = 7.89 \times 10^{10} /k_{\text{f}}^{1.6} f_{\text{prpt}}^{0.404} = 7.89 \times 10^{10} / \\ & \quad 220,000^{1.64} \times 0.38^{0.404} = 201.96\,{\text{ft}}^{ - 1} \\ \end{aligned} $$

$$ \begin{aligned} B_{\text{g}} & = 0.0283\,ZT /p = 0.0283\left( {0.96} \right)\left( {640} \right)/ \\ & \quad 2500 = 0.006955\,{\text{scf/cf}} \\ \end{aligned} $$

$$ \begin{aligned} k_{\text{f}} & = 220,000 \times 10^{{{-}2}} \left( {9.869 \times 10^{{{-}13}} } \right)\left( {3.280} \right)^{2} \\ & = 2.34 \times 10^{{{-}9}} {\text{ft}}^{2} \\ \end{aligned} $$

$$ \begin{aligned} v & = B_{\text{g}} q_{\text{g}} /2h\,w_{\text{opt}} = 0.006955\left( {1560} \right)\left( {1000} \right)/ \\ & \quad 2\left( {3600 \times 24} \right)\left( {100} \right)\left( {5.23 \times 10^{{{-}3}} } \right) = 0.12\,{\text{ft/sec}} \\ \end{aligned} $$

$$ \begin{aligned} N_{{\text{Re} ,nD}} & = \beta k_{f} v\,\rho_{g} /\mu = \left( {201.96} \right)\left( {2.34 \times 10^{ - 9} } \right) \\ & \quad \left( {0.12} \right)\left( {7.38} \right)/\left( {1.67 \times 10^{ - 5} } \right) = 0.025 \\ \end{aligned} $$

$$ \begin{aligned} J_{nD} /J_{Do} & = \left[ {\ln \left( {r_{\text{e}} /r_{\text{w}} } \right){-}0.75{-}\ln \left( {0.28k_{\text{f}} w_{\text{opt}} } \right)/\left( {k\,r_{\text{w}} } \right)} \right]/ \\ & \quad \left\{ {\ln \left( {r_{\text{e}} /r_{\text{w}} } \right){-}0.75{-}\left[ {\ln \left( {0.28k_{\text{f}} w_{\text{opt}} } \right)/\left( {kr_{\text{w}} \left( {1 + N_{{\text{Re} ,nD}} } \right)} \right)} \right]} \right\} \\ & = \left( {\ln \left( {1867/0.328} \right)} \right.{-}0.75{-}\ln \left( {0.28 \times 220,000 \times 5.23 \times 10^{ - 3} } \right)/ \\ & \quad \left( {0.01 \times 0.328} \right)/\left\{ {\ln \left( {1867/0.328} \right){-}0.75{-} \ln } \right. \\ & \quad \left. {\left( {0.28 \times 220,000 \times 5.23 \times 10^{ - 3} } \right)/\left[ {0.01 \times 0.328 \, \left( {1 + 0.025} \right)} \right]} \right\} = 1 \\ \end{aligned} $$

$$ J_{nD} = J_{Do} $$

Appendix B

Predicting long-term pre-fracturing production profile

See Fig. 9.

For p_r = 4500 psi, p_wf = 2500 psi, and S = 0.

$$\begin{aligned} Q_{{g,{\text{before}}\,{\text{HF}}}} & = kh\left[ {m\left( {p_{i} } \right){-}m\left( {p_{\text{wf}} } \right)} \right]/\left\{ {1424T\left[ {\ln \left( {0.472\,r_{\text{e}} /r_{\text{w}} } \right) + S} \right]} \right\} \\ & = \left[ {0.01 \times 100 \times \left( {1.22 \times 10^{9} {-}4.65 \times 10^{8} } \right)} \right]/ \\ & \quad \left[ {1424 \times 640 \times \ln \left( {0.472 \times 1867/0.328} \right) + 0} \right] \\ & = 105\,{\text{Mscf/day}} \\ \end{aligned}$$

Since there is no production history, then constant -percentage decline is assumed

Assuming nominal daily decline rate D_d = 0.000417 day ⁻¹

The monthly decline rate D_m = 30.4 D_d = 30.4 * 0.000417 = 0.0127 month ⁻¹

The nominal yearly decline rate D_a = 12 D_m= 365 D_d = 365 × 0.000417 = 0.152 year ⁻¹

Effective monthly rate D′_m = 1 − e^−Dm = 1 − e^−0.0127 = 1.26% per month

Predicting long-term post-fracturing production profile

See Fig. 10.

$$\begin{aligned} t_{{\left( {{\text{l}}.{\text{f}}} \right){\text{end}}}} & = 438f\mu c_{\text{t}} x_{\text{f}}^{2} /k = 438 \times 0.14 \times 0.0249 \times 1.25 \times 10^{ - 5} \times 1864^{2} /0.01 \\ & = 6631.37\,{\text{hrs}} = 9\,{\text{months}} \\ t & = 0.75\,{\text{years}} \\ \end{aligned}$$

$$\begin{aligned} Q_{{{\text{g}}\,{\text{sc,L}}}} & = \left[ {m\left( {p_{i} } \right) - m\left( {p_{\text{wf}} } \right)} \right)\left. {/64.35} \right]\left( {h/T} \right)\left( {x_{{{\text{f}},{\text{opt}}}} } \right)\left( {k\varphi \mu c_{t} } \right)^{0.5} \left( t \right)^{ - 0.5} \\ & = \left[ {\left( {1.22 \times 10^{9} } \right){-}\left( {4.65 \times 10^{8} } \right)/64.35} \right]\left( {100/640} \right)\left( {1866.7} \right) \\ & \quad \left( {0.01 \times 0.14 \times 0.0249 \times 1.25 \times 10^{ - 5} } \right)^{0.5} \left( {6631.37} \right)^{ - 0.5} \\ & = 881{\text{MScf/d}} \\ \end{aligned}$$

$$G_{\text{p}} = Q_{{{\text{g}}\,{\text{sc,L}}}} \times t = 1526 \times 2190\left( {1/24} \right) = 39 \times 10^{3} \,{\text{Mscf}}$$

• No pseudoradial regime, because half-fracture length extends all the way to the boundary. (Transition directly from ETR to LTR; no MTR)

• Assume initial reservoir pressure depletes by a certain constant for every time increment once boundary conditions are reached

t_{beginning of pss} = 0.75 years

Assume p_bar − p_i = 200 psi and depletion drive mechanism

$$c_{\text{t}} = DV/\left[ {V\left( {p_{\text{bar}} {-}p_{\text{wf}} } \right)} \right]$$

$$\begin{aligned} B_{\text{gi}} & = 0.0283Z_{i} T_{i} /p_{i} = 0.0283\left( {0.96} \right)\left( {640} \right)/4500 \\ & = 0.00386\,cf /scf \\ \end{aligned}$$

$$ \begin{aligned} V & = 43,560\,\phi AhS_{\text{gi}} /B_{\text{gi}} = \left( {43,560\left( {0.38} \right)\left( {320} \right)\left( {100} \right)\left( {1 - 0.27} \right)} \right)/ \\ & \quad 0.00386 = 100\,{\text{MMMscf}}({\text{Constant}}) \\ \end{aligned} $$

$$ \Delta V = c_{\text{t}} V\left( {p_{i} {-}p_{\text{avg}} } \right) = \left( {1.25 \times 10^{ - 5} } \right)\left( {100} \right)\left( {4500{-}4300} \right) = 0.25\,{\text{MMMscf}} $$

$$ \begin{aligned} Q_{{{\text{g}}\,{\text{sc,pss}}}} & = \left( { 70 3\times 10^{ - 6} } \right)\left[ {m\left( {p_{\text{avg}} } \right){-}m\left( {p_{\text{wf}} } \right)} \right]kh/ \\ & \quad \left\{ {T\left[ {0. 5 {\text{ln}}\left( { 10.0 6A/C_{\text{A}} r_{\text{w}}^{ 2} } \right){-}0. 7 5+ S} \right]} \right\} \\ \end{aligned} $$

$$ C_{\text{A}} = 0.7887\left( {{\text{for}}\;{\text{bounded}}\;{\text{reservoir}}\;{\text{where}}\;{\text{the}}\;{\text{ratio}}\;{\text{between}}\;x_{\text{f}} \;{\text{and}}\;x_{\text{e}} \;{\text{equals}}\;1} \right) $$

$$ m\left( {p_{\text{avg}} } \right) = 1.14 \times 10^{9} \,{\text{psi}}^{2} /{\text{cp}} $$

$$ \begin{aligned} x_{\text{f}} & = 2r_{\text{w}} {\text{e}}^{ - S} = 1866.7\;{\text{and}}\;{\text{thus}}\;2\left( {0.328} \right){\text{e}}^{ - S} \\ & = 1866.7\;{\text{and}}\;{\text{solving}}\;{\text{for}}\;S = - 7 \\ \end{aligned} $$

As a rule, if Q_gsc,psss is greater than last Q_linear, then set Q_gsc,psss= Q_linear

$$\begin{aligned} Q_{{{\text{g}}\,{\text{sc,pss}}}} & = \left( {703 \times 10^{ - 6} } \right)\left( {1.14 \times 10^{9} {-}4.65 \times 10^{8} } \right)\left( {0.01} \right)\left( {100} \right)/ \\ & \quad \left( {640} \right)\left\{ {0.5\ln \left[ {\left( {10.06 \times 320 \times 43560} \right)/\left( {0.7887 \times 0.328^{2} } \right)} \right]} \right. \\ & \quad {-}0.75{-}7.9\} = 378\,{\text{Mscf/d}} \\ \end{aligned}$$

$$\begin{aligned} \Delta t & = \Delta V/Q_{{{\text{g}}\,{\text{sc,pss}}}} = \left( {0.25 \times 10^{9} } \right)/\left( {377 \times 10^{3} } \right) \\ & = 661\,d \times 1/365 = 1.8\,{\text{years}} \\ \end{aligned}$$

$$t = \Delta t + t_{\text{o}} = 1.8 + 0.75 = 2.55\,{\text{years}}$$