Introduction

Some quantitative evaluation methods of remaining oil saturation, such as drilling core method, logging method, and reservoir dynamic production simulation method, have their limitations. It has become a practical and effective method to comprehensively determine the remaining oil saturation of oil reservoirs from the aspects of geology, logging, production dynamics, etc. (Elkins and Poppe 1973; Li and Chen 2001); especially, it is more meaningful to study the distribution characteristics of remaining oil by using the data of seal coring wells at present (Hirasaki 1996). Based on the numerical simulation of experimental data, the effects of relative permeability, capillary pressure, and reservoir parameters on the recovery rate of the water-driven reservoir are deduced (Alfarge et al. 2017). Li  et al. (2016) reasonably deduced the water flooding status of underground strata based on seal coring samples. Andersen et al. (2017) constructed a theoretical relationship of the water saturation equation about porosity, relative permeability, and capillary pressure from the perspective of core experiment; Zahoor (2015) used relative permeability data to study the saturation state of the displacement fluid in porous media.

The porosity (\(\varphi\)), absolute permeability (\(k\)) (according to the convention, the word permeability in the text refers to absolute permeability except for the relative permeability), and shale content of core samples are routine measurement items of reservoir physical property experiments. They have been perfected from measuring instruments to measuring techniques (Shen et al. 1995). As the basic data of scientific research, core samples are all to measure porosity, air permeability, and shale content. When conducting immiscible fluid displacement experiments in porous media, Dullien et al. (1972) found that the fluid flow state in pores and the capillary pressure suffered by the fluid were firmly related to the pore structure. Experiments show that the pore structure parameter (\(R_{c}\)) has a good correlation with \(\sqrt {{k \mathord{\left/ {\vphantom {k \varphi }} \right. \kern-0pt} \varphi }}\), i.e., the root mean square of the ratio of permeability (\(k\)) and porosity (\(\varphi\)) (Pittman 1992; Lala and El-Sayed 2015). At present, this parameter has been used to establish the calculation formula of the oil saturation (\(S_{\text{o}}\)) suitable for low porosity–permeability reservoirs and obtained excellent results in the evaluation of the distribution of oil and water in complex reservoirs (Zhang et al. 2013).

The water cutting rate of the dynamic reservoir production reflects the characteristics of water flooding remaining oil in actual oil engineering (Renard et al. 1998). Hu et al. (2005) established the linear equation between water cutting rate and water saturation by taking the tertiary oil layers of Jiyang depression as the research object and pointed out that the coefficients in the formula are closely related to the porosity of the rock.

The experimental relative permeability is the link that establishes the relationship between water flooding characteristics and remaining oil saturation. This procedure is called percolating saturation formula. Zhang et al. (2018) studied the relationship between water cutting rate content and relative permeability measured from the experiment, which was used to study the variation trend of water cutting rate in the actual production, and the relatively suitable results were obtained. Feng et al. (2017) established a water-driven state prediction model from the linear correlation between relative permeability and water saturation. Xu et al. (2014) used the regression analysis method to fit the relative permeability curve and established the calculation formula of oil–water relative permeability and water saturation, to predict the remaining oil reserves. At present, the percolating saturation formula commonly used includes the exponential method and indexing method (Cobb and Marek 1997). The exponential method is simple and does not take the irreducible water and residual oil saturation into account, and the form is commonly used to analyze the relationship between oil displacement efficiency and water cutting rate (Gong et al. 2018). The formula of index percolating saturation formula contains two parameters of bound water saturation and residual oil saturation, which can reflect the prediction of remaining oil saturation more practically. Yang (1998) used index percolating saturation formula with fixed coefficients (\(c\), \(n\)) to establish the compute method of remaining oil saturation in the west part of the seventh block of Gudong oilfield.

The percolation saturation relationship is from the core experiment, which combines the water production rate and water saturation, and reflects the reasonable formula of fluid seepage. Based on the experimental relative permeability in the coring wells, we were combining the index percolating saturation formula and the water-driving seepage formula and got the formula for calculating the remaining oil saturation by water cutting rate. In this paper, we found the coefficients of the index percolating saturation formula are related to the porosity and permeability of rock samples, so we optimally established the variable coefficients’ formula. The introduction of the variable coefficients index method is innovative because it can effectively investigate the variation trend of remaining oil saturation in reservoirs with different porosity and permeability, even though under the condition that the variation of water cutting rate is the same. Moreover, it reflects the actual situation that the flowing fluid in the rock layer is subject to porosity and permeability conditions (An et al. 2016), and the calculation results are more reliable with strong practicality. The realization process of this method is reasonable that can be extended to other oilfields that have been developed for many years to predict the remaining oil saturation or determine the position of drilling new wells.

Methodology

Because of the complexity of the pore structure, water cannot thoroughly wash away the oil where it sweeps. From the injection side to the production side, the distribution of water saturation of a sand layer is discontinuous unless the injection water arrived at the production well, and the oil–water front is formed at the abrupt change of water saturation. The water saturation of the area between the oil–water front and the injection side increases gradually, where the oil and water typically flow in a two-phase way. Between the oil–water front and the oil-producing end, the pure oil flow zone occurs where the water is bound, and oil can flow freely. The oil–water front moves in the direction of the injection toward production over time, that is, the two-phase flow zone keeps expanding, and the pure oil zone keeps shrinking. When injection water appears at the producing end, only the two-phase flow zone remains in the reservoir (Rathmell et al. 1973). Based on Buckley–Leverett’s one-dimensional two-phase leading-edge displacement theory, we proposed an unsteady oil–water relative permeability measurement method for displacement experiment data (Welge et al. 1962). According to the simulation conditions, The experiment with the constant pressure difference or constant velocity is carried out on the rock sample, then  the outputs (\(q_{\text{o}}\), \(q_{\text{w}}\)) of oil and water at the rock sample outlet are recorded. While the pressure difference across the core changes with time, we can use the Darcy formula to calculate oil–water relative permeability (\(k_{\text{ro}}\), \(k_{\text{rw}}\)). Meanwhile, we use the weighing method or the material balance method to calculate the corresponding oil–water saturation value (\(S_{0}\), \(S_{\text{w}}\)) of the rock samples. During the experiment, the ratio of oil to water was changed, the proportion of oil gradually decreased, the proportion of water gradually increased, and the distribution of water and oil saturation in porous media was a function of distance and time.

In this way, we obtained a series of oil and water relative permeability values at different water saturation values, and the relationship curve between the oil and water relative permeability and water saturation of rock samples can be drawn (Xie et al. 2003).

The oil–water relative permeability displacement experiment can also give the measured values of bound water saturation and residual oil saturation. In the process of displacing water with oil rapidly, as the oil saturation of the pore space gradually increases, the oil first occupies the part of the pore space where the fluid flow resistance is the smallest, the relative permeability \(k_{\text{rw}}\) gradually approaches 0, the water yield \(q_{\text{w}}\) → 0, water cutting rate \(f_{\text{w}}\) → 0, and water is mainly distributed in tiny capillaries where the fluid is not natural to flow or adsorbed on the surface of the rock particles, which is the bound water saturation \(S_{wi}\). In the process of displacing oil with water, the oil relative permeability \(k_{\text{ro}}\) gradually approaches 0, oil yield \(q_{\text{o}}\) → 0, the water cutting rate \(f_{\text{w}}\) → 1, while the oil saturation is the residual oil saturation \(S_{\text{or}}\).

Suppose that the cross section of the horizontal stratum remains constant, one side injected water and the other side produces oil. \(k\) is the permeability (i.e., absolute permeability) of the horizontal formation, mD (i.e., 10−3 μm2), and \(\mu_{\text{o}}\) and \(\mu_{\text{w}}\) are the viscosity of oil and water, respectively, \({\text{mPa}}\;{\text{s}}\). The pressure gradient at some time point on a cross section is \(\frac{\partial p}{\partial x}\), and the seepage velocity of water at the interface multiplied by the cross-sectional area (\(A^{\prime}\)) of the formation should be equal to the flow water yield, \(q_{\text{w}}\). According to Darcy’s law,

$$q_{\text{w}} = k \cdot A^{\prime } \cdot \frac{{k_{\text{rw}} }}{{\mu_{\text{w}} }} \cdot \frac{\partial p}{\partial x}$$
(1)

Capillary pressure is not considered in the same section. The pressure gradient of water and oil is the same. The flow of oil yield \(q_{\text{o}}\) is equal to:

$$q_{\text{o}} = k \cdot A^{\prime } \cdot \frac{{k_{\text{ro}} }}{{\mu_{\text{o}} }} \cdot \frac{\partial p}{\partial x}$$
(2)

From Eqs. (1) and (2), we obtained the water cutting rate on the cross section:

$$f_{\text{w}} = \frac{{q_{\text{w}} }}{{q_{\text{w}} + q_{\text{o}} }} = \frac{1}{{1 + \frac{{\mu_{\text{w}} }}{{\mu_{\text{o}} }} \cdot \frac{{k_{\text{ro}} }}{{k_{\text{rw}} }}}}$$
(3)

Equation (3) indicates that the relative permeability of oil and water determines whether the reservoir produces oil, water, or both. Moreover, the change of relative permeability of oil phase and water phase with water saturation can be expressed by index percolating saturation formula (Yu 1982):

$$\frac{{k_{\text{ro}} }}{{k_{\text{rw}} }} = c\left( {\frac{{S_{\text{w}} - S_{\text{wi}} }}{{1 - S_{\text{or}} - S_{\text{w}} }}} \right)^{ - n}$$
(4)

where \(S_{\text{w}}\)—water saturation, decimal; \(S_{\text{or}}\)—residual oil saturation after water flooding, decimal; \(S_{\text{wi}}\)—formation bound water saturation, decimal.

Some studies show the relative permeability is related to many factors such as rock pore structure, rock wettability, and oil–water viscosity ratio (Burdine 1953; Singh et al. 2019; Crotti and Cobenas 2001), so the coefficients \(c\) and \(n\) in formula (4) are naturally influenced by oil–water viscosity ratio and rock pore structure. Formula (4) indicates that the oil–water relative permeability and water saturation of a core sample have various corresponding relationships. Through Eqs. (3) and (4), the relationship between \(f_{\text{w}}\), \(S_{w}\), \(S_{\text{wi}}\), and \(S_{\text{or}}\) can be deduced, see (5):

$$S_{\text{w}} = \frac{{\left( {\frac{{cf_{\text{w}} }}{{1 - f_{\text{w}} }} \cdot \frac{{\mu_{\text{w}} }}{{\mu_{\text{o}} }}} \right)^{{\frac{1}{n}}} \left( {1 - S_{\text{or}} } \right) + S_{\text{wi}} }}{{1 + \left( {\frac{{cf_{\text{w}} }}{{1 - f_{\text{w}} }} \cdot \frac{{\mu_{\text{w}} }}{{\mu_{\text{o}} }}} \right)^{{\frac{1}{n}}} }}$$
(5)
$$S_{\text{o}} = 1 - S_{\text{w}}$$
(6)

According to formulas (5) and (6), when the water productivity at the outlet of a rock layer is known, the water saturation \(S_{\text{w}}\) and remaining oil saturation \(S_{\text{o}}\) of a rock can be calculated.

Determination of coefficients \(c\) and \(n\)

According to the standard of relative permeability in the oil and gas industry and related experiment implementation methods (Jones and Roszelle 1978), we selected 17 rock samples from six seal coring wells in Daqing Changyuan oilfield for relative permeability test in this paper. The porosity of these cores ranges from 24.5 to 32.2%, and the permeability ranges from 14.6 to 1632.7 mD. They can capture the porosity and permeability characteristics of Daqing Changyuan oilfield (Hou et al. 2009). Table 1 shows the test parameters. The simulated oil viscosity, density, and the injection viscosity and density are consistent with the produced oil and injected water in the block where the core wells located.

Table 1 Experimental conditions for oil–water relative permeability test
Full size table

According to formula (4), the coefficients \(c\) and \(n\) are influenced by the rock pore structure, wettability, and oil–water viscosity ratio. Because the samples come from the same oil group in a development block, they have almost the same wettability and oil–water viscosity ratio. In the actual calculation, it can be determined uniformly according to the development time stage and the block position. We focused on establishing the relationship between coefficients \(c\) and \(n\) and the rock pore structure parameter \(R_{c}\):

$$R_{c} = \sqrt {{\raise0.7ex\hbox{$k$} \!\mathord{\left/ {\vphantom {k \varphi }}\right.\kern-0pt} \!\lower0.7ex\hbox{$\varphi $}}}$$
(7)

Take the natural logarithm of both sides of Eq. (4) to obtain Eq. (7):

$$\ln \left( {\frac{{k_{\text{ro}} }}{{k_{\text{rw}} }}} \right)\ln (c) - n\ln \left( {\frac{{S_{\text{w}} - S_{\text{wi}} }}{{1 - S_{\text{or}} - S_{\text{w}} }}} \right)$$
(8)

Let

$$x = \ln \left( {\frac{{S_{\text{w}} - S_{\text{wi}} }}{{1 - S_{\text{or}} - S_{\text{w}} }}} \right)$$
(9)
$$y = \ln \left( {\frac{{k_{\text{ro}} }}{{k_{\text{rw}} }}} \right)$$
(10)

\(x\) and \(y\) of each sample are calculated, respectively, according to Eqs. (9) and (10). From Eq. (8), we can fit a linear regression line about \(y\) with respect to \(x\) of each sample. The slope of the line is (\(- n\)), and the intercept is \(\ln \left( c \right)\). Figure 1 shows \(y\) and \(x\) cross-plot of 17 rock samples. For clearly showing, we put the samples into four sub-figures. And Table 2 shows the formula of the relationships between \(\ln \left( {\frac{{S_{\text{w}} - S_{\text{wi}} }}{{1 - S_{\text{or}} - S_{\text{wi}} }}} \right)\) and \(\ln \left( {\frac{{k_{\text{ro}} }}{{k_{\text{rw}} }}} \right)\). Table 2 also gives the correlation coefficients (R2), standard deviations of \(x\) and \(y\) of each sample, and the root mean square error (RMSE). From the data, we can find good fitness of \(x\) and \(y\) for each sample.

Fig. 1
figure 1

Cross-plots of different samples between \(\ln \left( {\frac{{S_{\text{w}} - S_{\text{wi}} }}{{1 - S_{\text{or}} - S_{\text{wi}} }}} \right)\) and \(\ln \left( {\frac{{k_{\text{ro}} }}{{k_{\text{rw}} }}} \right)\). (Numbers in the legend are the sample numbers. The lines in the sub-figures are linear regression trend lines)

Full size image
Table 2 The formula of the relationships for 17 samples and the relative analysis data on fitness
Full size table

Table 3 shows the data of porosity (\(\varphi\)), permeability (\(k\)), bound water saturation (\(S_{\text{wi}}\)), residual oil saturation (\(S_{\text{or}}\)), and shale content (\(V_{\text{sh}}\)) of 17 samples, and the last two columns in Table 3 are \(\ln \left( c \right)\) and \(n\). Figure 1 shows each sample has a good correlation between \(y\) and \(x\), and the range of \(n\) between different samples is small. In these samples, No. 363 has the lowest value (\(n\) = 1.461), and No. 520 has the highest value (\(n\) = 1.788); but \(\ln \left( c \right)\) varies widely: change from − 0.204 of sample No. 1107 to 1.701 of sample No. 733, that is, the varying range of \(c\) value is 0.815–5.480.

Table 3 Experimental parameters of different samples and the values of \(\ln \left( c \right)\) and \(n\)
Full size table

There is a good positive correlation between the size of the pore throat and \(R_{c}\) (\(\sqrt {{k \mathord{\left/ {\vphantom {k \varphi }} \right. \kern-0pt} \varphi }}\)) value (Ma and Morrow 1996). Formula (7) is used to calculate the \(R_{c}\) values of 17 samples, as shown in column 7 in Table 3. Analyze the relationship between \(\varphi\), \(k\), \(R_{c}\) values with \(n\) and \(\ln \left( c \right)\) of each sample: Sample No. 363 has the minimum value of \(n\), and its values of \(\varphi\), \(k\), and \(R_{c}\) are 30.6%, 1632.7 mD, and 7.306; sample No. 520 has the maximum value of n, and its \(\varphi\), \(k\), and \(R_{c}\) values are 24.6%, 35.6 mD, and 1.203; sample No. 1107 has the minimum value of \(\ln \left( c \right)\), and its values of \(\varphi\), \(k\), and \(R_{c}\) are 30.6%, 1632.7 mD and 7.306; sample No. 733 has the maximum value of \(\ln \left( c \right)\), and its values of \(\varphi\), \(k\), and \(R_{c}\) are 30.6%, 1632.7 mD, and 7.306. These data further illustrate the point above that \(n\) and \(\ln \left( c \right)\) are affected by the porosity and permeability of a rock layer. Figure 2 shows the relationship between \(R_{c}\) and \(\ln \left( c \right)\) and reflects the positive correlation between the two; the correlation equation is shown in Eq. (11), correlation coefficient (R2) is 0.801, and the root mean square error (RMSE) is 0.132. It shows that the larger the pore throat, the larger the coefficient c; Fig. 3 shows the relationship between \(R_{c}\) and \(n\), \(R_{c}\) is negatively correlated with \(n\), and the relation is shown in Eq. (12), correlation coefficient (R2) is 0.859, and the root mean square error (RMSE) is 0.311:

Fig. 2
figure 2

Correlation diagram between \(R_{c}\) and \(\ln (c)\) of 17 samples

Full size image
Fig. 3
figure 3

Correlation diagram between \(R_{c}\) and \(n\) of 17 samples

Full size image
$$\ln (c) = 0.2595R_{c} - 0.2335$$
(11)
$$n = - 0.044R_{c} + 1.8221$$
(12)

Determination of bound water saturation (\(S_{\text{wi}}\)) and residual oil saturation (\(S_{\text{or}}\))

The bound water and residual oil remain in the micropores of sandstone or are adsorbed on the surface of the particles with large pore by the molecular surface force and cannot flow freely. The good residual oil saturation and bound water saturation can be deduced by the core analysis data in the water flooding area (Abrams 1975).

The study area has shaly sandstone sedimentary strata, the more micro-channels in the sandstone strata, the lower permeability, and the more residual stagnant water. The more the shaly particles in sandstone, the higher the shale content, and the higher the adsorbed water content on the surface of shaliness particles. Figure 4a, b shows the relationship between shale content (\(V_{\text{sh}}\)), permeability (\(k\)), and bound water saturation (\(S_{\text{wi}}\)), respectively. The formula of bound water saturation with \(V_{\text{sh}}\) and the logarithm term (base 10) of \(k\) was established, see Eq. (13). The correlation coefficient (R2) is 0.952, and the root mean square error (RMSE) is 0.103:

Fig. 4
figure 4

a Correlation diagram of permeability (\(k\)) and bound water saturation (\(S_{\text{wi}}\)), b correlation diagram of shale content (\(V_{sh}\)) and bound water saturation (\(S_{\text{wi}}\))

Full size image
$$S_{\text{wi}} = 0.4364 - 0.0799\log (k) + 0.4156V_{\text{sh}}$$
(13)

Residual oil saturation is related to the oil viscosity, porosity, and permeability of the rock strata. Core experiments show that with the same viscosity, the higher the porosity and permeability, the lower the residual oil saturation (Xie et al. 2017). It is found that the porosity and permeability distribution of core samples can affect the sweep rate of oil–water seepage. Figure 5a, b shows the relationship between porosity (\(\varphi\)) and the logarithm term (base 10) of permeability (\(\ln k\)) with residual oil saturation (\(S_{\text{or}}\)), respectively. Furthermore, use them to establish the formula of residual oil saturation, see Eq. (14). The correlation coefficient (R2) is 0.861, and the root mean square error (RMSE) is 0.293:

Fig. 5
figure 5

a Correlation diagram of porosity (\(\phi\)) and permeability (\(k\)), b correlation diagram of porosity (\(\phi\)) and residual oil saturation (\(S_{\text{or}}\))

Full size image
$$S_{\text{or}} = 0.447 - 0.386\phi - 0.0426\log (k)$$
(14)

Discuss the changing trend of \(S_{\text{w}}\) with \(f_{\text{w}}\)

After determining the \(n\) and \(c\) values of each sample, formula (5) can be used to investigate the changing relationship between the water cutting rate \(f_{\text{w}}\) and the remaining oil saturation (\(1 - S_{\text{w}}\)) at the oilfield development stage. For Eq. (5), the derivative of \(S_{\text{w}}\) with respect to \(f_{\text{w}}\) is calculated as \(S^{\prime}_{\text{w}} (f_{\text{w}} )\), and we get Eq. (15):

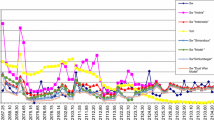
$$S_{\text{w}}^{\prime } (f_{\text{w}} ) = \frac{{(1 - S_{\text{or}} - S_{\text{wi}} )}}{{\left( {1 + \xi^{{\tfrac{1}{n}}} } \right)^{2} }}\left( {\xi^{{\tfrac{1}{n}}} } \right)^{\prime }$$
(15)

where \(\xi = \frac{{cf_{\text{w}} }}{{1 - f_{\text{w}} }} \cdot \frac{{\mu_{\text{w}} }}{{\mu_{\text{o}} }}\) \((\xi^{{\tfrac{1}{n}}} )^{\prime} = \frac{1}{n}\xi^{{\tfrac{1}{n} - 1}} \xi^{\prime}(f_{\text{w}} )\) \(\xi^{\prime}(f_{\text{w}} ) = \frac{{\mu_{\text{w}} }}{{\mu_{\text{o}} }}\frac{c}{{(1 - f_{\text{w}} )^{2} }}\) \(S^{\prime}_{\text{w}} (f_{\text{w}} )\) is defined as the change rate of water saturation with \(f_{\text{w}}\), \(S_{\text{or}}\), \(S_{\text{wi}}\), \(c\), and \(n\) of the 17 samples in Table 3, and the \(\mu_{\text{o}}\), \(\mu {}_{\text{w}}\) values in Table 1 are substituted into Eq. (15). For \(f_{\text{w}}\) to go from 1 to 99%, with a span of 5%, the change of \(S^{\prime}_{\text{w}} (f_{\text{w}} )\) can be calculated. We tried to use the computer way to divide these samples into clusters (Haralick and Shanmugam 2007) and found that dividing them into three types according to the values of \(R_{c}\) and \(V_{\text{sh}}\) has the most apparent degree of data separation. This also coincides with the view that porosity, permeability, and mud content are the main factors of stratification (Lu et al. 1995). In the first type group, \(R_{c} \ge 5.0\) and \(V_{\text{sh}} < 10\%\), which means the samples of this type own the best porosity and permeability characteristic with little shaleness. In the second type group, \(R_{c} \ge 3.0\) and \(10\% \le V_{\text{sh}} < 25\%\), which means the samples are shale-bearing sandstone with better porosity and permeability characteristic. In the third group, \(R_{c} < 3.0\) or \(V_{\text{sh}} \ge 25\%\), which means the samples own the common porosity and permeability characteristic or contain more shaleness. It can be seen that the changing trend of \(S^{\prime}_{\text{w}} (f_{\text{w}} )\) with \(f_{\text{w}}\) of samples in the same type is similar in Fig. 6a–c. Figure 6d shows the average trend of each type.

Fig. 6
figure 6figure 6

a The correlation diagram between the water cutting rate and change rate of water saturation of samples in the first type group, b the correlation diagram between moisture content and change rate of water saturation of samples in the second type group, c the correlation diagram between moisture content and change rate of water saturation of samples in the third type group, d correlation diagram between the average water cutting rate and the average change rate of water saturation for individual type

Full size image

Figure 6 shows that as the water cutting rate \(f_{\text{w}}\) increases, when the water cutting rate \(f_{\text{w}}\) is less than 20%, the change rate of water saturation \(S^{\prime}_{\text{w}} (f_{\text{w}} )\) shows a decreasing trend. When the water cutting rate \(f_{\text{w}}\) is between 20 and 80%, the change rate \(S^{\prime}_{\text{w}} (f_{\text{w}} )\) is about a constant. When the water cutting rate \(f_{\text{w}}\) reaches more than 80%, the change rate of water saturation \(S^{\prime}_{\text{w}} (f_{\text{w}} )\) presents a rapidly rising trend. Because the physical properties of samples are different, their changing states are also different. By analyzing Fig. 6d, we obtained the following laws:

  1. 1.

    Samples in the first type group have fine porosity and permeability conditions and low shale content. When the water cutting rate \(f_{\text{w}}\) is 1%, the change rate of water saturation \(S^{\prime}_{\text{w}} (f_{\text{w}} )\) is 0.831; with the increase in the water cutting rate, the change rate of water saturation \(S^{\prime}_{\text{w}} (f_{\text{w}} )\) decreases. When the water cutting rate \(f_{\text{w}}\) reaches 20%, the change rate of water saturation \(S^{\prime}_{\text{w}} (f_{\text{w}} )\) is 0.305. When the water cutting rate \(f_{\text{w}}\) is between 20% and 80%, the change rate of water saturation \(S^{\prime}_{\text{w}} (f_{\text{w}} )\) is flat, and the mean value is 0.331. When the water cutting rate \(f_{\text{w}}\) is 80%, the change rate of water saturation \(S^{\prime}_{\text{w}} (f_{\text{w}} )\) reaches 0.546, and then, the change rate of water saturation \(S^{\prime}_{\text{w}} (f_{\text{w}} )\) increased rapidly. When the water cutting rate \(f_{\text{w}}\) reaches 99%, the change rate of water saturation \(S^{\prime}_{\text{w}} (f_{\text{w}} )\) is up to 2.972.

  2. 2.

    Samples in the second type group have medium porosity and permeability conditions and medium shaleness. When the water cutting rate \(f_{\text{w}}\) is 1%, the change rate of water saturation \(S^{\prime}_{\text{w}} (f_{\text{w}} )\) is 0.557; with the increase in water cutting rate, the change rate of water saturation decreases. When the water cutting rate \(f_{\text{w}}\) reaches 20%, the change rate of water saturation \(S^{\prime}_{\text{w}} (f_{\text{w}} )\) is 0.183. When the cutting rate \(f_{\text{w}}\) is between 20 and 80%, the change rate of water saturation \(S^{\prime}_{\text{w}} (f_{\text{w}} )\) is flat, and the mean value is 0.211. When the cutting rate \(f_{\text{w}}\) is 80%, the change rate of water saturation \(S^{\prime}_{\text{w}} (f_{\text{w}} )\) reaches 0.382, and then, the change rate of water saturation \(S^{\prime}_{\text{w}} (f_{\text{w}} )\) increased rapidly. When the cutting rate \(f_{\text{w}}\) reaches 99%, the change rate of water saturation \(S^{\prime}_{\text{w}} (f_{\text{w}} )\) is up to 3.09.

  3. 3.

    Samples in the third type group have poor pore-permeability conditions and high shale content. When the water cutting rate \(f_{\text{w}}\) is 1%, the change rate of water saturation \(S^{\prime}_{\text{w}} (f_{\text{w}} )\) is 0.298; with the increase in water cutting rate \(f_{\text{w}}\), the change rate of water saturation \(S^{\prime}_{\text{w}} (f_{\text{w}} )\) decreases. When the water cutting rate \(f_{\text{w}}\) reaches 20%, the change rate of water saturation \(S^{\prime}_{\text{w}} (f_{\text{w}} )\) is 0.100. When the water cutting rate \(f_{\text{w}}\) is between 20% and 80%, the change rate of water saturation \(S^{\prime}_{\text{w}} (f_{\text{w}} )\) is flat, and the mean value is 0.125. When the water cutting rate \(f_{\text{w}}\) is 80%, the change rate of water saturation \(S^{\prime}_{\text{w}} (f_{\text{w}} )\) reaches 0.254, and then, the change rate of water saturation \(S^{\prime}_{\text{w}} (f_{\text{w}} )\) increased rapidly. When the water cutting rate \(f_{\text{w}}\) reaches 99%, the change rate of water saturation \(S^{\prime}_{\text{w}} (f_{\text{w}} )\) is up to 3.01.

  4. 4.

    To summarize the change rate of water saturation \(S^{\prime}_{\text{w}} (f_{\text{w}} )\) with water cutting rate of three types of samples: The condition of porosity and permeability varies from good to bad, and the change rate of water saturation varies from high to low. It indicates that the remaining oil in reservoirs with good porosity and permeability conditions can be reduced quickly. This is consistent with the fact that in actual oilfield exploitation, the injected water flooding of highly porous and permeable reservoirs is more serious (Zhang et al. 2016).

Method application

The method in this paper is applied to an inject-product unit in the study area, which includes six wells, namely one injection well#f and five oil production wells (#a, #b, #c, #d, and #e); the connected sand layers between the water injection wells and the oil production wells in the unit are S22 and S26. The unit has been water flooded, and some oil production wells have produced a certain amount of injected water. Since the layers S22 and S26 in the study area are sand layers with high porosity and permeability, the logging data can be used to establish the effective calculation formula of porosity (\(\phi\)), permeability (\(k\)), and shale content (\(V_{\text{sh}}\)) (Hong 2008; Wang et al. 2019). Equations (16), (17), and (20), respectively, are the calculation formulas of \(\phi\), \(V_{\text{sh}}\), and \(k\) in the study area. The water saturation \(Sw_{0}\) from deep lateral resistivity (LLD) can be calculated by using Archie’s formula (Bussian 1982), see Eq. (21):

$$\varphi = - 0.001AC^{2} + 0.7887AC - 117.48({\text{R}}^{ 2} = 0. 9 3 3, {\text{RMSE}} = 1. 3 5 1 9 )$$
(16)
$$V_{\text{sh}} = \frac{{2^{2 \cdot dgr} - 1}}{{2^{2} - 1}} ( {\text{RMSE}} = 1.0 5 2 )$$
(17)
$$dgr_{1} = {\raise0.7ex\hbox{${(GR - gr\hbox{min} )}$} \!\mathord{\left/ {\vphantom {{(GR - gr\hbox{min} )} {(gr\hbox{max} - gr\hbox{min} )}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${(gr\hbox{max} - gr\hbox{min} )}$}}$$
(18)
$$dgr_{2} = 1 - {\raise0.7ex\hbox{${PSP}$} \!\mathord{\left/ {\vphantom {{PSP} {SSP}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${SSP}$}}$$
(19)
$$\ln (k) = - 27.4096 - 0.0681dgr + 0.1124AC \left( {R^{2} = 0.901,\;{\text{Mean}}\;{\text{Relative}}\;{\text{Error}} = 81.352\% } \right)$$
(20)
$$Sw_{0} = \sqrt {\frac{{R_{w} }}{{LLD \cdot \phi^{2} }}}$$
(21)

where \(AC\) is acoustic log value, \(\upmu{\text{s}}/{\text{m}}\). When the rock layer does not contain radioactive elements, and the natural gamma curve does not show abnormal values, \(dgr\) is taken as \(dgr_{1}\); otherwise, \(dgr\) is taken as the minimum value of \(dgr_{1}\) and \(dgr_{2}\). \(dgr_{1}\) is the change value of natural gamma measurement value relative to pure shale, decimal. In the formula (18), \(GR\) is the natural gamma measurement value, API. \(gr\hbox{max}\) is the natural gamma value of pure shale, API. \(gr\hbox{min}\) is the natural gamma value of pure sandstone, API. In the formula (19), \({\text{PSP}}\) is the amplitude difference of the spontaneous potential curve deviating from the shale baseline, mV; \({\text{SSP}}\) is the amplitude difference of the natural potential curve of the pure sandstone deviating from the shale baseline in the area, mV. \(R_{\text{w}}\) is the formation water resistivity value, which is taken as the measured values of the resistivity of the produced water from the S22 and S26 layers of adjacent oil wells in this paper. The \(R_{\text{w}}\) values of S22 and S26 are 0.62 Ω m and 0.55 Ω m, respectively. LLD is the deep lateral resistivity log, Ω m.

It is assumed that the influence of water flooding mining on the water saturation, porosity, permeability, and shale content of the rock layer is negligible. Logging is a continuous measurement process, and there are many measurement points in a section of the rock layer, but according to the layering and valuing rule of the logging curve, the logging value representing the sand body layer can be reasonably given out (Zhang et al. 2009). The porosity, permeability, and shale content of S22 and S26 sand layers of six wells were calculated using formulas (16)–(20), see Table 4. Also, Table 4 gives the current water cutting rate of each layer. And the water cutting rate of the water injection well#f was taken as 1.0. The coefficients \(c\) and \(n\), bound water saturation \(S_{\text{wi}}\), and residual oil saturation \(S_{\text{or}}\) were calculated by using formulas (11–14), respectively. The water cutting rates of the S22 and S26 layers of each well were, respectively, brought into formula (5) and formula (15) to calculate the water saturation \(S_{\text{w}}\) and the change rate of water saturation \(S^{\prime}_{\text{w}}\). The calculation results are shown in Table 5. The remaining oil saturation of each layer was calculated by formula (6), and the contour map of the remaining oil saturation distribution of the inject-product unit was drawn in the way of interpolation, as shown in Fig. 7a, b. Table 5 shows that the remaining oil saturation \(S_{o}\) of the S22 and S26 layers is about 60%. In Table 5, the type of each rock layer was determined by its \(R_{c}\) and \(V_{sh}\) values. According to the analysis of \(S^{\prime}_{\text{w}}\) above, the \(S^{\prime}_{\text{w}}\) values of layers in the first type group all are less than 0.331, and the \(S^{\prime}_{\text{w}}\) values of layers in the second type group all are less than 0.211; the \(S^{\prime}_{\text{w}}\) values of layers in the third type group all are less than 0.125. That means the change rates of water saturation of the S22 and S26 layers of the six production wells are laying in the stable section, the remaining oil distribution is proper, and the sand body is suitable for continuous mining.

Table 4 Reservoir parameters calculated from logging data and current water cutting rates of S22 and S26 in the injection-production unit
Full size table
Table 5 The relevant parameters of S22 and S26 layers were calculated from the water cutting rates in the inject-product unit
Full size table
Fig. 7
figure 7

a Distribution of remaining oil saturation of S22 layer in the injection and production unit, b distribution of remaining oil saturation of S26 layer in the injection and production unit

Full size image

Therefore, two infill wells #1 and #2 were deployed. Layered mining for these two wells individually was carried out, the water cutting rate of the two layers S22 and S26 in well#1 reached 95% and 50%, respectively, and the water content of the two layers S22 and S26 in well#2 reached 30% and 40%, respectively. According to the remaining oil saturation distribution results of this unit, it is unreasonable that the water cutting rate of the S22 layer in well#1 reaches 95%. Table 6 shows the porosity, permeability, and mud content calculated from logging data in wells #1 and #2, as well as the current water cutting rate. The coefficient \(c\) and \(n\), bound water saturation \(S^{\prime}_{\text{w}}\), residual oil saturation \(S_{\text{or}}\), water saturation \(S_{\text{w}}\), and the change rate of water saturation \(S^{\prime}_{\text{w}}\) were calculated by using the relevant formulas above. Table 7 shows the calculation results. \(S_{\text{w}}\) of the S22 and S26 layers of well#1 is 68.4% and 41.7%, respectively, and \(S^{\prime}_{\text{w}}\) is 1.316 and 0.294. \(S_{\text{w}}\) of the S22 and S26 layers of well#2 is 34.4% and 42.6%, respectively, and \(S^{\prime}_{\text{w}}\) is 0.133 and 0.141.

Table 6 Water cutting rates and reservoir parameters calculated by logs of infill well#1 and well#2
Full size table
Table 7 The relative parameters deduced from water cutting rates of infill well#1 and well#2
Full size table

According to Eq. (21), the \(Sw_{0}\) values of S22 and S26 in well#1 are 37.1% and 43.2%, respectively. \(Sw_{0}\) values of S22 and S26 in wells #2 are 36.9% and 44.6%, respectively. Compared with Table 5, it is found that except for well#1 layer S22, the \(Sw\) values of the other three layers are equivalent to \(Sw_{0}\), indicating that the water saturation method calculated from the water cutting rate in this paper is reasonable. Figure 8 shows the logging curves of the natural gamma ray (GR), spontaneous potential (SP), deep lateral resistivity (LLD) log, acoustic log (AC), and the porosity (), permeability (\(k\)), shale content (\(V_{\text{sh}}\)), and water saturation curve (\(Sw_{0}\)) are calculated by logging curves. From \(Sw_{0}\) curve,in the bottom part (well section is 1012.5–1014.5 m) \(Sw_{0}\) is about 55% deviating from 37% in the up part (well section is 1009.2–1012.5 m). And from \(k\) curve, \(k\) changes from 231 to 1913 mD, and it means S22 layer is severe heterogeneity. It is conceivable that there are macrochannels for injection water to circulate it low efficiently in the high-permeability strip (Chen et al. 2019; Skjaerstein et al. 1997). Under this suggestion, profile control and plugging treatments were carried out on the high-permeability strip of S22, and the water cutting rate lowered down to 39%. It is consistent with the log calculation \(Sw_{0}\), and it indicates that this layer is in a period of stable exploitation.

Fig. 8
figure 8

Logging curves and related parameters calculated by logs of infill well#1. (From the left track to the right track, the first track is well depth, in m; the second track is the layer’s number; the third track is deep dual lateral resistivity log, LLD Ω m; the fourth is acoustic log, us/m; the fifth track is shale content curve Vsh, %, and porosity \(\varphi\),  %; the sixth track is permeability \(k\), mD; the last track is the saturation curve from well logs \(Sw_{0}\),  %)

Full size image

Conclusion

  1. 1.

    The index percolating saturation formula reflects the productive relationship between permeability, water saturation, and water cutting rate. However, it is not the unique relationship; the coefficients in the formula are strictly related to the porosity and permeability characteristics of samples. The relationship between pore structure parameters \(R_{c}\) and index formula’s coefficients was established by optimizing core experimental data which have a good fit.

  2. 2.

    The coefficients, bound water saturation, and residual oil saturation in the index saturation formula can be determined by the porosity, permeability, and shale content of a rock layer. These three parameters can be calculated from the logs effectively. The percolating saturation formula with variable coefficients constructed in this way conforms to the actual situation of different rock properties and different exploit effects.

  3. 3.

    The law of rock saturation changing with water yield is given by establishing the derivative relationship between water saturation and water cutting rate. When the water cutting rate is less than 20%, that is, under the condition of low water flooding, the change of water saturation is slower than that of water cutting rate. Under medium water flooding condition (water cutting rate is 20–80%), reservoir water saturation decreases uniformly. Under high water flooding condition (water cutting rate is greater than 80%), the water saturation in the layer changes sharply with the water cutting rate; at this point, the reservoir is almost depleted, and injected water completely replaces the original underground fluid.

  4. 4.

    Although the study did not consider actual conditions such as gravity and capillary forces, it can be used as an ideal background to analyze the dynamic information in actual mining. For instance, the water cutting rate of some oil reservoirs is above 95% at the beginning of exploitation. The reservoir likely has a “macrochannel” for inefficient circulation. It does not mean that the remaining oil saturation in the layers tends to 0.

  5. 5.

    According to the research method of the paper, the remaining oil saturation is predicted for a well block that has been exploited for many years, while the water cutting rate in the production process of the oil layers was combined with the reservoir parameters such as porosity, permeability, and shale content of the rock layer. Because no new drilling is required, it saves a lot of drilling cost and guarantees the improvement in the oil recovery capacity of the oilfield that has been developed for many years. This job has a vital promotion significance.