Introduction

In geomechanical projects, having information about the in situ stresses is necessary to ensure wellbore stability to prevent occurrence of breakout and mud loss (Khaksar Manshad et al. 2014; Molaghab et al. 2017). In situ stresses can be evaluated through leak of test (LOT), pressure integrity test (PIT) and drilling mud information. However, in addition to being costly and time-consuming, the number of tests that can be done for oil and gas wells is very limited. The reason is that in most cases, performing many such experiments will cause well collapse (Liu et al. 2018; Boness and Zoback 2004; Castillo et al. 2000). It is possible to determine the in situ stresses using well logs, and the purpose of this study is to perform such a task for a well in the South Pars field, Iran.

In general, a strength–physical property relationship for a specific rock formation is developed based on calibration through laboratory tests on rock cores from the given field. If there are no core samples available for calibration, the next best way would be to use empirical strength relations based on measurable physical properties (Chang et al. 2006). In situ stress and geomechanical properties play important roles in the drilling, well bore stability analysis, fracture design and reducing asymmetric fractures in a pad area to increase the recovery rate in shale gas extraction with hydraulic fracturing (Han and Yin 2018). Assuming that the rock properties are isotropic, the horizontal stresses will be equal and act in all directions in the horizontal plane; hence, the horizontal stresses are expressed as a function of the Poisson’s ratio and \(\sigma_{1}\) (Jepson et al. 2019). If a foreign factor disturbs the stress field, the horizontal stresses will no longer be isotropic. In such a case, \(\sigma_{2}\) is parallel to the tectonic stress and \(\sigma_{3}\) in the horizontal plane is perpendicular to \(\sigma_{2}\).

Pore pressure

Pore pressure refers to the pressure applied to the fluids in the pore space (ArabAmeri et al. 2019; Colmenares and Zoback 2003). The pore pressure can be either normal, underpressure or overpressure and is calculated as:

$$ P_{{\text{P}}} {\text{hydro}} = \mathop \int \limits_{0}^{z} \rho_{{\text{w}}} \left( z \right)g{\text{d}}z = \rho_{{\text{w}}} gZ_{{\text{w}}} $$
(1)

where \(\rho_{{\text{w}}}\) is the density of water. The average gradient of normal or hydrostatic pressure is 10 MPa/km. Abnormal pressure is a pressure that is greater or smaller than the normal pressure. Formations with unusual pressure are found in many sedimentary basins and have different origins. These formations cause problems in drilling and completion of oil and gas wells. High-pressure formations can cause hazards in drilling the wells (Dutta 2002; Peters et al. 2019).

Overburden pressure

The overburden pressure at each depth is a function of the weight of the rock and the liquids in the pore spaces above that point (Oloruntobi et al. 2018). In order to calculate this pressure at any depth, the average density of rocks and fluids above that point should be calculated. The average density of rocks and fluids in the pore spaces is called bulk density and is calculated using the following equation:

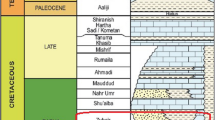
$$ \rho_{{\text{b}}} = \rho_{{\text{m}}} - \left( {\rho_{{\text{m}}} - \rho_{{\text{f}}} } \right)\varphi $$
(2)

where \(\rho_{{\text{b}}} \) is the bulk density, \(\rho_{{\text{m}}}\) is the density of the rock matrix, \(\rho_{{\text{f}}}\) is the density of the fluids contained in the pores and \(\varphi\) is the porosity. Due to the lithology, porosity and fluid content varying in different depths, the bulk density is not constant. Having the bulk density, the overburden pressure is at depth Z is calculated using the following equation: (Fig. 1).

$$ {\text{OB}} = \mathop \int \limits_{0}^{Z} \rho_{{\text{b}}} \left( z \right)g{\text{d}}z $$
(3)
Fig. 1
figure 1

The overburden pressure at a well no. 8 and b well no. 44

Full size image

where the OB is the overburden pressure at depth Z.

Methodology

In situ stress determination using well logs

The first step in determining the in situ stresses is to estimate the overburden pressure at the desired depth, which is given by:

$$ {\text{OB}} = g\mathop \int \limits_{0}^{z} \rho_{{\text{b}}} z{\text{d}}z $$
(4)

Determination of hydrostatic pressure at well no. 44

Hydrostatic pressure is the pressure caused by the weight of the fluid column. To calculate the hydrostatic pressure, we use the following equation (Zhang 2011):

$$ P_{{{\text{hyd}}}} = \left( {0.433} \right)\rho_{{\text{f}}} gz $$
(5)

in which g is the gravitational acceleration of the earth, \(\rho_{{\text{b}}}\) is the average density of the rocks and fluids and z is the depth.

Figure 2 shows the comparison between the two proposed formulas for hydrostatic pressure at well no. 8 and no. 44. As can be seen, the hydrostatic pressure increases with increasing depth.

Fig. 2
figure 2

Hydrostatic pressure at a well no. 8 and b well no. 44

Full size image

Determination of pore pressure at well no. 44 using well logs

As it is mentioned, pore pressure refers to the pressure applied to the fluids in the pore spaces. Equation (7) is the relationship presented by Eaton (1972) for pore pressure estimation. As it is evident from the relationship, in order to estimate the pore pressure, the overburden pressure, the hydrostatic pressure and the velocity of layers are required to be known. The layer velocities can be calculated using sonic logs.

$$ P_{{{\text{pg}}}} = {\text{OBG}} - \left( {{\text{OBG}} - P_{{{\text{ng}}}} } \right)\left( {\frac{{\Delta t_{{\text{n}}} }}{\Delta t}} \right)^{x} $$
(6)

Or, the other form of this equation is as follows:

$$ P_{{\text{p}}} = {\text{OB}} - \left( {{\text{OB}} - P_{{\text{n}}} } \right)\left( {\frac{{\Delta t_{{\text{n}}} }}{\Delta t}} \right)^{x} $$
(7)

In this case,\( P_{{\text{p}}}\) is the pore pressure, \({\text{OB}}\) is the overburden pressure and \(P_{{\text{n}}}\) is the hydrostatic pressure.

The hydrostatic pressure and overburden pressure have already been calculated. The value of Δt can be obtained from the sonic log in the desired well. To obtain \(\Delta t_{{\text{n}}}\), which is the values of the sonic log on the normal line, we use Eq. (8). Zhang's equation (2011) is as follows:

$$ \Delta t_{{\text{n}}} = \Delta t_{{\text{m}}} + \left( {\Delta t_{{{\text{ml}}}} - \Delta t_{{\text{m}}} } \right){\text{e}}^{ - cz} $$
(8)

The advantage of using the Zhang's method is that the normal trend of the sonic log can be generalized to deeper zones and a fairly straightforward answer to overpressure zones can be achieved. Additionally, the pore pressure is obtained in depth too. The value of \(\Delta t_{{\text{m}}}\) is considered to be 56 us/ft as an average value, according to the lithology of the area. The value for \(\Delta t_{{{\text{ml}}}}\) is considered to be equal to 169 us/ft, which is the velocity of the lithology identified in the studied region.

Any significant deviation from the normal trend corresponds to overpressure zones. According to Fig. 3, for the interval between 2200 and 2400 m, the pressure deviates from the normal trend line, which is identified as abnormal pressure zones (Fig. 3).

Fig. 3
figure 3

The sonic log (blue), normal sonic log (red) and gamma ray are sketched versus depth (vertical axis) in the overpressure area at well no. 44

Full size image

Having the values of well logging data, the pore pressure can be estimated. In Fig. 4, the estimated pore pressures are sketched against the formation pressures obtained using the repeated formation tests (RFT). As it can be seen, the estimated pore pressure is achieved with good precision.

Fig. 4
figure 4

The comparison of estimated pore pressure values (red spots) and the RFT values (blue spots) in well no. 44 and well no. 8

Full size image

As shown in Fig. 5, we identify an increase in pore pressure at a depth of 2200 m. At this depth, we see an abnormal change in the pore pressure, which is identified as the overpressure zone.

Fig. 5
figure 5

The pore pressure (red) and overburden pressure (blue) at well no. 44. The overpressure zone is identified at a depth of 2200 m. The pressures are measured in PSI

Full size image

Figure 6 shows the effective pressure in well no. 44 from the surface to the desired depth. As can be seen, effective pressure increases with increasing depth. It is important to notice that in the overpressure zone, the effective pressure is reduced due to an increase in the pore pressure.

Fig. 6
figure 6

Effective pressure in well no. 44 and well no. 8. As can be seen, effective pressure increases with increasing depth. Meanwhile, the effective pressure decreases in the overpressure zone

Full size image

Determination of in situ stresses using well logs

Determination of maximum and minimum horizontal stresses using vertical stress and pore pressure at well no. 44

Several methods are presented for estimating maximum and minimum horizontal stresses from the well logs. Zoback (2007) presents the following equations in order to determine the minimum and maximum horizontal stresses using vertical stress and the estimated pore pressure:

$$ \frac{{\sigma_{1} }}{{\sigma_{3} }} = \frac{{S_{{\text{V}}} - P_{{\text{P}}} }}{{S_{{{\text{hmin}}}} - P_{{\text{P}}} }} \le \left[ {\left( {\mu^{2} + 1} \right)^{\frac{1}{2}} + \mu } \right]^{2} $$
(9)
$$ \frac{{\sigma_{1} }}{{\sigma_{3} }} = \frac{{S_{{{\text{Hmax}}}} - P_{{\text{P}}} }}{{S_{{{\text{hmin}}}} - P_{{\text{P}}} }} \le \left[ {\left( {\mu^{2} + 1} \right)^{\frac{1}{2}} + \mu } \right]^{2} $$
(10)
$$ \frac{{\sigma_{1} }}{{\sigma_{3} }} = \frac{{S_{{{\text{Hmax}}}} - P_{{\text{P}}} }}{{S_{{\text{V}}} - P_{{\text{P}}} }} \le \left[ {\left( {\mu^{2} + 1} \right)^{\frac{1}{2}} + \mu } \right]^{2} $$
(11)

In these equations, \(S_{{\text{V}}}\) is the vertical stress, \(P_{{\text{P}}}\) is the pore pressure, μ is the coefficient of friction of the region which is considered to be 0.6 in this region. \(S_{{{\text{hmin}}}}\) is the minimum horizontal stress, \(S_{{{\text{Hmax}}}}\) is the maximum horizontal stress, \(\sigma_{1}\) and \(\sigma_{3}\) are the largest and smallest measured stresses, respectively. Equation (9) is presented in areas with normal faults, Eq. (10) is for regions with strike-slip faults, and Eq. (11) is used for regions with reverse faults.

As it is evident in Fig. 7, the minimum and maximum horizontal stresses increase with increasing depth. Notice that the minimum horizontal stress increases slightly in the overpressure zone, whereas the maximum horizontal stress decreases slightly in this zone. Hence, the mud window decreases in the overpressure zone.

Fig. 7
figure 7

Maximum and minimum horizontal stresses at well no. 44. Both stresses increase with increasing depth. In the overpressure zone, we see a slight increase in the minimum horizontal stress and a decrease in the maximum horizontal stress

Full size image

Figure 8 indicates a comparison between the vertical, maximum horizontal and minimum horizontal stresses, sketched against the calculated pore pressure at well no. 44.

Fig. 8
figure 8

Pore pressure (yellow graph), vertical stress (blue graph), minimum horizontal stress (green graph) and maximum horizontal stress (red graph) at well no. 44 and well no. 8

Full size image

Figure 9 shows the graph of the mud window in the studied well. As it can be seen, the mud window increases by increasing depth; however, the mud density decreases by entering the overpressure zone.

Fig. 9
figure 9

The mud window calculated at well no. 44. The mud window indicates a slight decrease in the overpressure zone

Full size image

Determination of the mud density using a pore pressure gradient

The mud density can be determined by dividing the pressure gradient to 0.052 (Zoback 2007).

Figure 10 indicates the graph of mud density (in ppg) for the studied well. This figure indicates that up to a depth of 2200 m, the well can be drilled with a mud density of about 8.33 ppg. However, in the overpressure interval the mud density should be increased to a value of 8.81 ppg in order to avoid formation collapse.

Fig. 10
figure 10

Suitable density of drilling mud at well no. 44 and well no. 8. In the overpressure interval, the mud density should be increased to 8.8 (ppg) and 9.1 (ppg) in well no. 8 and well no. 44, respectively, in order to avoid the formation collapse

Full size image

Conclusion

In this study, the pore pressure was estimated using the Zhang’s method and the results were compared with the RFT data for a case study at a well drilled in the South Pars field, Iran. The results indicate that the pore pressure of the formation is estimated with a good precision at the studied well location. In the overpressure interval, the vertical stress does not deviate from the normal trend, because the vertical stress depends essentially on the density and the fluids of the overburden rocks.

Upon entering the overpressure zone at the studied wells, the amount of vertical stress does not change, since the amount of vertical stress depends only on the density of the overlaying rocks and fluids. However, the minimum horizontal stress and maximum horizontal stress will change. These changes were examined at the well locations. Therefore, one of the alternative methods to determine an overpressure zone is that simultaneous abnormal changes in the minimum and maximum horizontal stresses will occur.

In the overpressure zone, the mud window is reduced which makes it difficult for the reservoir engineers to choose the appropriate mud density. In our case study, for the intervals above the overpressure zone (depth of 2200 m), a mud density of 8.33 ppg should be chosen; however, in the overpressure interval, the drilling mud density should be increased to a value of 8.8 ppg, in order to overcome the increase in the pore pressure. Integration of other types of data, such as seismic data attributes, can help in increasing the accuracy to estimate the in situ stresses.