Calculation of temperature profile in injection wells

Abstract

Injection wells have long been an essential asset in enhanced oil recovery, wastewater disposal and carbon dioxide sequestration in petroleum industries. The temperature profile of fluid flow in the injection well is one of the main parameters of interest for petroleum engineers to determine optimum injection conditions and wellbore completion design especially in thermal injection projects and deep wells. In this study, the calculation involved in determining the temperature profile along the depth of wellbore has been revised to be newer and more robust via solving governing wellbore equations. The wellbore is segmented into discrete counterparts for it to be solved simultaneously in terms of mass, momentum and energy balance via wellbore governing equations. Five injection cases from the literatures, incompressible and compressible fluid flows, were used to confirm that the procedure is reproducible in terms of its behaviour, which is similar to field data. The new results acquired from the new procedure are in good agreement with field data collected with a maximum absolute error less than 3 °C.

Introduction

Injection wells have long been an essential asset in enhanced oil recovery (EOR), wastewater disposal and carbon dioxide sequestration in petroleum industries (Hasan et al. 2002; Moradi 2013; Hamdi et al. 2014). The temperature of fluid flow in wellbore is one of the main parameters of interest for petroleum engineers. In-depth understanding of the pressure and temperature profiles along the depth of the well is a requirement for the appropriate design of well. The performance of hydrocarbon reservoirs can only be gauged with precise determination of downhole pressure and temperature. In addition to that to prevent damaging the formation by injecting above threshold pressure, extensive knowledge of the bottomhole pressure is useful. Although temperature can be measured by bottomhole gauge, the possibility of downhole gauge failure increases over a long period of time. Thus, the ability to calculate downhole parameters from surface injection parameters would be of great convenience (Paterson et al. 2008).

Currently, there are several accurate software packages that are available to calculate the temperature profile of flowing fluid along the depth of wellbore based on computational fluid dynamics (CFD) solutions (Fluent 2011). However, CFD solutions are rather slow and need a high capacity machine to run it; there is also the difficulty in model building for inexperienced users (Apak 2006). Also there are other types of software packages (Wellflo 2001; VFPi 2011) available for the determination of pressure and temperature profiles in the wellbore based on Ramey’s model (Ramey Jr 1962). The running speed of these packages is fast but Ramey’s model has been developed based on some assumptions that are not suitable for fluid flow at near critical point or deep injection wells (Messer et al. 1974; Alves et al. 1992; Yasunami et al. 2010). In addition to that there are some users who have reported difficulties in defining fluid thermodynamic properties in some of these commercial wellbore simulators.

In order to overcome these issues, this study is objectively conducted to develop a rapid and reliable procedure to determine pressure and temperature profiles free from the aforementioned limitations.

Methodology

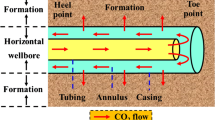
Simultaneous solving of equations governing the wellbore in terms of momentum, mass and energy balance has to be carried out for the calculation of temperature profile (Herrera et al. 1978; Fontanilla and Aziz 1982; Hasan et al. 2002; Paterson et al. 2008). The main components involved in the systems include tubing, insulation, casing and formation. Other elements involved are the fluid flowing through the tubing, annulus between the insulation and casing as well as the cement surrounding the casing (Moradi 2013). To begin finding resolution for the equations governing the wellbore, the system shown in Fig. 1 is discretized into N segments in the vertical direction to consider various fluid thermodynamic properties, overall coefficient of heat transfer, rate of heat transfer and heterogeneity of layers around the wellbore along the wellbore depth. The optimum value for length of segments is calculated by performing a sensitivity analysis (Yasunami et al. 2010). It is assumed that all variables within a segment remain constant. As shown in Fig. 2, the pressure and temperature of every segment are (Livescu et al. 2010):

Fig. 1

A schematic of the injection wellbore configuration

Fig. 2

A schematic of control volume

$$P_{\text{f}} = \frac{{P_{z} + P_{{z +\Delta {\text{z}}}} }}{2}$$

(1)

$$T_{\text{f}} = \frac{{T_{z} + T_{{z +\Delta {\text{z}}}} }}{2}$$

(2)

The density (ρ_f), viscosity (µ_f) and velocity (u_f) of the fluid in the segment can be calculated by knowing T_f, P_f and using a fluid thermodynamic properties table (Peng and Robinson 1976; National Institute of Standards and Technology 2011). For the calculation of fluid properties in the thermodynamic module, data published by the National Institute of Standards and Technology (NIST) is used for pure materials, and Peng–Robinson equation of state (Peng and Robinson 1976) is applied for calculating mixture properties.

Comparatively, the heat transferred along the wellbore is faster than the heat transferred in the layers surrounding the wellbore and the formation attributed to the small wellbore radius. Besides, the small wellbore radius also contributed to the rate of heat transfer reaching a steady state much sooner than in the formation as heat is transferred under unsteady state (Ramey Jr 1962; Fontanilla and Aziz 1982). Therefore, steady-state rate of heat transfer is made to solve the wellbore governing equations, while unsteady-state rate of heat transfer is made for the formation governing equation, without introducing significant errors.

Mass balance equation

The calculation of velocities at level z and z + ∆z is done using mass balance equation. In a steady-state condition and a given volume (Fig. 2), the flow of fluid within the tubing in accordance with the conservation of mass law is (Kreith et al. 2010):

$${\text{Mass}}\,{\text{in}} = {\text{Mass}}\,{\text{out}}$$

$$\dot{m}_{\text{in}} = \dot{m}_{\text{out}} = \dot{m}_{\text{f}}$$

(3)

where $\dot{m}$ is defined by:

$$\dot{m} = \rho uA$$

(4)

The combination of Eqs. (3) and (4) calculates the velocities at level z and z + ∆z as follows:

$$u_{z} = \frac{{\dot{m}_{\text{f}} }}{{\rho_{z} *A_{z} }}$$

(5)

and

$$u_{{z +\Delta {\text{z}}}} = \frac{{\dot{m}_{\text{f}} }}{{\rho_{{z +\Delta {\text{z}}}} *A_{{z +\Delta {\text{z}}}} }}$$

(6)

The radius of the tubing is constant (Ali 1981; Fontanilla and Aziz 1982). The Internal area of the tubing equals:

$$A_{\text{tubi}} = A_{z} = A_{{z +\Delta {\text{z}}}} = \pi r_{\text{tubi}}^{2}$$

(7)

Momentum balance equation

In a steady-state condition, momentum equation is the basic governing equation utilized for the calculation of its pressure gradient. The total forces acting on the fluid element is equivalent to the momentum change in the fluid; in the wellbore, the forces present are pressure, friction and gravity (Hasan et al. 2002; Pan et al. 2007; Paterson et al. 2008; Livescu et al. 2010). For a given control volume (Fig. 2):

$$(P_{z} A_{z} - P_{z + \Delta z} A_{z + \Delta z} ) - F + (A_{\text{tubi}} g\rho_{\text{f}} { \sin }\left( \theta \right)\Delta z) = (\dot{m}_{\text{f}} u_{z + \Delta z} - \dot{m}_{\text{f}} u_{z} )$$

(8)

The term F is the loss in momentum as a result of friction, and it is depicted by (Hasan et al. 2002; Pan et al. 2007; Paterson et al. 2008; Livescu et al. 2010):

$$F = \pi r_{\text{tubi}} \frac{{fv_{\text{f}}^{2} \rho_{\text{f}} }}{4}\Delta z$$

(9)

By substituting (7) and (9) in (8), simplifying, rearranging and dividing both sides of (9) by A_tubi, there will be:

$$P_{{z +\Delta {\text{z}}}} = P_{z} - \frac{{f*u_{\text{f}}^{2} *\rho_{\text{f}} }}{{4*r_{\text{tubi}} }}\Delta z + g\rho_{\text{f}} { \sin }(\theta )\Delta z - \frac{{\dot{m}_{f} }}{{\pi *r_{\text{tubi}}^{2} }}(u_{{z +\Delta {\text{z}}}} - u_{z} )$$

(10)

For calculating pressure by (10), the Moody friction factor (f) should be defined is usually an expression of Reynolds number:

$$Re = \frac{{2*r_{\text{tubi}} *u_{\text{f}} *\rho_{\text{f}} }}{{\mu_{\text{f}} }}$$

(11)

Generally, empirical correlations in computer calculations are used to determine Moody friction factor. Laminar flow is defined when Reynolds number (Re) is < 2400, friction factor is inversely related to Reynolds number [40].

$$f = \frac{64}{Re}$$

(12)

Turbulent flow is defined when Reynolds number (Re) ≥ 2400. In this condition, the friction factor is dependent on both Reynolds number and pipe roughness (Chen 1979; Pan et al. 2007). In a turbulent flow condition, the empirical correlation presented by Chen (1979) for determining f is:

$$f = \left( { - 2{ \log }\left( {\frac{{\frac{{\varepsilon_{\text{tubi}} }}{{2r_{\text{tubi}} }}}}{3.7065} - \frac{5.0452}{Re}\log \varLambda } \right)} \right)^{ - 2}$$

(13)

where

$$\varLambda = \frac{{\left( {\frac{{\varepsilon_{\text{tubi}} }}{{2r_{\text{tubi}} }}} \right)^{1.1098} }}{2.8257} + \left( {\frac{7.149}{Re}} \right) ^{0.8981}$$

(14)

Energy Balance Equations

The difference in temperatures between wellbore fluid flow and strata around the wellbore leads to an exchange of energy. The energy balance equation for every segment must be solved to calculate heat transfer rate in each element of the system as shown in Fig. 2 (Ramey Jr 1962; Hasan et al. 2002, 2010). In a steady-state system, the general energy balance is (Ramey Jr 1962; Hasan et al. 2002; Kreith et al. 2010):

$$\begin{array}{c}{{\text{rate}}\,{\text{of}}\,{\text{energy}}} \\{{\text{leaving}}\,{\text{system}}\,{\text{by}}} \\{{\text{outflow}}} \end{array}- \begin{array}{c}{{\text{rate}}\,{\text{of}}\,{\text{energy}}} \\{{\text{entering}}\,{\text{system}}\,{\text{by}}} \\{{\text{inflow}}} \end{array}= \begin{array}{c}{{\text{rate}}\,{\text{of}}\,{\text{heat}}\,{\text{added}}\,{\text{or}}} \\{{\text{left}}\,{\text{to}}\,{\text{system}}} \end{array}+ \begin{array}{c}{{\text{rate}}\,{\text{of}}\,{\text{work}}\,{\text{done}}} \\{{\text{on}}\,{\text{system}}} \end{array}$$

$$\Delta e + \Delta {\text{k}} + \Delta {\text{p}} = q - w$$

(15)

From (15) for the given control volume (Fig. 2), there is:

$$\left( {e_{z + \Delta z} - e_{z} } \right) + \frac{{(u_{z + \Delta z}^{2} - u_{z}^{2} )}}{2} - g\sin \left( \theta \right)\Delta z = \frac{Q}{{\dot{m}_{\text{f}} }} - (P_{z + \Delta z} v_{z + \Delta z} - P_{z} v_{z} )$$

(16)

The definition of enthalpy gives (Kreith et al. 2010):

$$h = Pv + e$$

(17)

Rearrangement of (17) and replacement of Pv + u by h yield:

$$\left( {h_{z + \Delta z} - h_{z} } \right) + \frac{{(u_{z + \Delta z}^{2} - u_{z}^{2} )}}{2} - g \sin \left( \theta \right)\Delta z = \frac{Q}{{\dot{m}_{\text{f}} }}$$

(18)

In (18), heat generation rate is only accounted for by a single term on the right due to the loss in flow friction and the rate of conductive heat transfer between wellbore and surrounding formation. Nevertheless, the rate of heat generated by flow friction loss is so minute that it is negligible (Pan et al. 2007; Paterson et al. 2008).

By rearranging (18), the following equation is obtained:

$$h_{z + \Delta z} = h_{z} - \frac{{(u_{z + \Delta z}^{2} - u_{z}^{2} )}}{2} + g*\sin \theta *\Delta z + \frac{Q}{{\dot{m}_{\text{f}} }}$$

(19)

In a steady-state condition, the rate of heat flowing through a wellbore of the segment is written as (Hasan et al. 2010):

$$Q = 2*\pi *r_{\text{tubo}} U_{\text{to}} \left( {T_{\text{f}} - T_{\text{cemo}} } \right)\Delta z$$

(20)

that

$$U_{\text{to}} = \left( {\frac{{r_{\text{tubo}} }}{{r_{\text{tubi}} h_{\text{f}} }} + \frac{{r_{\text{tubo}} \ln \frac{{r_{\text{tubo}} }}{{r_{\text{tubi}} }}}}{{k_{\text{tub}} }} + \frac{{r_{\text{tubo}} \ln \frac{{r_{\text{inso}} }}{{r_{\text{insi}} }}}}{{k_{\text{ins}} }} + \frac{{r_{\text{tubo}} }}{{r_{\text{ins}} \left( {h_{\text{r}} + h_{\text{c}} } \right)}} + \frac{{r_{\text{tubo}} \ln \frac{{r_{\text{caso}} }}{{r_{\text{casi}} }}}}{{k_{\text{cas}} }} + \frac{{r_{\text{tubo}} \ln \frac{{r_{\text{cemo}} }}{{r_{\text{cemi}} }}}}{{k_{\text{cem}} }}} \right)^{ - 1}$$

(21)

where

$$h_{\text{r}} = \frac{{\left( {T_{\text{inso}} + 273.15 + T_{\text{casi}} + 273.15} \right)\left((T_{\text{inso}} + 273.15)^{2} + (T_{\text{casi}} + 273.15)^{2} \right)\sigma }}{{\frac{1}{{\epsilon_{\text{inso}} }} + \frac{{r_{\text{inso}} }}{{r_{\text{casi}} }}\left( {\frac{1}{{\epsilon_{\text{casi}} }} - 1} \right)}}$$

(22)

and

$$h_{\text{c}} = \frac{{k_{\text{c}} }}{{r_{\text{inso}} \ln \frac{{r_{\text{casi}} }}{{r_{\text{inso}} }}}}$$

(23)

and

$$h_{\text{r}} = \frac{{\left( {T_{\text{inso}} + 273.15 + T_{\text{casi}} + 273.15} \right)\left((T_{\text{inso}} + 273.15)^{2} + (T_{\text{casi}} + 273.15)^{2} \right)\sigma }}{{\frac{1}{{\epsilon_{\text{inso}} }} + \frac{{r_{\text{inso}} }}{{r_{\text{casi}} }}\left( {\frac{1}{{\epsilon_{\text{casi}} }} - 1} \right)}}$$

(24)

h_r can be calculated if T_inso and T_casi are known.

Heat flow rate through the earth and wellbore/formation interface

The surrounding of the wellbore system that acts as a heat source or sink is known as the formation. The transfer of heat between wellbore fluid and the surrounding earth is attributed to their temperature difference. For modelling heat flow in the earth, first, the temperature profile has to be modelled in the formation. Heat transfer in the formation around the wellbore is dictated by the conduction mechanism instead of the convection mechanism (Ramey Jr 1962; Hasan and Kabir 1991; Moradi 2013; Moradi and Awang 2013). The Laplace transform was used by Hasan and Kabir (1991) to model the temperature profile of the formation. This was done following an approach taken by Van Everdingen and Hurst (1949) for pressure transients using a comparable set of equations. Thus, the definition of dimensionless temperature, T_D, is:

$$T_{\text{D}} = \frac{{2\pi k_{\text{e}} (T_{\text{cemo}} - T_{\text{e}} )}}{Q}\Delta z$$

(25)

where

$$T_{\text{e}} = \left( {T_{\text{s}} + a*\left( {z + \frac{\Delta z}{2}} \right)} \right)$$

(26)

They assumed surrounding layers around the wellbore are homogeneous with constant heat flow rate at the wellbore/formation interface. It is discovered that the following algebraic expressions for dimensionless temperature, T_D, in terms of dimensionless time, t_D, have quite accurately represented the solution.

$${\text{If}}\, \,t_{\text{D}} \le 1.5: T_{\text{D}} = 1.1281\sqrt {t_{\text{D}} } (1 - 0.3\sqrt {t_{\text{D}} } )$$

(27)

$${\text{If}}\,\, t_{\text{D}} > 1.5: T_{\text{D}} = \left( {0.4063 + 0.5\ln (t_{\text{D}} )} \right)\left( {1 + \frac{0.6}{{t_{\text{D}} }}} \right)$$

(28)

where

$$t_{\text{D}} = \frac{{k_{\text{e}} t}}{{\rho_{\text{e}} C_{\text{e}} r_{\text{cemo}}^{2} }}$$

(29)

By rearranging (25):

$$Q = \frac{{2\pi k_{\text{e}} (T_{\text{cemo}} - T_{\text{e}} )}}{{T_{\text{D}} }}\Delta z$$

(30)

Temperature for the fluid flow and wellbore assembly

Fluid temperature

The assumption that temperature, pressure and flow velocity are constant in a cross section of inside the tubing (T_f, P_f and v_f) is made due to the small ratio between tubing diameter and length. Thus, the flow is considered being one-dimensional (Hasan et al. 2002; Yasunami et al. 2010). The high heat transfer film coefficient [e.g. h_f of water is 2839–11,356 W/(m² °C)] renders the thermal resistance of fluid flow negligible as it offers little resistance to heat flow. Since T_f = T_tubi (Yasunami et al. 2010).

Tubing temperature

High conductivity metal is used to make the tubing [e.g. k of steel is 43.275 W/(m °C)]; hence, the temperature distribution is considered negligible and T_tubi = T_tubo (Ali 1981).

Insulation temperature

By using heat connectivity equation (Kreith et al. 2010):

$$T_{\text{inso}} = T_{\text{tubo}} - \frac{{\frac{\Delta Q}{\Delta z}\ln \frac{{r_{\text{inso}} }}{{r_{\text{tubo}} }}}}{{2*\pi *k_{\text{ins}} }}$$

(31)

Annulus temperature

There is a temperature profile across the annulus. Normally, an average temperature of the outer surface of the insulation and inner surface of the casing is assumed as annulus temperature, T_an (Pourafshary et al. 2009; Hasan et al. 2010):

$$T_{\text{an}} = \frac{{T_{\text{inso}} + T_{\text{casi}} }}{2}$$

(32)

Casing temperature

High conductivity metal is used to make the casing [e.g. k of steel is 43.275 W/(m °C)]; hence, the temperature distribution is considered negligible and T_casi = T_caso (Yasunami et al. 2010); so by neglecting the thermal resistance of the casing:

$$T_{\text{casi}} = T_{\text{caso}} = T_{\text{cemo}} + \frac{{r_{\text{tubo}} *U_{\text{to}} *\ln \frac{{r_{\text{cemo}} }}{{r_{\text{caso}} }}}}{{k_{\text{cem}} }}\left( {T_{\text{f}} - T_{\text{cemo}} } \right)$$

(33)

Cement temperature

Equating (20) and (25), then solving for T_cemo, gives:

$$T_{\text{cemo}} = \frac{{r_{\text{tubo}} *U_{\text{to}} *T_{\text{D}} *T_{\text{f}} + k_{\text{e}} *T_{\text{e}} }}{{r_{\text{tubo}} *U_{\text{to}} *T_{\text{D}} + k_{\text{e}} }}$$

(34)

Calculation steps of the new procedure

As stated in the objectives, a procedure is presented to predict the fluid flow pressure and temperature profiles in the injection well by using equations derived in the previous sections. Input data needed to run the new procedure include P, T and $\dot{m}_{\text{f}}$ of injection flow at wellhead, r_tubi, r_tubo, r_inso, r_casi, r_caso, r_cemo, k_ins, k_cem, k_e, $\rho_{\text{e}}$, $C_{\text{e}}$, T_s, $\varepsilon_{\text{tubi}}$, $C_{\text{an}}$, $\mu_{\text{an}}$, $k_{\text{a}}$, $\epsilon_{\text{inso}}$, and $\epsilon_{\text{casi}}$. The well is discretized into N segments and a procedure as shown below is use in all segments:

• Step 1 Assign a random value for T at level z + ∆z. The temperature at level z can be used for initial guess.

• Step 2 Assign a random value for P at level z + ∆z. The pressure at level z can be used for initial guess.

• Step 3 Using a thermodynamic module determines the density, enthalpy and viscosity of fluid at level z and z + ∆z.

• Step 4 Determine the average properties of the segment at P_f and T_f by (1) and (2), respectively. Then, calculate ρ_f, µ_f and v_f at T_f and P_f in the thermodynamic module.

• Step 5 Resolve momentum equation and calculate P at level z + ∆z by (10).

• Step 6 Compare the calculated P at level z + ∆z from step 5 with the assumed P from step 2. If (calculated P − assumed P) < 0.001 (kPa), the procedure has converged and vice versa. When non-convergent of the procedure occurs, return to step 2, assumed P = calculated P and repeat the procedure until same values are obtained.

• Step 7 Assign a random value for the ∆Q/∆z (for initial guess ∆Q/∆z = 0).

• Step 8 Determine the geothermal temperature (T_e) by (26).

• Step 9 Equate T_casi to the geothermal temperature, T_e.

• Step 10 Calculate the value T_ins by (31).

• Step 11 Calculate U_to by (21).

• Step 12 Calculate the T_cemo by (34).

• Step 13 Calculate the T_casi by (33).

• Step 14 Compare the calculate T_casi from step 13 with step 9, if ABS(old T_casi− new T_casi) < 0.01 (°C), the procedure is assumed to have converged and go to step 17 else go to step 15.

• Step 15 Determine the corresponding ∆Q/∆z from (20) based on the calculated T_cemo from step 12 and go to Step 10 and repeat until convergent of the procedure.

• Step 16 Determine the specific enthalpy at level z + ∆z by (19).

• Step 17 Determine the T_z+∆z at P_z+∆z and h_z+∆z in developed thermodynamic module.

• Step 18 Compare the calculated T at level z + ∆z from step 17 with the assumed T from step 1, if ABS(calculated T − assumed T) < 0.01 (°C), convergent of the procedure is assumed. If there is a non-convergent of procedure, return to step 1, assumed T = calculated T and repeat until convergent of procedure is obtained.

Figure 3 represents the flowchart of the calculation procedure.

Fig. 3

Procedure for calculating the pressure and temperature profiles along the borehole

Validation

Validation is a necessity in ensuring the validity of the mathematical formulation, solution techniques, and program coding. The validity of the new procedure is examined against three water injection cases, one carbon dioxide injection case and one steam injection case to confirm that the procedure is reproducible in terms of its behaviour, and in agreement with collected field data. A computer code in Visual C#.net environment has been programmed in order to easily implement the new procedure shown in Fig. 3 for various cases.

Case 1 Figure 4 compares results of the new procedure against the field data taken from Nowak (1953). Water at a surface temperature of 28.33 °C was injected at the rate of 0.0016 m³/s through 0.1778 m casing diameter for three years. There, the calculated temperature exceeded the measured temperatures, but the difference is small. The maximum discrepancy over the depth is 2.39 °C.

Fig. 4

Comparison of temperature distribution with well depth from Nowak (1953) and predicted by the new procedure

Case 2 For further verification on the performance of the procedure presented, newly calculated results using the procedure are compared with those presented by Squier et al. (1962). The problem concerned hot water injection at a surface temperature of 148.8889 °C into a 914.4 m vertical well at a rate of 0.0018 m³/s through 0.178 m casing diameter. The comparison made between the results from the new procedure and those presented by Squier et al. is shown in Fig. 5. The temperature profiles from both Squier et al. and the new procedure agreed quite well with each other. Comparison of the results predicted by the new procedure with the data reported by Squier et al. showed average absolute per cent relative deviation of 0.22.

Fig. 5

Comparison of bottomhole temperature versus time from Squier et al. (1962) with predicted by the new procedure

Case 3 As a third case, the computer code was examined with cold water injection, data from Ramey Jr (1962). Water was injected at 0.0088 m³/s through 0.162 m casing diameter for a period of 75 days. Injection temperature was 14.7222 °C at the wellhead. The results from the new procedure agree quite well with Ramey’s results as shown in Fig. 6. Comparison of the results predicted by the new procedure with Ramey’s data showed that the maximum discrepancy over the depth is 0.81 °C.

Fig. 6

Comparison of temperature distribution with well depth from Ramey Jr (1962) and predicted by the new procedure

Case 4 For the confirmation of the validity of the proposed procedure for compressible fluid, a comparison was made with the data presented in the study of Cronshaw and Bolling (1982). At the time of the survey, carbon dioxide at a surface temperature of 13.39 °C was injected at a rate of 163.871 m³/s. Figure 7 revealed a fairly good match between bottomhole temperatures of carbon dioxide after 7 days of injection as reported by Cronshaw and Bolling with that predicted by the new procedure. Cronshaw and Bolling reported the bottomhole temperature as 25.22 °C. The present procedure predicted a value of 26.36 °C.

Fig. 7

Comparison of bottomhole temperatures from Cronshaw and Boling (1982) and predicted by the new procedure

Case 5 For further validation of the model, results calculated using the new procedure are compared with those presented by Satter (1965). Superheated steam was injected into a vertical well at a mass flow rate of 0.63 kg/s at 537.78 °C and 3.45 MPa. Figure 8 showed a good agreement between the calculated results and Satter’s results after 3.65 days injection. Comparison of the results predicted by the new procedure with the results reported by Sattar showed an average absolute per cent relative deviation of 0.15.

Fig. 8

Comparison of temperature distribution with well depth from Satter (1965) and predicted by the new procedure

Application of the new procedure

Input data needed to run the new procedure are listed as the following:

• Surface parameters: P, T and $\dot{m}_{\text{f}}$ of injection flow at wellhead.

Well completion facilities:

• I. Radius: r_tubi, r_tubo, r_inso, r_casi, r_caso and r_cemo.

• II. Thermal properties: k_ins, k_cem, $\varepsilon_{\text{tubi}}$, $C_{\text{an}}$, $\mu_{\text{an}}$, $k_{\text{a}}$, $\epsilon_{\text{inso}}$$\epsilon_{\text{casi}}.$

• • Formation properties: T_s, k_e, ρ_e and C_e.

The main outputs of the new procedure are pressure and temperatures profiles along the depth of wellbore.

Beside those, the new procedure calculates the below items:

• Geothermal temperature versus depth.

• Heat transfer through each facility of the well completion.

• Heat transfer through layers around the wellbore.

• Kinetic energy, potential energy.

• Contribution of changing the kinetic energy and potential energy for building the temperature profile.

• Contribution of changing the hydrostatic gradient, acceleration gradient, and frictional gradient for building the pressure profile.

The new procedure that was proposed in this study is useful for the following applications:

• Comparing measured data with calculated data This could be for one of several purposes, such as evaluating “match parameters” which are difficult or impossible to measure, pipe roughness, or determining if a well is behaving the way it is expected to (i.e. to detect faulty components).

• Monitoring work such as predicting bottomhole pressure from measured surface pressure and flow rate.

• Conducting a design work where it is required to calculate the pressure and temperature drop in the wellbore such as: to determine the best diameter of the tubing and injection flow rate.

The coupled response from fluid movement in the wellbore to the reservoir is neglected that is the main limitation of the new workflow. This is important during early stage of production or injection as the fluid flows under unsteady conditions specially during well testing. To handle this issue, the new producer must be coupled to a reservoir simulator. Also it needs to add unsteady-state formulations to calculate the energy balance.

Conclusions

The main output of this study is a non-isothermal wellbore simulator. This new simulator discretizes the wellbore to several segments and considers various thermodynamic properties and overall heat transfer coefficient for every segment. The ability of the new simulator to calculate its own overall heat transfer coefficient holds substantial benefit over commercial software packages. The validity of the new procedure and computer code has been examined in various scenarios against the results from the literatures and they agreed quite well with each other.