Introduction

Transient flow forms the basis of a domain of reservoir engineering called pressure transient analysis (PTA), also known as well test interpretation, which is used for volumetric estimation, well deliverability, reservoir characterisation and efficient field management. However, its accuracy depends on precise analysis and integrated reservoir studies. For over four decades, well testing has been transformed from a level mainly interested in determining a well’s productivity to a sophisticated discipline capable of characterising the reservoir geometry, boundary and heterogeneity (Weiland 2008; Nnadi and Onyekonwu 2004; Freddy 2004; Kamal et al. 2005; Jackson and Banerjee 2000; Landa et al. 2000; Zakirov et al. 2006). Pressure transient analysis (PTA) depends strongly on complex equations of fluid flow for a well flowing at a constant rate, and its analytical solution is limited to single-phase flow (Zheng 1997, 2006) which in real case is never the situation due to well operational constraints and fluid mobility.

This paper introduced the statistical and numerical density derivative developed from the fundamental of PTA which assumed that there is a small change in fluid-phase densities at the wellbore and the phases flow independently. In this study, the density derivatives from the DTA solution and pressure–density equivalent derivative are generated from Horne (1995) mathematical derivative equation or the new statistical derivative equation by Biu and Zheng (2015). The statistical and numerical density derivative serves as a support tool for better interpretation and estimation of reservoir properties in these conditions.

The statistical method

This section introduces the new statistical method for diagnosing flow regime for both flowing and shut-in conditions. The method utilises the 2nd differencing of pressure and time series since pressure change and subsurface flow rate are nonstationary series and then integrate the residual of its 1st differences using simple statistical functions such as sum of square error SSE, standard deviation, moving average MA and covariance of data to formulate the model.

The statistical approach utilised simple statistical function such as the product and exponential of 1st and 2nd difference of a well bottom-hole flowing or shut-in pressure tied to the standard deviation; and sum of square difference of 1st difference residual series to generate the statistical diagnostic models such as StatDiv, StatSSE, StatDev, StatExp, StattDev and StatDdev. These models help to identify key flow regimes for reservoir description and serve as checkbox to the derivative approach for better interpretation of complex features.

If n values P 1, P 2,…, P n of a time series are observed, the first difference of the time series values P 1, P 2,…, P n are;

$$ \Delta P_{t} = P_{0} - P_{i} $$
(1)

where i = 1, 2, 3,…, t n

$$ {\text{StatDiv}}\left( i \right) = \frac{{\Delta P_{i} }}{{P_{i} }} $$
(2)

and

$$ {\text{StatSSE}}\left( i \right) = \left[ {\frac{{\Delta P_{i} }}{{P_{2} }}} \right]^{{\frac{{\delta {\text{dev}}}}{\text{SEE}}}} $$
(3)

where \( \frac{{\delta {\text{dev}}}}{\text{SEE}} = \left[ {\frac{{{\text{STDEVP}}\left( {{\text{StatDiv}}(\Delta P)} \right)}}{{{\text{STEYX}}\left( {{\text{StatDiv}}\left( {\Delta P} \right),\Delta^{2} P\left( i \right)} \right)}}} \right]^{{}} \) and Δ2 P(i) = ΔP(i + 1) − ΔP(1)

Equations (2) and (3) are known as model A and B. These are similar to semi-log pressure–time curve developed by Miller et al. (1950) and Horner (1951) but differ completely in terms of sharp contrast between each flowing regimes which is clearly seen, thus better approach for wellbore and reservoir parameters estimation to support interpretation from conventional, type-curve and derivative methods. These semi-log models are simple to generate and good for easy identification of different flow regimes to obtain reliable reservoir properties.

For better reservoir characterisation, six statistical models mimicking the log–log pressure derivative approach are derived using the steps below;

First, the 1st pressure and time differencing are obtained:

$$ \begin{aligned} \Delta P_{t} = P_{0} - P_{i} \hfill \\ \Delta t_{t} = t_{i + 1} - t_{i} \hfill \\ \end{aligned} $$
(4)

Then, the divided 1st differencing for pressure and time is derived:

$$ \Delta {\text{dev}}\left( i \right) = \frac{{\Delta P\left( {i + 1} \right)}}{\Delta P\left( 2 \right)} $$
(5)
$$ \Delta tt_{t} = \Delta t_{i} /\Delta t_{i + 1} $$
(6)

The residual for the pressure and time differencing are generated using the statistical functions such as standard deviation between data points:

$$ \delta \Delta pt\left( i \right) = {\text{STDEV}}\left( {\Delta tt\left( {i + 1} \right),\left( {i + 2} \right),\Delta^{2} P\left( {i + 1} \right),\left( {i + 2} \right)} \right) $$
(7)

To reduce the noise effect arising from the differencing, the square root of the standard deviation of the 1st differencing and the divided 1st differencing for pressure is obtained:

$$ pdd\left( i \right) = {\text{SQRT}}\left( {\delta \Delta pt\left( i \right) \times {\text{STDEV}}\left( {\Delta {\text{dev()}},\Delta^{2} P()} \right)} \right) $$

Finally, the six statistical models for flow regime diagnosis are given as:

Model 1:

$$ {\text{StatDev}}1\left( i \right) = {\text{SQRT}}\left( {pdd\left( i \right) \times \Delta {\text{dev}}\left( i \right) \times \Delta^{2} P\left( i \right)} \right) $$
(8)

Model 2: The exponential function

$$ {\text{StatExp}}\,\left( i \right) = {\text{SQRT}}\left( {{\text{EXP}}\left( {{\text{SQRT}}\left( {\Delta^{2} P} \right)} \right)} \right) \times pdd\left( i \right) \times \Delta^{2} P\left( i \right) $$
(9)

Model 3:

$$ {\text{StatdDev}}\left( i \right) = {\text{SQRT}}\left( {pdd\left( i \right) \times \Delta {\text{dev}}\left( i \right) \times \Delta^{2} P\left( i \right) \times \Delta^{2} P\left( i \right)} \right) $$
(10)

Model 4: The time function

$$ {\text{StattDev}}\left( i \right) = {\text{STDEV}}\left( {\Delta tt\left( i \right),\Delta tt\left( {i + 1} \right),{\text{StatDev}}\left( i \right),{\text{StatDev}}\left( {i + 1} \right)} \right) $$
$$ {\text{StatDev}}2\left( i \right)^{0.4} = \left( {\Delta p(i + 1) - \Delta p(i)} \right) \times pdd(i) \times \frac{{\Delta {\text{dev}}(i)}}{\Delta p(i)} \times {\text{Exp}}\left( {\frac{\Delta tt(i)}{\Delta tt(i + 1)}} \right) $$

Model 5:

$$ + \sqrt {\left( {t_{i + 1}^{2} + t_{i}^{2} } \right) - \left( {t_{i}^{2} - t_{i - 1}^{2} } \right)} \times \frac{\delta \Delta pt(i)}{\Delta p(i)} $$
(11)

Model 6:

$$ {\text{StatDev}}3\left( i \right)^{2} \,= \left( {\frac{\Delta p(i + 1)}{\Delta p(0)}} \right) \times \sqrt {\Delta p(i)} + {\text{Exp}}\left( {\frac{\Delta tt(i)}{\Delta tt(i + 1)}} \right) \times \delta \Delta pt(i) \times pdd(i) $$
(12)

Equations (8)–(12) are regarded as statistical pressure diagnostic models for interpreting pressure transient data. These are similar to the log–log derivative method developed by Tiab (1975), Tiab and Kumar (1976a, b) and Bourdet et al. (1983), and are reliable diagnostic tools for flow regimes identification and reservoir characterisation. They are also used for estimating wellbore and reservoir parameters in order to support the interpretation from the derivative method or type-curve after the analysis. The workflows for generating these models are shown in Figs. 17 and 18, and summary of the models is presented in Fig. 1. The statistical models are tested with design, field and synthetic data.

Fig. 1
figure 1

Summary of statistical models for flow regime identification

Full size image

Theoretical concept of the density derivatives

The basic concept involved in the derivation of fluid flow equation (Ayestaran et al. 1989; Tiab and Kumar 1976a, b; Bourdet et al. 1983) includes:

  1. 1.

    Conservation of mass equation,

  2. 2.

    Transport rate equation (e.g. DARCY’s Law),

  3. 3.

    Equation of State

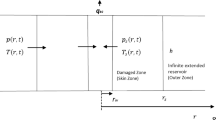
Consider a flow in a cylindrical coordinates with flow in angular and z-directions neglected, the equations are given as follows:

$$ {\text{Mass}}\,{\text{rate}}\,{\text{in}} - {\text{Mass}}\,{\text{rate}}\,{\text{out}}\,{\text{Mass}}\,{\text{rate}}\,{\text{storage}} $$
(13)

The above Eq. (1) represents the conservation of mass. Since the fluid is moving, the equation

$$ q = - \frac{k}{\mu }A\frac{\partial p}{\partial r} $$
(14)

is applied. By conserving mass in an elemental control volume and applying transport rate equation, the following equation is obtained:

$$ - \left[ {\frac{2\pi rhk}{\mu }\rho \frac{\partial p}{\partial r}} \right]_{r} = - \left[ {\frac{2\pi rkh}{\mu }\rho \frac{\partial p}{\partial r}} \right]_{r + \Delta r} +\, 2\pi r\Delta rh\frac{\partial }{\partial t}\left( {\rho \phi } \right) $$
(15)

Expanding the equation using Taylor Series

$$ \frac{1}{r}\frac{\partial }{\partial r}\left[ {\frac{rk\rho }{\mu }\frac{\partial p}{\partial r}} \right] = \frac{\partial }{\partial t}\left[ {\rho \phi } \right] $$
(16)

For slight or compressibility liquid,

$$ \rho = \rho_{i} e^{{c\left[ {p - p_{i} } \right]}} $$
(17)

Substituting for pressure in the equation, the diffusivity equation in terms of density is given as:

$$ \frac{{\partial^{2} \rho }}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial \rho }{\partial r} = \frac{{\phi \mu \left[ {c + cr} \right]}}{k}\frac{\partial \rho }{\partial t} $$
(18)
$$ \frac{{\partial^{2} \rho }}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial \rho }{\partial r} = \frac{{\phi \mu c_{t} }}{k}\frac{\partial \rho }{\partial t} $$
(19)

Equation (19) is known as the density radial diffusivity equation which can also be rewritten in form of pressure. Equations (13)–(19) applies to both liquid and gas. The density or pressure term in Eq. (19) can be replaced by the correct expression in terms of density or pressure. Over four decades, the pressure transient test analysis has applied the general diffusivity equation in pressure term to generate several nonunique solutions applying different well, reservoir and boundaries condition constraints with pressure-rate data. Equation (19) is rewritten for each phase as shown below assuming independent fluid-phase behaviour.

For gas phase

$$ \frac{1}{r}\frac{\partial \rho }{\partial r}\left[ {r\frac{{\partial \rho {}_{g}}}{\partial r}} \right] = \frac{{\phi \mu_{g} c}}{{k_{g} }}\frac{{\partial \rho_{g} }}{\partial t} $$
(20)

For oil phase

$$ \frac{1}{r}\frac{\partial \rho }{\partial r}\left[ {r\frac{{\partial \rho {}_{o}}}{\partial r}} \right] = \frac{{\phi \mu_{o} c}}{{k_{o} }}\frac{{\partial \rho_{o} }}{\partial t} $$
(21)

For water phase

$$ \frac{1}{r}\frac{\partial \rho }{\partial r}\left[ {r\frac{{\partial \rho {}_{w}}}{\partial r}} \right] = \frac{{\phi \mu_{w} c}}{{k_{w} }}\frac{{\partial \rho_{w} }}{\partial t} $$
(22)

Invariably as in pressure term for outer and inner boundary conditions, the density term is also implored as follows:

$$ \frac{{\partial^{2} \rho }}{\partial r} + \frac{1}{r}\frac{\partial \rho }{\partial r} = \frac{1}{r}\frac{\partial }{\partial r}\left( {r\frac{\partial \rho }{\partial r}} \right) = 0 $$
(23)

For inner boundary condition

$$ \left[ {r\frac{\partial \rho }{\partial r}} \right]_{rw} = \frac{q\mu }{2\pi kh}c_{\text{oi}} \rho_{\text{oi}} \, = \,{\text{Constant}} $$
(24)

Outer boundary condition

$$ \rho = \rho_{e} \,{\text{at}}\,r = r_{e} $$
(25)

Density radial flow equation derivation for each fluid phase

For slightly and small compressibility fluid such as water and oil, the isothermal compressibility coefficient c, in terms of density is given as:

$$ c = \frac{1}{\rho }\frac{\partial \rho }{\partial p} $$
(26)

Rearranging the parameters w.r.t ∂P and ∂ρ

$$ - c\int_{{p_{i} }}^{p} {{\text{d}}p = \int_{{\rho_{i} }}^{\rho } {\frac{\partial \rho }{\rho }} } $$
(27)

Integrating

$$ e^{{c\left[ {P_{i} - P} \right]}} = \frac{\rho }{{\rho_{i} }} $$
(28)
$$ p = p_{i} - \frac{{\ln \left[ {\frac{\rho }{{\rho_{i} }}} \right]}}{c} $$
(29)

OrApplying the e x expansion series,

$$ e^{x} = 1 + x + \frac{{x^{2} }}{2!} + \frac{{x^{3} }}{3!} + \cdots + \frac{{x^{n} }}{n!} $$
(30)

Because the term c[ρ i  − ρ] is very small, the e x term can be approximated as:

$$ e^{x} = 1 + x $$

Therefore, Eq. (29) can be rewritten as:

$$ \rho = \rho_{i} \left[ {1 - c\left( {p_{i} - p} \right)} \right] $$
$$ p = p_{i} - \left[ {\frac{{\frac{\rho }{{\rho_{i} }} + 1}}{c}} \right] $$
(31)

Presently, there are limited oil and gas wells installed with bottom-hole fluid density gauges for measuring fluid densities changes at the wellbore during flowing and shut-in testing conditions. However, for simplification and application of the density derivative in existing well test softwares, the density-pressure equivalent equation is derived.

For slight or compressibility liquid such as oil and water, the pressure–density equivalent algorithm of the fluid density changes at the wellbore as derived is given as:

PDENO and PDENW:

$$ p = p_{\text{oi}} - \left[ {\frac{{\frac{\rho }{{\rho_{\text{oi}} }} + 1}}{{c_{o} }}} \right]\quad {\text{and}}\quad p = p_{\text{wi}} - \left[ {\frac{{\frac{\rho }{{\rho_{\text{wi}} }} + 1}}{{c_{w} }}} \right] $$
(32)

Equations (29) and (31) are the pressure–density equivalent algorithm for slightly compressible fluid such as oil and water

From Eqs. (29) and (31),

$$ p = p_{\text{oi}} - \frac{{\ln \left[ {\frac{\rho }{{\rho_{\text{oi}} }}} \right]}}{c}\,{\text{or}}\,p = p_{\text{oi}} - \left[ {\frac{{\frac{\rho }{{\rho_{\text{oi}} }} + 1}}{c}} \right] $$

Differentiating with respect to ρ

$$ \frac{\partial P}{\partial \rho } = - \frac{1}{{c_{\text{oi}} \rho_{\text{oi}} }}\quad{\text{and}}\quad\partial P = - \frac{\partial \rho }{{c_{\text{oi}} \rho_{\text{oi}} }} $$
(33)

From Darcy equation flow equation

$$ q = - \frac{2\pi kh}{\mu }r\frac{\partial P}{\partial r} $$
(34)

Substitute for ∂P

$$ q = - \frac{2\pi kh}{\mu }{\raise0.7ex\hbox{$r$} \!\mathord{\big/ {\vphantom {r {c_{\text{oi}} \rho {}_{\text{oi}}}}}\kern-0pt} \!\lower0.7ex\hbox{${c_{\text{oi}} \rho {}_{\text{oi}}}$}}\frac{\partial \rho }{\partial r} $$
(35)

To derivate the density transient analytical equation for slightly and small compressibility phase, the following assumption is applicable:

  • There is small change in fluid densities at the wellbore

  • The fluid phase flow independently

  • Rock density is constant

Radial diffusivity equation for oil phase from Eq. (21) is given as

$$ \frac{1}{r}\frac{\partial \rho }{\partial r}\left[ {r\frac{\partial \rho }{\partial r}} \right] = \frac{\phi \mu c}{k}\frac{\partial \rho }{\partial t} $$
(36)

Initial condition

$$ \rho \left( {r,t = 0} \right) = \rho_{i}^{{}} $$
(37)

BC at the wellbore

$$ \mathop {\lim }\limits_{r \to 0} \frac{2\pi kh}{\mu }{\raise0.7ex\hbox{$r$} \!\mathord{\big/ {\vphantom {r {c_{\text{oi}} \rho {}_{\text{oi}}}}}\kern-0pt} \!\lower0.7ex\hbox{${c_{\text{oi}} \rho {}_{\text{oi}}}$}}\frac{\partial \rho }{\partial r} = Q $$
(38)

BC at infirmity

$$ \mathop {\lim }\limits_{r \to \infty } \rho \left( {r,t} \right) = \rho_{i} $$
(39)

Applying boundary conditions

Then

$$ \rho \left( {r,t} \right) = \rho_{i} - \frac{{\mu Qc_{\text{oi}} \rho_{\text{oi}} }}{4\pi kh}\left[ {\ln \left[ {\frac{2.246kt}{{\phi \mu cr^{2} }}} \right] + 0.80907} \right] $$
(40)

Plotting ρ wb(t) versus ln (t) will yield a straight line at longer time and the slope of the line is given as:

$$ \frac{{\partial \rho_{\text{wb}} }}{\partial \ln t} = m_{\text{oil}} = \frac{{\mu Qc_{\text{oi}} \rho_{\text{oi}} }}{4\pi kh} $$
(41)

Therefore,

$$ kh = \frac{{\mu Qc_{o} \rho_{o} }}{{4\pi m_{\text{oil}} }} $$
(42)

Similarly for water phase, the radial density equation is given as:

$$ \rho \left( {r,t} \right) = \rho_{i} - \frac{{\mu Qc_{\text{wi}} \rho_{\text{wi}} }}{4\pi kh}\left[ {\ln \left[ {\frac{2.246kt}{{\phi \mu cr^{2} }}} \right] + 0.80907} \right] $$
(43)

Plotting ρ wb(t) versus ln (t) will yield a straight line at longer time and the slope of the line is given as:

$$ \frac{{\partial \rho_{\text{wb}} }}{\partial \ln t} = m_{\text{water}} = \frac{{\mu Qc_{\text{wi}} \rho_{\text{wi}} }}{4\pi kh} $$
(44)

where

$$ kh = \frac{{\mu Qc_{\text{wi}} \rho_{\text{wi}} }}{{4\pi m_{\text{water}} }} $$
(45)

Equations (40) and (43) are the density transient analytical solution for slightly compressible fluid such oil and water used for generating density derivatives and specialised density time plot for further interpretation.

For gas phase: for compressible fluid for isothermal conditions

$$ c = - \frac{1}{v}\left[ {\frac{\partial v}{\partial p}} \right]_{T} $$
(46)

For real gas equation of state

$$ v = \frac{nRTz}{p} $$

Differentiating the above equation with respect to pressure at constant temperature

$$ \left( {\frac{\partial v}{\partial p}} \right)_{T} = nRT\left[ {\frac{1}{p}\left( {\frac{\partial z}{\partial p}} \right) - \frac{z}{{p^{2} }}} \right] $$
(47)

Substituting into Eqs. (47) into (46) gives

$$ c_{g} = \frac{1}{p} - \frac{1}{z}\left[ {\frac{{{\text{d}}z}}{{{\text{d}}p}}} \right] $$

In terms of density

$$ c_{g} = \frac{1}{p} - \frac{1}{\rho }\left[ {\frac{\partial \rho }{\partial p}} \right] $$
(48)

This equation is applicable for real gas condition.

Rearranging the parameters w.r.t to ∂P and ∂ρ

$$ \int_{{\rho_{i} }}^{\rho } {\frac{\partial \rho }{\rho }} = \int_{{p_{i} }}^{p} {\left[ {\frac{\partial p}{p} - \partial pc_{g} } \right]} $$

Applying the power series for ln p

$$ \ln \left[ \rho \right] = \left[ {\rho - 1} \right] - \frac{{\left[ {\rho - 1} \right]^{2} }}{2} + \cdots + \frac{{\left[ { - 1} \right]^{n} \left[ {\rho - 1} \right]^{n} }}{n} + \cdots 0 < \rho \le 2 $$
(49)

Limit ln x to only the 1st term only

$$ \left[ {\frac{\rho }{{\rho_{i} }}} \right] - 1 = \left[ {\frac{p}{{p_{i} }}} \right] - 1 - \left[ {p - p_{i} } \right]c_{g} $$
(50)

For compressible fluid such as gas, the pressure–density equivalent algorithm as derived is given as: PDENG

$$ p = \frac{{\frac{{p_{\text{gi}} \rho }}{{\rho_{o} }} - p_{\text{gi}}^{2} c_{g} }}{{1 - p_{\text{gi}} c_{g} }} $$
(51)

Equation (51) is the pressure–density equivalent algorithm for compressible fluid such as gas. Bottom-hole flowing or shut-in fluid-phase densities from field, design or synthetic data generated from simulation software with wellbore densities keywords for each phase can be converted to pressure–density equivalent using Eqs. (32) and (51). Pressure equivalent from the fluid-phase densities are then analysed in any of the well test software.

Also the density weighted average, PDENA, is used to obtain the pressure–density equivalent for a two or three phase combination. The pressure–density equivalent derived from the densities for all three fluid components such as gas, oil and water is given as

$$ {\text{PDENA}}\,P{}_{i} = \frac{{\rho_{g} p_{i} + \rho_{o} p_{o} + \rho_{w} p_{w} }}{{\rho_{g} + \rho_{o} + \rho_{w}^{{}} }} $$
(52)

From Eq. (51)

$$ p = \frac{{p_{\text{gi}} \rho - p_{\text{gi}}^{2} \rho_{\text{gi}} c_{g} }}{{\rho_{\text{gi}} \left( {1 - p_{\text{gi}} c_{g} } \right)}} $$

And

$$ \partial p = \frac{{p_{\text{gi}} }}{{\rho_{\text{gi}} \left( {1 - p_{\text{gi}} c_{g} } \right)}}\partial \rho $$
(53)

From the fundamental real gas equation

$$ n = \frac{pv}{zRT} $$
(54)

At standard condition

$$ \frac{pv}{zT} = \frac{{p_{\text{sc}} v_{\text{sc}} }}{{T_{\text{sc}} }} $$
$$ q = \frac{{p_{\text{sc}} }}{{T_{\text{sc}} }}\frac{{Q_{\text{sc}} }}{5.615}\left( {zT} \right) = \frac{2\pi kh}{\mu }r\frac{p\partial p}{\partial r} $$
(55)

where \( \partial p = \frac{{p_{\text{gi}} }}{{\rho_{\text{gi}} \left( {1 - p_{\text{gi}} c_{g} } \right)}}\partial \rho \) and \( \alpha = \frac{{p_{\text{gi}} }}{{\rho_{\text{gi}} \left( {1 - p_{\text{gi}} c_{g} } \right)}} \)

$$ \partial p = \alpha \partial \quad \rho \quad {\text{and}}\,p = \rho RzT $$

From the diffusivity equation for gas

$$ \frac{1}{r}\frac{\partial \rho }{\partial r}\left[ {r\frac{{\partial \rho {}_{g}}}{\partial r}} \right] = \frac{{\phi \mu_{g} c}}{{k_{g} }}\frac{{\partial \rho_{g} }}{\partial t} $$
(56)

Initial condition

$$ \rho \left( {r,t = 0} \right) = \rho_{i}^{{}} $$
(57)

BC at the wellbore

$$ \mathop {\lim }\limits_{r \to 0} \frac{4\pi kh\alpha R}{\mu }\left( {\frac{{5.615T_{\text{sc}} }}{{\rho_{\text{sc}} }}} \right)r\rho \frac{\partial \rho }{\partial r} = Q $$
(58)

BC at infirmity

$$ \mathop {\lim }\limits_{r \to \infty } \rho \left( {r,t} \right) = \rho_{i} $$
(59)

Applying boundary conditionsThen

$$ m\left( {\rho_{\text{wf}} } \right) = m\left( {\rho_{i} } \right) - \frac{\mu Q}{4\pi kh\alpha R}\left( {\frac{{p_{\text{sc}} }}{{5.615T_{\text{sc}} }}} \right)\left[ {\ln \left[ {\frac{2.246kt}{{\phi \mu cr^{2} }}} \right] + 0.80907} \right] $$
(60)
$$ \frac{{\partial m\left( {\rho_{\text{wb}} } \right)}}{\partial \ln t} = m_{\text{gas}} = \frac{\mu Q}{4\pi kh\alpha R}\left( {\frac{{p_{\text{sc}} }}{{5.615T_{\text{sc}} }}} \right) $$
(61)

Equation (60) is the density transient analytical solution for compressible fluid such as gas used for generating density derivatives and specialised density time plot for further interpretation.

Plotting ρ 2wb (t) or m(ρ wb) versus ln (t) will yield a straight line at longer time, and the slope of the line is given as:where

$$ kh = \frac{\mu Q}{4\pi kh\alpha R}\left( {\frac{{p_{\text{sc}} }}{{5.615T_{\text{sc}} }}} \right)\frac{1}{{m_{\text{gas}} }} $$
(62)

Figure 2 shows example of the specialised semi-log plot of fluid densities versus time (Horner/Agarwal time, Horner 1951; Agarwal et al. 1970) for permeability estimation, and Fig. 3 depicts the expected density derivatives for each fluid phase generated from Horne (1995) and Biu and Zheng (2015).

Fig. 2
figure 2

Specialised diagnostic semi-log plot of fluid densities (gas, oil and water phase) versus Horner time

Full size image
Fig. 3
figure 3

Diagnostic log–log plots of fluid densities (gas, oil and water) derivatives versus time

Full size image

The logarithm density derivative function can be expressed as;

$$ \frac{{{\text{d}}\Delta \rho }}{{{\text{d}}\ln t}} = t\frac{{{\text{d}}\Delta \rho }}{{{\text{d}}t}} $$
(63)

Horne (1995) formulates a mathematical model for the pressure derivative which can be written in terms of fluid density as follow;

$$ \left( {\frac{\partial \rho }{\partial \ln t}} \right) = t\left( {\frac{\partial \rho }{\partial t}} \right)_{i} - A $$
(64)
$$ A = \frac{{\ln \left( {{\raise0.7ex\hbox{${t_{i} }$} \!\mathord{\left/ {\vphantom {{t_{i} } {t_{i - k} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${t_{i - k} }$}}} \right)\Delta \rho_{i + j} }}{{\ln \left( {{\raise0.7ex\hbox{${t_{i + j} }$} \!\mathord{\left/ {\vphantom {{t_{i + j} } {t_{i} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${t_{i} }$}}} \right)\ln \left( {{\raise0.7ex\hbox{${t_{i + j} }$} \!\mathord{\left/ {\vphantom {{t_{i + j} } {t_{i - k} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${t_{i - k} }$}}} \right)}} + \frac{{\ln \left( {{\raise0.7ex\hbox{${t_{i + j} t_{i - k} }$} \!\mathord{\left/ {\vphantom {{t_{i + j} t_{i - k} } {t_{i}^{2} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${t_{i}^{2} }$}}} \right)\Delta \rho_{i} }}{{\ln \left( {{\raise0.7ex\hbox{${t_{i + j} }$} \!\mathord{\left/ {\vphantom {{t_{i + j} } {t_{i} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${t_{i} }$}}} \right)\ln \left( {{\raise0.7ex\hbox{${t_{i} }$} \!\mathord{\left/ {\vphantom {{t_{i} } {t_{i - k} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${t_{i - k} }$}}} \right)}} - \frac{{\ln \left( {{\raise0.7ex\hbox{${t_{i + j} }$} \!\mathord{\left/ {\vphantom {{t_{i + j} } {t_{i} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${t_{i} }$}}} \right)\Delta \rho_{i + k} }}{{\ln \left( {{\raise0.7ex\hbox{${t_{i} }$} \!\mathord{\left/ {\vphantom {{t_{i} } {t_{i - k} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${t_{i - k} }$}}} \right)\ln \left( {{\raise0.7ex\hbox{${t_{i + j} }$} \!\mathord{\left/ {\vphantom {{t_{i + j} } {t_{i - k} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${t_{i - k} }$}}} \right)}} $$

or the statistical pressure derivative formulated by Biu and Zheng (2015), transformed into density form as follows:

$$ {\text{StatdDev}}\left( i \right)^{0.4} \,= \left( {\Delta \rho (i + 1) - \Delta \rho (i)} \right) \times \rho dd(i) \times \frac{{\Delta {\text{dev}}(i)}}{\Delta \rho (i)} \times {\text{Exp}}\left( {\frac{\Delta tt(i)}{\Delta tt(i + 1)}} \right) $$
$$ + \sqrt {\left( {t_{i + 1}^{2} + t_{i}^{2} } \right) - \left( {t_{i}^{2} - t_{i - 1}^{2} } \right)} \times \frac{\delta \Delta \rho t(i)}{\Delta \rho (i)} $$
(65)
$$ {\text{StatdDev}}\left( i \right)^{2} = \left( {\frac{\Delta \rho (i + 1)}{\Delta \rho (0)}} \right) \times \sqrt {\Delta \rho (i)} + {\text{Exp}}\left( {\frac{\Delta tt(i)}{\Delta tt(i + 1)}} \right) \times \delta \Delta \rho t(i) \times \rho dd(i) $$
(66)

In this study, the fluid-phase density and pressure–density equivalent derivatives are generated from Eqs. (64) or (65), (66) (Horne 1995; Biu and Zheng 2015).

Average permeability k estimation

An empirical model integrating the fluid-phase permeabilities for a given set of bottom-hole fluid density data is formulated to estimate the average reservoir permeability. The mathematical model is given as:

$$ k_{\text{ave}} = \sqrt[4]{{k_{\text{o}} k_{\text{w}} k^{2}_{\text{g}} }} $$
(67)

where

k o = oil phase permeability

k g = gas phase permeability

k w = water phase permeability

With the estimation of the phase’s permeabilities, it is therefore possible to estimate the possible relative permeability for each phase and the percentage each phase contribution to flow at one point analysis; hence at several point, the relative k can be generated.

To investigate comprehensively the application of this approach, three case studies in oil and gas reservoirs are considered. Case 1 is an example design data from application well test software; case 2 is a field data from offshore Nigeria, while case 3 is a synthetic data generated from numerical model built with commercial simulator. The simulator keywords were local refinement bottom-hole pressure, LBPR; local refinement oil density, LDENO; local refinement water density, LDENW; local refinement gas density, LDENG; and well bottom-hole pressure, BHP, were outputs to obtain the density and pressure change around the well and as far as the perturbation could extend.

Examples

Example 1: design data—low k reservoir with closed boundary

Table 1 presents a summary of the well and reservoir data of a designed BHP obtained from the examples of application well test software (Windowstm Application Well test Software 1995) simulating the drawdown test using parameters in Table 1. The reservoir permeability range is ≥70 mD, with light oil PVT properties. The well capacity is above 2500 bbl/days with initial reservoir pressure close to 6000 psi. It is required to generate the pressure–density equivalent and derivative for each phase, compare their diagnostic signatures and also estimate the phases permeabilities and average reservoir permeability

Table 1 Reservoir and fluid data (Windowstm Application Welltest Software 1995)
Full size table

This drawdown test shows the effect of a closed boundary response at late time period. In Fig. 4, the StatDev depicts a radial flow regime with a unit slope straight line at late time indicating a close boundary response. The derivative also exhibits similar radial and boundary response. The StatDiv and StatSSE plots as shown in Fig. 5 also indicate two flow regimes (radial pseudosteady) supporting the reservoir and boundary response diagnosed by the StatDev. Nevertheless, noisy data is noticed within the radial region of both StatDev and the derivative.

Fig. 4
figure 4

Comparisons of StatDdev and StattDev diagnostics approach

Full size image

Another validation of the radial pseudosteady response is clearly seen by plotting three other statistical models such as StatDdev, StatExp and StattDev as shown in Figs. 4 and 6. All three models depict same reservoir response at both the middle and late time period. This also serves as checkbox to improve interpretation of reservoir features diagnosed with the log–log pressure derivative.

Fig. 5
figure 5

StatSSE and StatDiv semi-log for low K boundary response

Full size image

Reservoir characterisation

Estimated permeability and skin are 71.3 mD and 12.1, respectively, using the statistical derivative approach. In comparison with the pressure derivative method, k and S differ by 13 and 77%, respectively. Difference in result is related to the slope of the pressure time semi-log specialised plot which depends on the extent of the transient period as identified from the statistical models and conventional derivative log–log plot. Figure 7 shows the pressure time semi-log plot for reservoir properties estimation. Table 2 is a summary of calculated results from the conventional, type-curve and statistical approach.

Fig. 6
figure 6

Comparisons of four statistical diagnostic models for reservoir with boundary conditions

Full size image
Table 2 Build-up analysis results
Full size table
Fig. 7
figure 7

Miller et al. (1950) semi-log for low K boundary response

Full size image

Example 2: field data—homogenous system, no boundary limit

Table 3 presents a summary of the well and reservoir data of Field Y in Offshore Niger Delta Nigeria used for the build-up interpretation with additional well log information given in Fig. 8. In this example, only the statistical and convention ‘pressure’ derivative method will be analysed and used to estimate average reservoir permeability.

Table 3 Reservoir and fluid data
Full size table
Fig. 8
figure 8

Well log and petrophysical data

Full size image

Other information includes:

  • Appraisal well, penetrated several reservoir levels, located in conventional offshore Niger Delta

  • Structural maps indicating hydrocarbons in crestal part of the block with some possible potential in the eastern part

  • Reservoir facies associations and their lateral correlation, high sand to shale ratio, suggesting very good reservoir potential.

  • Amalgamated channel fill or delta front facies associations constituting continuous coalescing sandstone bodies in a rather constant stacking pattern.

Data screening and derivative calculation

Figure 9 shows the flowing and shut-in pressure with distortion prior to the beginning of flow with the main section for interpretation unaffected. Six hundred pressure points per log circle are applied to the conventional and statistical ‘pressure’ derivative.

Fig. 9
figure 9

Production and shut-in data

Full size image

Method comparison and permeability k calculation

An exponential smoothing method with α = 0.02 was used to smooth all three cases. The statistical ‘pressure’ derivative shown in Fig. 10 depicts a clear radial stabilisation fingerprint without boundary effect. The response behaves like an infinite acting system which is continuous, without noise. StatDev depicts a continuous drop in derivative which could be increasing mobility features away from the well which can be seen from the well log in Fig. 8; however, there is no available geological information on increasing thickness away from the well.

Fig. 10
figure 10

Comparison of conventional and statistical derivatives versus time

Full size image

The k ave estimated from equation \( k = \frac{141.2qB\mu }{mh} \) is between 3100 and 4100 mD depending on the movement of the derivative flat line. This is within the range of uniform k from core sample and existing well test interpretation for this reservoir; a good estimation of permeability is justifiable.

Generally, the field cases reviewed show the robustness of the statistical ‘pressure’ and numerical density derivatives applicable in pressure transient analysis. The results demonstrated that clearer radial flow regimes can be visualised with increasing confidence on formation permeability estimation. Also, individual fluid-phase permeability can be estimated in multiphase condition for better reservoir characterisation with improved understanding of the true contribution of each phase to flow at the sand face.

Example 3: synthetic data

a → : Flowing + Build-up Sequence: Well perforated hp = 30 ft between oil and water layer. Net sand thickness h = 250 ft.

In this case, the well is completed between the oil and water layer to mimic multiphase conditions at the wellbore and some distance away from the well in order to capture the pressure distribution, fluid densities change around the wellbore, then analyse their pressure–density equivalent and density derivatives fingerprint and estimate the fluid-phase permeabilities k using the specialised density time plot and k ave from the empirical model for three phase condition (Table 4).

Table 4 Reservoir and fluid data
Full size table

Pressure–density equivalent derivatives

The derivative in Fig. 11 shows a good radial flow but drop in derivative at late time driven by numerical artefact and constant pressure effect. A continuous drop is seen from 10 h in all fluid phase’s derivative signatures, confirming the strong presence of this feature. The derivatives for all fluid phase depict same well and reservoir fingerprint (3 flow regimes, early to late time response) but with different dp’ stabilisation. PDENA derivative displays a better and longer stabilisation period compared to BHP (Fig. 12).

Fig. 11
figure 11

Conventional BHP and three fluid phases pressure–density equivalent derivatives versus time and k estimates. All three fluid phase (gas, oil and water) with good stabilisation with estimated k for each phase \( k = \frac{141.2qB\mu }{mh} \)

Full size image
Fig. 12
figure 12

Conventional BHP derivative versus time showing good stabilisation with numerical artefact effect \( \frac{{{\text{d}}\Delta \rho }}{{{\text{d}}\ln t}} = t\frac{{{\text{d}}\Delta \rho }}{{{\text{d}}t}} \)

Full size image

A permeability value of 50.8 mD is estimated from the BHP where \( k = \frac{162.7qB\mu }{mh} \) and m obtained from the specialised plot. This is an approximate of the input value in the simulation model. Also PDENG and PDENO give 15.8 and 403.7 mD, respectively, while PDENA = PDENW = 50.8 mD. At h = 50 ft, the best k estimate is obtained depicting h = 50 ft as the optimise thickness contributing to flow. At h > 50 ft, k drop below the k imputed in the model. Using empirical Eq. (67):

$$ k_{\text{ave}} = \sqrt[4]{{k_{o} k_{w} k^{2}_{g} }} $$
$$ k_{\text{ave}} = \sqrt[4]{{403.7 \times 50.8 \times 15.8^{2} }} $$
$$ k_{\text{ave}} = 47.3\,{\text{mD}} $$

Obtained k ave = 47.3 mD is approximately close to the BHP estimates, hence a good estimate of the fluid-phase permeabilities.

Direct numerical density derivatives

Result from each phase density derivatives derived from the DTA solution depicts better reservoir fingerprint which is continuous and without noise for the gas and water phase density derivatives as shown in Figs. 13 and 14. This is in support of the PDENA interpretation with longer stabilisation. However, the oil phase derivative shows similar fingerprint as the pressure–density equivalent and BHP derivatives response in Figs. 11 and 12.

Fig. 13
figure 13

Oil and gas densities derivative versus time showing good stabilisation without numerical artefact in the gas density derivative \( \frac{{{\text{d}}\Delta m\left( {\rho_{w} } \right)}}{{{\text{d}}\ln t}} = t\frac{{{\text{d}}\Delta m\left( {\rho_{w} } \right)}}{{{\text{d}}t}},\,\frac{{{\text{d}}\Delta \rho_{o} }}{{{\text{d}}\ln t}} = t\frac{{{\text{d}}\Delta \rho_{o} }}{{{\text{d}}t}} \)

Full size image
Fig. 14
figure 14

Fluid phase (water) density derivative versus time showing good stabilisation without numerical artefact in the water density derivative \( \frac{{{\text{d}}\Delta \rho_{w} }}{{{\text{d}}\ln t}} = t\frac{{{\text{d}}\Delta \rho_{w} }}{{{\text{d}}t}} \)

Full size image

Applying the radial DTA solution derived in Eqs. (40), (43) and (60), the data are analysed with the semi-log plot of wellbore flowing density for each phase (oil, water and gas) plotted against Horner time as shown in Figs. 15 and 16.

Fig. 15
figure 15

Specialised semi-log oil and gas phase densities versus Horner time

Full size image
Fig. 16
figure 16

Specialised semi-log water phase density versus Horner time

Full size image

** Q used for k calculation is the average rate for all flowing periods.

The calculated slope of the radial flowing period from the semi-log plot for oil and water phases are given as:

$$ \frac{{\partial \rho_{w} }}{\partial \ln t} = m_{\text{oil}} = \frac{{162.7\mu Qc_{o} \rho_{o} }}{kh} = - 0.009 $$

and

$$ \frac{{\partial \rho_{w} }}{\partial \ln t} = m_{\text{water}} = \frac{{162.7\mu Qc_{o} \rho_{o} }}{kh} = - 0.0003 $$

The estimated phase permeabilities are

$$ k_{\text{oil}} = \frac{{162.7\mu Qc_{o} \rho_{o} }}{{hm_{\text{oil}}^{{}} }} = 445\,{\text{mD}} $$

and

$$ k_{\text{water}} = \frac{{162.7\mu Qc_{o} \rho_{o} }}{{hm_{\text{water}}^{{}} }} = 50\,{\text{mD}} $$

Also for the gas phase:The calculated slope from the semi-log plot is given as:

$$ \frac{{\partial m\left( {\rho_{w} } \right)}}{\partial \ln t} = m_{\text{gas}} = \frac{1637\mu Q}{kh\alpha R} = - 1.2195 $$

And estimated gas phase permeability is given as:

$$ k_{\text{gas}} = \frac{{1637\mu Q_{o} }}{{h\alpha Rm_{\text{gas}}^{{}} }} = 17.0\,{\text{mD}} $$

Using the empirical model for all three phase, the average estimated permeability

$$ k_{\text{ave}} = \sqrt[4]{{50 \times 445 \times 17.0^{2} }} $$
$$ k_{\text{ave}} = 50\,{\text{mD}} $$

Discussion and conclusion

In this study, we introduced a new technique for analysing and interpreting reservoir pressure transient data as well as estimating reservoir properties. So far, two PTA diagnostic methods have been discussed and tested with synthetic and field data, these include: (1) statistical ‘pressure’ derivative and (2) numerical density transient analytical DTA (numerical density derivative). Also we present the workflow for easy application of the algorithms and the mathematical radial density diffusivity equation and analytical DTA solutions for PTA interpretation (Figs. 17, 18). We have described in detail how the models were developed and their application.

Fig. 17
figure 17

Workflow for statistical models formulation using pressure data

Full size image
Fig. 18
figure 18

Statistical models for flow regime identification

Full size image

In the field data in example 1, the statistical derivative depicts good radial stabilisation, indicating the robustness of approach. Likewise for the synthetic data presented in example 2, result shows the same wellbore and reservoir fingerprint for the conventional method (BHP) and fluid-phase pressure–density equivalent derivatives except the PDENA with longer stabilisation. However, from the direct numerical density analysis, the gas and water phase density derivatives depict better radial stabilisation making it suitable for permeability estimation. Each of the fluid-phase permeabilities is determined (k oil = 445 mD, k gas = 17 mD, k water = 50 mD), and the three phase fluid empirical model developed for average effective k ave is used to estimate the actual k. Result ranges from 43 to 50 mD which is within that used in the simulation model and also estimated from BHP.

With synthetic and field data, the numerical density and statistical derivatives yield a clearer reservoir radial flow regime and therefore estimate formation permeability with higher level of confidence. Additionally, there was a better estimation of individual fluid phase permeability, reflecting the contribution of each phase to flow at a given point; therefore, the formation effective and phase permeabilities can be derived with confidence. Summarily, the numerical density transient analysis DTA solution is a robust approach for interpreting multiphase flow condition which is presently limited to only numerical well testing approach. The pressure–density equivalent and numerical density derivatives can derive individual phase permeability along with good visualisation of each phase derivative response which gives the true picture of the reservoir response, and this ensures that the derived permeability is right from the formation radial flow.