Introduction

Steamflooding is a process in which steam is injected into the reservoir that it transfers its heat to the rock and fluids. Generally, there are four separated zones in a steamflooding process namely (1) oil bank, (2) hot water bank, (3) solvent bank, and (4) steam zone (Hong 1994). This process occurs while the oil bank moves toward the production well. After the pore is saturated with steam, the steam tends to move to the top of the reservoir since it is lighter than reservoir fluids. Therefore, in a continuous injection process, the steam will breakthrough early to the production well. Even though the steam injection rate remains constant, the oil production rate decreases while the steam oil ratio (SOR) increases. Because the steam is produced by way of burning natural gases, in such a process the CO2 emission per produced-oil volume also increases.

In order to avoid early steam breakthrough, the first approach was steamflooding followed by hot water-flooding, which was successfully applied in the Kern River field. It was found that the production increased after the hot water had been injected. The main reason for such a strategy is that it would prevent a significant loss in production rate. It might also improve the sweep efficiency and prevents the migration of the left-behind oil into the portions of the reservoir which had been swept by the steam (Ault et al. 1985). The further approach was water alternating steam process (WASP). Section 13D of West Coalinga Field was the first WASP pilot project. They claimed that WASP eliminated early steam breakthrough and channeling problems, reduced fuel consumption for steam generation and improved incremental oil sale (Hong and Stevens 1990). A successful WASP has also been reported in some other fields such as North Palo Seco, Apex Quarry, Central Las Bajo, and Bennett Village (Ramlal and Singh 2001).

Although most of WASP projects have been applied successfully, studies on WASP have rarely been reported in the literature. To fill this gap, this paper proposes a “response surface correlation” generated by an experimental design and response surface methodology to investigate the economy and CO2 emission problems. In this method, the operating conditions are varied to achieve the maximum NPV, the side effect CO2 emission is calculated, and the most sensitive operating conditions are identified.

Methodology overview

Response surface methodology is a collection of mathematical and statistical techniques that is useful for modeling and analyzing problems. In this method, the relationships between response and unknown-independent variables are established (Douglas 2001). If the problem is simple enough, then the response might be well modeled by a linear function. Furthermore, if the problem is more complicated, the equation may be described by second order as follows:

$$y = \beta_{0} + \beta_{1} x_{1} + \beta_{2} x_{2} + \beta_{3} x_{1}^{2} + \beta_{4} x_{2}^{2} + \cdots + \beta_{k} x_{k}^{n} + \hbox{C}$$
(1)

where β k are constant coefficients, x is the independent variable, k is the factor coefficient, n is the order of equation, and Є is an error. In order to estimate the response, the ANOVA method is applied. There are several functions which can used to approximate the response such as first-order, second-order, or third-order functions depending on the complexity of variable relationships. To understand the response, one needs to do the experiment design. The foundational principle of this is to select a set of variable combinations from a number of scenarios while it is still adequate to build the relationship among the independent variables and the response at a certain confidence level.

To achieve such an objective, three-level factorial design is used in this study. Four variables including WASP-start, WASP-cycle, steam injection rate, and oil price are varied. The full combination variables generate 81 scenarios. Afterward, D-optimal design with a confidence level of 95% is used to create 27 scenarios to minimize the number of runs. In each of the scenarios, an economic analysis and CO2 emission calculation are performed. Figure 1 displays the workflow used in this study. First, a basic reservoir model is built. After that, steamflooding is applied to the model. Following the standard term of CO2 emission from gas fuel (US Environmental Protection Agency 2004), the amount of CO2 emission generated is observed. The NPV and CO2 emission equations are shown briefly below:

$${\text{NPV}} = \sum\limits_{t = 0}^{N} {\frac{{{\text{NCF}}_{t} }}{{\left( {1 + i} \right)^{t} }}}$$
(2)
$${\text{CO}}_{2} \;{\text{emission}}\;\left( {\text{kg}} \right) = 50 \times {\text{heat}}\;{\text{employed}}\;\left( {\text{GJ}} \right)$$
(3)
Fig. 1
figure 1

Flowchart of the work

Full size image

The next step is evaluating the outcomes of each scenario. If the optimum condition cannot be found in this area of design space, the search is continued in another area following a steepest-ascent direction.

Reservoir model

A thermal reservoir simulator, STARS Version 2012 developed by Computer Modeling Group, is used to construct the reservoir model and to investigate the performance of the WASP. The reservoir model which represents a generic formation in Duri Field, Indonesia, is selected for this study with the pertinent data described in Table 1. A reversed seven-spot pattern is used with an injection well is located in the center surrounded by 6 production wells as illustrated in Fig. 2.

Table 1 Pertama/kedua reservoir properties (Gael et al. 1995)
Full size table
Fig. 2
figure 2

Schematic 3D view of the model

Full size image

The assumptions in this model include homogeneous reservoir, no gas cap, and no bottom water drive. The distance between the production and injection wells is 75 m representing the typical well configuration in Duri Field. The total grid number is 47 × 41 × 5 (i, j, k), and the size is 3.19 m in i- and j-directions and 7.52 m in k-direction. The temperature of the steam and hot water injection is 204 and 95 °C, respectively. Furthermore, the reservoir model uses 0.65 of steam quality.

Result and discussions

As mentioned, four variables are analyzed to generate the correlation. The first variable is WASP-start, which defines the time when the WASP is started to apply. There are three values for this variable which are 1, 4, and 8 years. When the maximum value is used, it means the WASP is not applied because the project life is 8 years. The second variable is WASP-cycle, which defines the period of a cycle in which the steam and hot water injection are alternated. The third variable is steam injection rate, which defines the steam or hot water injection rate per day. The fourth variable is oil price, which is the oil price per barrel. Table 2 shows the independent variables and their range of values used in this work.

Table 2 Range of parameters for this research
Full size table

Economic assumptions

An economic analysis is performed for each scenario using a common set of general assumptions in steamflooding projects in shallow reservoirs. The steam generation capital cost is $1.1E6 for a 150 m3/day-capacity, and the water treatment capital cost is $1.1E6 for a 200 m3/day-capacity (Frauenfeld et al. 2006). The well cost is assumed to be $0.3E6 for the thermal well and $0.4E6 for the two production wells (equivalent to 6 wells in a seven-spot pattern). The exploration cost is set to be $0.1E6 per pattern. The natural gas cost is assumed to be $4.33/GJ. The water treatment cost is $1/barrel of water production and the fixed cost is assumed to be 0.45 MM$/year and the interest rate is 12% per annual. In order to calculate the net cash flow (NCF), we used equation below:

$${\text{NCF}} = \left[ {{\text{Gross}}\;{\text{revenue}}} \right] - \left[ {{\text{Well}}\;{\text{cost}}\;\left( {{\text{thermal}}\;{\text{well}} + {\text{Non}}\;{\text{thermal}}\;{\text{well}} + {\text{Exploration}}\;{\text{cost}}} \right)} \right] - \left[ {{\text{Steam}}\;{\text{generation}}\;{\text{cost}}} \right] - \left[ {{\text{Water}}\;{\text{treatment}}\;{\text{cost}}} \right] - \left[ {{\text{Natural}}\;{\text{gas}}\;{\text{cost}}} \right] - \left[ {{\text{Fixed}}\;{\text{cost}}} \right]$$
(4)

By using standard term on CO2 and economy above, Table 3 displays the NPV and CO2 emission calculation results. To calculate the NPV, Eqs. (2) and (4) have been employed. The gross revenue is function of oil production rate as result from reservoir simulation. The CO2 emission is calculated by Eq. (3). The heat employed is also calculated by reservoir simulation.

Table 3 NPV and CO2 calculations for each scenario
Full size table

Fitted model

The relationship between the independent variables and the response is constructed using the quadratic model. By using this model, the relationship between the independent variables and the response can be described as:

$${\text{NPV}}\left( {MM\$ } \right) = - 12.0871 + 0.375491\left( {\text{A}} \right) + 0.505609\left( {\text{B}} \right) + 0.092169\left( {\text{C}} \right) + 0.38321\left( {\text{D}} \right) - 0.0547919\left( {{\text{A}}^{2} } \right) + 0.0322998\left( {\text{AB}} \right) - 0.00136669\left( {\text{AC}} \right) - 0.00158124\left( {\text{AD}} \right) - 0.0386117\left( {{\text{B}}^{2} } \right) - 0.00101391\left( {\text{BC}} \right) - 0.00560595\left( {\text{BD}} \right) - 0.000460315\left( {{\text{C}}^{2} } \right) + 0.000932527\left( {\text{CD}} \right) - 0.000453058\left( {{\text{D}}^{2} } \right)$$
(5)
$${\text{CO}}_{2} \left( { \times 10^{3} \,{\text{tonnes}}} \right) = 3.26189 - 1.04622\left( {\text{A}} \right) - 1.93923\left( {\text{B}} \right) + 0.216004\left( {\text{C}} \right) + 0.112553\left( {{\text{A}}^{2} } \right) - 0.00933755\left( {\text{AB}} \right) + 0.0185834\left( {\text{AC}} \right) + 0.236503\left( {{\text{B}}^{2} } \right) + 0.00052458\left( {\text{BC}} \right) - 0.000361654\left( {{\text{C}}^{2} } \right)$$
(6)

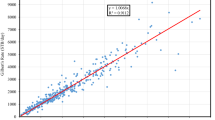
where A is WASP-start (year), B is WASP-cycle (month), C is steam/water injection rate (m3/day), and D is oil price per barrel. To validate the equation, Figs. 3 and 4 showing the plot between the observed and the predicted NPV and CO2 emission, respectively, are evaluated. The predicted parameters are calculated using Eqs. (5) and (6). The determination coefficient (R 2) and the adjusted determination coefficient (R 2 Adj) are close to one exhibiting the model is adequate. The low value of the residual standard deviation (RSD) indicates the accuracy of the relationship.

Fig. 3
figure 3

Relationship between NPV observed and predicted

Full size image
Fig. 4
figure 4

Relationship between CO2 emission observed and predicted

Full size image

Interaction effects

The interaction effects between the independent variables and the response are shown in Figs. 5 and 6. These effects are calculated from the polynomial model described by Eqs. (5) and (6). The Pareto graph consists of two groups. One group of factor coefficients is positive meaning that if the values of these factors increase, then the NPV and CO2 emission also increase. The other group is negative meaning that increasing the value of the factors will cause the response to decrease.

Fig. 5
figure 5

Pareto chart for selecting response to NPV

Full size image
Fig. 6
figure 6

Pareto chart for selecting response to CO2 emission

Full size image

In the economic analysis, two parameters have positive effects on the NPV. These are steam injection rate and oil price. The effect of oil price is larger than the steam injection rate. On the other hand, the parameters that have negative effects are WASP-start and WASP-cycle. However, the WASP-start has a little effect on the NPV.

In the CO2 emission part, the oil price does not include in the calculation since it will be not affected by the CO2 emission. There are two parameters that have positive effect. These are WASP-start and steam injection rate. The effect of injection rate is the higher compared to WASP-start. The WASP-cycle has a little negative effect on the CO2 emission. As a result, increasing the WASP-start and steam injection rate will increase the CO2 emission.

Proposed response surface correlation for economy and CO2 emission

Figure 7 displays the surface correlation for the economic analysis. At the same steam injection rate, if the oil price increases, the NPV will dramatically increase. For example, at the injection rate of 50 m3/day, if the oil price increases from 30 to 60 $/barrel, the NPV will increase from 5.53 to 16.11 MM$. The degree of the increment is analogous to the injection rate of 100 m3/day case and a little bit comparable to the 150 m3/day case. Based on Eq. (5), the NPV will be negative if the oil price is lower than 17 $/barrel. This value depends on the assumption on the economic variable above.

Fig. 7
figure 7

Response surface correlation to prediction of maximum NPV

Full size image

In order to get the optimum economy, each oil price will need different operation conditions. If the oil price is 30 $/barrel, the optimum operating condition will be 5.1 years of WASP-start, 2.3 months of WASP-cycle, 122 m3/day of injection rate and then the NPV will be 7.3 MM$. The other condition, if the oil price is 45 $/barrel, the optimum operating condition will be 3 years of WASP-start, 3.5 months of WASP-cycle, 141 m3/day of injection rate and then the NPV will be 14.1 MM$. While, if the oil price is 60 $/day, the optimum operating condition will be 1.1 years of WASP, 4.7 months of WASP-cycle, 149 m3/day of injection rate and then the NPV will be 20.54 MM$. Increasing the oil price at the same steam injection rate will decline the WASP-start and raise the WASP-cycle.

Figure 8 shows the surface correlation between the WASP operating condition and the side effect CO2 emission. In the low steam injection rate case, the CO2 emission is more favorable. At this condition, WASP-cycle has not an effect on the CO2 emission. In the contrary, at the WASP-start and steam injection rate have a significant effect on the CO2 emission. The increasing of WASP-start also tends to increase the CO2 emissions for all cases of the steam injection rate. This phenomenon is quite different compared to that observed in the economic analysis part. The CO2 emission is only a function of heat consumption while the NPV is related to the oil production, oil price, and economic assumptions.

Fig. 8
figure 8

Response surface correlation to prediction of CO2 emission on maximum NPV

Full size image

Finally, the CO2 emission based on the above optimum operating conditions for each the oil price shows if the oil price is 30, 45, and 60 $/barrel, the CO2 emission will be approximately 30.21 × 103, 28.53 × 103, and 25.88 × 103 Tonnes, respectively. In the optimum case, increasing oil price will influence to decrease CO2 emission. Hence, by using surface correlations for the NPV and CO2 emission, the operating condition can be set up to select which one is more favorable.

Conclusions

This study demonstrates the water alternating steam process (WASP) that can be economically optimized by applying a response surface correlation. Four parameters used are WASP-start, WASP-cycle, steam/water injection rate, and oil price. The oil price significantly influences to the NPV, while the WASP-start does not have significant effects on the NPV. In the maximum NPV case, increasing oil price at the same steam injection rate reduces the WASP-start and raises the WASP-cycle. Similar circumstance is obtained when the injection rate increases at the same oil price. In our specific case, if the economy is prioritized and oil price is 45 $/barrel, the optimum case will be achieved in which the WASP-start is 3.0 years, the WASP-cycle is 3.5 months, and the steam/water injection rate is 141 m3/day. Then, the NPV and the CO2 emission results will be 14.1 MM$ and 28.53 × 103 Tonnes, respectively. Combining the NPV correlation and the CO2 emission correlation resulted from the steam generation will bring significant advantages in the selection of a favorable operating condition for a WASP.