Introduction

Today, due to climate change, the occurrence of heavy rains with low duration has increased. As a result of these rains, a large amount of sediments in the upstream basin are washed away and the flow concentration of the alluvial channels suddenly increases. The hyperconcentrated flow occurs as a result of this type of heavy precipitation, in which a significant proportion of coarse-grained sediment particles is observed, so collisions and friction between particles are expected (Takahashi 2014). Various researchers have stated that if the flow concentration is more than 10 percent by volume, the behavior of the fluid will be non-Newtonian (Coussot 1994; Sloff 1993). In a considerable range of shear stress, the rheological behavior of this type of fluid can be described by the Herschel–Bulkley model. While in flows with a free surface, the simplified Bingham model is used for most visible shear stresses (O’Brien et al. 1993 and O’Brien and Julien 1988). In very low shear stresses, the pseudo-plastic model is recommended (Qian and Wan 1986).

For use in numerical models, it is necessary to provide relations and diagrams to calculate the coefficient of friction loss in non-Newtonian fluid. So far, many researches have been done in this regard and relations have been presented to model the friction coefficient of the Darcy–Weisbach relationship for non-Newtonian fluid in the conditions of laminar and turbulent particles in open channels and pipelines. El-Emam et al. (2003) by collecting and analyzing some of these relations which are given in Table 1, finally presented relation 1 to calculate the pressure loss in turbulent non-Newtonian fluid flow:

$$\Delta P = f\;L\rho \;V^{2} /2D$$
(1)
$$f = \left( {[N^{\prime}/\{ 3.072 - (0.1433.N^{\prime})\} ] \cdot N_{{{\text{R}} e^{\prime}}}^{{[N^{\prime}/0.282 - \{ 4.211 \cdot N^{\prime}\} ]}} } \right) - 0.00065$$
(2)
$$N_{{{\text{Re}}^{\prime } }} = D^{{N{\prime} }} V^{{2 - N{\prime} }} \rho /K^{\prime } 8^{{N^{\prime } - 1}}$$
(3)

where \(\Delta P\) the pressure loss is in Pascal’s, L is the length of the pipeline in meters, \(\rho \,\) volumetric mass of the fluid is in kilograms per cubic meter, V is the flow rate in meters per second, D is the internal diameter of the pipe in meters, f is the dimensionless Blasius friction coefficient, N \({\text{R}} e^{\prime}\) Reynolds number, \(^{{N{\prime} }}\) fluid behavior index, \(K^{\prime}\) compatibility index (viscosity of non-Newtonian fluid) in terms of Newton seconds per square meter. For non-Newtonian fluid flow in laminar conditions, the following relation is presented in its Blasius form (Metzner and Reed 1955):

$$f = \frac{64}{{N_{{{\text{Re}}{^{\prime}} }} }}$$
(4)
Table 1 Relationships for calculating friction loss coefficient in turbulent non-Newtonian fluid flow (quoted by El-Emam et al. 2003)
Full size table

The research conducted by Wan and Wang (1994) has shown that the standard relations presented for Newtonian fluids can be used for non-Newtonian fluids, provided that the Reynolds number used to calculate the Darcy–Weisbach loss coefficient is modified. Komatina (1999) presented the following relationship for the extended Reynolds number (\({\text{Re}}_{{{\text{ext}}}}\)) in the Herschel–Buckley model.

$${\text{Re}}_{{{\text{ext}}}} = {\text{Re}} \cdot \Phi^{m}$$
(18)

where:

$${\text{Re}} = \frac{{4\rho U^{2 - m} h}}{{\eta \cdot 3^{m - 1} }}^{m}$$
(19)
$$\Phi = \frac{3m}{{2m + 1}}\left[ {1 + \frac{m}{m + 1}\xi_{c} } \right](1 - \xi_{c} )^{{\left( {\frac{m + 1}{m}} \right)}}$$
(20)
$$\xi_{c} = \frac{{\tau_{c} }}{{\tau_{ \circ } }} = 1 - \frac{{y_{c} }}{h}$$
(21)

where, \(\tau_{ \circ }\) is the bed shear stress, \(\tau_{c}\) is the yield flow stress of non-Newtonian fluid, h is the flow depth, \(y_{c}\) is the distance from bed where the flow shear stress is equal to the yield flow stress (\(\tau\) = \(\tau_{c}\)), \(\eta\) is consistency index and \(m\) is fluid behavior index. It should be mentioned that three parameters \(\eta\) \(m\), and \(\tau_{c}\) are fluid rheology parameters that can be measured in a laboratory.

This researcher introduced the following relationship to calculate the friction coefficient in laminar flow:

$$f = \frac{24}{{{\text{Re}}_{{{\text{ext}}}} }}$$
(22)

For turbulent flow conditions, the Blasius relation was used as follows:

$$f = \frac{0.079}{{{\text{Re}}_{ext}^{1/4} }}$$
(23)

Julien and Paris (2010), using the collection of 350 measured data, presented the following relationship to calculate the friction loss coefficient of the Darcy–Weisbach relationship in a turbulent flow of mud and gravel:

$$\sqrt {\frac{8}{{f_{{\text{t}}} }}} = 5.75\log \frac{\alpha h}{{d_{s} }}$$
(24)

where: ft is the Darcy–Weisbach friction coefficient for turbulent flows. The \(\alpha\) value for the glued elements on a smooth bed is equal to 12.2. In natural rivers where it \(d_{s}\) refers to \(d_{90}\) of bed materials \(\alpha = 3\) can be used. In the high flow regime with smooth bed form and sediment transfer conditions, \(\alpha = 2\). h is the average flow depth.

Takashi (1991) has presented a relationship for describing the flow resistance using the dispersed stress approach for high concentrations of coarse-grained materials:

$$\sqrt {\frac{8}{{f_{d} }}} = \frac{V}{u*} = \frac{2h}{{5d_{s} }}\left[ {\frac{1}{{a_{1} }}\left\{ {C_{v} + (1 - C_{v} )\frac{1}{G}} \right\}} \right]^{1/2} \left\{ {\left( {\frac{{C_{v} *}}{{C_{v} }}} \right)^{1/3} - 1} \right\}$$
(25)

where fd is the Darcy–Weisbach friction coefficient for turbulent flows with high concentration, Cv is the sediment concentration, V is the average velocity, u* is the shear velocity and h is the average flow depth. For a certain amount of sedimentation error, the values \(C_{{_{v} }}^{*}\), \(a{}_{1}\) and \(G\) are constant. Therefore, the values inside the brackets are constant, in other words, the relationship between \(\sqrt {\frac{8}{{f_{d} }}}\) and \(\frac{\,h}{{d_{s} }}\) is linear. Hashimoto (1997) also provided a linear relationship between the mentioned values for high concentration flows:

$$\sqrt {\frac{8}{{f_{d} }}} = \frac{V}{u*} = 0.4\frac{h}{{d_{s} }}$$
(26)

In order to explain the rheological behavior of hyperconcentrated sediment flows, O’Brien et al. (1993) provided relations to calculate the bottom shear stresses τb1 and τb2 along the ξ and η directions:

$$\tau_{b1} = \frac{{\tau_{{\text{B}}} u}}{{\sqrt {u^{2} + v^{2} } }} + \frac{{{\text{K}}\mu_{{\text{B}}} u}}{8h} + cf\rho_{{\text{m}}} u\sqrt {u^{2} + v^{2} }$$
(27)
$$\tau_{b2} = \frac{{\tau_{{\text{B}}} v}}{{\sqrt {u^{2} + v^{2} } }} + \frac{{{\text{K}}\mu_{{\text{B}}} v}}{8h} + cf\rho_{{\text{m}}} v\sqrt {u^{2} + v^{2} }$$
(28)

where τB is the Bingham yield stress. μB is the Bingham viscosity. u and v are the depth-averaged velocity components in the ξ and η directions, respectively. g is the gravitational acceleration; K is the resistance parameter for laminar flow. \(cf=g/{C{\text{c}}}^{2}\) is friction coefficient and Cc is the Chézy coefficient. The resistance parameter K varies from 90 to 300. In general, Bingham's yield stress τB and Bingham's viscosity μB increase exponentially with the average volume concentration C of sediments at depth (O’Brien et al. 1988), which are expressed as follows:

$$\tau_{{\text{B}}} = \alpha_{1} e^{{C(\% )\beta_{1} }}$$
(29)
$$\mu_{{\text{B}}} = \alpha_{2} e^{C(\% )\beta 2}$$
(30)

In these relationships, α1, β1, α2, β2 are coefficients that need to be determined by conducting experiments. For streams with low concentration of suspended sediment C, the value of the third term on the right side of Eqs. (27) and (28) is much larger than the first and second terms. Therefore, the first and second terms on the right side of the mentioned equations can be ignored when C is small. However, using the Bingham model has almost no effect on clear water simulations.

To calculate yield flow stress (τc) and plastic viscosity (η), the following relations are provided by Komatina and Jovanovic (1997):

$$\tau_{c} = 0.002\,\,{\text{exp}}(0.342\;C_{v} )$$
(31)
$$\eta = 0.621\,\,{\text{exp}}(0.173\;C_{v} )$$
(32)

In these relationships, Cv is the volume concentration of the flow in percent.

Due to the importance of the phenomenon of dam break, a lot of research has been devoted to it. Most of the research done on dam break is caused by the Newtonian fluid of water. The phenomenon of non-Newtonian fluid dam break has been studied numerically and especially in laboratory.

Komatina and Jovanovic (1997) by conducting 69 tests on a flume with a slope of 0–1% investigated the phenomenon of fluid barrier failure with a concentration of 0–36.1% and investigated the effect of faulting on the speed of the advancing wave caused by one-dimensional failure. Contract analysis. Their results showed that in a certain concentration, with the increase in the depth of the flow and the slope of the channel bottom, the ratio of the velocity of the progressive wave of the hyperconcentrated fluid to the clear water has decreased. In addition, these researchers have presented relations and diagrams for calculating the coefficient of friction loss in non-Newtonian fluid for use in numerical models, in which the coefficient of friction can be extracted for the Reynolds and Hedström numbers.

So far, the dam break flow of liquid–solid mixtures with high viscosity has been studied numerically using the various relationships presented. The use of Newtonian models in research Hunt 1994 and Aguirre-Pe et al. 1995, Bingham model in research McArthur and Schamber 1986 and Herschel–Buckley fluid models in research Laigle and Coussot (1997) have been used to model laminar flow. Also, hybrid models have been used in many researches for turbulent flows. Liu and Lai (2000), O'Brien et al. (1993) used the extended Bingham model to consider turbulent and scattered stresses. Also, Han and Wang (1996) used the model created by combining Bingham and Chezy relations. Chen et al. (2018) developed a depth-averaged two-dimensional numerical model for hyperconcentrated flows in steep alluvial channels used a rheological relation for Bingham fluid and sediment transport capacity formula, developed through laboratory experiments, to describe the behavior of hyperconcentrated flow in the model. Their results showed that at the peak discharge during Typhoon Morakot, the bed shear stress from the hyperconcentrated flow model can be 150% larger than the clear water model. These researchers stated that the temporal evolution of bed changes obtained from the model can be used to provide credible descriptions regarding the causes of embankment failure during Typhoon Toraji.

In this research, a two-dimensional numerical model based on solving shallow water equations in orthogonal curvilinear coordinates has been developed to simulate two-dimensional non-Newtonian flow. In this model, it is possible to use the Bingham model or the Herschel-Buckley model, as well as the use of different friction loss coefficient relationships. Explicit finite difference method and the simultaneous application of leapfrog and Lex algorithms on the staggered grid were used in numerical discretization. By increasing the number of points involved in the discretization and creating more connections between them without using artificial viscosity, this action smooths the sharp geometric and hydraulic gradients and reduces the possibility of oscillation and divergence.

Methods and materials

Governing equations

As stated before, in hydraulic engineering, shallow water equations are used as governing equations to study many physical phenomena, including dam break. These equations are obtained in two-dimensional form with the initial assumption of hydrostatic pressure distribution and also incompressible fluid from the averaging of three-dimensional Navier–Stokes equations in depth (Chaudhry 2007; Hadian and Zarati 2008). Two-dimensional shallow water equations for incompressible fluid in the Cartesian coordinate system along the x and y axes are presented by Sobey et al. 1980 as relations (33–35):

$$\frac{\partial h}{{\partial t}} + \frac{\partial U}{{\partial x}} + \frac{\partial V}{{\partial y}} = 0$$
(33)
$$\begin{aligned} \frac{\partial U}{{\partial t}} & + \beta \frac{\partial }{\partial x}(\frac{{U^{2} }}{h - d}) + \beta \frac{\partial }{\partial y}(\frac{UV}{{h - d}}) - f\;V \\ = & - g(\eta - d)\frac{\partial h}{{\partial x}} - \frac{(h - d)}{{\rho_{w} }}\frac{{\partial P_{s} }}{\partial x} + \frac{1}{{\rho_{{\text{w}}} }}(\tau_{sx} - \tau_{bx} ) \\ \quad & + \overline{\varepsilon }(h - d)\left[ {\frac{{\partial^{2} (U/(h - d))}}{{\partial y^{2} }} + \frac{{\partial^{2} (U/(h - d))}}{{\partial x^{2} }}} \right]\, \\ \end{aligned}$$
(34)
$$\begin{aligned} \frac{\partial V}{{\partial t}} & + \beta \frac{\partial }{\partial x}\left( {\frac{UV}{{h - d}}} \right) + \beta \frac{\partial }{\partial y}\left( {\frac{{V^{2} }}{h - d}} \right) + f\,U \\ = & - g(h - d)\frac{\partial h}{{\partial y}} - \frac{(h - d)}{{\rho_{{\text{w}}} }}\frac{{\partial P_{s} }}{\partial y} + \frac{1}{{\rho_{{\text{w}}} }}(\tau_{sy} - \tau_{by} ) \\ \quad & + \overline{\varepsilon }(h - d)\left[ {\frac{{\partial^{2} (V/(h - d))}}{{\partial x^{2} }} + \frac{{\partial^{2} (V/(h - d))}}{{\partial y^{2} }}} \right] \\ \end{aligned}$$
(35)

That in these equations:

$$f = 2\omega \,\sin \phi$$
(36)
$$\overline{\varepsilon } = 0.7 \times u^{ * } (h - d)$$
(37)
$$u^{ * } = \sqrt {\frac{{\tau_{b} }}{{\rho_{{\text{w}}} }}}$$
(38)
$$\tau_{{{\text{s}}y}} = C_{{_{f} }} \rho_{{_{{\text{a}}} }} W_{y} W_{{\text{s}}}$$
(39)
$$\tau_{{{\text{s}}x}} = C_{{_{f} }} \rho_{{_{{\text{a}}} }} W_{x} W_{{\text{s}}}$$
(40)
$$\tau_{bx} = \frac{{\tau_{{\text{B}}} U}}{{\sqrt {U^{2} + V^{2} } }} + \frac{{{\text{K}}\mu_{{\text{B}}} U}}{{8\left( {\eta - d} \right)^{2} }} + \frac{\lambda }{8}\rho_{{\text{w}}} \frac{{U\sqrt {U^{2} + V^{2} } }}{{\left( {\eta - d} \right)^{2} }}$$
(41)
$$\tau_{by} = \frac{{\tau_{{\text{B}}} V}}{{\sqrt {U^{2} + V^{2} } }} + \frac{{{\text{K}}\mu_{{\text{B}}} V}}{{8\left( {\eta - d} \right)^{2} }} + \frac{\lambda }{8}\rho_{{\text{w}}} \frac{{V\sqrt {U^{2} + V^{2} } }}{{\left( {h - d} \right)^{2} }}$$
(42)
$$\frac{1}{\lambda } = \frac{{C_{{\text{c}}}^{2} }}{8g},\quad C_{{\text{c}}} = \frac{{(h - d)^{1/6} }}{n},\quad \beta = \left( {1 + \frac{g}{{C_{c}^{2} \kappa^{2} }}} \right)$$
(43)
$$\begin{aligned} {\text{for}} & \quad W_{{\text{s}}} \le 1\;{\text{m}}/{\text{s}} \to C_{{_{f} }} = 1.25 \times 10^{{ - 3}} W_{{\text{s}}} ^{{ - 0.2}} \\ {\text{for}} & \quad 1 < W_{{\text{s}}} < 15\;{\text{m}}/{\text{s}} \to C_{{_{f} }} = 0.5 \times 10^{{ - 3}} W_{{\text{s}}} ^{{0.5}} \\ {\text{for}} & \quad W_{{\text{s}}} \ge 15\;{\text{m}}/{\text{s}} \to C_{{_{f} }} = 2.6 \times 10^{{ - 3}} \\ \end{aligned}$$
(44)

In the above relations: U is flow rate per unit width in x direction, V is flow rate per unit width in y direction, h = h(x,y,t) is water surface elevation, d = d(x,y,t) is bed elevation, τs = τs (x,y,t) is shear stress caused by wind, τb = τb (x,y,t) is shear stress caused by bed roughness, Ps = Ps(x,y,t) is atmospheric pressure, f is Coriolis parameter, g is gravitational acceleration ρw is the volumetric mass of water, ρa is the volumetric mass of air, β is momentum coefficient, Ws is the wind speed, Wx and Wy are the wind speed components in the x and y directions, respectively, ω is the angular velocity of the Earth's rotation, φ is the latitude, and κ is Van-Karman's constant. u* is shear velocity, λ is Darcy–Weisbach coefficient, Cc is Chézy coefficient, n is Manning roughness coefficient, \(\overline{\varepsilon }\) is mean eddy viscosity in depth that in this research, in order to speed up calculations, it is estimated from the zero-equation turbulence model, τB is Bingham's yield stress, μB is Bingham's viscosity, and K is the resistance parameter for laminar flow.

Transferring the governing equations to curvilinear coordinate system

Due to the inability of the Cartesian coordinate system to reflect the irregular boundaries of the physical domain, the curvilinear coordinate system method has been used in this research. This system was first defined by Thomson with the conventional axes ξ and η (Wood and Wang 2015). According to the above, the governing equations in the curvilinear coordinate system will be in the form of relations (45–47) (Hoffmann and Chiang 2000):

$$h_{t} + \frac{1}{J}\left( {y_{\eta } U_{\xi } - y_{\xi } U_{\eta } } \right) + \frac{1}{J}\left( {x_{\xi } V_{\eta } - x_{\eta } V_{\xi } } \right) = 0$$
(45)
$$\begin{aligned} U_{t} & + \beta \frac{1}{J}\left[ {\begin{array}{*{20}c} {y_{\eta } \left( {\frac{{U^{2} }}{h - d}} \right)_{\xi } - y_{\xi } \left( {\frac{{U^{2} }}{h - d}} \right)_{\eta } + } \\ {x_{\xi } \left( {\frac{UV}{{h - d}}} \right)_{\eta } - x_{\eta } \left( {\frac{UV}{{h - d}}} \right)_{\xi } } \\ \end{array} } \right] - fV \\ = & \frac{{ - \left( {h - d} \right)}}{J}\left[ {\begin{array}{*{20}c} {g\left( {y_{\eta } h_{\xi } - y_{\xi } h_{\eta } } \right) + } \\ {\frac{{\left( {y_{\eta } P_{\xi } - y_{\xi } P_{\eta } } \right)}}{{\rho_{{\text{w}}} }}} \\ \end{array} } \right] + \frac{1}{{\rho_{{\text{w}}} }}\left( {\tau_{{{\text{s}}x}} - \tau_{bx} } \right) \\ \quad & + \overline{\varepsilon }\left( {\eta - d} \right)\left\{ {\begin{array}{*{20}c} {\frac{1}{{J^{2} }}\left\{ {C_{1} \times \left( {\frac{U}{h - d}} \right)_{\xi \xi } - 2C_{2} \times \left( {\frac{U}{h - d}} \right)_{\xi \eta } + C_{1} \times \left( {\frac{U}{h - d}} \right)_{\eta \eta } } \right\}} \\ { + \frac{1}{{J^{3} }}\left\{ {\begin{array}{*{20}c} {\left( {\frac{U}{h - d}} \right)_{\xi } \left[ {x_{\eta } \left( {A_{1} + B_{1} } \right) - y_{\eta } \left( {A_{2} + B_{2} } \right)} \right]} \\ { + \left( {\frac{U}{h - d}} \right)_{\eta } \left[ {y_{\xi } \left( {A_{2} + B_{2} } \right) - x_{\xi } \left( {A_{1} + B_{1} } \right)} \right]} \\ \end{array} } \right\}} \\ \end{array} } \right\} \\ \end{aligned}$$
(46)
$$\begin{aligned} V_{t} & + \beta \frac{1}{J}\left[ {\begin{array}{*{20}c} {y_{\eta } \left( {\frac{UV}{{h - d}}} \right)_{\xi } - y_{\xi } \left( {\frac{UV}{{h - d}}} \right)_{\eta } + } \\ {x_{\xi } \left( {\frac{{V^{2} }}{h - d}} \right)_{\eta } - x_{\eta } \left( {\frac{{V^{2} }}{h - d}} \right)_{\xi } } \\ \end{array} } \right] + fU \\ = & \frac{{ - \left( {h - d} \right)}}{J}\left[ {g\left( {x_{\xi } h_{\eta } - x_{\eta } h_{\xi } } \right) + \frac{{\left( {x_{\xi } P_{\eta } - x_{\eta } P_{\xi } } \right)}}{{\rho_{{\text{w}}} }}} \right] + \frac{1}{{\rho_{{\text{w}}} }}\left( {\tau_{{{\text{s}}x}} - \tau_{bx} } \right) \\ \quad & + \overline{\varepsilon }\left( {\eta - d} \right)\left\{ {\begin{array}{*{20}c} {\frac{1}{{J^{2} }}\left\{ {C_{1} \times \left( {\frac{V}{h - d}} \right)_{\xi \xi } - 2C_{2} \times \left( {\frac{V}{h - d}} \right)_{\xi \eta } + C_{1} \times \left( {\frac{V}{h - d}} \right)_{\eta \eta } } \right\}} \\ {\frac{1}{{J^{3} }}\left\{ {\left( {\frac{V}{h - d}} \right)_{\xi } \left[ {x_{\eta } \left( {A_{1} + B_{1} } \right) - y_{\eta } \left( {A_{2} + B_{2} } \right)} \right] + \left( {\frac{V}{h - d}} \right)_{\eta } \left[ {y_{\xi } \left( {A_{2} + B_{2} } \right) - x_{\xi } \left( {A_{1} + B_{1} } \right)} \right]} \right\}} \\ \end{array} } \right\} \\ \end{aligned}$$
(47)

The coefficients in relations (46) and (47) are defined as relation (48–53):

$$A_{1} = \left( {y_{\eta }^{2} y_{\xi \xi } - 2y_{\xi } y_{\eta } y_{\xi \eta } + y_{\xi }^{2} y_{\eta \eta } } \right)$$
(48)
$$A_{2} = \left( {y_{\eta }^{2} x_{\xi \xi } - 2y_{\xi } y_{\eta } x_{\xi \eta } + y_{\xi }^{2} x_{\eta \eta } } \right)$$
(49)
$$B_{1} = \left( {x_{\eta }^{2} y_{\xi \xi } - 2x_{\xi } x_{\eta } y_{\xi \eta } + x_{\xi }^{2} y_{\eta \eta } } \right)$$
(50)
$$B_{2} = \left( {x_{\eta }^{2} x_{\xi \xi } - 2x_{\xi } x_{\eta } x_{\xi \eta } + x_{\xi }^{2} x_{\eta \eta } } \right)$$
(51)
$$C_{1} = \left( {x_{\eta }^{2} + y_{\eta }^{2} } \right)$$
(52)
$$C_{2} = \left( {y_{\xi } y_{\eta } + x_{\xi } x_{\eta } } \right)$$
(53)

Which in the above equations J is Jacobin (J = xξ yη−yξ xη) and xξ, ξy, ηy, xη are transformation derivatives, transfer metrics or more simply called metrics.

Mesh generation of the studied area

Mesh of the studied domain generated by solving the elliptic differential equation set which is introduced in the form of Poisson's equation (Hadian and Zarati 2008; Hoffmann and Chiang 2000):

$$A x_{\xi \xi } - 2 B x_{\xi \eta } + C x_{\eta \eta } = - J^{2} (P x_{\xi } + Q x_{\eta )}$$
(54)
$$A y_{\xi \xi } - 2 B y_{\xi \eta } + C y_{\eta \eta } = - J^{2} (P y_{\xi } + Q y_{\eta )}$$
(55)

where:

$$A = \left( {x_{\eta }^{2} + y_{\eta }^{2} } \right)$$
(56)
$$B = x_{\xi } x_{\eta } + y_{\xi } y_{\eta }$$
(57)
$$C = \left( {x_{\xi }^{2} + y_{\eta }^{2} } \right)$$
(58)
$$P\left( {\xi ,\eta } \right) = - \mathop \sum \limits_{1}^{M} a_{m} \frac{{\xi - \xi_{m} }}{{\left| {\xi - \xi_{m} } \right|}}\exp \left( {c_{m} \left| {\xi - \xi_{m} } \right|} \right) - \mathop \sum \limits_{1}^{N} b_{n} \frac{{\xi - \xi_{n} }}{{\left| {\xi - \xi_{n} } \right|}}\exp \left\{ { - d_{n} \left[ {\left| {\xi - \xi_{m} } \right|^{2} + \left| {\eta - \eta_{n} } \right|^{2} } \right]^{\frac{1}{2}} } \right\}$$
(59)
$$Q\left( {\xi ,\eta } \right) = - \mathop \sum \limits_{1}^{M} a_{m} \frac{{\eta - \eta_{m} }}{{\left| {\eta - \eta_{m} } \right|}}\exp \left( {c_{m} \left| {\eta - \eta_{m} } \right|} \right) - \mathop \sum \limits_{1}^{N} b_{n} \frac{{\eta - \eta_{n} }}{{\left| {\eta - \eta_{n} } \right|}}\exp \left\{ { - d_{n} \left[ {\left| {\xi - \xi_{m} } \right|^{2} + \left| {\eta - \eta_{n} } \right|^{2} } \right]^{\frac{1}{2}} } \right\}$$
(60)

The amplification factors a and b as well as the decay factors c and d are entered into the model by the user. P and Q control functions are used to condense grid lines near a certain line or point. M is the number of constant grid lines around which clustering is done. Also, N is the number of grid points around which clustering is done.

Set of Eqs. (54) and (55) are solved in computational space (\(\xi\),\(\eta\)) to obtain the coordinates of grid points in physical space (x,y). Due to the use of Poisson's equation, it is possible to create mesh density anywhere in the domain or adjacent to rigid boundaries. Figure 1 shows an example of a constructed mesh for one of the studied area related to the partial and asymmetric dam break.

Fig. 1
figure 1

Example of generated mesh for a computational domain

Full size image

Discretization of governing equations

In this research, the governing equations on grid points in the curvilinear coordinates, which are located at distances Δξ and Δη from each other, have been discretized by the staggered method. The discretization method is an explicit Leap-Frog method, which also uses the Lax algorithm. The momentum equation in the ξ direction at the node (i + 1/2, j, n + 1/2), the momentum equation in the η direction at the node (i, j + 1/2, n + 1/2) and the continuity equation at the node (i, j, n + 1); are discretized, that symbols i, j are used for space and n is used for time. For example, the method to discretize each term of the momentum equation in the ξ direction at node (i + 1/2, j) in Fig. 2 is given in relations (61–67). The decoupling of the continuity relation and the momentum equation in the direction of η is done in a similar way, which has been omitted due to the reduction of the volume of the article.

$$U_{t} = \frac{{U_{i + 1/2,j}^{n + 1/2} - \overline{U}_{i + 1/2,j}^{n - 1/2} }}{\Delta t}$$
(61)
$$\overline{U}_{i + 1/2,j}^{n - 1/2} = 0.25 \times U_{i - 1/2,j}^{n - 1/2} + 0.5 \times U_{i + 1/2,j}^{n - 1/2} + 0.25 \times U_{i + 3/2,j}^{n - 1/2}$$
$$\begin{aligned} {\varvec{\beta}}\frac{1}{{\varvec{J}}}\left[ {{\varvec{y}}_{{\varvec{\eta}}} \left( {\frac{{{\varvec{U}}^{2} }}{{{\varvec{h}} - {\varvec{d}}}}} \right)_{{\varvec{\xi}}} - {\varvec{y}}_{{\varvec{\xi}}} \left( {\frac{{{\varvec{U}}^{2} }}{{{\varvec{h}} - {\varvec{d}}}}} \right)_{{\varvec{\eta}}} } \right] = & {\varvec{\beta}}\frac{{{\varvec{y}}_{{\varvec{\eta}}} }}{{\varvec{J}}}\left[ {\frac{{\left( {\frac{{{\varvec{U}}^{2} }}{{{\varvec{h}} - {\varvec{d}}}}} \right)_{{{\varvec{i}} + \frac{3}{2},{\varvec{j}}}}^{{{\varvec{n}} - \frac{1}{2}}} - \left( {\frac{{{\varvec{U}}^{2} }}{{{\varvec{h}} - {\varvec{d}}}}} \right)_{{{\varvec{i}} + \frac{1}{2},{\varvec{j}}}}^{{{\varvec{n}} - \frac{1}{2}}} }}{{{\varvec{\xi}}_{{{\varvec{i}},{\varvec{j}} + 1}} - {\varvec{\xi}}_{{{\varvec{i}},{\varvec{j}} - 1}} }}} \right] \\ \quad & - {\varvec{\beta}}\frac{{{\varvec{y}}_{{\varvec{\xi}}} }}{{\varvec{J}}}\left[ {\frac{{\left( {\frac{{{\varvec{U}}^{2} }}{{{\varvec{h}} - {\varvec{d}}}}} \right)_{{{\varvec{i}} + \frac{1}{2},{\varvec{j}} + 1}}^{{{\varvec{n}} - 1/2}} - \left( {\frac{{{\varvec{U}}^{2} }}{{{\varvec{h}} - {\varvec{d}}}}} \right)_{{{\varvec{i}} + \frac{1}{2},{\varvec{j}} - 1}}^{{{\varvec{n}} - 1/2}} }}{{{\varvec{\eta}}_{{{\varvec{i}} + 1,{\varvec{j}}}} - {\varvec{\eta}}_{{{\varvec{i}},{\varvec{j}}}} }}} \right] \\ \end{aligned}$$
(62)
$$\begin{aligned} {\varvec{\beta}}\frac{1}{{\varvec{J}}}\left[ {{\varvec{x}}_{{\varvec{\xi}}} \left( {\frac{{{\varvec{UV}}}}{{{\varvec{h}} - {\varvec{d}}}}} \right)_{{\varvec{\eta}}} - {\varvec{x}}_{{\varvec{\eta}}} \left( {\frac{{{\varvec{UV}}}}{{{\varvec{h}} - {\varvec{d}}}}} \right)_{{\varvec{\xi}}} } \right] = & \frac{{{\varvec{x}}_{{\varvec{\xi}}} }}{{\varvec{J}}}\left[ {\frac{{\left( {\frac{{{\varvec{U}}_{{{\varvec{i}} + \frac{1}{2},{\varvec{j}} + 1}}^{{{\varvec{n}} - \frac{1}{2}}} \overline{\user2{V}}_{{{\varvec{i}} + \frac{1}{2},{\varvec{j}} + 1}}^{{{\varvec{n}} - \frac{1}{2}}} }}{{\frac{1}{2}\left( {{\varvec{h}} - {\varvec{d}}} \right)_{{{\varvec{i}},{\varvec{j}} + 1}} + \frac{1}{2}\left( {{\varvec{h}} - {\varvec{d}}} \right)_{{{\varvec{i}} - 1,{\varvec{j}} + 1}} }}} \right)}}{{{\varvec{\eta}}_{{{\varvec{i}} + 1,{\varvec{j}}}} - {\varvec{\eta}}_{{{\varvec{i}},{\varvec{j}}}} }}\user2{ } + \frac{{\left( {\frac{{{\varvec{U}}_{{{\varvec{i}} + \frac{1}{2},{\varvec{j}} - 1}}^{{{\varvec{n}} - \frac{1}{2}}} \overline{\user2{V}}_{{{\varvec{i}} + \frac{1}{2},{\varvec{j}} - 1}}^{{{\varvec{n}} - \frac{1}{2}}} }}{{\frac{1}{2}\left( {{\varvec{h}} - {\varvec{d}}} \right)_{{{\varvec{i}},{\varvec{j}} - 1}} + \frac{1}{2}\left( {{\varvec{h}} - {\varvec{d}}} \right)_{{{\varvec{i}} - 1,{\varvec{j}} - 1}} }}} \right)}}{{{\varvec{\eta}}_{{{\varvec{i}} + 1,{\varvec{j}}}} - {\varvec{\eta}}_{{{\varvec{i}},{\varvec{j}}}} }}\user2{ }} \right] \\ \quad & - \frac{{{\varvec{x}}_{{\varvec{\eta}}} }}{{\varvec{J}}}\left[ {\frac{{\left( {\frac{{{\varvec{U}}_{{{\varvec{i}} + \frac{3}{2},{\varvec{j}}}}^{{{\varvec{n}} - \frac{1}{2}}} \overline{\user2{V}}_{{{\varvec{i}} + \frac{3}{2},{\varvec{j}}}}^{{{\varvec{n}} - \frac{1}{2}}} }}{{\frac{1}{2}\left( {{\varvec{h}} - {\varvec{d}}} \right)_{{{\varvec{i}} + 1,{\varvec{j}}}} + \frac{1}{2}\left( {{\varvec{h}} - {\varvec{d}}} \right)_{{{\varvec{i}} + 2,{\varvec{j}}}} }}} \right)}}{{{\varvec{\xi}}_{{{\varvec{i}},{\varvec{j}} + 1}} - {\varvec{\xi}}_{{{\varvec{i}},{\varvec{j}} - 1}} }} + \frac{{\left( {\frac{{{\varvec{U}}_{{{\varvec{i}} - \frac{3}{2},{\varvec{j}}}}^{{{\varvec{n}} - \frac{1}{2}}} \overline{\user2{V}}_{{{\varvec{i}} - 1\frac{3}{2},{\varvec{j}}}}^{{{\varvec{n}} - \frac{1}{2}}} }}{{\frac{1}{2}\left( {{\varvec{h}} - {\varvec{d}}} \right)_{{{\varvec{i}} - 1,{\varvec{j}}}} + \frac{1}{2}\left( {{\varvec{h}} - {\varvec{d}}} \right)_{{{\varvec{i}} - 2,{\varvec{j}}}} }}} \right)}}{{{\varvec{\xi}}_{{{\varvec{i}},{\varvec{j}} + 1}} - {\varvec{\xi}}_{{{\varvec{i}},{\varvec{j}} - 1}} }}} \right] \\ \end{aligned}$$
(63)
$$fV = f \times \frac{1}{4}\left[ {V_{i,j}^{n - 1/2} + V_{i,j - 1}^{n - 1/2} + V_{i - 1,j}^{n - 1/2} + V_{i - 1,j - 1}^{n - 1/2} } \right]$$
(64)
$$\begin{aligned} \frac{{ - \left( {h - d} \right)}}{J}\left[ {\frac{{\left( {x_{\xi } P_{\eta } - x_{\eta } P_{\xi } } \right)}}{{\rho_{{\text{w}}} }}} \right] = & \left[ {\frac{{ - g\left( {h - d} \right)_{i,j} + g\left( {h - d} \right)_{i - 1,j} }}{2}} \right] \\ \quad & \times \left[ {\frac{{x_{\xi } \left( {\frac{{\left( {\frac{{P_{i,j + 1 } + P_{i - 1,j + 1} }}{2}} \right)^{n} - \left( {\frac{{P_{i,j - 1} - P_{i - 1,j - 1} }}{2}} \right)^{n} }}{{\eta_{i,j + 1} - \eta_{i.j - 1} }}} \right)}}{J} - \frac{{x_{\eta } }}{J}\left( {\frac{{P_{i,j} - P_{i - 1,j} }}{{\xi_{i,j} - \xi_{i - 1,j} }}} \right)^{n} } \right] \\ \end{aligned}$$
(65)
$$\begin{aligned} \frac{1}{{\rho_{{\text{w}}} }}\left( {\tau_{{{\text{s}}x}} - \tau_{bx} } \right) = & \frac{{\tau_{sx\;i,j}^{n} }}{{\rho_{{\text{w}}} }} - \frac{{\tau_{{\text{B}}} U_{i,j}^{{n + \frac{1}{2}}} }}{{\rho_{{\text{w}}} \sqrt {\left( {U_{i,j}^{{n - \frac{1}{2}}} } \right)^{2} + \left( {\overline{\user2{V}}_{i,j}^{{n - \frac{1}{2}}} } \right)^{2} } }} - \frac{{{\text{K}}\mu_{{\text{B}}} U_{i,j}^{{n + \frac{1}{2}}} }}{{8\rho_{{\text{w}}} \times \left[ {\frac{1}{2}(h - d)_{i + 1,j} + \frac{1}{2}(h - d)_{i,j} } \right]^{2} }} \\ \quad & - \frac{\lambda }{8}\frac{{U_{i,j}^{{n + \frac{1}{2}}} \times \sqrt {\left( {U_{i,j}^{{n - \frac{1}{2}}} } \right)^{2} + \left( {\overline{\user2{V}}_{i,j}^{{n - \frac{1}{2}}} } \right)^{2} } }}{{\left[ {\frac{1}{2}(h - d)_{i + 1,j} + \frac{1}{2}(h - d)_{i,j} } \right]^{2} }} \\ \end{aligned}$$
(66)
$$\begin{aligned} \overline{\varepsilon }\left( {h - d} \right) & \times \left\{ {\begin{array}{*{20}c} {\frac{1}{{J^{2} }}\left\{ {C_{1} \times \left( {\frac{U}{h - d}} \right)_{\xi \xi } - 2C_{2} \times \left( {\frac{U}{h - d}} \right)_{\xi \eta } + C_{1} \times \left( {\frac{U}{h - d}} \right)_{\eta \eta } } \right\}} \\ { + \frac{1}{{J^{3} }}\left\{ {\left( {\frac{U}{h - d}} \right)_{\xi } \left[ {\begin{array}{*{20}c} {x_{\eta } \left( {A_{1} + B_{1} } \right)} \\ { - y_{\eta } \left( {A_{2} + B_{2} } \right)} \\ \end{array} } \right] + \left( {\frac{U}{h - d}} \right)_{\eta } \left[ {\begin{array}{*{20}c} {y_{\xi } \left( {A_{2} + B_{2} } \right)} \\ { - x_{\xi } \left( {A_{1} + B_{1} } \right)} \\ \end{array} } \right]} \right\}} \\ \end{array} } \right\} \\ = & \overline{\varepsilon }\left[ {\frac{1}{2}\left( {h - d} \right)_{i + 1,j} + \frac{1}{2}\left( {h - d} \right)_{i,j} } \right] \\ \quad & \times \left[ {\begin{array}{*{20}c} {\frac{1}{{J^{2} }}\left\{ {C_{1} \times \left( {\left( {\frac{U}{h - d}} \right)_{\xi \xi } } \right)_{{i + \frac{1}{2},j}}^{n - 1/2} - 2C_{2} \times \left( {\left( {\frac{U}{h - d}} \right)_{\xi \eta } } \right)_{{i + \frac{1}{2},j}}^{n - 1/2} + C_{1} \times \left( {\left( {\frac{U}{h - d}} \right)_{\eta \eta } } \right)_{{i + \frac{1}{2},j}}^{n - 1/2} } \right\}} \\ { + \frac{1}{{J^{3} }}\left\{ {\left( {\left( {\frac{U}{h - d}} \right)_{\xi } } \right)_{{i + \frac{1}{2},j}}^{n - 1/2} \left[ {x_{\eta } \left( {A_{1} + B_{1} } \right) - y_{\eta } \left( {A_{2} + B_{2} } \right)} \right] + \left( {\left( {\frac{U}{h - d}} \right)_{\eta } } \right)_{{i + \frac{1}{2},j}}^{n - 1/2} \left[ {y_{\xi } \left( {A_{2} + B_{2} } \right) - x_{\xi } \left( {A_{1} + B_{1} } \right)} \right]} \right\}} \\ \end{array} } \right] \\ \end{aligned}$$
(67)
Fig. 2
figure 2

a U-momentum, b continuity equations discretization

Full size image

Boundary conditions and stability

In the open outlet boundary, the specific flow depth and zero gradient for the velocities perpendicular to the boundary are defined as the boundary condition. Also, in the exit and inlet boundaries, the tangential velocity on the boundary is considered equal to zero.

In some cases, such as the flow falling at the end of the flume, a critical depth is likely to occur. In this situation, using relation (68), which is derived from the continuity relationship and integrating the critical depth relationship (for example, in the X direction), the flow water surface (h) at the downstream boundary for the next time step is calculated. Then, discharge per unit width (U) at the downstream boundary is calculated from equation (69).

$$h_{t} + \frac{1}{J} \times \frac{3}{2} \sqrt {g(h - d} h_{\xi } y_{\eta } + \frac{3}{2} \sqrt {g(h - d} \times S_{0} = 0$$
(68)
$$U = \sqrt {g\left( {h - d} \right)^{3} }$$
(69)

where \({S}_{0}\) is flume bed slope.

In the symmetry boundaries at hypothetical points outside the boundary, the depth of flow and the velocity component parallel to the boundary were considered equal to the depth and velocity of the internal neighboring points of the boundary and the velocity component perpendicular to the boundary. In rigid boundaries, for hypothetical points outside the wall, the vertical velocity has been replaced by changing the sign of the inner neighboring points, which results in asymmetric reflection, while the tangential velocity at the hypothetical point is considered equal and the same sign as the inner neighboring point. In rigid boundaries, where the wall of the computational domain is not parallel or perpendicular to the horizon axis, but makes an angle θ, in reflective boundaries, the result of the velocity vector at the virtual point outside the boundary with the velocity vector at the point inside the boundary is parallel to the wall. Since the model prepared in this research is based on the explicit method, the condition of its stability is that the Courant number is less than one.

$$C_{{\text{r}}} = \sqrt {g\left( {h - d} \right)} \frac{\Delta t}{{{\text{min}}\left( {\Delta \xi ,\Delta \eta } \right)}}$$
(70)

Results and discussion

Model validation

In order to validate the current model for hydraulic simulation of non-Newtonian fluid flow, measurement data by Komatina (1999) was used. In his experiments, a mixture of water and pieces of copper taken from the copper mine (Veliki Krivelj) in Serbia and Montenegro was used as a fluid in the experiments. The average diameter of the particles is 0.025 mm, 8% of the materials are smaller than 0.002 mm and 70% are smaller than 0.062 mm. The volumetric mass of the particles is 2650 kg/m3 and its chemical composition: 63% SiO2, 14% Al2O3, 3.5% Fe, 3% K2O, 3% CaO, 3% MgO and 3% Na2O. The clay component is kaolinite-illite material. The rheological parameters of the mixtures were obtained using two types of measurements by a commercial rotary viscometer and in the laboratory flume shown in Fig. 3. The measurement errors were estimated to be 13% (viscometer) and 16% in flume, respectively (Komatina 1999).

Fig.3
figure 3

Laboratory flume and measurement equipment: 1—flume, 2—lower tank, 3—pump, 4—upper tank, 5—deflector, 6—control weir, 7—fluid supply rubber tube, 8—membrane probes, 9—electromagnetic probe, 10—data acquisition and processing system (Komatina 1999)

Full size image

The data related to the rheological behavior of the fluid mixture in different ranges of small shear rate (0.5–20/s) in the free surface flow test in the laboratory flume and larger shear rates from 50 to 250/s were obtained using a rotational viscometer. For each mixture, two linear relationships (Bingham model) were defined for each of the shear rate ranges. Finally, a power relation (Herschel-Buckley model) is defined to match the linear relations. The values of the rheological parameters obtained in the aforementioned research are presented in Table 2. In this table, CV indicates the volumetric concentration of the solid phase.

Table 2 Rheological properties of mixtures (Komatina 1999)
Full size table

The test of the dam was carried out in a laboratory flume with a glass wall 4.5 m long and 0.15 m wide, with an adjustable slope (Fig. 3). The flow caused by the dam failure started with the release of the mixture from a tank 2 m long and 0.155 m wide, which is located in the upstream part of the flume. A design of the experiment is shown in Fig. 4. The initial depth of the fluid in the reservoir was considered to be between 10 and 30 cm, the slope of the flume was between 0 and 1%, and the amount of volumetric sedimentation was considered variable from 0 to 45.6%.

Fig.4
figure 4

Sketch of a dam-break flow experiment (Komatina 1999)

Full size image

In this research, in order to validate the model in the numerical simulation of non-Newtonian fluid dam break, the information related to the longitudinal slope of the flume is 1% and the flow depth in the upstream reservoir is 30 cm. The studied area was gridded with 680 longitudinal meshes and 17 transverse meshes. The time step for testing with different concentrations was considered variable from 0.001 to 0.0005 s. Figure 5 shows some fluid depth measured at different points and times and the surface profile calculated by the present model for concentrations of 13.8, 18.1 and 32.2%.

Fig. 5
figure 5

Measured (blue point) and calculated fluid depth

Full size image

As can be seen, the graphs presented in Fig. 5 show that the current model correctly predicts the profile of the measured fluid surface and the position of the head of the advancing wave downstream. The statistical analysis between all measured and calculated flow depth values at different times and errors (only some results are presented here due to the reduction of the volume of the article) shows that the model has an error of less than 14% and a correlation coefficient of 99% in approximates the measurement results.

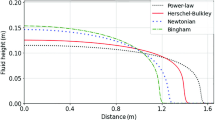
Figure 6 shows the profile of the fluid surface calculated at different times for concentrations of 13.8 and 36.4%. As the concentration increases, the speed of propagation the positive wave downstream and the negative wave toward the reservoir decreases. For example, in the time of 1 s after the dam failure at a concentration of 13.8%, the front of the downstream advancing wave reached from the dam break point (a position of 2 m along the flume) to a position of about 4.25 m, while for the concentration of 36.4, after almost 1 s, the flood wave stands from the movement at a position of about 3 m and the high concentration does not allow further progress. For comparison, the results of dam break on clear water are also presented in Fig. 6c. To achieve this goal, the fluid rheology parameters in relations 18–21 were defined as m = 0, \(\eta\) = 0.001 Pas and \({\tau }_{c}=0\). The downstream boundary condition was considered as critical depth. For this purpose, relation 68 was discretized by using the backward scheme and explicit method on all nodes over the downstream boundary. As shown in mentioned figure, after 0.8 s, the flood wave reached the downstream end of the flume. While at this time for concentration of 13.8%, the flood wave has not yet reached the end of the flume and it is even one meter away from the end of the flume.

Fig. 6
figure 6

The profile of the fluid surface calculated with current model a Cv = 13.8%, b Cv = 36.4% and c Cv = 0%

Full size image

In the problem of ideal dam failure, before the negative wave reaches the upstream wall of the reservoir, the flow depth (y) at the dam break location is constant and equal to 4/9 y0 (y0 = depth of flow in the reservoir). The results of the present research showed that fluid concentration has an effect on the flow depth at the break location. As shown in Fig. 7, the depth of flow at the break site has increased with the increase in fluid concentration.

Fig.7
figure 7

The effect of fluid concentration on the relative flow depth at the dam break site

Full size image

Asymmetric partial dam break of a non-Newtonian fluid

In order to investigate the two-dimensional hydraulic properties of the non-Newtonian fluid dam break flow and compare it with the Newtonian fluid, the computational domain shown in Fig. 1 was used. This area, one-meter-long and one-meter-wide, is divided by a 5-cm thick wall into two parts of the tank and its downstream. Initial flow depth in the tank is 50 cm and 5 mm downstream of the wall. The break wall is asymmetrically located at a distance of 45 cm from the upstream of the tank. The breaking length of this wall is 30 cm and its thickness is 5 cm. The grid independency studies were done and Finally, 191 meshes were selected in the direction of length (ξ) and 120 meshes in the direction of width (η). Also, the time step of performing the calculations was considered to be 1 × 10−5 s. Relations 27 and 28 were used to calculate the shear stress in the two mentioned directions. In these relations, the average value of coefficient k = 200 was considered. Dam failure was done for fluid with a concentration of 32.2%, whose rheological properties were calculated from relations 31 and 32. In Fig. 8a and b, the three-dimensional view of the water surface is displayed for 0.5 s after dam break for the sample. As expected, with increasing fluid concentration volume of water remaining inside the tank at a certain moment after dam break is greater. In other words, the tank is emptied later. By zoning and comparing the iso-velocity line in the flow direction, it is observed (Fig. 8c and d) at any specific time after dam break, pattern of flow velocity in flow direction is different for Newtonian and non-Newtonian fluid. For example, at the moment of half a second after of dam break, the maximum flow velocity in the nose of progressive wave, has occurred approximately 2.6 m/s in the Newtonian fluid. While at this moment, the maximum velocity occurs on the right and left sides of the progressive wave and its value is about 0.8 m/s for the non-Newtonian fluid. On the other hand, the observation of Fig. 8e and f shows that velocity pattern in the y direction for both Newtonian and non-Newtonian fluids is almost the same, although the velocity value in the non-Newtonian fluid is much lower than in the Newtonian fluid.

Fig. 8
figure 8

Three-dimensional view of the flow surface (a, b), u velocity (c, d) and v velocity (e and f) 0.5 s after dam break

Full size image

For a more detailed investigation, in Fig. 9a, the values of the flow velocity at the center of the broken wall, i.e., the position (x = 0.5, y = 0.65) are shown. For the Newtonian fluid, the maximum flow velocity in this position is 1.4 m/s, which is more than double the maximum velocity observed in the non-Newtonian fluid with a concentration of Cv = 32.2%, i.e., 0.66 m/s. Figure 9b shows the trend of flow depth changes at the failure location. A similar process occurred for both Newtonian and non-Newtonian fluids, however, at the same moment, the depth of flow is greater for non-Newtonian fluid. A similar trend for changes in flow depth at different times has been reported by other researchers (Fraccarollo and Toro 1995).

Fig. 9
figure 9

The values of a flow velocity and b flow depth at different time at the center of the break wall (x = 0.5, y = 0.65)

Full size image

Conclusion

Due to the importance of hyperconcentrated flow in sediment transport and its significant effects on river morphology, simulation of its movement is always of interest to researchers. Fluid characteristics in hyperconcentrated flows, such as density and viscosity, are different from Newtonian fluid and clear water. In this research, two-dimensional model was developed in curvilinear coordinates for two-dimensional dam-breaking of hyperconcentrated fluid flow. In the validation phase of the model, one-dimensional dam-break data measured in the laboratory by Komatina (1999) were used. In this step, the extended Reynolds number was used to calculate the flow resistance coefficient in laminar and turbulent flow conditions (Relations 22 and 23). The statistical analysis between all the measured and calculated flow depth values at different times and errors showed that the model approximates the measurement results with an error of less than 14% and a correlation coefficient of 99%. In other words, the present model has correctly measured the profile of the fluid surface and predicts the position of the avalanche of the advancing wave downstream. In addition, it was shown that fluid concentration affects the flow depth at the fracture site. With the increase in the fluid concentration, the flow depth at the failure location has increased. In the two-dimensional simulation, relations 27 and 28 were used to calculate the shear stresses of non-Newtonian fluid. The simulation results showed that the maximum flow velocity in the center of the fracture wall is 1.4 m/s, which is more than twice the maximum velocity observed in the non-Newtonian fluid with a concentration of Cv = 32.2%, i.e. 0.66 m/s. In addition, as in the one-dimensional case, the depth of the non-Newtonian fluid flow at the fracture location is greater than that of the Newtonian fluid throughout the simulation period.