Introduction

Climate change, aggregated agricultural activity, population growth, and rapid urbanization all pose serious threats to groundwater quantity and quality (Green et al. 2011; Swain et al. 2022; Zango et al. 2022). Groundwater contamination is an important problem not only in areas where groundwater is the primary source of drinking water but also for the sustainable use of water resources. Especially, nitrate contamination in groundwater systems remains a major problem affecting human health. Various approaches to nitrate contamination have been reported in rural and coastal areas where agricultural activities involve the intensive use of organic manure and chemical fertilizers (Almasri and Kaluarachchi 2004; Kim et al. 2021; Kwon et al. 2021; Jannat et al. 2022). The primary sources of nitrate contaminants are manure, fertilizers, and waste in septic tanks (Koh et al. 2009b; Pham et al. 2022); therefore, groundwater nitrate contamination depends on numerous factors, such as land use, agricultural fertilizer application rates, and hydrogeological parameters (Zhang et al. 2015).

Although the establishment of nitrate concentration monitoring is essential for the utilization and management of groundwater resources, nitrate concentrations at all points cannot be investigated and monitored because this process is costly and time-consuming. Therefore, statistical analyses using hydro-chemical components and numerical modeling were performed. Utilizing modeling approaches can assist scientists and managers of groundwater resources in preventing nitrate contamination and improving monitoring quality (Almasri 2008; Locatelli et al. 2019). However, these approaches require large amounts of data and intensive processing steps (Pham et al. 2022). They also require detailed information on the hydrogeological and contamination characteristics, which are difficult to measure or estimate at a field scale (Knoll et al. 2019; Koh et al. 2020). Machine learning techniques have recently received increased attention in the field of groundwater research because they can assess unknown groundwater vulnerability and susceptibility of groundwater changes (e.g., groundwater flooding, Allocca et al. 2021), and predict contamination with relatively high resolution using available hydrogeological parameters and chemical characteristics (Ahn et al. 2012; Yoo et al. 2016; Sajedi-Hosseini et al. 2018; Islam et al. 2022).

Several different machine learning methods, including standard algorithms such as artificial neural network (ANN), support vector machine (SVM), and tree-based models, have been applied to evaluate groundwater nitrate contamination susceptibility and make predictions (Nolan et al. 2015; Ransom et al. 2017; Sajedi-Hosseini et al. 2018; Rodriguez-Galiano et al. 2018; Knoll et al. 2019). Recently, more advanced data-driven algorithms and hybrid optimized algorithms have been developed and applied to more accurately predict nitrate concentrations (Elzain et al. 2021; Pham et al. 2022; Ransom et al. 2022; Islam et al. 2022). These prediction methods mainly utilize the hydrogeological characteristics of total nitrogen leaching into groundwater, where each land-use type contributes to the nitrate load in groundwater (Xue et al. 2009; Burow et al. 2010).

Chemical reactivity plays a major role in the occurrence of nitrates in aquifers, and nitrate reduction, such as denitrification, is usually controlled by hydrological and geochemical factors (Jahangir et al. 2012). Nitrate is generally accompanied by other chemical elements from anthropogenic sources, including agricultural and industrial activities (Bui et al. 2020). Previous studies have successfully estimated the environmental risk and contamination associated with nitrate within agricultural and industrial areas using hydrogeochemical parameters and machine learning methods (Rodriguez-Galiano et al. 2014; Darwishe et al. 2017; Bui et al. 2020; Islam et al. 2022). As groundwater quality is determined by chemical reactions such as water–rock interactions or the inflow of substances at the surface into aquifers, a prediction model using dissolved ions in groundwater as input parameters can achieve high prediction performance (Bui et al. 2020). However, prediction models that rely on chemical composition suffer from the following disadvantages: it is difficult to obtain groundwater samples that have representative values for all areas. In addition, analyzing and validating chemical composition data is expensive and time-consuming.

Field-measured parameters are indirect indicators of groundwater quality that can be easily measured and used to predict long-term fluctuations when continuous measurement data are consistently obtained using automatic monitoring devices (El Bilali et al. 2021; Stylianoudaki et al. 2022). In South Korea, the prediction of nitrate contamination fluxes using machine learning algorithms in mixed land-use areas has rarely been studied. The field measurements were collected periodically within the groundwater monitoring network system. Using machine learning methods combined with geographic information system (GIS) techniques, these monitoring data could be useful for assessing spatiotemporal variations in nitrate contamination, including those at unmeasured or unknown locations.

Therefore, we applied standard algorithms to evaluate the prediction of nitrate concentration using indirect groundwater data, such as field measurements of parameters (pH, water temperature, electrical conductivity, dissolved oxygen, and redox potential), on a small catchment scale. To validate the prediction performance of the model-applied field measurement parameters, we estimated and compared the prediction models for nitrate concentration using chemical elements as input variables. In addition, we identified the most important variables with regard to model prediction performance to better understand nitrate behavior and the relationships between nitrate and field measurement parameters, considering GIS-based hydrogeochemical properties. The results of this study can help guide the development of local groundwater nitrate management measures in areas with agricultural activities using easily accessible monitoring or measurement data.

Materials and methods

Study area

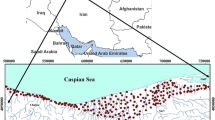
The study area, the Nonsan Stream Watershed (NSW), is located in the midwestern region of South Korea (35°59′ N–36°22′ N, 127°0′ E–127°24′ E). The basin area is 666.1 km2, and the watershed contains 33 small streams as well as the main stream of Nonsan-cheon, with 5 sub-watersheds (Fig. 1). The average elevation of the area is 119.3 m (maximum: 874 m), the slope direction is mainly western, and the average slope is 24.6%. Plains with low slopes (< 10) occupy most of the land (approximately 48%), and agricultural land is widely distributed (Water Resources Management Information System (WAMIS); http://www.wamis.go.kr). The bedrock of the western plains is mostly Mesozoic Jurassic granodiorite from intrusive magmatic activity. The eastern area bedrock is covered with forest and is composed of metasedimentary rocks of the Choseon and Okcheon supergroups from the Paleozoic Ordovician period to the Cambrian period (Korea Institute of Geoscience and Mineral Resources (KIGAM); https://data.kigam.re.kr/mgeo). Some metamorphic and volcanic rocks (tuff) are also distributed in the area (Fig. 1a).

Fig. 1
figure 1

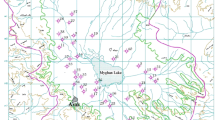
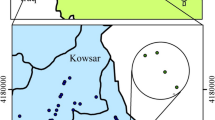
Map of the Nonsan Stream Watershed: a simplified geological map and distribution of the groundwater wells (n = 183), and b hydrogeological map (hydrogeological unit; modified from ME 2023, groundwater contour lines and flow direction; simplified from www.gims.go.kr), c land use and land cover in the study area with the distribution of the NO3-N concentration data

Full size image

Hydrogeological setting helps understand the infiltration and transport of nitrate contaminants in groundwater systems. The hydrogeological units in the study area are classified into seven groups (Fig. 1b modified from ME 2023). In the western region, unconsolidated alluvial deposits are widely distributed, surrounded by intrusive igneous rocks (Jurassic to Cretaceous). Due to the influence of sedimentation and erosional processes, rice paddy and uplands are mainly distributed in this plain area. In the eastern region, clastic sedimentary rocks, meta-sedimentary rocks, and non-porous volcanic rocks are distributed, and groundwater utilization is not high because forests mainly cover it, and nitrate concentration is low. Intrusive igneous rocks (Cretaceous-Paleogene) are distributed in some areas to the southeast.

In Nonsan region (administrative district), which covers most of the NSW, the specific capacity for groundwater of each hydrogeological unit is as follows (MOLIT and K-water 2015); The average specific capacity in unconsolidated clastic sedimentary rocks is 40.9 m2/d (bedrock aquifer 19.6 m2/d, alluvial aquifer 97.6 m2/d), and the particular capacity in metamorphic and intrusive rocks is 27.1 m2/d (bedrock 16.5, alluvial 80.4 m2/d) and 13.1 m2/d (bedrock 12.1, alluvial 28.8 m2/d), respectively. The average transmissivity values for each hydrogeological unit in metamorphic, unconsolidated clastic sedimentary, and intrusive igneous rocks were 8.2, 7.5, and 4.8 m2/d (bedrock 5.4, 4.7, 4.6 m2/d; alluvial 17.8, 19.3, 7.8 m2/d), respectively. The hydrologic characteristics of the NSW were high in both specific capacity and transmissivity in the unconsolidated clastic sedimentary layer by hydrogeological unit. In the bedrock aquifer, the difference in particular capacity and hydrogeological unit transmissivity was insignificant. Still, in the alluvial aquifer, the intrusive igneous rock's specific capacity and transmissivity were relatively small.

In the study area, highlands (recharge areas) are mainly distributed in the eastern region, and plains (discharge areas) are distributed in the western region. The average recharge rate by groundwater modeling was about 17% (about 220 mm/year estimated from MOLIT and K-water 2015). The groundwater level distribution and flow characteristics in the NSW were analyzed using the groundwater information map of the "National Groundwater Information Center” operated by K-water (https://www.gims.go.kr). Due to the topographical characteristics, the groundwater flow direction is approximately east–west oriented in the basin scale, and the groundwater converges in the direction of the river in each sub-basin (MOLIT and K-water 2015).

Land cover is an intensive agricultural activity that combines paddy fields, uplands, and greenhouses (Fig. 1c). The forest area within the basin is 303.1 km2 (45.5%), agricultural land is 235.9 km2 (35.4%), urban area is 49.5 km2 (7.4%), and others (grassland, waterbody, etc.) comprise 77.7 km2 (11.7%). The ratio of upland to paddy fields, including greenhouses, was approximately 3:7, and is higher for paddy fields. The main crops grown in the Nonsan area are strawberries, rice, pears, watermelons, and tomatoes. Previous studies have assessed the characteristics and sources of nitrate contamination in groundwater owing to differences in geological properties (lithology), aquifer type (alluvial and bedrock), and land use in the study area (Kim et al. 2008; Koh et al. 2009b; Kwon et al. 2020).

The average annual temperature over the past 10 years (2011–2020) recorded by the automated weather station (AWS) in NSW is approximately 12.7 °C, and the annual average rainfall is approximately 1221 mm. Most precipitation occurs during the wet season (June to September, average 792 mm), and the average precipitation during the dry season (October to May) is 429 mm (Korea Meteorological Administration (KMA); https://data.kma.go.kr). In 2018, the number of inhabitants in NSW was approximately 130,000, most of whom were distributed near paddy fields in the lowlands. The total groundwater use was approximately 31 Mm3/year, of which approximately 21 Mm3/year (70%) was used for agriculture and 9 Mm3/year (29%) for drinking or domestic water. The water supplied to this area was calculated at 15 Mm3/year, indicating that the area is highly dependent on groundwater (WAMIS; http://www.wamis.go.kr).

Data acquisition and datasets

A total of 183 groundwater well data were constructed by selecting points corresponding to NSW from the data in the Basic Groundwater Survey Report in the Nonsan/Gyeryong, Gongju, and Geumsan regions (MOLIT and K-water 2013, 2015; ME and K-water 2019). The aquifer where the groundwater wells were installed is classified as an alluvial or bedrock aquifer. The database for water quality parameters comprised the raw data presented in the Basic Groundwater Survey Report. Field data from the groundwater samples, such as pH, water temperature (Temp.), electrical conductivity (EC), dissolved oxygen (DO), and redox potential (ORP), were collected. The dissolved major and minor elements, including Ca, Mg, Na, K, SiO2(aq), Fe, Mn, and major anions, including HCO3, F, Cl, SO4, and NO3-N, were collected in groundwater samples, allowing the prediction performance to be compared to that of the prediction model based on field measurements. The database of chemical components in the Basic Groundwater Survey Report was analyzed by a certified agency for water quality inspection. In addition, we calculated the charge balance error (CBE) for the major elements and selected samples within ± 5% CBE for dataset quality control.

The parameters related to the hydrogeological characteristics of NSW were used for data mining. The parameters used as input data were land cover, lithology, aquifer type (alluvial and bedrock), well depth, and soil drainage. Using ArcGIS (ver. 10.5.1), point data regarding the location of the groundwater wells were extracted from the spatial information of the polygon types, such as land use and soil drainage (Table 1). Because the other parameters, except well depth and soil drainage, were unstructured (non-numeric) data, the information was categorized by assigning a random number. Because the main source of groundwater nitrate contamination is the intensive use of organic manure and fertilizers in farming activities, land use is the main determining factor, while the main agricultural type in NSW is a water-curtain-type greenhouse (Cho et al. 2012; Kwon et al. 2020). Usually, greenhouse facilities are built on an existing rice paddy field (Son et al. 2018). For the points where land cover was classified as paddy fields in the GIS data, each point was shown on a Google map (Google Earth), and points with greenhouse facilities were separately extracted and compared.

Table 1 Information on the input variables
Full size table

Characteristics of field parameters and nitrate contamination

The characteristics of the field-based measurements of the 183 groundwater samples in the study area are summarized in Table 2. The pH ranged from 5.8 to 8.3, and the median DO was 8.3 mg/L, which was high in most groundwater samples and indicated shallow groundwater or oxidizing conditions. The EC value range was 80–1420 µS/cm; however, the median value was 210 µS/cm, and the CV was as low as 67%. The temperature of the groundwater samples ranged from 9.4 to 20.2 °C (median = 15.5 °C), which may be due to differences in well depth and survey period among the various sampling points. The median values of Ca, Mg, Na, and K, which are the major cations, were as low as 23.6, 4.3, 12.7, and 1.9, respectively. The median values of the anions HCO3, Cl, SO4, and NO3-N were also low at 63, 14.5, 8.0, and 4.0, respectively.

Table 2 Summarized statistics of the measured parameters for the groundwater samples
Full size table

The majority of water types in the groundwater samples were the Ca–HCO3-type, and some samples with elevated NO3-N concentrations were the Ca–Cl (SO4)-type. Only some groundwater samples were the Na–HCO3-type (Fig. 2). The lithology of the study area is mostly granitic rock, with some metasedimentary rock and volcanic rock in the southeast and metamorphic rock on a small scale in the north. In the Piper diagram, the water type according to the lithology of the study area was not clearly classified, and most groundwater samples were of the Ca–HCO3-type. Groundwater samples of the Na–HCO3-type are associated with the dissolution of silicate minerals in granitic rocks (Chae et al. 2006).

Fig. 2
figure 2

Piper diagram of the hydro-chemical and nitrate concentrations of the groundwater samples

Full size image

The NO3-N concentration of the groundwater samples ranged from 0.1 to 42.9 mg/L (median = 4.0 mg/L, Table 2). The drinking water standard for nitrate is 10 mg/L NO3-N (WHO 1996). In South Korea, the drinking water standard for NO3-N is 10 mg/L, and the agricultural water standard is less than 20 mg/L. Even if the NO3-N concentration in the groundwater exceeds 20 mg/L, it can be used as industrial water. Figure 3 shows a histogram of NO3-N concentrations in the groundwater samples in the study area. Only 75% (n = 138) of the total groundwater samples had a concentration within the drinking water standard limit. However, the concentration of NO3-N in the remaining 25% of the groundwater samples (n = 45) exceeded the drinking water standard, and 12 of them were highly contaminated, limiting their use to industrial purposes. The distribution of NO3-N concentrations in groundwater samples from the forests in the eastern and southern regions indicated a range of conditions suitable for drinking water.

Fig. 3
figure 3

Histogram of the NO3-N concentrations of the groundwater samples (n = 183) in the Nonsan Stream Watershed according to the water quality standards of South Korea (below 10 mg/L for drinking water, below 20 mg/L for agricultural water, and above 20 mg/L for industrial water)

Full size image

Elevated nitrate concentrations in groundwater were found in mixed land-use areas, where the distribution of paddy fields and uplands was dominant (Fig. 1c). NO3-N concentrations were plotted in a box plot to compare land-use types (Fig. 4). The median NO3-N concentrations were 4.2, 4.0, 3.8, 1.8, and 7.0 mg/L in paddy fields, greenhouses, uplands, forests, and residential areas, respectively. The cultivation type of the greenhouse facility is similar to that of an upland area. Regarding land use categories, greenhouses were classified and analyzed as upland land. The median concentration of NO3-N in the groundwater samples distributed in the forested regions was less than 3 mg/L, indicating that the natural background concentration was unaffected by anthropogenic pollution (Medison and Brunett 1985). A comparison of the distribution of nitrate concentrations revealed that the central and western regions had high nitrate concentrations, but the distribution of nitrate among the agricultural land areas was consistent (Fig. 1c).

Fig. 4
figure 4

Box plot comparison of the groundwater nitrate concentrations classified by land use

Full size image

Data mining approaches and multivariate statistics

Four representative machine learning models, namely the random forest (RF) model, support vector machine (SVM) model, classification and regression tree (CART) model, and artificial neural network (ANN) model, were used to estimate the probability of contamination occurrence.

The RF model is a machine learning model, which consists of several decision trees (DT) using ensemble techniques (Breiman 2001). This model combines bagging and bootstrap techniques to compensate for the shortcomings of DT, which is data-dependent and has relatively low accuracy (Islam et al. 2022). Furthermore, unlike traditional machine learning methods such as neural networks, RF processes rapidly even with large amounts of data, and it is a model that accurately reflects the nonlinearity between variables (Breiman 2001). The SVM model is easy to generalize because it uses a decision function that minimizes the empirical errors for each group by subdividing the entire group based on structural risk minimization (SRM), which has the advantage of being able to analyze not only linear data, but also nonlinear data using various kernels (Cortes and Vapnik 1995). In addition, SVM can alleviate problems such as overfitting and local optimization by applying a penalty term that can provide better predictive power than ANN (Zhou et al. 2017). CART is a nonparametric classification and regression technique of decision trees, which is widely used because it is easy to understand and analyze results. It has the advantage that pre-processing processes such as scaling are relatively unnecessary and nonlinear relationships do not significantly affect results (Breiman 2001; Yoo et al. 2016). CART is nonparametric and can identify complex relationships between input and output variables. Therefore, CART also has the advantage of discovering nonlinear structures and variable interactions in training samples (Brezigar-Masten and Masten 2012). ANN is a set of connected units called neurons, similar to the human brain. ANN can identify complex nonlinear relationships or patterns between input and output data and has a flexible structure that can estimate output values based on training and testing processes (Breiman 2001). However, if the number of nodes in the hidden layer is too large, overfitting problems may occur, and if it is too small, underfitting problems may occur; therefore, determining the node of the hidden layer is most important when designing an ANN (Yoo et al. 2016). Therefore, in this study, the number of hidden-layer nodes was selected using a trial-and-error method.

The dataset was randomly partitioned into subsets, where 70% of the data (n = 128) were used to calibrate the models and 30% (n = 55) were used for testing, as described in previous studies (Yoo et al. 2016; Messier et al. 2019). Nitrate concentrations were used as the target variables, whereas field measurement parameters (pH, EC, DO, water temperature, and ORP), land use, soil drainage, depth, and aquifer media were used as input variables for modeling. During model training, tenfold cross-validation was used to avoid model overfitting (Cawley and Talbot 2003; Yoo et al. 2018). All machine learning models were developed on the training set, whereas the test set remained independent and was used to quantify the out-of-sample prediction accuracy (Yoo et al. 2016; Messier et al. 2019). Machine learning modeling and analysis were performed using the IBM SPSS modeler v.18.2 software (IBM; Armonk, NY 10504, USA). In addition, to compare the prediction performance, ten major elements dissolved in groundwater were included as model input variables and evaluated in the same manner. To determine the best algorithm for the database, we used hyperparameter tuning (Islam et al. 2022). The model hyperparameters were tuned for all models during calibration. The numbers of trees used for RF induction were set to 50, 100, 200, 300, 400, and 500, and sensitivity test from 1 to 1000 was performed to find optimal node size. To build the SVM, the gamma value was 2–1 ~ 21, the cost value was 2–2 ~ 25, and the optimal result was selected from the experimental results (gamma, cost) = (0.5, 1.0) because the optimal combination of the gamma value and the cost according to overfitting can be determined to create an SVM model that is not overfitting (Zhou et al. 2017). The CART was built considering tree depths from 2 to 29, with a minimum number of observations per node between 1 and 50. The complexity parameter (cp) is used to select the optimal size of the CART model with the default threshold cp value (0.001 to 0.01). For the ANN, the node and hidden layers were considered by setting 10, 20, and 30 nodes and 1, 2, 3, 4, 5, 6, 7, and 8 hidden layers, respectively.

To evaluate the performance of the different machine learning models, the coefficient of determination (R2), root mean square error (RMSE), and mean absolute error (MAE) were calculated using the following equations:

$$\begin{aligned} & R^{2} = { }\left[ {1 - \mathop \sum \limits_{i} \frac{{\left( {y_{i} - \hat{y}_{i} } \right)^{2} }}{{\left( {y_{i} - \overline{y}_{i} } \right)^{2} }}} \right] \\ & {\text{RMSE}} = { }\sqrt {\frac{{\mathop \sum \nolimits_{i = 1}^{n} \left( {\hat{y}_{i} - y_{i} } \right)^{2} }}{n}} \\ & {\text{MAE}} = \left[ {\frac{{\mathop \sum \nolimits_{i = 1}^{n} \left| {y_{i} - \hat{y}_{i} } \right|}}{n}} \right] \\ \end{aligned}$$

where \(y_{i}\) and \(\hat{y}_{i}\) are the observed and predicted values, respectively, \(\overline{y}_{i}\) is the mean of the observed data, i is the number of observed data points, and n is the number of data points (groundwater samples).

Principal component analysis (PCA) was performed to identify and classify the factors influencing the groundwater geochemistry by integrating information on the hydrogeochemical parameters of the groundwater samples into a single number (Horel 1981; Valdes et al. 2007). The PCA method was used to analyze 15 variables, including pH, temperature, DO, total dissolved solids (TDS), ORP, Ca, Mg, Na, K, HCO3, Cl, SO4, NO3-N, F, and SiO2(aq), from 183 groundwater samples using XLSTAT statistical software (Addinsoft, version 2020; Paris, France). Fe and Mn concentrations were not included in the PCA because they were found to be below detection levels in most groundwater samples. Principal components (PCs) were extracted using the Kaiser criterion and varimax rotation.

Results

Prediction of nitrate concentrations

The machine learning methods RF, CART, SVM, and ANN were applied to predict the nitrate concentration in groundwater in the mixed agricultural areas of paddy fields, uplands (including greenhouses), and forests, and the prediction performance of each model was evaluated (Table 3 and Fig. 5). A performance assessment that considers cross-validation or test datasets can yield realistic values of the prediction performance (Yoo et al. 2016; Knoll et al. 2019). To obtain dependable results and achieve output interpretation, we assessed the machine learning performance using the cross-validation method. The optimized parameters of the RF, CART, SVM, and ANN models are listed in Tables S2–S5. In this study, ntree = 200 and mtry = 7 was found to be the optimal model for the RF model, and 0.5 gamma and 1.0 cost were finalized as the optimal model for SVM, while 11 terminal node and cp of 0.03 produced the optimal RMSE in CART, and six neurons in the hidden layer were optimized for the ANN model based on the lowest RMSE value.

Table 3 Estimation of the model performance of the RF, CART, SVM, and ANN models based on the training and test data
Full size table
Fig. 5
figure 5

Results of the model-predicted versus observed NO3-N concentrations in groundwater using field-measured parameters for data mining; a RF, b CART, c SVM, and d ANN

Full size image

Analysis of the observed and predicted NO3-N concentrations revealed that the RF model achieved a satisfactory prediction performance using both field-based and chemical data. As shown in Figs. 5a and S1a, the prediction performance of the RF model was higher when chemical data were used (R2 = 0.78, RMSE = 2.5, and MAE = 2.0) than when field-based data were used (R2 = 0.74, RMSE = 3.5, and MAE = 2.6). Although the chemical data produced a better nitrate concentration fitting effect for model training purposes, no significant difference was observed in the contamination prediction performance (p > 0.05). However, the predicted concentration at the point with the highest actual NO3-N concentration (42.9 mg/L) in the groundwater sample was extremely low compared with the observed concentration, and the value was higher in the concentration range below 2.5 mg/L (Fig. 5a). Because of the CART model, the observed concentration was not correctly evaluated and was calculated using only the predicted values of the three intervals of approximately 3, 8, and 23 mg/L. The prediction performance of the CART model (Figs. 5b and S1b) was also low when both chemical (R2 = 0.54, RMSE = 4.8, and MAE = 3.4) and field-based data (R2 = 0.52, RMSE = 4.9, and MAE = 3.5) were used. The SVM model results indicated the best prediction performance among the four machine learning techniques applied to predict nitrate concentration in this study. The metrics used to evaluate the prediction performance of the SVM model were R2 = 0.80, RMSE = 2.8, and MAE = 2.4, whereas the model performance using the chemical data indicated the following values: R2 = 0.85, RMSE = 2.1, and MAE = 1.6 (Figs. 5c and S1c). Similar to the RF model results, the SVM model results using both chemical and field-based data revealed a problem, whereby the predicted values of the range of low nitrate concentrations in certain groundwater samples were higher than the observed values; however, the model calculation results were closer to the 1:1 line (Fig. 5c). The performance of the ANN model was not as good as that of the RF model; however, the fitting curve indicated a relatively high noise (error) level. The prediction performance of the ANN model (Fig. 5d and S1d) was satisfactory when using both chemical (R2 = 0.70, RMSE = 3.5, and MAE = 2.6) and field-based data (R2 = 0.65, RMSE = 4.3, and MAE = 3.2).

Identification of important variables

The relative importance of the field-based data variables was analyzed after the RF, SVM, CART, and ANN model-learning processes. The ten input variables of the field-based data and 29 input variables of the chemical data that could significantly affect the performances of the RF, SVM, CART, and ANN models are shown in Fig. S2. Remarkable differences were observed in the results when chemical- and field-based data were used (Fig. S3). With regard to chemical data, lithology, land use, soil drainage, SO4, and DO were the most important variables of the RF and CART models for nitrate concentration prediction. The most important variables in the SVM and ANN models were HCO3, Na, Mg, land use, and depth. Moreover, when using field-based data, the overall land use and aquifer type were the most important variables for nitrate concentration prediction for all models. Lithology and soil drainage were important variables in the RF, CART, and SVM models. However, in the ANN model, the DO variable was important for nitrate concentration prediction.

Discussion

Relationship between nitrate contamination and type of land cover

The relationship between land-use type and groundwater nitrate contamination has been previously reported (Koh et al. 2009b; Guzman et al. 2017; Lee et al. 2020). Nitrate contamination in agricultural areas is caused by using fertilizers and manure. In addition, differences in the fertilizer rate and correlations of N concentration in groundwater samples according to the type of land use have been reported (McLay et al. 2001; Zhang et al. 2022). Nitrate concentration is usually lower in paddy fields than in uplands (Kumazawa 2002; Chae et al. 2009; Kao et al. 2011; Ki et al. 2015). Paddy fields are usually water-saturated, and groundwater exhibits reducing conditions owing to the low-permeability layers of clay or silt and the saturation conditions at the top. These conditions can result in an environment in which denitrification occurs during the recharge of surface nitrates into groundwater.

However, in this study area, the variation in the nitrate concentration was the highest in paddy fields, with the median NO3-N concentrations in paddy fields and uplands (including greenhouses) being 4.2 and 3.9 mg/L, respectively. Nitrate concentrations in the groundwater of paddy fields may vary depending on the sampling period. During the dry season, the water-saturated state is not maintained and the groundwater state changes to eventually exhibit oxidizing conditions that may promote nitrification processes (Kumazawa 2002). Rice paddy farming in South Korea begins at the end of May and continues until June. As groundwater sampling was conducted from March to May in the study area, it is possible that the nitrate concentration in the paddy fields was high. High concentrations were detected in residential and bare-land areas. Because there are no central municipal sewer facilities in this area, the groundwater wells adjacent to the farmhouses are affected by nitrate contaminants derived from the septic tanks of each household (Koh et al. 2009b).

Some groundwater samples from the paddy field showed a high concentration of dissolved ions, but the low NO3-N concentration. The elevated concentration of dissolved ions was not affected by the inflow of chemical fertilizer or manure. Because these groundwater samples are located in granitic bedrock areas, their properties are likely due to the influence of deep circulating groundwater rather than water–rock interactions (Koh et al. 2009b). Considering the small scale of the study area, the inflow of nitrate from adjacent upland areas may affect groundwater quality in paddy fields. Nitrate sourced from uplands located at higher altitudes can infiltrate along flow paths and further contaminate groundwater in paddy fields in downstream lowland areas.

Comparison of the performance of the various prediction models according to the selection of input parameters

The results obtained with the four prediction models using field parameters (pH, EC, Temp., DO, and ORP) as input variables indicated the following: R2 0.52–0.80, RMSE 2.8–4.9, and MAE 2.4–3.5 (Fig. 5) for NO3-N prediction. The NO3-N prediction errors of the prediction model considering the 29 variables including major chemical elements as input variables revealed that R2 ranged from 0.54 to 0.85, RMSE ranged from 2.1 to 4.8, and MAE ranged from 1.6 to 3.4; hence, slightly better prediction results could be obtained (Fig. S1). However, the use of field measurement parameters is a more cost-effective approach for generating data easily and facilitating model construction than using chemical elements determined through water quality analysis. Field measurement parameters such as pH, EC, DO, and temperature can be easily measured in situ in groundwater. A prediction model using these parameters as input variables can also effectively predict indicators for determining groundwater quality for agricultural use (El Bilali et al. 2021). Similarly, Zhang et al. (2022) and Wang et al. (2023) used a standard machine learning algorithm with easily accessible indicators (such as pH, EC, DO, ORP, and temperature) as the main parameters and derived a high-predictive-performance model for groundwater nitrate concentration. Prediction models of nitrate concentration were developed for intensive agricultural areas near a lake in Yunnan Province, China, and major predictors were derived through a correlation analysis of input variables. The main indicators were EC, DO, and N fertilization rates. The availability of easily accessible indicators in the field for a nitrate concentration prediction model was verified. High predictive performances have also been derived from agricultural areas in other countries with different scales (data and site scales) and geological characteristics. Field-measured parameters are indirect indicators of groundwater quality and are closely related to geochemical properties or contaminant infiltration. The concentration of contaminants (such as NO3, Mn, and Fe) can be predicted with high accuracy using models combining hydrogeological factors and the GIS database (Rodriguez-Galiano et al. 2014; DeSimone and Ransom 2021).

The relative importance of the input variables used in the nitrate concentration prediction model were ranked and compared (Fig. S2). The relevant predictors with a major influence on the results differed for each model. Although the relative importance ranking for each model was different, land use was found to be suitable for model prediction, confirming that it is a major factor in relation to nitrate prediction in mixed land use areas. Lithology and hydrogeological units are the major factors affecting groundwater quality and are relevant predictors (Tesoriero et al. 2017). However, in this study area, all groundwater samples affected by nitrate contamination in agricultural areas were distributed in granitic rock regions. The groundwater samples with low nitrate concentrations in forests were distributed in metasedimentary or volcanic rock regions, making them unsuitable predictors (Fig. 1).

Machine learning-based model optimization

The results indicated that the RF and SVM methods outperformed the other methods and had the lowest error rates, while the CART method had the weakest performance. Because the RF method is resistant to overtraining, builds on a subset of the best estimators selected in a node, and is randomly applied to divide that node (Liaw and Wiener 2002), it does not create the risk of overfitting (Breiman 2001), and we obtained acceptable results with high accuracy. This feature represents one of the main advantages of RF over neural network models. In addition, the RF method is resistant to outliers in the predictors and automatically manages missing values (Breiman and Cutler 2004). Although CART is a powerful method for classification and prediction, the decision-tree algorithm is more sensitive to noise and outliers than the RF method (Last et al. 2002; Quinlan 2014). Previous studies have shown that the RF method generally achieves significantly higher accuracy than the CART method (Gislason et al. 2006; Cutler et al. 2007; Youssef et al. 2016). These observations may explain why the RF model achieved a stronger performance than the other models in this study.

The SVM method can generally achieve high accuracy with small sample sizes because of its low sensitivity to the training sample size and high capacity for generalization when compared to other machine learning methods (Anguita et al. 2010; Mountrakis et al. 2011; Zhao et al. 2019). Because this study used 183 samples to evaluate the prediction capability and interpretation, a less sensitive method, such as SVM, or a model with a high tolerance to noise and outliers may be more suitable and yield superior performance. Yang et al. (2023) also reported that the prediction performance of the SVM for phosphorus concentration was the best in a prediction model using easily accessible field-based data and a small amount of data from groundwater in agricultural areas. In addition, a high predictive performance can be obtained even with simple algorithms (RF, SVM, and NN) if key indicators are included (Wang et al. 2023). Therefore, RF- and SVM-based modeling approaches may provide more reliable results and better performance for interpretation in agricultural areas with mixed land use, such as the site in this research.

Implications and limitations of the study

The land use types and groundwater nitrate concentrations were highly correlated. The groundwater samples were classified by land use/land cover based on the GIS database to analyze the correlation between nitrate and each major chemical element (Fig. 6). Among the cations, Ca and Mg concentrations were highly correlated with NO3-N concentration, whereas among the anions, Cl and SO4 concentrations were highly correlated with NO3-N concentration. It was inferred that the use of chemical fertilizers or manure for plant growth on agricultural land affected groundwater quality, and this correlation showed similar characteristics to the correlations between the concentrations of nitrate and those of major chemical elements as shown in previous studies (Kaown et al. 2009; Menció et al. 2016). Based on the relationship between the concentrations of Cl and NO3-N, it was found that agricultural activities in the paddy fields and uplands in this area affected nitrate contamination. Elevated nitrate concentrations are associated with an increase in the dissolved ion concentration (Kent and Landon 2013; Menció et al. 2016). Therefore, the EC value (an easily accessible indicator), indicating the total dissolved ion content, can be used as the main indicator for predicting the nitrate concentration (Wang et al. 2023).

Fig. 6
figure 6

Relationships between the major parameters and nitrate in the groundwater samples for each land cover

Full size image

Using land use classification and GIS-based data in the study area as an input variable may weaken the prediction performance of the model. Strawberries, watermelons, and tomatoes are the main crops in the study area, and existing paddy fields are commonly converted into greenhouses for cultivation. Water curtain-type greenhouses can generate high levels of nitrate (Shi et al. 2009). In the GIS data, the land use or land cover of water curtain-type greenhouses was classified as paddy field type. Owing to the limitations of GIS data, elevated nitrate concentrations may be incorrectly determined in paddy fields. Because land use is an important input variable in the prediction model for nitrate concentration, the validation of GIS data can improve the prediction performance.

DO, Fe, and Mn concentrations are factors that indicate redox conditions and can be used as key indicators to evaluate nitrate contamination (Knoll et al. 2020; Zhang et al. 2022). The nitrate concentration in paddy fields is typically low because of the low DO and ORP values, owing to the low permeability of the topsoil layer and saturation conditions (Kumazawa 2002; Chae et al. 2009). However, the average DO value of the groundwater samples in the study area was 8.1 (± 1.0), indicating that most samples exhibited oxidized conditions (> 5 mg/L O2; Rivett et al. 2008). The use of this parameter as a key input variable is limited because of the non-significant difference in the average DO concentration between paddy fields and uplands in the study area, and errors could occur during the measurement of the DO content in groundwater samples using a portable meter. In addition, most of the Fe and Mn concentrations in the groundwater samples were below the detection limits, and there was insufficient data for evaluation.

PCA was performed to explain the characteristics of the major elements included in the input variables of the prediction model (Fig. 7). The component loading in the PCA results represents the correlation between the variable and component, and the component loading can reach a positive or negative value. PC1 explained 27.6% of the total variance and attained high positive loadings for TDS (indicating the EC value), Cl, Mg, and Na, which are indicators of mineralization (water–rock interaction). PC2 accounted for 13.3% of the total variance and attained a high positive loading for NO3-N (Table S1). Notably, PC2 indicated groundwater contamination by nitrate (Fig. 7). High TDS levels in groundwater are caused by the degree of mineralization via water–rock interactions or by the influx of pollutants such as nitrate (Koh et al. 2009a). SO4 can be considered a relevant predictor of groundwater contamination due to agricultural activities and the use of MgSO4 fertilizers. In addition, HCO3-and hardness (Ca + Mg) are associated with the lime (CaO) employed to prevent soil acidification, which is attributed to the inflow of N or MgSO4 fertilizers (Chae et al. 2004). Therefore, these models can suitably predict nitrate contamination under the influence of anthropogenic factors.

Fig. 7
figure 7

Principal component (PC) loadings and score plot of PC1 versus PC2

Full size image

The feasibility of a groundwater nitrate concentration prediction model using easily accessible field-measured parameters (pH, EC, DO, ORP, and temperature) as input variables was verified. However, the easily obtained field parameters may result in measurement errors. For example, pH and temperature, as well as DO and ORP, are major factors in chemical reactions, but model uncertainty can increase owing to data quality. As similar prediction models using easily accessible indicators have been tested for agricultural areas of different scales and in other countries, we believe that the validity and applicability of easily accessible indicators have been confirmed. Because the predictive performance of the models using easily measured parameters from the field or monitoring was evaluated similarly to that of the models using all chemical elements, the field measurement data could be used as a low-cost, high-efficiency predictive model. Although the prediction maps of groundwater nitrate susceptibility for unmeasured areas were not derived, the stand-alone models used in this study to predict the groundwater susceptibility have also uncertainty and variability. Therefore, it can contribute to assessing the susceptibility area for groundwater contamination and groundwater flooding by comparing the results of each prediction model and presenting the optimal ensemble model (Allocca et al. 2021).

Conclusion

The aim of this study is to predict nitrate concentrations in groundwater by employing a simple machine learning approach using field measurement parameters (such as pH, EC, water temperature, DO, and ORP) that can be easily obtained from field surveys or monitoring wells. Problems related to groundwater nitrate contamination have emerged in many agricultural regions of South Korea. Many studies have been conducted on the hydro-chemical behavior of nitrates; however, the nitrate prediction performed in this study using easily measured parameters in the field and hydrogeological characteristics was attempted for the first time. The findings of this study demonstrated that although easily accessible parameters may have measurement inaccuracies, the predictive performance derived by the prediction models using these easily accessible parameters has a significant value compared to the results of the prediction model using chemical components in groundwater.

Although the prediction performance differed among the various applied models, the RF and SVM models achieved relatively high performances, as evaluated by R2, RMSE, and MAE. Compared to the prediction model considering the chemical components in groundwater, the prediction model using field measurement parameters could effectively predict the nitrate concentration in groundwater with high prediction performance and low cost. It is possible to identify nitrate sources in areas with intensive agricultural activities and different land uses and to control and manage groundwater contamination. Automatic monitoring wells distributed across South Korea periodically collect field measurement parameters. Therefore, it is expected that applying the prediction model of this study to a monitoring system will provide spatial and temporal predictions of nitrate concentrations in groundwater. The results of this study can help decision makers and governmental agencies manage groundwater in rural areas by providing information on areas vulnerable to groundwater nitrate contamination and reducing the cost of acquiring water quality data. Although easily accessible parameters have been applied to different regions by other researchers, this prediction model may not be generalized or applicable to other areas with different land cover types and hydrogeological characteristics. Therefore, in the future, we intend to verify the above groundwater quality prediction model by ensuring the reliability of the field measurement parameters used as the main input variables and extending the model to the river basin scale considering various land-use characteristics.