Introduction

Accurate and reliable streamflow prediction is of great importance in designing, developing, and proper operation of water resources management, hydropower generation, and ecohydrological studies and plans. In this sense, various and vigorous modeling strategies have been introduced and implemented in the literature, such as numerical-based (Suiju and Minquan 2015), autoregressive moving average models (Liu et al. 2015), and conceptual models (Boulariah et al. 2019).

During the last decades, with the advent of high-speed processors and the development of novel Soft Computing (SC) techniques, a new era of data mining methods, e.g., Machine Learning (ML) models for modeling and simulating different phenomena in hydrology, has been emerged (Najafzadeh and Niazmardi 2021; Najafzadeh et al. 2021; Zounemat-Kermani et al. 2020a, b; Najafzadeh et al. 2021; Barzkar et al. 2022; Granata et al. 2022; Ikram et al. 2023; Mostafa et al. 2023). Accordingly, streamflow prediction using SC techniques and data-driven models has been one of the main targets for hydrologists and researchers in recent years (Adnan et al. 2020a). These models use ML techniques to map the complicated relationship between the predictors (like precipitation and/or previous observed discharge values) and the response variable (short-term or long-term streamflow) (Adnan et al. 2020b). Poul et al. (2019) challenged four different types of data-driven models, including Multi-Linear Regression (MLR), Artificial Neural Network (ANN), K-nearest neighbors, and Adaptive Neuro-Fuzzy Inference System (ANFIS) in monthly streamflow prediction based upon six input combinations. In general, the ANFIS and ANN models were slightly superior to the other methods. Fu et al. (2020) applied deep learning ML models for the prediction of daily streamflow in a tropical environment. They compared the results of the Long Short-Term Memory (LSTM), as the deep network, to the conventional backpropagation ANN. The findings of the study revealed the obvious advantages of the LSTM over the classic ANN.

It should be noted that among the successful applications of various types of ML models, the Extreme Learning Machine (ELM), which presents a simple structure yet fast learning speed single-layer ANN, has proven its accuracy and efficiency in simulating complex and nonlinear hydrological problems (Rezaie-Balf and Kisi 2018; Yaseen et al. 2020; Saberi-Movahed et al. 2020; Ikram et al. 2022).

In a study, Niu et al. (2020) utilized the ELM for the annual prediction of streamflow using data series of three hydropower reservoirs in China. It was shown that the developed ELM model outperformed several traditional methods. According to the previous researches, the majority of ML applications for streamflow prediction confirm the proper potential and accuracy of ML in comparison with the conventional statistical or conceptual models in addressing this hydrological issue (Riahi-Madvar et al. 2019). Subsequently, new ideas for upgrading and enriching ML models, especially using integrative (hybrid) ML-heuristic methods, have been being developed and tested recently (Fadaee et al. 2020).

In the field of hydrology, several researchers have reported the successful application of heuristic algorithms embedded with ML models. Sudheer et al. (2014) developed a hybrid (integrative) ML model using Support Vector Regression (SVR) and Particle Swarm Optimization (PSO) for forecasting monthly streamflow in the USA. Analyzing the forecasted results indicated that the SVR–PSO model gave a better performance than the ANN and statistical model, namely ARMA (autoregressive moving average model). Malik et al. (2020) employed several integrative models based on the SVR and six heuristic algorithms in predicting daily streamflow in India. Comparing the results showed that SVR–HHO (SVR and Harris Hawks Optimization algorithm) during calibration/validation periods had superior performance to the other developed integrative models. Jiang et al. (2020) developed an integrative (hybrid) ELM–PSO model for monthly streamflow forecasting. The findings of the study demonstrated the superiority of the ELM–PSO over standard ELM, SVR, and ANFIS models.

Considering conventional heuristic algorithms, the PSO and Simulated Annealing (SA) are among the most widely used optimization algorithms in hydrology, and numerous applications have been applied using these algorithms (Bazargan and Norouzi 2018; Hosseini et al. 2020). Recently, some new heuristic algorithms have been introduced and claimed with high capability in optimizing sophisticated problems, such as Mayfly Optimization Algorithm (MOA) (Zervoudakis and Tsafarakis 2020), Grey Wolf Optimization (GWO) (Mirjalili et al. 2014), and hybrid PSOGWO (Şenel et al. 2019). However, there has not been a report on the comprehensive assessment of the capabilities of these algorithms in dealing with hydrological issues compared to the conventional ones (here, the PSO and SA). In this regard, this study utilizes the extreme learning machine (ELM) as the main model embedded with conventional (PSO and SA) and novel (GWO, hybrid PSOGWO, MOA, and hybrid SAMOA) as predictive models to realize streamflow in subhumid region of Bangladesh.

The main contribution and innovation of this study lie in (1) developing four integrative ELM models and analyzing their performance on simulation of a complicated engineering problem, namely streamflow prediction, and (2) appraisal of all developed models based on seven different input combinations scenarios including lagged streamflow values, precipitation, and temperature. To have a clear comprehension, these new approaches include simple (ELM–MOA and ELM–GWO) and hybrid integrative (ELM–PSOGWO and ELM–SAMOA) ML models. Continuously, the results of the new mention models will be compared with the standard ELM and integrative ELM–PSO and ELM–SA to achieve an inclusive perception for their usefulness and accuracy.

Case study

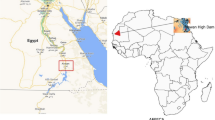
For the current research, the Padma river, a large river basin, is the major downstream stretch of the Ganges River, which runs more than 2561 km2 derived from the Gangotri glacier of the Himalayan system which was chosen as a case study. This river basin is regarded as one of the highly populated residents on the globe. The Padma River acts a crucial role in the socio-economic conditions of the country. The stretch of the Padma river flows for 108 km2 before the confluence with Meghna River at Chandpur point. Gorai River is one of the tributaries of the Padma River. The accumulated discharge of the Padma and Brahmaputra River is 30,000 m3/s−1, and sometimes, it reaches 75,000 m3/s−1 during the bank full phase (Dewan et al. 2017). Geographically, the study basin is positioned between 23° 48′ and 25° 18′ north latitudes and 88° 27′ and 89° 48′ east longitudes. Annually, 900 metric tons of sediment load passes through the river, out of which, 60% of sediment is either silt or clay, while the rest is bed load (Islam 2016). Islam et al. (2021) stated the floodplain of the river as a ‘wandering’ form. Padma River basin is vital for sustaining livelihood through agricultural activities, navigation, nourishment, aquaculture, and environmental sustainability perspective. For instance, the freshwater distributed by this basin is truly imperative to sustaining a riparian ecosystem of the south-western region of Bangladesh, mostly in the world’s largest mangrove forest, the Sundarbans, by holding the salinity anterior downstream side into the Bay of Bengal (BOB) (Mirza 2004). Apart from this, this basin reports extreme variability of flow regime (water and sediment), triggering from monsoonal precipitation and the melting of the Himalayan ice, which causes frequent large floods of high magnitude in Bangladesh. Further, bank erosion and river shifting are common phenomena in this basin, which led to environmental degradation and population migration. This is anticipated to enhance in forthcoming years (CDMP 2014) since elevated precipitation triggered by climate change will raise the runoff into the Ganges–Brahmaputra–Meghna River systems (Moors et al. 2011). Four seasons, such as summer (March–May), monsoon (June–September), post-monsoon (October–November), and winter (December–February), have predominated in this region with significant temperature and precipitation differences (Akhter et al. 2019). Runoff in the Padma river was mostly distributed in June–October, accounting for 72.5% of the accumulated annual runoff. The dry season is from December to April, accounting for l2.1% of the accumulated annual runoff. From December to February, it was the lowest, accounting for solely 5.87% of the annual total (Islam et al. 2016). Runoff in this river basin mostly originates from heavy rainfall. Therefore, in the current study, two hydro-meteorological sites on the Padma River basin, e.g., Padma Hardinge bridge and Gorai stations were employed for predicting monthly streamflow (see Fig. 1). The data adopted in this work were collected from Bangladesh Water Development Board (BWDB).

Fig. 1
figure 1

Study area

Full size image

Methods

Extreme learning machine (ELM)

ELM is a form of the single-layer feed-forwarding network (FFN) that aims to intertwine the traditional neural networks and biological learning mechanism. Due to its special structure based on the random hidden neurons mechanism—in which hidden neurons do not need to be tuned similar to the conventional ANNs—it can provide precise modeling results having a lower computational cost. Moreover, ELM offers other advantages such as ease of implementation, better generalization ability, and minimal human intervention. As a result of the mentioned arguments and reasons, ELM has been chosen as the core machine learning tools in this study. The main mathematical methodology of ELM is described in the following.

As can be seen in Fig. 2, a single hidden layer resides in the ELM network. The input weights between the input and hidden layers are only initialized once and do not need to be conditioned (Zhu et al. 2019; Prasad et al. 2018; Yadav et al. 2017; Zhang et al. 2020). Iterative testing is used to prepare the outcome weights between the un-seen and outcome layers. The training and process time of an ELM is much quicker than that of the comparable single-layer FFN since the input weights remain in their initial state and only the output weights are trained. Huang et al. (2006) suggested the ELM, a basic three-layer structure algorithm, to address the shortcomings of conventional soft computing techniques. The input weight and the bias values are generated at random in the ELM structure. ELM uses a basic simplified inverse operation of the hidden layer output matrix to measure the output weight matrix between hidden and output layers analytically (Fan et al. 2018; Zhu et al. 2020). The ELM is a promising time series prediction method because of its interpolation and uniform approximation capabilities. ELM can be represented mathematically as a function with L hidden nodes and N training data, as seen in Huang et al., (2006):

$$\mathop \sum \limits_{i = 1}^{L} w_{i} g\left( {W_{{{\text{in}}\left( i \right)}} ,b_{i} ,x_{j} } \right) = \mathop \sum \limits_{i = 1}^{L} w_{i} g\left( {W_{{{\text{in}}\left( i \right)}} ,x_{j} + b_{i} } \right) = Y_{j} ,\;j = 1, \ldots ,N.$$
(1)

where \({x}_{j}\) represent the input vector, \({W}_{\mathrm{in}\left(i\right)}\) denotes the weight vtor of the input, \({W}_{\mathrm{in}\left(i\right)}\).\({x}_{j}\) corresponds the inner product of \({W}_{\mathrm{in}\left(i\right)}\) and \({x}_{j}\), bi denotes the bias of the ith hidden node, g(∙) denotes the sigmoid function, wi refers to the weight matrix of the output, and yj is the modeled output of the ELM. At the start of the ELM algorithm, the input weight and bias are selected at random.

Fig. 2
figure 2

ELM structure

Full size image

Particle swarm optimization (PSO)

The PSO algorithm is a type of optimization algorithm to simulate the behavior of swarm intelligence (Qi et al. 2018; Xi et al. 2021). It is an efficient globally optimized search algorithm through the system intelligence guidelines that comes from the collaboration and rivalry between parts of the group. In the research space of N-dimensional, it can specifically be represented randomly as a particle group (the quantity is m) and each implemented a special structure of ANN (Chen et al. 2020; Wang et al. 2018). The primary architectural theory of PSO is closely related to two studies: the first is the evolutionary algorithm; the PSO swarm mode where the mostly optimized objective solution space can be searched simultaneously. The other is synthetic life and in particular the examination of artificial systems with life-characteristics. The efficiency of the particles location was measured by the statistical error in the training phase. More specifically, at generating the lowest values of MSE, the ANN structure is defined by a particle with a superlative performance (Elsheikh and Abd Elaziz 2019). The next swarm was produced based on updating the particles’ locations, which takes into account the best position of swarm and particle. Particle swarms gradually shifted to the optimal location up to the maximum number of iterations. The velocity and direction of the particle can be modified as follows:

$$V_{i}^{k + 1} = \omega \times V_{i}^{k} + c_{1} \times {\text{rand}} () \times \left( {P_{i}^{k} - X_{i}^{k} } \right) + c_{2} \times {\text{rand}}() \times \left( {G_{i}^{k} - X_{i}^{k} } \right)$$
(2)
$$X_{i}^{k + 1} = X_{i}^{k} + V_{i}^{k + 1}$$
(3)

where \({V}_{i}^{k+1}\) and \({V}_{i}^{k}\) denote the particle (\(i\)) velocity at iteration (\(k\)) and (\(k+1\)), rand () represents a random value between 0 and 1. c1, c2 are called a learning or acceleration factor and equaled 2 for both in this work. \(\omega\) refers to the coefficient of inertia. P and G represent the best place for a particle and a swarm, respectively. In the present work, number of iterations, population, and runs were 100, 25 and 7, respectively. \(\omega\) ranged from 0.2 to 0.9.

Mayfly optimization algorithm (MOA)

The suggested process of optimization considers as a PSO adjustment and the combination of main PSO, genetic and firefly algorithms benefits (Gao et al. 2020; Zervoudakis and Tsafarakis 2020). In reality, it offers for researchers who seek to advance the efficiency of the PSO algorithm with certain techniques and local search, a powerful hybrid algorithm, dependent upon the mayflies’ actions, as PSO has proved that modifications are required to ensure optimum performance in high-dimensional areas. The algorithm functions like this. Initially, the random generation of two groups of mayflies is male and female, respectively (Mansouri et al. 2019). The individual fly can be put on a random basis as a d-dimensional vector solution x = (x1,…,xd) in problem space, and its output is assessed on the previous definition of objective function f (x). The velocity of the mayfly v = (v1,…,vd) is known as the shift of its path, and each mayfly’s flying path is a complex relationship between individual and social experience. In specific, they will change their direction to their best (Pbest) location and the best position achieved by any swarm flying (Gbest) (Haddad et al. 2006). In Swarms, male’s mayflies will continue to investigate or manipulate during iterations. The speed will be modified to their present fitness data and historical optimal values of fitness (Chen and Shi 2019; Mansouri et al. 2019; Zhou et al. 2018). The females will update their speeds in a particular way. In biological terms, the female only live with wings in one day to at most seven days, so the female mayflies need to search the male mayflies to intermarriage and spread. They will then update their speeds on the basis of their masculine flies. The top best male and female mayflies are regarded as the first mate and the second best female/male mayflies as the second mates and so on. In the present study, the parameters used for this algorithm are presented in Table 1.

Table 1 Parameters setting of each optimization algorithms
Full size table

Simulated annealing algorithm (SA)

The SA is an algorithm that belongs to meta-heuristic methods and is known also as Monte Carlo Annealing (Shao and Zuo 2020; Tufano et al. 2020; Turhan and Bilgen 2020). The SA algorithm is a physical annealing method based on simulation that has successfully extended to multiple dynamic problem optimization. The concept behind the SA stems from thermodynamics and illustrates how to mirror the solidifying mechanism of the fluid into a crystalline solid (Abdel-Basset et al. 2021; Redi et al. 2020; Silva et al. 2020; Tang et al. 2020). Annealing is a physical mechanism utilized to tend to harden metals beginning at maximum temperature and cool off slowly. At first, SA parameters including the initial temperature T0, final temperature Tfinal and cooling rate are initialized. The original temperature is the maximum and will be gradually refreshed using the rate of cooling before the end temperature is reached (Ben Messaoud 2020; Meng et al. 2020). A sharp decline in temperature causes the molecules to select the right location, normally not the best possible case, therefore quench the object. The algorithm starts with a randomly created solution. The approach is based on progressive improvement of the present solution. During iterations process, a new neighboring solution for the current solution is chosen. If the latest neighboring solution is stronger, the existing solution is modified. In addition, when the adjacent solution is stronger, the optimal solution is refreshed. When the end temperature is hit, the model stops (Liu et al. 2020; Zhao et al. 2020). For each iteration (), the actual temperature T is modified by:

$$T = T * \tau , \, 0 < \tau < {1}$$
(4)

Boltzmann distribution gives the probability according to mathematical thermodynamics that a molecule is at a certain energy degree as follows:

$$P\left( {\varepsilon_{i} } \right) = \frac{{{\text{exp}}^{{ - \varepsilon_{i/kT} }} }}{{\mathop \sum \nolimits_{j = 1}^{m} {\text{exp}}^{{ - \varepsilon_{j/kT} }} }}$$
(5)

where \({\varepsilon }_{i}\) is the energy at the state (\(i\)), k represents the constant of Boltzmann, T equals the thermodynamic temperature and m denotes the overall states number. In this study, the initial and final temperatures were 100 and 0.01, respectively, and the rate of cooling was 0.7 (Table 1).

Grey wolf optimizer (GWO)

GWO is an advanced successful introduced swarm intelligence algorithm suggested by Mirjalili et al. (2014) in last decade. The kind of algorithms is based on the imitation of the social order and hunting activities of the Grey Wolf Herd. GW is purely hierarchical social species comprising \(\propto\), β, δ, and \(\omega\). In this respect, \(\propto\) is the leader who distributes several assignments to individuals at various levels to achieve global optimization. Due to its simple structure, insignificant parameter change required and high accuracy, the GWO algorithm has always been used for functional optimization (Dehghani et al. 2019; Himanshu et al. 2020; Wang et al. 2018). The location of the ith wolf is defined as Xi = XI1, XI2…, XId. XId stands for the position of the ith wolf is d-dimensional space, for a population containing N grey wolves (X = X1, X2,…, XN). The specific role of hunting is as follows:

$$D = \left| {C* X_{i } \left( t \right) - X\left( t \right)} \right|$$
(6)
$$X_{i} \left( {t + 1} \right) = X \left( t \right) - A*D$$
(7)

where A and C stand for the coefficient vectors, t is number of iterations, X(t) is the position vector of GW, Xi (t) is target position vector of the GW, D corresponds to the distance between the prey and the grey wolf.

Defining the coefficient vector as follows:

$$A = 2*a*r_{1} - a$$
(8)
$$C = 2*r_{2}$$
(9)
$$a = 2 - i*\left( {\frac{2}{Maximum \; iteration}} \right)$$
(10)

where r1 and r2 correspond to the random vectors with values (0, 1) and a represents the iteration factor. In this study, the population, number of iterations, and number of runs for all algorithms were 25, 100, and 7, respectively, as demonstrated in Table 1. In addition, a decreased from 2 to 0. GW has strong food quest ability. ∝ is the boss who will serve in all activities and sometimes β and δ can participate. β and δ can also provide ∝ with successful goal information in the GWO as an ideal solution (Mohammadi et al. 2020; Tikhamarine et al. 2020, 2019; Yu and Lu 2018). Therefore, α, β, and δ are the three ideal alternatives in fact and their adjusted positions:

$$D_{ \propto } \;= \left| {C_{1} * X_{ \propto }\; \left( t \right) - X\left( t \right)} \right|$$
(11)
$$D_{{\upbeta }} = \left| {C_{2} * X_{{\upbeta }} \left( t \right) - X\left( t \right)} \right|$$
(12)
$$D_{{\updelta }} = \left| {C_{3} * X_{{\updelta }} \left( t \right) - X\left( t \right)} \right|$$
(13)
$$X_{1} = X_{ \propto } - A_{1} *D_{ \propto }$$
(14)
$$X_{2} = X_{{\upbeta }} - A_{2} *D_{{\upbeta }}$$
(15)
$$X_{3} = X_{{\updelta }} - A_{3} *D_{{\updelta }}$$
(16)
$$X \left( {t + 1} \right) = \frac{{X_{1} + X_{2} + X_{3} }}{3}$$
(17)

where Xα, Xβ, and Xδ correspond to the current positions of the three optimal solutions α, β, and δ, respectively; X(t) stands for the target position; Dα, Dβ, and Dδ denote the distances from the prey to the three solutions, respectively; X(t + 1) is the position vector with updated searching factor; C and A represent the random vectors.

Hybrid PSO–GWO algorithm

Without modifying the overall operation of PSO and GWO algorithms, our hybrid PSO–GWO algorithm has been built. In nearly all real-world issues, the PSO can produce good results. Nevertheless, the PSO algorithm has to be reduced to minimal in the local solution. The GWO algorithm in our approach suggested follows the PSO algorithm in order to minimize the risk of slipping through a minimum local level (Şenel et al. 2019). The PSO algorithm leads those particles into the random spot, as discussed in PSO description section, with no potential to escape local minima. These directions can be risky for going away from the global minimum. The GWO algorithm’s scanning ability can be used to avoid these threats by directing those particles into locations which are partly enhanced by the GWO algorithm rather than randomly guided. The runtime therefore is expanded, since besides the PSO algorithm, the GWO algorithm is still used. The longer time will be considered tolerable, based on the optimization problem solved, when the results are effective and the additional time required is considered. The improved success will accommodate extra time in the sector like leather, in which losses are much more important as long as the solution is accomplished in a proper time. The flowchart of this algorithm is presented in Fig. 3.

Fig. 3
figure 3

Flowchart of the PSO–GWO Algorithm

Full size image

Proposed hybrid MOA–SA algorithm

For on-going optimization issues, the MOA algorithm was designed above. The new hybrid algorithm called MOA–SA is for fitness function problems of each particle in the current population and selecting the best particle and swam. Our hybrid MOA–SA algorithm was created without altering the overall operation of MOA and SA algorithms. Each MOA solution vector shall be transformed, i.e., only 0 s and 1 s and evaluated in binary form. The S-shaped transition mechanism is used for this conversion. The option of selecting a specific feature in a solution vector is given by this function. The initial temperature is the highest and will be steadily refreshed using the cooling rate to reach the final temperature, as discussed in the SA algorithm description. The algorithm begins with a solution generated at random. The method is focused on gradual changes to the existing approach. A new neighboring solution for the current solution is selected during the iteration process. The final steps are checking the iteration process and terminate the computational process and store the optimal solution. The flowchart for the new hybrid algorithm (MOA–SA) is shown in Fig. 4.

Fig. 4
figure 4

Flowchart of the MOA–SA Algorithm

Full size image

Application and results

The ability of two-phase optimized ELM models, ELM–PSOGWO and ELM–SAMOA, is investigated in monthly streamflow prediction. Various combinations of streamflow, precipitation and temperature data obtained from two stations, Pakistan, are used as model inputs. The outcomes acquired from the ELM–PSOGWO and ELM–SAMOA are compared with two single-phase optimized models, ELM–PSO, ELM–MOA, and standalone ELM. The following criteria are utilized in assessment of the employed models:

$${\text{RMSE}}:{\text{Root}}\; {\text{Mean}}\; {\text{Square}}\; {\text{Error}} = \sqrt {\frac{1}{N}\mathop \sum \limits_{i = 1}^{N} \left[ {(S_{{\text{o}}} )_{i} - (S_{{\text{c}}} )_{i} } \right]^{2} }$$
(18)
$${\text{MAE}}:{\text{Mean}}\; {\text{Absolute}}\; {\text{Error}}\; = \frac{1}{N}\mathop \sum \limits_{i = 1}^{N} |\left( {S_{{\text{o}}} } \right)_{i} - \left( {S_{{\text{c}}} } \right)_{i} |$$
(19)
$${\text{MAPE}}:{\text{Mean}} \;{\text{Abs}}.\; {\text{Percentage}} \;{\text{Error}} = \frac{1}{N}\mathop \sum \limits_{i = 1}^{N} \frac{{|(S_{{\text{o}}} )_{i} - (S_{{\text{c}}} )_{i} |*100}}{{(S_{{\text{c}}} )_{i} }}$$
(20)
$${\text{NSE}}:{\text{Nash}} - {\text{Sutcliffe}} \;{\text{efficiency}} = 1 - \frac{{\mathop \sum \nolimits_{i = 1}^{N} \left[ {(S_{{\text{o}}} )_{i} - (S_{{\text{c}}} )_{i} } \right]^{2} }}{{\mathop \sum \nolimits_{i = 1}^{N} \left[ {(S_{{\text{o}}} )_{i} - \overline{S}_{{\text{o}}} } \right]^{2} }}, - \infty < {\text{NSE}} \le 1$$
(21)

where \({S}_{\mathrm{c}}, {S}_{\mathrm{o}}, {\overline{S}}_{\mathrm{o}}\) are calculated, observed and mean of the observed streamflows, respectively, and N is the quantity of the data. Several control parameter values were considered in model development phase, and the optimal ones were decided with respect to lowest square error (Najafzadeh and Niazmardi 2021; Najafzadeh et al. 2021). These values are listed in Table 1 for each algorithm. The table also shows the population and iteration numbers and the number of runs which are necessary to get more robust results from the meta-heuristic algorithms. Input combinations listed in Table 2 were decided taking into account the correlation analysis (autocorrelation and/or partial auto-correlation functions). As seen from Table 2, first three involve lagged streamflow values, in the inputs iv and v, precipitation data are imported and after temperature data are included in the input combinations.

Table 2 The input combinations used for model development
Full size table

Table 3 represents training and testing statistics of single-phase optimized, two-phase optimized and standalone ELM models in predicting streamflows of Padma Station. As it is clear from the table, two-phase optimized models are superior to the other models, while the standalone model has the worst results in streamflow prediction. It is also clear that the two-phase optimized ELM–SAMOA has the lowest RMSE, MAE and MAPE and the highest NSE and R2 in both training (RMSE = 3448 m3/s, MAE = 2282 m3/s, NSE = 0.928, R2 = 0.928, MAPE = 10.78%) and testing (RMSE = 4042 m3/s, MAE = 2413 m3/s, NSE = 0.896, R2 = 0.897, MAPE = 15.24%) stages; an increase in RMSE of ELM, ELM–PSO, ELM–MOA, ELM–PSOGWO is by 31%, 27%, 19% and 14% applying the ELM-SAMOA in the test stage, respectively. All models’ outcomes reveal that importing precipitation information deteriorates the accuracy while lagged temperature inputs improve the efficiency of the single-phase optimized ELM–MOA and the two-phase optimized ELM–SAMOA models (compare the inputs iii and iv/v). The RMSE and MAE of the ELM–SAMOA decrease from 4488 and 2419 m3/s to 4042 and 2413 m3/s by 11% and 0.2%; the NSE and R2 increase from 0.872 and 0.878 to 0.896 and 0.897 by 3% and 2%.

Table 3 The results of the single-phase, two-phase optimized and standalone ELM models in prediction streamflows of Padma Station
Full size table

Training and testing results of the ELM-based models in predicting streamflows of Gorai Station are compared in Table 4. Here, also the superiority of the two-phase optimized ELM models over other models and the standalone model has the last rank in accuracy. The ELM-SAMOA with third input combination produced lower RMSE (413.1 m3/s), MAE (240.4 m3/s), MAPE (18.94%) and higher NSE (0.855) and R2 (0.857) than those of the best ELM with input iii (RMSE = 531.3 m3/s, MAE = 289.6 m3/s, NSE = 0.760, R2 = 0.762, MAPE = 27.29%), ELM–PSO with input vii (RMSE = 523.38 m3/s, MAE = 281.17 m3/s, NSE = 0.767, R2 = 0.788, MAPE = 27.15%), ELM–MOA with input iv (RMSE = 492.8 m3/s, MAE = 276.2 m3/s, NSE = 0.793, R2 = 0.810, MAPE = 23.68%) and ELM–PSOGWO with input iv (RMSE = 470.5 m3/s, MAE = 275.1 m3/s, NSE = 0.811, R2 = 0.819, MAPE = 23.17%) in the testing stage. By applying the two-phase optimized ELM–SAMOA, the RMSE was improved by 29%, 27%, 19% and 14% compared to ELM, ELM–PSO, ELM–MOA and ELM–PSOGWO, respectively. On the contrary to Padma Station, here adding precipitation information into the inputs improves the accuracy of the ELM–MOA (RMSE from 521.5 to 482.8 m3/s, MAE from 281.17 to 276.2 m3/s, NSE from 0.767 to 0.793 and R2 from 0.788 to 0.810) and ELM–PSOGWO (RMSE from 600.6 to 470.5 m3/s, MAE from 324.7 to 275.1 m3/s, NSE from 0.693 to 0.811 and R2 from 0.812 to 0.819). Importing temperature input slightly improves efficiency of ELM–PSO; from input combination iii to vii, the RMSE, MAE, NSE and R2 were improved by 0.6%, 6.9%, 0.4% and 3% in the testing stage, respectively.

Table 4 The results of the single-phase, two-phase optimized and standalone ELM models in prediction streamflows of Gorai Station
Full size table

Figures 5 and 6 illustrate the time variation diagrams of the observed and predicted streamflows by the best ELM-based models for the Padma and Gorai stations, respectively. From the figures, the two-phase optimized ELM-SAMOA model appears to be better simulate the streamflows compared to other models while the standalone ELM cannot adequately catch the observed values in both stations. The scatter diagrams of the streamflow predictions are compared in Figs. 7 and 8 for two stations. From these graphs, it is also apparent that the ELM-SAMOA offers better accuracy with less scattered estimates compared to other alternatives. The implemented models are further compared on Taylor and violin diagrams in Figs. 9 and 10 for the Padma and Gorai stations. It is apparent from the Taylor graphs that the ELM–SAMOA has the closest standard deviation to observed one with the highest correlation and the lowest square error and it is followed by the other two-phase optimized ELM–PSOGW, single-phase optimized ELM–MOA, ELM–PSO and standard ELM models, respectively. It is clear from the violin diagrams that the distribution of the ELM–SAMOA predictions is closer to the observed one while the standard ELM model has the most different distribution. All the graphs justify the testing statistics provided in Tables 3 and 4 that the ELM–SAMOA acted better than the other models in prediction of monthly streamflows.

Fig. 5
figure 5

Time variation graphs of the observed and predicted streamflows by different ELM-based models in the test period of Padma River Station

Full size image
Fig. 6
figure 6

Time variation graphs of the observed and predicted streamflows by different ELM-based models in the test period of Gorai Station

Full size image
Fig. 7
figure 7

Scatterplots of the observed and predicted streamflows different ELM-based models in the test period of Padma

Full size image
Fig. 8
figure 8

Scatterplots of the observed and predicted streamflows different ELM-based models in the test period of Gorai

Full size image
Fig. 9
figure 9

Taylor and violin diagrams of different ELM-based models in the test period of Padma Station

Full size image
Fig. 10
figure 10

Taylor and violin diagrams of different ELM-based models in the test period of Gorai Station

Full size image

Table 5 compares the single-phase, two-phase optimized and standalone ELM models with respect to t-test for both stations. In the table, the statistics were calculated according to the significance level of 5% (two-tailed test). Higher t-statistics (t-stat) than the critical one shows that there is no significant difference in mean between the computed and observed data. The model having higher t-stat indicates better robustness. It is clearly seen from Table 5 that the two-phase optimized ELM–SAMOA has higher statistics compared to the other models in Padma and Gorai stations.

Table 5 t-test of single-phase, two-phase optimized and standalone ELM models for both stations using best input combination results
Full size table

Two-phase optimized ELM models were also compared with the single-phase optimized and standalone ELM models in estimating streamflows of Gorai Station (downstream) using data of Padma Station (upstream). Same input combinations were taken into account, and the model outcomes are listed in Table 6 with respect to RMSE, MAE, NSE, R2 and MAPE. In this application, also two-phase optimized ELM models perform superior to the single-phase optimized and standalone ELM models; however, the difference between the ELMSAMOA and ELM–PSO is marginal. The best two-phase optimized ELM–PSOGWO model with input ii has lower RMSE (511.9 m3/s) and higher NSE (0.777) than those of the best ELM with input iv (RMSE = 612.1 m3/s, NSE = 0.681), ELM–PSO with input v (RMSE = 538 m3/s, NSE = 0.753), ELM–MOA with input ii (RMSE = 543.4 m3/s, NSE = 0.749) and ELM-SAMOA with input iv (RMSE = 535.7 m3/s, NSE = 0.756) in the testing stage. Implementing the ELM–PSOGWO improved the RMSE of the best ELM, ELM–PSO, ELM–MOA and ELM–SAMOA by 20%, 5.1%, 6.2% and 4.6% in the testing stage, respectively. By including precipitation inputs, the accuracy of standalone ELM (input iv), (ELM–PSO (input v) and ELM–SAMOA (input iv) was improved, whereas the temperature data did not increase the efficiency of the models in estimating Gorai’s streamflows utilizing data of upstream station. Time variation and scatter diagrams of the estimated streamflows by different ELM-based models are illustrated in Figs. 11 and 12. It is clear from the visual comparisons; two-phase optimized ELM models have closer streamflow estimates to the observed values, and their scatters are less compared to single-phase optimized and standalone ELM models. This part of study is very useful especially for the basins having missing streamflow data. In such basins, streamflow can be easily estimated using external (e.g., upstream) data.

Table 6 The results of the single-phase, two-phase optimized and standalone ELM models in estimation of Gorai’s streamflow using data of Padma Station (Upstream)
Full size table
Fig. 11
figure 11

Time variation graphs of the observed and predicted streamflows by different ELM-based models in the test period of Gorai station (d/s) using Padma station data (u/s)

Full size image
Fig. 12
figure 12

Scatterplots of the observed and predicted streamflows by different ANFIS-based models in the test period of Gorai Station (d/s) using Padma station (u/s) data

Full size image

Overall, two-phase optimized ELM models, ELM–PSOGWO and ELM–SAMOA models, perform superior to the single-phase and standalone ELM models in streamflow prediction. Among the two-phase optimized ELM models, the ELM–SAMOA acted better than the other. In the second application, the ELM–PSOGWO offered better efficiency compared to other ELM-based models. The main advantages of the two-phase optimization approaches are improvement in exploration and exploitation abilities of single-phase metaheuristic algorithms. Because for a robust and generalizable optimization algorithm is to balance the ability of exploitation and exploration efficiently in order to find best solution/parameters of a machine learning model. Results of this study also endorsed the effectiveness of PSOGWO- and SAMOA-based ELM models by improving exploration and exploitation capabilities.

Concluding remarks

The ability of two-phase optimized ELM models was investigated in monthly streamflow prediction using lagged streamflow, precipitation and temperature data as inputs. The outcomes were compared with the single-phase optimized and standalone ELM models. In the first application, each station’s streamflows were predicted using local data while in the second application, streamflows of one station were estimated using other station data. The following conclusions were reached from the benchmark outcomes.

  • Based on the RMSE, MAE, NSE, R2 and MAPE criteria and graphical methods (e.g., time variation, scatter, Taylor and violin diagrams), the two-phase optimized ELM–SAMOA offered the best accuracy in prediction of monthly streamflows using local data; improvement in RMSE of ELM, ELM–PSO, ELM–MOA and ELM–PSOGWO is by 31%, 27%, 19% and 14% for one station and 29%, 27%, 19% and 14% for other station, in the testing stage, respectively.

  • In the second application, the two-phase optimized ELM–PSOGWO acted as the best model in streamflow estimation with external data; improvement in RMSE of ELM, ELM–PSO, ELM–MOA and ELM–SAMOA is by 20%, 5.1%, 6.2% and 4.6% in the testing stage, respectively.

  • The outcomes suggested the use of two-phase optimization compared to single-phase one while the standalone ELM model provided the worst efficiency.